Atomically phase-matched second-harmonic generation in a 2D crystal

Abstract

Second-harmonic generation (SHG) has found extensive applications from hand-held laser pointers to spectroscopic and microscopic techniques. Recently, some cleavable van der Waals (vdW) crystals have shown SHG arising from a single atomic layer, where the SH light elucidated important information such as the grain boundaries and electronic structure in these ultra-thin materials. However, despite the inversion asymmetry of the single layer, the typical crystal stacking restores inversion symmetry for even numbers of layers leading to an oscillatory SH response, drastically reducing the applicability of vdW crystals such as molybdenum disulfide (MoS₂). Here, we probe the SHG generated from the noncentrosymmetric 3R crystal phase of MoS₂. We experimentally observed quadratic dependence of second-harmonic intensity on layer number as a result of atomically phase-matched nonlinear dipoles in layers of the 3R crystal that constructively interfere. By studying the layer evolution of the A and B excitonic transitions in 3R-MoS₂ using SHG spectroscopy, we also found distinct electronic structure differences arising from the crystal structure and the dramatic effect of symmetry and layer stacking on the nonlinear properties of these atomic crystals. The constructive nature of the SHG in this 2D crystal provides a platform to reliably develop atomically flat and controllably thin nonlinear media.

Introduction

The optical second-harmonic generation (SHG) is the nonlinear frequency doubling process that has been demonstrated over 50 years ago in quartz¹ with numerous applications, including those in microscopic² and spectroscopic techniques³. However, as SHG arises from χ⁽²⁾, strong SH signals may only be observed from noncentrosymmetric crystals. As the demand for smaller and thinner nonlinear media becomes higher in next-generation optoelectronic devices, great efforts have been devoted to solve the phase-mismatch problems in nonlinear crystals. While techniques such as quasi-phase matching⁴ or creating zero-index metamaterials⁵ are viable methods, reducing the dimensionality of such nonlinear media to two dimensions would eliminate the requirement for phase matching as the crystal thickness is far below the coherence length. Naturally, two-dimensional (2D) van der Waals (vdW) crystals may serve as an ideal candidate for such materials, as the SH polarization is confined within a single molecular layer that may be exfoliated and isolated from a bulk crystal. Unfortunately, the vdW crystals that exhibit nonlinearity within a single layer typically do not produce SH signals when inversion symmetry is restored in their multilayer counterparts.

Group VI transition metal dichalcogenides (TMDCs), such as MoS₂, WS₂, MoSe₂ and WSe₂ have gained prominent attention due to many unique emerging properties once these materials are thinned down to single or a few atomic layers. Rich physical properties, such as the emerging photoluminescence^{6, 7}, excellent transistor on-off ratio⁸, optical valley polarization^{9, 10, 11}, large exciton and trion binding energies^{12, 13}, exciton electroluminescence¹⁴, ambipolar transport¹⁵, superconductivity¹⁶ and piezoelectricity^{17, 18} have been demonstrated in this 2D crystal system. Many of these properties arise as a result of the layer-dependent evolution of crystal symmetry.

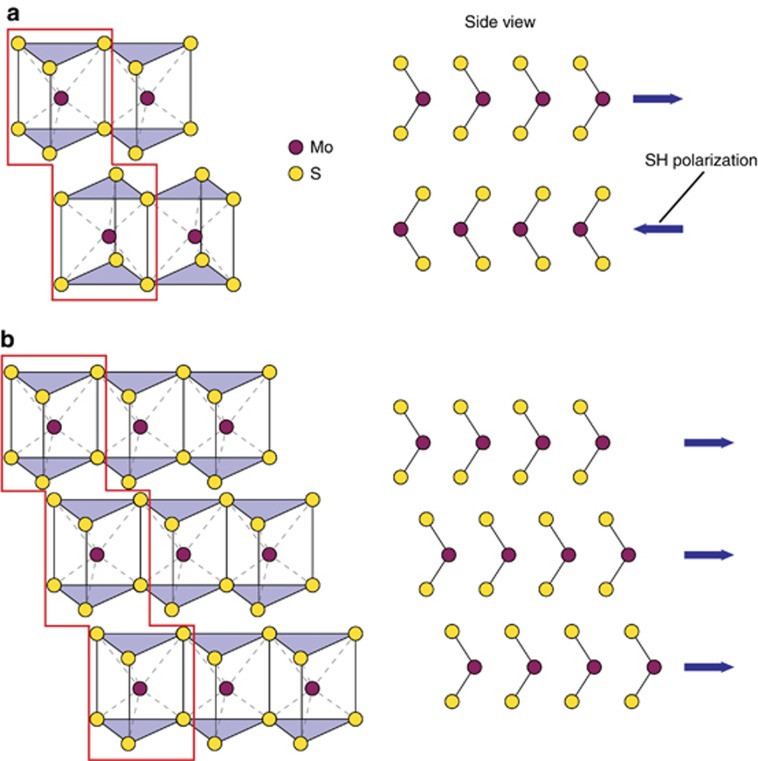
Thus far, the most commonly studied bulk crystal phase of MoS₂ is the 2H polytype, with two S–Mo–S unit cells of trigonal prismatic coordination and space group D_6h (P6₃/mmc) (Figure 1a). The symmetry of the 2H phase dictates that the flakes with odd-numbered layers are noncentrosymmetric, retaining a net nonlinear dipole, while centrosymmetric even layers do not. This net nonlinear dipole in odd-layered TMDCs (along with h-BN) has enabled the probing of SHG from 2D crystals due to the finite second-order nonlinearity (χ⁽²⁾≠0)^{19, 20, 21, 22, 23}. The SH signal from single-layer TMDCs has been utilized to study the crystal orientation and grain boundaries²⁴, while also enabling a spectroscopic method to study the excitonic structure²⁵. This all-optical technique allows for non-destructive crystal structure studies, and has advantages over transmission electron microscopy and atomic-force microscopy (AFM) based techniques due to the simplicity of sample preparation. Unfortunately, the crystal symmetry constrains the SHG in the 2H phase to noncentrosymmetric odd-numbered layers. Coupled with a typically decaying SH intensity as odd layers become thicker due to the finite absorption¹⁹, the applicability of the SHG from 2H-MoS₂ is significantly reduced.

Figure 1.

Crystal structure of 2H and 3R-MoS₂. (a) Schematic of the crystal structure of 2H-MoS₂ (two layer unit cell outlined in red) with Mo atoms in maroon and S atoms in yellow. The Mo atoms are hexagonally packed within each layer and trigonal prismatically coordinated with S atoms on the top and bottom. The side projection shows the flipped orientation of each layer and the anti-parallel orientation of the SH dipoles that allow for SHG. (b) Crystal structure of 3R-MoS₂ (three layer unit cell outlined in red). Individual layers are identical to the 2H structure, however the unit cell and bulk crystal are noncentrosymmetric. The layers are oriented in such a way that the dipoles are parallel allowing for constructive interference of the SHG light.

Aside from the 2H phase, MoS₂ coexists in the equally stable bulk noncentrosymmetric 3R polytype. The orientation of the atomic layers in the 3R phase, of space group C_3v (R3m), leads to parallel in-plane nonlinear dipoles (Figure 1b), making the crystal an excellent candidate for a cleavable, atomically flat, phase-matched 2D nonlinear crystal. The single-layers of these two crystal phases are identical (‘1H’, group D_3h). However, adjacent layers of the 2H are mirrored to restore the inversion symmetry, while the layers in the 3R phase retain the same orientation but shift along the in-plane direction. The alignment of the in-plane dipole of each 3R layer allows for an atomic phase match and leads to the constructive interference of the SH polarization in the thin-film limit below the coherence length, where we expect the intensity to scale quadratically with the layer number. In the bulk crystalline forms (over 10 μm thick), the SHG of the 3R and 2H has been studied over a decade ago showing the observable and nearly zero SHG, respectively²⁶. While the SHG observed in chemically grown MoS₂ spirals²⁷ as well as folded MoS₂ bilayers^{28, 29, 30} yield some insight, there have not yet been reports on the nature of the SHG from the 3R phase in the atomically phase-matched regime, crucial for the development of ultra-thin nonlinear optical devices.

Materials and methods

Growth and characterization of MoS₂ polytypes

Bulk 3R and 2H-MoS₂ crystals were grown using chemical-vapor transport technique with Cl₂ and I₂ as the carrier gas, respectively³¹. Crystals (3R and 2H-MoS₂) were mechanically exfoliated onto a fused quartz substrate. Layer number assignment was determined using a combination of photoluminescence imaging, Raman spectroscopy (Horiba LabRAM HR Evolution, Edison, NJ, USA)^{31, 32} and AFM (Dimension 3100, Digital Instruments, Santa Barbara, CA, USA) (Supplementary Fig. S3).

Optical measurements

The SH measurement was conducted with a reflection geometry with the excitation normal to the sample at room temperature. We used a Ti-Sapphire oscillator (Chameleon, Coherent, Glasgow, Scotland) to pump an optical parametric oscillator (Chameleon Compact OPO, Coherent, Berlin, Germany) with 80 MHz repetition to achieve tunable near-infrared wavelength from 1000 to 1550 nm in 200 fs pulses. The laser is directed to a microscope with a scanning stage. The average laser power was kept at 90 mW for the 3R excitation and a similar power for the 2H excitation at each excitation energy before entering the microscope. The laser is focused by a 63 × objective with a numerical aperture of 0.75 to a spot size of around 2 μm. The reflected signal is directed to an 805 nm short-pass dichroic mirror and two band-pass filters (315–725 and 350–700 nm) to eliminate the reflected pump beam. The signal is detected using a photomultiplier tube with a detection range of 300–720 nm (H7422-40, Hamamatsu, Japan). Each SH intensity is normalized using the transmission of our optical setup.

Results and discussion

We probed the layer dependence of the SHG from the 3R and 2H-MoS₂ across a broad energy range, and found that the SH intensity in the 3R polytype scales quadratically with layer number up to six layers. By mapping out the SH signal with energies from 1.77 to 2.30 eV, two strong SH resonances are found. Compared with linear optical absorption measurements, we showed the resonances are due to the A and B excitonic transitions in the MoS₂, arising from spin–orbit coupling and interlayer interaction-induced splitting. We show that the SHG in a 3R crystal allows for the nonlinear probing of the bulk excitons beyond an odd-layer limit, while also providing an alternative all-optical method of layer number determination.

The optical image of the 3R crystal with the layer number overlaid is presented in Figure 2a. In this crystal, we assign the few-layers 1–4 and 6 by Raman spectroscopy and AFM (Supplementary Figs. S1–S3). This can be immediately compared with the respective SH image pumped at an energy of 1.14 eV in Figure 2b. We can easily distinguish between the 3R and 2H polytypes through the image produced through the SH scanning. The SH intensity produced by the 3R crystal is highest in the thickest of layers, while the SHG from a 2H crystal is only noticeable in the odd-numbered layers (Supplementary Fig. S4)²⁰.

Figure 2.

Optical and SH microscopy images of 3R-MoS₂. (a) Optical image of the 3R-MoS₂ crystal exfoliated onto a fused quartz substrate. Here, we overlay the layer number on top of the corresponding thickness, which was verified via using a combination of photoluminescence mapping, Raman spectroscopy and atomic-force microscopy. (b) Image produced via scanning and gathering the SH light produced by the 3R-MoS₂ (excitation energy of 1.14 eV). We see that the SH intensity in increases with layer thickness, shown in a with the single-layer having the lowest intensity. The strongest emissions at the left and bottom of the crystal (given by yellow and red) correspond to layer numbers greater than six. Scale bars shown in a and b correspond to 15 μm.

Following a similar approach to the reported SHG in single-layer MoS₂^{(refs. 19, 21)} and assuming weak interlayer coupling, the inclusion of the parallel SH polarizations in the 3R crystal from N layers leads to the summation of N polarizations. Thus, we predict a crystal of N layers to produce a SH intensity given by:

where C is a proportionality constant describing the local field factors, and φ and φ₀ describe the angle of the laser polarization and initial crystallographic orientation, respectively. This predicts the observed intensity to quadratically vary with respect to the layer number within the thin-film limit. However, as the linear absorption in MoS₂ may become non-negligible in our SH photon energy range from 1.77 to 2.30 eV, the attenuation from reabsorption is expected to be nontrivial, particularly as the layer numbers increase. In addition, changes in the refractive index^{33, 34, 35} at the fundamental and SH energies play a role in the attenuation of the experimental SHG (Supplementary Fig. S6).

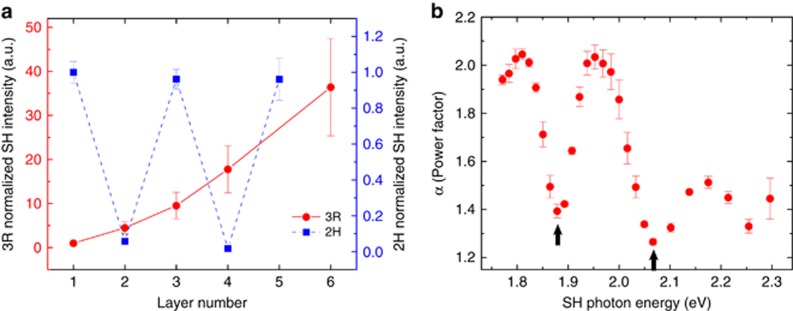
The observed SH layer dependence of the 3R and 2H crystal polytypes a SH energy of 1.82 eV are shown in contrast in Figure 3a. We have normalized the SH intensity of different layer numbers to that of the respective single-layer intensity, resulting in the larger deviations as the layer number increased. Representative data before the normalization is shown in Supplementary Fig. S7. The SHG from the 3R crystal is distinct from the oscillating signal of the 2H crystal, with only observable SHG in odd layers. Using the log–log relationship, we mapped out the N layers’ power dependence, α, across the entire bandwidth (Figure 3b). We observed a quadratic dependence in good agreement with our model of the SHG intensity produced by the 3R crystal from energies of 1.77 to 1.83 eV, as well as from 1.93 to 1.98 eV. Two clear dips are observed in the power dependence at energies of around 1.87 and 2.07 eV, corresponding to excitonic enhancements in the single-layer intensity.

Figure 3.

Layer dependence and scaling of the SH light. (a) SH intensity of the 3R and 2H-MoS₂ normalized to the respective single-layer intensity at a SH energy of 1.81 eV. The dependence of the SH intensity is roughly squared with relation to the layer number in the 3R crystal, while it oscillates with layer number in the 2H crystal. The left axis corresponds to the 3R intensity, while the right axis corresponds to the 2H intensity. (b) Power law (N^α, where N is the layer number) derived from the log–log relationship in data such as a across energies from 1.77 to 2.3 eV to determine the range of the expected phase-matching relationship, N². We note the energies below 1.85 eV and energies between 1.9 and 2.0 eV correspond to scaling accordingly to N². Two dips marked by arrows correspond to the A (1.85 eV) and B (2.05 eV) excitons of the single-layer MoS₂. The enhancement due to the excitons in the single layer decreases the expected scaling of the SHG across the other layers. The deviations above 2.1 eV are noted to arise from the broader linear absorption at energies above the B exciton.

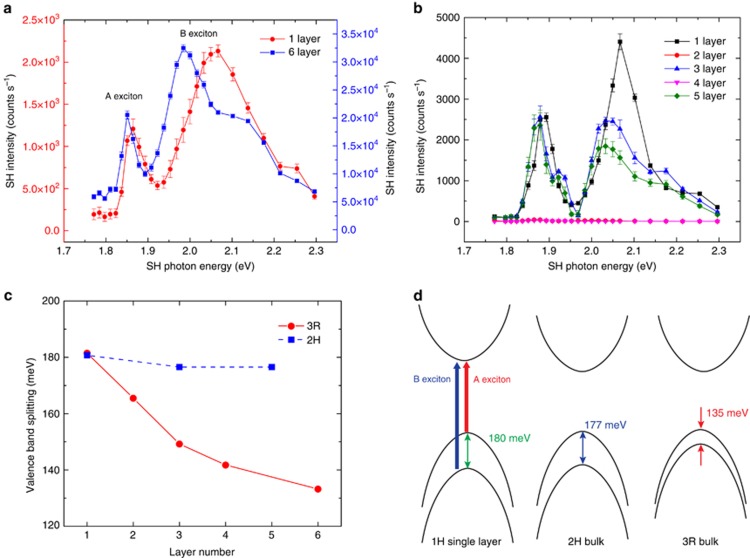
In order to understand the range of the predicted N² dependence, we performed SH spectroscopy on the 3R crystal using excitation energies ranging from 0.88 to 1.22 eV. From the SHG spectra of single-layer and six-layer 3R-MoS₂ (Figure 4a), we observe two dramatic enhancements in the SH intensity. These two enhancements at around 1.85 and 2.00 eV correspond well to the known A and B excitons, also observed in the linear absorption (Supplementary Fig. S5), correspond directly to the dips observed in the power law. The two resonances are the excitonic transitions originated from the conduction band and two split valence bands at the K-point of the Brillouin zone.

Figure 4.

SH spectroscopy. (a) SH spectra of the 3R-MoS₂. The two peaks occurring at around 1.85 and 2.0 eV correspond to the A and B excitons of K-point transitions in MoS₂. The six-layer intensity is one order larger than the single-layer intensity. Increasing the layer number decreases both exciton energies, with the B exciton experiencing a much larger shift (roughly 50 meV). (b) SH spectra of the 2H-MoS₂, showing a similar response as the 3R crystal. Only odd layers show SH intensities with comparable amplitudes in the layers. The two and four-layered intensities are overlapped. (c) The A and B exciton energy differences, corresponding to the valence-band splitting, of the 3R and 2H crystal are plotted. The 2H exciton splitting remains close to 180 meV up to five layers, while the 3R exciton splitting dramatically decreases to 130 meV at six layers (which agrees to the bulk value obtained from linear absorption). (d) Simplified electronic band structure showing transitions from the valence band to the excitonic band, derived from the SH spectroscopy data at the K-point of the single layer and bulk 2H and 3R phases. The energy of the A exciton decreases from single layer to bulk in both crystal phases by around 10 meV (exemplified in a lower excitonic band of the bulk crystals), however the valence-band splitting is dramatically different, which effects the large difference between the B exciton energy in the two phases. This splitting difference is due to the different stacking geometries and suppressed-interlayer hopping, resulting in an inequality of the electrostatic potential energy at the MoS₂ prisms in the two layers.

Due to the atomically thin nature of the sampled crystal, we expect that the deviations from the N² dependence arise primarily from the sensitivity of the SHG to small shifts in resonant energy. At high SH energies (roughly beyond 2 eV) the linear absorption remains non-negligible, effectively attenuating the SH intensity as the thickness increases through reabsorption. Furthermore, an obvious red shift in the A and B excitons were observed when changing from a single layer to six layers (Figure 4a), due to electronic changes as a result of interlayer interactions. These exciton shifts dramatically influence the observed layer dependence due to the high enhancements of the SH intensity around the exciton resonances. The SH resonances produced by the A (B) exciton has a red shift of 10 (50) meV from layers one to six. These energy offsets causes the SH enhancements of each layer to occur at different energies and reveals why the quadratic dependence is observed at the lowest probed energies, as well as select energies between the two resonant enhancements, where SH absorption and excitonic enhancements do not strongly affect the SHG. Considering the finite absorption even at lower energies, we have observed a very close to N² dependence up to six layers. Beyond six layers the SH light is attenuated due to a combination of the reabsorption and the phase accumulation from the refractive index change. These two factors become significant even at ten layers, as there is roughly a 20% decrease in the idealized SH intensity (Supplementary Fig. S6).

SH spectroscopy was also performed on the 2H crystal in the same energy range using the same experimental setup (Figure 4b). It was noted that many of the works on SHG in 2H-MoS₂^{(refs. 19, 20, 21)} used an excitation around 1.5 eV, corresponding to SH energies of around 3 eV. These energies fall into the range of the broad exciton feature at the Γ-point²¹. As a result, large SH enhancement produced from the single-layer 2H-MoS₂, as well as the high sensitivity of the SH intensity produced by the odd-numbered layers was observed. Using SH spectroscopy, we observed that the overall SHG between the odd layers are of comparable magnitude, with the even layers showing no detectable SHG, as expected. The A and B exciton features are observed here as well. In our experimental range, the single-layer SHG is enhanced most by the B exciton, while the A exciton seems to enhance the odd layers to a comparable degree. As with the 3R sample, both SHG peaks are red-shifted as the odd layer number increases, though to a lesser extent.

We expect that our results provide more insight into the electronic evolution of the 3R crystal with increasing layer number. Theoretical calculations show that the single-layer valence-band splitting (around 180 meV, Figure 4c) at the K-point arises solely from spin–orbit interactions, while the splitting in two and more layers of the 2H crystal is primarily a result of the interlayer-hopping interactions. Due to the symmetry, the wave functions form interlayer bonding and anti-bonding states^{36, 37}. In contrast, calculated wave functions at the K-point of the 3R crystal are localized, suppressing interlayer hopping. The effects of which are apparent (Figure 4c), the valence-band splitting from a 1H single-layer to a 3R two layer decreases by 20 meV, while the 2H splitting is nearly constant regardless of layer number. The lack of interlayer hopping suggests that the origin of the valence-band splitting in the bulk 3R crystal arises from the unique crystal stacking geometry, resulting in an inequality of the electrostatic potential energy at the MoS₂ prisms in the two layers^{29, 31, 38}. We probe a splitting of 135 meV in six layers, nearly 50 meV smaller than the splitting found in the 2H bulk crystal, in agreement with the reported bulk splitting found from linear absorption and angle-resolved photoemission spectroscopy³¹. Our findings are summarized in the simplified band structure in Figure 4d. We were able to experimentally measure the layer by layer evolution of the valence-band splitting in the 3R phase for the first time, using SH spectroscopy.

Conclusions

In conclusion, we have measured the atomically phase-matched SHG arising from a 3R-MoS₂ crystal with layer numbers up to six. The SHG intensity scales with the layer number, N, as N² in the range of SH energies of 1.77–1.84 and 1.95–1.98 eV. The SH spectrum from 1.77 to 2.30 eV showed two strong enhancements corresponding to the A and B excitons in MoS₂, which cause the deviations in the N² dependence, even though the SH photons are phase-matched. These findings enable the probing of the 3R-MoS₂ excitons with SH spectroscopy in the bulk, as well as provide an all-optical tool for the determination of layer number in the 3R polytype of TMDCs. We demonstrated that 3R-MoS₂ is a cleavable nonlinear crystal that generates SH light in all of its crystalline layers. Coupled with the potential of tuning the excitonic states and thus SH intensities through electric gating^{13, 39}, the 3R crystal polytype is an exceptional material choice in the development of ultra-thin nonlinear optical devices. The 3R polytype of TMDCs along with recently engineered twisted bilayers^{28, 29, 30} and CVD grown MoS₂ spirals²⁷ show promise for an additional avenue in controlling the rich physical properties of vdW materials through the manipulation of interlayer symmetries.

Author contributions

MZ, ZY and RS designed the experiment; RS grew the MoS₂ crystals; HZ prepared the quartz substrate for the experiment; MZ and ZY conducted the optical experiments; MZ, ZY, YY, JX and HZ analyzed the data. XZ guided the research. All authors contributed to the discussion and preparation of the manuscript.