Generating scattering dark states through the Fano interference between excitons and an individual silicon nanogroove

Abstract

Effective interactions between excitons and resonating nanocavities are important for many emerging applications in nanophotonics. Although plasmonic nanocavities are considered promising substitutes for diffraction-limited dielectric microcavities, their practical applications are hindered by large ohmic loss and Joule heating. Other than plasmonic materials, high-refractive-index dielectric nanocavities is a new way to trap light in subwavelength scales. However, studies on the interaction between dielectric nanocavities and excitons are still scarce. Here, for the first time, we demonstrate that the Fano interference between molecular excitons and an individual silicon nanogroove can generate scattering dark modes. By placing J-aggregate excitons into a silicon nanogroove, the leaky magnetic resonant modes filling in the groove can tailor their scattering directivity and reduce the uncoupled radiation decay in a specific direction. This unidirectional ‘dark state’ brings a new approach to tailor the interaction between excitons and nanocavities without large near-field enhancement. By adjusting the resonant modes, the scattering spectra can change from a Fano asymmetric line shape to a significantly suppressed scattering dip. These findings indicate that silicon nanogrooves can provide a platform for integrated on-chip silicon–exciton hybrid optical systems in the future.

Introduction

Strong interactions between nanocavities and excitons is important for both fundamental studies and designing functional nanophotonics devices¹. Bringing together plasmonic nanocavities and molecular excitons results in strong light–matter interactions because of the high density of electromagnetic modes and light trapping in deep subwavelength scales^{2, 3}. Recently, many groups have studied plasmon–exciton coupling systems based on gold or silver^{4, 5, 6, 7}. However, the advantages of plasmonic nanocavities also hinder the realization of simultaneous effective coupling. On the one hand, the strong near-field enhancement leads to the high photothermal conversion and Joule heating of the local environment⁸. Temperatures higher than 60 °C lead to J-aggregates further growing to larger crystallites⁹, which influences the stability of the hybrid system. On the other hand, although plasmonic nanocavities are able to confine light to small mode volumes called ‘hot spots’, these confined ‘hot spots’ prevent more effective overlap between the surrounding J-aggregates and localized plasmon modes¹⁰.

As an alternative, high-index dielectric nanocavities that can manipulate light at a subwavelength scale owing to Mie magnetic and electric resonances^{11, 12, 13, 14, 15} have shown promising applications, such as surface-enhanced spectroscopies⁸ and third-harmonic generation¹⁶. The magnetic resonances in silicon structures are driven by the electric field of light that couples to the displacement of current loops. The interaction between magnetic and electric modes in silicon nanostructures can generate directional scattering^{17, 18, 19}, which brings new insights into zero-index metamaterials^{20, 21}, Fano resonances^{22, 23} and biosensing²⁴. If the magnetic responses can interact with the surrounding excitons, then interesting scattering behaviors may occur. Unfortunately, these modes are internally distributed in silicon nanodisks or nanospheres, which prevent effective interactions with excitons.

Here, for the first time, we demonstrate tunable Fano interferences between excitons (J-aggregates) and individual silicon nanogrooves (NGs). Silicon NGs as slot waveguides have been utilized to overcome the diffraction limit of optical manipulation²⁵. They are different from traditional microcavities in that they confine light on at least a half-wavelength scale owing to the presence of mirrors or surrounding photonic crystals¹. We also establish that silicon NGs hold different resonant modes compared with silicon nanodisks or nanoblocks²⁶, that is, leaky magnetic resonant mode (LMRM). Unlike the internal modes in the usual Mie resonators, the LMRM is able to leak out and fill in the groove, which is beneficial for realizing an effective light–matter interaction. The LMRMs ‘shield’ J-aggregates from the incident light backward and direct the scattering light mainly forward. In this way, a unidirectional scattering dark state²⁷ can be observed, which significantly suppresses backward scattering at the specific wavelength. Using Kerker’s scattering theory and a coupled-oscillator model^{28, 29, 30}, we theoretically explain why silicon NGs can realize prominent Fano interference with excitons without large near-field enhancement and why this scattering dark state can be generated only in silicon NGs and not in other silicon-based nanocavities. Silicon NGs guiding the radiation via strongly confined magnetic resonant modes provide a path for designing various types of integrated nanophotonics devices based on their interactions with excitons^{31, 32, 33}.

Materials and methods

Fabrication of silicon NGs

Silicon NGs with different geometries were fabricated by focused ion beam FIB (FIB-SEM crossbeam workstation, Zeiss Auriga-4525) milling techniques on a single-crystal silicon substrate. The beam current was set to 10 pA for high-resolution structuring. The width and depth of the silicon NGs were determined by top and 85°-tilted SEM (scanning electron microscope), respectively. Before spin-coating, the silicon substrate was treated by ultrasonic cleaning and plasma cleaning to improve its hydrophilicity. TDBC (5,6-dichloro-2-[[5,6-dichloro-1-ethyl-3-(4-sulfobutyl)-benzimidazol-2-ylidene]-propenyl]-1-ethyl-3-(4-sulfobutyl)-benzimidazolium hydroxide, inner salt, sodium salt) J-aggregates were formed by adding 0.25 mol/l Na₂SO₄ to 0.1 mM TDBC monomers (FEW Chemicals GmbH, Wolfen, Germany) after 10 min ultrasonic treatment. The J-aggregates were then spin-coated on patterned silicon substrate (3000 r.p.m. for 60 s), forming a J-aggregate thin film. The thickness was confirmed using atomic force microscopy (AFM). For comparison, silicon nanospheres with diameters from 100 to 200 nm were fabricated using the method reported in our former work^{17, 22}.

Dark-field measurements

The dark-field backward scattering spectra were obtained using a dark-field optical microscope (BX51, Olympus) integrated with a spectrograph (IsoPlane 160, Princeton Instruments) and a charge-coupled device (CCD) camera (PiXis 400B-eXcelon, Princeton Instruments). During the measurements, the oblique incident white light was illuminated with a 53° incident angle on the entire nanostructures. The scattered light from a certain section of the silicon NG was collected through a dark-field objective on top (numerical aperture=0.80) and a slit in front of the spectrograph.

Numerical calculations

The finite difference time domain method was used to calculate the scattering spectra, near-field distributions and far-field scattering patterns of the silicon NGs and hybrid systems. Four total-field scattered-field area sources with 53° incident angles from four sides at visible wavelengths (300–900 nm) were used to simulate the dark-field scattering in an experiment. Geometrical parameters were obtained from SEM images of each of the NGs. The interaction between the J-aggregates and the NG was simulated by setting 10-nm-thick J-aggregates in the top side of the grooves. The dielectric function of the silicon was obtained from Palik. The dielectric permittivity of the J-aggregates was described by the Lorentz model as

where ε_∞=1 is the high-frequency component, f=0.1 is the reduced oscillator strength, 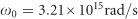is the exciton transition frequency and 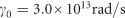is the exciton linewidth.

Results and discussion

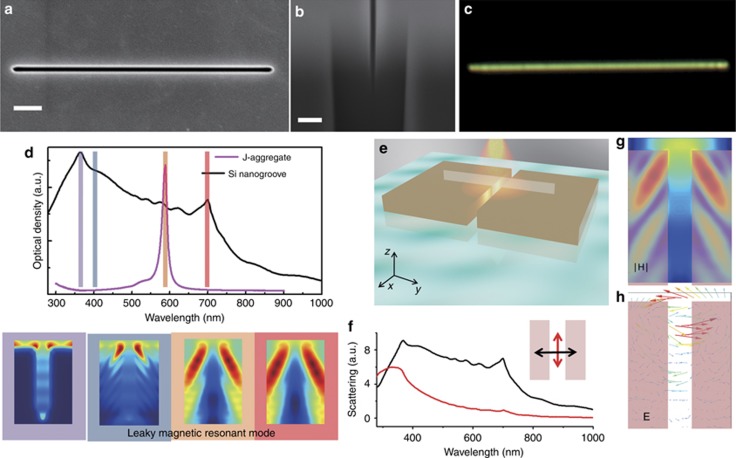
In our case, silicon NGs with different sizes were fabricated by FIB milling on a single-crystal silicon substrate (Supplementary Fig. S1). A typical silicon NG with a width of ~100 nm is shown in Figure 1a. The longitudinal section graph in Figure 1b indicates that the NG possesses a tapering shape and that the rate of narrowing becomes faster at the bottom. The dark-field scattering image in Figure 1c embodies a bright scattering light, with a broad resonant spectrum in the visible region. As for a silicon nanosphere, the strongest resonant mode is the magnetic dipole resonance generated from the displacement current loops (see Supplementary Fig. S2). This nanostructure can be explained by Mie theory. Although the scattering from other silicon nanostructures such as cubic and conical shapes cannot be described by Mie theory, they still possess the displacement current loops and the induced magnetic responses^{34, 35}. To confirm whether silicon NGs also possess the magnetic response, we simulated the scattering spectrum from a silicon NG and the magnetic field distributions on the vertical cross-section at different wavelengths shown in Figure 1d. The pink curve in Figure 1d is the measured absorption spectrum of the TDBC J-aggregating dyes. At λ=365 nm, the scattering light is generated mainly from the surface, and no internal modes were excited. Above λ=400 nm, the light field begins to penetrate into the silicon along the groove and generate a magnetic response. Then, at λ=587 nm (the absorption peak of J-aggregate) and λ=698 nm, the internal magnetic resonances become the dominant mode. The schematic graph in Figure 1e shows the distribution of the magnetic field (bright dots) inside the groove, and the white plane (y–z plane) represents the investigated vertical cross-section. The scattering spectra under different polarization directions shown in Figure 1f indicate that the scattering intensity excited by vertical polarization is much stronger. Therefore, we can use the magnetic field distribution (Figure 1g) and electric vector distribution (Figure 1h) under vertically polarized excitation to analyze the resonant mode. Owing to the nanoscale gap, the former regular internal electromagnetic distribution in the silicon slab is damaged, and the magnetic field expands into the top of the NG, which we called LMRM. The electric vector distribution shown in Figure 1h is similar to that observed in the silicon nanosphere (Supplementary Fig. S2), which represents the capability to generate an obvious magnetic response.

Figure 1.

Resonant modes in an individual silicon NG. (a) Top-view SEM image of a fabricated silicon NG with a width of 100 nm and a length of 5 μm. Scale bar=500 nm. (b) The tilted SEM image of a typical silicon NG with a depth of 800 nm (scale bar=300 nm). (c) Dark-field scattering image of a typical silicon NG with a length of 20 μm. (d) The calculated scattering spectrum of a typical silicon NG and the absorption spectrum of TDBC J-aggregates. Longitudinal section magnetic field distributions in boxes reveal the resonant modes at specific wavelengths. The field distributions and the corresponding locations in the spectrum are marked in the same color. (e) A schematic shows the generation of LMRMs inside the groove. The white plane reveals the investigated y–z plane. (f) Scattering spectra of the silicon NG under different polarization directions. The black curve represents the spectrum under y-axis polarization, and the red curve represents the spectrum under x-axis polarization. (g) Magnetic field distribution under y-axis polarization. (h) Electric field lines under y-axis polarization.

Comparing the electric and magnetic field distributions at λ=587 nm between a silicon NG and plasmonic NGs (Supplementary Fig. S3), we can find that the near-field enhancements of gold or silver NGs mainly distribute on the surface. For a silicon NG, however, the resonant modes can be excited inside; therefore, the electromagnetic fields distributed in the groove mainly leak from the bilateral internal resonant modes. The field distributions in Supplementary Fig. S3 also indicate that the field enhancements are much stronger in plasmonic NGs than they are in the silicon NGs. The absorption performance can be evaluated by using a simple formula 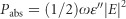, where ω is the frequency, 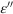is the imaginary part of permittivity and |E| is the total electric field^{36, 37}. Through the curves of the imaginary part of permittivity (Supplementary Fig. S4)³⁸ and the electric field enhancement amplitude obtained from Supplementary Fig. S3, we can calculate the absorptivity of different types of NGs, and the average absorptivity of the silicon NG is 2% of the gold NG and 2.3% of the silver NG. This result confirms the low-loss feature of the silicon nanostructures. Admittedly, the densities of the electromagnetic modes in the silicon NGs are much lower than are those in the plasmonic NGs; therefore, there should be a new mechanism in the interacting process with excitons.

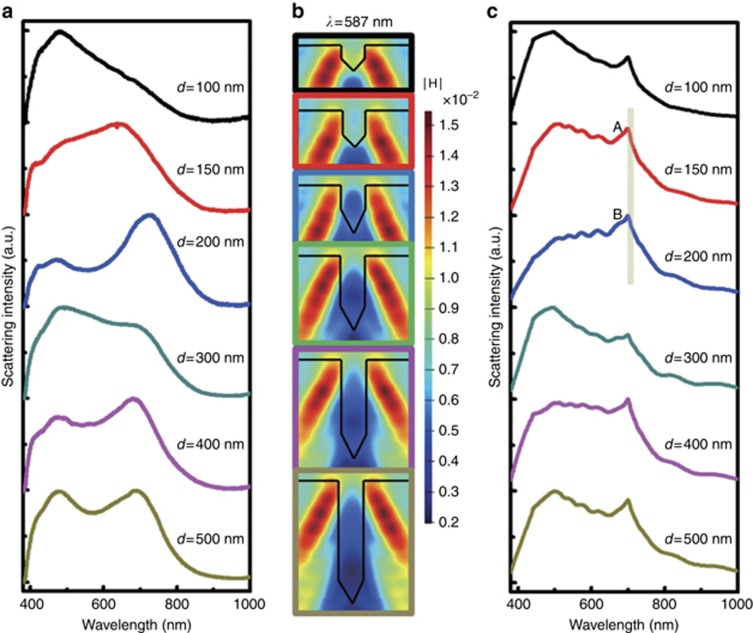
To generate a scattering dark state in a silicon NG-J-aggregate hybrid system, the dimensions of the silicon NG should first be carefully designed to adjust the resonant peak overlapping with the exciton energy. By adjusting the depth and width of the silicon NGs, the scattering behaviors are changed. For a shallow groove with a depth of 100 nm, the resonant peak at approximately λ=500 nm generated from the surface scattering is dominated as shown in Figure 2a (black curve). At the same time, the magnetic field distribution at λ=587 nm in Figure 2b indicates that the magnetic resonance is formed. When increasing the depth to 150 nm, the usual surface scattering is weakened, but the scattering at longer wavelengths generated from the LMRMs is enhanced (see red curve in Figure 2a). This enhanced scattering occurs because of the larger mode volume of the LMRMs. As shown in Figure 2b, the LMRM can fully fill in the groove. Further increasing the depth brings different distributions of the LMRM and then engineers the resonant peaks. From d=150 to d=300 nm, the mode volumes of the LMRMs at λ=587 nm first decrease and then slightly increase, which is in accordance with the scattering fluctuation at λ=587 nm in Figure 2a. For a silicon NG with a depth of more than 400 nm, the distributions of the LMRMs become stable. In addition, the scattering spectra remain unchanged when increasing the depth further (see Figure 2a). The scattering spectra of the silicon NGs calculated using the finite difference time domain method (Figure 2c) agree well with the experimental dark-field observation. The detailed comparison between the magnetic field distributions of the silicon NGs with different depths (d=150 and 200 nm) in Supplementary Fig. S5 illustrates how LMRMs influence the scattering intensities. For a NG with a depth of 150 nm, the groove always fills the magnetic fields at λ=587 and λ=700 nm (point A in Figure 2c); therefore, the scattering intensities at these two wavelengths are almost the same. For a NG with a depth of 200 nm, the leaky magnetic field is more obvious at 700 nm (point B in Figure 2c) than at 587 nm; therefore, the scattering intensity is weaker at 587 nm than it is at 700 nm. Because of our system limitations, we show our experimental data in the range of 400–1000 nm. The lower quantum efficiency of the CCD below λ=500 nm and the visible-range incident light lead to the quick drop of the light-source spectrum approaching λ=400 nm (see Supplementary Fig. S6). To simulate this phenomenon well, the raw simulated spectra below 500 nm have multiplied coefficients to simulate the scattering behavior below 500 nm more precisely (see Figure 2c). Other deviations between the simulation and experiment may arise from different incident situations. A ‘dark-field circle’ (Supplementary Fig. S6a) was used to realize the oblique incidence in the experiment, and four oblique incident plane waves were used in simulation (see Supplementary Fig. S6b) because the ‘dark-field circle’ is difficult to simulate. The scattering behaviors can also be adjusted by increasing the width of the silicon NGs, as shown in Supplementary Fig. S7. The scattering signals are increased when widening the groove from w=100 nm to w=400 nm. This phenomenon arises from a larger volume of the submicron cavity, whose mechanism of light confinement is similar to that of Fabry–Perot resonators^{39, 40}. Usually, the mode volume of Fabry-Perot cavities is larger than 1.6(λ/n)³. Therefore, wider silicon NGs cannot obtain a small mode volume and support LMRMs to realize strong light–matter interactions.

Figure 2.

Depth dependence of silicon NGs. (a) Measured scattering spectra of silicon NGs with different depths. The width is fixed at 100 nm. (b) Longitudinal section magnetic field distributions in the y–z plane at λ=587 nm. (c) Calculated scattering spectra of silicon NGs with depths corresponding to the sizes in the experiments.

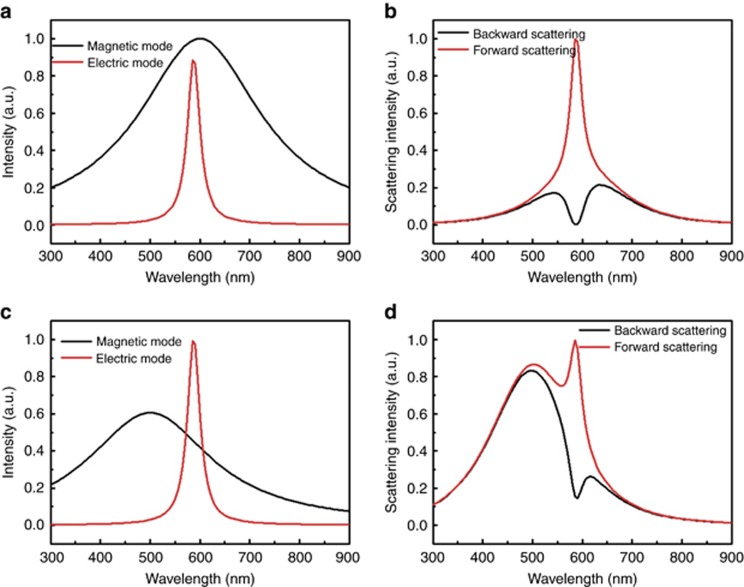
Although the LMRM as a type of resonant mode that in dielectric materials cannot generate as high of a near-field enhancement as plasmon resonances can to realize strong dipole coupling², the effective overlap and electromagnetic interaction^{17, 22} with excitons are expected to generate ‘far-field coupling’ or ‘the coupling of scattering resonances’^{2, 27}. Therefore, for the silicon NG–exciton hybrid system that is scattering-dominant, the constructive or destructive interference between these optical pathways is expected to analyze the interaction characteristics. For a single silicon nanosphere, the interaction between the electric and magnetic dipole can generate directional scattering⁴¹. For a dipolar source coupled to a magnetodielectric scatterer, directional emission can also be observed⁴². Therefore, we expected that the interference between the J-aggregates (dipole source) and LMRMs (magnetic modes) in the silicon NG would also lead to directional scattering. These phenomena can be explained by Kerker's theory¹⁸, in which directional scattering could occur depending on the relative strength between the electric dipole mode and the magnetic dipole mode according to the equation below

where θ is the scattering angle. For forward scattering, θ equals 0°, and for backward scattering, θ equals 180°. a_ED and b_ED represent the scattering coefficients contributed by the electric dipole and magnetic dipole. If the dipole moments of the electric mode and magnetic mode are comparable (Figure 3a), then pronounced scattering of the dark state can be produced backward, whereas a strong scattering peak can be seen forward (Figure 3b). If the magnetic mode becomes weaker (see Figure 3c), then the unidirectional scattering effect is weakened (Figure 3d).

Figure 3.

Analysis of unidirectional scattering using the Kerker's theory. (a) and (c) Scattering intensities contributed by electric and magnetic modes with different strengths. (b) Calculated scattering spectra in both forward and backward directions arising from modes in a. (d) Calculated scattering spectra in both forward and backward directions arising from modes in c.

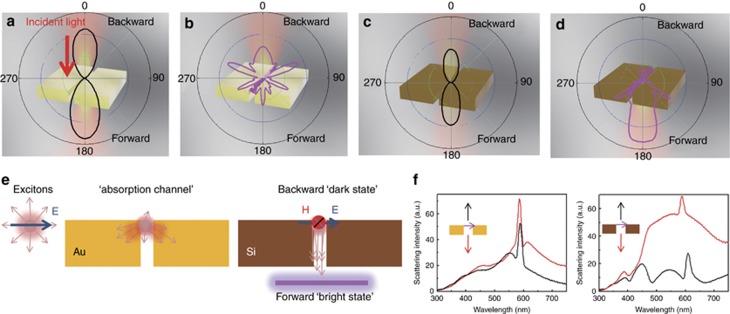
To fully understand the interference between J-aggregates and silicon NGs in different directions by simulation, we use bi-pass grooves with a thickness of 100 nm to replace the actual NGs. The radiation pattern in Figure 4a describes the forward and backward scattering from a gold NG. The localized surface plasmon resonance (LSPR) distributed on the edges interacting with the incident light leads to strong scattering in both the forward and backward directions. Using the Lorentz model to describe the dielectric permittivity of J-aggregates in a simulation⁴, we can investigate the radiation property from this plasmon–exciton hybrid structure as shown in Figure 4b. At λ=587 nm, J-aggregates with high oscillator strengths filled in the groove experience strong interactions with LSPRs and cause scattering quenching. The coupling between J-aggregates and LSPRs mainly occurs on the top surface because the LSPR distributes mainly on the top-surface edges. This interaction directs most uncoupled energies radiating backward, and little light escapes in the forward direction.

Figure 4.

Unidirectional ‘dark states’ in silicon NGs. (a) The schematic and calculated scattering pattern from a gold bi-pass NG with a thickness of 100 nm under the incident wavelength of λ=587 nm. (b) Schematic illustration and calculated scattering pattern of the Au NG-J-aggregate hybrid nanostructure. (c) Schematic illustration and calculated scattering pattern of a bi-pass Si NG under the incident wavelength of 587 nm. (d) Schematic illustration and calculated scattering pattern of the Si NG-J-aggregate hybrid nanostructure. (e) Schematic explains the ‘absorption channel’ in a gold-exciton hybrid system and the unidirectional ‘dark state’ in a silicon–exciton hybrid system. (f) Simulated backward and forward scattering from single-dipole emitter–NG hybrid systems.

The radiation pattern in Figure 4c exhibits scattering in the forward and backward directions from a bi-pass silicon NG with a thickness of 100 nm. LMRMs interact with the incident light and generate both forward and backward scattering light. Upon filling the groove with the J-aggregates, the J-aggregates can be considered electric dipole oscillators interacting with the LMRMs. This situation is exactly Kerker's type of scattering, in which unidirectional scattering can be achieved. As shown in Figure 4d, the scattering can be engineered only toward the forward direction. In Figure 4e, the different interaction mechanisms in gold NGs and silicon NGs is illustrated clearly. The plasmon–exciton coupling process is dominated by an ‘absorption channel’ because of the strong localized plasmon resonances^{2, 43}. The energy exchange rate between the excitons and the plasmonic cavity is much higher than are their individual radiative decay rates. However, the situation is different in silicon NGs. The interaction between the excitons and the silicon cavity is realized from the far-field interference between two radiating resonances. On the basis of the unidirectional scattering induced by the electromagnetic interaction, the LMRM cuts off the radiation decay of the J-aggregates and produces a scattering dark state in the backward direction. There is thus no scattering signal found at λ=587 nm in the backward direction (see Figure 4d). At the same time, strong forward scattering can be obtained through the bi-pass silicon NG. The silicon NGs in the experiment are single pass, which prevents the leak of uncoupled light forward and forces the uncoupled light to penetrate much deeper into the hybrid structure, which in turn further enhances the coupling between the J-aggregates and silicon NGs. A simulation was also performed by placing a single electric dipole source in the middle of the NGs and calculating the forward and backward scattering spectra as shown in Figure 4f. For the dipole in a gold NG, the forward and backward scattering intensities are nearly equal. For the dipole in a silicon NG, we can see obvious intensity differences between the forward and backward directions, especially at λ=587 nm. In addition, we performed a simulation to explore whether the unidirectional ‘dark state’ also exists in other silicon nanostructures, such as the silicon nanosphere shown in Supplementary Fig. S8. A silicon nanosphere with a diameter of 140 nm was chosen whose strong magnetic dipole response is located at approximately λ=587 nm. In addition, the radiation pattern in Supplementary Fig. S8 indicates that no backward scattering suppression occurs because the magnetic modes only distribute inside the sphere and cannot form effective LMRMs for an effective interaction.

In the experiment, after coating a thin-layer TDBC J-aggregate, the scattering spectra of the silicon NGs with different depths were re-measured as shown in Figure 5a. From the AFM characterization in Supplementary Fig. S9, we can see that the thickness of the J-aggregates layer is ~10 nm and that the J-aggregates distribute on the top of silicon NGs. For a silicon NG with a depth of 100 nm, the scattering spectrum is dominated by a surface-scattering peak below λ=500 nm, which cannot effectively realize overlap with the exciton energy; therefore, only a shallow Fano dip can be observed at λ=587 nm. Meanwhile, for a silicon NG with a depth of 150 nm whose LMRM can fully overlap with the exciton mode, the significantly suppressed scattering dip at approximately λ=587 nm reveals an effective destructive interference between the excitons and the silicon NG. When increasing the depth to 200 nm, the red-shifted LMRM weakens the Fano destructive interference between the excitons and the silicon NG; therefore, only a shallow Fano dip can be observed in Figure 5a (blue curve). For a silicon NG with a depth of 300 nm, although the overlap between the resonant energies of the exciton and LMRM can be satisfied in spectrum, the lower overlapping degree in space leads to an incomplete unidirectional ‘dark mode’ (see radiation patterns in Supplementary Fig. S10). The effect of peak splitting thus becomes slightly weaker (green curve) compared with the NG with d=150 nm (red curve). For silicon NGs with depths greater than 400 nm, the nonoverlapping resonant peaks further weaken the destructive interference; therefore, only the Fano asymmetric line shape can be observed (pink curve). Using the thickness and location of the J-aggregates obtained from AFM, we simulated the scattering spectra in Figure 5b, which confirm our experimental spectra above. However, some differences between the experiment and simulation still exist that may arise from the optical and geometrical parameters of the J-aggregates used in the simulation not fitting the actual situation accurately.

Figure 5.

Scattering spectra of J-aggregate-coated silicon NGs. (a) Measured scattering spectra of TDBC J-aggregate-coated silicon NGs with different depths (up to down: d=100, 150, 200, 300 and 400 nm). (b) Simulated scattering spectra of J-aggregate-coated silicon NGs.

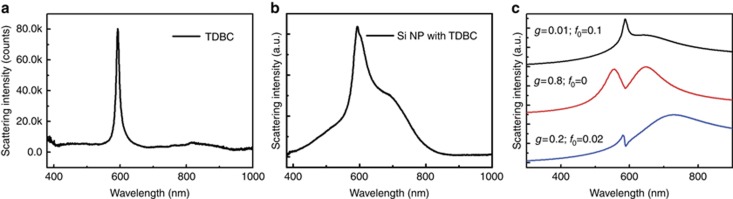
The scattering spectra of pure J-aggregates and a silicon nanosphere coated with J-aggregates were also measured. For pure J-aggregates, the large harmonic force from the incident field exerts on the J-aggregates directly and leads to the strong backward scattering from the dipole-like excitonic resonance as the measured scattering spectrum shown in Figure 6a. A silicon nanosphere with a diameter of 170 nm exhibits a broad magnetic dipole resonance in the visible region⁴⁴, and the experimental and simulated scattering spectra are shown in Supplementary Fig. S11. After coating the silicon nanosphere with J-aggregates, we can see a strong and narrow exciton-scattering peak overlapped on the scattering from the nanostructure in the experiment as shown in Figure 6b. We also measured the backward scattering of other sizes of silicon nanospheres spin-coated with J-aggregates. In addition to Figure 6b, the measured scattering spectra in Supplementary Fig. S12 embody strong scattering resonances from excitons. The interaction strength is therefore much lower than that in a J-aggregate–silicon NG system, and the main reason is the different magnetic mode distributions.

Figure 6.

Theoretical analysis of the interaction between silicon nanostructures and excitons. (a) Measured scattering spectrum of pure TDBC J-aggregates layer. (b) Measured scattering spectrum of a J-aggregate-coated silicon nanosphere. (c) The calculated scattering spectra from two interacting oscillators (J-aggregate and Si nanostructures) under different harmonic forces on excitons and different interaction strengths.

The coupled-oscillator model was widely used to analyze the Fano resonances in a system that consists of two interacting oscillators^{28, 29}. Using the coupled-oscillator model³⁰, we can fit the scattering spectra of different silicon–exciton systems using different parameters (f₀ and g) and clarify the general criteria for observing pronounced Fano interference in silicon NGs and silicon nanospheres. The scattering spectra can be described as

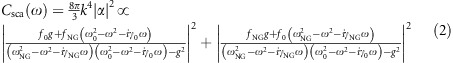where ω_NG and ω₀ are the resonant frequencies of LMRM and J-aggregate, respectively, and γ_NG and γ₀ are the decay rates of LMRM and exciton energies, respectively. g is the interaction strength, and f_NG and f₀ represent the incident field imposed on the silicon NG and excitons, which describe the scattering excited directly by the incident field. g and f₀ are two main factors that explain different scattering behaviors in different silicon nanostructures. In our case, the scattering from excitons (f₀) cannot be ignored because considerable J-aggregates have been added in this hybrid system that can generate obvious scattering light around λ=587 nm under the incident field (see Figure 6a). f₀ reflects whether excitons couple to the external field or to the NG. If the harmonic force exerting on the excitons approaches zero, then the resonant mode of the excitons can be considered the dark mode. If the harmonic force exerting on excitons is large, then it becomes a bright mode, which hinders the generation of Fano destructive interference.

Interaction strength g determines how pronounced the Fano dip is. It can be given by^{3, 45}

where μ_J is the excitonic transition dipole moment, n_x is the density of the J-aggregates, V_x is the result of the overlap integral between the LMRMs and the distribution of J-aggregates and V is the LMRM volume. For dielectric nanocavities, we added coefficient k/f₀ that represents the contribution of Kerker's scattering from the electromagnetic dipole interaction. It can be seen that the interaction strength is influenced by two aspects. First, the LMRMs interacting with excitons greatly decreased the uncoupled scattering decay backward (f₀) and enhanced the light–matter interaction. Second, such as plasmonic nanocavities, silicon NGs with widths below 100 nm, can realize light trapping under a subwavelength scale. At the same time, unlike solid silicon nanostructures with field enhancements concentrated inside, the leaky magnetic modes diffusing into the groove can fully overlap with the J-aggregates in the groove (large V_x), which dramatically enhances the ratio 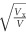. These two factors lead to high ‘g’ and make silicon NGs realize the Fano-type scattering dark state without strong near-field enhancement.

After knowing the meanings of g and f₀, we can explain and fit the scattering spectra of different silicon–exciton hybrid systems. Because no effective LMRMs are generated in the silicon nanosphere–exciton hybrid system, the large harmonic force from the incident field exerts on the J-aggregates directly and leads to strong backward scattering from the dipole-like excitonic resonance. In this situation, as shown in the black curve in Figure 6c, f₀ is large (equals 0.1) and g is small (equals 0.1), which exactly describes the situation in the silicon nanosphere coated with J-aggregates (Figure 6b). When an effective electromagnetic interaction occurs between the excitons and the silicon NG, then Kerker's directional scattering can be obtained and uncoupled radiation decay generating backward would be weakened; therefore, the coupling between the incident field and excitons (f₀) becomes much weaker. In contrast, the excitons under unidirectional scattering decay most energies through the silicon nanocavity and boost the interaction strength (g). This interacting case (g=0.8; f₀=0) is revealed by the red curve in Figure 6c, which can describe the spectrum from NG with a depth of 150 nm (Figure 5). When changing the depth of the silicon NG, the Kerker’s type unidirectional scattering is weakened; therefore, f₀ increases to 0.02 and g decreases to 0.2. We plotted this status in Figure 6c (the blue curve), which is correlated with the scattering spectrum of the silicon NG with a depth of 200 nm. More precise values of the g and f₀ of different silicon–exciton hybrid systems can be deduced from further numerical fitting using the estimated initial values.

Although silicon NGs cannot obtain strong field enhancement, the unidirectional scattering produced by the electromagnetic interaction (small f₀) and the large interaction strength are favorable to obtain a pronounced Fano dip. However, it should be noted that more excitons should be added in this system to realize a strong interaction; therefore, applications such as one-photon nonlinearity⁴⁶ and nonlinear quantum optics³⁹ cannot be easily realized. This all-dielectric system also has potential applications in all-optical ultrafast circuits⁴⁷, induced transparency² and the design of novel optical devices with precisely tailored responses⁴⁸.

Conclusions

In conclusion, we have investigated the interaction between molecular excitons and resonant modes in silicon NGs. The high-refractive index silicon NG can trap electromagnetic fields on subwavelength scales and produce LMRMs. The LMRMs interacting with J-aggregates produce directional scattering and enhance the interaction strength. This new mechanism gives rise to Fano resonances or scattering dark states without large near-field enhancement. By changing the depth of silicon NGs, the scattering spectra of the hybrid system can be engineered. In the emerging applications based on light–matter interactions, silicon NGs provide possibilities to realize on-chip optical processing networks.