Long-lived electron emission reveals localized plasmon modes in disordered nanosponge antennas

Abstract

We report long-lived, highly spatially localized plasmon states on the surface of nanoporous gold nanoparticles—nanosponges—with high excitation efficiency. It is well known that disorder on the nanometer scale, particularly in two-dimensional systems, can lead to plasmon localization and large field enhancements, which can, in turn, be used to enhance nonlinear optical effects and to study and exploit quantum optical processes. Here, we introduce promising, three-dimensional model systems for light capture and plasmon localization as gold nanosponges that are formed by the dewetting of gold/silver bilayers and dealloying. We study light-induced electron emission from single nanosponges, a nonlinear process with exponents of n≈5...7, using ultrashort laser pulse excitation to achieve femtosecond time resolution. The long-lived electron emission process proves, in combination with optical extinction measurements and finite-difference time-domain calculations, the existence of localized modes with lifetimes of more than 20 fs. These electrons couple efficiently to the dipole antenna mode of each individual nanosponge, which in turn couples to the far-field. Thus, individual gold nanosponges are cheap and robust disordered nanoantennas with strong local resonances, and an ensemble of nanosponges constitutes a meta material with a strong polarization independent, nonlinear response over a wide frequency range.

Introduction

Nanoporous metal nanoparticles have attracted attention due to their high surface to volume ratio and their tunable optical properties. In this paper, we demonstrate their potential as disordered nanoantennas that can efficiently funnel far-field light into a few nanolocalized, long-lived surface plasmon (SP) modes. Ordered metal nanoantennas with well-controlled geometries have been the focus of extensive research for several decades^{1, 2}. Among other features, they provide the possibility to control light on the subwavelength scale^{3, 4} and to produce highly enhanced optical near fields via surface plasmon polariton (SPP) excitations^{5, 6, 7, 8}. This has shown to be beneficial for nonlinear optical and near-infrared sensing⁹ and for photocatalytic applications because the nonlinear response of the sample is dominated by localized hot spots of high field intensity. Applications in which plasmonic field enhancement is crucial in the vicinity of nanoparticles have already been demonstrated for vibrational sensing^{10, 11}, ultrasensitive measurements of circular dichroism^{12, 13, 14}, plasmon-driven dissociation of hydrogen molecules¹⁵ and solar water splitting^{16, 17}. Other sensing applications have been demonstrated by employing the shift of the plasmon resonance itself^{18, 19}. Strong-field emission along with the all-optical control of plasmonic electron sources also depends on the plasmonic field enhancement^{20, 21, 22}. Long-lived SPPs that are realized with certain antenna geometries or clusters can be used for optical data processing, and their long lifetime is desirable for narrow linewidths in sensing applications. However, the large-scale production of such computer-designed, ordered antenna systems is costly due to the precision required in the manufacturing process.

Exciting alternatives for these conventionally manufactured nanostructures are disordered metallic structures, which also show ubiquitous field localization and are significantly cheaper to produce. Disorder-induced localization and longevity have been reported for randomly disordered dielectrics^{23, 24} and quasi-two-dimensional metallic films^{25, 26, 27, 28, 29}, where the benefits for surface-enhanced Raman scattering (SERS) spectroscopy have been noted^{30, 31}. Localization in such films results from the random, multiple scattering of surface-bound SPP modes in the percolated metal film³². A particular advantage of such disordered structures is the inherent robustness of their resonance effects. Although the specific realization of mode localization may be changed by temperature or environmental variations, the overall characteristics remain largely unaffected.

To date, SPP localization has mostly been studied in quasi-two-dimensional metal films. Quite recently, gold nanosponges, which are produced by the dewetting of gold/silver bilayers and dealloying, have emerged as an interesting prototype for quasi-three-dimensional SPP localization^{31, 33, 34, 35}. These morphologies are nearly micron-sized gold half spheres that are perforated with a fine, random network of unfilled pores. The pore diameter, which is typically 10–20 nm, can be controlled by the fabrication conditions. Finite-difference time-domain (FDTD) simulations^{31, 34} predict SPP localization due to multiple random scattering. However, little is known about the local field enhancement, that is, the size of the localized modes and, more importantly, the mechanisms and the dynamics of their coupling to the optical far-field. Without such knowledge, it is very challenging to assess the potential of those new nanoparticles for applications in, for example, nanosensing or for enhancing the optical nonlinearity. In addition, the development of strategies to improve their optical properties urgently requires a thorough understanding of their basic optical properties.

Here we study these properties at the level of single nanosponges using far-field extinction measurements and ultrafast two-photon photoemission experiments. We observe persistent photoemission, even some tens of femtoseconds after the decay of the near-infrared excitation pulse. This demonstrates the existence of long-lived, highly spatially localized SPP modes at the surface of the nanosponge. Our results show that the nanosponge acts as a disordered type of nanoantenna, in which far-field light is captured by the dipolar resonance of the gold sphere and concentrated into local, strongly enhanced SP modes with lifetimes of more than 20 fs. This observation enables the rational design of this new class of nanoantenna by tailoring the nanopore disorder.

Materials and methods

The gold nanosponges were fabricated from a combination of the solid-state dewetting of a 10 nm Au/20 nm Ag bilayer and a subsequent dealloying, as reported before³³. The gold nanosponges were transported onto a transparent and conductive indium tin oxide (ITO)-glass substrate for photoemission and scattering measurements. A scanning electron microscopy (SEM) image (Figure 1d) shows that nanosponges are dispersed at a low density on the substrate. For such nanosponges, the pore size can be adjusted, and the fundamental plasmon resonance in the optical spectra can be shifted by changing the filling fraction of the pores³⁴. Importantly, many nanosponges can be produced in regular arrays³⁵.

Figure 1.

The gold-nanosponge sample. (a, b) Scanning electron microscopy (SEM) images of two representative gold nanosponges, henceforth called nanosponges A and B, respectively. (c) Cross-sectional model geometry for finite-difference time-domain (FDTD) calculations. The spherical inclusions are overlapping and form a percolating network with a filling fraction of 0.36, comparable to the experimental results. (d) SEM image of the sample surface with several nanosponges. (e) Photoelectron emission microscopy image of the same area of the sample with a single sponge visible. All nanosponges show strong electron emission. (f) Cross-sectional SEM image of a nanosponge underneath a protecting platinum layer that has been cut open by a focused ion beam, revealing the internal percolated structure.

Ultrafast photoemission experiments are performed using few-cycle light pulses at a wavelength of 1600 nm and with a pulse duration of 16 fs. The pulses are generated in a home-built, non-collinear optical parametric amplifier, pumped by a regenerative Ti:sapphire amplifier operating at a repetition rate of 5 kHz (Ref. 36) (details are given in the Supplementary Information). A phase-locked pair of these pulses is created in a Mach–Zehnder interferometer. The pulses are focused onto the sample by using an all-reflective objective. Photoemission is recorded under high vacuum conditions as a function of the time delay between the pulses using a microchannel plate detector followed by a phosphor screen.

Results and discussion

We examine the light scattering of two individual gold nanosponges and time-resolved photoemission properties. The nanosponges are referred to as nanosponges A and B, respectively, as depicted in Figure 1a and 1b, and are taken as representatives of the larger set of nanosponges. Although some detailed aspects of the spectrum differ for individual nanosponges—specifically the exact position of the resonances—the most relevant properties, such as the existence of long-lived plasmonic modes and the high field enhancement, can be observed for essentially all of the nanosponges that we investigated. The nanosponges can be approximated as prolate half-ellipsoids with a semi-major axis of 515 nm (nanosponge A) and 525 nm (nanosponge B), and a semi-minor axis of 384 nm (A) and 339 nm (B). This corresponds to aspect ratios of 1.34 and 1.55, respectively. The nanosponges are transported on a 200-nm-thick layer of ITO coated onto a glass substrate, and the feature size of the pores is ~12 nm. The cross-section image of Figure 1f is evidence that the porous structure is indeed percolated and homogenous throughout the nanosponge, as conceptually illustrated in Figure 1c, and is not just restricted to the surface. The cross section was prepared by milling with a focused ion beam microscope (FIB, Carl Zeiss Auriga 60 crossbeam), and a Pt layer was previously deposited on the nanosponge for protection during the milling.

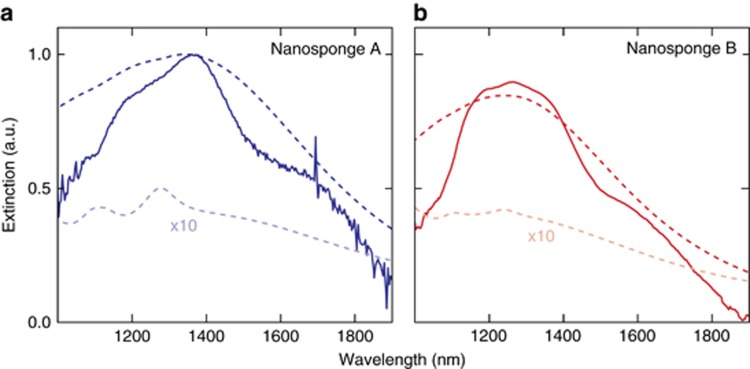
In a first set of experiments, we evaluate the linear light scattering properties of individual nanosponges. For this, we use a confocal optical microscope in a transmission geometry and excite the nanosponge with a white-light supercontinuum source. Figure 2 shows the near-infrared extinction spectra of the two individual nanosponges, A and B. The incident light is polarized along the semi-minor axis of the ellipsoidal nanosponges. A broad maximum of the extinction is visible at ~1.3 μm, which is identified as the fundamental plasmonic dipole resonance by comparison with elementary Mie-scattering calculations. On top of this broad resonance, several faint, narrower resonances with often dispersive, Fano-like lineshapes are clearly visible. The exact positions, amplitudes and linewidths of the resonances are different for both nanosponges, suggesting a dependence on the exact realization of disorder in the sponges. The occurrence of these features, however, appears to be a universal feature of this type of nanosponge, as observed in Ref. 34 and in the optical spectra of several other sponges that are not shown here. It thus appears that the continuum of the broad fundamental mode is interacting with several comparatively long-lived and, therefore, spectrally much narrower modes. Compared to more marked Fano resonances in other types of plasmonic nanoresonators^{37, 38, 39}, these peaks are not very pronounced and do not display strongly asymmetric lineshapes. This finding suggests that the total amount of light that is scattered from the main, dipolar resonance is much larger than that scattered from each of the narrower modes. From the average width of these resonances, we estimate the lifetimes of the intensity stored in the narrower modes as being up to a few 10s of fs. Such comparatively long lifetimes may suggest that these modes are spatially localized within a small region of the nanosponge. This assumption will be supported by the FDTD calculations and nonlinear experiments reported below.

Figure 2.

Spectral characterization of the nanosponges. Experimentally measured (full lines) and calculated (dark dashed lines) extinction spectra for nanosponges A (a) and B (b) from Figure 1. The incident field is polarized along the semi-minor axis of the ellipsoids. The spectra are normalized to the extinction maximum of nanosponge A. The narrower resonances on top of the fundamental dipole resonance are attributed to the coherent, resonant interaction of the dipole mode with the localized long-lived modes. Calculated scattering spectra (dark dashed lines) for the half-ellipsoidal nanosponges with the same overall dimensions are in good general agreement with the experimental data but underestimate the mode-coupling. Long-lived modes can, however, be seen in the calculated absorption spectra (light dashed lines, 10-fold enhanced).

To test the assertion that these spectrally narrow resonances arise from spatially localized SP modes with strongly enhanced fields, we now examine the nonlinear optical properties of the nanosponges. To accomplish this, we use multiphoton photoemission as a particularly sensitive probe. We excite the nanosponges with few-cycle pulses from a noncollinear optical parametric amplifier centered at 1600 nm (0.78 eV). With such long wavelength pulses, approximately n=7 photons are needed to overcome the 5.5 eV work function of gold. Therefore, the total number of photoelectrons N_el emitted from the nanosponge scales with the spatial and temporal integral over the local electric field 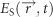at the nanosponge surface to the power 2n: 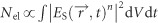. Hence, this high optical nonlinearity largely amplifies the locally enhanced electric fields and causes the photoemission signal to be highly sensitive to local hot spots of light at the nanosponge surface.

In our setup, the incident pulses are focused without measurable pulse broadening to a spot size of ~2 μm with an all-reflective objective. Using this spatial resolution, the photoemission from individual nanosponges is easily resolved (Figure 1e). Each nanosponge appears as an emission spot with a diameter of ∼ 1 μm (full width at half maximum), which is much smaller than the laser spot size due to the high nonlinearity of the emission process. This spot size is larger, however, than the diameter of a single nanosponge and, therefore, the spatial resolution of this measurement is not sufficient to resolve individual hot spots at the nanosponge surface.

To experimentally demonstrate the existence of these long-lived hot spot resonances, we perform time-resolved photoemission measurements on single nanosponges. For this, we excite the nanosponge with a phase-locked pair of 16 fs pulses centered at a 1600 nm wavelength. In the measurements, the pulse energy of the incident pulses is set to 7 pJ, resulting in a maximum recorded electron signal of approximately one electron per pulse. The time-dependent electric field E_L(t) of the excitation pulses has carefully been characterized by frequency-resolved, interferometric autocorrelation measurements (see Supplementary Information), and the measured pulse duration of 16 fs is close to the limit set by the spectral bandwidth of the laser pulses.

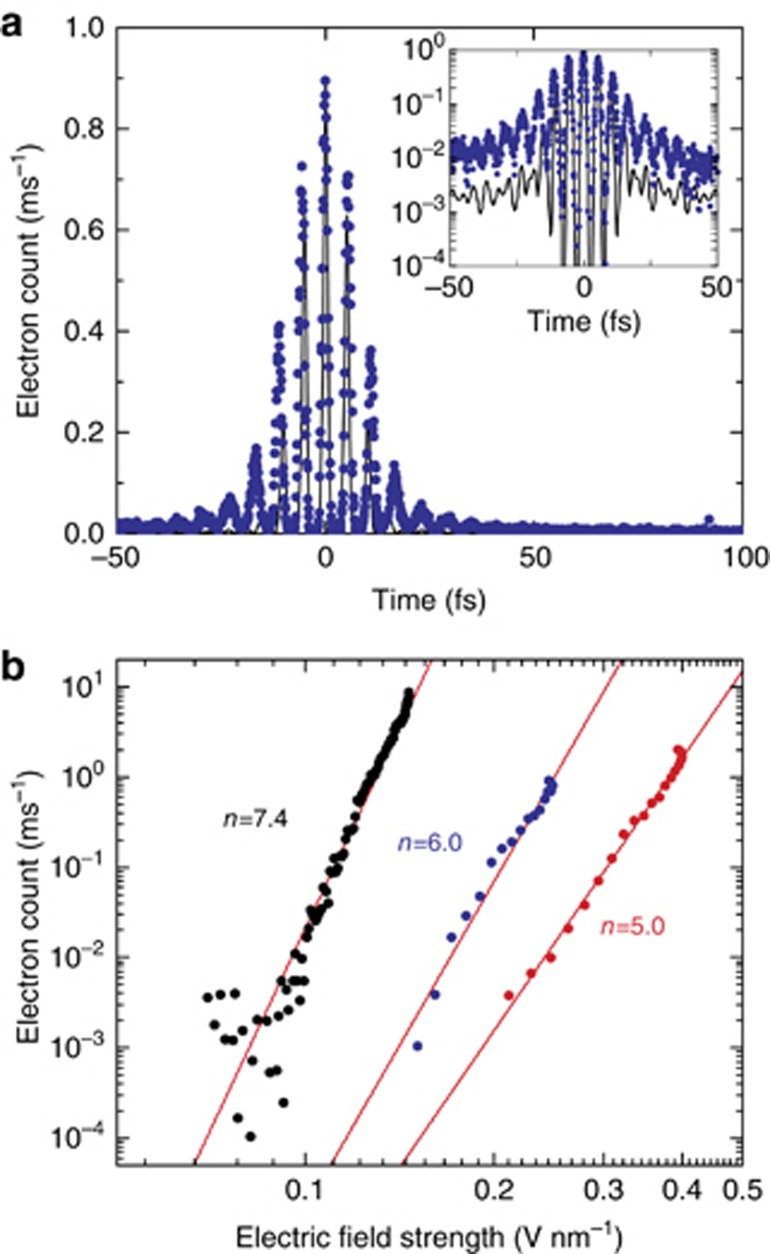
A typical interferometric autocorrelation trace C(Δt), displaying the photoemission signal recorded from a single nanosponge as a function of the time delay Δt between the pulses, is shown in Figure 3a. The following aspects of the experimental data are particularly important. First, the photoemission persists even for time delays of more than 40 fs, that is, much beyond the time overlap of the two pulses. This is seen by comparing the measured data (filled circles) to an instrument response C₀(Δt) that is calculated using the known time structure E_L(t) and assuming a fifth-order nonlinearity n=5 (solid line in Figure 3a). Experimentally, we find eight clear oscillations at both positive and negative time delays. Interestingly, the fringe spacing is slightly larger than that in the instrument response function. A comparison between C(Δt) and C₀(Δt) on a logarithmic intensity scale (inset of Figure 3a) highlights the difference in the fringe spacings and, importantly, the strong photoemission from the nanosponge at long delay times. This is direct experimental evidence that the local electric field at the surface of the nanosponges still persists at time delays that are much longer than the duration of the incident laser field.

Figure 3.

Electron photoemission from nanosponges. (a) Interferometric autocorrelation trace C(Δt) of the photoemission from a single nanosponge. The data (filled circles) are taken from nanosponge A in Figure 1. The nanosponge is illuminated with a phase-locked pair of few-cycle near-infrared pulses (center wavelength 1600 nm, pulse duration 16 fs) and time delayed by Δt. The energy of each pulse is set to 7 pJ. Photoemission persists for delay times of up to 40 fs, as is seen more clearly when showing the data on a logarithmic intensity scale (inset). The instrument response C₀(Δt) simulated from the measured electric field of the laser pulses E_L(t) for a fifth-order optical nonlinearity is shown as a solid line. (b) The optical nonlinearity of the photoemission is deduced by plotting the recorded photoelectron signal from three representative nanosponges as a function of the maximum electric field amplitude of the laser pulses. The blue and red circles show the measurements taken for nanosponges A and B, respectively. Optical nonlinearities of order n=5...7 are deduced. The power law fits of order 2n are shown as solid lines.

At the same time, the data give evidence for a high-order optical nonlinearity of the emission process. This is reflected in the very high dynamic range (four orders of magnitude) for the change in the photoemission signal during the first interference fringes. In addition, the emission signal at delay times of more than 50 fs, that is, in the limit when each pulse interacts individually with the nanostructure, the photoemission is very weak and amounts to <1/200 of the maximum signal at a zero time delay. We can extract information about the nonlinearity of the emission process from the autocorrelation tracing by plotting the photoemission signal, C(Δt), against the maximum amplitude of the total incident laser field E_L(t)+E_L(t+Δt) at the given time delay. These plots, taken from the central interference fringe of C(Δt), are given in Figure 3b for three different nanosponges. The data plotted as blue and red circles denote the measurements taken for nanosponges A and B, respectively. In these three cases, the data match well with a nonlinear, multiphoton emission process of order n=5…7, in reasonable agreement with the simple estimate given by the ratio between the work function and the photon energy. Photoemission sets in at incident field amplitudes of 0.1–0.2 V nm⁻¹, smaller than what we observed for photoemission from a single gold nanotip under similar excitation conditions⁴⁰. Again, this points to a high local field enhancement at the surface of the nanosponges. Experimentally, we find that we cannot increase the field amplitude beyond ~0.5 V nm⁻¹ before an irreversible reduction in the photoemission yield sets in. At these incident fields, approximately one photoelectron per pulse is detected, and the yield still follows a nonlinear power law, suggesting that strong-field phenomena still play a minor role in the photoemission process^{40, 41}.

We now attempt to deduce information about the local electric field at the surface of the nanosponges from these experiments. Specifically, we wish to extract knowledge about the lifetimes of the local fields. For this, we assume that the photoemission process itself is quasi-instantaneous on the time-scale of our experiment and that the process scales with the nth power of the local field. Then, the interferometric autocorrelation trace for the surface field E_S(t) of a nanosponge can be approximated as 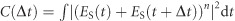, where n is the order of the nonlinear photoemission process. We assume that the photoemission primarily stems from N hot spots (spot index j) and that at each of these hot spots, the local field 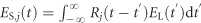is given as the convolution between the incident field and the local response R_j(t) of all of the relevant plasmonic modes of the nanosponge. This response function will then consist of the following two contributions: the response of the short-lived dipolar mode of the nanosponge, which is the fundamental Mie resonance, with a resonance frequency ω_P and a lifetime τ_P/2 of the field intensity, and the response of a localized hot spot mode ω_j with frequency ω_j and lifetime τ_j/2. In the following, we refer to the dipolar mode as ‘delocalized’ because it extends over the entire nanosponge, as opposed to localized modes, which stretch only over a few pores, that is, a few tens of nanometers. Taking these modes as the usual Lorentzian oscillators, the response function at each hot spot can be written as R_j(t)=Θ(t)(A_P exp(−i(ω_P−i/τ_P)t)+A_jexp(−i(ω_j−i/τ_j)t)). Here, A_P and A_j denote the amplitudes of the respective modes and Θ(t) is the Heaviside function. Finally, we assume that the photoemission signals C_j(Δt) from the individual hotspots on the sample add up incoherently, given 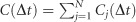. The instrument function shown as a black line in Figure 3a is then calculated from the same model by taking an instantaneous, delta-like response R_j(t)=δ(t). In addition, an estimate of the linear extinction spectrum is deduced from these simulations as 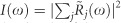, where 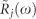is the Fourier transform of R_j(t). The details of the simulations are described in Supplementary Information.

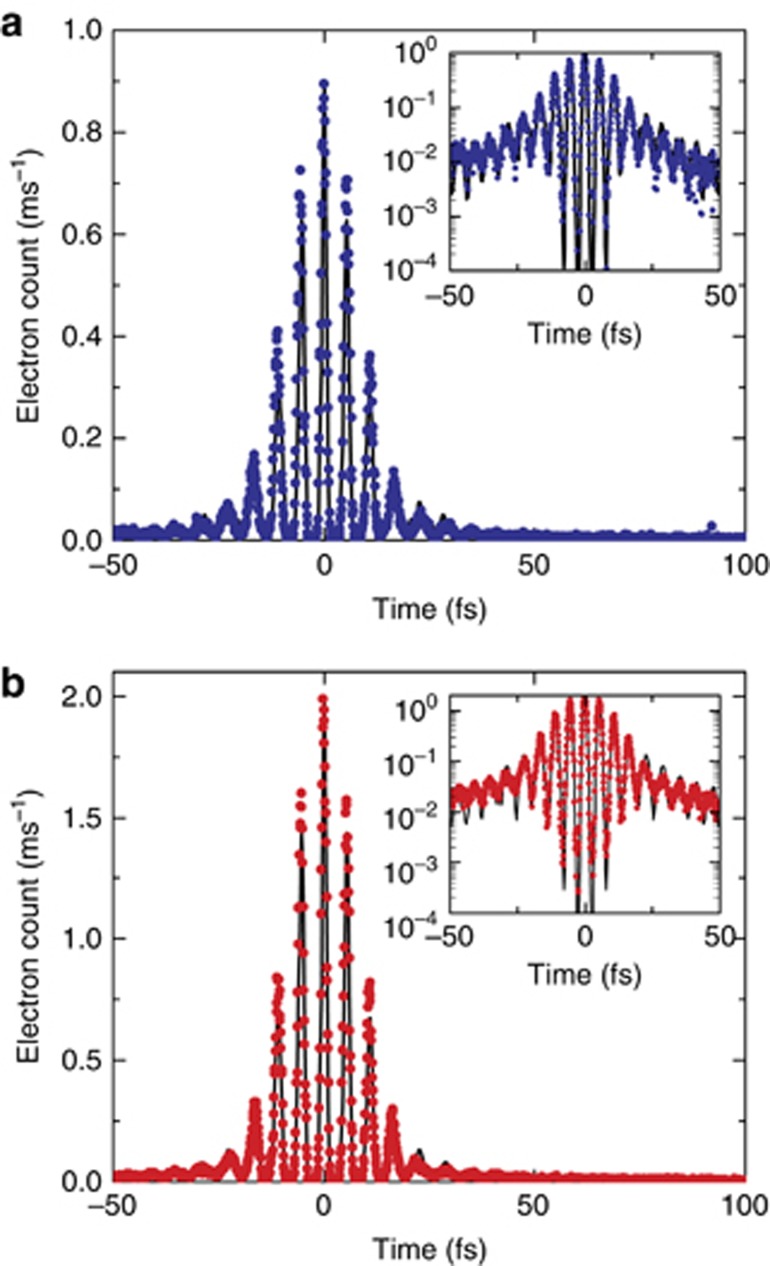
The following conclusions can be drawn from these simulations. The overall shape of the extinction spectrum is well reproduced by taking a plasmon resonance at 1500 nm with a lifetime of 2.5 fs (τ_P=5 fs). Since this lifetime is much shorter than the laser pulse duration, the autocorrelation function C(t) of a sponge without any localized modes would be very similar to the instrument response function. This points to the existence of at least one localized mode on the nanosponge surface. When modeling C(t) for a single localized mode, N=1, resonant at 1700 nm and with τ_H=40 fs, we can indeed reproduce the total number of fringes in the autocorrelation function as well as their overall decay and fringe spacing (Supplementary Fig. S5). This sets a lower limit for the lifetime of the localized plasmon intensity of ~20 fs. However, the modulation contrast of the individual fringes, that is, the ratio between the maximum and minimum emission signal, can only be matched for the central three fringes. This points to an inhomogeneous broadening of the localized plasmon field, that is, the contribution of several hot spots to the photoemission. We find that at least four hot spot modes are needed to reasonably match the experimentally measured autocorrelation. To reach an acceptable match of both the autocorrelation function and the linear extinction spectrum of nanosponge A, we choose N=7 hot spot modes and set their resonant wavelengths to those deduced from the extinction spectrum in Figure 2a. With a dynamic range of the autocorrelation data of less than two decades (Figure 4), we cannot reliably deduce the hot spots, for example, N=7 separate decay rates. Thus, we choose the same field decay time τ_j=τ_H=50 fs for all modes and adapt their amplitudes to approximate the measured autocorrelation function. With this choice, we can now also quantitatively describe the fringe modulation in C(Δt) by comparing the experimental and simulated traces both on a linear and logarithmic (inset) intensity axis, as shown in Figure 4a. From this, we conclude that the average intensity lifetime of the hot spot amounts to 25±5 fs, which is almost 10 times longer than the lifetime of the nanosponge plasmon resonance. This lifetime is still smaller than the lifetime of an SPP mode at a planar gold/air interface (~100 fs in this wavelength range^{38, 42}). The lifetime may be further increased by optimizing the nanoporosity of the nanosponge.

Figure 4.

Experimentally measured interferometric autocorrelation traces of the photoemission from a single nanosponge and the simulation based on a phenomenological localization model. The data (filled circles) are taken from nanosponges A (a) and B (b) and are compared to the model simulations (solid line). In the insets, the measurements and simulations are shown on a logarithmic intensity scale. In the simulation, the response of nanosponge A is taken as the sum of a short-lived, delocalized, dipolar plasmon mode (field decay time τ_P=5 fs; nanosponge B: τ_P=3 fs) and seven (nanosponge B: nine) localized, long-lived plasmon modes with decay times of τ_H=50 fs (nanosponge B: τ_H=40 fs). In the simulation, a fifth-order optical nonlinearity is assumed.

Similar conclusions are reached for nanosponge B (Figure 4b). Here we take a short-lived nanosponge resonance (1400 nm, τ_P=3 fs) and 9 localized modes with a field decay time of τ_H=40 fs for the simulation of C(Δt).

In summary, the interferometric autocorrelation measurements suggest that the linear and nonlinear optical response of the nanosponges in the near-infrared region is governed by the coupling of the incident far-field light to the dominant collective SP resonance of the nanosponge. The resulting plasmon field is coupled to a series of localized hot spot resonances at the surface of the nanosponge. The associated plasmon modes have relatively long lifetimes of ~25 fs, which is much longer than that of the collective plasmon mode for the nanosponge (~2.5 fs). In the linear optical spectra, the interference between the fields emitted by the collective plasmon resonance and the different hot spots gives rise to weak, dispersive, Fano-type spectral modulations. When exciting the nanosponge with intense near-infrared laser pulses, however, the highly local field enhancement in the hot spots and the highly nonlinear characteristics of the multiphoton photoemission process results in electron autocorrelation traces being almost completely dominated by the photoemission from the localized hot spots. Hence, the time-resolved photoemission experiments with sufficiently short laser pulses, as presented here, can provide direct measurements of the lifetimes of the localized hot spots.

To shed more light on the details of the plasmon excitations of these nanosponges, extensive simulations of the time-dependent local electromagnetic fields at the nanosponge surface were carried out. Simulations were performed using the FDTD method⁴³, using the freely available software package Meep⁴⁴. We used a model geometry that is very similar to the experiments but did not attempt to reproduce the exact realization of the porosity for either sample. The procedure for creating the model geometry on the computer was as follows. Prolate metal semi-ellipsoids were placed on a dielectric substrate with a refractive index matching that of ITO. Small, slightly overlapping spheres were generated inside the ellipsoid. Starting from the exterior, the gold was removed from these spheres if they had contact to the surface, in analogy to the etching process during the sample preparation. Therefore, isolated inclusion spheres remain metallic and a percolating porous network is created inside the metallic nanoparticle, see Figure 1c. The filling factor of the pores in the nanosponge can be adjusted. Filling factors of ~36% for the pores reproduce the experimental dipolar plasmonic resonance well, as is evident in Figure 2. A higher filling factor shifts the resonances toward the infrared, consistent with Maxwell–Garnett effective-medium theory. To model the optical properties of gold, we use an analytical Drude-model fit to experimental data^{45, 46}. The Drude relaxation times in the model of ~10 fs (Refs. 42, 46) are considerably shorter than the observed SPP decay times because a large fraction of the SPP energy is stored in vacuum. A plane-wave source with a wave-vector perpendicular to the substrate was used for the 3D geometry to calculate the scattering properties and field dynamics. The excitation was a Gaussian pulse with the same 16-fs pulse duration as in the experiments and polarized along the semi-minor axis. The extinction spectra from the FDTD calculations are presented as the dark dashed lines in Figure 2. They reproduce the fundamental plasmonic dipole mode frequency well for the given filling fraction, but the Fano-type resonances are barely visible in the extinction spectra. They can, however, be observed in absorption spectra, depicted by the light dashed lines in Figure 2, which are increased 10-fold in the plot because the absorption is comparatively weak. In the calculated spectra, there are no visible peaks in the long wavelength part of the spectra, whereas in the experimental results, the dips in the spectrum appear to be spread out over the entire frequency range in the plot.

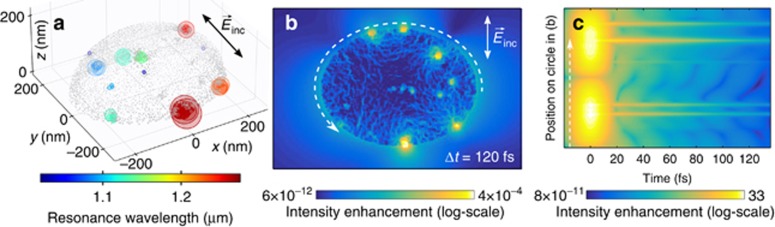
Figure 5a shows details of the spatial dynamics of the long-lived modes that cause the features in the scattering and autocorrelation spectra. To obtain this plot, the decaying fields after the excitation period were evaluated at the center of each individual pore and then spectrally analyzed using harmonic inversion^{47, 48}. A model for nanosponge A yields several independent modes with different frequencies. All modes are concentrated near the surface and are highly localized to a few pores (Figure 5b), with the most prominent ones—not only for sample A, but for most nanosponges—being situated roughly along the ellipse vertices, where the semi-minor axis meets the surface of the ellipsoid. The intensity of the dipolar excitation is maximal in this region, indicating that the localized modes are excited indirectly via the dipole plasmonic mode that couples to the far-field. Proof for this is found in the detailed temporal dynamics. At each point on the surface, we find the presence of an intense and short-lived plasmon field that vanishes within the first 20 fs. The time dynamics of the field intensity follows the intensity profile of the laser pulse, which shows that the lifetime of this delocalized plasmon mode is shorter than the pulse duration of the laser (16 fs). In addition, we find, at selected positions, that there is a coherent and delayed excitation of localized modes with a phase difference of ≈π/2 between them. The field dynamics matches that of the multi-exponential decay model used for the fit of the experimental data in Figure 4. Clearly, the localized modes are long-lived, as seen in Figure 5b and 5c. The former shows the field intensity that remains at a time delay of 120 fs in a cross section through the nanosponge, that is, long after the initial dipolar excitation of the nanosponge has died out. The latter shows the temporal evolution of the field intensity on a circle along the surface of the nanosponge (see the dashed line in Figure 3b). In both plots, we see that a few tens of femtoseconds after the excitation, the whole remaining intensity is localized in the same modes that are already visible in Figure 5a. The initial dipolar excitation is delocalized and short-lived, as seen in Figure 5c.

Figure 5.

Numerical simulation of the local field distribution. (a) Calculated intensity distribution and resonance wavelengths of the localized modes from a model of nanosponge A in Figure 1 with 10-nm inclusions for incident light polarized along the y-direction. The field intensity is measured at the centers of all overlapping inclusion spheres forming the network. The diameter of the circles corresponds to the amplitude of the dominating mode found by harmonic inversion at that specific point. The wavelength of the dominating mode is depicted by the displayed color code. (b) The local field intensity (logarithmic scale) for the model nanosponge, calculated along a cross section through a plane parallel to the substrate, 5 nm above the substrate, and at a time delay of 120 fs after the arrival of the excitation pulse. (c) The time-dependent field intensity calculated along a circle close to the surface of the nanosponge (see white dashed line in b). The y-axis gives the position on the circle. The maximum of the incident pulse is at 0 fs. The decay times for the short-lived and delocalized dipolar and the distinct, long-lived localized SP modes are clearly distinguished.

An intuitive explanation for the dynamical behavior of the nanosponges is readily found in terms of the coupled electromagnetic modes. The localized modes on the surface of the nanosponges show almost no far-field coupling and, thus, are not directly excited by an incoming laser beam but rather by the strong fundamental dipole mode. The latter is spectrally quite broad. Thus, its time dependence is well approximated by that of the laser field E_L(t). Disorder caused by the porosity of the nanosponges breaks the symmetry and leads to a finite coupling between the dipole and localized modes. The excitation process for the localized modes is therefore indirect. First, the dipole mode is excited by the laser and decays partially radiatively and partially into the localized modes. The longevity of the localized modes is caused by the suppression of the direct radiative decay because of the low far-field coupling. Localized modes can re-excite the dipole mode or decay through Joule heating, which contributes significantly to the overall absorption signal of the entire nanosponge (Figure 2).

Of great importance both for basic science experiments and potential practical applications is the massive field enhancement caused by the localization. In our calculations, a maximum enhancement of the local field intensity over that of the incident far-field of ~40...45 is found. The corresponding field enhancement factor f≈6...7 is consistent with earlier works on nanoporous gold rods⁴⁹. The distribution of the field enhancements inside the pores (not shown) decays sub-exponentially, hinting at a log-normal intensity distribution and, thus, strong localization^{24, 50}. The strong localization also explains the high photoemission yield of the nanosponges. If the energy of the incoming pulse is concentrated on a volume fraction V/V₀ then the yield of a process with nonlinearity n is on average increased as (V/V₀)ⁿ⁻¹≫1.

Although the calculations qualitatively reproduce all the important aspects of the experiment, they show two quantitative differences. First, the localized, long-lived modes are less efficiently excited in the calculation, as evidenced by their low visibility in the extinction spectra (Figure 2) and by comparing the experimental autocorrelation spectra with spectra calculated from the FDTD results (not shown here). From the latter, we can estimate that the mode coupling and, therefore, the energy in the localized mode are underestimated by approximately a factor of 4. Second, the localized modes occur only in a relatively narrow spectral range compared to the experiment. We suggest that this can be explained by the simplified geometry that was chosen in the calculations. The overlapping inclusion spheres build a network with a relatively uniform feature size, especially on the surface. As shown in the SEM figures (Figure 1a and 1b), this is not true for the actual geometry of the nanosponge. The uniform feature size leads to a rather uniform effective, that is, averaged over a few tens of nanometers, dielectric function, whereas the stronger disorder in the real nanosponges might lead to a non-uniform effective dielectric function. As the resonance frequency of the localized modes depends on the effective dielectric function around the hotspot, we expect a broader distribution of mode frequencies for a less correlated geometry. In addition, in the simulated geometries, there is no localized mode that is in perfect resonance with the fundamental mode for the nanosponges. This limits the coupling, which means that we do not see as much of the localized modes in the calculated scattering spectra. This can, in theory, be overcome with a slightly more sophisticated model geometry. However, the additional degrees of freedom make an intuitive interpretation of the results more difficult. We note that for uniform inclusions and equal filling factors in the calculation, we find only a very weak dependence on the statistical properties of the localized mode spectrum on the inclusion size, that is, the feature size of the pores, as seen in Figure 1f. In contrast, for a different wavelength regime, there is experimental evidence for a dependence of the field enhancement on the pore size⁵¹.

Conclusions

In summary, we have presented, based on ultrafast photoemission experiments and FDTD simulations, strong support for an intuitive physical picture that can explain the linear and nonlinear optical properties of gold nanosponges, and model systems for three-dimensional random nanoresonators for SP polariton excitations. Far-field light couples to the short-lived dipole mode of the nanosponge, thus creating a spatially delocalized SPP excitation at the nanosponge surface. This delocalized plasmon mode efficiently couples to a series of localized hot spots, formed by coherent plasmon scattering within the randomly disordered nanoporous network. Long hot-spot lifetimes of several tens of femtoseconds are observed experimentally, and large local field enhancement factors of five to seven are deduced from the simulations. This scenario comprises the same steps as most experiments on nanoantennas. The incident far-field light is efficiently captured by the antenna and localized to, for example, the gap of a bow-tie antenna where nonlinear processes occur. The striking difference is that a small number of computer-designed nanostructures written, for example, via focused ion beam lithography are replaced by potentially mass-producible and comparatively cheap gold nanosponges, which can be studied individually or as an ensemble. A nanosponge ensemble shows a strong nonlinear and polarization-independent response over a wide frequency range. This makes such nanosponges interesting and flexible resonators with high potential for a series of applications, for example, in random lasing, SERS or plasmonic sensing. Experiments aimed at exploiting this potential are currently underway in our laboratories. Future studies will also aim to take a closer look at the disorder-induced plasmon localization phenomenon. This will enable further progress in tailoring disorder for specific applications, such as sensing, by exploiting the enormous field enhancement potential of the nanosponges.

Author contributions

ER, CL and PS initiated the project. CL conceived the experiments. DW and PS designed and fabricated the samples. GH, JV and HK carried out the experiments. FS and ER performed the FDTD calculations. GH and JV simulated the (electron) IACs. FS and CL prepared the manuscript. All authors contributed to the interpretation of the data and the final version of the manuscript.