Modelling compound cytotoxicity using conformal prediction and PubChem HTS data

The assessment of compound cytotoxicity is an important part of the drug discovery process.

Abstract

The assessment of compound cytotoxicity is an important part of the drug discovery process. Accurate predictions of cytotoxicity have the potential to expedite decision making and save considerable time and effort. In this work we apply class conditional conformal prediction to model the cytotoxicity of compounds based on 16 high throughput cytotoxicity assays from PubChem. The data span 16 cell lines and comprise more than 440 000 unique compounds. The data sets are heavily imbalanced with only 0.8% of the tested compounds being cytotoxic. We trained one classification model for each cell line and validated the performance with respect to validity and accuracy. The generated models deliver high quality predictions for both toxic and non-toxic compounds despite the imbalance between the two classes. On external data collected from the same assay provider as one of the investigated cell lines the model had a sensitivity of 74% and a specificity of 65% at the 80% confidence level among the compounds assigned to a single class. Compared to previous approaches for large scale cytotoxicity modelling, this represents a balanced performance in the prediction of the toxic and non-toxic classes. The conformal prediction framework also allows the modeller to control the error frequency of the predictions, allowing predictions of cytotoxicity outcomes with confidence.

Introduction

Cytotoxicity assessment is often one of the earliest toxicity tests conducted in the drug discovery process. These tests are important as cytotoxicity is a highly undesired feature in drug candidates, and the results from cytotoxicity screening are used both to remove toxic compounds and to help interpret the results of the subsequent assays.1 It has also been shown that cytotoxicity can be linked to organism level toxicities,2,3 raising hopes that it will be possible to replace in vivo acute toxicity studies with predictive in vitro cytotoxicity testing.4 However, experimental screening for cytotoxicity not only requires that compounds are available in sufficient quantities but also needs both time and resources for the running of the screening assays. Prioritising what compounds to test by means of in silico methods has the potential to save considerable amounts of time and money.5

Cell death can occur through a multitude of mechanisms, either through acute structural breakdown or through stress that triggers cellular apparatus leading to regulated cell death.6 However, many assays cannot distinguish between different mechanisms behind cell death or growth arrest. For an in depth understanding of the cytotoxic properties of a compound it is therefore important to investigate the underlying mechanisms.

For predictive methods to be useful for cytotoxicity assessment it is important to know under which circumstances the predictions are likely to be accurate. Conformal prediction is a modelling framework that outputs predictions with a guaranteed error rate.7 The controlled error rate makes conformal prediction attractive for important decision steps as the domain expert can adjust the confidence level to suit the particular problem at hand and be guaranteed about the corresponding level of correct predictions. The application of this has recently been demonstrated for problems in QSAR and predictive modeling.8–12 Eklund et al. describe the application of conformal prediction on AstraZeneca preclinical drug development data and show that conformal prediction greatly improves the predictions compared to traditional QSAR methods.10,11 Norinder et al. demonstrate how conformal prediction can serve as a more transparent alternative to traditional applicability domain determination.8,9

An additional advantage of conformal prediction is that the framework can be extended to each outcome class. Such a class conditional conformal predictor is guaranteed to be valid for each class.13 This means that for imbalanced data, the error rate for the minority class can be controlled, offering a solution to many of the problems14 associated with modelling imbalanced data.12,15 This feature has the potential to make conditional conformal predictions a useful approach when building models on data from screening assays since this type of data often is highly imbalanced, i.e. a large number of compounds have been screened to find a few active (or toxic) compounds.

PubChem is a publicly available repository of chemical compounds and associated assay data.16,17 Various assays for cell viability and cell proliferation inhibition (in this study collectively referred to as cytotoxicity) have been made available through this service. The deposited assays include high throughput screening, qHTSs, and smaller dose–response assays.

Several machine learning approaches have been applied for the prediction of compound cytotoxicity based on in vitro data.18–24 These approaches include neural networks,18 random forests (RF),19 decision trees,20 linear regression,20 and Bayesian learning.21 Different techniques to handle the data imbalance have also been applied, including undersampling,19 oversampling,22 and Bayesian learning.21 The main source used for obtaining cytotoxicity data for modelling has been PubChem, but Langdon et al. also used internal data from assays carried out at Pfizer.21 The investigation by Molnár et al.18 using neural networks on some 12 000 compounds, with a toxic to non-toxic ratio of 1 : 1.5, divided into a training set (8298 compounds) and 2 equally sized test sets (2000 compounds) which resulted in predicted accuracies of 77.6%, 73.4% and 73.4% for the 3 sets, respectively. The Guha and Schürer19 study using RF included 13 smaller datasets of 1300–1400 compounds with toxic to non-toxic ratios between 1 : 7 and 1 : 22. The reported predicted accuracies from the derived models were between 56–80% with a large variation on how well the minority class, i.e. the toxic class, was correctly classified. The investigation by Chang et al.,22 where oversampling of the toxic compounds was employed, resulted in some models for the training set where the internally validated accuracy, sensitivity and specificity were satisfactory and in the 80% range. However, the corresponding results for the test set were, for the most part, disappointing with values for accuracy, sensitivity or specificity in the 25–65% range. Thus, despite the previous efforts, modelling of highly imbalanced cytotoxicity assay data is still challenging, especially in regard to generating models with a balanced performance between toxic and non-toxic compounds. There is therefore a need for further research on how to best address this problem.

In this study we introduce conformal prediction as a tool for predictive toxicology. Conformal predictors are used to generate predictive models for highly imbalanced cytotoxicity data from sixteen PubChem assays. The models are shown to deliver accurate predictions of compound cytotoxicity as well as being valid with respect to each individual class according to the set confidence level. Thus, allowing for predictions with the level of confidence required for making important decisions in early stage compound toxicity assessments.

Methods

Data collection and characterization

The PubChem BioAssay database was manually queried for cytotoxicity screening with more than 20 000 tested compounds (Table 1). The selected datasets were downloaded and the structures were neutralised and the salts were removed using CORINA.25 Structure standardization was performed using the IMI eTOX project standardizer26 in combination with the MolVS standardizer27 for tautomer standardization where defined SMARTS patterns were used for these operations. Activity was assigned to compounds based on the PubChem outcome annotation and records with missing or conflicting annotations were removed.

Table 1. The studied cytotoxicity bioassay records from PubChem. The number of unique Bemis–Murcko scaffolds for the toxic compounds in parenthesis.

AID	Tested compounds a	Toxic compounds a	Cell line	Depositor
463	56 465	706 (538)	Jurkat	Scripps Research Institute Molecular Screening Center
1486	217 851	2408 (1672)	Ba/F3	Scripps Research Institute Molecular Screening Center
1825	290 605	2259 (1468)	IEC-6	Scripps Research Institute Molecular Screening Center
598	85 162	5139 (3694)	H69AR	Southern Research Molecular Libraries Screening Center
648	86 121	924 (735)	HUVEC	Southern Research Molecular Libraries Screening Center
719	84 841	937 (748)	LL47	Southern Research Molecular Libraries Screening Center
847	41 152	194 (184)	SK-BR-3	Southern Research Molecular Libraries Screening Center
903	52 783	338 (209)	H1299	NIH Chemical Genomics Center
504648	367 995	600 (499)	A549	NIH Chemical Genomics Center
588856	404 016	3018 (2183)	HEPG2	NIH Chemical Genomics Center
624418	386 360	524 (441)	HEK293	NIH Chemical Genomics Center
430	62 627	1121 (920)	HPDE-C7	Burnham Center for Chemical Genomics
620	86 701	364 (287)	HT1080	Burnham Center for Chemical Genomics
602141	359 040	1302 (956)	KKLEB	Burnham Center for Chemical Genomics
2275	29 938	193 (145)	BJeLR	Broad Institute
2717	299 957	3181 (2248)	HMLE_sh_Ecad	Broad Institute

^aNumber of compounds after processing.

The collected data sets were highly imbalanced with a fraction of toxic compounds spanning from 0.13 to 6.03% with an average of 0.8%. Many of the tested compounds are shared between the assays, and in total the data includes 441 396 unique PubChem compound identifiers (CIDs). A total of 16 228 unique CIDs were toxic in at least one assay with just 3967 CIDs being toxic in more than one (see ESI Table S4†). To assess the chemical diversity within the collected data sets the number of Bemis–Murcko scaffolds28 was counted using the RDKit29 MurckoScaffold function.

The PubChem data set AID 364, that served as an external test set for AID 463 as it was deposited by the same assay provider and run using the same protocol, was also downloaded and prepared in the same way. After processing the AID 364 data set contained 3247 non-toxic and 48 toxic compounds.

All the screening experiments were carried out at major NIH screening centres but used different cell lines, primarily human cancer cell lines and also two cell lines from rodents (AID 1825 and 1486). The detection method in most assays was a luminescence30 readout but AID 430, 620, and 504648 utilised fluorescence. Also, the concentration and incubation time varied between the assays and they used different cut-offs for outcome assignment. For details regarding a specific assay the reader is referred to the PubChem entry for that AID.

Descriptor calculation

97 different physiochemical descriptors were calculated using RDKit (complete list in the ESI†). Molprint2D fingerprints31,32 were calculated using Canvas applying Mol2 atom types and a maximum path length of two.33,34 In order to limit the memory usage in the random forest (RF) algorithm only bits present in at least 0.1% of the molecules were used.

Model generation

A conformal predictor will make valid predictions according to a user defined confidence level. For a classification problem this is achieved by assigning a set of class labels to new instances (compounds) through comparison to a calibration set with known labels. If the prediction outcome for a new instance (compound) is similar enough (higher than the set cut-off) to the prediction outcomes on the calibration set instances (compounds) with a certain label, the new instance (compound) is assigned that class label. This process is then repeated for each label (class) in the data. Consequently, for a binary classification problem there are four possible outcomes. A new instance can be labelled with either of the two classes or it could be assigned both labels (both classification) or neither one (empty classification). For an illustrative example of how conformal prediction is carried out we refer the reader to ref. 8.

The performance of a conformal predictor is often measured by its validity. A conformal predictor is said to be valid if the frequency of errors does not exceed the set confidence level. Towards this end, a prediction is considered correct if it includes the correct class label, meaning that both predictions are always correct and empty predictions never are (i.e. always erroneous). The trade off in conformal prediction is that between the validity of the model and the efficiency, in other words, between correctness and the number of single class predictions.

We used RF35 as the underlying model in our predictors. RF has been shown to deliver robust results even without case specific calibration.36 However, it is not the primary objective of this study to present the optimal model and settings but rather to introduce the framework of conformal prediction and its usefulness for predictive toxicology.

Models were developed using Python, Scikit-learn37 version 0.17, and the nonconformist package38 version 1.2.5. Binary classification models were built based on RF using the Scikit-learn RandomForestClassifier with 500 trees and all other options set at default. Conformal predictions were performed using the ProbEstClassifierNC and IcpClassifier functions in the nonconformist package with options for class conditional conformal predictions enabled.

Model validation

We applied the aggregated conformal prediction method described by Carlsson et al.39 Each data set was randomly divided in the training (80%) and test set (20%). The training set was then further divided into a proper training set and calibration set using 70% and 30% of the training data, respectively. The size of the calibration set, important for the performance of conformal prediction in terms of validity, was chosen within the recommended range previously investigated and identified for conformal prediction in combination with RF by Linusson et al.40 This whole process was repeated 100 times, each time storing the predictions on the test set. The median predicted probability for each compound was then calculated and used for class assignment in accordance with the set confidence levels.

We also performed further evaluation by randomly selecting 20% of each data set as a fixed external test set, trained 100 models on the remaining training data for each data set (with new random splits for proper training and calibration set at each iteration) and then used these to predict the external test sets. Also, for the model built on the data from AID 463 we applied AID 364 as an external test set.

Results and discussion

Dataset description

Even though many compounds were tested in several assays, most toxic compounds were not toxic in more than one of the assays. This highlights the fact that cytotoxic effects quite often are cell-type specific.41 Structurally the toxic compounds are quite diverse as illustrated by the number of unique Bemis–Murcko scaffolds among them (Table 1). The lowest fraction of unique Bemis–Murcko scaffolds was observed for AID 903 where the ratio of scaffolds to compounds was 0.62.

To further characterize the data we investigated the correlation between the physiochemical descriptors calculated using RDKit and the assay outcome (see the ESI† for top correlated features and correlation coefficients). Although no single feature was strongly correlated (highest Pearson correlation was 0.155) to the outcome MolLogP, MolMR, the number of aromatic rings, and the number of aromatic carbocycles were the most frequently appearing features over all the data sets, being among the top ten correlated features 12, 10, 9 and 9 times respectively. These are features known to often correlate with toxicity.42

Modelling results

For each of the sixteen cell lines one model was constructed. The validities of the models using RDKit descriptors are shown in Table 2. The validity corresponds to the set confidence level both for the toxic and non-toxic class, showing that the conditional conformal predictors are valid for our data sets despite the strong imbalances existing between the two classes.

Table 2. Validity for models built using RDKit descriptors at different confidence levels. It can be seen that the predictions are valid for both the toxic and the non-toxic class.

Conf. level	70		75		80		85		90
AID	Toxic	Non-toxic	Toxic	Non-toxic	Toxic	Non-toxic	Toxic	Non-toxic	Toxic	Non-toxic
463	73.2	71.4	79.3	76.5	83.6	81.6	88.8	86.6	93.2	91.5
1486	71.9	72.6	76.9	77.7	82.0	82.5	87.6	87.2	92.9	91.7
1825	73.0	72.1	78.4	77.2	83.6	82.2	89.1	87.0	93.7	91.6
598	72.1	70.5	76.9	75.4	82.3	80.6	87.0	85.7	91.5	90.4
648	74.2	71.3	78.4	76.3	82.9	81.3	87.4	86.0	92.6	90.8
719	71.8	71.4	78.4	76.5	82.5	81.5	87.7	86.2	92.0	91.0
847	74.7	73.4	83.0	78.2	90.2	82.9	95.9	87.5	99.5	92.0
903	71.9	72.6	75.7	77.4	79.9	82.3	86.4	86.8	93.5	91.2
504648	71.7	77.1	77.5	81.1	83.5	85.8	89.5	89.1	97.2	92.7
588856	72.2	72.3	77.2	77.2	82.1	82.0	88.1	86.7	93.0	91.2
624418	71.8	77.2	78.1	81.9	84.0	86.5	92.9	89.8	98.9	93.2
430	72.4	70.9	77.7	76.1	82.9	81.1	88.3	85.9	92.0	90.8
620	73.9	73.4	79.1	78.1	84.9	82.9	89.0	87.5	94.2	91.9
602141	72.1	73.4	78.3	78.2	83.1	82.5	88.9	87.1	93.9	91.5
2275	68.4	70.9	78.2	76.4	81.9	81.5	87.6	86.4	92.2	91.2
2717	72.3	71.3	77.0	76.3	82.7	81.2	87.3	86.0	91.9	90.7

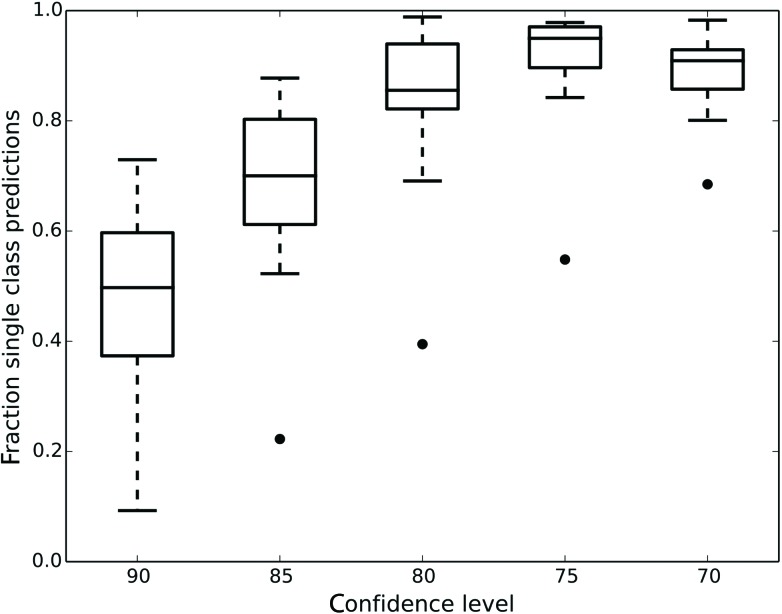
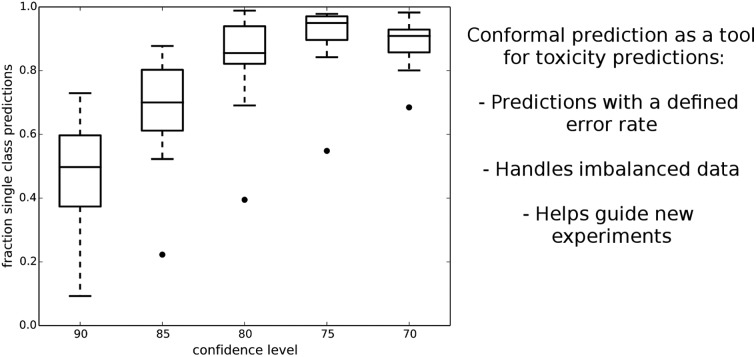
Fig. 1 shows how the number of single class predictions is affected by the confidence level. At higher confidence levels a large portion of compounds are classified in the both class. For example at the 90% confidence level the median number of single class predictions across all data sets is 49.7% with all the other predictions being both. When the confidence level is decreased the number of both predictions also decreases but instead the number of empty class predictions increases. The highest number of single class predictions for our data is therefore observed at the 75% confidence level where the median number of single class predictions is 95%.

Fig. 1. Box plot showing the fraction of single class predictions for all the datasets at five different confidence levels. Whisker extends up to a 1.5 inter quartile range. The number of single class predictions is the highest at the 75% confidence level.

Ultimately, what confidence level has to be used is dependent on the aim of the modelling. For a general model of assay outcome a lower confidence level can give good predictions for most compounds whereas a more confident model might be useful to select cytotoxic molecules with a low number of false positives. Since our aim was to construct predictive models of the assay outcomes further analysis was focused on the lower confidence levels in order to generate single class predictions for the majority of compounds.

The coverage (fraction single class predictions) and the accuracy of these single class predictions at 70 and 80% confidence levels are shown in Table 3. Both the majority and the minority classes are well predicted in our models despite the large imbalance in the ratio of toxic to non-toxic compounds. For the toxic class the average coverage at the 80% confidence level is 87% and the average accuracy for the single predictions 80%. At the same confidence level the non-toxic class is also well predicted with an average coverage of 83% and an average accuracy of 78%.

Table 3. Coverage and accuracy per class at 70 and 80% confidence levels. The accuracy is similar for the toxic and the non-toxic classes.

AID	70%				80%
	Accuracy non-toxic	Coverage non-toxic	Accuracy toxic	Coverage toxic	Accuracy non-toxic	Coverage non-toxic	Accuracy toxic	Coverage toxic
463	71.6	98.3	73.8	97.9	75.6	75.5	79.5	80.3
1486	72.1	97.6	71.5	98.3	74.6	69.0	77.7	80.6
1825	79.7	90.5	78.9	92.5	79.1	85.2	81.6	88.9
598	75.6	93.2	77.0	93.7	77.4	85.8	79.4	85.9
648	83.4	85.5	83.8	88.6	80.1	93.9	82.0	95.2
719	77.0	92.8	77.6	92.5	78.0	84.3	79.9	87.0
847	61.2	68.5	64.7	71.6	56.6	39.4	79.1	46.9
903	84.1	86.3	76.7	93.8	79.7	87.2	78.7	94.4
504648	88.7	86.9	82.9	86.5	84.9	93.9	82.7	94.7
588856	79.2	91.3	77.9	92.7	78.8	85.1	79.9	89.4
624418	84.2	91.7	79.7	90.1	84.1	84.9	81.6	87.0
430	77.2	91.9	78.4	92.4	78.0	86.2	80.5	87.7
620	73.6	97.0	73.9	97.0	76.9	74.0	80.6	77.7
602141	85.6	85.8	84.7	85.2	81.6	95.0	82.4	95.5
2275	88.5	80.1	86.8	78.8	82.0	97.5	81.8	96.9
2717	85.8	83.2	86.8	83.3	81.1	98.8	82.5	98.7

Overall the models showed good performance on the investigated data sets, with a high efficiency and accuracy. However, the models built for AID 847 have clearly worse performance than the models for any of the other data sets with both fewer single class predictions and lower accuracy within these single class predictions. This is surprising since the data set contains largely the same pool of compounds as several other successfully modelled data sets used in this study. The results could be due to high levels of noise in the screening data making confident predictions impossible or failure of the chosen representation of the compounds to capture the effects important to separate the two classes.

Models using Molprint2D fingerprints

In order to investigate the impact of the chosen descriptors on the model performance we also conducted the modelling using Molprint2D fingerprints as compound descriptors (ESI†). The average accuracy at the 70% confidence level was 79% for the non-toxic class and 79% for the toxic class. At the same confidence level the models built using RDKit had an average accuracy of 79% and 78% for the non-toxic and toxic classes respectively. Also at the 80% confidence level the average accuracy is similar to the values of 75% and 83% for the non-toxic and toxic classes using Molprint2D and 78% and 81% for the non-toxic and toxic classes using RDKit. The results are similar with respect to performance which indicates that the models are not sensitive to the choice of the descriptor.

Since the Molprint2D models had a similar performance to the ones built using RDKit descriptors but with a much higher computational cost due to the high number of features we chose to perform additional analyses using only the RDKit descriptors.

Performance on external data

When the models were trained on 80% of the data with the remaining 20% kept as a fixed test set the results in Table 4 were obtained. The average accuracy for the toxic compounds in the test set and the training set, using the same internal validation as described before, were in both cases 80%. The same close correspondence can be seen for the non-toxic class where the average accuracy from internal validation and on the test set in both cases was 78%. These results indicate that the internal validation procedure from the aggregated conformal predictors gives accurate estimates of the performance of the models also for new data.

Table 4. Accuracy of the single class predictions and coverage on randomly assigned test sets as well as from internal validation of the training data at the 80% confidence level. The performance on the training data closely reflects the performance obtained for the test set.

AID	Test data				Training data
	Accuracy non-toxic	Coverage non-toxic	Accuracy toxic	Coverage toxic	Accuracy non-toxic	Coverage non-toxic	Accuracy toxic	Coverage toxic
463	75.1	75.3	86.7	77.2	74.6	72.6	79.2	74.4
1486	74.3	69.3	77.5	80.9	73.4	66.1	77.8	78.5
1825	79.0	85.0	77.6	88.1	78.4	82.3	81.3	86.6
598	77.3	85.9	79.2	87.0	76.9	84.2	78.4	84.8
648	80.3	94.3	81.2	95.7	79.6	92.3	81.8	93.4
719	76.9	84.3	76.5	87.4	77.9	84.1	80.1	84.6
847	59.5	44.7	61.5	41.9	60.9	43.8	74.4	52.8
903	78.6	85.9	77.8	92.6	79.1	85.5	80.8	92.6
504648	84.8	92.9	87.6	90.5	84.3	91.1	82.2	90.5
588856	78.9	86.1	77.6	90.6	78.7	84.5	79.5	88.5
624418	84.4	85.0	86.3	88.0	83.4	80.9	82.0	85.3
430	77.2	87.0	81.9	85.0	77.5	84.2	79.8	85.7
620	76.7	75.2	75.5	79.0	75.6	70.2	78.7	76.2
602141	81.9	95.4	83.3	92.7	81.2	92.8	82.3	93.3
2275	80.9	99.1	85.0	100	81.6	97.2	80.4	96.7
2717	80.9	99.7	79.1	99.2	80.8	98.4	82.2	98.9

For AID 463 we also used the additional assay AID 364 as an external test set. The screening of AID 364 was performed by the same PubChem depositor using the same assay protocol as AID 463 and should thus constitute a suitable method to evaluate model performance. The predictions made on the external set AID 364 and the internal validation of the model built on AID 463 are shown in Table 5. The validity slightly drops for the completely external test set, from 84% to 77% for the toxic class and from 82% to 73% for the non-toxic class. Also the accuracy drops for the external data, for the toxic class from 80% to 74% and for the non-toxic class from 76% to 65%. The coverage on the other hand remained practically unchanged for the non-toxic class but increased for the toxic class from 80% to 88%.

Table 5. Results for AID 463 internal validation and prediction on external test set (AID 364) at the 80% confidence level. The performance drops slightly for the external data compared to the training data.

AID	Validity non-toxic	Validity toxic	Accuracy non-toxic	Coverage non-toxic	Accuracy toxic	Coverage toxic
463 (internal)	81.6	83.6	75.6	75.5	79.5	80.3
364 (external)	73.2	77.1	64.5	75.6	73.8	87.5

On AID 364 we are able to compare model performance to previous models which were also based on data from the Jurkat cell line. Guha and Schürer19 report a model built on PubChem dose response data with a sensitivity of 56% and a specificity of 80%. Langdon et al.21 use PubChem percent inhibition data to develop a model with a sensitivity of 82% and specificity of 35%, and Chang et al.22 report a sensitivity of 41% and a specificity of 77% for predictions on data from AID 364 and AID 464. Although a direct comparison is not possible due to the different methods, descriptors, and data used, the results from previous studies show the difficulties in generating balanced models with similar predictive power for both the toxic and the non-toxic classes, respectively.

The performance of cytotoxicity modelling has to be measured in relation to the noise often present in this kind of data potentially limiting the accuracy of the results.43 A further source of uncertainty in this study is that the compounds are classified to be either toxic or non-toxic by a hard cut-off, usually at around three times the assay standard deviation. However, the potential toxicity of a compound scoring just below the cut-off is not necessarily less than one scoring just above.

Aside from the good predictive performance on these datasets, conformal prediction offers a number of advantages over traditional predictive models. Foremost, and mentioned above, is that the predictions have a guaranteed error rate, allowing for predictions to be made with confidence. Furthermore, the predictions can also serve to guide further experiments. Screening of additional compounds in the both category can increase the separation of the two classes and screening of compounds from the empty category can serve to expand the model. In our study random forest was used as the underlying machine learning algorithm but the conformal prediction framework allows any machine learning technique to be applied as long as it is paired with a suitable conformity function. This allows already validated modelling workflows to be rapidly converted into a conformal prediction framework as well, underlining the versatility of the method presented here.

Conclusions

In this study we report the prediction of compound cytotoxicity against 16 different cell lines. The data were obtained from high throughput screening records deposited in PubChem. Despite a large imbalance between the number of toxic and non-toxic compounds the models built using conformal prediction with random forest were predictive for both classes. The internal validation of the models was also shown to be indicative of the model performance on external data, aiding in the evaluation of the constructed models.

Overall, our results show that conditional conformal prediction can be a useful tool for modelling the outcomes of large scale imbalanced cytotoxicity assays. The conditional conformal prediction framework combines two much desired features for this kind of modelling: the reliability of the results can be chosen to suit the needs of the decision making process, and highly imbalanced data are handled without additional considerations such as over- or undersampling that may cause modelling complications. Conformal prediction can also be used as a valuable guide to what compounds are to be screened next in order to improve the model.

Conflict of interest

There are no conflicts of interest to declare.