Rapid and robust control of single quantum dots

Abstract

The combination of single particle detection and ultrafast laser pulses is an instrumental method to track dynamics at the femtosecond time scale in single molecules, quantum dots and plasmonic nanoparticles. Optimal control of the extremely short-lived coherences of these individual systems has so far remained elusive, yet its successful implementation would enable arbitrary external manipulation of otherwise inaccessible nanoscale dynamics. In ensemble measurements, such control is often achieved by resorting to a closed-loop optimization strategy, where the spectral phase of a broadband laser field is iteratively optimized. This scheme needs long measurement times and strong signals to converge to the optimal solution. This requirement is in conflict with the nature of single emitters whose signals are weak and unstable. Here we demonstrate an effective closed-loop optimization strategy capable of addressing single quantum dots at room temperature, using as feedback observable the two-photon photoluminescence induced by a phase-controlled broadband femtosecond laser. Crucial to the optimization loop is the use of a deterministic and robust-against-noise search algorithm converging to the theoretically predicted solution in a reduced amount of steps, even when operating at the few-photon level. Full optimization of the single dot luminescence is obtained within ~100 trials, with a typical integration time of 100 ms per trial. These times are faster than the typical photobleaching times in single molecules at room temperature. Our results show the suitability of the novel approach to perform closed-loop optimizations on single molecules, thus extending the available experimental toolbox to the active control of nanoscale coherences.

Introduction

Spectroscopy and microscopy at the single molecule level provide the most detailed insight in complex environments, revealing unprecedented detail about molecular structure and dynamics even at ambient conditions^{1, 2, 3, 4}. Indeed, applications of single molecule spectroscopy are numerous, ranging from the determination of molecular interactions in biological systems⁵ to the development of super-resolution microscopy techniques⁶, and the implementation of quantum optics protocols in the solid state⁷. The next step is to facilitate single molecule spectroscopy with ultrafast laser pulses and thus gain access to the intrinsic ultrafast molecular processes such as vibrational motions, excitation energy transfer, charge transfer and electronic dephasing, all of which have femto- to picosecond characteristic times, with the major advantage to overcome the loss of information inherent to conventional ensemble pump-probe measurements⁴.

To capture the ultrafast dynamics in single molecules and nanoparticles, one needs to excite with sophisticated well-tailored pulse sequences, generally referred to as ‘coherent control’. The field of coherent control^{8, 9, 10, 11, 12} has developed two generic approaches in this context, open-loop and closed-loop control. Both strategies are being applied to ensembles of systems, yet the step towards the optimal control of single nanoparticles has remained challenging and is the key point of this paper.

The open-loop approach relies on optimal control theory, in which the ‘best’ laser pulse sequence for inducing a desired response is calculated a priori from the assumed system’s Hamiltonian^{9, 13}. For complex systems like molecules and nano-emitters in dense environment and at room temperature, complete a priori calculations are often very complicated or even impossible. For this reason, in recent works, the coherence properties of single molecules and energy transfer complexes were investigated using simplified and more intuitive electric fields—for example, a sequence of two pulses whose relative phase and time delay could be varied—chosen based on the ensemble absorption spectra^{14, 15, 16}. Even if these simplified fields led to some insight into the coherence of the molecules investigated, they were not optimal for controlling the ultrafast dynamics, especially given that for each single molecule the spectrum does deviate from the ensemble¹⁷.

The closed-loop approach, often the preferred one to control arbitrarily complex systems, consists in resorting to an adaptive closed-loop feedback optimization following the seminal paper by Judson and Rabitz¹⁸. A specific experimental observable (for example, one-photon- or multi-photon-induced fluorescence in molecules or second harmonic (SH) generation in crystals) guides a learning algorithm that varies the spectral phase and time profile of the laser pulses. Closed-loop control schemes were successfully applied to ensembles of different systems^{19, 20, 21, 22, 23}, yet the ultimate target of extending this approach to single molecules has remained challenging. Closed-loop approaches typically need many iterations and strong signals to converge to the optimal solutions⁴. However, these requirements are generally in conflict with the nature of single molecules and nano emitters. As one moves from ensemble measurements to the investigation of single systems, the observable signal reduces to the few photon level with a shot-noise that can be of the order of several percent for ideal single quantum emitters²⁴. To overcome this difficulty, one needs to increase the integration time for every step in the optimization process, which considerably extends the experimental time. On the other hand, photo-induced processes—such as blinking and photobleaching—that molecules and quantum dots (QDs) undergo at room temperature²⁵, together with experimental drifts that become particularly important when measuring on single emitters and nanoparticles, limit the total observation time to few minutes at best.

A recent experiment demonstrated enough sensitivity to attempt a closed-loop control experiment on single molecules in the linear weak-excitation limit²⁶. By using a genetic algorithm, similar to those used in bulk measurements, no optimization could be obtained and the fluorescence signal from the molecules remained unchanged. Learning algorithms that work well for ensembles are, in general, not applicable to the investigation of weak single photon emitters. For a closed-loop algorithm to work for single molecules at room temperature, two requirements need to be fulfilled: (i) the trial phases applied by the algorithm need to produce an effect larger than the intrinsic (shot) noise of the signal; (ii) the optimal solution has to be found in a reduced amount of trials (time) to overcome experimental drift and photobleaching of the molecules.

Here we demonstrate an improved all-optical closed-loop phase-control scheme capable of rapidly optimizing the photoluminescence of a single quantum emitter at room temperature, thus satisfying both the above conditions. The method is demonstrated on single QDs at room temperature using as feedback variable, the two-photon-induced photoluminescence (TPPL). The spectral phases from broadband femtosecond laser pulses are deterministically varied based on a multiple one-dimensional search (MODS)²⁷ that allows rapid global optimization of the observable using reduced amount of trials even at the few photon level. This approach is possible because in the case under study no local minima exist that can hamper the optimization, as explained below. Because the theoretical dependence of the two-photon absorption (TPA) process on the spectral phase of the incident field in these systems is well known^{12, 28}, the experiment allows us to validate the correctness of the found solution.

Materials and methods

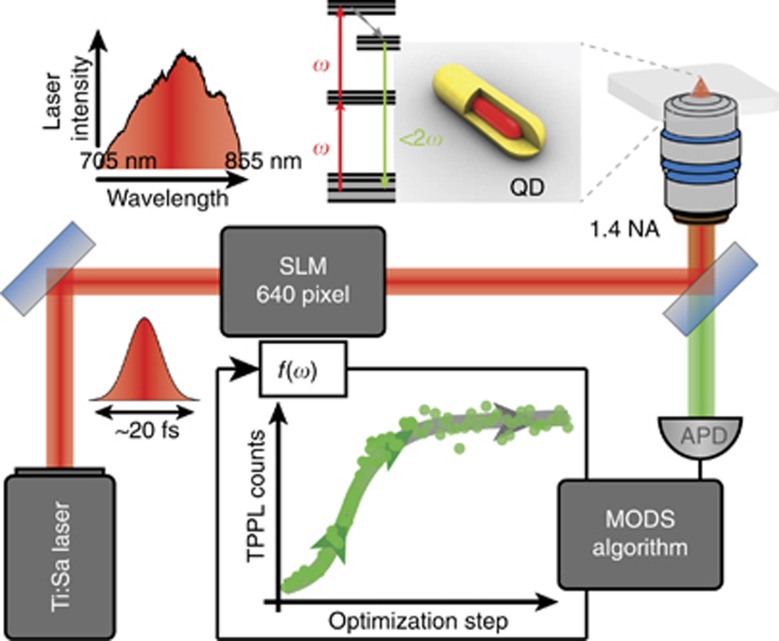
A schematic of the experimental procedure is shown in Figure 1. In short, a 20-fs-laser pulse (central wavelength 800 nm, bandwidth 100 nm) entered a phase-only pulse shaper, arranged in a 4-f configuration, in which a spatial light modulator (SLM) made up of two liquid crystal masks of 640 pixels each (SLM-640 CRi) controlled the spectral phase of the laser pulse. The laser beam was then sent through an oil-immersion microscope objective (1.4 numerical aperture) and focused on the sample plane, inducing TPA in the studied QDs. We used colloidal CdSe/CdS core/shell QDs characterized by a 4.8 × 15 nm CdSe core rod embedded in a CdS shell, yielding an overall QD size of 9.8 nm by 44 nm. They were synthesized according to the procedure described in Ref. 29, dispersed in toluene and finally spin-coated in a PMMA matrix on a 180-μm-thick glass coverslip for microscope imaging. Due to the large volume of the CdS shell, these QDs are known to be efficient two-photon absorbers^{30, 31, 32}. In these systems, the total volume determines the cross-section for TPA and is given mostly by the CdS shell volume, whereas the exciton confinement and thus the emission spectrum can be tuned independently by changing the dimensions of the CdSe core. Our QDs have an absorption spectrum that is dominated by the CdS shell absorption with an onset at 515 nm, and a Stokes-shifted luminescence emission centered at 670 nm.

Figure 1.

Schematic of the experiment. Laser pulses from a broadband femtosecond laser induce two-photon absorption in rod-shaped CdSe/CdS quantum dots, after passing through a phase-only pulse shaper. TPPL signal collected using an oil-immersion objective is spectrally filtered and sent to a single photon avalanche photodiode (APD). For each optimization step, the multiple one-dimensional search optimization algorithm searches for the spectral phase on the spatial light modulator pixels that maximizes the TPPL signal using it as feedback variable.

The resulting TPPL emitted by the QDs was collected through the same objective, detected with an avalanche photodiode in Geiger mode after spectrally filtering the signal and constituted the feedback variable for the MODS algorithm. The algorithm changed the spectral phase on the SLM and searched for the phase mask that maximized the TPPL signal. In this manuscript, we show that it is experimentally feasible to perform such closed-loop TPPL maximization even on individual QDs.

Results and discussion

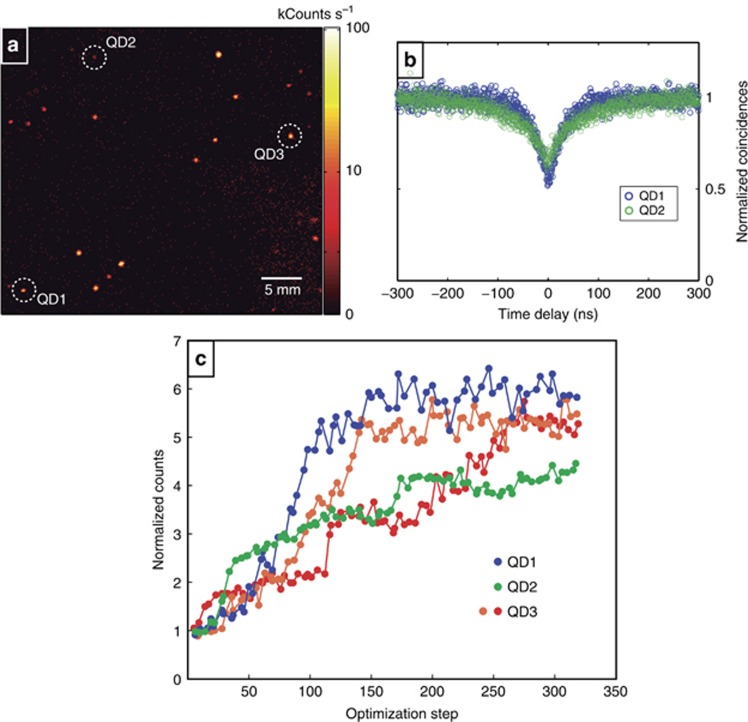
We present the main result of this work in Figure 2, namely the realization of a phase-only closed-loop optimization of the TPPL emitted by single QDs at room temperature. First, we acquired a confocal image by raster scanning the QD sample while recording the TPPL signal (Figure 2a). Due to the low concentration of used QDs, we could spatially resolve isolated bright spots corresponding to single QDs or small clusters of QDs. We further chose QDs presenting low TPPL signal (circled QDs) as candidates for the optimization experiment on single emitters. Photon correlation measurements performed on these QDs confirm that these were non-classical emitters, as can be deduced from the photon anti-bunching dip at time zero in the graph of Figure 2b. For these measurements, we used a helium–neon laser that linearly excited the QDs; we subsequently divided the collected photoluminescence from the QDs with a beam splitter and sent it to two different avalanche photodiodes arranged in a Hanbury-Brown and Twiss intensity interferometer configuration. We note that the second-order photon autocorrelation traces were neither corrected for accidental coincidences arising from detector dark counts nor for the presence of biexcitons in QDs. Thick-shell QDs, like the ones we used, present high bi-exciton photoluminescence quantum yields³³. This has the effect of increasing the normalized coincidences at zero-time delay up to half for high-excitation powers as the ones used in these experiments³⁴. After selecting the suitable QDs behaving as single emitters, the MODS optimization algorithm was used to optimize the TPPL signal on the chosen QDs. We present optimization routines in Figure 2c, showing the TPPL for three different QDs for every step of the optimization algorithm (cf. algorithm description). As different spectral phases were applied by the SLM in a deterministic way, the TPPL signal increased until it reached a maximum value. For all the investigated QDs, the TPPL increased by a factor between 4 and 6.

Figure 2.

(a) TPPL confocal image of the QD sample obtained before closed-loop optimization with 50 μW excitation power. Isolated bright spots, corresponding to TPPL emitted by individual QDs, are clearly resolved. (b) Second order intensity correlation functions corresponding to QD1 and QD2 in a show photon antibunching. The non-classical characteristics of the photon statistics confirm the individual character of QD1 and QD2. (c) Closed-loop optimization of the TPPL signal emitted from the specific single QDs indicated in a. In the case of QD3, we report two different optimization traces to show reproducibility under different conditions.

These optimizations were performed under the following conditions:

• Low-signal conditions. For these QDs, the typical TPPL intensity detected by the avalanche photodiode was in the range 2000–7500 photons per second with an average excitation power of 20–50 μW, which is comparable to the power and signal levels for typical single molecule experiments.¹⁴

• Few total acquisitions. With a total number of only 300 acquisitions, the algorithm was able to find the best solution. In order to have sufficient signal-to-noise ratio, we used typical integration times of 100–800 ms for each acquisition. This means that the full maximization was carried out in about a minute, which is in stark contrast to orthodox optimization strategies based on evolutionary algorithms that typically perform hundreds of generation steps with a pool of hundreds of measurements per generation. Hence, our algorithm typically needs two orders of magnitude fewer measurements to find an optimum.

On the basis of these numbers, closed-loop coherent control experiments even in single molecules at room temperatures become possible. Our optimization scheme is sufficiently robust to handle signals on the few photon level and at the same time sufficiently rapid to beat photobleaching and experimental instability, which take place on a few minutes timescale.

Since the maximization algorithm is crucial to the feasibility of the experiment, we now describe in detail the strength of this strategy. In general, the objective of closed-loop coherent control experiments is to find the optimal set of control variables that maximize the signal of a particular observable of the system under study. In our case, the control variable is the spectral phase of a broadband femtosecond laser pulse, and the observable is the TPPL signal of individual QDs. We remark that we are dealing with QDs that emit a limited number of photons. The intrinsic noise of these systems, roughly the square root of the number of photons, is of the order of 1% of the signal, in addition to the stability of the optical setup (laser and microscope) that, especially when looking at single emitters, can produce signal drifts over time also of the order of a few percent. Hence, the change produced by different sets of control variables on the observables need to be larger than the intrinsic noise in the measurement.

Our femtosecond-laser pulse shaper incorporates a SLM with 640 pixels (control dimension), with 4096 different phase-delay values at each pixel. It is obvious that performing a brute-force global search over such a vast solution landscape is unrealistic due to the long time required to perform such an experiment and the constraints of our particular QD sample.

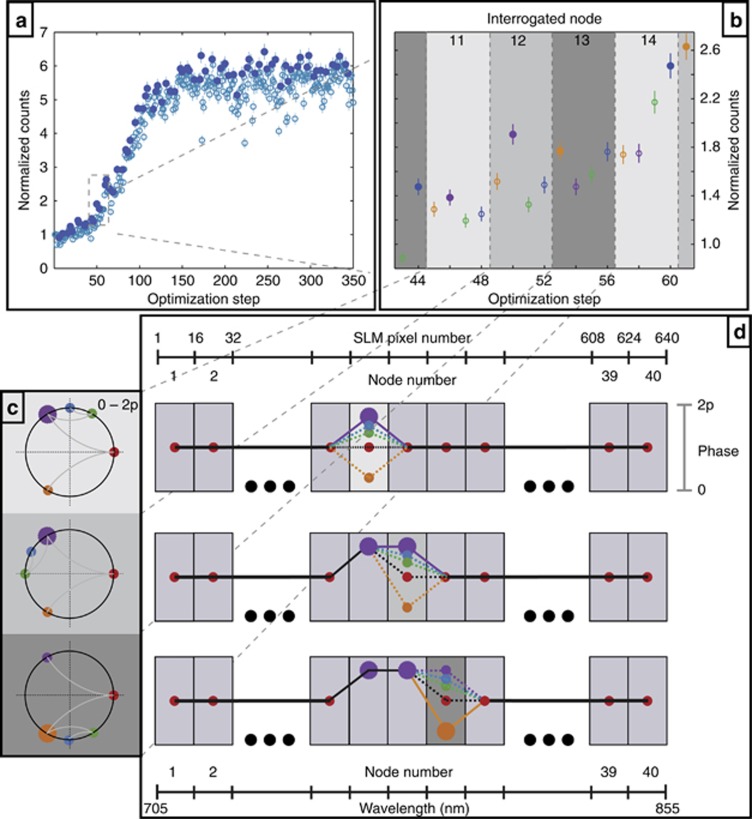
The MODS algorithm, whose working principles are illustrated in Figure 3 (and explained in detail in the figure caption), is based on two general assumptions. (1) The time profile of the laser field can be expressed as a linear superposition of its frequency components, which stems from the property of the Fourier transform; (2) in the majority of the quantum control landscapes there are no local traps, namely no local maxima that differ from the global maximum^{8, 35, 36}. The first assumption allows separating the maximization problem in simpler one-dimensional maximization problems, one for every frequency component. In practice, since different SLM pixels (16 in this case) are grouped together in the experiment to form 40 control nodes, the search for the optimal phase mask is reduced to 40 one-dimensional searches. For each node, the algorithm searches for the phase value in the 0–2π domain (4 different tries are performed in the experiment described) that maximizes the targeted observable (TPPL from single QDs), while keeping the rest of the nodes fixed. Once the optimal phase value for a node has been found, the algorithm fixes its value in the mask and repeats the same procedure in the next node. Because in the case under study, as in many different quantum control problems³⁵, no local traps exist, there is only one real maximum for every node once the previous are set. This is the reason why the optimization progresses in a very efficient way towards the global maximum, even when acting on low-signal levels.

Figure 3.

Schematic of the fast-converging optimization algorithm. (a) Trace of TPPL signal (observable) evolution in a typical deterministic closed-loop optimization run on a single quantum emitter. Full symbols represent optima for each individual interrogated node, with empty symbols representing discarded phase masks. (b) Close up look of the optimization trace. For every node, the phase is changed four times and the phase value producing the highest TPPL signal is kept before moving to the next node. The colors used in the plot correspond to the phases shown in (c). For every node, the algorithm performs a progressive segmentation of the phase space starting with an equally spaced trisection (red, purple and orange points) where the red vertex corresponds to the default phase (zero phase) loaded on the SLM at the start of the optimization. Based on the TPPL signal for the three applied phase masks, the phase interval that produces highest signal is selected and bisected again (green and blue points). This refinement procedure can be iteratively applied at discretion in each node; in practice, we make two refinement measurements at each node, since the intrinsic observable noise prevents us from finding arbitrarily refined solutions. (d) Represents the total phase mask at each run of the optimization algorithm. All the nodes are set to zero (red points) at the beginning. As the algorithm proceeds, the phase of individual nodes is changed separately and interpolation between adjacent nodes is performed to produce a smooth phase mask.

The number of nodes used, as well as the number of different phases applied at each node by the algorithm, which are called phase jumps, is very critical for the success of the optimization and should be carefully chosen as a compromise between two counteracting effects. On one hand, the number of nodes determines the sampling rate of the algorithm or the effective optical resolution at the SLM. A bad optical resolution (low number of nodes used) in turn implies two great limitations in the phase functions that the algorithm can produce¹¹. First, phase functions varying more rapidly than the sampling rate cannot be generated, or, in the time domain, delays longer than the inverse of the optical resolution are beyond the shaper capability. Thus, the number of nodes determines the magnitude of the search space that the algorithm is restricted to. However, for most solid-state quantum systems at room temperature, the coherence time is limited to few tens of femtoseconds at best. Long time delays are therefore, in general, not needed when performing coherent control in these cases. Second, when using a limited amount of nodes, smooth phase functions can only be approximately reproduced. In this case, a bad optical resolution generates jagged phase functions and the effect is amplified when low numbers of phase jumps are used. This limitation implies that the best solution might only be approximated to a certain level of precision. In order to maximally extend the search space and produce smooth phase functions, the number of nodes and phase jumps has to be as high as possible. On the other hand, the frequency band of a node, and the amount of phase variation between consecutive phase jumps, also determine how large the total change in the feedback variable (in this case the TPPL from a QD) will be when varying the phase of that node in the search for the maximum. As discussed above, an important criterion for the optimization success is that the variation of the feedback signal produced by the application of different phases should be larger than the intrinsic noise of the system. Too large amount of nodes, that is, a too small frequency band associated to every node, or too many phase jumps would result in only small variations of the feedback signal, which might hamper the optimization. As shown below (see also Supplementary Information), in the case of the current experiment, a good compromise between the two effects could be found. By using 40 nodes and four phase jumps, we ensured at the same time that the TPPL signal could be quickly optimized, and that the MODS algorithm could find the best solution to a good approximation (with 80% precision, as demonstrated below).

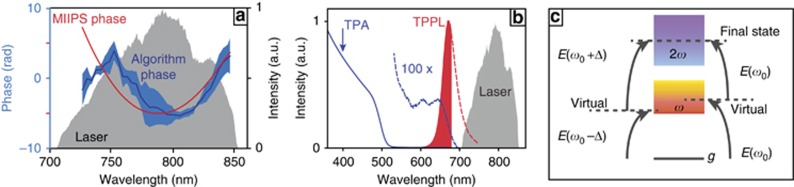
In order to prove the correctness of the optimization experiment presented here, we need to demonstrate that the solution found by the MODS algorithm is indeed close enough to the real optimum for the QDs studied. The algorithm starts with an initial phase mask on the SLM and produces a final phase mask that optimizes the TPA. Looking at the difference between initial and final phase masks, we can compare the results of this experiment with theoretical predictions. The phase difference, in the case of the experiments illustrated in Figure 2c, is plotted as a blue curve (called the Algorithm Phase) in Figure 4a and has a well-defined shape.

Figure 4.

(a) Laser spectrum (shaded grey curve), initial spectral phase measured with MIIPS (red curve) and the inverse phase mask obtained with the closed-loop optimization on QDs (blue curve). The light blue shaded region represents the uncertainty on the determination of the phase mask, corresponding to the standard deviation calculated repeating the maximization process several times. (b) Laser spectrum (shaded grey curve), absorption (blue solid curve) and TPPL (red curve) spectrum of the QDs. The red-colored region is the portion of the TPPL we detected in the experiment using a 680 nm short pass filter to block the laser. The blue-dashed curve is the magnified (100 × ) absorption spectrum in the 700 nm range. The blue arrow at 400 nm indicates the spectral region where the TPA takes place. (c) Sketch of two possible sum frequency processes, for electric fields E(ω₀−Δ)+E(ω₀+Δ) or E(ω₀)+E(ω₀), leading to the same final state. Here ω₀ is the central frequency of the laser and E(ω₀±Δ) represents a frequency component within the laser bandwidth. The total TPA is maximal when all the possible pathways constructively interfere.

To understand this phase, we separately measured the initial spectral phase of the laser pulse with the multiphoton intrapulse interference phase scan (MIIPS)³⁷ on a SH crystal, plotted as a red curve in Figure 4a. This curve represents the spectral phase of the laser pulse when the starting phase mask on the SLM was applied. As discussed in literature³⁷, a non-flat spectral phase, as the red curve of Figure 4a, corresponds to a distorted pulse, which is not the shortest possible for a given laser spectrum, that is, it is not a transform-limited (TL) pulse. The similarity between the red and the blue curves implies that the optimization process can be thought of as an attempt to produce TL pulses at the position of the QDs. This is confirmed by pulse autocorrelation measurements corresponding to nearly TL pulses (Supplementary Information). The same experiment was repeated with different starting phase masks and the maximization process always ended up close to the TL optimization point (see Supplementary Information).

In order to understand the outcome of the experiment, in Figure 4b, we report the absorption spectrum of the QDs studied, which is dominated by the CdS, having an onset around 515 nm and increasing for smaller wavelengths. As the graph shows, there is no overlap between the laser spectrum and the tail of the QDs absorption, meaning that the fundamental laser cannot induce any single photon transition in the QDs and only pure two-photon transitions around 400 nm (in the region of the SH spectrum of the laser) are possible. Moreover, at the SH wavelength, the absorption spectrum of the QDs is very broad, and no discrete state is expected to be resolved at room temperature even in a single QD. In other words, the QDs absorb all the wavelengths within the SH spectrum of the laser with a similar efficiency. As can be theoretically demonstrated^{11, 38}, in these conditions, namely for very broad absorbers at the SH wavelength with no real intermediate state, the TL pulse is the unique solution that maximizes the TPA. By choosing these QDs, we therefore can verify that the algorithm converges to the theoretically predicted solution, which demonstrates the correctness of our closed-loop experiment.

As shown in Figure 4c, this optimization experiment may be seen as the simplest example of coherent control, based on the interference of the different possible sum frequency processes (pathways) leading to the same final state^{8, 12}. Non-resonant two-photon transitions for a broadband field involve many routes through a continuum of virtual levels, where the interference pattern excited by the multiple-frequency components can enhance or diminish the total transition probability. Since the interference effect depends on the spectral phase distribution of the laser field, controlling the spectral phase gives access to the control of the two-photon transition probability⁸.

We want to address now the limitations of the current approach, both in terms of the search space and the precision of the found solution. The applicability of this scheme to real coherent control experiments on the nanoscale depends on how severe these limitations are.

As discussed above, the magnitude of the search space is limited by the optical resolution. In this case, for a laser bandwidth of ~100 nm, centered around 800 nm, dividing the spectrum on 40 nodes corresponds to an effective time window for the algorithm to operate of ~200 fs. The initial pulse, namely the pulse that corresponds to the MIIPS phase of Figure 4a, is about 100 fs long (see simulations in Supplementary Information), therefore well within the search space of the algorithm, which is why the optimization can converge to a solution close to the real optimum (the TL pulse). In many cases of interest, for instance for molecules¹⁴, light-harvesting complexes¹⁶, QDs³⁹ and plasmonic nanoparticles^{40, 41} at room temperature, the coherence time was measured to be shorter than 100 fs. The current implementation of the MODS algorithm would therefore lead to a large enough search space to make coherent control of single molecules and nanoparticles at room temperature possible, in all the problems for which conditions (1) and (2) for the applicability of the approach are satisfied.

As shown in Figure 4a, the Algorithm Phase does not perfectly coincide with the MIIPS phase. In order to address the precision of the found solution, we also measured the increase in the SH signal obtained after the MODS optimization and compared it with what the MIIPS algorithm obtains (see Supplementary Information). The increase in the SH signal obtained with the current implementation of the MODS algorithm was always about the 80% of what the MIIPS method could obtain. In other words, the best solution could be found very rapidly, with an 80% precision when maximizing on a single QD. Considering that MIIPS is a dedicated method for compressing pulses and takes advantage of the good theoretical knowledge of nonlinear optical processes, whereas the MODS algorithm does not need any preknowledge and can optimize on arbitrary signals, we believe that this is a very remarkable demonstration of closed loop optimization on single-quantum emitters that almost reaches the best solution. Furthermore, the MODS algorithm does not need any spectral information to work, as opposed to the MIIPS algorithm that needs the complete SH spectrum. Refining the solution with successive iterations, using higher number of nodes and phase jumps would lead to a better optimum, but would also require longer measurement times, which might become incompatible with the nature of single quantum emitters.

Conclusions

With the current experiment, we pushed closed-loop optimization techniques to the limit of single-quantum emitter sensitivity, demonstrating maximization of the TPPL emitted by single QDs at room temperature. At the same time, our strategy satisfied all the conditions required to achieve closed-loop coherent control of single molecules at room temperature: the signal levels were as low as the ones found in single molecule experiments; the TPPL optimization was performed in <4 min (faster than typical photobleaching times), made possible by a speed up of about two orders of magnitude over widely used traditional evolutionary strategies; the algorithm succeeded in finding a solution that well reproduced the theoretical expectation.

The fact that, in our experiment, the best solution for the targeted problem is the TL pulse, used here to validate our approach, is a consequence of the physics of the QDs studied and does not limit the general applicability of the method. Applied to different problems with different underlying physics, our optimization strategy would maximize the targeted observable by inducing constructive interference between the pathways connecting to the desired final state. Optimizations in systems, characterized by non-trivial responses within the laser bandwidth would in general lead to optimal solutions that differ from the TL pulse. We speculate that our method can be applied to the study and control of plasmonic fields in complex nanostructures⁴²; the steering of coherences in individual molecular systems with specific laser fields^{16, 26}, allowing time-resolved quantum state tomography of molecular systems⁴³; and the selective excitation of different absorptive species with high spatial resolution^{39, 40, 41, 42, 43, 44}.