Skip to main content
PMC home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2017 Feb 10;6(2):e16204. doi: 10.1038/lsa.2016.204

Effects of edge on graphene plasmons as revealed by infrared nanoimaging

Qingyang Xu 1, Teng Ma 2, Mohammad Danesh 3, Bannur Nanjunda Shivananju 1, Sheng Gan 1, Jingchao Song 4, Cheng-Wei Qiu 3, Hui-Ming Cheng 2, Wencai Ren 2,*, Qiaoliang Bao 1,4,*
PMCID: PMC6062181  PMID: 30167226

Abstract

We used scattering-type scanning near-field optical microscopy (s-SNOM) to investigate the plasmonic properties of edges in well-defined graphene nanostructures, including sharp tapers, nanoribbons and nanogaps, which were all fabricated via the growth-etching chemical vapor deposition (GECVD) method. The obtained near-field images revealed the localized plasmon modes along the graphene nanoribbon; these modes strongly depended on the size of the graphene pattern, the angle of the tapered graphene and the infrared excitation wavelength. These interesting plasmon modes were verified by numerical simulations and explained by the reflection, and interference of electromagnetic waves at the graphene–SiO2 edge. The constructive interference at the graphene nanogap caused by charge accumulation was demonstrated for the first time. Using the infrared nanoimaging technique, greater plasmon broadening was observed in the zigzag edge than in the armchair edge. Our study suggests that graphene edges should be separated by an effective working distance to avoid the overlapping of localized plasmon modes, which is very important for the design of graphene-based plasmonic circuits and devices.

Keywords: edge chirality, graphene, graphene plasmon, nanoribbon, nanogap, near-field microscopy, s-SNOM

Introduction

Graphene, an attractive, atomically thin carbon material, has been demonstrated to possess excellent electrical, optical, mechanical, magnetic and thermal properties, and has many exciting applications1, 2, 3. Surface plasmons in graphene are electromagnetic waves that propagate along the surface of the graphene as a result of the infrared light-induced oscillation of surface charges. Because of its low plasmon damping, remarkable tunability and high quantum efficiency for light–matter interactions, graphene has intriguing potential applications in a new area of two-dimensional (2D) plasmonics4, 5, 6, 7, 8. Graphene plasmons can efficiently enhance optical absorption, which can be tuned by changing the micro/nanopattern size or the in situ electrostatic doping, thus enabling applications in graphene-based terahertz metamaterials9, tunable far-infrared notch filters10, strongly enhanced light–matter interactions for quantum devices11, modulation, light harvesting, spectroscopy and biosensing12.

Intrinsic plasmons can be observed using various direct and indirect methods. Infrared transmission spectroscopy of graphene micro-ribbon arrays indicated that infrared light polarized in a direction perpendicular to the graphene nanoribbon axis is able to excite plasmon resonance caused by bounded electron oscillation9. Because of a lack of mid-infrared light excitation and high spatial resolution, graphene plasmons could be launched and detected in real space only using high-spatial-resolution scattering-type scanning near-field optical microscopy (s-SNOM). Infrared nanoimaging experiments revealed that graphene plasmons are strongly reflected at graphene edges5, 6, grain boundaries13 and nanometer-sized steps in monolayer graphene formed on SiC substrates14. The interference patterns at the graphene grain boundaries were imaged by recording the interference between tip-launched and reflected plasmons13. The extracted plasmon wavelength is ~200 nm at the relevant incident infrared frequency for the common graphene/SiO2/Si structure; this plasmon wavelength and the plasmon interactions can be tuned via electrical gating5, 6. Theoretically, graphene-based nanoribbon-like waveguides and Y-shaped waveguides can be constructed by precisely designing the non-uniform conductivity pattern and applying different gate voltages at different locations across the structure15. Recently, the usage of resonant antennae and spatial conductivity patterns has opened up exciting avenues for the design of nanoscale graphene photonic circuits and devices by launching and controlling the propagating graphene plasmons16.

Notably, the surface plasmons in graphene nanostructures behave distinctly because of the finite-size effect17. The real-space observation of surface plasmons in graphene nanoribbons and nanogaps, and the investigation of edge effects are fundamentally important to further understand the finite-size effect, but have not yet been demonstrated. Infrared imaging of these nanostructures could conclusively unveil the plasmonic phenomena in confined 2D systems, thereby facilitating the fabrication of miniaturized 2D plasmonic devices. However, real-space imaging of the plasmonic modes in nanoscaled graphene remains challenging because of the lack of a mature fabrication technique able to produce fresh edges of patterned graphene nanostructures with precise control over the shape and quality. Moreover, conventional lithography cannot deliver patterned graphene nanostructures with well-defined edges.

In this study, we adapted a growth-etching method in a chemical vapor deposition (GECVD) process18 to produce patterned nanoribbon and nanogap structures with well-defined edges in graphene films and single crystals (Supplementary Information). Using infrared nanoimaging technology, we captured optical amplitude images of the graphene nanoribbon and nanogap for the first time. The special localized plasmon modes at the graphene nanoribbon were clearly shown to strongly depend on the width of the nanoribbon, the apex angle and the wavelength of the incident light. We also observed interference enhancement in the graphene nanogap and attributed this effect to the small gap size, which enables accumulation of carriers at the gap19. Moreover, we experimentally investigated the effect of graphene edge chirality on plasmonic reflection and interference, verifying the theoretically predicted chirality-dependent photon–plasmon interactions17. The obtained results may pave the way for the development of active sub-wavelength optics and a plethora of nano-optoelectronic devices and functionalities, such as graphene-based waveguides, quantum information devices, optical signal processing and ultra-sensitive sensing applications.

Materials and methods

Characterization

We characterized the GECVD-grown graphene using an optical microscope (Nikon LV100D, Nikon Company, Tokyo, Japan), Raman (JY HR800, Horiba Jobin Yvon Company, Villeneuve d' Ascq, France) and a field emission scanning electron microscope (SEM; FEI Quanta 200, Field Electron and Ion Co., Hillsboro, OR, USA).

Plasmon nanoimaging

A commercial s-SNOM (Neaspec Company, Munich, Germany; www.neaspec.com) equipped with mid-infrared quantum cascade lasers (Daylight Solutions Company, San Diego, California, USA; www.Daylightsolutions.com) and a CO2 laser (Access Laser Company, Everett, WA, USA; www.accesslaser.com) with wavelengths of 4, 7 and 10.6–11.3 μm was used to launch and detect propagating and localized graphene plasmons. Infrared nanoimaging was based on an atomic force microscopy (AFM) operated in tapping mode, with a tapping frequency Ω of ~270 KHz and a tapping amplitude Δz=40 nm.

In a near-field nanoimaging experiment, the AFM tip scans a sample surface and simultaneously acts as an optical antenna. The infrared laser beam is focused onto the AFM tip using a parabolic mirror. The sharp metal tip can concentrate the incident optical field at its apex to a small spot with a diameter of only a few tens of nanometers. When a flat sample is located near the tip, the highly confined field at the apex interacts with the sample, and because of the near-field interaction between the tip and the sample, the tip-scattered light contains information regarding the local optical properties of the sample surface. The backscattered light and the topography are recorded simultaneously via pseudo-heterodyne detection, yielding nanoscale-resolution infrared near-field images.

Results and discussion

Plasmon modes in a sharp graphene taper

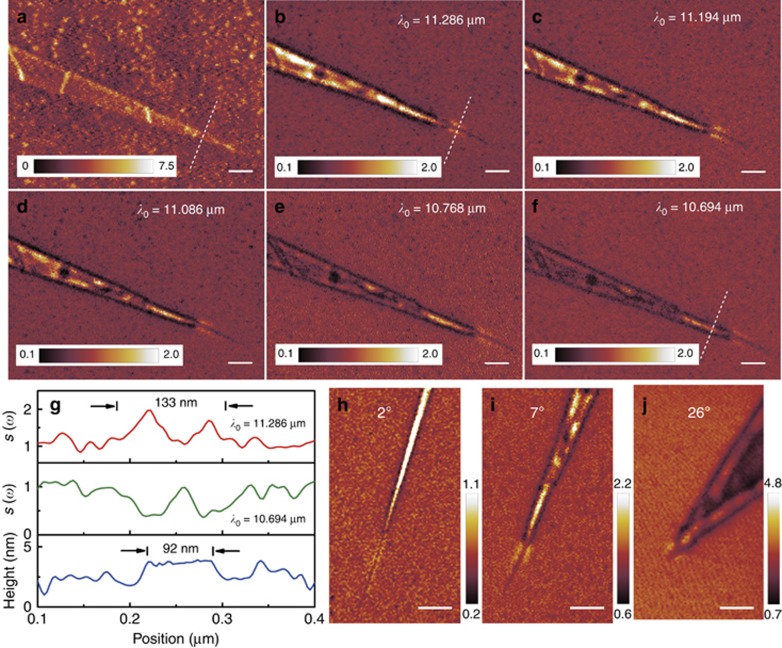
In conventional noble metal-based plasmonics, the tapered waveguide structure has been suggested to be one of the most efficient approaches to achieving light focusing20, 21. In this study, we first fabricated a sharp graphene taper (with an apex angle of ~7o) and then investigated the notably tight confinement of electromagnetic energy in the graphene plasmonic waveguide. We produced large-area graphene films on a Pt substrate with conversional CVD growth conditions in the presence of methane and hydrogen. After we cut off the methane flow rate, with the other parameters remaining constant during the CVD process, the graphene films switched from growth to etching, forming several hexagonal holes randomly distributed over the entire graphene plane. As the reaction time increases, the holes expand and encounter neighboring holes to generate the tapered structure. The AFM topography (Figure 1a) confirms that the width of the tapered graphene gradually decreases from ~280 to ~50 nm at the end. To probe the plasmonic properties, we used a CO2 laser (wavelength range from 10.694 to 11.286 μm) to illuminate the AFM tip of a commercial s-SNOM. Figure 1b–1f shows near-field images of a tapered graphene nanocrystal with a size smaller than the plasmon wavelength λp (~200 nm, see Supplementary Information). The optical amplitude images clearly reveal two distinct localized modes that coexist with a resonant enhancement of the near-field signal comparable to previous reports5, 6. In this study, we focus special attention on the light confinement in such a sharp tapered single-crystal graphene sample. The light confinement, which can be defined as λ0/w, becomes stronger as the excitation wavelength λ0 decreases, as evidenced by the shorter and narrower hotspot at the apex of the nanocrystal (Figure 1f). The observed highest confinement (λ0/w) is 218 for λ0=10.694 μm, which is 1.45 times stronger than that of previous reports6 because of the high quality of our single-crystal graphene domains and the much sharper tip of the graphene taper.

Figure 1.

Figure 1

Open in a new tab

Visualization of localized modes at different excitation wavelengths and apex angles. (a) AFM topography images of tapered graphene with a sharp apex angle of ~7o. (b–f) Near-field optical images, taken simultaneously with the AFM topography in a, at imaging wavelengths (λ0) of 11.286 μm (b), 11.194 μm (c), 11.086 μm (d), 10.768 μm (e) and 10.694 μm (f). Scale bar=200 nm. (g) Line profile obtained along the white dashed line in b, f and a (from top to bottom), normalized to the optical amplitude of the SiO2 substrate and illustrating that the localized modes move toward the tip of the graphene taper as the excitation wavelength decreases. (h–j) Near-field optical images of tapered graphene, with angles of 2º, 7º and 26º, respectively. The imaging wavelength is λ0=11.086 μm. Scale bar=300 nm.

Moreover, if the graphene ribbon is narrow enough, the lowest-order mode6 manifests as a pair of bright spots near the sharp tip. The separation of the lowest-order mode (133 nm) is larger than the width of the graphene taper at that location (92 nm) for λ0=11.286 μm, as depicted in Figure 1b and 1g. This phenomenon can be understood by considering the bright edge as a localized light source that can illuminate the surrounding area. Corresponding to the amplitude images at the same location for λ0=10.694 μm, a resonance mode can be found inside the taper (Figure 1f and 1g). Thus, the localized modes strongly depend on the width (w) and the excitation wavelength (λ0) and move toward the tip of the graphene ribbon as the excitation wavelength decreases. Similar to a fixed excitation wavelength, the incident light is confined inside the taper if the width is sufficiently large, revealing a dark edge mode. In contrast, the lowest-order mode is observed if the taper is quite sharp.

Another interesting phenomenon is that the plasmon localization in the tapered graphene strongly depends on the vertex angle (θ) of the tapered structure, as shown in Figure 1h–1j. It is observed that additional light is confined along the length of graphene nanoribbons with smaller angles (2o in Figure 1h) compared with those with larger angles (26o in Figure 1j), as evidenced by an elongated hotspot or localized mode. Moreover, the localized mode inside the ribbon shifts away from the tip of the tapered graphene as the vertex angle decreases. This tendency is accompanied by a relatively enhanced optical amplitude in terms of brightness and localized area because of the occurrence of multiple plasmon reflections between the graphene edge and the AFM tip.

Plasmon modes in a narrow graphene nanoribbon

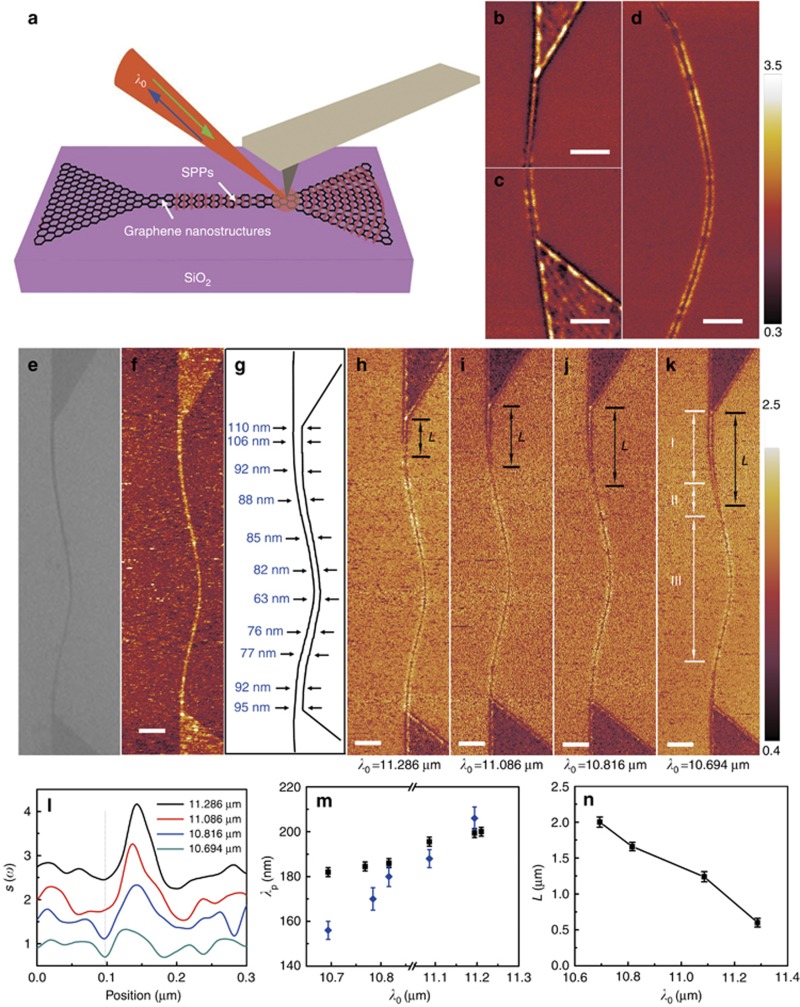
Figure 2a shows a schematic diagram of the infrared nanoimaging experiment. The AFM tip is scanned over a graphene nanoribbon on the SiO2 substrate, which is prepared via the GECVD method. The width of the nanoribbon depends on the etching time (Supplementary Information). The metallic tip is illuminated by broadband (10.694–11.286 μm) infrared light to produce a focused optical field at its apex, which further interacts with the plasmon modes inside the graphene nanoribbon22 and results in surface propagating waves. Consequently, these plasmonic standing waves interact with the AFM tip and affect the total scattered field collected by the measurement system23. Two tapered graphene sheets and a connecting graphene nanoribbon are clearly visible in the SEM image and AFM topography (Figure 2e and 2f). The width of the graphene nanoribbon changes gradually from ~110 nm at one end to the smallest value of ~63 nm at the center and eventually to ~95 nm at the other end.

Figure 2.

Figure 2

Open in a new tab

Scanning plasmon interferometry of a graphene nanoribbon. (a) Diagram of an infrared nanoimaging experiment for a graphene nanoribbon on SiO2. The AFM tip is illuminated by an incident infrared light (green arrow) and launches surface plasmon waves (red circles) into the graphene nanostructure. The near-field optical images are collected by detecting the backscattered light (blue arrow). (b–d) Infrared amplitude images of three components of the graphene nanoribbon: top (b), bottom (c) and middle (d) at an infrared wavelength of λ0=11.086 μm. (e, f) SEM image and AFM topography of tapered graphene and connecting nanoribbon. (g) Sketch of the geometry width along the nanoribbon, imaged by SEM (e) and AFM (f). (h–k) Near-field amplitude images of tapered graphene and connecting nanoribbon at infrared wavelengths of λ0=11.286 μm (h), 11.086 μm (i), 10.816 μm (j) and 10.694 μm (k). L indicates the length of the edge plasmon mode confined inside the graphene nanoribbon. I, II and III indicate three different plasmon interaction behaviors. Scale bar=500 nm. (l) Maximum O3 optical amplitude of the bright spot in b, as a function of λ0 normalized to the optical amplitude of the substrate SiO2. (m) Theoretically (black) and experimentally (blue) extracted graphene plasmon wavelength as a function of λ0. (n) Length of light confined inside the nanoribbon at different incident wavelengths λ0. The brightest point at the apex of the graphene ribbon is chosen as a reference point.

The corresponding near-field optical images are shown in Figure 2b–2d and 2h–2k. A bright spot can be observed at the end of each graphene taper where the taper connects with the graphene nanoribbon. At this particular position, the plasmonic surface waves excited from the center of the taper and those reflected back from the edges are completely in phase and thus produce a peak or hotspot in the standing wave function. Similar to the effect shown in Figure 1, graphene tapers with smaller vertex angles produce stronger plasmon confinements, as evidenced by the brighter hotspot shown in Figure 2b (taper vertex angle: 31o) and the relatively weak hotspot shown in Figure 2c (taper vertex angle: 43o). In particular, a rich variety of bright and dark features can be observed along the whole graphene nanoribbon. The interference pattern, manifesting as numerous black dots along the edge of the wide nanoribbon (Figure 2b), can be assigned as the edge mode of graphene plasmon24. It is also interesting to observe a chain of black dots in between bright fringes along the narrow region (Figure 2c and 2d), which can be considered as the waveguiding mode25.

Figure 2h–2k shows the wavelength-dependent optical field images in the graphene nanoribbon, in which three different behaviors of the plasmon interaction were observed. First, in the wider region (I), the plasmonic waves reflected from the edges constructively interact with each other to produce an edge mode, with line-shape confinement at the center of the nanoribbon. Second, as the nanoribbon becomes narrower, the constructive interference shifts toward destructive interference, leading to a dark region (II) within the nanoribbon. Finally, as the width becomes even narrower, localized plasmon resonance occurs and produces the waveguide mode along the nanoribbon in region (III). The data shown in Figure 2h–2k possess a weaker contrast, which is attributed to the limited number of data points while scanning over a large area. Note that the localized edge modes decay quite rapidly because of interactions with surface polar phonons in SiO2 at such small dimensions4. Unlike the upper region of the nanoribbon, the waveguide mode is always dominant in the bottom region, where the nanoribbon width is slightly smaller than that of the upper region, as revealed by the zoomed-in scanning image in Figure 2b and 2c. This observation is in good agreement with a recent discovery that the waveguide mode exists in the graphene nanoribbon, with widths w<λp/225. The plasmon properties of such a nanostructure at shorter excitation wavelengths were also investigated. The optical amplitudes at both tapers are similar to those at longer wavelengths for λ0=7.26 μm (Supplementary Fig. S3a). Moreover, the waveguide-like mode also occurs in the nanoribbon and high contrast can be observed between the graphene and the substrate. In contrast, a lack of graphene plasmons and weak contrast are observed for λ0=4.67 μm (Supplementary Fig. S3b) (see Supplementary Information for detail).

Interestingly, the length (L) of the second-order sheet mode confined inside the graphene nanoribbon becomes longer as the excitation wavelength decreases. This observation is attributed to the balance between the plasmon wavelength in graphene and the width of the graphene nanoribbon, which confines the light to a small volume. More specifically, the plasmonic properties of graphene are related to the effective dielectric function of the environment, κ(ω)=[1+εsub(ω)]/2, and its optical conductivity8, 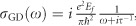Inline graphic, where ω is the infrared excitation wavelength and τ−1 is the charge-scattering rate in graphene. We obtain the equation for the plasmon wavelength, λp=2π/Re(qp), from the plasmon dispersion of graphene at the interface between the air and the SiO2 substrate5, 13, qp=(i2ωε0κ(ω)/σ(ω)). According to these formulas, the amplitude of the hotspot and the period of the plasmon in the graphene nanoribbon strongly depend on the excitation wavelength, as shown in Figure 2l and 2m. Shorter excitation wavelengths lead to smaller plasmon periods, in turn leading to longer second-order sheet modes in the upper wide region of the graphene nanoribbon, as revealed in Figure 2h–2k and 2n.

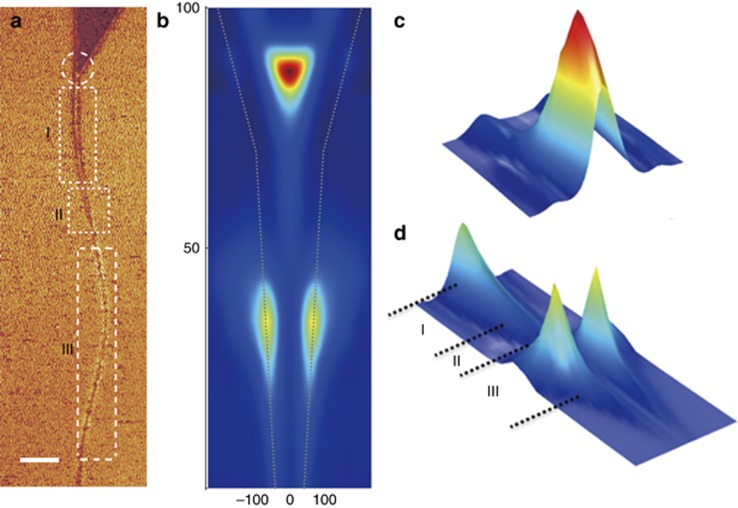
To better understand the plasmons in the graphene nanoribbon, numerical modeling was performed, considering all the experimental parameters (see Supplementary Information for details), as shown in Figure 3. It was assumed that the width of the graphene taper changes from 200 to 100 nm and that of the graphene nanoribbon changes from 100 to 10 nm. The simulation results also reveal a bright spot at the end of the taper and three regions with distinct plasmonic near fields in the nanoribbon section, which are consistent with the experimental observations depicted in Figure 3a. Region I displays high intensity at the center because of constructive interference of the reflected wave, which produces a peak in the standing wave pattern at the center point. Region II is a transition zone, where the reflected waves from both edges interfere with each other and form a prolonged higher-order sheet mode25. Localized plasmon resonances manifesting as bright edge modes appear along the ribbon in region III and could be considered an elongated analog of the lowest-order modes, similar to those observed in tapered graphene5, 6. In summary, two main resonance modes can be excited in the graphene nanoribbon, that is, the edge mode appearing at the center of the wide ribbon because of constructive interference and the waveguide mode observed in the narrow ribbon. The appearance of these modes strongly depends on the excitation wavelength.

Figure 3.

Figure 3

Open in a new tab

Theoretical simulations. (a) Infrared experimental amplitude of tapered graphene and connecting nanoribbon at an infrared wavelength of λ0=10.694 μm, revealing the bright spot (dashed circle) and three localized modes I, II and III (dashed rectangle). Scale bar=300 nm. (b–d) Numerical results of the plasmonic near fields on a graphene nanoribbon changing from 10 to 100 nm. Regions I, II and III exhibit three different localized mechanisms at the graphene ribbon and the numerical simulation of a taper changing from 100 to 200 nm. (c) confirms that the experimental results are in accordance with the theoretical simulation.

Plasmons in a graphene nanogap

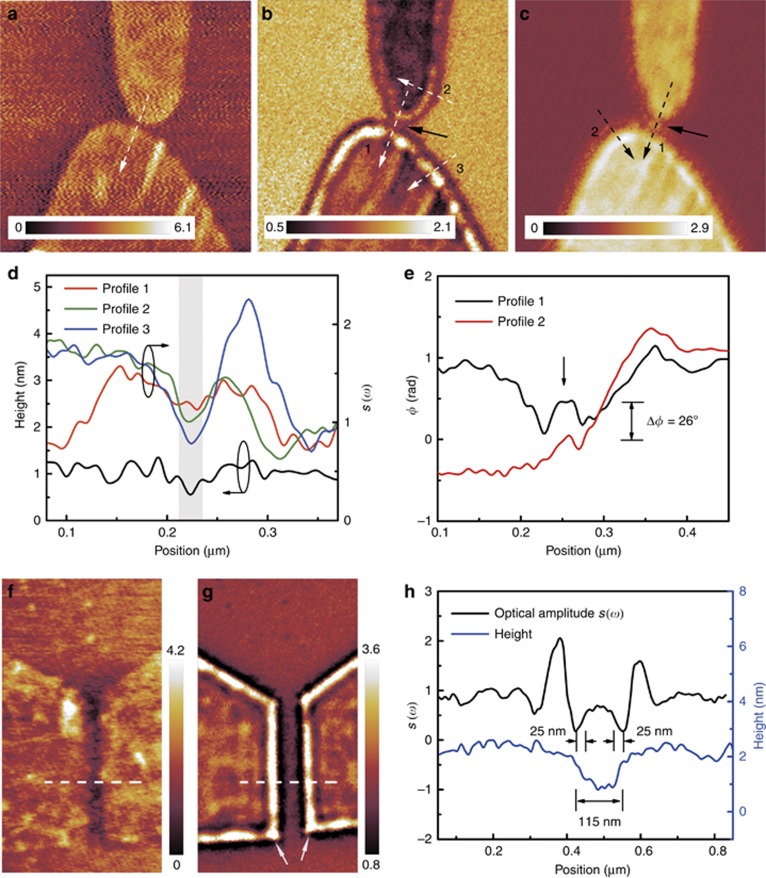
The interference of the graphene plasmon wave is known to cause a bright fringe pattern in near-field optical images. The bright fringe near the edge is usually accompanied by two black fringes on both sides; the dark fringe near the substrate is much darker than that in graphene, as observed in previous reports6, 24, 25, 26, which corresponds to destructive interference and thus yields a negative near-field contrast. One interesting question pertains to what would occur if two edges were placed so close that the dark fringes overlapped with each other. Experimentally, we prepared two graphene tapers separated by a small gap of ~25 nm and performed s-SNOM measurements, as shown in Figure 4a–4e. The scattering amplitude s(ω) along the white dashed lines is plotted in Figure 4d. We found that the amplitude inside the gap exhibits strong increases of ~15 and 50% compared with the amplitude across the edge (see traces 2 and 3 in Figure 4d). We attribute this effect to the interaction of graphene plasmons at the edge, which enables charge accumulation in the gap19. The phase image (Figure 4c), taken at an infrared wavelength of 11.086 μm, further verifies the enhancement in the near-field amplitude image26 and reveals a larger phase gradient of ~26º (Figure 4e).

Figure 4.

Figure 4

Open in a new tab

Scanning plasmon interferometry of the graphene nanogap. (a) AFM topography of the graphene nanogap, with a geometric slot of ~25 nm. The height profile along the dashed line is plotted in d (the arrow means the direction of plotting). (b, c) Infrared amplitude image and phase image taken simultaneously with the AFM topography shown in a, with an illuminating wavelength of λ0=11.086 μm. Scan size=1.5 μm × 1.5 μm. (d, e) Line profiles obtained along the white and black dashed lines in b and c, revealing amplitude enhancement and phase jump in the gap, as indicated by the black arrows in b and c. (f) AFM topography of the graphene nanogap, with a geometric slot of ~115 nm. (g) Near-field optical image taken at an infrared wavelength of λ0=11.086 μm. The arrows mark the positions of plasmon localization modes that appear at two corners of the graphene flakes. (h) Line profiles obtained along the white dashed lines in f and g. No plasmon interaction is observed in such large gaps. Scan size=1 μm × 2 μm.

To further investigate how the separation of the graphene nanogap affects the plasmon interactions, we observed a graphene nanogap with a separation of ~115 nm, as depicted by the AFM topography in Figure 4f. The scanning plasmon interferometry image, taken at an infrared wavelength of 11.086 μm, is shown in Figure 4g. Two black fringes parallel to each bright fringe can be observed at the edge: one in graphene and the other near the substrate. More interestingly, the black dots were observed at the bottom corners of graphene flakes, which is possibly due to the interference of edge plasmons25.

Comparing the optical amplitude with the AFM topography, we confirm that the outer black fringes, which originate from the dark mode of the edge plasmon in graphene, lie partially on the substrate. We further plot the scattering amplitude s(ω) along the white dashed line in Figure 4h; the scattering signal shows that the period of the fringe pattern is ~100 nm (λp/2) for our high-quality graphene. The black fringe expands to the substrate with a width of ~25 nm (~λp/8). No plasmon interaction was observed in such a large gap, but interactions were noted in the small 25 nm gap (Figure 4a–4c). Therefore, we conclude that the amplitude and phase enhancement inside the small gap result from the constructive interference of the graphene plasmon mode at the edge when the gap width is sufficiently small (that is, ~λp/8).

Effect of edge chirality on graphene plasmons

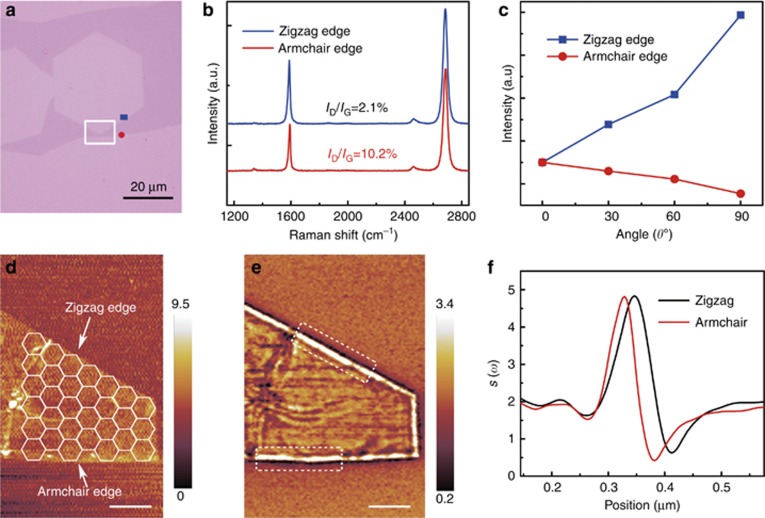
The edge chirality of graphene is critically significant for various fundamental properties, such as magnetic properties27, 28, optical properties29, phonons30, 31, 32 and superconductive33 properties. Similarly, because of the different edge terminations, the edge chirality also imprints certain signatures in the plasmonic near field. Quantum mechanical simulations have suggested that zigzag edges with a small ribbon width can produce additional plasmon broadening17, 34. To acquire different types of edges, hexagonal single-crystal graphene domains were first synthesized and subsequently etched in a pure hydrogen atmosphere18. Because of the structural defects generated during the nucleation stage, hexagonal holes appear at the center of the domain and quickly expand, resulting in different crystallographic orientations between the inner and outer edges. The edge structure of the graphene domains was identified via Raman spectroscopy through combined analyses of both the D and G peaks18, 30, 31. During the D peak measurements, the polarization of the incident laser was tuned parallel to the edge orientation to avoid the effect of laser polarization on the D peak intensity32. For the G peak measurements, the polarization of the incident laser was tuned by rotating a half-wave plate, and the angle of the laser polarization relative to the edge orientation was defined as θ. Figure 5a shows the optical image of a graphene domain with a hexagonal hole in its center, which was etched in pure hydrogen for 2 min after growth under a gas flow of 500 standard-state cubic centimetre per minute (sccm) of hydrogen and 4.5 sccm of methane for 30 min at 1000 °C. The Raman spectra and polarized G peak spectra shown in Figure 5b and 5c were collected from the edges, denoted by the blue squares and red dots in Figure 5a, respectively. The outer edge exhibits a notably high ID/IG, and its G peak intensity decreases with θ, which indicates that the outer edge has an armchair direction. The inner edge shows a low ID/IG and opposite G peak polarization dependence on θ, suggesting that the edge is zigzag type.

Figure 5.

Figure 5

Open in a new tab

Effect of edge chirality on graphene plasmon. (a) Optical image, scale bar=20 μm. (b) Typical Raman spectra measured at the zigzag edge and armchair edge (inner and outer edges). (c) Polarization dependence of the G peaks of the zigzag edge and armchair edge indicated by blue square and red circle in a. (d) AFM topography of a graphene ribbon with controlled edges (indicated by white arrows). (e) Near-field optical amplitude, obtained simultaneously with the AFM topography shown in d, at an infrared wavelength of λ0=11.086 μm. Scale bar=500 nm. (f) Experimental s(ω) line profiles obtained by averaging 20 such profiles in the region (white dashed rectangles in e) at edges with different chirality (zigzag or armchair), revealing a broader plasmon at the zigzag edge.

We excited and visualized the graphene plasmons at the zigzag edge and armchair edge using the high-resolution scattering-SNOM system. Figure 5d shows the AFM topography of etched graphene with known edge chirality; Figure 5e shows the corresponding near-field optical image. The bright mode at the top zigzag edge is broader than that at the armchair edge. Nevertheless, it is found that the right edge is not as broad as the top edge. We speculate that the right edge may not have perfect zigzag arrangement, as it was formed by a mechanical tear during the transfer process. To quantitatively compare the plasmons at the edges, 20 amplitude profiles were plotted across each edge (white rectangles) and averaged to produce a single profile, as shown in Figure 5f. The plasmon wavelength is λp=149 nm at the zigzag edge and λp=117 nm at the armchair edge. Clearly, the width of the zigzag edge plasmon is larger than that of the armchair edge plasmon, possibly because of the different carrier densities at the two edges, which support different surface states35. In particular, it has been theoretically proposed that localized states are supported by zigzag ribbons, resulting in extra plasmon broadening compared with that of an armchair ribbon with a similar width18, 36. Considering that the size of the graphene edge described here is much larger than the quantum finite size17, 34, the AFM tip of the s-SNOM system excites the propagation of the confined electronic states near the Dirac points rather than the finite width for the zigzag edges.

Conclusions

In conclusion, we have developed a GECVD method to synthesize sharp graphene tapers, nanoribbons, nanogaps and different types of edges, and investigated their effects on graphene plasmons using an infrared nanoimaging technique. The scanning plasmon interferometry technique reveals that the plasmonic effects strongly depend on the geometry, the size of the graphene nanostructure, the vertex angle of the tapered graphene and the excitation wavelength. Moreover, we probed the effect of edge chirality on the graphene plasmon and found that zigzag edges produce greater plasmon broadening than armchair edges. The main findings could provide important guidance for the design and fabrication of miniaturized nanophotonic devices, such as graphene plasmon waveguides and plasmonic circuits.

Author contributions

QX and TM contributed equally to this work. The manuscript was written based on all authors’ contributions. All authors have approved the final version of the manuscript.

Acknowledgments

We acknowledge support from the National Key Research & Development Program (2015CB932700 and 2016YFA0201902), the National Natural Science Foundation of China (grant No. 51290273, 91433107, 51325205 and 51521091), the Doctoral Fund of the Ministry of Education of China (grant No. 20123201120026), ARC (DP140101501 and FT150100450), the Collaborative Innovation Center of Suzhou Nano Science & Technology, the Priority Academic Program Development of Jiangsu Higher Education Institutions, A*STAR Pharos Programme (grant No. 152 70 00014, with Project No. R-263-000-B91-305), and Competitive Research Program (CRP Award No. NRF-CRP15-2015-03) by the National Research Foundation, Prime Minister’s Office, Singapore. This work was performed in part at the Melbourne Centre for Nanofabrication in the Victorian Node of the Australian National Fabrication Facility.

Footnotes

Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website(http://www.nature.com/lsa).

The authors declare no conflict of interest.

Supplementary Material

Supplementary Information
Click here for additional data file. (8.6MB, doc)

References

  1. Geim AK, Novoselov KS. The rise of graphene. Nat Mater 2007; 6: 183–191. [DOI] [PubMed] [Google Scholar]
  2. Geim AK. Graphene: status and prospects. Science 2009; 324: 1530–1534. [DOI] [PubMed] [Google Scholar]
  3. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y et al. Electric field effect in atomically thin carbon films. Science 2004; 306: 666–669. [DOI] [PubMed] [Google Scholar]
  4. Yan HG, Low T, Zhu WJ, Wu YQ, Freitag M et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat Photon 2013; 7: 394–399. [Google Scholar]
  5. Fei Z, Rodin AS, Andreev GO, Bao W, McLeod AS et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 2012; 487: 82–85. [DOI] [PubMed] [Google Scholar]
  6. Chen JN, Badioli M, Alonso-González P, Thongrattanasiri S, Huth F et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012; 487: 77–81. [DOI] [PubMed] [Google Scholar]
  7. Woessner A, Lundeberg MB, Gao YD, Principi A, Alonso-González P et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat Mater 2014; 14: 421–425. [DOI] [PubMed] [Google Scholar]
  8. Jablan M, Buljan H, Soljačić M. Plasmonics in graphene at infrared frequencies. Phys Rev B 2009; 80: 245435. [Google Scholar]
  9. Ju L, Geng BS, Horng J, Girit C, Martin M et al. Graphene plasmonics for tunable terahertz metamaterials. Nat Nanotechnol 2011; 6: 630–634. [DOI] [PubMed] [Google Scholar]
  10. Yan HG, Li XS, Chandra B, Tulevski G, Wu YQ et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat Nanotechnol 2012; 7: 330–334. [DOI] [PubMed] [Google Scholar]
  11. Koppens FH, Chang DE, García de Abajo FJ. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett 2011; 11: 3370–3377. [DOI] [PubMed] [Google Scholar]
  12. Grigorenko AN, Polini M, Novoselov KS. Graphene plasmonics. Nat Photon 2012; 6: 749–758. [Google Scholar]
  13. Fei Z, Rodin AS, Gannett W, Dai S, Regan W et al. Electronic and plasmonic phenomena at graphene grain boundaries. Nat Nanotechnol 2013; 8: 821–825. [DOI] [PubMed] [Google Scholar]
  14. Chen JN, Nesterov ML, Nikitin AY, Thongrattanasiri S, Alonso-Gonz´lez P et al. Strong plasmon reflection at nanometer-size gaps in monolayer graphene on SiC. Nano Lett 2013; 13: 6210–6215. [DOI] [PubMed] [Google Scholar]
  15. Vakil A, Engheta N. Transformation optics using graphene. Science 2011; 332: 1291–1294. [DOI] [PubMed] [Google Scholar]
  16. Alonso-González P, Nikitin AY, Golmar F, Centeno A, Pesquera A et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 2014; 344: 1369–1373. [DOI] [PubMed] [Google Scholar]
  17. Thongrattanasiri S, Manjavacas A, Garcıa de Abajo FJ. Quantum finite-size effects in graphene plasmons. ACS Nano 2012; 6: 1766–1775. [DOI] [PubMed] [Google Scholar]
  18. Ma T, Ren WC, Zhang XY, Liu ZB, Gao Y et al. Edge-controlled growth and kinetics of single-crystal graphene domains by chemical vapor deposition. Proc Natl Acad Sci USA 2013; 110: 20386–20391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Schnell M, García-Etxarri A, Huber AJ, Crozier K, Aizpurua J et al. Controlling the near-field oscillations of loaded plasmonic nanoantennas. Nat Photon 2009; 3: 287–291. [Google Scholar]
  20. Krenn JR, Lamprecht B, Ditlbacher H, Schider G, Salerno M et al. Non–diffraction-limited light transport by gold nanowires. Europhys Lett (EPL) 2002; 60: 663–669. [Google Scholar]
  21. Stockman MI. Nanofocusing of optical energy in tapered plasmonic waveguides. Phys Rev Lett 2004; 93: 137404. [DOI] [PubMed] [Google Scholar]
  22. Hillenbrand R, Taubner T, Keilmann F. Phonon-enhanced light–matter interaction at the nanometre scale. Nature 2002; 418: 159–162. [DOI] [PubMed] [Google Scholar]
  23. Cvitkovic A, Ocelic N, Hillenbrand R. Analytical model for quantitative prediction of material contrasts in scattering-type near-field optical microscopy. Opt Express 2007; 15: 8550–8565. [DOI] [PubMed] [Google Scholar]
  24. Fei Z, Goldflam MD, Wu JS, Dai S, Wagner M et al. Edge and surface plasmons in graphene nanoribbons. Nano Lett 2015; 15: 8271–8276. [DOI] [PubMed] [Google Scholar]
  25. Nikitin AY, Alonso-González P, Vélez S, Mastel S, Centeno A et al. Real-space mapping of tailored sheet and edge plasmons in graphene nanoresonators. Nat Photon 2016; 10: 239–243. [Google Scholar]
  26. Gerber JA, Berweger S, O’Callahan BT, Raschke MB. Phase-resolved surface plasmon interferometry of graphene. Phys Rev Lett 2014; 113: 055502. [DOI] [PubMed] [Google Scholar]
  27. Son YW, Cohen ML, Louie SG. Half-metallic graphene nanoribbons. Nature 2006; 444: 347–349. [DOI] [PubMed] [Google Scholar]
  28. Yazyev OV, Katsnelson MI. Magnetic correlations at graphene edges: basis for novel spintronics devices. Phys Rev Lett 2008; 100: 047209. [DOI] [PubMed] [Google Scholar]
  29. Yang L, Cohen ML, Louie SG. Excitonic effects in the optical spectra of graphene nanoribbons. Nano Lett 2007; 7: 3112–3115. [DOI] [PubMed] [Google Scholar]
  30. You YM, Ni ZH, Yu T, Shen ZX. Edge chirality determination of graphene by Raman spectroscopy. Appl Phys Lett 2008; 93: 163112. [Google Scholar]
  31. Cong CX, Yu T, Wang HM. Raman study on the g mode of graphene for determination of edge orientation. ACS Nano 2010; 4: 3175–3180. [DOI] [PubMed] [Google Scholar]
  32. Casiraghi C, Hartschuh A, Qian H, Piscanec S, Georgi C et al. Raman spectroscopy of graphene edges. Nano Lett 2009; 9: 1433–1441. [DOI] [PubMed] [Google Scholar]
  33. Moghaddam AG, Zareyan M. Graphene-based superconducting quantum point contacts. Appl Phys A 2007; 89: 579–585. [Google Scholar]
  34. García de Abajo FJ. Graphene plasmonics: challenges and opportunities. ACS Photon 2014; 1: 135–152. [Google Scholar]
  35. Brey L, Fertig H. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys Rev B 2006; 73: 235411. [Google Scholar]
  36. Christensen T, Wang W, Jauho AP, Wubs M, Mortensen NA. Classical and quantum plasmonics in graphene nanodisks: role of edge states. Phys Rev B 2014; 90: 241414(R). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (8.6MB, doc)

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES