Skip to main content
PMC home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2017 Jul 28;6(7):e17017. doi: 10.1038/lsa.2017.17

Fano-resonance-assisted metasurface for color routing

Chen Yan 1,✝, Kuang-Yu Yang 1,✝, Olivier J F Martin 1,*
PMCID: PMC6062224  PMID: 30167273

Abstract

Controlling the phase of an electromagnetic field using plasmonic nanostructures provides a versatile way to manipulate light at the nanoscale. Broadband phase modulation has been demonstrated using inhomogeneous metasurfaces with different geometries; however, for many applications such as filtering, hyperspectral imaging and color holography, narrowband frequecy selectivity is a key functionality. In this work, we demonstrate, both theoretically and experimentally, a narrowband metasurface that relies on Fano resonances to control the propagation of light. By geometrically tuning the sub-radiant modes with respect to a fixed super-radiant resonance, we can create a phase modulation along the surface within a narrow spectral range. The resulting anomalous reflection measured for such a Fano-resonant metasurface exhibits a 100 nm bandwidth and a color routing efficiency of up to 81% at a central wavelength of λ=750 nm. The design flexibility provided by this Fano-assisted metasurface for color-selective light manipulation is further illustrated by demonstrating a highly directional color-routing effect between two channels, at λ=532 and 660 nm, without any crosstalk.

Keywords: color filtering, Fourier imaging, metasurfaces, plasmonic Fano resonance, wavefront manipulation

Introduction

The ability to manipulate and change the course of light when it reaches a surface has expanded markedly since the first description of refraction in the 17th century and the demonstration of the first known gratings in the 19th century1, up through modern subwavelength dielectrics2, 3, 4 and plasmonic nanostructures5, 6, 7, 8, 9. Recently, two-dimensional metamaterials—so-called metasurfaces—have received increasing attention owing to their outstanding and unusual properties regarding the manipulation of light at an interface6, 10, 11, 12, 13. The versatile control provided by metasurfaces over the momentum of light at an interface, which is determined by their spatial phase discontinuity, has enabled the development of various flat devices, such as optical elements6, 14, 15, 16, 17, 18, surface plasmon couplers11, 19, holograms20, 21, 22, 23, cloaks24 and analog computing circuits25. In such efforts, dispersionless broadband phase control by means of the rotation of plasmonic nanostructures is an important effect that can be achieved under circular polarization conditions14, 26, since the phase of cross-polarized light depends solely on the orientation of the antennas, not on their spectral response14, 26. Another class of devices utilizes anisotropic plasmonic constituents with various geometries6, 11, 23, 27, 28, 29, in which metal losses at optical frequencies and inhomogeneous broadening automatically produce a broadband response. Generally, in these previous works, the angular response, which is determined by the generalized laws of refraction6, has been spectrally homogeneous. There are, however, several important practical applications that require a much higher level of control over the emission angle as a function of the operating frequency band: multi-junction solar cells, integrated spectroscopy and optical multiplexing30, 31, 32, 33, 34. To unleash the full versatility of metasurfaces for achieving arbitrary control over light in terms of both spectrum and momentum, it is necessary to engineer optical modes that contribute to the phase modulation produced by the surface.

In terms of wavelength selectivity, it has emerged over the last few years that optical sub-radiant resonances—with strongly suppressed radiation losses—can overcome the broad spectral response of lossy plasmonic materials. These sub-radiant modes couple only weakly to free space through their coherent interaction with a broader super-radiant mode, thereby producing unique, narrow spectral features known as plasmonic Fano resonances35, 36, 37, 38. Compared with conventional plasmonic nanostructures, Fano-resonant systems show a strongly increased sensitivity to geometric changes and perturbations to the local environment and can be used as plasmonic nano-rulers39, 40 or biochemical sensors41, 42, 43, 44. Furthermore, because Fano resonances arise from the interference between a sub-radiant and a super-radiant mode, equivalent to a bound state in the continuum45, they are intrinsically well suited for altering the far-field properties of light in narrow regions to enable wavelength filtering46, imaging47 and spectrally dependent scattering48.

In this work, we combine spectrum engineering with light manipulation in a phase-gradient metasurface constructed from Fano-resonant nanostructures to demonstrate a color-routing device with a spectrally narrow operation band. The required phase modulation is achieved by carefully detuning the resonance frequency of the sub-radiant mode from a fixed super-radiant mode, thereby modifying, in a controlled manner, the phase of the light scattered from the metasurface. With this approach, we first experimentally demonstrate a phase-gradient metasurface with an active band for wavelengths between λ=700 and 800 nm. To further reveal the benefits of both spatial and spectral beam steering, we demonstrate a dual-color (with maxima at λ=532 and 660 nm) routing metasurface with high directionality and 60 nm operation bandwidths for both channels. We further discuss the underlying limits on the tuning efficiency and the design principles for the band-pass regimes to enhance the freedom of light manipulation provided by such a metasurface.

Materials and methods

Nanofabrication

A float glass substrate was first prepared by depositing a 200 nm-thick Ag backplane followed by a 30 nm-thick SiO2 spacer within a single thermal evaporation run at a rate of 4 Å s−1 to ensure a uniform thin film surface. Silver Fano-resonant nanostructures were then fabricated on top of the SiO2 spacer using a previously introduced method49. In brief, a double-layer PMMA photoresist coating was exposed via electron beam lithography (Vistec EBPG5000 system, Germany) using a 100 keV and 200 pA electron beam. The nanostructures were obtained through the thermal evaporation of a 1 nm silver oxide adhesion layer and 39 nm of Ag followed by a lift-off process. The fabricated metasurface arrays cover an area of 40 × 40 μm2.

Fourier imaging setup

A Fourier imaging setup for spectral-angular measurements was assembled using an inverted microscope (Olympus IX73, Japan, Supplementary Fig. S7). A supercontinuum light source (Fianium FemtoPower 1060, UK) combined with an 8-channel acousto-optical tunable filter was used to focus light of the desired wavelength on the back focal plane of the oil immersion objective (Olympus × 60 OTIRFM, numerical aperture=1.45). This produced a collimated plane wave for the excitation of the sample. A two-axis translation stage was placed before the input port of the microscope to move the focal point off the optical axis to enable tuning of the incidence angle. The reflected light was collected by the same objective and a Fourier lens placed at the output to probe the wavevector information. An iris was placed in the intermediate image plane to select the reflection from a specific area on the sample. Finally, Fourier images were captured using a three-layer color sensor camera (Foveon X3, USA). All signals from the camera were calibrated using a power meter. The measured intensity was normalized with respect to the light reflected from a bare 200 nm-thick silver mirror.

Surface integral equation simulation method

All simulations were performed using a custom-developed numerical program based on the surface integral equation (SIE) for two-dimensional periodic nanostructures50. The complete supercell was used as the unit cell for the calculations and was repeated with Bloch periodic boundary conditions. The complete supercell was considered, including the silver metallic backplane, and the surfaces of the structures were discretized with a typical mesh size of 10 nm. A finite array (20 periods) was considered to match the simulation results with the measured angular divergence of the reflection peaks.

Results and discussion

The reflection from an interface can be described using the generalized Snell’s law6: 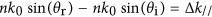Inline graphic, where θi and θr are the angles of the incident and reflected rays, n is the refraction index of the background medium above the surface, k0 is the wavevector in vacuum, and 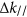Inline graphic is the additional in-plane wavevector provided by the interface, which depends on how the interface is structured:

graphic file with name lsa201717e3.jpg
graphic file with name lsa201717e4.jpg
graphic file with name lsa201717e5.jpg

For a conventional grating, the additional momentum is 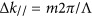Inline graphic, where m is an integer and 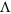Inline graphic is the grating period1; thus, the incoming light is reflected at multiple orders, both positive and negative, as shown in Figure 1a. For a broadband dispersionless gradient metasurface (Figure 1d), which is composed of dipole antennas with varying orientations14, the entirety of the incoming light is bent into a single channel, with additional momentum determined by the wavelength-independent phase gradient 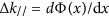Inline graphic along the interface (Equation (1b)). Here we introduce a frequency-selective metasurface, for which the additional momentum depends on the illumination wavelength, such that only specific colors are affected by the metasurface (Figure 1g).

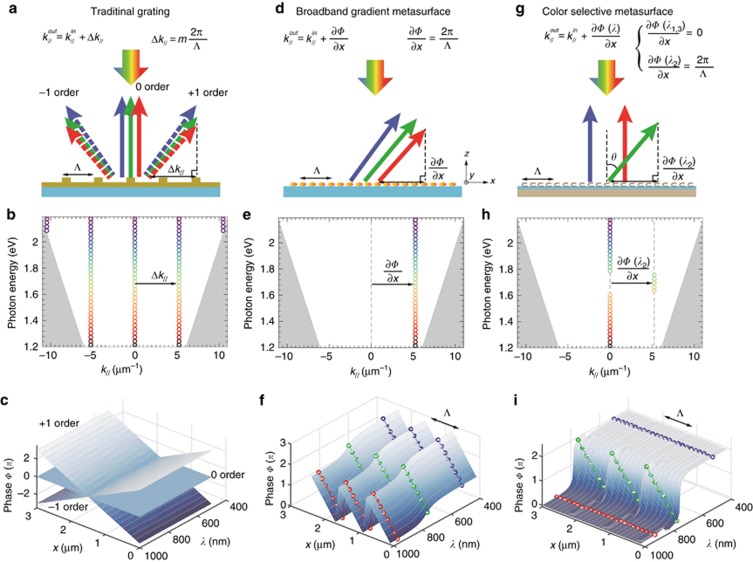
Figure 1.

Figure 1

Open in a new tab

Comparison between a traditional grating, a broadband metasurface and a color-selective metasurface. (a) For a traditional grating, light is diffracted at various orders, as given by the grating equation. (b) In the diffraction diagram, integer multiples of the momentum Δk are added to the incoming light, regardless of its frequency. (c) Phase map along the interface for diffraction orders of –1, 0, and 1. (d) A broadband metasurface induces anomalous reflections over a large spectral range; (e) its diffraction diagram consists of a single channel. (f) Phase map induced by a gradient antenna array with an orientation axis that is independent of frequency. (g–i) A metasurface that selectively induces a gradient phase at a certain wavelength; as shown by h, its diffraction diagram and (i) its phase map, only light with the wavelength indicated by green dots accrues a growing phase along the interface.

To compare the responses of these three different systems, it is insightful to consider the corresponding dispersion diagrams for the reflected waves in the momentum-energy plane. In the case of a grating, the different diffraction orders correspond to the addition or subtraction of integer multiples of the momentum 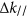Inline graphic (Figure 1b). For a broadband-gradient metasurface, where all light is bent into a single channel, all incoming light receives a fixed additional momentum regardless of its wavelength (Figure 1e). For the color-selective metasurface introduced here, only the incoming light within a narrow spectral range is bent into a specific channel; compare Figure 1e and 1h.

Another perspective to consider is the phases introduced by these different surfaces along their interfaces. For a grating, each diffraction order corresponds to a specific constant phase gradient along the interface, which manifests as a plane in the phase map (Figure 1c). For a broadband-gradient surface, the phase increases linearly along the interface, regardless of the spectral response of the antennas (Figure 1f). Note that in this figure, the phase has been wrapped between 0 and 2π to emphasize that the phase variation is generated by an array of nanostructures with different orientations that are repeated with a specific period 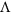Inline graphic (Ref. 14). We note in Figure 1f that incoming rays with different wavelengths, marked with red (λ1), green (λ2) and blue (λ3) circles, will all accrue the same phase along the interface. For a color-selective metasurface, however, the phase must be different for different wavelengths, as illustrated in Figure 1i. In the illustrated case, only a wave of wavelength λ2 accrues an increasing phase along the interface (green dots), whereas waves with other wavelengths do not accrue any phase (red and blue dots in Figure 1i). Consequently, the metasurface bends light to an arbitrary angle determined by the in-plane wavevector 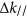Inline graphic only at the designed wavelength λ2.

Fano-resonant plasmonic metasurface

As illustrated in Figure 2a, we use dolmen nanostructures that support Fano resonances to implement our color-selective metasurface. The Fano lineshape associated with such a dolmen structure arises from the interaction between a sub-radiant quadrupolar mode supported by the two parallel nanorods and a super-radiant dipolar mode supported by the central nanorod35, 51. The narrowband phase gradient metasurface presented here is composed of an array of Ag dolmen structures located on top of an Ag metallic backplane with a 30 nm SiO2 spacer (ε=2.25). Figure 2b illustrates the detailed geometry of the supercell, which consists of four dolmens constructed from nanorods with widths and thicknesses of w=40 nm. The central nanorod, with a fixed length of 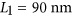Inline graphic, supports the dipolar mode and acts as an antenna for receiving and emitting light from/to the far field; it determines the operation frequency of the color-selective metasurface. By adjusting the length of the two parallel nanorods, it is possible to manipulate the spectral position of the Fano resonance, thereby controlling the phase gradient along the interface generated by the metasurface at its operation wavelength of 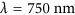Inline graphic. We choose to discretize the full 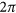Inline graphic phase range into four levels along the x direction, corresponding to the relative phases 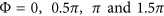Inline graphic. This is achieved by choosing the following lengths for the two parallel nanorods: L2=60, 85, 100 and 125 nm (Figure 2b).

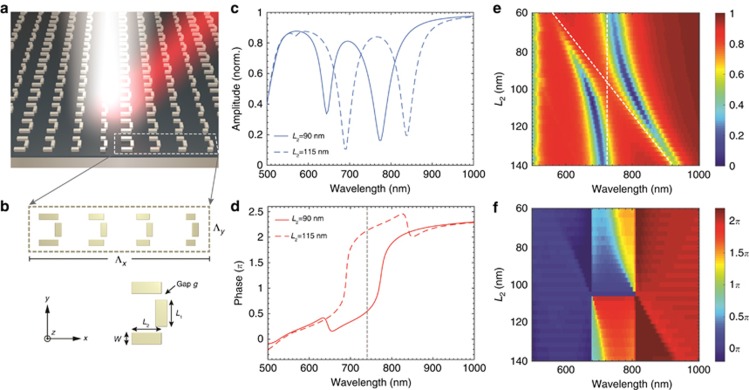
Figure 2.

Figure 2

Open in a new tab

Design principle of a narrowband metasurface. (a) Three-dimensional schematic view of a metasurface based on dolmen structures on a metal backplane. The nanostructures are made of silver, with a 30 nm-thick SiO2 spacer. (b) Top view of the optimized supercell, with periods of 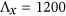Inline graphic nm and 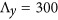Inline graphic nm. The length 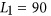Inline graphicnm of the central nanorod along the y direction is fixed, whereas the length of the pair of parallel nanorods along the x direction is 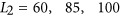Inline graphic or 125 nm; the width and thickness are 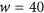Inline graphic nm for all structures. (c, d) Calculated (c) amplitude and (d) phase spectra of the fields reflected from two periodic arrays with parallel nanorod pairs of different lengths: 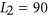Inline graphic and 115 nm. (e, f) The amplitude and relative phase maps as a function of both wavelength and length L2. The phase is expressed as the relative phase shift with respect to that in the case of L2=105 nm.

The operation principle of the system is illustrated in Figure 2c and 2d, which show the normalized amplitude and phase, respectively, of the light reflected by an array of identical dolmen structures for two different lengths L2. These two lengths are presented here to demonstrate the extremes of the phase-tuning range of the system. The calculations were performed using the periodic SIE, a full-wave method for solving Maxwell’s equations50; see the Materials and methods section. Normally, one would expect an asymmetric dip in the scattering spectrum, but in the case of reflection from a metallic backplane, the spectrum is inverted, such that the Fano resonance feature becomes a reflection window. We observe in Figure 2c that for both lengths L2, the amplitude of the reflected light remains rather constant in this window surrounding the operation wavelength λ=750 nm. By contrast, the phase at this wavelength exhibits a rapid variation when L2 is changed from 90 to 115 nm (Figure 2d). Thus, changing the dolmen geometry modifies the phase of the reflected wave without significantly affecting its amplitude. Further insights into the system are obtained by considering its response as a function of the length of the two parallel nanorods, L2. The corresponding normalized amplitude is shown in Figure 2e, where we clearly observe anti-crossing behavior between the fixed dipolar resonance (vertical dashed line) and the quadrupolar resonance, whose resonance wavelength decreases as the two parallel nanorods are shortened (oblique dashed line). The corresponding phase difference is shown in Figure 2f, where we observe an increase in the phase of as large as 1.9π over the wavelength band between λ=700 and 800 nm. The phase in this figure corresponds to the relative phase difference with respect to the value for L2=105 nm. This remarkably large phase interval is caused by the coupling between the dolmen structure and the backing silver mirror27, 28. Note also in Figure 2f that the relative phase vanishes (that is, takes a value of 0 or 2π) for wavelengths smaller than λ=680 nm or larger than 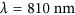Inline graphic. This operation bandwidth, which corresponds to the spectral range in which the phase is modulated, is defined by the energy splitting between the super-radiant and sub-radiant modes and is controlled by the coupling between them, as will be discussed later. According to Figure 2f, we are able to select four different lengths L2 that correspond to four phase levels with relative phases of 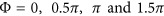Inline graphic for the construction of metasurfaces; the exact phases and amplitudes for these four chosen unit cells are shown in detail in Supplementary Fig. S1 of the Supplementary Information. In summary, the unit cell shown in Figure 2b provides two degrees of freedom: the length of the central nanorod controls the central operation frequency, whereas the length of the two parallel nanorods controls the phase of the reflected light within the operation band. Note that this narrowband mode of operation requires the incident light to be polarized parallel to the central nanorod; the perpendicular polarization leads to a broadband response of the metasurface, as described in Supplementary Figs. S4 and S5 of the Supplementary Information.

Optical characterization

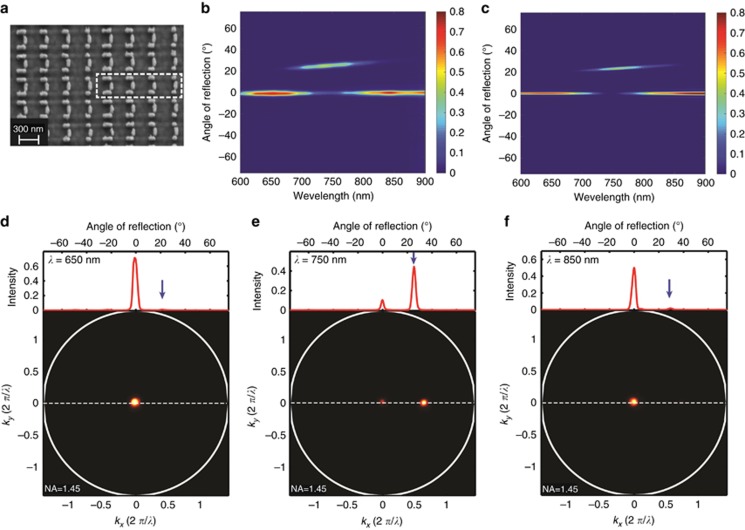
The color-selective metasurface was fabricated following the design shown in Figure 2a using a recently developed technique for the realization of smooth plasmonic nanostructures in silver49; see the Materials and methods section. Silver exhibits much weaker absorption in the visible part of the spectrum and narrower spectral features compared with gold—the metal of choice for plasmonics. The fabricated structure is shown in Figure 3a, where a supercell corresponding to a phase gradient of 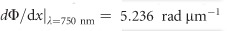Inline graphic along the x direction is highlighted with a white dashed box. Figure 3b presents the far-field reflection intensity as a function of the excitation wavelength and reflection angle, as measured using the Fourier imaging setup (see the Materials and methods section). In addition to the ordinary reflection band at 0° visible in the middle of the figure, anomalous reflection is clearly visible between 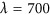Inline graphic and 800 nm, corresponding to the operation band of the device. In this wavelength range, the wavefront of the reflected beam is bent along the phase-gradient direction in accordance with the generalized Snell’s law and Equation (1c). The measured reflection map is in very good agreement with the SIE simulations shown in Figure 3c. Figure 3d–3f shows Fourier images corresponding to three specific excitation wavelengths. The red curves on top represent the corresponding reflection intensity, with the blue arrows indicating the calculated position of the anomalous reflection angle according to Equation (1c). At the center of the designed operation band, 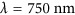Inline graphic (Figure 3e), ordinary reflection almost vanishes and a strong reflection peak appears at 25°, which contributes ~81% of the total reflected power (routing efficiency). By contrast, for the wavelengths of λ=620 and 880 nm, which are outside the designed operation band, only ordinary reflection is observed in Figure 3d and 3f. For these wavelengths, the metasurface simply acts as a flat mirror.

Figure 3.

Figure 3

Open in a new tab

Experimental characterization of the color-selective phase gradient metasurface. (a) SEM image of a fabricated phase gradient metasurface with a supercell consisting of four dolmen structures, acquired at 30°. (b, c) Reflection intensity as a function of both wavelength and reflection angle under normal incidence conditions: (b) measurements and (c) SIE simulations. 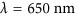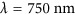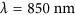(d–f) Experimental Fourier images of the light reflected from the metasurface at three different wavelengths: (d) Inline graphic, (e) Inline graphic and (f) Inline graphic. The red curves on top show the intensity profile along the principle reflection plane, indicated by the white dashed line.

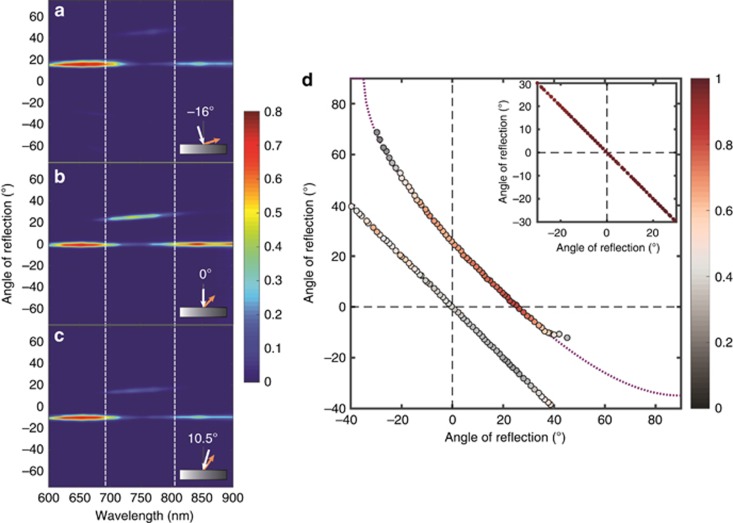
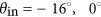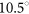It is important for practical applications to note that the response of the designed metasurface exhibits a relatively high tolerance with respect to the incidence angle. Figure 4a–4c shows the measured reflection intensity as a function of the wavelength for three different incidence angles, Inline graphic and Inline graphic. For all cases, the anomalous reflection band remains within the designed frequency range (indicated by the white dashed lines in Figure 4). Because of the subwavelength thickness of the surface, changing the incidence angle does not generate any additional phase accumulation along the direction of propagation through the device. As a consequence, the operation band does not suffer from spatial dispersion. In Figure 4d, we further characterize the reflection angle as a function of the incidence angle for a fixed wavelength of λ=750 nm. Both ordinary reflection and anomalous reflection are observed. The color scale in that panel indicates the output efficiency, which is defined as the portion of energy in a specific channel compared with all possible emission channels. The angular dependence well follows the generalized reflection law, indicated by a purple dashed line. By contrast, only specular reflection is observed when the excitation wavelength is outside the operation band, for example, for λ=650 nm; see the inset in Figure 4d.

Figure 4.

Figure 4

Open in a new tab

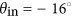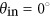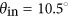Optical response at oblique incidences. (a–c) Reflection intensity as a function of wavelength and reflection angle for various incidence angles: (a) Inline graphic, (b) Inline graphic, and (c) Inline graphic. (d) Reflection angle versus incidence angle under excitation at a wavelength of 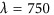Inline graphicnm. The purple dashed curve represents theoretical calculations of the anomalous dispersion based on the generalized reflection law, and the colors of the symbols indicate the normalized routing efficiency extracted from the experimental data. Inset: reflection angle versus incidence angle for ordinary reflection at an excitation wavelength of 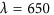Inline graphicnm. A positive (negative) sign on the angles corresponds to the right (left) side of the normal axis.

Multiple-wavelength color routing

In the preceding, we have shown that, on the one hand, the operation band of the metasurface is controlled by the spectral position of the Fano resonance, and on the other hand, the direction in which light is anomalously reflected is governed by the direction of the phase gradient along the unit cell of the metasurface. By combining different unit cells within the same metasurface, we demonstrate here a new class of plasmonic devices that can selectively route two different wavelengths from a broadband incident beam into two different directions, as shown in Figure 5a. We fabricated such a plasmonic metasurface using supercells with periodicities of 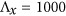Inline graphic nm and 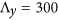Inline graphic nm, as indicated in Figure 5b. Two different supercells, highlighted in blue and red in that panel, were combined into the same metasurface: the blue supercell corresponds to one set of dolmens, with a central nanorod length of L1=55 nm, which produce a resonance near λ=532 nm, whereas the red dashed box indicates a second set of dolmens, with a central nanorod length of L1=75 nm, exhibiting a resonance near λ=660 nm (Figure 5b). The phase gradient was designed to be 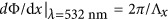Inline graphic for the blue cell and 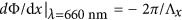Inline graphic for the red cell, thus establishing opposite anomalous reflections in the corresponding operation bands. Experimentally, as shown in Figure 5c, we measured two anomalous reflection branches on opposite sides of the normal axis, one centered at λ=660 nm and the other centered at λ=532 nm, with bandwidths as narrow as 60 nm. Note that no spectral overlap appears between the two operation bands; consequently, in the Fourier image, one can distinguish the red and blue light as separated spots in the k-space (Figure 5d). This image was captured using a three-layer color sensor camera and plotted directly in the RGB basis without any post-processing.

Figure 5.

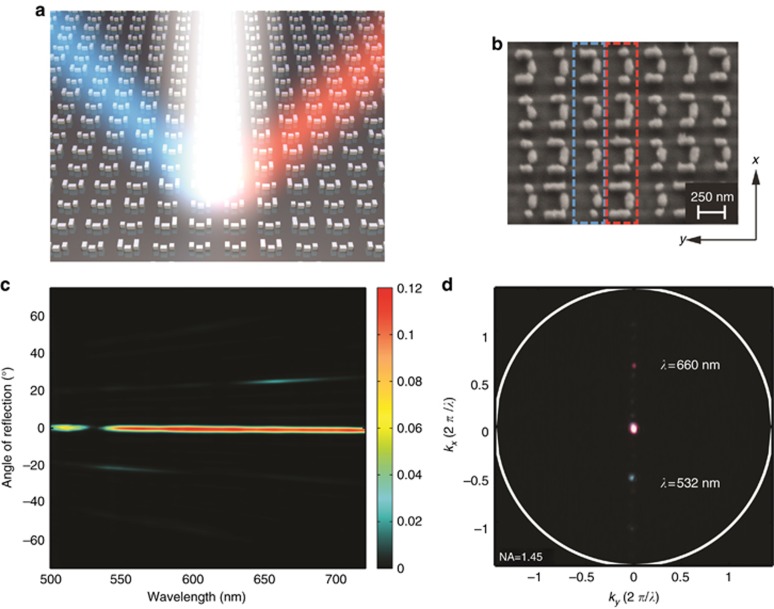
Figure 5

Open in a new tab

Realization of a dual-band color routing device. (a) A three-dimensional schematic view of a color-routing metasurface that reflects red and blue light in different directions. (b) SEM image of the fabricated color-routing metasurface. The blue and red dashed squares indicate the supercells that are responsible for routing the two different wavelengths. (c) Intensity of the reflected light as a function of the input wavelength and reflection angle for the metasurface shown in a. Spectral components with different wavelengths are redirected in opposite directions. (d) Measured Fourier image of reflection from the metasurface under illumination with two different wavelengths. The blue spot in the −y direction corresponds to the wavelength of 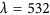Inline graphic nm, and the red spot in the +y direction corresponds to 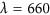Inline graphic nm.

Let us emphasize that this color-routing metasurface should be distinguished from color-routing devices based on asymmetric plasmonic dimers7, whose performances are limited by the wide angular emission and broad resonance spectrum associated with plasmonic dimers. In our case, the Fano resonance produces a narrow resonance lineshape, and the angular emission is highly directional owing to the effect of the phased array geometry52. The dolmen structures provide complete control over the various operation parameters: the color of the anomalous reflection band is chosen by selecting the resonance frequency of the central nanorod, whereas the two parallel nanorods control the phase modulation. The measured routing efficiency for each color channel is ~5%, which is consistent with the simulated results shown in Supplementary Fig. S6. The decrease in efficiency compared with the metasurface shown in Figure 3 is explained by three main reasons. First, the effective area that is responsible for the phase tuning of each color channel is reduced by half. Second, to maintain a subwavelength unit cell in the lateral direction, the unit cell must be arranged such that the anomalous reflection has a TM polarization. Unfortunately, the bright mode radiates less at higher angles in the case of TM polarization, which decreases the routing efficiency. Third, silver exhibits higher material losses at these shorter wavelengths, which markedly increases the absorption of the system. One can foresee that this technology could be refined to narrow the spectral response of the system for colorful on-chip holographic devices32, 33. Moreover, the current properties of a reasonably narrow linewidth and pronounced spatial separation are very well suited for applications that are not highly sensitive to wavelength but require flexible light manipulation, such as solar concentrators that focus different sunlight bands onto different regions of a multi-junction solar cell or security devices that cause different spectral signals to be observed when the orientation of the substrate is changed30, 31, 34.

The bandwidth of the proposed metasurface can be controlled by modifying the gap in the dolmen structures. For example, in Supplementary Fig. S3a–S3c of the Supplementary Information, we present the anomalous bands measured for three metasurfaces with different dolmen gap sizes of g=6, 15 and 25 nm (SEM images are shown as insets). A bandwidth as large as 150 nm is observed for the smallest gap size of g=6 nm, whereas a 60 nm bandwidth is obtained with a larger gap size of g=25 nm. A small gap produces strong coupling between the super-radiant and sub-radiant modes, leading to larger energy splitting for the hybrid modes and thus producing a broader operation band; see Supplementary Fig. S3c. When the gap size is increased to 25 nm, the quadrupolar mode is only weakly coupled to the dipolar mode, resulting in a narrower operation band with inappropriate phase variation; see Supplementary Fig. S3a. Consequently, the efficiency drops as a result of insufficient phase modulation. The proposed metasurface operates in the visible range of the optical spectrum, where material losses and fabrication imperfections can impair the overall efficiency. To further reduce the bandwidth at optical wavelengths without affecting the efficiency in the visible range, one could employ other materials, such as aluminum or single-crystalline silver, or could even resort to a dielectric metasurface. Meanwhile, the same design principle could be utilized in the infrared, for example, at telecom wavelengths, where much narrower spectral features can be anticipated.

Conclusions

In summary, we have demonstrated a new class of reflective metasurfaces based on Fano-resonant nanostructures for narrowband operation. The central position and width of the anomalous band can be controlled by varying the geometry of the constituent elements, thanks to the narrow linewidth and strong spectral sensitivity of Fano resonances. Although here we have considered dolmen structures, this concept can be generalized to any Fano-resonant plasmonic system based on the coupling between a super-radiant resonance and a sub-radiant resonance. Moreover, such a color-routing device exhibits highly directional emission, whereas its operation bands are quite insensitive to the angle of illumination. The proposed design can be extended to cover a wide range of frequencies, from the visible to the mid-infrared. Together with their subwavelength unit cells, these metasurfaces represent a new family of devices for color-sensitive nanophotonic applications, including color computer-generated holograms, multi-channel data storage, demultiplexers and on-chip plasmonic spectrometers, to name a few.

Author contributions

CY and KYY designed and conceived the experiments under the supervision of OJFM. Both CY and KYY performed the numerical simulations, fabrication procedures and experiments. CY developed the measurement setup and performed the data analysis. All authors contributed to the writing of the paper, discussed the results and commented on the manuscript.

Acknowledgments

This work was financially supported by the Swiss National Science Foundation (grants 200020_153662 and 200021_162453).

Footnotes

Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website(http://www.nature.com/lsa).

The authors declare no conflict of interest.

Supplementary Material

Supplementary Information
Click here for additional data file. (2.8MB, doc)

References

  1. Gaylord TK, Moharam MG. Analysis and applications of optical diffraction by gratings. Proc IEEE 1985; 73: 894–937. [Google Scholar]
  2. Bomzon Z, Biener G, Kleiner V, Hasman E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt Lett 2002; 27: 1141–1143. [DOI] [PubMed] [Google Scholar]
  3. Lin DM, Fan PY, Hasman E, Brongersma ML. Dielectric gradient metasurface optical elements. Science 2014; 345: 298–302. [DOI] [PubMed] [Google Scholar]
  4. Jahani S, Jacob Z. All-dielectric metamaterials. Nat Nanotechnol 2016; 11: 23–36. [DOI] [PubMed] [Google Scholar]
  5. Fang YR, Li ZP, Huang YZ, Zhang SP, Nordlander P et al. Branched silver nanowires as controllable plasmon routers. Nano Lett 2010; 10: 1950–1954. [DOI] [PubMed] [Google Scholar]
  6. Yu NF, Genevet P, Kats MA, Aieta F, Tetienne J-P et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 2011; 334: 333–337. [DOI] [PubMed] [Google Scholar]
  7. Shegai T, Chen S, Miljković VD, Zengin G, Johansson P et al. A bimetallic nanoantenna for directional colour routing. Nat Commun 2011; 2: 481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Yin XB, Ye ZL, Rho J, Wang Y, Zhang X. Photonic spin hall effect at metasurfaces. Science 2013; 339: 1405–1407. [DOI] [PubMed] [Google Scholar]
  9. Dregely D, Lindfors K, Lippitz M, Engheta N, Totzeck M et al. Imaging and steering an optical wireless nanoantenna link. Nat Commun 2014; 5: 4354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Liu N, Guo HC, Fu LW, Kaiser S, Schweizer H et al. Three-dimensional photonic metamaterials at optical frequencies. Nat Mater 2008; 7: 31–37. [DOI] [PubMed] [Google Scholar]
  11. Sun SL, He Q, Xiao SY, Xu Q, Li X et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 2012; 11: 426–431. [DOI] [PubMed] [Google Scholar]
  12. Yu NF, Capasso F. Flat optics with designer metasurfaces. Nat Mater 2014; 13: 139–150. [DOI] [PubMed] [Google Scholar]
  13. Papaioannou M, Plum E, Valente J, Rogers ETF, Zheludev NI. Two-dimensional control of light with light on metasurfaces. Light Sci Appl 2016; 5: e16070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Huang LL, Chen XZ, Mühlenbernd H, Li GX, Bai BF et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett 2012; 12: 5750–5755. [DOI] [PubMed] [Google Scholar]
  15. Yu NF, Aieta F, Genevet P, Kats MA, Gaburro Z et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett 2012; 12: 6328–6333. [DOI] [PubMed] [Google Scholar]
  16. Fedotov VA, Wallauer J, Walther M, Perino M, Papasimakis N et al. Wavevector selective metasurfaces and tunnel vision filters. Light Sci Appl 2015; 4: e306. [Google Scholar]
  17. Wang Q, Rogers ETF, Gholipour B, Wang C-M, Yuan GH et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat Photon 2016; 10: 60–65. [Google Scholar]
  18. Khorasaninejad M, Chen WT, Devlin RC, Oh J, Zhu AY et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 2016; 352: 1190–1194. [DOI] [PubMed] [Google Scholar]
  19. Lin J, Mueller JPB, Wang Q, Yuan GH, Antoniou N et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 2013; 340: 331–334. [DOI] [PubMed] [Google Scholar]
  20. Larouche S, Tsai Y-J, Tyler T, Jokerst NM, Smith DR. Infrared metamaterial phase holograms. Nat Mater 2012; 11: 450–454. [DOI] [PubMed] [Google Scholar]
  21. Huang LL, Chen XZ, Mühlenbernd H, Zhang H, Chen SM et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun 2013; 4: 2808. [Google Scholar]
  22. Ni XJ, Kildishev AV, Shalaev VM. Metasurface holograms for visible light. Nat Commun 2013; 4: 2807. [Google Scholar]
  23. Chen WT, Yang K-Y, Wang C-M, Huang Y-W, Sun G et al. High-efficiency broadband meta-hologram with polarization-controlled dual images. Nano Lett 2014; 14: 225–230. [DOI] [PubMed] [Google Scholar]
  24. Ni XJ, Wong ZJ, Mrejen M, Wang Y, Zhang X. An ultrathin invisibility skin cloak for visible light. Science 2015; 349: 1310–1314. [DOI] [PubMed] [Google Scholar]
  25. Pors A, Nielsen MG, Bozhevolnyi SI. Analog computing using reflective plasmonic metasurfaces. Nano Lett 2015; 15: 791–797. [DOI] [PubMed] [Google Scholar]
  26. Kang M, Feng TH, Wang H-T, Li J. Wave front engineering from an array of thin aperture antennas. Opt Express 2012; 20: 15882–15890. [DOI] [PubMed] [Google Scholar]
  27. Sun SL, Yang K-Y, Wang C-M, Juan T-K, Chen WT et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett 2012; 12: 6223–6229. [DOI] [PubMed] [Google Scholar]
  28. Pors A, Albrektsen O, Radko IP, Bozhevolnyi SI. Gap plasmon-based metasurfaces for total control of reflected light. Sci Rep 2013; 3: 2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li ZY, Palacios E, Butun S, Aydin K. Ultrawide angle, directional spectrum splitting with visible-frequency versatile metasurfaces. Adv Opt Mater 2016; 4: 953–958. [Google Scholar]
  30. Atwater HA, Polman A. Plasmonics for improved photovoltaic devices. Nat Mater 2010; 9: 205–213. [DOI] [PubMed] [Google Scholar]
  31. Polman A, Atwater HA. Photonic design principles for ultrahigh-efficiency photovoltaics. Nat Mater 2012; 11: 174–177. [DOI] [PubMed] [Google Scholar]
  32. Redding B, Liew SF, Sarma R, Cao H. Compact spectrometer based on a disordered photonic chip. Nat Photon 2013; 7: 746–751. [Google Scholar]
  33. Calafiore G, Koshelev A, Dhuey S, Goltsov A, Sasorov P et al. Holographic planar lightwave circuit for on-chip spectroscopy. Light Sci Appl 2014; 3: e203. [Google Scholar]
  34. Eisler CN, Abrams ZR, Sheldon MT, Zhang X, Atwater HA. Multijunction solar cell efficiencies: effect of spectral window, optical environment and radiative coupling. Energy Environ Sci 2014; 7: 3600–3605. [Google Scholar]
  35. Zhang S, Genov DA, Wang Y, Liu M, Zhang X. Plasmon-induced transparency in metamaterials. Phys Rev Lett 2008; 101: 047401. [DOI] [PubMed] [Google Scholar]
  36. Verellen N, Sonnefraud Y, Sobhani H, Hao F, Moshchalkov VV et al. Fano resonances in individual coherent plasmonic nanocavities. Nano Lett 2009; 9: 1663–1667. [DOI] [PubMed] [Google Scholar]
  37. Luk'yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater 2010; 9: 707–715. [DOI] [PubMed] [Google Scholar]
  38. Miroshnichenko AE, Flach S, Kivshar YS. Fano resonances in nanoscale structures. Rev Mod Phys 2010; 82: 2257–2298. [Google Scholar]
  39. Liu N, Hentschel M, Weiss T, Alivisatos AP, Giessen H. Three-dimensional plasmon rulers. Science 2011; 332: 1407–1410. [DOI] [PubMed] [Google Scholar]
  40. Gallinet B, Siegfried T, Sigg H, Nordlander P, Martin OJF. Plasmonic radiance: probing structure at the ångström scale with visible light. Nano Lett 2013; 13: 497–503. [DOI] [PubMed] [Google Scholar]
  41. Wu C, Khanikaev AB, Adato R, Arju N, Yanik AA et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat Mater 2012; 11: 69–75. [DOI] [PubMed] [Google Scholar]
  42. Zhao J, Zhang CJ, Braun PV, Giessen H. Large-area low-cost plasmonic nanostructures in the nir for fano resonant sensing. Adv Mater 2012; 24: OP247–OP252. [DOI] [PubMed] [Google Scholar]
  43. Zhang Y, Zhen Y-R, Neumann O, Day JK, Nordlander P et al. Coherent anti-Stokes Raman scattering with single-molecule sensitivity using a plasmonic Fano resonance. Nat Commun 2014; 5: 4424. [DOI] [PubMed] [Google Scholar]
  44. King NS, Liu LF, Yang X, Cerjan B, Everitt HO et al. Fano resonant aluminum nanoclusters for plasmonic colorimetric sensing. ACS Nano 2015; 9: 10628–10636. [DOI] [PubMed] [Google Scholar]
  45. Lovera A, Gallinet B, Nordlander P, Martin OJF. Mechanisms of fano resonances in coupled plasmonic systems. ACS Nano 2013; 7: 4527–4536. [DOI] [PubMed] [Google Scholar]
  46. Chang W-S, Lassiter JB, Swanglap P, Sobhani H, Khatua S et al. A plasmonic fano switch. Nano Lett 2012; 12: 4977–4982. [DOI] [PubMed] [Google Scholar]
  47. Kumar K, Duan HG, Hegde RS, Koh SCW, Wei JN et al. Printing colour at the optical diffraction limit. Nat Nano 2012; 7: 557–561. [DOI] [PubMed] [Google Scholar]
  48. Guo R, Decker M, Setzpfandt F, Staude I, Neshev DN et al. Plasmonic fano nanoantennas for on-chip separation of wavelength-encoded optical signals. Nano Lett 2015; 15: 3324–3328. [DOI] [PubMed] [Google Scholar]
  49. Thyagarajan K, Santschi C, Langlet P, Martin OJF. Highly improved fabrication of Ag and Al nanostructures for UV and nonlinear plasmonics. Adv Opt Mater 2016; 4: 871–876. [Google Scholar]
  50. Gallinet B, Kern AM, Martin OJF. Accurate and versatile modeling of electromagnetic scattering on periodic nanostructures with a surface integral approach. J Opt Soc Am A 2010; 27: 2261–2271. [DOI] [PubMed] [Google Scholar]
  51. Yan C, Martin OJF. Periodicity-induced symmetry breaking in a fano lattice: hybridization and tight-binding regimes. ACS Nano 2014; 8: 11860–11868. [DOI] [PubMed] [Google Scholar]
  52. Dregely D, Taubert R, Dorfmüller J, Vogelgesang R, Kern K et al. 3D optical Yagi-Uda nanoantenna array. Nat Commun 2011; 2: 267. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (2.8MB, doc)

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES