Broadband spin Hall effect of light in single nanoapertures

Abstract

With properties not previously available, optical metamaterials and metasurfaces have shown their great potential in the precise control of light waves at the nanoscale. However, the use of current metamaterials and metasurfaces is limited by the collective response of the meta-atoms/molecules, which means that a single element cannot provide the functionalities required by most applications. Here, we demonstrate for the first time that a single achiral nanoaperture can be utilized as a meta-macromolecule to achieve giant angular spin Hall effect of light. By controlling the spin-related momenta, we show that these nanoapertures can enable full control of the phase gradient at a deep-subwavelength level, thus forming unique building blocks for optical metasurfaces. As a proof-of-concept demonstration, a miniaturized Bessel-like beam generator and flat lens are designed and experimentally characterized. The results presented here may open a door for the development of meta-macromolecule-based metasurfaces for integrated optical systems and nanophotonics.

Introduction

The past decade has witnessed the rapid development of artificially structured metasurfaces. Owing to the unique electromagnetic responses of the meta-atoms or meta-molecules arranged in the two-dimensional (2D) plane, metasurfaces have enabled many exciting applications, such as imaging below the diffraction limit^{1, 2, 3, 4}, controlling light rays beyond Snell’s law^{5, 6, 7, 8, 9}, changing polarizations and chirality^{10, 11, 12, 13, 14, 15, 16} and mimicking the physical processes in quantum systems^{17, 18, 19, 20, 21}. Compared with traditional bulk optical components, metasurfaces hold great advantages since only one single layer with vanishing thickness is required to achieve complete control of the light fields^{22, 23, 24, 25, 26, 27}. Regarding the light–matter interaction in metasurfaces, the role of circularly polarized light (CPL) has drawn special attention in recent years^{10, 28}. As indicated in quantum theory, the polarization state of CPL corresponds to the spin angular momentum, which is coupled with the phase gradient of light following a process named optical spin–orbit interaction (OSOI)^{29, 30, 31, 32, 33}. The spin-related phase can also be used to generate the angular spin Hall effect of light (SHEL), where a handedness-dependent momentum shift is introduced to the incident CPL^{17, 18, 19}.

The phase shift originating from the OSOI is often termed geometric phase because of its geometric nature²⁹. Although the first demonstration of such phase at the radio frequency can be dated back to the 1960s³⁴, the realization of functional devices in the optical range has only been accomplished lately. In the polarization gratings²⁹ and q-plates³⁰, linear momentum and angular momentum could be converted to CPL by properly designing the continuous anisotropic structures. Nevertheless, because of the lack of a general design procedure and precise fabrication techniques, it is difficult to realize arbitrary phase modulation with subwavelength resolution³⁵. To overcome this obstacle, discrete or quantized optical antennas were proposed to construct metasurfaces and achieve various optical functionalities^{6, 35, 36, 37, 38}. These metasurfaces relied on the combination of different elements to create the phase gradient, while each individual element (meta-atom) introduced only a locally constant phase. The finite dimension of the discrete elements, however, may severely limit the accuracy of the phase distribution, as well as the diffraction efficiency. Consequently, it would be much more appealing for both the theoretical understanding and practical application if a single nanostructure can be used to realize an arbitrary phase profile³⁹. Note that, although some pioneering lines of work on the polarization-dependent transmission of light through single holes have been reported^{11, 32}, they were not optimized in the framework of the geometric phase.

In this paper, we demonstrated that a perfect continuous and dispersion-free phase gradient can be observed in a single catenary-shaped nanoaperture perforated on a thin metallic screen. The phase gradient is attributed to the OSOI in the space-variant anisotropic aperture, which leads to a giant and broadband angular SHEL. We also designed and experimentally characterized a single deformed catenary aperture, as well as a catenary array, to generate various types of phase distribution. The results may open many perspectives regarding the design of optical metasurfaces.

Materials and methods

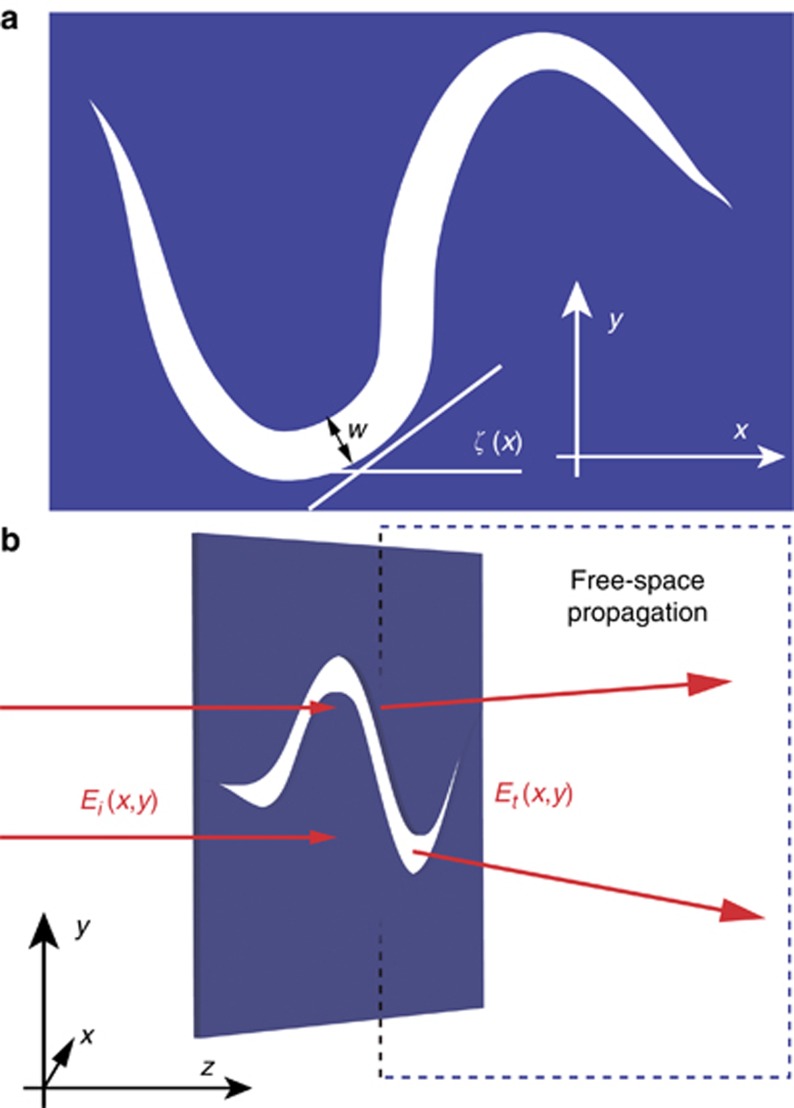
We focus on a slim subwavelength aperture perforated on a metallic screen with vanishing thickness. By ‘slim’, we mean that the aperture has a length much larger than the width, while the width is much smaller than the operating wavelength. As shown in Figure 1a, such an aperture could be mathematically treated with two parameters, that is, the inclination angle ζ(x) with respect to the x axis and the width w.

Figure 1.

Diffraction of light by an arbitrary aperture on a conducting screen. (a) Geometry of the structure. (b) Sketch of the diffraction problem. Here, E_i(x, y) and E_t(x, y) denote the incident and transmitted electric fields, respectively. Once E_t(x, y) is obtained via the boundary conditions, the diffraction fields can be evaluated via the free-space propagation methods.

Since the early work of Bethe in 1944⁴⁰, it is known that traditional Kirchhoff’s diffraction theory does not fulfill the electromagnetic boundary conditions for small apertures even if the thickness of the screen is decreased to zero. In particular, owing to the polarization-dependent transmission⁴¹, the incident fields do not equal the fields at the output side of the aperture and the diffraction (or scattering) phenomena may become completely different from that predicted by Kirchhoff’s theory (Figure 1b).

As depicted in Figure 2a, the aperture we used is obtained by connecting two ‘catenary of equal strength’^{42, 43, 44} curves with a vertical shift of Δ:

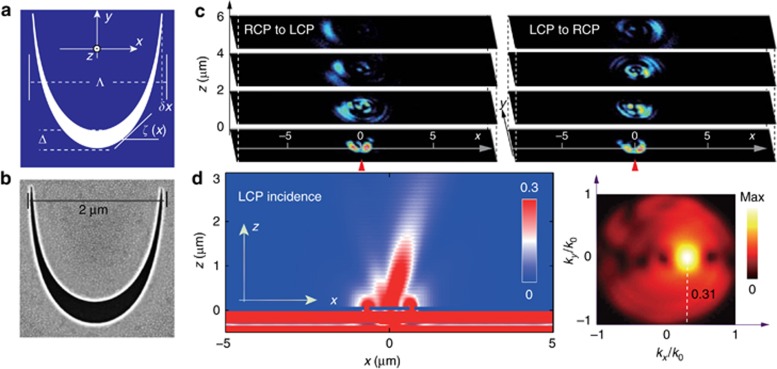
Figure 2.

Angular SHEL observed in a single catenary aperture. (a) Schematic of the catenary aperture. (b) Scanning electron microscope (SEM) image of the fabricated catenary aperture with Λ=2 μm, Δ=200 nm and δx=50 nm. (c) Measured cross-polarized intensity patterns in the xy planes for z=0, 2, 4, 6 μm under RCP (left panel) and LCP (right panel) illumination (λ=632.8 nm). The top surface of the sample is set at z=0. (d) Simulation of a single catenary aperture under LCP incidence. The left panel represents the cross-polarized electric intensity in the xz plane (y=1 μm). The right panel shows the amplitude of the far-field angular spectrum in the k-space, where k_x and k_y are the horizontal wavenumbers in the x and y directions, respectively.

where Λ is the horizontal length of the catenary. Because the value of Equation (1) is infinite for x=±Λ/2, the curves should be truncated at the two ends with a value of δx; thus, the span of x is (−0.5Λ+δx, 0.5Λ−δx).

Under CPL illumination, the anisotropic transmission would result in a geometric phase for the cross-polarized light, which is twice the inclination angle of the aperture and can be written as Φ=−2σζ(x)²⁸. Here, σ=±1 denotes the left-handed circular polarization (LCP, σ=−1) and right-handed circular polarization (RCP, σ=1), respectively. Because the inclination angle of the catenary aperture has a form of:

there is a linear and dispersion-free phase distribution of Φ(x)=−2σπx/Λ at the output boundary of the catenary aperture. Note that the phase is distributed along a curved aperture; thus, it can also be written as a function of y:

Owing to the geometric phase, the diffraction of the cross-polarization violates the Kirchhoff’s theory. Intuitively speaking, a single element of the catenary aperture can act as an artificial bias for the incident CPL and show dramatic angular SHEL, that is, a handedness-dependent beam-steering effect. In general, the theoretical deflection angle of the cross-polarized light (at normal incidence) is θ=−σsin⁻¹(λ/Λ), corresponding to an additional horizontal momentum of Δk=−2σπ/Λ. In contrast to the cross-polarization, the co-polarized light will not be deflected because it does not acquire any geometric phase (see Supplementary Fig. S2a).

Results and discussion

As shown in Figure 2b, a catenary aperture with Λ=2 μm and Δ=200 nm was fabricated via focused ion beam milling on a 120-nm-thick gold film deposited on a SiO₂ substrate. In the experiments, the incident light was set to propagate perpendicularly to the sample plane. Under LCP and RCP illumination at λ=632.8 nm, the cross-polarized (RCP and LCP) fields transmitted from the aperture were measured using a home-made microscope (see Supplementary Fig. S2e). Figure 2c represents the intensity distribution in the xy planes, revealing that the CPL has been deflected by the catenary aperture along the x axis with an angle of ~±18° (the theoretical value is ±18.42°) for LCP and RCP, respectively. In Figure 2d, we investigated the cross-polarized near-field electric fields and far-field scattering of this aperture using a commercial electromagnetic software (CST Microwave Studio, Darmstadt, Germany). This far-field scattering corresponds well with the experimental results (Figure 2c). In the simulations, the metal film was assumed to be a perfect electric conductor because the excited surface plasmon polariton (SPP) does not contribute to the far-field pattern, in contrast to the case of the beaming effect⁴⁵. We also noted that the phase retardation originating from the SPP propagation²⁵ can be neglected because it is much smaller than the geometric phase for such thin metallic film (see Supplementary Fig. S1).

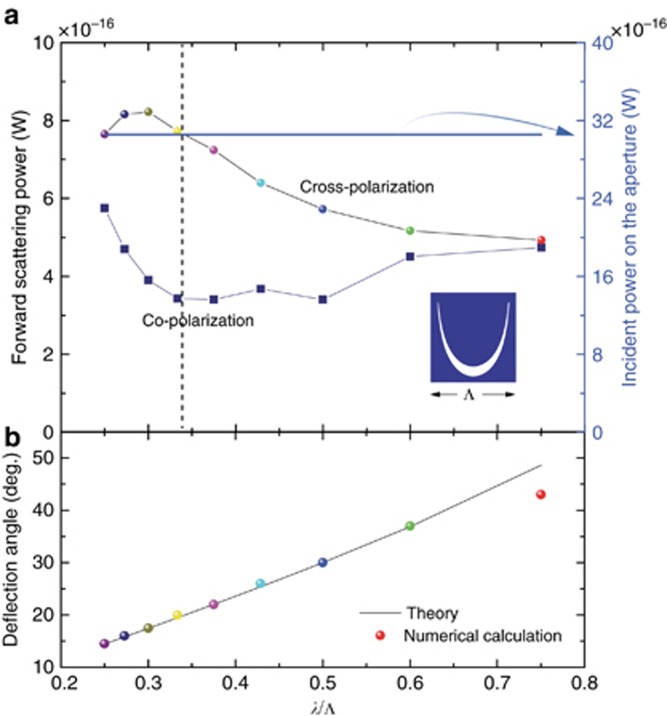
Owing to the geometric nature of the spin–orbit conversion, we anticipate that the handedness scattering can be observed within a broadband frequency range. To demonstrate this, we calculated the far-field scattering power of the single catenary aperture illuminated by LCP light at different wavelengths. As shown in Figure 3a, the cross-polarized scattering is larger than the co-polarization within the whole range. Because the amplitude of the electric field of the incident plane wave is set as 1 V m⁻¹, the power of the light incident on the aperture can be evaluated as 30 × 10⁻¹⁶ W. Clearly, the conversion efficiency, defined as the ratio of the cross-polarization power to the input power, is typically below 25%, except for the range where 0.25≤λ/Λ≤0.35. The relatively low efficiency can be attributed to the reflection of the CPL. Moreover, the cross-polarized component becomes evanescent and does not contribute to the far field when λ/Λ>1. In the short wavelength region (λ/Λ<0.25), the degradation of performance would be attributed to the increased diffraction because the wavelength is comparable to Δ.

Figure 3.

Broadband light scattering by a single catenary aperture. (a) Calculated scattering powers in forward direction for co- and cross-polarized components (left axis) and the total input LCP power integrated on the aperture (right axis). The scattering powers are obtained by integrating the power pattern given by CST. (b) Theoretical (θ=sin⁻¹(λ/Λ)) and numerically calculated deflection angles at different wavelengths.

Figure 3b plots the deflection angles evaluated from CST Microwave Studio at different wavelengths, showing good agreement with the theoretical results obtained via the relation θ=−σsin⁻¹(λ/Λ). The deviation at large angles is mainly because the beam width increases with the deflection angle, which would in turn induce stronger scattering by the edge of the aperture.

In the following section, we would like to show that a simple deformation of the catenary aperture can provide more freedom for the light manipulation at the nanoscale. As shown in Figure 4a and 4b, the left half part of the catenary was flipped upside down; thus, the geometric phase can be written as:

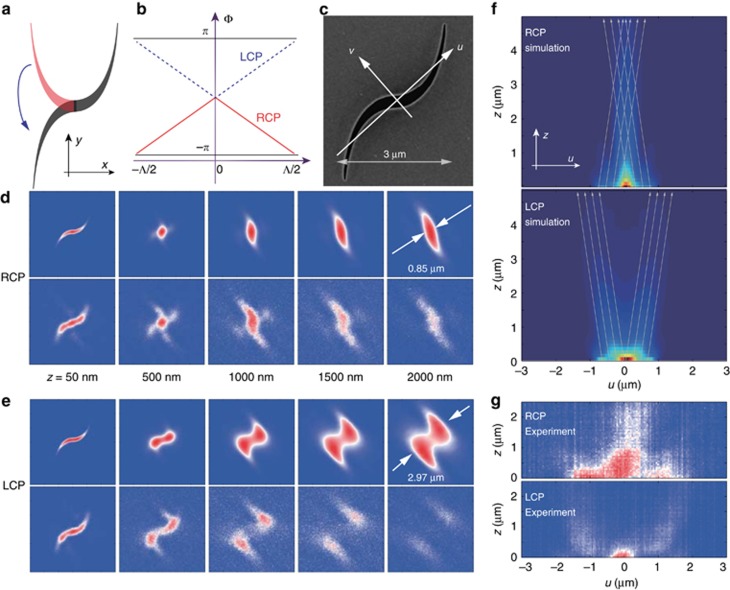
Figure 4.

Deformed catenary aperture. (a) Schematic of the deformed catenary aperture. The left side is flipped upside down compared to a normal catenary. (b) Phase distribution of the deformed catenary under LCP (dashed blue) and RCP (solid red) illumination. (c) SEM image of the deformed catenary with Λ=3 μm, Δ=300 nm and δx=50 nm. (d,e) Theoretical (top rows) and experimental (bottom rows) cross-polarized intensity for RCP (d) and LCP (e) incidence. The patterns are recorded at different distances away from the aperture, as indicated by the value of z. The dimensions of all panels in d,e are 6 μm × 6 μm. (f) Numerically calculated intensity distribution in the uz plane for RCP and LCP incidence. The angle between the u and x directions is 30°. The gray arrows indicate the ray approximation of the light path, which is similar to the case of common Bessel beam generation. (g) Experimental intensity distribution in the uz plane.

The phase distribution along the y direction can be obtained as:

From Equation (4), we find that such a deformed catenary aperture can be utilized to create two counterpropagating waves along the x direction, similar to the case of the diffraction-free Bessel beam, which is made up of plane waves traveling on a cone⁴⁶. To test the optical performance of the deformed catenary, a sample with Λ=3 μm and Δ=300 nm was fabricated and measured by adopting the methods used above (Figure 4c). The intensity distribution for cross-polarized components was measured at different distances away from the sample and compared with the results obtained from vectorial diffraction theory, where the phase distribution is assumed to follow Equations (4) and (5). As illustrated in Figure 4d and 4e, the experimental results agree very well with the theoretical evaluations, except that there is some quantitative mismatch resulting from the approximation made in Equations (4) and (5).

In addition to the phase modulation in the x direction, the deformed catenary also possesses a phase gradient in the y direction, as indicated in Equation (5). Thus, the deflection direction of the CPL is actually along the diagonal direction (the u direction), as indicated in Figure 4c, and the last column of Figure 4d and 4e. For LCP illumination, the cross-polarized light fields are gradually separated, along with its propagation. At z=2 μm, the separating width becomes 2.97 μm. In contrast, a narrow light spot was obtained for RCP illumination, with a beam width of 0.85 μm at z=2 μm. Figure 4f and 4g plots the intensity profiles in the uz plane for both the numerical and experimental results. Owing to the low transmission and the noise stemming from the incomplete polarization conversion, the measured intensity becomes blurred for z>2.5 μm. Nevertheless, the ray approximation shown in Figure 4f demonstrates that the light diffraction behavior in the single aperture is the same as a common Bessel beam.

Owing to the continuous phase gradient, the catenary aperture can be used as a unique building block in optical metasurfaces. For instance, we demonstrated a one-dimensional flat lens that can focus the incident CPL into a straight line. Under paraxial approximation, the required phase is obtained in a quadratic form:

where k is the wavenumber in free space and f is the focal length. Such phase distribution could make the metasurface function as an ideal optical Fourier analyzer⁴⁷. To realize such phase distribution using catenary-shaped apertures, the curve shape can be obtained using an integration algorithm:

where x_n and x_n+1 indicate the left and right sides of each catenary on the x axis, respectively. In general, they can be written as:

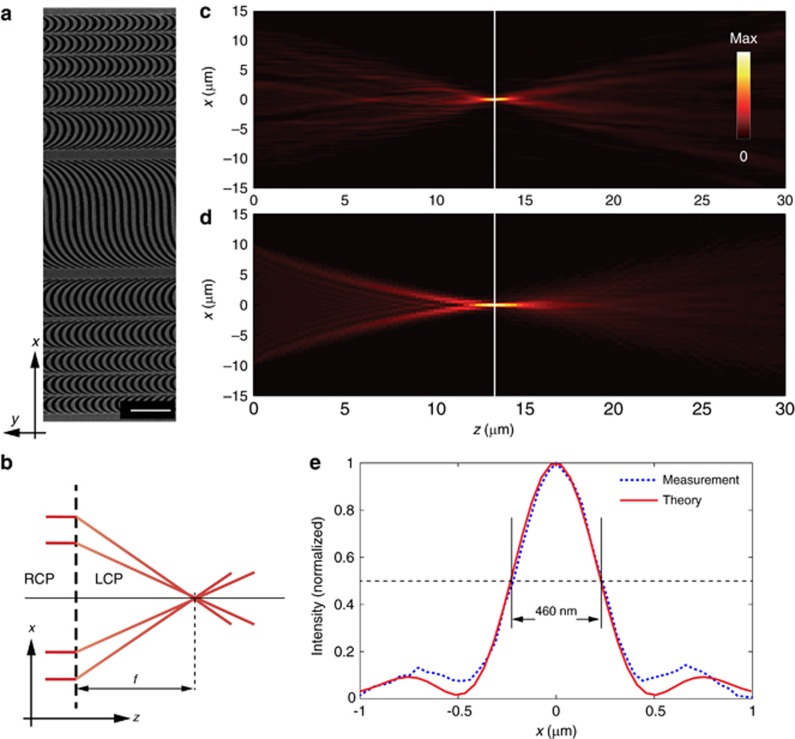
where n is an integer. In the design of the catenary lens, we set σ=1 (RCP incidence), λ=632.8 nm and f=15 μm. The sample was fabricated with a dimension of 20 × 20 μm². As shown in Figure 5a, the flat lens is composed of many catenary apertures. Because the catenaries are arranged periodically along the y axis, the phase distribution is independent of y. This is different from the single catenary, where the values of x and y are defined in a closed aperture.

Figure 5.

Catenary array serving as a one-dimensional flat lens. (a) SEM image of the fabricated sample. Scale bar=2 μm. (b) Schematic of the ray path for the flat lens. (c) Measured and (d) theoretically calculated (vectorial diffraction theory) intensity distribution for the cross-polarized component in the xz plane. The white line indicates the focal plane at z=13.5 μm. (e) Normalized intensity at the cross-section indicated in c,d.

As shown in Figure 5b, the RCP light propagating along the z direction can be converted to LCP and tightly focused by the catenary array. Since the quadratic phase described by Equation (6) is an approximation, the focal length is actually 13.5 μm, as observed in both the measurement (Figure 5c) and theoretical results (Figure 5d). Figure 5e shows the normalized intensity at the cross-section z=13.5 μm. Obviously, the measured full width at half maximum is ~460 nm, agreeing well with the theoretical result. It is also interesting to note that such a lens can serve as a concave lens when the incident light is tuned as LCP^{35, 36}.

Conclusions

In summary, we presented a new class of catenary-shaped nanoapertures to realize arbitrary phase gradient at the nanoscale and to modify the diffraction behavior predicted by classical Kirchhoff’s theory. Different from the meta-atoms/molecules included in traditional metasurfaces and metamaterials, the proposed aperture can generate a phase gradient, that is, many different phase levels, in a single unit based on the nanostructure-enhanced OSOI. Such apertures can be regarded as meta-macromolecules, which have optical properties beyond a single molecule.

We noted that the handedness-dependent scattering (SHEL) in the catenary apertures may be regarded as a form of circular dichroism (CD), that is, the differential absorption and transmission for different CPL^{11, 12, 48}, if the scattering in a certain direction is assumed as the transmission coefficient. This result is interesting because the structure of the catenary is achiral (superimposable on its mirror image). We anticipate that such CD signal may be observed in biological samples where the macromolecules have similar geometric structures as the catenaries. Moreover, both the CD and OSOI can be understood in the framework of symmetries, although they have different physical origins. While CD is determined by the mirror symmetry of both the structure of light and materials, the OSOI is related to the breaking of translational and rotational symmetries in inhomogeneous and anisotropic materials³⁰.

In addition to the giant SHEL, the catenary can be utilized as a powerful building block of optical metasurfaces, considering that the phase gradient can be quasi-continuously controlled over the 2D plane. Since the performance is independent of the excitation of SPP⁴⁵, it is straightforward to scale the device to other frequency bands by taking advantage of the scalability of Maxwell’s equations.