Skip to main content
PMC home page
Light, Science & Applications logoLink to Light, Science & Applications
. 2016 Feb 12;5(2):e16032. doi: 10.1038/lsa.2016.32

Efficient photon coupling from a diamond nitrogen vacancy center by integration with silica fiber

Rishi N Patel 1,2, Tim Schröder 1, Noel Wan 1, Luozhou Li 1, Sara L Mouradian 1, Edward H Chen 1, Dirk R Englund 1,*
PMCID: PMC6062425  PMID: 30167144

Abstract

A central goal in quantum information science is to efficiently interface photons with single optical modes for quantum networking and distributed quantum computing. Here, we introduce and experimentally demonstrate a compact and efficient method for the low-loss coupling of a solid-state qubit, the nitrogen vacancy (NV) center in diamond, with a single-mode optical fiber. In this approach, single-mode tapered diamond waveguides containing exactly one high quality NV memory are selected and integrated on tapered silica fibers. Numerical optimization of an adiabatic coupler indicates that near-unity-efficiency photon transfer is possible between the two modes. Experimentally, we find an overall collection efficiency between 16% and 37% and estimate a single photon count rate at saturation above 700 kHz. This integrated system enables robust, alignment-free, and efficient interfacing of single-mode optical fibers with single photon emitters and quantum memories in solids.

Keywords: diamond nanophotonics, fiber optics, nitrogen vacancy center, quantum optics, single photon source

Introduction

Efficient coupling of stationary quantum memories to a single spatial mode in silica fiber is of central importance in a range of quantum information processing applications, including long-distance entanglement of stationary qubits and quantum networks1,2,3,4,5. Recently, the efficient fiber coupling of atomic quantum memories also enabled large atom-cavity coupling6,7,8 and strong single-atom nonlinearities9,10. Among solid-state qubits, the nitrogen vacancy (NV) center in diamond has emerged as an attractive quantum memory due to its optically addressable and long coherence electronic and nuclear spin states11,12. These properties have enabled recent demonstrations of heralded quantum entanglement13 and teleportation14 between two separated NV centers. To improve the entanglement probability in such schemes, an open experimental challenge is to improve the efficiency with which single photons from an NV center can be channeled into a single-guided optical mode. This has motivated a variety of light collection approaches, including diamond micro-posts15, solid immersion lenses16,17,18, grating structures19,20, and inverse tapered coupling to photonic integrated circuits21. Several research efforts have also sought to integrate quantum emitters directly with optical fibers, as a way of eliminating non-essential optical components and achieving compact and nearly monolithic interfaces. Recently, fluorescence collection from colloidal quantum dots and diamond nanocrystals containing single NVs was proposed22,23 and demonstrated, often using a tapered fiber section24,25,26,27,28,29,30. However, these approaches use point-like emitters that exhibit poor collection efficiency; in addition, the spin and optical properties of NVs in diamond nanocrystals are degraded compared to bulk diamond23. It is desirable instead to transfer photons from emitters in a wave-guiding structure to an optical fiber, as was recently demonstrated for quantum dots31. Here we introduce an approach that uses adiabatic power transfer between a tapered silica fiber and a single-mode diamond micro-waveguide fabricated from high-quality CVD-grown diamond. This integrated diamond–silica waveguide system enables efficient optical collection from high-quality NV centers.

Materials and methods

Device description

We consider a tapered single-mode diamond micro-waveguide in direct contact with the tapered section of a single-mode optical fiber, as illustrated in Figure 1. The diamond micro-waveguide is positioned by van der Waals forces directly on the tapered fiber resulting in coupling between the optical modes of the two structures.

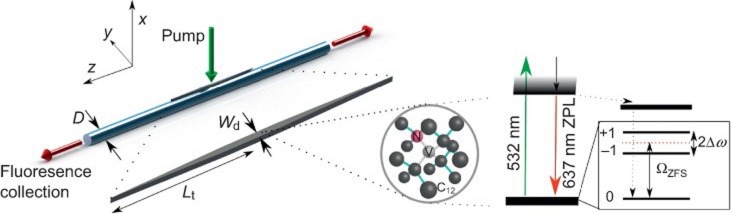
Figure 1.

Figure 1

Open in a new tab

System overview. A diamond micro-waveguide containing an NV center (gray) in parallel contact with a tapered fiber segment (blue) is schematically shown. Excitation and collection pathways are shown in green and red, respectively. The inset shows the diamond crystal lattice and the NV center spectrum. The parameters in this experiment are the fiber diameter D≈500 nm, the diamond width (at z = 0), Wd (0) = 200 nm, and the taper length Lt = 5 μm. In the NV energy level diagram, the zero-phonon line is denoted by ZPL, the zero-field-splitting frequency of 2.87 GHz by ΩZFS and the Zeeman splitting between the +1 and –1 states in a direct current (DC) magnetic field by 2Δω.

For a slowly varying diamond width, corresponding to a slowly varying effective refractive index, light in the diamond micro-waveguide remains in the fundamental mode of the combined diamond–silica structure. We analyze this problem using coupled mode analysis, following a similar analysis for coupling between a silicon waveguide to a tapered fiber32. Figure 2a plots the effective indices of the diamond and fiber modes as a function of the diamond waveguide cross-section, for a fixed fiber diameter of 500 nm. Near a diamond cross-section of 140 nm, a clear anti-crossing is observed as the matching group indices of the waveguides results in strong mode-coupling between them. The corresponding mode fields are shown in Figure 2b. If the diamond taper is swept slowly such that the optical mode remains in the ground state through the transition from the diamond into the silica waveguide, nearly 100% power transfer is possible. Specifically, the diamond taper width Wd (z) must satisfy:

graphic file with name lsa201632e1.jpg

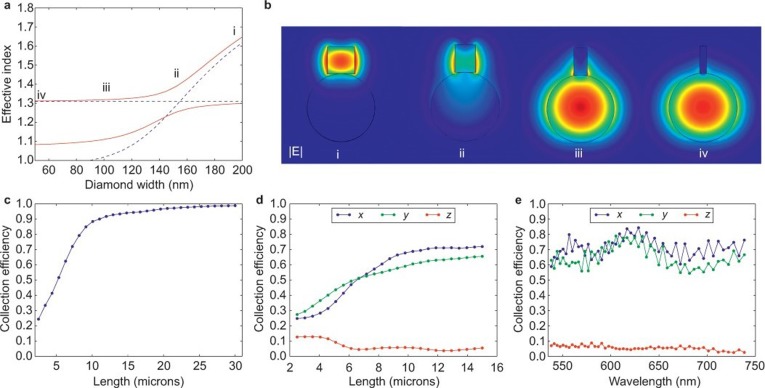
Figure 2.

Figure 2

Open in a new tab

System simulation. (a) Plot of the effective mode index of the fundamental mode of the fiber and diamond micro-waveguide versus diamond width. The blue dotted lines show the uncoupled fundamental modes of each structure. The horizontal line is the effective index of the lowest-order fiber mode. The red lines are the coupled supermodes, which show an anti-crossing. (b) The field profile of the norm of the electric field is shown for the fundamental supermode of the combined structure. From left to right, the diamond width ranges from 200 nm, 150 nm, 100 nm, and 50 nm. (c) FDTD calculation showing the fiber collection efficiency, given that only the fundamental supermode of the diamond–fiber structure is excited. (d) FDTD calculation using a dipole source of three different polarizations. Blue, green, and red are oriented along the x, y, and z directions, respectively. See Figure 1 for a coordinate inset. (e) Detailed view of the FDTD results versus wavelength for a 15 um long diamond micro-waveguide.

where 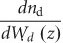Inline graphic, the rate of change of the fundamental diamond mode effective index versus diamond width, can be computed from the derivative of the uncoupled diamond band plot shown in Figure 2a. The parameters on the right-hand side of Equation (1) can be estimated from the simulation shown in Figure 2a. Using λ0 = 637 nm, Δneff = 0.13, and 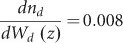Inline graphic, we thus obtained a bound 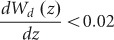Inline graphic. For Wd (0) = 200 nm, this corresponds to a taper length Lt = 10 μm. This is consistent with the finite-difference time-domain (FDTD) calculation shown in Figure 2c, confirming that the coupling efficiency increases with the length of the diamond waveguide, as expected.

Next, we consider how the orientation of the NV, which is assumed to be located at the center of the diamond micro-waveguide (see Figure 1), affects the coupling efficiency. In our simulation, we consider three orthogonal dipole polarizations along the axes shown in the inset of Figure 1a. For an x-polarized dipole, a theoretical overall collection efficiency of over 70% can be achieved, as can be seen from the collection efficiency plot for the three dipole orientations in Figure 2d. We also note that the adiabatic coupling approach has the advantage of being highly broadband, as is apparent from the FDTD calculations plotted versus excitation wavelength (Figure 2e).

Device fabrication

The system fabrication involves three main stages. First, tapered fibers were fabricated from single-mode optical fibers (Thorlabs 630HP) using a standard heat-and-pull technique33 while secured in a tapered fiber mount that is sealed to maintain a clean-air environment and to block air flow. Our setup uses a fixed hydrogen flame and two motorized stages. To prepare the fiber for tapering, we strip a 1 cm region of the outer jacket and preheat the region for 120 s. We then pull the stages in opposite directions at a speed of 30 μm s−1. Laser transmission at 630 nm is monitored throughout the pulling process, and the stages are stopped manually when the transmission begins to fall. We confirmed with scanning electron micrscope and optical images that this diameter is on the order of 500 nm.

The fiber tapering results in an adiabatic fiber mode conversion to maintain a high (≈90%) transmission of 633 nm laser light. Although especially long tapers can provide efficiencies around 97%34, we used here shorter tapers as they are easier to manipulate. Second, diamond micro-waveguides were fabricated from a 200 nm thin film of [1 0 0] electronic grade synthetic diamond using transferred hard mask lithography35. They are 12 μm long, with a 5 μm triangular taper on either side of a 2 μm section of constant width (Figure 3a). Third, we characterized and selected individual diamond micro-waveguides containing exactly one NV center before placing them onto the waist of the tapered fiber, where they adhere readily by van der Waals forces. This detachment and placement is done using a tungsten micro-manipulator tip (Ted Pella). We use a rotation stage for the fiber to align it parallel to the micro-waveguide, while the tungsten probe is controlled by a separate three-axis piezo stage. Figure 3b and 3c shows a completed device under a scanning electron microscope and optical confocal microscope, respectively.

Figure 3.

Figure 3

Open in a new tab

Device fabrication. (a) Scanning electron microscope (SEM) image of diamond micro-waveguides. (b) SEM image of a functionalized tapered fiber, in contact with a diamond micro-waveguide. (c) Optical image of assembled device. (d) Confocal scans of fluorescence detected from two fiber ends (shown in top and bottom panel). The micro-waveguide is optically pumped with a green (532 nm) laser excitation source. Light originating from a single NV center is shown in the dotted circles.

Confocal excitation and autocorrelation measurements

A home-built confocal microscope is used to excite the NV center. We use a 532 nm pump laser and focus it onto our sample using a Zeiss NA = 0.75 cover-glass corrected objective. We couple the signal from each fiber end to free-space in order to filter out the pump with two 550 nm long-pass filters. The resulting signal is coupled back into single-mode (SMF-28, Corning) fiber before being directed to two avalanche photo-diodes (APDs; Perkin-Elmer). We perform cross-correlation measurements with a histogram of start-stop time intervals using a counting module with a bin width of 0.256 ns. In a confocal scan, the NV can be identified as a bright fluorescence spot to the left of the center of the micro-waveguide (Figure 3d). Here, we excited the NV from the top while collecting photons through the left and right fiber ends, as seen in the top and bottom panels, respectively. The ends of the diamond micro-waveguides are also apparent as bright fluorescence spots on the scan. At these positions, more laser power is scattered into the fiber, causing increased fluorescence background. The bright extended spot at the right of the top panel is due to additional asymmetric scattering from the tip of the diamond waveguide. This scattering signal does not originate from NV center fluorescence, as determined from the photon statistics and spectra from these points (see Supplementary Fig. S4).

Results and discussion

Optical characterization

Optical measurements reveal the efficient collection of NV fluorescence directly coupled into a single-guided mode. We detected NV fluorescence through both the left and right fiber ends, as evidenced by the typical NV spectrum with a pronounced zero phonon line around 637 nm (Figure 4a).

Figure 4.

Figure 4

Open in a new tab

Optical characterization of tapered fiber-coupled diamond micro-waveguides. (a) Spectra in blue (red) show NV fluorescence collected through left (right) ends. The zero-phonon line and sideband are clearly detected. We observe stronger signal from the right side, as both spectra are taken under the same integration time. (b) Saturation curves showing photon count rates from NV center versus pump power collected through the fiber. The blue (red) shows collection from the left (right) without background correction. The collection from the right fiber end exhibits more background due to increased scattering into this direction of the fiber (see Figure 3d). The green curve is the sum of the left and right collection curves, with the linear background subtracted. (c) Saturation curve using objective collection with an NA = 0.75 objective. (d) Second order autocorrelation function taken using both fiber ends in a Hanbury Brown–Twiss setup. Strong photon anti-bunching with g(2) (0) < 0.2 is observed with an incident pump power on the objective of 114 μW. (e) Strong photon anti-bunching is detected with g(2) (0) < 0.5 over a range of powers below about 2.3 mW. The blue line is a guide to the eye, while the red dotted line denotes 0.5. (f) Measurements of the g(2) (τ) time constant (describing the central dip at low pump power) fitted to a linear model yield a lifetime of 15.7 ns. Error bars denote a one standard deviation error on fit parameters. (Inset) Electron-spin-resonance fluorescence dip in zero external DC magnetic field.

By varying the pump power, we observe a saturation behavior in the NV signal (Figure 4b and 4c). All fits are to a model of the form:

graphic file with name lsa201632e2.jpg

where I is the measured intensity in counts per second (cps), P is the pump power, Isat the saturation intensity, Psat the saturation pump power, and C is a fitting parameter that characterizes the linear background contribution. The fits estimate an overall Isat of 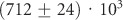Inline graphic cps from both fiber ends combined versus 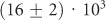Inline graphic cps from the objective. The corresponding saturation powers are approximately 380 and 485 μW, respectively. We measured the normalized second-order autocorrelation function of the fiber-coupled light with a Hanbury Brown–Twiss setup, using the fiber itself as the intrinsic beamsplitter. At an incident pump power of 114 μW, the anti-bunching with g(2) (0) = (0.15±0.02) < 0.5 indicates the presence of a single NV center; no background was subtracted from this measurement (Figure 4d). This autocorrelation data is fit to a three-level model:

graphic file with name lsa201632e3.jpg

where pf is the single photon emission probability, τ1 is a time constant for the central anti-bunching dip, τ2 is the time constant for correlation function decay at intermediate times, and c is a parameter describing the amplitude of the bunching shoulders. We then estimated the background by plotting the parameter 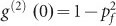Inline graphic for different values of the excitation pump power (Figure 4e). Here we identify a maximum incident pump power of 2.25 mW focused to a spot size of approximately 0.6 μm, beyond which the background emission causes g(2) (0) > 0.5. At this pump power, we use the green curve in Figure 4b to show that over 600 000 single photons per second are detected. Fitting Equation (3) for a number of different pump powers, allows us to extract the inverse time constant, 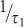Inline graphic (Figure 4f)15. We see that 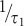Inline graphic varies linearly for small pump power and extrapolation to zero power yields a lifetime, τNV, of 15.7 ± 1.1 ns.

System efficiency

We use two different metrics to characterize our observed system efficiency. The first, relating the number of guided photons to the total possible number of photons emitted with a unity quantum efficiency, is given by:

graphic file with name lsa201632e4.jpg

where Γguided is the total excited state decay rate into the guided modes (into the fiber), and Γdecay is the total decay rate of the NV center (including both non-radiative and radiative pathways). β is a lower bound on the observed system efficiency if one assumes an NV quantum efficiency of unity. We estimate the parameter Γguided from our measurements of the observed count rate:

graphic file with name lsa201632e5.jpg

where ηapd is the quantum efficiency of our APD detectors, κtaper the transmission efficiency of our tapered fiber, and κtg the transmission efficiency of our filtering stages. In our experiment, ηapd ≈ 65%, κtaper ≈ 95%, and κtg ≈ 43%. κtaper is obtained from transmission measurements of the fiber during fabrication, and represents an upper bound on the taper transmission. It is defined as the single-sided transmission, from the center of the taper to either of the fiber ends. κtg is obtained from measuring the transmission of a 635 nm laser signal through both left and right filtering ports, providing an upper bound for the filter stage transmission. We take a weighted average of these two measurements for our estimated κtg and 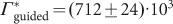Inline graphic cps directly from the parameter Isat above. Dividing out the transmission factors gives a total single photon count rate of about Γguided = (2.7±0.1) · 106 cps. We determine Γdecay as the inverse of the lifetime, 15.7 ± 1.1 ns. Finally, this gives a value of β ≈ 4.2%. This lower bound of β does not take into account the NV’s charge instability or the non-unity quantum efficiency.

In a second method of estimating the collection efficiency, we use the ratio of the guided photons to the total number of radiated photons:

graphic file with name lsa201632e6.jpg

where Γfree is the decay rate into free space modes. ηc differs from the first metric because it requires an estimation of the total number of radiated photons as opposed to the total decay rate, which includes both non-radiative and radiative terms. That is, we can write 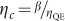Inline graphic, where ηQE is the quantum efficiency of the NV. We estimate the free space decay rate from:

graphic file with name lsa201632e7.jpg

where κtf is the transmission efficiency of our confocal microscope setup and κNA gives the fraction of photons collected into the acceptance angle of our microscope objective (NA = 0.75, cover glass-corrected Zeiss). This fraction requires an estimate of the NV orientation, which in our case can be obtained because we work with a [1 0 0] oriented diamond thin film and the facet of this sample, to a good approximation, faces the objective (See Supplementary Information for additional details)36. With FDTD simulations, we then obtained κNA. We also estimated a range for κtf based on transmission measurements of our confocal setup, and taking into account losses from the cover glass enclosing our sample. From saturation measurements acquired via the objective, we have 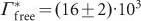Inline graphic cps. 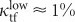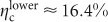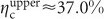Using the factors Inline graphic, Inline graphic, and κNA ≈ 18%, we estimate an efficiency of Inline graphic and Inline graphic. The large range of κtf is caused by our collection optics, as the fiber coupling efficiency is strongly dependent on the position of the sealing cover slip in the focus, and the setting of the correction ring of the objective. By comparison, our FDTD-based calculation yields a lower and upper bound on the collection efficiency of 0.36 and 0.61, respectively. We attribute the discrepancy primarily to the assumption in our simulation of a triangularly shaped diamond micro-waveguide tapered with ends going to zero width, an assumption that is not valid in the experimental system. In addition, the NV is not located exactly in the center of the adiabatic coupler, and may have different coupling efficiencies to either side. In practice, we can achieve micro-waveguide tips of about 50 nm which creates a sudden index step at which scattering losses can occur. 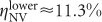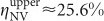Using the above estimates for the collection efficiency, we obtain quantum efficiency bounds of Inline graphic and Inline graphic.

The inset of Figure 4f shows continuous wave optically detected magnetic resonance of our NV electron spin. Separate Hahn-echo measurements on waveguides produced in the same way indicate long phase coherence times in excess of 100 μs (see Supplementary Fig. S2)37.

Discussion

For our system to be useful in larger photonic networks, multiple working devices must be fabricated. In our study, we assembled four devices similar to the one discussed in detail. In three of these systems, we measured anti-bunching with g(2) (0) < 0.5, and in one g(2) (0) ≈ 0.5 indicating the presence of a single emitter and two closely spaced emitters, respectively. The count rates for these devices were on the order of several hundred thousand counts, similar to the device discussed above. In addition, we note that the yield of the diamond waveguides we fabricated was between 5% and 10%. This is defined as the fraction of waveguides that contain a single NV near the center.

It is important to cover several limitations of our system, and to highlight some aspects for future work. We observed that the tapered fiber transmission degrades over time because of the deposition of large scatterers, such as dust. In future experiments, this can be averted by mounting the tapered section in a sealed container. Furthermore, presently our method is limited by diamond fabrication capabilities to make slowly tapering structures, as we currently attach the waveguides on the ends to a diamond substrate. With improved fabrication techniques, diamond waveguides could be made with longer taper lengths and thinner tips, improving adiabatic power transfer up to the theoretical limit close to unity. Regarding our optical pumping scheme, we currently use confocal excitation to excite individual NV centers in our devices. For a completely fiber-integrated approach, it would be interesting to use a fiber-integrated Bragg filter to allow excitation from one fiber end and collection through the second fiber end. Such a system could be cooled by simple immersion in a cryogenic fluid, eliminating the need for a confocal microscope and in principle allowing for lifetime-limited ZPL emission, an important requirement for a number of quantum information experiments.

Conclusion

We have demonstrated an approach for the efficient integration of a high-quality quantum memory directly with a silica fiber. With a raw single photon detection rate exceeding 6 · 105 cps and g2 (0) < 0.5, we show a roughly fourfold improvement over previous fiber-coupled approaches that used diamond point emitters instead of wave-guiding structures16. In addition, the fiber background is strongly suppressed allowing exceptionally low g2 (0)≈0.15 (without background subtraction) for cross-correlation measurements in a fiber-integrated system. This geometry can be used for coherent spin manipulation of a fiber-coupled spin qubit, thereby providing efficient optical access to a long-lived quantum memory. The deterministic pick and place method presented here is amenable to larger scale integration and can be extended to the evanescent integration of diamond-based nano-cavities38. Furthermore, a transmission configuration could open up possibilities for long-distance quantum communication experiments with completely fiber-integrated components.

Acknowledgments

R.N.P. thanks Amir H. Safavi-Naeini for helpful discussion and Christopher Foy for useful comments on the manuscript. R.N.P. was supported in part by the MIT SuperUROP (Undergraduate Research Opportunities Program). T.S. was supported by the Alexander von Humboldt-Foundation. E.H.C. was supported by the NASA Office of the Chief Technologist’s Space Technology Research Fellowship. Experiments were carried out in part with support from the Air Force Office of Scientific Research PECASE (supervised by G. Pomrenke). S.L.M. was supported in part by the AFOSR Quantum Memories MURI and by a fellowship from the NSF iQuISE program, award number 0801525. Fabrication of the diamond micro-waveguides was carried out in part at the Center for Functional Nanomaterials, Brookhaven National Laboratory, which is supported by the US Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-98CH10886.

Note: Accepted article preview online 8 October 2015

Footnotes

Note: Supplementary information for this article can be found on the Light: Science & Applications' website(http://www.nature.com/lsa/).

Supplementary Information

Supplementary information
Click here for additional data file. (1.6MB, pdf)

References

  1. Kimble HJ. The quantum internet. Nature 2008; 453: 1023–1030. [DOI] [PubMed] [Google Scholar]
  2. Northup TE, Blatt R. Quantum information transfer using photons. Nat Photonics 2014; 8: 356–363. [Google Scholar]
  3. Childress L, Hanson R. Diamond NV centers for quantum computing and quantum networks. MRS Bull 2013; 38: 134–138. [Google Scholar]
  4. Lončar M, Faraon A. Quantum photonic networks in diamond. MRS Bull 2013; 38: 144–148. [Google Scholar]
  5. Sprague MR, Michelberger PS, Champion TFM, England DG, Nunn J et al. Broadband single-photon-level memory in a hollow-core photonic crystal fibre. Nat Photonics 2014; 8: 287–291. [Google Scholar]
  6. Thompson JD, Tiecke TG, de Leon NP, Feist J, Akimov AV et al. Coupling a single trapped atom to a nanoscale optical cavity. Science 2013; 340: 1202–1205. [DOI] [PubMed] [Google Scholar]
  7. Tiecke TG, Thompson JD, de Leon NP, Liu LR, Vuletić V et al. Nanophotonic quantum phase switch with a single atom. Nature 2014; 508: 241–244. [DOI] [PubMed] [Google Scholar]
  8. Tiecke TG, Nayak KP, Thompson JD, Peyronel T, de Leon NP et al. Efficient fiber-optical interface for nanophotonic devices. Optica 2015; 2: 70–75. [Google Scholar]
  9. O′Shea D, Junge C, Volz J, Rauschenbeutel A. Fiber-optical switch controlled by a single atom. Phys Rev Lett 2013; 111: 193601. [DOI] [PubMed] [Google Scholar]
  10. Mitsch R, Sayrin C, Albrecht B, Schneeweiss P, Rauschenbeutel A. Directional nanophotonic atom–waveguide interface based on spin-orbit interaction of light. arXiv: 1406.0896. 2014.
  11. Maurer PC, Kucsko G, Latta C, Jiang L, Yao NY et al. Room-temperature quantum bit memory exceeding one second. Science 2012; 336: 1283–1286. [DOI] [PubMed] [Google Scholar]
  12. Bar-Gill N, Pham LM, Jarmola A, Budker D, Walsworth RL. Solid-state electronic spin coherence time approaching one second. Nat Commun 2013; 4: 1743. [DOI] [PubMed] [Google Scholar]
  13. Bernien H, Hensen B, Pfaff W, Koolstra G, Blok MS et al. Heralded entanglement between solid-state qubits separated by 3 meters. Nature 2013; 497: 86–90. [DOI] [PubMed] [Google Scholar]
  14. Pfaff W, Hensen BJ, Bernien H, van Dam SB, Blok MS et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 2014; 345: 532–535. [DOI] [PubMed] [Google Scholar]
  15. Babinec TM, Hausmann BJM, Khan M, Zhang YN, Maze JR et al. A diamond nanowire single-photon source. Nat Nanotechnol 2010; 5: 195–199. [DOI] [PubMed] [Google Scholar]
  16. Schröder T, Gädeke F, Banholzer MJ, Benson O. Ultrabright and efficient single-photon generation based on nitrogen-vacancy centres in nanodiamonds on a solid immersion lens. New J Phys 2011; 13: 055017. [Google Scholar]
  17. Hadden JP, Harrison JP, Stanley-Clarke AC, Marseglia L, Ho YLD et al. Strongly enhanced photon collection from diamond defect centers under microfabricated integrated solid immersion lenses. Appl Phys Lett 2010; 97: 241901. [Google Scholar]
  18. Siyushev P, Kaiser F, Jacques V, Gerhardt I, Bischof S et al. Monolithic diamond optics for single photon detection. Appl Phys Lett 2010; 97: 241902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Choy JT, Bulu I, Hausmann BJM, Janitz E, Huang IC et al. Spontaneous emission and collection efficiency enhancement of single emitters in diamond via plasmonic cavities and gratings. Appl Phys Lett 2013; 103: 161101. [Google Scholar]
  20. Li LZ, Chen EH, Zheng JB, Mouradian SL, Dolde F et al. Efficient photon collection from a nitrogen vacancy center in a circular bullseye grating. Nano Lett 2015; 15: 1493–1497. [DOI] [PubMed] [Google Scholar]
  21. Hausmann BJM, Shields B, Quan QM, Maletinsky P, McCutcheon M et al. Integrated diamond networks for quantum nanophotonics. Nano Lett 2012; 12: 1578–1582. [DOI] [PubMed] [Google Scholar]
  22. Chonan S, Kato S, Aoki T. Efficient single-mode photon-coupling device utilizing a nanofiber tip. Sci Rep 2014; 4: 4785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Almokhtar M, Fujiwara M, Takashima H, Takeuchi S. Numerical simulations of nanodiamond nitrogen-vacancy centers coupled with tapered optical fibers as hybrid quantum nanophotonic devices. Opt Express 2014; 22: 20045–20059. [DOI] [PubMed] [Google Scholar]
  24. Yalla R, Le Kien F, Morinaga M, Hakuta K. Efficient channeling of fluorescence photons from single quantum dots into guided modes of optical nanofiber. Phys Rev Lett 2012; 109: 063602. [DOI] [PubMed] [Google Scholar]
  25. Schröder T, Schell AW, Kewes G, Aichele T, Benson O. Fiber-integrated diamond-based single photon source. Nano Lett 2011; 11: 198–202. [DOI] [PubMed] [Google Scholar]
  26. Schröder T, Fujiwara M, Noda T, Zhao HQ, Benson O et al. A nanodiamond-tapered fiber system with high single-mode coupling efficiency. Opt Express 2012; 20: 10490–10497. [DOI] [PubMed] [Google Scholar]
  27. Liebermeister L, Petersen F, Münchow AV, Burchardt D, Hermelbracht J et al. Tapered fiber coupling of single photons emitted by a deterministically positioned single nitrogen vacancy center. Appl Phys Lett 2014; 104: 031101. [Google Scholar]
  28. Liu XD, Cui JM, Sun FW, Song XR, Feng FP et al. Fiber-integrated diamond-based magnetometer. Appl Phys Lett 2013; 103: 143105. [Google Scholar]
  29. Fujiwara M, Toubaru K, Noda T, Zhao HQ, Takeuchi S. Highly efficient coupling of photons from nanoemitters into single-mode optical fibers. Nano Lett 2011; 11: 4362–4365. [DOI] [PubMed] [Google Scholar]
  30. Henderson MR, Gibson BC, Ebendorff-Heidepriem H, Kuan K, Afshar V et al. Diamond in tellurite glass: a new medium for quantum information. Adv Mat 2011; 23: 2806–2810. [DOI] [PubMed] [Google Scholar]
  31. Davanço M, Rakher MT, Wegscheider W, Schuh D, Badolato A et al. Efficient quantum dot single photon extraction into an optical fiber using a nanophotonic directional coupler. Appl Phys Lett 2011; 99: 121101. [Google Scholar]
  32. Gröblacher S, Hill JT, Safavi-Naeini AH, Chan J, Painter O. Highly efficient coupling from an optical fiber to a nanoscale silicon optomechanical cavity. Appl Phys Lett 2013; 103: 181104. [Google Scholar]
  33. Hauer BD, Kim PH, Doolin C, MacDonald AJR, Ramp H et al. On-chip cavity optomechanical coupling. EPJ Tech Instrum 2014; 1: 1–21. [Google Scholar]
  34. Vetsch E, Reitz D, Sagué G, Schmidt R, Dawkins ST et al. Optical interface created by laser-cooled atoms trapped in the evanescent field surrounding an optical nanofiber. Phys Rev Lett 2010; 104: 203603. [DOI] [PubMed] [Google Scholar]
  35. Li LZ, Bayn I, Lu M, Nam CY, Schröder T et al. Nanofabrication on unconventional substrates using transferred hard masks. Sci Rep 2015; 5: 7802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Alegre TPM, Santori C, Medeiros-Ribeiro G, Beausoleil RG. Polarization-selective excitation of nitrogen vacancy centers in diamond. Phys Rev B 2007; 76: 165205. [Google Scholar]
  37. Mouradian SL, Schröder T, Poitras CB, Li LZ, Goldstein J et al. Scalable integration of long-lived quantum memories into a photonic circuit. Phys Rev X 2015; 5: 031009. [Google Scholar]
  38. Li LZ, Schröder T, Chen EH, Walsh M, Bayn I et al. Coherent spin control of a nanocavity-enhanced qubit in diamond. Nat Commun 2015; 6: 6173. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information
Click here for additional data file. (1.6MB, pdf)

Articles from Light, Science & Applications are provided here courtesy of Nature Publishing Group

RESOURCES