BIOMECHANICS OF THE SOFT-PALATE IN SLEEP APNEA PATIENTS WITH POLYCYSTIC OVARIAN SYNDROME

Abstract

Highly compliant tissue supporting the pharynx and low muscle tone enhance the possibility of upper airway occlusion in children with obstructive sleep apnea (OSA). The present study describes subject-specific computational modeling of flow-induced velopharyngeal narrowing in a female child with polycystic ovarian syndrome (PCOS) with OSA and a non-OSA control. Anatomically accurate three-dimensional geometries of the upper airway and soft-palate were reconstructed for both subjects using magnetic resonance (MR) images. A fluid-structure interaction (FSI) shape registration analysis was performed using subject-specific values of flow rate to iteratively compute the biomechanical properties of the soft-palate. The optimized shear modulus for the control was 38 percent higher than the corresponding value for the OSA patient. The proposed computational FSI model was then employed for planning surgical treatment for the apneic subject. A virtual surgery comprising of a combined adenoidectomy, palatoplasty and genioglossus advancement was performed to estimate the resulting post-operative patterns of airflow and tissue displacement. Maximum flow velocity and velopharyngeal resistance decreased by 80 percent and 66 percent respectively following surgery. Post-operative flow-induced forces on the anterior and posterior faces of the soft-palate were equilibrated and the resulting magnitude of tissue displacement was 63 percent lower compared to the pre-operative case. Results from this pilot study indicate that FSI computational modeling can be employed to characterize the mechanical properties of pharyngeal tissue and evaluate the effectiveness of various upper airway surgeries prior to their application.

1. Introduction

Obstructive sleep apnea (OSA) is a disorder that involves frequent collapse of the pharynx followed by arousal to maintain airway patency (Fogel et al., 2001). OSA decreases cognitive performance and increases daytime sleepiness. Increased collapsibility of the upper airway in snorers and subjects with OSA could be attributed to neuromuscular deficiencies of the pharyngeal dilator muscles and abnormal stiffness of airway structures (Ayappa and Rapoport, 2003). Upper airway obstruction in OSA has been frequently reported to occur in the velopharyngeal region (Hillman et al., 2003). Treatment options for sleep apnea include noninvasive methods such as continuous positive airway pressure (CPAP) and the use of mandibular advancement devices and invasive surgical procedures that involve excision of tissue to increase airway caliber (Ayappa and Rapoport, 2003). Polycystic ovarian syndrome (PCOS) is an endocrine disorder that affects 5 to 10% of pre-menopausal women, is often characterized by oligoanovulation and chronic hyperandrogenism (Vgontzas et al., 2001) and is commonly associated with OSA (Fogel et al., 2001). It has been suggested that high androgen levels increase visceral fat in these subjects resulting in obesity and sleep-disordered breathing (Fogel et al., 2001). However, high prevalence of OSA in PCOS (Vgontzas et al., 2001) cannot be fully explained by elevated body mass index (BMI) or hyperandrogenism (Tasali et al., 2008).

Computational fluid dynamics (CFD) has been employed to describe airflow patterns in adult (Wei et al., 2017) and pediatric female subjects (Wootton et al., 2014; Wootton et al., 2016). The assumption of a rigid airway wall in these aforementioned studies is applicable to subjects with high stiffness of tissue supporting the pharynx. Computational structural mechanics (CSM) has been employed to study the collapsibility of upper airway tissue in OSA patients (Liu et al., 2018; Moxness et al., 2018). Airflow-induced motion of compliant pharyngeal tissue has also been modeled using fully coupled fluid-structure interaction (FSI) simulations (Pirnar et al., 2015; Wang et al., 2012; Zhao et al., 2013; Zhu et al., 2012). However, the stiffness prescribed to the structural domain was obtained from measurements of tissue compliance that were not subject-specific. Mechanical properties of the human soft-palate have been estimated previously using uniaxial testing of tissue specimens (Birch and Srodon, 2009), and MR elastography (MRE) (Cheng et al., 2011). CSM has also been employed to estimate mechanical properties of airway tissue in adults (Carrigy et al., 2016) and pediatric OSA subjects (Subramaniam et al., 2017; Subramaniam et al., 2016b). These computational models assumed a uniformly distributed static pressure on the pharyngeal wall and required prior knowledge of the critical closing pressure. Flow-induced forces that deform airway tissue consist of shear and normal components (Zhu et al., 2012) and can be computed using FSI. FSI simulations have been employed previously to noninvasively compute viscoelastic properties of adherent osteocytes in fluid flow (Qiu et al., 2014). The present study describes a non-invasive method that combines medical image analysis and simulations of flow-induced airway tissue motion to estimate biomechanical properties of the soft-palate in a female child with PCOS and OSA and a non-OSA matched control. The estimated mechanical properties are then employed in the FSI model to simulate the effectiveness of a virtual surgical procedure to minimize the possibility of airway occlusion.

2. Methods

2.1 Subjects

We studied two Hispanic female subjects with PCOS, one with OSA and one without. The OSA subject was 15.3 years old with a Body Mass Index (BMI) of 42 kg/m² (BMI z-score 2.5) and apnea-hypopnea index (AHI) of 36 events per hour. The control was 14.9 years old with a BMI equivalent to 43 kg/m² (BMI z-score 2.6) and AHI of 0.8 events per hour. Both were recruited at the Montefiore Medical Center, Bronx, NY (Wagshul et al., 2013). Informed consent was obtained from the subjects and the study was approved by the Institutional Review Board at the Albert Einstein College of Medicine.

2.2 MR Imaging and Flow Waveform Acquisition

Breathing airflow waveforms were collected from a nasal cannula coupled to a pressure transducer (TSD-160B, Biopac Systems Inc., Goleta, CA). A National Instruments data acquisition board (DAQCard-6036E coupled to a SCB-68 board) was used to digitize the signal and was displayed on a custom graphical user interface written for Labview (National Instruments, Austin, TX). Magnetic resonance (MR) image acquisition was performed during wakefulness without any sedation. The MR images were collected on a 3T Philips Achieva scanner (Philips Medical System, Best, Netherlands). The patient was positioned in the radiofrequency (RF) coil and head and neck motion were constrained using padding on both sides of the head. The dynamic study used a 3D, retrospectively-gated, turbo gradient echo sequence. Images (1.2 mm isotropic resolution) were acquired over the complete respiratory cycle in 10 equal phase increments. Additional details regarding the gating system, imaging protocol and acquisition of airflow waveforms have been described elsewhere (Wagshul et al., 2013; Wootton et al., 2016).

2.3 Reconstruction and Discretization of Fluid and Solid Domains

Sagittal MR images corresponding to the end of the inspiratory phase (i.e. beginning of exhalation) and the peak expiratory phase of the breathing cycle were employed in our study. The choice of modeling the expiratory phase stemmed from previous observations of reduction in the nasopharyngeal and velopharyngeal cross-sectional areas during peak exhalation in PCOS patients with severe OSA (Wootton et al., 2016). We hypothesized that differences in the magnitude of flow-induced forces on the anterior and posterior faces of the soft-palate resulted in posterior movement of the velum and reduced airway caliber. The images were imported into the Mimics (Materialise Inc., Plymouth, MI) image processing software for reconstruction of anatomically accurate geometries of the upper airway and soft-palate. Three-dimensional (3D) models of the soft-palate and airway comprising of the pharynx, oral airway between the tongue and soft-palate, trachea and nasal airway were segmented using a thresholding algorithm for the control and apneic subjects. To simulate the effects of the surgical technique of adenoidectomy, palatoplasty and genioglossus advancement, 10 mm of adenoid tissue, 6 mm of palate tissue and 2 mm of tongue tissue were ‘virtually’ removed (Subramaniam et al., 2017) for the OSA case (Fig. 1a). The ratio of the excised tissue length to the total length of the soft-palate was 15 percent. The proportion of excised tissue was comparable to the same employed in a previous study from our research group (Mylavarapu et al., 2016). The influence of individual virtual surgeries on pharyngeal airflow has been described previously (Mylavarapu et al., 2013) and was not considered in this analysis. The lateral extents of the soft-palate were similar to previous computational studies involving flow-induced motion of upper airway structures in pediatric OSA patients (Subramaniam et al., 2017). The levator veli palitini and musculus uvulae were not included in the computational model due to the relatively lower image contrast between individual muscle groups and limited lateral extents of the MR images (Wagshul et al., 2013). Previous studies involving computational modeling of soft-palate movement in response to airflow assumed that the tissue was immersed in the pharynx (Wang et al., 2012; Zhu et al., 2012) and a similar approach was adopted in our study (Fig. 1b).

Figure 1.

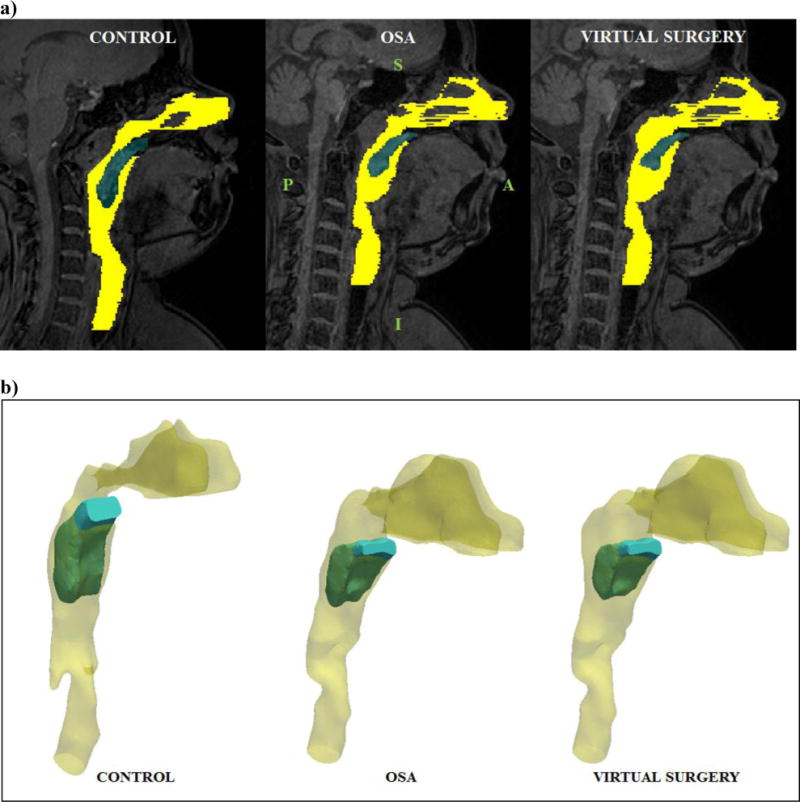
a) Mid-sagittal MR image (end inspiratory phase) corresponding to the control, OSA patient and virtual surgery (Note: yellow – pharynx, blue – soft-palate, S – Superior, I – Inferior, A – Anterior, P – Posterior, Virtual surgery – palatoplasty: 6 mm, adenoidectomy: 10 mm, genioglossus advancement – 2 mm, Removal of soft tissue increases airway caliber locally) b) Three-dimensional views of the reconstructed airway and tissue geometries corresponding to the control, apneic and virtual surgery cases.

Surface artifacts were then removed by smoothing the coarse geometric models. A fixation surface was created for the soft-palate at the hard palate. Inlet and outlets for the airway were generated at the trachea and nostrils respectively using Mimics. Common interfaces between the soft-palate and airway were then identified by exporting the pre and post-operative geometries to 3-Matic (Materialise Inc., Plymouth, MI). Surface meshes of the airway for the control, OSA and virtual surgery (VS) cases were refined at the fluid-solid interface and at narrow cross-sections using 3-Matic, to obtain better resolution of flow variables. Volume meshes for the airway and soft-palate (Fig. 2a) were then generated using ANSYS T-Grid (ANSYS Inc., Canonsburg, PA). Immersion of the soft-palate resulted in a thin layer of fluid elements on the lateral walls of the soft-palate (Zhu et al., 2012). The thickness of this layer was ensured to be less than 10% of the local tissue width to minimize airflow leakage. This layer of fluid maintained the continuity of the fluid-solid interface and reduced the possibility of solver instabilities while updating the mesh for the flow domain. We employed tetrahedral cells for the flow (Wootton et al., 2016) and structural domain (Subramaniam et al., 2017). Linear tetrahedral elements generated for the tissue were converted into quadratic tetrahedrons (Carrigy et al., 2016) since the latter are preferable for modeling nearly incompressible materials. Table 1 summarizes the mesh resolutions for the fluid and structural domains. It should be noted that the mesh resolution of the flow and solid domains were of the same order of magnitude as that employed in a previous study (Subramaniam et al., 2017).

Figure 2.

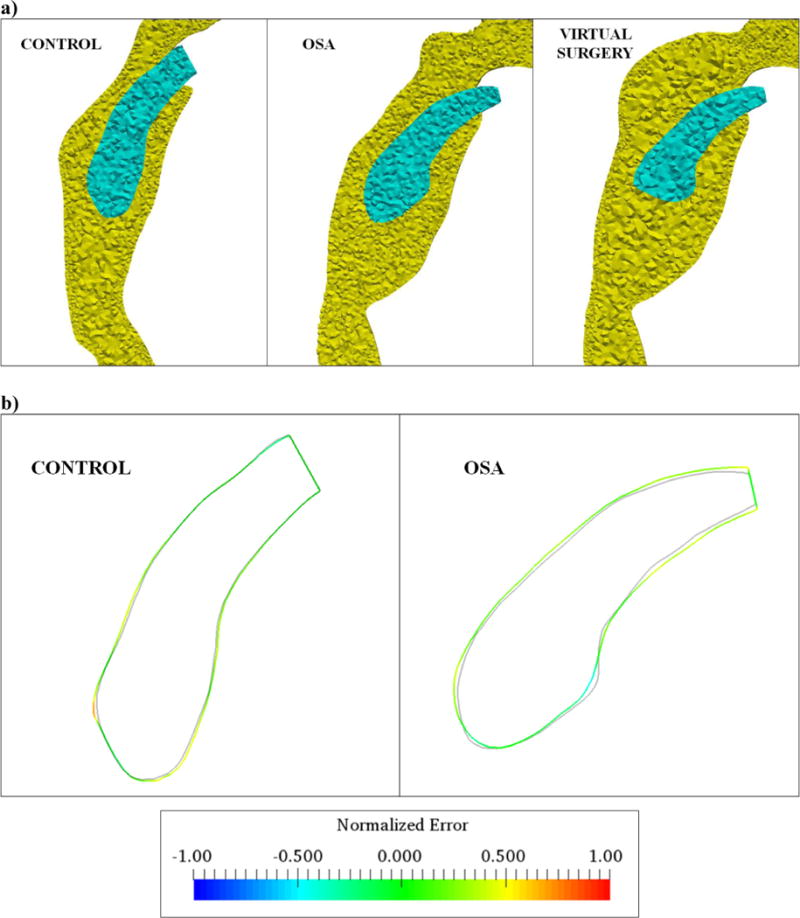
a) Discretization of the flow (yellow) and structural (blue) domains corresponding to the control, OSA and virtual surgery cases b) Mid-sagittal outlines of the soft-palate at peak exhalation obtained from MR imaging (lines colored by the normalized error) and computational modeling (solid gray line) for the control and OSA patients considered in the study (Note: Error computed as the signed distance between the imaged and simulated outlines).

Table 1.

Summary of mesh resolutions for flow and structural domains (Note: Four node and ten node tetrahedrons employed for fluid and solid domains. 1600 quadratic tetrahedrons were employed over the maximum thickness of the soft-palate).

Case	Flow Domain	Structural Domain
Control	800000	90000
OSA	700000	60000
Virtual surgery	900000	50000

2.4 Computational Modeling of Flow-induced Tissue Motion

Transitional or fully turbulent flow in the human upper airway corresponding to physiological flow rates has been modeled previously using the incompressible Reynolds Averaged Navier Stokes (RANS) equations expressed in Einstein notation,

$$\begin{gathered} \frac{\partial \overline{v_i}}{\partial x_i}=0 \\ {\rho }_f\left(\frac{\partial \overline{v_i}}{\partial t}+\overline{v_i}\frac{\partial \overline{v_f}}{\partial x_i}\right)=-\frac{\partial \overline{P}}{\partial x_i}+\frac{\partial }{\partial x_i}\left(2\mu S_{ij}-R_{ij}\right) \\ {S}_{ij}=\frac{1}{2}\left(\frac{\partial \overline{v_i}}{\partial x_j}+\frac{\partial \overline{v_j}}{\partial x_i}\right) \\ {R}_{ij}={\rho }_f\overline{v_i^{{ }^{\prime }}{v}_j^{{ }^{\prime }}} \end{gathered}$$

Where P is the fluid pressure, v is the flow velocity, μ is the dynamic viscosity, ρ _f is the fluid density, S_ij is the mean rate of strain tensor, R_ij is the Reynold’s stress tensor and the bar denotes time average. The present study employs the k-ω shear stress transport (SST) turbulence model to close the RANS equations since it provides an enhanced description of flows involving adverse pressure gradients and curved boundary layers (Subramaniam et al., 2017). A no-slip boundary condition was prescribed on the airway wall. Flow waveforms for 10 normal tidal breaths were averaged for the control and apneic subject (Wootton et al., 2014) to compute the peak expiratory flow rate. Accordingly a flow rate corresponding to 10 liters per minute was prescribed at the inlet in the trachea (Wootton et al., 2016) and an ambient pressure boundary condition was applied at the nostrils. Simulations of soft tissue movement in response to airflow at peak inspiratory and expiratory flows have been performed previously using a transient flow solver (Wang et al., 2012) and the same was utilized in our study. It should also be noted that although boundary conditions were steady in time, we employed the unsteady solver to account for possible unsteadiness in the velocity field arising from the vortex shedding, as described in previous studies (Wootton et al., 2014; Wootton et al., 2016). Pressure, momentum and turbulence terms were discretized using a second-order upwind scheme. A coupled formulation was adopted to achieve pressure-velocity coupling (Subramaniam et al., 2017). A least-squares cell-based scheme was employed to evaluate gradients. Time integration was performed using a second-order implicit scheme that enabled selection of larger time steps since the scheme is unconditionally stable (Wang et al., 2012).

The incremental form of the momentum conservation law describing the displacement of the soft-palate, in the updated Lagrangian formulation (Wiedemair et al., 2012) is given by,

$${\displaystyle \underset{V_u}{\int }{\rho }_s\frac{\partial }{\partial t}\left(\frac{\partial \delta \mathit{u}}{\partial t}\right)d{V}_u={\displaystyle \underset{V_u}{\int }{\rho }_s\delta {\mathit{f}}_{\mathbf{b}}d{V}_u+{\displaystyle \underset{S_u}{\int }{n}_u•(\delta {\sum }_u+{\sum }_u•\delta F_u^T+\delta {\sum }_u•\delta F_u^T)d{S}_u}}}$$

Where u is the displacement vector, f_b is the body force vector, ρ_s is the density of the solid, F is the deformation gradient tensor, Σ is the second Piola-Kirchhoff stress tensor and subscript u indicates quantities corresponding to the preceding time step (Wiedemair et al., 2012). The nonlinear behavior of the soft-palate was approximated using the neo-Hookean material (Subramaniam et al., 2017). Body forces arising from gravity were not considered since the MR images were acquired in supine position (Wootton et al., 2014). A zero displacement boundary condition was prescribed at the fixation surface. The density and Poisson’s ratio of the soft-palate was assumed to be 1100 kg/m³ and 0.475 respectively. A FSI boundary condition was applied at the interface between the airway and tissue (Wang et al., 2012),

$$\begin{gathered} {\sigma }_{ij}^s•{\mathit{n}}_s+{\sigma }_{ij}^f•{\mathit{n}}_f=0 \\ {v}_i=\frac{\partial u_i}{\partial t} \end{gathered}$$

Where σ^s and σ^f correspond to the solid and fluid stress tensors, n_s and n_f denote the outward normal vectors corresponding to the structural and flow domains. In order to maintain the aforementioned boundary condition, the mesh for the flow domain was moved using the arbitrary lagrangian-eulerian (ALE) method. The grid was remeshed at every time step and smoothed using a diffusion based scheme to maintain mesh quality and minimize the possibility of negative cell volumes. Governing equations for the flow and structural domain were solved using ANSYS multi-physics software. The ANSYS System Coupling code was employed to communicate forces from the ANSYS Fluent flow solver to the ANSYS Mechanical structural solver and relay the resulting displacements to the flow solver to update the mesh and flow variables. The coupling code employs a stagger loop to ensure that flow, structural and data transfer variables are converged at the end of each step. 20 iterations were observed to be sufficient for each stagger loop. A time step corresponding to 0.0025 s was employed in our study and 70 coupling steps were simulated to fulfill the convergence criteria defined in previous studies (Subramaniam et al., 2017).

3. Results

3.1 Inverse Estimation of Biomechanical Properties

Mechanical properties of the soft-palate for the control and apneic subjects were estimated using a shape registration method described in this section. An initial guess value of the shear modulus corresponding to 2420 Pa obtained previously using MRE (Brown et al., 2015) was employed in this study. FSI computations of soft-palate movement were performed for the flow boundary conditions described in the previous section and the shear modulus was iteratively changed to match peak expiratory tissue displacements obtained using MR imaging. A ‘registration error’ was computed at the end of the iteration by comparing the mid-sagittal profiles of the soft-palate obtained from simulations with the same obtained from imaging. The registration error was defined as the signed distance between the two profiles. The iterative process was continued until the error was minimized (Qiu et al., 2014). Figure 2b indicates the simulated (gray color) and imaged (colored by the normalized error) tissue outlines at peak expiration. As can be seen, good agreement was obtained between the two profiles for both subjects. The shear modulus estimated from the optimization was 10000 Pa and 7250 Pa for the control and apneic subjects respectively.

3.2 Virtual Surgery

Figure 3a shows contour plots of flow velocity magnitude in the velopharynx for the control, OSA and virtual surgery cases at peak exhalation. As can be seen for the control and preoperative OSA case, the flow accelerated at the narrowest cross-section. The magnitude of flow velocity, size and strength of the separation region in the oral airway were comparable for the healthy and pre-operative apneic subjects. The flow remained attached to the posterior surface of the soft-palate for both subjects. For the post-operative case, magnitude of flow velocity at the narrowest cross-section in the velopharynx was 80 percent lower than the corresponding preoperative magnitude. Moreover, palatoplasty resulted in separation of flow on the posterior surface of the soft-palate. We recognized that the absence of the flow separation for the preoperative case could be attributed to the streamline shape of the soft-palate prior to the palatoplasty surgery. Additionally, the genioglossus advancement increased the stagnation region in the oral airway. The resistance of the retropalatal airway was computed as the ratio of the velopharyngeal pressure drop to the peak expiratory flow rate. The velopharyngeal resistance for the control (0.5 Pa/lpm) was 67 percent higher than the apneic subject (0.3 Pa/lpm). Following surgery, the resistance decreased by 66 percent. The higher resistance for the normal subject resulted from a smaller airway cross-sectional area in the choanae. Higher airway resistance in controls compared to OSA has been documented in previous computational studies involving a rigid pharynx (Wootton et al., 2014).

Figure 3.

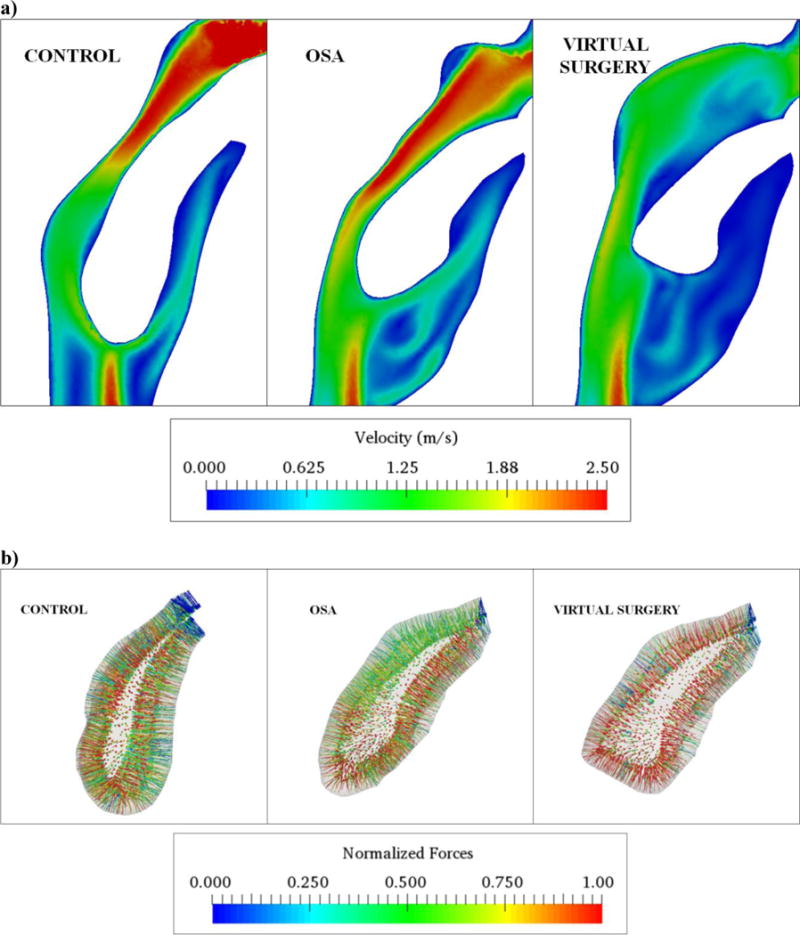
a) Contour plots describing velopharyngeal airflow patterns in the mid-sagittal plane for the control, apneic and virtual surgery cases at peak exhalation b) Vector plots describing the three-dimensional distribution of normalized flow-induced forces at the fluid-solid interface for the control, apneic and virtual surgery cases at peak exhalation (Note: Forces normalized by the respective maximum values. Normalization performed to enable comparison between the three cases).

3D distribution of forces at the fluid-solid interface is indicated in Fig. 3b. As can be seen, the forces were equilibrated for the control and virtual surgery cases. Higher forces were obtained on the anterior face of the soft-palate adjacent to the oral airway as compared to the same on the posterior face for the pre-operative case. This observation was in good agreement with recently concluded CFD studies for PCOS patients (Wootton et al., 2016). Furthermore, forces on the right and left walls were equilibrated for all cases and resulted in negligible lateral tissue motion. Figure 4 summarizes the mid-sagittal contour plots of peak expiratory palate displacement and mechanical stress for the three cases. As indicated in Fig. 4a, maximum tissue displacement was observed in the velum for the control, apneic and virtual surgery cases. However, the magnitude of displacement for the pre-operative case was nearly 300 percent higher than the control. The displacement decreased by 63 percent following surgery. The location and magnitude of displacements were in good agreement with previous FSI studies involving the soft-palate (Wang et al., 2012; Zhu et al., 2012). Maximum mechanical stresses were observed in the proximity of the hard palate for all the cases (Fig. 4b). Stresses for the OSA case were greater than the control by 67 percent. Higher stresses in the apneic subject resulted from a smaller tissue cross-sectional area at the fixation. The stresses for the virtual surgery were lower than the control by 34 percent. The aforementioned flow and mechanical variables for the control, apneic and virtual surgery cases are summarized in Table 2.

Figure 4.

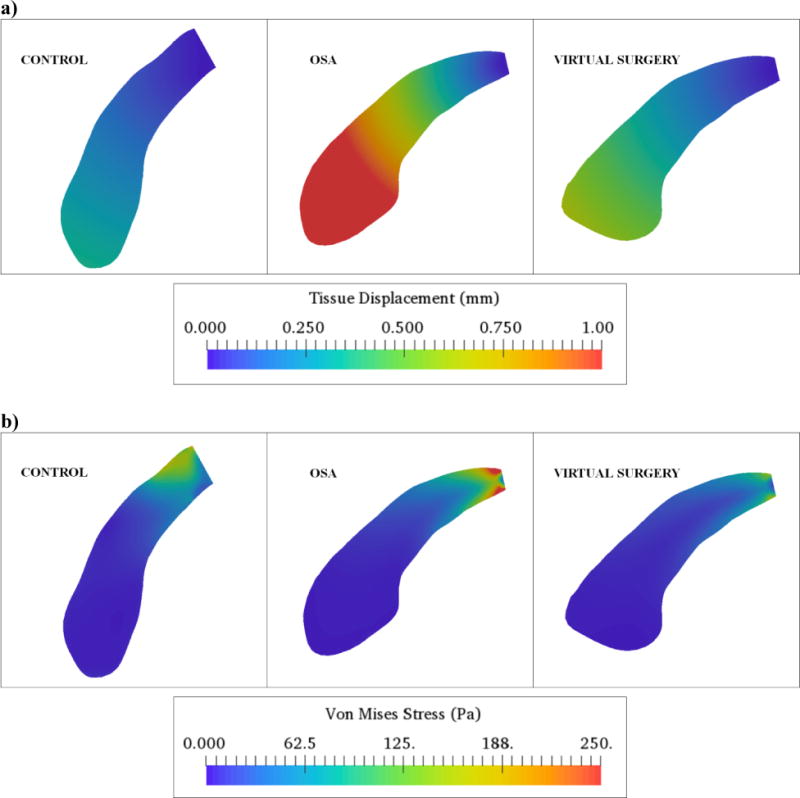
a) Tissue displacement contours in the mid-sagittal plane for the control, apneic and virtual surgery cases at peak expiratory airflow b) Mechanical stress variation in the mid-sagittal plane for the control, apneic and virtual surgery cases at peak expiratory airflow.

Table 2.

Comparison of flow and mechanical variables for control, apneic and virtual surgery cases (Note: Maximum flow velocity evaluated at narrowest cross-section in velopharynx).

Case	Maximum Flow Velocity (m/s)	Velopharyngeal Resistance (Pa/lpm)	Maximum Stress (Pa)	Maximum Displacement (mm)
Control	2.4	0.5	240	0.4
OSA	2.5	0.3	400	1.6
Virtual Surgery	0.5	0.1	160	0.6

4. Discussion

The shear modulus of the soft-palate was comparable to the values employed in previous computational studies (Huang et al., 2005; Wang et al., 2012). However, the estimated stiffness was significantly greater than the same obtained from mechanical testing and MRE. The deformed geometry of the soft-palate could be a result of both passive and active neuromuscular response, since the scans were acquired during wakefulness. Previous experimental (Wakeling et al., 2002) and computational (Pelteret and Reddy, 2012) studies have shown that muscle activity can damp tissue motion by decreasing the compliance (i.e. increasing the stiffness). The higher value of the estimated shear modulus could be potentially attributed to the activation of muscle fibers. Truly passive mechanical properties of airway tissue would have to be estimated using mechanical testing, although some studies have also proposed to obtain the same using MRE with respiratory gating (Cheng et al., 2011). Activation of the levator veli palitini and musculus uvulae has been studied previously using CSM (Inouye et al., 2016) and the same would have to be considered in a future study to model flow-induced palate movement during wakefulness. Modeling the same would necessitate MR images with higher image contrast between individual tissue structures (Perry et al., 2014). Tissue viscoelasticity (Bilston and Gandevia, 2014) would also have to be suitably incorporated into the constitutive model chosen in this study. The neo-Hookean material model would have to be eventually substituted with the Fung model (Pelteret and Reddy, 2012), since the latter provides a better approximation of the exponential stress-strain response of airway tissue.

As described in a previous study, shear modulus of pharyngeal tissue estimated iteratively is sensitive to the choice of volumetric airflow (Subramaniam et al., 2017). Recognizing the possible breath-to-breath variations in airflow volume, it would be necessary to repeat the optimization process for the highest and lowest values of expiratory airflow and determine a range of tissue elasticity for each subject. The present study described estimation of material properties for one of several upper airway structures, to minimize the number of unknowns. Inclusion of the tongue, lateral wall tissue, adenoid and posterior wall mucosa could significantly increase the complexity of the optimization problem. Anisotropic material properties of upper airway tissue would also have to be estimated since previous imaging studies have indicated variations in tissue compliance along the length and circumference of the pharynx (Brown et al., 2015; Subramaniam et al., 2016a). The presented methodology would have to be repeated for the same subjects under conditions of sedation-induced or natural sleep to evaluate possible variations in tissue elasticity resulting from reduced neuromuscular control. Notwithstanding the aforementioned limitations, the proposed registration method offers a promising technique to estimate mechanical properties of upper airway tissue. Although lateral movements of the uvula were not observed in the dynamic MR images, the same could potentially increase the complexity of the profile matching methodology. Besides, a higher spatial resolution of the MR images would significantly enhance the shape registration technique employed in this study.

The virtual surgery was performed to demonstrate the effect of increasing the airway caliber on flow-induced motion and stresses of supporting tissue. The genioglossus advancement and adenoidectomy surgeries were performed in addition to palatoplasty since previous computational studies indicated significantly reduced airway resistance in pediatric OSA patients following virtual excision of adenoid and tongue tissue (Mylavarapu et al., 2016). Besides, palate shortening surgeries could potentially result in nasal regurgitation of fluids while drinking, difficulty swallowing, voice changes, smell and taste disturbances as reported previously (Franklin et al., 2009). Palate implant surgeries have been shown to minimize discomfort to patients (Nordgård et al., 2004) and the influence of the same would be evaluated using FSI in a future study. The virtual surgeries presented here would also be validated subsequently using post-operative MR images (Luo et al., 2014). Although occlusion of the velopharyngeal airway was observed and modeled during the expiratory phase, inspiratory airway collapse could potentially occur when the tongue and soft-palate are in contact. Removal of the adenoids would significantly decrease the airway resistance and tissue stresses in this scenario as observed in a recent study (Subramaniam et al., 2017). The conformal mesh FSI method adopted in this study is suitable for moderate displacements of the soft-palate (~1 to 2 mm) and partial airway occlusion. Modeling complete airway closure could be potentially achieved using non-conformal grid methods such as the immersed boundary technique (Zheng et al., 2009).

The least airway tissue stress has been previously reported to occur at the end of exhalation (Bilston and Gandevia, 2014). Tissue pre-stress resulting from inspiratory flow-induced forces would thereby have to be considered and the effectiveness of additional invasive and non-invasive treatments for sleep disordered breathing would have to be estimated by modeling the complete respiratory cycle. Future studies would also include more subjects to define endpoints based on tissue elasticity and aid clinicians in obtaining an improved description of sleep apnea in patients with polycystic ovarian syndrome.

5. Conclusions

We presented an in-vivo methodology to estimate the subject-specific stiffness of the soft-palate using image-based computational modeling. Airway tissue was more compliant for the apneic subject as compared to the healthy control. The effectiveness of a surgical procedure was virtually assessed using the proposed computational model. The surgical procedure equilibrated the flow-induced forces acting on the soft-palate and damped the tissue motion thereby minimizing the possibility of airway occlusion, at least for the conditions tested in this study.