Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2018 Jun 20;4(7):832–839. doi: 10.1021/acscentsci.8b00157

Improving the Mechanical Stability of Metal–Organic Frameworks Using Chemical Caryatids

Seyed Mohamad Moosavi †, Peter G Boyd †, Lev Sarkisov ‡, Berend Smit †,§,*
PMCID: PMC6062841  PMID: 30062111

Abstract

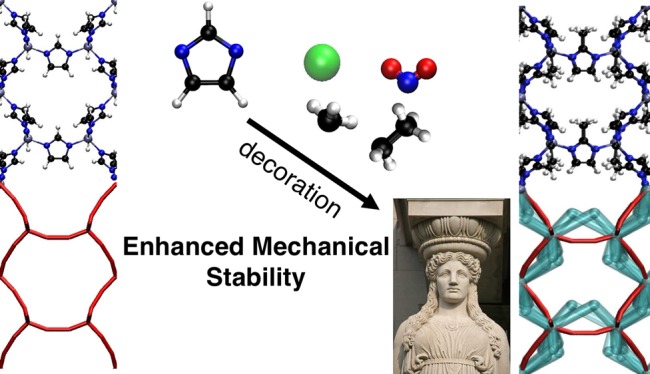
graphic file with name oc-2018-001578_0006.jpg

Metal–organic frameworks (MOFs) have emerged as versatile materials for applications ranging from gas separation and storage, catalysis, and sensing. The attractive feature of MOFs is that, by changing the ligand and/or metal, they can be chemically tuned to perform optimally for a given application. In most, if not all, of these applications one also needs a material that has a sufficient mechanical stability, but our understanding of how changes in the chemical structure influence mechanical stability is limited. In this work, we rationalize how the mechanical properties of MOFs are related to framework bonding topology and ligand structure. We illustrate that the functional groups on the organic ligands can either enhance the mechanical stability through formation of a secondary network of nonbonded interactions or soften the material by destabilizing the bonded network of a MOF. In addition, we show that synergistic effect of the bonding network of the material and the secondary network is required to achieve optimal mechanical stability of a MOF. The developed molecular insights in this work can be used for systematic improvement of the mechanical stability of the materials by careful selection of the functional groups.

Short abstract

The mechanical stability of metal−organic frameworks can be significantly enhanced and/or tuned by rational decoration of ligands with functional groups via secondary networks.

Introduction

Like any other material, metal–organic frameworks (MOFs), as an important class of porous materials with large diversity of pore shapes and sizes, and rich chemical functionalities must pass the stability criteria to be used in most practical applications.1−3 Despite having superior performance for many applications, MOFs are vulnerable with respect to stability compared to the competing materials. For instance, due to the relatively weak metal–ligand coordination bonds, many MOFs are chemically unstable and have low endurance in different types of chemicals environments, e.g., acidic or basic environment.3 Significant progress has been made in developing MOFs that are chemically stable, e.g., zirconium-based MOFs.4 Since applications of MOFs often involve repetitive, cyclic temperature and pressure variations and capillary forces exerted by guest molecules, sufficient mechanical stability is of equal importance.5,6 The mechanical stability for porous materials measures the stiffness of a material to withstand its pore size and structure under mechanical load. Clearly, deformations due to external pressure will disrupt pore shape and size, resulting in significantly reduced performance. In this study, we focus on strategies to improve the mechanical stability of a particular MOF.

The mechanical properties of materials vary by several orders of magnitude with changing atomic composition and/or crystal structure.7−9 As the mechanical stiffness, i.e., modulus of elasticity, typically scales quadratically with the density,10 mechanical stability is of particular importance for applications of low-density materials, such as MOFs.6,11,12 For these materials special strategies are often required to improve their mechanical stability. Often these strategies are inspired by nature (e.g., wood and bones13,14) and involve a fractal and hierarchical design to make highly connected materials over multiple length scales.15−17 Indeed, improving the mechanical stability of MOFs by tuning the chemistry has become an important focus of attention.3,18−20 In analogy to the concept of high connectivity of the hierarchical design of materials, it has been shown that the MOFs with high degrees of framework interconnectivity, i.e., high coordination number of metal nodes, have improved the mechanical stability.18,21 However, a particular MOF can not be easily replaced for all applications, and therefore, Kapustin et al. developed a strategy to retrofit a particular MOF by adding additional ligands to the framework.20 This strategy is robust but limited to the MOFs that permit ligand installation.22,23 In both cases, the mechanical stability is improved by increasing the connectivity of the bonding topology.

In this work, we explore the option of decorating the organic ligands of a MOF with functional groups. The significant progress in computational material science in in silico generation of MOFs24,25 and reliable prediction of their mechanical properties11,26 permits studying a large and diverse set of materials to extract structure–property relationships to design materials with enhanced mechanical stability. We show that the nonbonded interactions play an important role in the stiffness of the materials, and therefore, strategically placed functional groups can introduce extra framework connectivity via nonbonded interactions. This secondary network of nonbonded interactions can enhance the mechanical stability of the framework considerably. We use the term “chemical caryatids” for those functional groups that are contributing in carrying the mechanical load applied to the material. In addition, we show that the optimum mechanical stability of a MOF framework is obtained by the cooperative effect of the primary network, determined by the bonding topology, and the secondary network, which is governed by the nonbonded interactions.

Results and Discussion

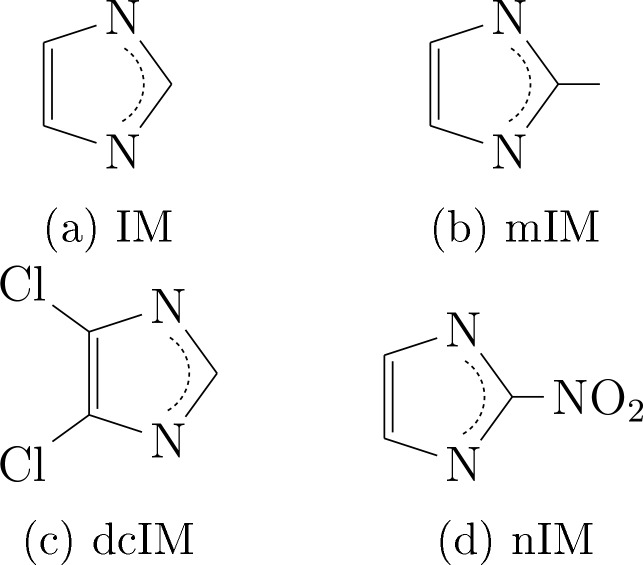
In this work, we focus on zeolitic imidazolate frameworks (ZIFs), which are a special class of MOFs composed of four coordinated metals, typically zinc, with imidazolate (IM) derivative ligands. ZIFs are an ideal case study for our work because they all have the same coordination environment, but diverse bonding topologies and functional groups.27,28 This allows us to focus on the effects of bonding topology and functional groups on the mechanical properties, while keeping coordination environment fixed, i.e., keeping the same metal node. In addition, because of the pioneering work of Cheetham and co-workers, ZIFs are among the very few MOFs for which systematic research has been done on their mechanical stability.5,6,12 To characterize the mechanical properties of ZIFs, Cheetham and co-workers used nanoindentation to measure the Young’s modulus, i.e., the resistance of materials to the tensile stress.6 These and related studies concluded that for these materials the mechanical properties can be described with the low density–stiffness correlation.6,29−32 As these experiments require sufficiently large single crystals, the number of studied structures is relatively small compared to the total number of possible ZIFs. In this work, we expand the studied materials to, in addition to the known ZIF structures, a large set of in silico constructed materials using 50 different zeolite topologies33 with four types of ligands. Such a large set of materials allows us to cover a representative range of bonding topologies and functional groups. The ligands used for in silico construction of materials include the commonly27,34 used derivatives of IM shown in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Four different ligands used to construct hypothetical materials. (a) IM = imidazolate, (b) mIM = 2-methylimidazolate, (c) dcIM = dichloroimidazolate, and (d) nIM = 2-nitroimidazolate.

Theoretically, mechanical properties of materials are described by their stiffness matrix.35 Young’s and other moduli of elasticity, including bulk and shear modulus, which characterize material’s resistance to hydrostatic pressure and shear stress, respectively, can be extracted from the stiffness matrix. Since the mechanical properties of the materials in our study do not involve the breaking/formation of chemical bonds and other quantum effects, we used an approach based on a classical force field to compute the stiffness matrix for each material. The reliability of our force field is evaluated by comparison with the experimental and ab initio calculated values of Young’s modulus reported in the literature. Figure 2 shows a comparable agreement between the ab initio and force field results with the experimental data, supporting the conclusion of our previous work that these classical force fields yield sufficiently reliable data on the mechanical properties of these materials.36

Figure 2.

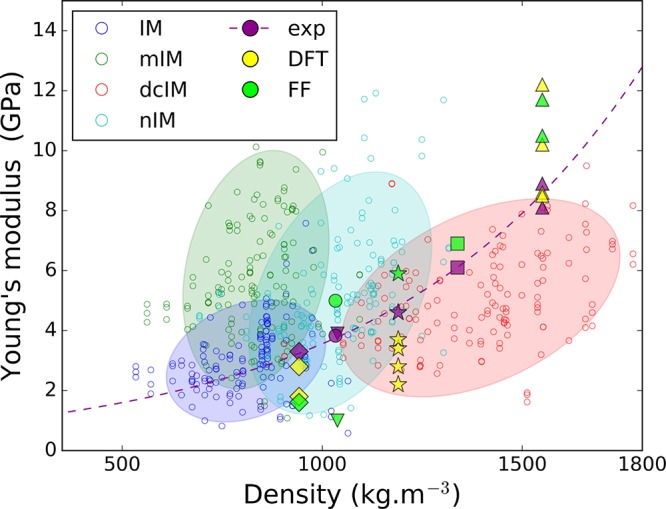
Figure 2

Open in a new tab

Young’s modulus versus density; for each material we plot the value along each of the three lattice principle axes. The filled markers with unique marker for each structure are used for those structures we can compare our force field (FF) with experimental (exp) or ab initio density functional theory (DFT) calculations, with the markers representing as follows: ◆, ZIF-8;6,12 ●, ZIF-20;6 ▼, ZIF-68;6 ★, ZIF-4;6,30,31 ■, ZIF-7;6 and ▲, ZIF-zni.6,30,32 The color coding is used to indicate the different ligands. If the density–stiffness correlation were perfectly obeyed, a principal component analysis would give a narrow cloud around the dashed line. The clouds derived from principal component analysis demonstrate the deviations for the different ligands. The complete set of data can be found in the SI.

If we focus on those materials in Figure 2 for which experimental data are available, we observe the same low density–stiffness correlation as found experimentally.6 However, if we include all our data, the picture becomes quite different. By expanding the chemistry and topology of ZIF structures, Figure 2 shows large deviations from the density–stiffness correlation. Changing the underlying network topology and/or ligand can lead to larger variations in mechanical stability than changes in density, and in some cases, even reverse the trend. For instance, many ZIF structures with dcIM ligand have similar or lower stiffness in comparison to the structures in mIM and nIM ligand families, although they have higher density. A molecular-level explanation of these deviations is provided below, the understanding of which will allow us to exploit the chemical and topological features of a material to improve its mechanical stability.

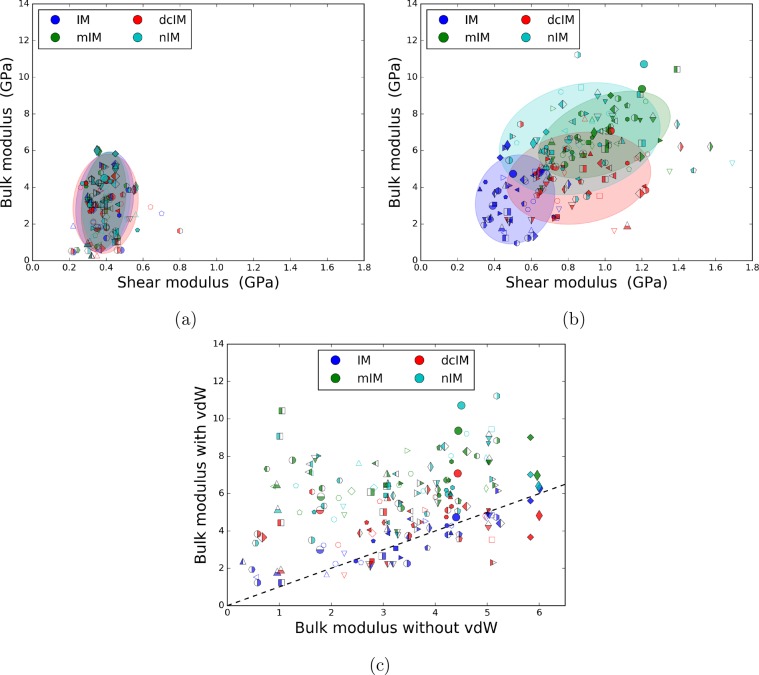
The structures in Figure 2 differ in their bonding topology and/or functional group of ligand. We introduce a computational approach to disentangle the effects of changes of the topology from changes of the ligand. To distinguish the role of the bonding topology on the mechanical properties, we first look at the mechanical stability of a simplified network of atoms composed of atomic bonding, and we refer to this network as the primary network. Several approaches have been used to define such a primary network.21,37 Here, we define the primary network as the ZIF structure in the absence of nonbonded interactions. Since the ligands in our study only differ in their functional groups, the primary network of the structures with the same underlying network topology but different ligands are nearly identical. Hence, we expect similar mechanical properties for the structures with the same underlying network topology. Indeed, Figure 3a shows that all ZIFs with the same topology have similar bulk and shear modulus, and hence, superpose on each other.

Figure 3.

Figure 3

Open in a new tab

Differentiating the contributions from bonding topology (primary network) and nonbonded interactions (secondary network) in mechanical properties. Considerable contribution from the secondary network is observed in some of the materials with functional groups. (a, b) Bulk modulus with respect to shear modulus of the materials computed without and with nonbonded interactions, respectively. (c) Bulk modulus of the materials versus the bulk modulus of them without nonbonded interactions. Dashed line represents identical properties computed with and without nonbonded interactions, i.e., no contribution from the secondary network. In all parts, each marker (open, half-filled, and filled) represents a unique underlying network topology while the colors represent the ligand.

Figure 3b,c shows the effects of switching on the nonbonded interactions where a large effect of functionalization on mechanical properties is observed. As there is no functional group on the IM ligand, it can be seen as bare backbone, and we see that the mechanical properties for this ligand are indeed dominated by the primary network. However, for the other ligands, functionalization can have a large effect on some topologies while on others surprisingly little. Moreover, although mIM, dcIM, and nIM exhibit observable contributions to the stiffness of ZIF structures in comparison to IM, depending on the topology one functional group might show greater enhancement. For instance, for LTA topology, mIM gives higher stiffness, while for GIS topology (ZIF-634,38) dcIM has higher stiffness. Similar changes in the mechanical properties were observed experimentally for ZIFs with the same underlying net but different functional groups and were associated with the ligand–ligand interactions.6 It is instructive to try to explain these deviations with a simple extension of the density–stiffness model. This model assumes a solid which has only nonbonded interactions, for example, a primitive cubic lattice with only nearest neighbor, (Lennard-Jones type) pairwise interactions. In this simple model, the only variable is the density-dependent nearest neighbor distance. The bulk modulus is given by the second derivative of the potential energy of the crystal with respect to isotropic deformations. The second derivative of the Lennard-Jones potential changes sign from positive to negative at ∼1.2 σ, where σ is the van der Waals radius (see the SI). As the second derivative for each pairwise interaction can be positive or negative depending on the nearest neighbor distance, the bulk modulus of this simple solid consists of a sum of positive or negative contributions, giving the well-known density–stiffness correlation. In a ZIF structure, however, there is a distribution of interatomic distances; some have a positive contribution (i.e., stiffening interactions), and some have a negative contribution (i.e., softening interactions) to bulk modulus. One can argue that this distribution depends on the topology and functional group. If we now assume that the contributions of the nonbonded interactions are independent of the contribution of the primary network, we can obtain a simple correction to the density–stiffness correlation by adding the sum of the contribution of the nonbonded interactions to the bulk modulus resulting from the primary network.

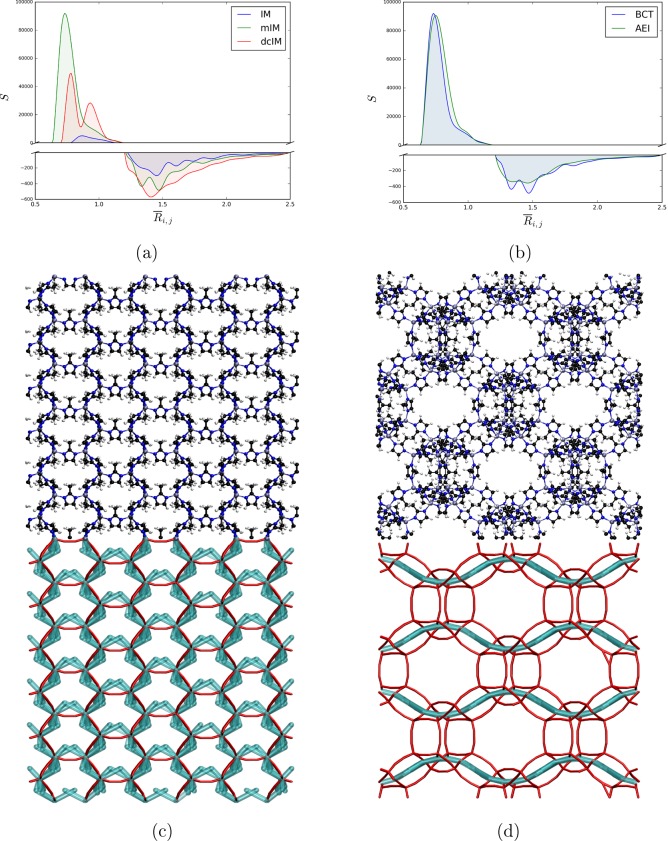
In Figure 4a, we plot the distribution of stiffening/softening contributions for the ZIFs with BCT topology for three different ligands. The BCT zeolite topology includes some known ZIFs, e.g., ZIF-1.34,38 As expected, for IM, which has no functional group, this contribution is small. For the mIM and dcIM ligands, Figure 4a shows higher peaks in the stiffening regime which is consistent with the observed increase in mechanical stability due to functionalization. Figure 4b shows an example of two materials in which the distributions of the stiffening and softening contributions are nearly identical. For the BCT topology structure we observe the expected stiffening compared to the primary network. However, for AEI topology we observe only a small effect of the nonbonded interactions on the bulk modulus. This is where our simple correction to the density–stiffness correlation breaks down. This example illustrates that the contributions of nonbonded interactions and the primary network to the stiffness can be highly nonadditive. The reason for this nonadditive behavior becomes clear by introducing the concept of a secondary network.

Figure 4.

Figure 4

Open in a new tab

Distribution of stiffening/softening nonbonded contributions for (a) structures with BCT topology and IM, mIM, and dcIM ligands, and (b) structures with mIM ligand and BCT and AEI topologies. The vertical axes represent the sum of second derivative of van der Waals (vdW) energy (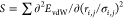Inline graphic) plotted with respect to the interatomic distances normalized with vdW radii (R̅i,j = ri,j/σi,j). The bulk moduli are 4.7, 9.4, and 7.1 for the BCT structures with IM, mIM, and dcIM ligands, and 6.3 and 7.0 for the AEI structures with IM and mIM ligands, respectively (values are in GPa). (c, d) Atomic representation and primary and secondary networks for the mIM ligand structures with BCT and AEI topologies, respectively. Details of ligands and metals were omitted in visualization of the primary and secondary networks for clarity. The primary net is demonstrated with red tubes and secondary net with cyan tubes; white, black, blue, and gray spheres represent H, C, N, and Zn atoms, respectively. The corresponding structures with IM ligand have the same primary net and no secondary net.

We define the secondary network by connecting pairs of atoms with nonbonded interactions that have a stiffening contribution to the bulk modulus. Figure 4c,d shows the primary (red tubes) and secondary (cyan tubes) networks for the BCT and AEI topologies, respectively. Both materials have a 3D percolating primary network, but the pronounced difference is in the secondary networks. For BCT the secondary network is percolating in all three dimensions, while for AEI topology it percolates only in one dimension, and there are no contributions in the other two dimensions. Inspection of the primary network of AEI topology shows that the weak spots are on the ligands while the backbone is relatively stiff. Figure 4d shows that the corresponding secondary network reinforces this stiff backbone, but not the links between the backbones. Hence, the secondary network is only supporting AEI topology in a direction in which the primary network is already strong. As the mechanical properties are dominated by the weakest link, we now understand why we see such a small effect of the secondary network on the mechanical properties. To have an effect, we need to add a functional group that would form a secondary network orthogonal to the current network which would significantly increase the bulk modulus. This type of synergy between the primary and secondary networks explains why some topologies show a large effect of functionalization, while for others this effect can be small.

It is interesting to apply our concept of primary and secondary networks to MOF-520-BPDC. Kapustin et al.20 retrofitted the mechanically unstable MOF-520 by adding an additional linker to allow for its use at high pressures. This retrofitting procedure changes the underlying network topology from a fon net to a more connected skl net.39 This improved mechanical stability can be explained in terms of changes of the primary network (see the SI). This form of topological tunability is very robust. However, it does rely on the ability to add extra linkers to support the weak spots of the primary network, which can be challenging from a chemical point of view for most materials.

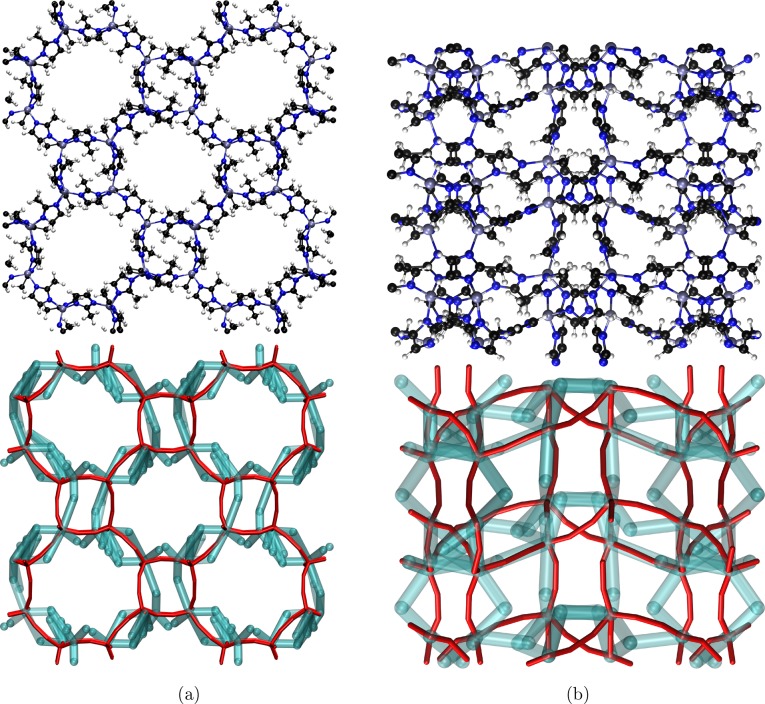
Alternatively, the mechanical properties of MOFs can be tuned by creating a secondary network via ligand functionalization. The presence of such a secondary network can shed some light on the experimental observation on the amorphization of ZIFs.40 Amorphization is directly related to the mechanical stability of these materials.41 Cheetham and co-workers showed that ZIFs with the bare IM ligand amorphize relatively easily under pressure and heating, while the corresponding ZIFs with functionalization ligands required extreme conditions; specifically, they observed thermal amorphization only in ZIFs with the bare IM ligand.40,42 These results are consistent with our molecular dynamics simulations (see the SI). Our analysis of the mechanical stability shows that “switching on” the secondary network in ZIF-3 and ZIF-4 improves the mechanical stability by as much as ∼80% in shear modulus of both structures, and 300% and 150% in their bulk modulus, respectively. Figure 5 shows that for both ZIFs the functionalized structures have a secondary network that spans the entire unit cell in all three directions. Such increased mechanical stability explains why these materials are stable at conditions where the unsubstituted IM structure amorphizes.

Figure 5.

Figure 5

Open in a new tab

(a, b) Atomic representation and the primary and secondary networks of ZIF-3 and ZIF-4 structures with mIM ligands, respectively. The corresponding structures with IM ligand have the same primary net and no secondary net. The bulk and shear moduli for ZIF-3 (ZIF-4) are 2.0 and 0.53 (3.1 and 0.80) for IM and 7.8 and 0.96 (7.6 and 1.49) for mIM structures, respectively (values are in GPa). The functional groups of the ligands form a secondary network which enhance the mechanical stability considerably. The primary net is demonstrated with red tubes and secondary net with cyan tubes; white, black, blue, and gray spheres represent H, C, N, and Zn atoms, respectively.

Conclusions

Our study shows that there are two strategies to improve the mechanical stability of a nanoporous material: modifying the primary and/or secondary network. Changing the primary network can be challenging as it requires the addition of extra linkers. In this respect the work of Kapustin et al.20 is a remarkable, but exceptional, achievement. Functionalization of ligands to create or modify the secondary network, much like the caryatids holding up the porch of the Erechtheion on the Acropolis, might be a more generally applicable route. Our study shows that such a network, however, is only effective if it supports the weak points of the primary network.

It is interesting to envision how these results can be used from an experimental perspective. Suppose we have a particular MOF for a given application, but the mechanical stability needs to be improved. As the tools developed in this work are applicable to any MOF, we can determine the primary and secondary network of this material. If this analysis shows weak spots, a simple screening of different functional groups should give a clear prediction whether the mechanical properties of the material can be improved. As these functional groups may change the details of the pores, other computational tools should be used to ensure that these changes do not influence the performance of the modified material.

Methods

To compute the mechanical properties of a material we start with the crystal structure either from experimental or from an in silico predicted structure. The procedure of computing the mechanical properties relies on the assumption that the structure corresponds to the minimum energy configuration that is consistent with the force field used to describe the potential energy surface of the material. We developed a structural minimization procedure to efficiently obtain this minimum energy configuration for all materials. All calculations were carried out within the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) molecular simulation package.43 The VMD–Visualize Molecular Dynamics package was used for the structural figures and visualization of the primary and secondary networks.44 No unexpected or unusually high safety hazards were encountered. Below we summarize the computational procedures that we have used. A more detail description can be found in the Supporting Information.

Hypothetical Material Generation

Each material was assembled with the ToBasCCo algorithm,45 using a representative set of 50 zeolite topologies. Inputs into the program were the underlying networks, as obtained from the International Zeolite Association web site,33 and two geometric building blocks; a 4-connected tetrahedral (Zn2+) and 2-connected imidazole type ligands. This procedure yielded 200 materials, i.e., 50 structures for each of the four types of ligands, IM, nIM, mIM, and dcIM. All the structures are available through the materials cloud Web site and the Supporting Information.

Structure Minimization

Simulated annealing algorithm was used to minimize lattice parameters and atomic sites using DREIDING force field46 as implemented36 in LAMMPS for all the structures. To avoid getting trapped in local minima we combined temperature annealing with expansion/relaxation cycles. The details of the algorithm and its efficiency are discussed in the Supporting Information.

Calculation of the Mechanical Properties

The moduli of elasticity were extracted from the stiffness tensor based on Voigt–Reuss–Hill averages. The stiffness tensor was calculated for the minimized structures based on the curvature of the potential energy surface with respect to lattice deformations estimated by second order polynomials (see the SI for details).

Acknowledgments

This project was supported by the MARVEL National Centre of Competence in Research of the Swiss National Science Foundation. Simulation time was provided by the Swiss National Supercomputing Centre (CSCS). S.M.M. was supported by the Deutsche Forschungsgemeinschaft (DFG, priority program SPP 1570). P.G.B. and B.S. were supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 666983, Magic). S.M.M. thanks Dr. Leopold Talirz and Dr. Aliaksandr Yakutovich for materials cloud implementation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00157.

  • Discussion on structure minimization procedure, calculation of the mechanical properties, force field, Lennard-Jones lattice model, mechanical properties of MOF-520 and MOF-520-BPDC, and amorphization of ZIF-3 and ZIF-4 (PDF)

  • Videos showing the primary and seondary networks of the discussed ZIFs (ZIP)

The authors declare no competing financial interest.

Notes

The hypothetical materials, minimized structures, molecular simulation input files for LAMMPS and primary and secondary networks are available in “Materials Cloud” via https://doi.org/10.24435/materialscloud:2018.0004/v1. Access to any of other data sets can be requested by writing to the corresponding author.

Supplementary Material

oc8b00157_si_001.pdf (4.9MB, pdf)
oc8b00157_si_002.zip (69.2MB, zip)

References

  1. Furukawa H.; Cordova K. E.; O’Keeffe M.; Yaghi O. M. The chemistry and applications of metal-organic frameworks. Science 2013, 341, 1230444. 10.1126/science.1230444. [DOI] [PubMed] [Google Scholar]
  2. Mueller U.; Schubert M.; Teich F.; Puetter H.; Schierle-Arndt K.; Pastre J. Metal–organic frameworks–prospective industrial applications. J. Mater. Chem. 2006, 16, 626–636. 10.1039/B511962F. [DOI] [Google Scholar]
  3. Howarth A. J.; Liu Y.; Li P.; Li Z.; Wang T. C.; Hupp J. T.; Farha O. K. Chemical, thermal and mechanical stabilities of metal–organic frameworks. Nature Reviews Materials 2016, 1, 15018. 10.1038/natrevmats.2015.18. [DOI] [Google Scholar]
  4. Cavka J. H.; Jakobsen S.; Olsbye U.; Guillou N.; Lamberti C.; Bordiga S.; Lillerud K. P. A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability. J. Am. Chem. Soc. 2008, 130, 13850–13851. 10.1021/ja8057953. [DOI] [PubMed] [Google Scholar]
  5. Tan J. C.; Cheetham A. K. Mechanical properties of hybrid inorganic–organic framework materials: establishing fundamental structure–property relationships. Chem. Soc. Rev. 2011, 40, 1059–1080. 10.1039/c0cs00163e. [DOI] [PubMed] [Google Scholar]
  6. Tan J. C.; Bennett T. D.; Cheetham A. K. Chemical structure, network topology, and porosity effects on the mechanical properties of Zeolitic Imidazolate Frameworks. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 9938–9943. 10.1073/pnas.1003205107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hill R. Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. 10.1016/0022-5096(63)90036-X. [DOI] [Google Scholar]
  8. Sigmund O. Tailoring materials with prescribed elastic properties. Mech. Mater. 1995, 20, 351–368. 10.1016/0167-6636(94)00069-7. [DOI] [Google Scholar]
  9. De Jong M.; Chen W.; Angsten T.; Jain A.; Notestine R.; Gamst A.; Sluiter M.; Ande C. K.; Van Der Zwaag S.; Plata J. J.; Toher C.; Curtarolo S.; Ceder G.; Persson K. A.; Asta M. Charting the complete elastic properties of inorganic crystalline compounds. Sci. Data 2015, 2, 150009. 10.1038/sdata.2015.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fan H.; Hartshorn C.; Buchheit T.; Tallant D.; Assink R.; Simpson R.; Kissel D. J.; Lacks D. J.; Torquato S.; Brinker C. J. Modulus–density scaling behaviour and framework architecture of nanoporous self-assembled silicas. Nat. Mater. 2007, 6, 418–423. 10.1038/nmat1913. [DOI] [PubMed] [Google Scholar]
  11. Ortiz A. U.; Boutin A.; Fuchs A. H.; Coudert F.-X. Anisotropi elastic properties of flexible metal-organic frameworks: how soft are soft porous crystals?. Phys. Rev. Lett. 2012, 109, 195502. 10.1103/PhysRevLett.109.195502. [DOI] [PubMed] [Google Scholar]
  12. Tan J.-C.; Civalleri B.; Lin C.-C.; Valenzano L.; Galvelis R.; Chen P.-F.; Bennett T. D.; Mellot-Draznieks C.; Zicovich-Wilson C. M.; Cheetham A. K. Exceptionally Low Shear Modulus in a Prototypical Imidazole-Based Metal-Organic Framework. Phys. Rev. Lett. 2012, 108, 095502. 10.1103/PhysRevLett.108.095502. [DOI] [PubMed] [Google Scholar]
  13. Mandelbrot B. B.; Pignoni R.. The fractal geometry of nature; WH Freeman New York, 1983; Vol. 1. [Google Scholar]
  14. Aizenberg J.; Weaver J. C.; Thanawala M. S.; Sundar V. C.; Morse D. E.; Fratzl P. Skeleton of Euplectella sp.: structural hierarchy from the nanoscale to the macroscale. Science 2005, 309, 275–278. 10.1126/science.1112255. [DOI] [PubMed] [Google Scholar]
  15. Lakes R. Materials with structural hierarchy. Nature 1993, 361, 511–515. 10.1038/361511a0. [DOI] [Google Scholar]
  16. Zheng X.; Lee H.; Weisgraber T. H.; Shusteff M.; DeOtte J.; Duoss E. B.; Kuntz J. D.; Biener M. M.; Ge Q.; Jackson J. A.; Kucheyev S. O.; Fang N. X.; Spadaccini C. M. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. 10.1126/science.1252291. [DOI] [PubMed] [Google Scholar]
  17. Meza L. R.; Zelhofer A. J.; Clarke N.; Mateos A. J.; Kochmann D. M.; Greer J. R. Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 11502–11507. 10.1073/pnas.1509120112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wu H.; Yildirim T.; Zhou W. Exceptional mechanical stability of highly porous zirconium metal–organic framework UiO-66 and its important implications. J. Phys. Chem. Lett. 2013, 4, 925–930. 10.1021/jz4002345. [DOI] [PubMed] [Google Scholar]
  19. Bouëssel du Bourg L.; Ortiz A. U.; Boutin A.; Coudert F.-X. Thermal and mechanical stability of zeolitic imidazolate frameworks polymorphs. APL Mater. 2014, 2, 124110. 10.1063/1.4904818. [DOI] [Google Scholar]
  20. Kapustin E. A.; Lee S.; Alshammari A. S.; Yaghi O. M. Molecular Retrofitting Adapts a Metal–Organic Framework to Extreme Pressure. ACS Cent. Sci. 2017, 3, 662–667. 10.1021/acscentsci.7b00169. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Sarkisov L.; Martin R. L.; Haranczyk M.; Smit B. On the flexibility of metal–organic frameworks. J. Am. Chem. Soc. 2014, 136, 2228–2231. 10.1021/ja411673b. [DOI] [PubMed] [Google Scholar]
  22. Yuan S.; Lu W.; Chen Y.-P.; Zhang Q.; Liu T.-F.; Feng D.; Wang X.; Qin J.; Zhou H.-C. Sequential linker installation: precise placement of functional groups in multivariate metal–organic frameworks. J. Am. Chem. Soc. 2015, 137, 3177–3180. 10.1021/ja512762r. [DOI] [PubMed] [Google Scholar]
  23. Zhai Q.-G.; Bu X.; Zhao X.; Li D.-S.; Feng P. Pore space partition in metal–organic frameworks. Acc. Chem. Res. 2017, 50, 407–417. 10.1021/acs.accounts.6b00526. [DOI] [PubMed] [Google Scholar]
  24. Boyd P. G.; Lee Y.; Smit B. Computational development of the nanoporous materials genome. Nature Reviews Materials 2017, 2, 17037. 10.1038/natrevmats.2017.37. [DOI] [Google Scholar]
  25. Wilmer C. E.; Leaf M.; Lee C. Y.; Farha O. K.; Hauser B. G.; Hupp J. T.; Snurr R. Q. Large-scale screening of hypothetical metal–organic frameworks. Nat. Chem. 2012, 4, 83. 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
  26. Rogge S. M.; Waroquier M.; Van Speybroeck V. Reliably Modeling the Mechanical Stability of Rigid and Flexible Metal–Organic Frameworks. Acc. Chem. Res. 2018, 51, 138–148. 10.1021/acs.accounts.7b00404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Banerjee R.; Phan A.; Wang B.; Knobler C.; Furukawa H.; O’keeffe M.; Yaghi O. M. High-throughput synthesis of zeolitic imidazolate frameworks and application to CO2 capture. Science 2008, 319, 939–943. 10.1126/science.1152516. [DOI] [PubMed] [Google Scholar]
  28. Yang J.; Zhang Y.-B.; Liu Q.; Trickett C. A.; Gutierrez-Puebla E.; Monge M. Á.; Cong H.; Aldossary A.; Deng H.; Yaghi O. M. Principles of Designing Extra-Large Pore Openings and Cages in Zeolitic Imidazolate Frameworks. J. Am. Chem. Soc. 2017, 139, 6448–6455. 10.1021/jacs.7b02272. [DOI] [PubMed] [Google Scholar]
  29. Bennett T.; Sotelo J.; Tan J.-C.; Moggach S. Mechanical properties of zeolitic metal–organic frameworks: mechanically flexible topologies and stabilization against structural collapse. CrystEngComm 2015, 17, 286–289. 10.1039/C4CE02145B. [DOI] [Google Scholar]
  30. Tan J.-C.; Civalleri B.; Erba A.; Albanese E. Quantum mechanical predictions to elucidate the anisotropic elastic properties of zeolitic imidazolate frameworks: ZIF-4 vs. ZIF-zni. CrystEngComm 2015, 17, 375–382. 10.1039/C4CE01564A. [DOI] [Google Scholar]
  31. Ryder M. R.; Tan J.-C. Explaining the mechanical mechanisms of zeolitic metal–organic frameworks: revealing auxeticity and anomalous elasticity. Dalton Transactions 2016, 45, 4154–4161. 10.1039/C5DT03514G. [DOI] [PubMed] [Google Scholar]
  32. Ryder M. R.; Bennett T. D.; Kelley C.; Frogley M.; Cinque G.; Tan J.-C. Tracking Thermal-Induced Amorphization of a Zeolitic Imidazolate Framework via Synchrotron In Situ Far-Infrared Spectroscopy. Chem. Commun. 2017, 53, 7041–7044. 10.1039/C7CC01985H. [DOI] [PubMed] [Google Scholar]
  33. Baerlocher C.; McCusker L. B.. Database of zeolite structures. http://www.iza-structure.org/databases/ (accessed October, 2016).
  34. Park K. S.; Ni Z.; Côté A. P.; Choi J. Y.; Huang R.; Uribe-Romo F. J.; Chae H. K.; O’Keeffe M.; Yaghi O. M. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 10186–10191. 10.1073/pnas.0602439103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nye J. F.Physical properties of crystals: their representation by tensors and matrices; Oxford University Press: New York, 1985. [Google Scholar]
  36. Boyd P. G.; Moosavi S. M.; Witman M.; Smit B. Force-Field Prediction of Materials Properties in Metal-Organic Frameworks. J. Phys. Chem. Lett. 2017, 8, 357–363. 10.1021/acs.jpclett.6b02532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Jacobs D. J.; Rader A. J.; Kuhn L. A.; Thorpe M. F. Protein flexibility predictions using graph theory. Proteins: Struct., Funct., Genet. 2001, 44, 150–165. 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
  38. Phan A.; Doonan C. J.; Uribe-Romo F. J.; Knobler C. B.; O’keeffe M.; Yaghi O. M. Synthesis, structure, and carbon dioxide capture properties of zeolitic imidazolate frameworks. Acc. Chem. Res. 2010, 43, 58–67. 10.1021/ar900116g. [DOI] [PubMed] [Google Scholar]
  39. O’Keeffe M.; Peskov M. A.; Ramsden S. J.; Yaghi O. M. The reticular chemistry structure resource (RCSR) database of, and symbols for, crystal nets. Acc. Chem. Res. 2008, 41, 1782–1789. 10.1021/ar800124u. [DOI] [PubMed] [Google Scholar]
  40. Bennett T. D.; Cheetham A. K. Amorphous metal–organic frameworks. Acc. Chem. Res. 2014, 47, 1555–1562. 10.1021/ar5000314. [DOI] [PubMed] [Google Scholar]
  41. Ortiz A. U.; Boutin A.; Fuchs A. H.; Coudert F.-X. Investigating the pressure-induced amorphization of zeolitic imidazolate framework ZIF-8: mechanical instability due to shear mode softening. J. Phys. Chem. Lett. 2013, 4, 1861–1865. 10.1021/jz400880p. [DOI] [PubMed] [Google Scholar]
  42. Bennett T. D.; Keen D. A.; Tan J.-C.; Barney E. R.; Goodwin A. L.; Cheetham A. K. Thermal amorphization of zeolitic imidazolate frameworks. Angew. Chem., Int. Ed. 2011, 50, 3067–3071. 10.1002/anie.201007303. [DOI] [PubMed] [Google Scholar]
  43. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  44. Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  45. Boyd P. G.; Woo T. K. A generalized method for constructing hypothetical nanoporous materials of any net topology from graph theory. CrystEngComm 2016, 18, 3777–3792. 10.1039/C6CE00407E. [DOI] [Google Scholar]
  46. Mayo S. L.; Olafson B. D.; Goddard W. A. DREIDING: a generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. 10.1021/j100389a010. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc8b00157_si_001.pdf (4.9MB, pdf)
oc8b00157_si_002.zip (69.2MB, zip)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES