Abstract
Adaptive introgression is common in nature and can be driven by selection acting on multiple, linked genes. We explore the effects of polygenic selection on introgression under the infinitesimal model with linkage. This model assumes that the introgressing block has an effectively infinite number of loci, each with an infinitesimal effect on the trait under selection. The block is assumed to introgress under directional selection within a native population that is genetically homogeneous. We use individual-based simulations and a branching process framework to compute various statistics of the introgressing block, and explore how these depend on parameters such as the map length and initial trait value associated with the introgressing block, the genetic variability along the block, and the strength of selection. Our results show that the introgression dynamics of a block under infinitesimal selection are qualitatively different from the dynamics of neutral introgression. We also find that, in the long run, surviving descendant blocks are likely to have intermediate lengths, and clarify how their length is shaped by the interplay between linkage and infinitesimal selection. Our results suggest that it may be difficult to distinguish the long-term introgression of a block of genome with a single, strongly selected, locus from the introgression of a block with multiple, tightly linked and weakly selected loci.
Keywords: introgression, linkage, infinitesimal model
LIMITED introgression of genetic material between closely related subspecies or species is common (Arnold 2004; Hedrick 2013; Racimo et al. 2015). Introgression may be adaptive if it supplies new genetic variation that facilitates a response to selection. Well-documented examples include adaptive introgression between different species of sunflowers, resulting in increased herbivore resistance in the recipient species (Whitney et al. 2006), introgression between the Algerian mouse and the European house mouse, which likely caused the latter to acquire increased pesticide resistance (Song et al. 2011), and possible introgression between Denisovans and the ancestors of modern-day Tibetans, resulting in adaptation to life at high altitude (Huerta-Sánchez et al. 2014).
Unlike de novo mutation, migration introduces multiple, linked allelic variants into a population. The likelihood of successful introgression or hybridization is thus sensitive to the density of selected loci among these variants and the distribution of their fitness effects, in addition to demography (Yeaman 2013). More generally, polygenic adaptation or introgression may involve minor shifts in allele frequencies as opposed to selective sweeps, leading to genomic signatures that are qualitatively distinct from those of major-effect loci (Pritchard et al. 2010). Similarly, background selection due to many weakly deleterious loci shapes diversity at linked sites differently from a few strongly deleterious loci (Good et al. 2014). Incorporating linked, polygenic selection into methods for detecting introgression is thus an important challenge for population genetic inference (Elyashiv et al. 2016).
Most polygenic models of introgression or hybridization analyze the dynamics of a single beneficial or neutral locus embedded within a deleterious genomic background (Barton and Bengtsson 1986; Visscher et al. 1996; Uecker et al. 2015). These analyses often make various simplifying assumptions about the genetic architecture of barriers to gene flow. For example, Barton and Bengtsson (1986) derive the effective migration rate between populations at a neutral locus in a variety of hybridization scenarios, by neglecting random drift and assuming that the neutral locus is embedded within a genome in which all loci are under divergent selection across populations. Similarly, Uecker et al. (2015) use a branching process approximation to analyze how the introgression probability of a beneficial locus is altered by the presence of multiple, linked and unlinked deleterious mutations. Qualitatively similar models have been used to investigate whether selecting on marker loci might reduce “linkage drag” during introgression in practical breeding programs (Visscher et al. 1996), where the objective typically is to introgress a single favorable allele from a donor population by repeated back-crossing, while minimizing the amount of background donor genome (which is assumed to be deleterious in the recipient).
Genomic regions with many tightly linked beneficial variants may, however, play an important role in adaptive introgression (Hedrick 2013). Fine-scale mapping of quantitative trait loci (QTL) reveals that these often consist of multiple alleles that affect the trait (Flint and Mackay 2009). In fact, recombination within QTL has been suggested as a possible explanation for the failure of simple marker-assisted introgression schemes when attempting to introgress QTL for polygenic traits such as yield (Hospital 2005). Thus, a step toward more realistic models is to consider linked, introgressing variants associated with a range of selective effects—both positive and negative. Such models also provide more general insight into the limits of selection acting on complex traits.
A particularly useful limit for studying the dynamics of multiple selected loci is the infinitesimal model, which assumes that a given phenotype is influenced by an effectively infinite number of loci, each of infinitesimally small effect (Bulmer 1980). It follows that the effect of selection on individual polymorphisms is negligible, so that, in the absence of drift and linkage, the genic variance can be assumed to be constant over short time scales.
The infinitesimal model is quite general, as the limit of a model where many discrete loci with a range of effects sum to determine trait value (Barton et al. 2017). However, it does neglect linkage, which becomes untenable if the density of selected variants on the genome is high. To explore the effect of linkage on introgression, we consider a trait determined by an effectively infinite number of loci, but now assume that these are uniformly distributed on a genomic block of map length This model, which we refer to as the “infinitesimal model with linkage” was first introduced by Robertson (1977). It is parameterized by a single parameter the genic variance per unit map length.
For simplicity, we assume that a single block of genome from a source population enters a genetically homogeneous native population having zero genic variance. By definition, the native population also has zero segregation variance, which is the variance in trait values among the offspring of any two randomly chosen individuals in the population. This implies that any adaptive response must be due entirely to genetic variation supplied by the introduced genome. We typically follow descendants of the introduced genome over a few hundred generations after the initial hybridization event, and neglect the creation of new variation by mutation over these time scales.
The assumption of a genetically homogeneous native population is unrealistic, but may approximate a situation where that population has much lower genetic variation, and hence lower segregation variance, than the source population. Such a situation might arise, for instance, if the native population went through a recent bottleneck. A later shift of the selection optimum would spur further evolution when new variation is introduced via migration. Assuming a genetically homogeneous native population allows us to focus on the dynamics of the introduced block, without considering additional effects due to the association of this block (or its descendants) with different native genomic backgrounds.
The assumption that most of the introduced genome is neutral, while only one block is under selection, may appear restrictive. However, even in a scenario where selected loci are spread across the entire introduced genome, a few generations of back-crossing with the native population would yield descendant individuals carrying single fragments of the donor genome. The spread of each of these fragments through the population is then independent of other fragments, and can thus be described using our framework, as long as introgressing fragments are rare (so that they do not encounter each other) and short (so that only single crossovers occur and genomes carry at most one fragment).
Under the infinitesimal framework, any block of genome contains a very large number of weakly selected loci. This is a highly idealized model, which we regard as a first step toward a fuller analysis. However, we shall see that it already shows quite rich behavior—in particular, the model allows for a long-term response to selection, at least in large populations. Thus, focusing on the dynamics of a single block can provide useful insight into the effect of polygenic selection during introgression.
The introgression of a neutral block of genome was modeled as a branching process by Baird et al. (2003). They found that a neutral block of map length y is lost very slowly—the probability that at least some portion of the block survives at time t falls as in contrast to the faster decay observed for a single neutral locus. This is because a large block has a higher chance of being transmitted to offspring than a small block (either as a whole or in part), resulting in a relatively large number of descendants that carry at least some portion of the block in the first few generations. Over longer times, as surviving fragments become smaller, this transmission advantage is lost. However, by this time there are so many () of these small descendant blocks, that the probability of all of them being lost from the population becomes very small.
The analysis by Baird et al. (2003) does not include selection per se, though it can describe a rather artificial situation in which any fragment of the block, howsoever small, has the same selective effect. However, in the infinitesimal limit, we expect the additive effects of short fragments to be smaller than those of long fragments (on average). Thus, recombination not only splits an originally beneficial block into smaller and smaller fragments, but also dilutes the selective (dis)advantage of descendants that carry fragments of the block. This can result in a complex feedback whereby the strength of recombination relative to selection shapes the distribution of block sizes and trait values, while this distribution itself determines the effective strengths of selection and recombination in the population. The main goal of our work is to use the infinitesimal framework to understand how the resultant, dynamically changing balance between selection and recombination influences the introgression of genomic blocks.
To this end, we focus on two questions. First, can the introgression of a block of genome that contains very many weakly selected beneficial and deleterious loci be distinguished from neutral introgression? Second, is an extended block, which contains a large number of loci with infinitesimally small (but, on average, positive) effects, less likely or slower to introgress than a single strongly selected locus? These questions also relate to the broader issue of whether weakly selected loci can, in aggregate, have discernible effects on evolution.
Methods
We consider a scenario where a single haplotype from a diverged source population enters a native population, for example from a backcross. Each individual in the native and source populations expresses a trait that is the sum of effects of many genes, which are uniformly distributed over a genomic block of map length The individuals are assumed to be diploid, but the analysis and results are essentially the same for haploids.
The native population is assumed to consist of individuals with identical haplotypes and hence the same trait value, defined as For ease of analysis, we define the additive contributions of any allele (or indeed, any small region) of the native haplotype to be zero, and ignore nongenetic effects on the trait throughout. The native haplotype thus provides a reference with respect to which the additive contributions of different tracts of the introduced block are measured.
The introduced block has an associated trait value which is obtained by integrating over the contributions from different regions of the block, over a map length These regions typically make unequal contributions to the trait. Thus, when the introduced block is split by recombination, descendants inherit fragments associated with a range of trait values, which differ from the trait value of the parent but also from each other.
The additive trait is under directional selection in the native population, such that individuals with trait value z have a Poisson-distributed number of offspring, with mean where β represents the strength of selection. Thus, each individual carrying native haplotypes produces two offspring on average, while individuals carrying fragments of the introduced block may expect to produce more or less than two, depending on the trait value associated with the fragment. This results in a response to selection, whose magnitude depends on the selection strength β, the trait value associated with the introduced haplotype, and the extent of genetic variation among descendants of this haplotype, which can be characterized in a simple way within the infinitesimal framework described below.
Infinitesimal model with linkage and no selection
The infinitesimal model with linkage was introduced by Robertson (1977), and can be thought of as the limiting case of a trait determined additively by L discrete loci uniformly distributed on a genomic block of map length Consider a population in linkage equilibrium (LE), in which the allelic states of different loci determining the trait are statistically independent of each other (irrespective of linkage between the loci). Then, the additive contributions of different loci () on any particular block are identical, independent random variables drawn from some distribution (with mean and variance denoted by μ and ). The contributions of all the loci sum to give the trait value of the block:
If we now adopt a coarse-grained view of this block, and consider the additive contributions of small genomic tracts of map length (instead of individual loci), then these are normally distributed with variance for This follows from the central limit theorem by assuming that the number of trait loci in a tract of length , given by is sufficiently large, and that there is no linkage disequilibrium (LD).
Thus, the variance in additive contributions of small tracts of map length is proportional to with coefficient which is the genic variance per locus () times the number of loci per unit map length (). We refer to as the genic variance per unit map length; the genic variance is just equal to the additive genetic variance minus the variance due to LD (which is zero here, assuming LE). Note that in the infinitesimal limit, the distribution of allelic effects becomes irrelevant: only matters.
If we define as the trait value associated with the genomic region of the block, then it follows that is a Brownian path, since there is no LD or correlation between the contributions of different genomic segments (see Table 1 for notation and terminology for infinitesimal introgression). The distribution of such Brownian paths is characterized by two quantities—the trait value associated with the full block (or the net displacement of the path in the interval ), and the variance per unit map length.
Table 1. Notation and terminology for infinitesimal introgression.
| y, | Map length of block; initial map length |
|---|---|
| z, | Trait value of block; initial trait value |
| Brownian path | Function specifying trait value for a particular genome under the assumption of LE |
| β | Selection gradient; expected number of offspring is |
| Genic variance per unit map length | |
| Moment generating function of offspring number of individual with trait value z; for Poisson-distributed offspring | |
| Path-conditioned BP | Branching process (BP) conditioned on a particular path |
| Probability that some part of the block survives till t | |
| Unconditioned BP | BP, averaged over all possible paths |
| Unconditioned BP approximation | Approximation to this, that ignores correlations between descendants inheriting different fragments of a particular block |
| Probability that some part of a block of initial length y and initial trait value z survives till t, averaged over paths | |
| Trait value scaled by genic variance of block | |
| Rescaled time | |
| Strength of selection relative to recombination | |
| Number of blocks; mean number of blocks | |
| Total length of surviving blocks; mean total length |
A key assumption of the infinitesimal model is that is independent of the trait value and is equal to the genic variance (per unit map length) in the source population. This implies that in the absence of selection, the variance of trait values among diploid individuals in the source population is simply (Appendix A). Thus, the parameter measures the extent of variability along a single genome as well as the variability between genomes in the source population.
Based on the above model, we can write down the probability that given a block of map length and trait value the trait values associated with two constituent fragments of map length and are and respectively. This is a product of two normal distributions:
| (1) |
Thus, the trait value of a daughter block (having map length ) is normally distributed with mean and variance . Equation (1) is the main equation describing inheritance under the infinitesimal model with linkage (see also Robertson 1977, p. 309).
Note that the distribution of trait values among descendant blocks under our model differs qualitatively from that in models where all allelic effects on the introduced block have the same sign (e.g., Barton (1983)). In those models, the trait value (or fitness) of the descendant block is deterministically proportional to its length. This case is recovered by taking the limit of the more general model described here.
Equation (1) is valid only when allelic states at physically linked loci are uncorrelated, i.e., in LE. Correlations may, however, arise due to selection or genetic drift. In particular, stabilizing selection in the source population can build up negative LD between linked genomic regions (Lande 1976). The variance released by recombination is then no longer described by Equation (1), but can be much lower than for . Thus, any one genome encodes information about the nature of multi-locus associations in the source population from which it originates. This information lies hidden in the distribution of trait values of its constituent sub-blocks, and is revealed gradually as recombination separates these.
We assume LE in the source population from which the “introduced block” originates, such that individual blocks within this population can be represented by Brownian paths. In principle, we could generate the Brownian path specifying the introduced block during the course of one simulation run of the introgression process as follows—each time an individual passes on a fragment of the introduced block to a descendant, we choose the trait value associated with this fragment by conditioning on the trait value of the parental block using Equation (1) (while also taking into account all known trait values of other fragments that have some overlap with this fragment). We would store trait values of different fragments of the introduced block in a master list and keep updating this list with the values of smaller and smaller fragments as these are generated by recombination. While this scheme would exactly simulate the infinitesimal model with linkage, it is quite cumbersome to implement.
Instead, we follow two different approximate simulation schemes that discretize the continuous Brownian path. In the first “discrete locus” scheme, we approximate the Brownian path by a large number L of discrete loci uniformly spread across the introduced block. The additive contribution of each locus is drawn from a normal distribution with mean and variance using an iterative scheme that ensures that all the add up to (see Appendix B). Whenever the introduced block is split by recombination, the trait value of the descendant block is obtained by summing over the contributions of all loci that it inherits from the introduced block.
In the second simulation scheme, we divide the introduced block into L sub-blocks and choose their additive contributions as in the first scheme. However, now when a portion of the parent block is transmitted to an offspring, the trait value of the descendant block is obtained by summing the contributions of all the complete sub-blocks inherited from the parent plus a random contribution ζ that corresponds to the partially inherited sub-block. If the crossover point lies within the sub-block such that the descendant inherits a fraction α of this sub-block, then ζ is a normally distributed random variable with mean equal to α times the additive contribution of the sub-block and variance Thus, under this approximation, the contribution of sub-blocks that are shorter than is uncorrelated across different individuals, which is not true for the actual model. However, this approximation makes very little difference to various quantities of interest as L becomes large (Appendix B).
An important difference between the discrete locus and sub-block-based schemes is that the maximum possible advance of trait value under selection is limited by the total number of loci with positive effect in the former, but can potentially be infinite under the latter, at least in an infinite population. Thus, the sub-block-based simulation scheme better represents the true infinitesimal model with linkage. However, in a finite population, the exact number of individual loci matters only if recombination can separate the loci within introgressing segments before these fix. Thus, we expect the two approximate simulation schemes and the true infinitesimal model with linkage to yield very similar predictions for various quantities in a finite population, as long as L is large (see Appendix B for details on the choice of L for both approximations).
Note that we only assume LE within the source population from which the introduced block is sampled. In the recipient population, LD is quite strong during early introgression—our model accounts for this by explicitly following the numbers of different blocks of genome in the population.
Modeling the initial spread of the introduced block as a branching process
During the initial phases of introgression, while the number of descendants of the introduced block is much smaller than the size of the recipient population, the likelihood of mating between two individuals, both bearing introgressed genetic material, is negligible. Further, if the map length of the introduced block is small enough that multiple crossovers can be neglected, then any individual genome will carry at most one introduced fragment (of map length y), surrounded by native blocks (map length ). Since the native population is assumed to be genetically homogeneous, it is sufficient to follow just the fragments of the introduced block down various lineages without considering the rest of the genome, as described below.
The first generation after hybridization is simulated by drawing the number of offspring of the individual carrying the introduced haplotype from a Poisson distribution with mean where is the trait value of the introduced block. Each of these offspring is either assigned no portion of the introduced block (probability ), or the whole block (probability ), or a fragment of the block (probability ). The fragment is generated by choosing a single crossover point x, uniformly distributed in the interval and then assigning to the offspring either the left or the right fragment with equal probability. If the descendant block is shorter than the parent block, then its trait value is decided using the sub-block-based simulation scheme described above.
This process is repeated in each generation for each descendant individual that carries any fragment of the introduced block, for a prespecified number of generations, or until no portion of the introduced block survives in the population. At the end of each generation, we ascertain the number of descendants carrying at least some introduced material, the total length of introgressed genome they carry, and various moments of the lengths and trait values of introgressing fragments in the population. For each set of parameters, we obtain statistics by averaging over many () realizations, each corresponding to a different Brownian path. All paths are chosen from the same distribution, parameterized by and .
Path-conditioned branching process:
The above formulation describes a branching process (BP), in that it ignores correlations between the offspring number of different individuals due to density-dependent regulation, and also ignores recombination between blocks. Note, however, that it is a BP conditioned on a particular Brownian path with end points at 0 and ; thus, descendants inheriting overlapping (or complementary) segments of a block have correlated (or anticorrelated) trait values and fitness. This also implies that various statistics of the BP, e.g., the “extinction probability” that a genomic block with end-points at and has no descendants t generations later, must also be conditioned on this Brownian path. We can write the following recursive equation relating at time to the corresponding probability at time t:
| (2) |
Here is the trait value associated with the genomic region and is specified by the Brownian path. The function is the moment generating function of the number of offspring of an individual carrying a block fragment with trait value z. If individuals have a Poisson-distributed number of offspring with mean then we have Thus, is nonlinear in x, resulting in a recursion (Equation (2)) that is also nonlinear.
The first term in the square brackets represents the probability that the block (of map length ) is not split by recombination and not transmitted to the offspring. The second term describes events in which the entire block is transmitted to the offspring without being split by recombination, but then is completely lost among the descendants of this offspring within the next t generations. The third term describes recombination events that result in the transmission of a fragment of the block to the descendant. The integral is over the map position x of the crossover point. It involves the probability that the immediate offspring inherits the or the fragment, and that none of this fragment survives among the descendants of this offspring after t generations. The sum of these three terms gives the net probability that the introduced block has no surviving descendants after t generations in the pedigree branch involving one of its offspring. The probability of extinction of the block within two such pedigree branches is the square of this net probability, and so on for three or more branches. This allows extinction probabilities to be expressed in terms of the moment generating function of the offspring distribution (Harris 1963).
Unconditioned branching process approximation:
Equation (2) describes the time evolution of extinction probabilities for a particular genomic block described by a particular Brownian path (i.e., with particular effects on the trait). We are interested in the outcome averaged over random paths, and can calculate this average numerically by drawing a large number of Brownian paths, solving (2) for each, and taking the average. However, since Equation 2 is nonlinear, this becomes computationally demanding.
In order to calculate the extinction probability (or other statistics), averaged over different Brownian paths, all characterized by the same value of , we introduce a different “unconditioned” BP approximation. The unconditioned BP is not conditioned on any particular path, but treats the trait values of two or more descendants inheriting portions of the parent block as independent random variables. These random variables have a distribution [specified by Equation (1)] which is only conditional on the map length and trait value of the parent block. This approximation thus ignores the correlations in trait values of offspring that inherit overlapping or even complementary tracts of a parent block. The underlying assumption is that the effects of these correlations on various quantities of interest get averaged out, when averaging over Brownian paths.
It then follows that under the unconditioned BP approximation, the extinction probability of a block depends only on its map length y and trait value z. Defining as the probability that a block of map length y and trait value z has no surviving descendants t generations after it enters the population, we can write the following recursions for
| (3) |
Equation (3) is similar to Equation (2) except that now the third term involves an integral over the map length and trait value associated with the descendant block. Note that is now a random variable drawn from the distribution in Equation (1), and is not prespecified by the chosen Brownian path, as in Equation (2). To numerically iterate Equation (3), we discretize (y,z) space and replace the two-dimensional integral by a double summation.
Equation (3) is analogous to Equation 1 in Baird et al. (2003), but, unlike that equation, involves extinction probabilities that depend on both the length and the trait value of the introduced block. This reflects the fact that blocks evolve under the joint influence of selection and recombination in our model, in contrast to the neutral dynamics modeled in Baird et al. (2003).
We can also express the Laplace transform of the joint distribution of the number, map lengths, and trait values of descendant blocks at time in terms of the corresponding Laplace transform at time t, as in Baird et al. (2003) (see Appendix C). These can be used to recursively compute moments of the total number of descendant blocks and the total amount of introgressed genome. In particular, the expected number of descendants of an introduced block with map length y and trait value z (after t generations) follows the linear recursion:
| (4) |
Effective parameters governing introgression:
Taking the continuous time limit of Equation (4) yields an integro-differential equation in terms of the map length y, the rescaled trait value rescaled time and the ratio of the selection strength to recombination strength, given by (see Appendix D):
| (5) |
Here denotes the expected number of descendants of a block of map length y and effective trait value at rescaled time τ. Note that the parameters and τ (as well as θ) are themselves functions of y. An identical equation describes the evolution of the average total amount of introgressed genetic material but with the initial condition In this case, we argue that these equations must have solutions of the form and Thus, the expected number of descendants depends on the map length of the introduced block only implicitly via the rescaled parameters θ, , τ. Similarly, the genic variance enters into the equations only via θ and
The above discussion highlights an important difference between the infinitesimal model and models with equal effect loci, used in other studies of multi-locus introgression (e.g., Barton 1983), where trait value is determined entirely by block length. With deterministic inheritance of trait values, the effective parameter governing introgression is the product while in the infinitesimal framework, the parameters θ and independently influence the dynamics (see Appendix D).
Individual-based simulations of long-term introgression into a finite population
To study the long-term dynamics of introgression into a finite population of size N, we also simulate individuals. These simulations start by randomly choosing a diploid individual to carry the introduced block. The introduced block is simulated via the discrete locus scheme, i.e., by assuming that there are L uniformly spaced loci embedded within it, and then iteratively choosing their additive contributions such that these sum to (see Appendix B). The remaining individuals are assumed to be identical and have zero genic variance.
In each generation, N individuals are created as follows. Two diploid parents are chosen for each offspring by sampling individuals in the previous generation in proportion to their fitness, defined as Here z is the sum of the trait values associated with the two haplotypes of the individual. Subsequently, a gamete is created from each parent either with no recombination (probability ) or with a single crossover (probability ) between parental haplotypes. With no recombination, one of the two parent haplotypes is chosen with equal probability to be the gamete. With recombination, the crossover point is sampled from a uniform distribution between 0 and the gamete inherits all loci to the right of the crossover point from one parental haplotype and all loci to the left from the second haplotype. The two gametes generated in this way together form a diploid individual. Note that, unlike in the BP framework, a gamete might contain multiple introgressed fragments, for example, if both parent haplotypes carry different fragments.
Data availability statement
FORTRAN 95 codes used to generate the simulated data can be found at https://git.ist.ac.at/himani.sachdeva/Introgression_source_codes/snippets. The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.
Results
We first consider the introduction of a single genomic block with trait value . This block is initially neutral with respect to the native population. However, its immediate descendants inherit fragments with various effects, resulting in a change in the average trait value in response to selection, with the response being stronger for higher values of This is in contrast to the purely neutral case (Baird et al. 2003), where there is no variability along the genome () or alternatively no selection (), so that descendants always inherit neutral fragments of the originally neutral genome.
The distinction between the limit considered in Baird et al. (2003) and the scenarios we study here is less obvious at long time scales. As time progresses, recombination splits the original block into smaller and smaller fragments that contribute less and less to trait value, and are thus expected to be effectively neutral. However, selection favors descendants carrying larger fragments with significantly positive contributions to trait value, and thus tends to amplify the frequency of such fragments in the population, in opposition to recombination. Do the resultant long-term signatures of introgression in the presence of selection differ from the neutral expectation, under the infinitesimal model?
Introgression of an initially neutral block: an example
Before computing various statistics of the descendants of the introduced block and exploring their dependence on parameters such as , and it is useful to visualize a few random realizations of the process by directly simulating the path-conditioned BP. Figure 1, A and C show two snapshots of the process at and respectively, while Figure 1, B and D in the right panel show the analogous snapshots for another realization of the process, corresponding to a different Brownian path. The x-axis denotes physical positions along the genomic region spanned by the introduced block (map length ). The numbers on the y-axis index the descendants of the introduced block, and are different in Figure 1, A and C due to the larger number of descendants carrying introgressed material at than . Each horizontal line within a plot represents an individual genome. The colored segment depicts the fragment that has descended from the introduced block; the color encodes the trait value associated with the fragment (see accompanying color scales).
Figure 1.
Snapshots of descendants of the introduced genome at (A) and (C) for a single realization of the introgression process for an initially neutral block () with map length and (B and D) show the corresponding snapshots for a second (independent) realization, obtained for introgression of a different genomic block (described by a different Brownian path). Each horizontal line represents the genome of an individual carrying a fragment of the introduced block; the colored portion represents the introgressed fragment while the white portions represent native blocks. The trait value associated with each introgressed fragment is encoded by the color of the block (green for positive trait values and red for negative values) and can be read off from the accompanying color scale. The y-axis of each plot indexes the descendants carrying introgressed block fragments—e.g., in (A), there are 41 descendants of the introduced block at ; thus, there are 41 lines representing 41 genomes in (A). The x-axis shows positions along the genomic region influencing trait value (here having map length ). Both realizations are obtained from direct simulations of the path-conditioned BP.
In each realization, descendant blocks are longer (on average) at than at . Different individuals carry blocks associated with different trait values, with both deleterious ( or red) and favorable ( or green) blocks present in the population at appreciable frequency at . These blocks can themselves be viewed as mosaics of smaller sub-blocks with positive and negative contributions to trait value. As time progresses, recombination tends to isolate small sub-blocks from their genomic backgrounds, allowing selection to amplify the frequency of those sub-blocks that have significantly positive contributions. Thus, at , surviving fragments are mostly associated with positive trait values (fewer red blocks).
Note that although the two Brownian paths corresponding to the two replicates are drawn from the same distribution, the two replicates look quite different. For instance, in the first realization (left panel), the introduced genome has a small sub-block with a significantly positive effect embedded within it (evident in the large number of dark green segments between genomic positions 0.179 and 0.216 in Figure 1C)— this results in rapid introgression, with >700 individuals carrying introgressed genetic material at . In the second realization (right panel), the original genome contains moderately favorable sub-blocks, which spread more slowly ( descendants at ). Interestingly, surviving blocks appear to be longer in the first realization than in the second (e.g., at ), which suggests a correlation between the trait values and lengths of surviving fragments.
In Appendix E, we also consider replicate simulations corresponding to the same introduced genome (represented by the same Brownian path), which differ from each other only in their stochastic histories of birth and recombination events. These replicates are also quite different from each other (see E1 in Appendix E), showing that both the stochasticity inherent in reproduction and recombination and the variation among introduced blocks are important sources of variability between replicates.
Introgression dynamics of an initially neutral block: branching process predictions
We now compute various statistics associated with individual fragments of the introduced block, first calculating the mean (or variance) of block lengths and trait values for any one realization of the introgression process, and then averaging the mean (or variance) over many such realizations, each corresponding to a different Brownian path.
Figure 2B shows that the average trait value of surviving fragments of a block, introduced with is positive and increases with time, even as the length of the fragments decreases (Figure 2A). This is consistent with Figure 1 and the observation that a large neutral block typically has small positively selected fragments embedded within it, which can be dislodged by a few generations of recombination. The increase in average trait values is thus most dramatic for large i.e., when there is high genetic variability along the introduced genome (which makes it more probable that some of its constituent sub-blocks have significantly positive effects) and selection is strong (which results in a quasi-deterministic increase in the frequency of such blocks).
Figure 2.
(A) Average length of surviving fragments of the introduced block in a population with at least one such fragment, and (B) average trait values of surviving fragments, vs. t, the number of generations since the initial hybridization event. (C) Probability of detecting an introgressed fragment of map length l, generations after the initial hybridization event, for various values of (D) Probability that an introgressed fragment present in the population at is associated with trait value z, for various . The introduced block has trait value and map length (main plots) or (insets). All plots are obtained from direct simulations of the path-conditioned BP, by averaging over realizations of the process, each corresponding to a different Brownian path.
However, once a small positively selected genomic sub-block has been isolated, further splitting dilutes its selective advantage (unless there is an even more strongly selected, short fragment embedded within it). Average trait value associated with descendant fragments continues to increase nevertheless over several hundred generations (in spite of recombination), due to selection which favors descendants inheriting the whole sub-block over those inheriting smaller portions of this sub-block. To see this, note that a sub-block with map length and trait value is passed on intact (i.e., without splitting) to an average of descendants, and is transmitted in part to an average of descendants. For and sufficiently smaller than 1, we have Thus any sub-block with a positive “growth rate,” i.e., spreads exponentially through the population as a nonrecombining unit, while also constantly generating smaller blocks by recombination, leading to the exponential growth of a “quasi-species” consisting of the focal block and its constituent fragments (Eigen et al. 1988).
The crucial point is that when individual loci have infinitesimal effects, a sub-block can only have a significant positive contribution and hence a significantly positive growth rate if it contains many positive-effect loci. Thus, the sub-block must be large enough to contribute substantially to the trait, but small enough that it does not undergo frequent recombination. The exponential proliferation of such medium-sized blocks that emerge from the extended neutral () block, is responsible for the increase in average trait value per descendant block over hundreds of generations (Figure 2B).
When selection is strong, fairly large sub-blocks with moderate positive contributions can still have positive growth rates and spread exponentially without being split. Thus, the average length of surviving fragments decays significantly slower than the neutral expectation for large values of (Figure 2B). Concomitantly, the distribution of block lengths l is shifted toward large l (Figure 2C) while the distribution of trait values among surviving blocks is significantly skewed toward positive values (Figure 2D) for strong selection (e.g., ).
Signatures of selection are evident in other statistics associated with the population as a whole (Figure 3). Figure 3A shows the probability that at least some part of the introduced block, i.e., one or more of its fragments, survive in the population t generations after the original hybridization event. This probability follows the neutral expectation (dashed line) over generations, irrespective of the selection strength, but then decays more slowly over longer time scales for larger values of .
Figure 3.
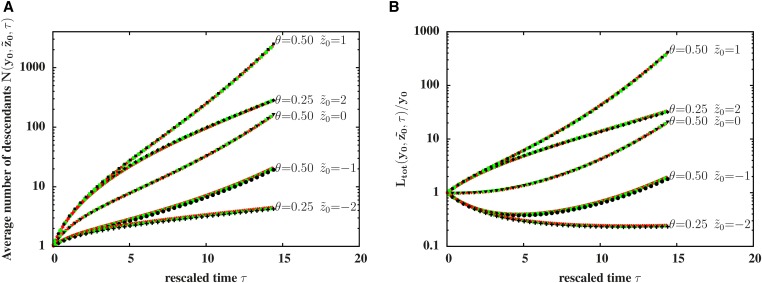
(A) Survival probability that at least one descendant of the introduced block survives (B) average number of descendants of the block, and (C) average of the total map length of introgressed genetic material in the population, vs. t, the number of generations after the initial hybridization event. The averages in plots (B and C) are conditional on survival of at least some part of the block, i.e., are normalized by The introduced block is assumed to have trait value and map length (main plot) or (inset). Both inset and main plot depict statistics for four different values of Points are calculated from direct simulations of the path-conditioned BP averaged over paths, while lines show predictions of the unconditioned BP and are obtained from numerical iteration of recursions such as Equations (3) and (4). Deviations from the neutral expectation (dashed line) become evident only after several tens of generations.
Marked deviations from neutral dynamics are also evident for the number of descendants of the introduced block and the total amount of introgressed material they carry. Figure 3B shows the average number of descendants carrying fragments of the introduced block, conditional on the survival of at least one such descendant. Figure 3C depicts the total amount of introgressed genetic material (obtained by summing over the map lengths of all introgressed fragments present in the population), again conditional on survival of some part of the block. At long times, both these quantities grow exponentially, as opposed to the linear in time spread of introgressed material predicted by Baird et al. (2003) in the absence of selection (see also dashed black lines corresponding to in Figure 3, B and C). This is consistent with our earlier observation that at long times, surviving fragments of the block are medium sized and have significantly positive trait values. Directional selection then results in exponentially fast introgression of some of these fragments.
Note that introgression is more likely (Figure 3A) and proceeds faster (Figure 3, B and C) when the introduced block (with ) is longer. This can be seen by comparing the curves in the inset () and the main plot () for any value of Longer genomic blocks have a twofold advantage—the overall probability that a block of length y is passed on (either in part or wholly) to a haploid gamete increases as (for ), resulting in a transmission advantage for longer blocks. Moreover, longer blocks display higher variability (proportional to ) and are thus more likely to contain medium-sized beneficial fragments, resulting in a long-term selective advantage for their descendants.
Interestingly, Figure 3 also shows that the predictions of the path-conditioned BP (points), when averaged over different Brownian paths, are indistinguishable from those of the unconditioned BP approximation (lines).
Long-term introgression of an initially neutral block into a finite population
Our BP analysis neglects the possibility of mating between individuals carrying introgressed fragments, and thus fails to describe introgression into a finite population of size N at long time scales. Moreover, the indefinite exponential spread of medium-sized blocks with significant contributions (), as predicted by the BP analysis, is also unrealistic for any finite N. To study long-term introgression dynamics, we simulate individuals in finite populations, and compare with BP predictions, to determine the domain of applicability of the latter.
Figure 4A shows the average total amount of surviving introgressed genome as a function of time t after the hybridization event. The predictions of the path-conditioned BP averaged over many paths (lines) agrees with finite N predictions from individual-based simulations (points) over a short time scale, whose duration is proportional to (for ). This is simply because the average number of descendants (as well as ) grows exponentially within the BP framework (Figure 3, B and C), and thus becomes comparable to any N at a time that scales as Further, the time scale is inversely proportional to the rate of introgression, which increases with the map length, for Thus, for a neutral introduced block, BP predictions are valid for a shorter time when the introduced block is long and recipient population small.
Figure 4.
Simulations of a finite population of N diploids: (A) Total length of introgressed genome surviving t generations after the initial hybridization event as a function of t, for various values of (B) Average trait value associated with a surviving block, vs. t. (C) Average trait value associated with individuals in the population, vs. t. (D) Variance of trait values associated with individuals in the population (averaged over replicates), vs. t. Lines in (A and B) represent predictions of the path-conditioned BP averaged over paths, while points are from individual-based simulations of (squares) and (circles) populations. All simulations are with discrete loci. The BP predictions match individual-based simulations of populations with N individuals, over an initial time scale that increases logarithmically with N.
Once descendants of the introduced block constitute a sizable fraction of the recipient population, mating between individuals carrying the introgressed genome becomes frequent, resulting in offspring with multiple introgressed fragments. For instance, with strong selection (), the average number of introgressed fragments per diploid genome ranges from (for ) to (for ) as early as at .
This has interesting implications for the evolution of trait values and hence, the rate of adaptation in finite populations (as shown in Figure 4, B and C). The average trait value associated with individual fragments in a finite population follows the BP prediction over a time scale of duration , but then starts declining over longer times (Figure 4B). However, since a typical descendant accumulates many such fragments over time, the average trait value associated with individuals keeps increasing (Figure 4C). The average trait value initially increases faster in the smaller () population, in which mating between descendants of the introduced block starts occurring soon after the hybridization event (Figure 4C). However, the fixation of sub-blocks and the accompanying decline in genetic variability is also faster with (Figure 4D). Since the trait mean advances each generation by an amount β times the genetic variance, the higher variance with allows for a longer selection response and a greater net advance of the trait value (Figure 4C).
Thus, in the present model, adaptive introgression into a finite population involves two distinct processes occurring on different time scales. The first phase is characterized by splitting of the original block by recombination, the separation of genomic fragments with positive fitness effects from their deleterious background and the amplification of these by selection. During this phase, the average trait value per descendant increases logarithmically in time and is well predicted by the BP. The second phase is characterized by increased probability of mating between individuals carrying introgressed genetic material and the emergence of individuals who bear multiple, beneficial introgressed fragments, and have a strong selective advantage. This causes a rapid increase in average trait value among individuals in the population at longer time scales, even as the average trait value per surviving fragment declines. This rapid increase is not predicted by the BP.
Nevertheless, the BP provides valuable intuition about the initial phases of introgression, and is easier to simulate since it only tracks single fragments. We now use the BP framework to explore how blocks that are originally non-neutral (with ) spread during early phases of introgression.
Introgression dynamics of a beneficial introduced block:
Suppose that a single copy of a beneficial block (with ) enters the native population. Unlike in the case of a neutral () introduced block, we expect the trait values associated with descendants to decrease as the original block splits into smaller fragments. Does this then imply that a long, positively selected genomic block is less likely to introgress than a discrete locus (which cannot be further split by recombination) with the same selective advantage? As before, we follow various attributes such as and the average size and effect of descendant blocks through time using the BP framework, but now with a focus on how these vary with (the map length of the introduced block).
Figure 5A shows that the survival probability a few hundred generations after the hybridization event, is actually minimum for the discrete locus and increases with map length but more weakly than in the case of the block. This is true for both selection strengths shown in Figure 5A (main plot and inset). The weak dependence of on reflects the tension between two opposing effects—the higher (overall) probability of transmission of longer blocks to the gamete during meiosis, vs. the fact that long blocks are more likely to be split by recombination and hence transmit only a part of their selective advantage to the next generation.
Figure 5.
(A) Probability that at least one descendant of an originally beneficial () introduced block survives (B) average of the total map length of introgressed genetic material in the population (conditional on survival of some part of the introduced block) (C) average length of surviving blocks and (D) average trait values of surviving block, vs. t, the number of generations since the initial hybridization event. Points are calculated from direct simulations of the path-conditioned BP, while lines in (A and B) show predictions of the unconditioned BP and are obtained from numerical iteration of Equations (3) and (4). Both inset and main plot depict statistics for four different values of Main plots show statistics for an introduced block with map length and inset for
However, within surviving lineages, short blocks introgress faster, i.e., leave more descendants and result in a higher total length of introgressed genome in the long run, than long blocks with the same selective advantage (Figure 5B). This is because short blocks undergo fewer divisions, and, hence, less dilution of selective effect. This is also evident in Figure 5D, which shows that the long-term average trait value associated with surviving fragments is highest for the shortest introduced block, for a given total value.
Since long blocks break up faster than short ones, fragments of the genomic block are already shorter on average at , than fragments of an originally smaller (e.g., ) block that had the same trait value (Figure 5C). Thus, at longer time scales, the average length of descendant blocks depends nonmonotonically on the map length of the original block—surviving fragments are longest when the initial selective advantage is spread over a block of intermediate length (Figure 5C).
As in the case, the BP fails to describe long-term introgression into finite populations. In a finite population, the average trait value associated with descendant individuals actually increases at long time scales, even as trait values of descendant blocks falls (results not shown). As before, this is due to the emergence of individuals carrying multiple introgressed fragments. Thus, recombination can be thought of as playing a dual role during the introgression of a beneficial genomic block. In the initial phase, recombination splits the original block into smaller and smaller fragments, thus diluting the selective advantage of descendants carrying block fragments over time. The most successful fragments that survive this phase are medium-sized and have a significant selective effect, causing them to be amplified faster by selection than they can be broken up by recombination. In later phases, recombination reassembles those fragments that have survived the initial phase, resulting in genomes with very large and positive trait values.
Note that the rate of introgression [reflected in the rate of growth of quantities such as and ] shows a qualitatively different dependence on the initial map length when the introduced block is strongly beneficial () vs. when it is neutral (), suggesting that there could be a crossover between these two kinds of dependence at some critical value of . To investigate this, we plot the average number of surviving descendants a 100 generations after the initial hybridization event, as a function of map length of the selected genomic block, for various initial trait values (Figure 6). For low or zero , the number of descendants increases with increasing . This is due to the higher genetic variation associated with longer blocks. When the introduced block is neutral (or nearly neutral) with respect to the native population, the response to selection must be driven by the release of this variation by recombination. By contrast, when the initial trait value is high, initial introgression depends more on the selective advantage of the introduced block over native blocks, and less on the generation of new variation. In this case, varying essentially alters the balance between selection and recombination, with longer blocks splitting faster, resulting in a rapid dilution of their selective effect. Thus, in this case, at actually falls with Interestingly, at intermediate values of the average number of surviving descendants exhibits a nonmonotonic dependence on (see and curves in Figure 6), signifying a switch from behavior (associated with strongly beneficial genomic blocks) to behavior (associated with initially neutral blocks).
Figure 6.
The average number of surviving descendants carrying some part of an introduced block for 100 generations after the initial hybridization event (conditional on survival of at least one such descendant), vs. where is the map length of the introduced block. The different colors correspond to different values of the (unscaled) trait value associated with the introduced block. All points are obtained from direct simulations of the path-conditioned BP.
Figure 6 also shows that, for a fixed map length, introduced blocks with higher trait value leave more descendants. This effect is particularly marked when map lengths are small and introgression depends more on the selective effect of the introduced block and less on the generation of new variation. This also implies that if there is random sampling of blocks from a source population with a distribution of trait values (with mean and variance ), then most successful introgression events will be initiated by outlier genomes with higher than average trait values within the source population. Thus, fragments of such genomes tend to be over-represented in the recipient population (relative to their frequency in the source population). As before, we expect this effect to be more pronounced when is small. This is confirmed in simulations (Figure F1, Appendix F).
Introgression dynamics of a deleterious introduced block
Finally, we consider the introgression of a block with which is at a selective disadvantage with respect to the native population. The role of selection in this scenario is subtle—on the one hand, stronger selection makes it likely that lineages containing (deleterious) fragments of the original block die out in the first few generations; on the other, small fragments of the block with even mildly positive contributions to trait value, once separated from the deleterious background, have a strong selective advantage that causes their number to rapidly increase. Thus, while the probability that at least part of the block survives declines more rapidly for larger in the first few generations (Figure 7A), it also approaches its asymptotic value faster.
Figure 7.
(A) Survival probability of at least one descendant of an originally deleterious () introduced block (B) average of the total map length of introgressed genetic material in the population (conditional on survival of some part of the introduced block) (C) average length of surviving blocks and (D) average trait values of surviving block, vs. t, the number of generations since the initial hybridization event. Points are calculated from direct simulations of the path-conditioned BP, while lines in (A and B) show predictions of the unconditioned BP and are obtained from numerical iteration of Equations (3) and (4). Both inset and main plot depict statistics for four different values of Main plots show statistics for an introduced block with map length and inset for
Moreover, the average number of descendant blocks (conditional on survival) and the total amount of introgressed genome they encompass, grows faster for larger i.e., for stronger selection against the original deleterious block and/or higher genic variance of the block (Figure 7B). The trait value associated with surviving descendant blocks also becomes rapidly positive when is large (Figure 7D). This is consistent with the general expectation that under strong selection, maladapted lineages must undergo rapid adaptation or else soon be lost from the population.
The average length of blocks descended from the originally deleterious block is shorter than that of descendant blocks of the neutral () block (Figure 7C). Shorter blocks are associated with less negative contributions to trait value (on average) and are favored by selection; thus, the stronger the selection, the more markedly the average block size deviates from the neutral expectation, at least at short times. At longer times, however, the decay in average block size slows down significantly for high values of . As before, this is due to the emergence of small positively selected fragments from the deleterious blocks. Selection opposes any further splitting of these fragments, and favors descendants who inherit the entire fragment, as opposed to a smaller portion.
Figure 7, A and B also show that large deleterious blocks are more likely to survive, and also leave more descendants within surviving lineages than small deleterious blocks with the same selective disadvantage (insets vs. main plots). This is both because of the higher transmission advantage of large blocks during meiosis as well as the higher segregation variation and superior adaptive potential associated with them.
Discussion
Adaptive introgression under infinitesimal selection
Under the infinitesimal model, individual loci have vanishingly small effects. Nevertheless, the introgression of a block of genome with many such loci under directional selection differs qualitatively from neutral introgression. Positive selection causes the average number of descendants of such a block, as well as the average total amount of introgressed genetic material, to grow exponentially, at least while the number of descendants is much smaller than population size. For introduced blocks that are neutral or nearly neutral, exponentially fast introgression emerges only several tens of generations after the hybridization event (Figure 3, B and C), once favorable fragments are dislodged by recombination. By contrast, if the introduced block has a significant selective advantage, exponential growth of descendant blocks starts almost immediately after hybridization (Figure 5B), and continues indefinitely in an infinite population. This is contrary to the intuitive expectation that, under the infinitesimal model, multiple rounds of recombination should progressively dilute the selective effect of descendant blocks, leading to patterns that are essentially indistinguishable from those of neutral introgression over longer time scales. Here, we show that this dilution of selective effect is countered by selection, which tends to amplify medium-sized fragments with significant contributions, so that they proliferate, essentially as nonrecombining units.
Linkage plays a qualitatively different role, depending on whether adaptive introgression is driven by the initial selective advantage of a very fit introduced block, or by the generation of new variation via recombination, for instance, if the introduced block is initially neutral or deleterious (Figure 6). When the introduced block is fit, tight linkage ensures that it is passed on intact to more descendants, leading to faster introgression by shorter blocks. When the introduced block is nearly neutral, larger map lengths are correlated with more hidden variation and a higher probability that a positively selected sub-block can escape from the neutral block to grow exponentially. Thus, introgression is faster if a neutral or nearly neutral introduced block is longer.
Length of surviving blocks
Under the infinitesimal model, the process of introgression depends on relatively few parameters: the map length of the introduced block, the trait value relative to the genic variance of the block, and the strength of selection relative to recombination. Specifically, the length of surviving blocks is shaped by two opposing effects—the block must be small enough that it is transmitted intact (without recombination) to the majority of offspring, but large enough that it contributes substantially to trait value.
“Successful” descendant blocks that emerge from a neutral block of map length have typical contributions that scale with where is the genic variance per unit map length. Note that can be high either if the density of selected loci per unit map length is high or if the variance of their fitness effects is large. Thus, it may not be possible to disentangle the number of selected loci within initially successful fragments from the distribution of their fitness effects. More generally, the initial survival of the genome depends on the growth rates of intermediate sized blocks, not on the finer-scaled variation that might eventually be uncovered and then reassembled by recombination in a large population. In fact, in a small population of size N, initially successful fragments may fix in generations, well before recombination can separate positive and negative effect loci within these. This also explains why in simulations with L discrete loci, quantities such as the net advance of trait value under selection in a finite population, reach a limit that is independent of L, and hence can be accurately described by the infinitesimal model (Figure B1, Appendix B).
Variability among replicate populations
Most of the systematic trends described above are only evident for the averages of various quantities, where the averaging is over thousands of replicates, each involving a different realization of the introduced block. Individual replicates can, however, differ dramatically from one another (see Figure 1 above and Figure E1 in Appendix E) and also from the average. Such variability between replicates presents a severe challenge for developing methods to infer population genetic parameters (typically from a single realization of the introgression process).
The high variability among replicates reflects two different kinds of underlying stochasticity. First, individual Brownian paths describing the introduced block can be quite different from each other, even if they are drawn from the same distribution. Positive-effect alleles may be physically clustered on an individual block just by chance even if the distribution of effect sizes of loci is the same across different genomic regions and there is no population-wide LD in the source population from which the block originated. Rapid introgression ensues when the introduced block happens to contain a genomic tract with strong positive effect (for instance in Figure 1, A and C), while introgression is much slower when the clustering is weaker and the constituent tracts only moderately beneficial (Figure 1, B and D). This also suggests that introgression would be more likely even with infinitesimal effect loci, if the underlying distribution of effect sizes were nonuniform across the genome, resulting in particular genomic regions that contribute significantly to the trait. Conversely, introgression becomes less likely if the source population is under very strong stabilizing selection (which would create negative LD and reduce the likelihood that a genome contains stretches with significant positive effect).
Second, different replicates corresponding to the same Brownian path can also be very different due to the stochasticity inherent in reproduction and recombination events (see Figure E1 of Appendix E). Various stretches of a long, nearly neutral, introduced block may be lost from the population by chance early on, when segregating sub-blocks are also long, have weak effects, and are present in small numbers. At longer times, once medium-sized blocks with a substantial contribution to trait value (i.e., with positive growth rate ) have been isolated, we expect introgression to be dominated by the proliferation of the sub-block with the largest growth rate. Understanding whether the interplay between early stochasticity and long term, essentially deterministic dynamics can cause parallel introgression signatures in replicate populations that receive the same introduced genome, remains an interesting direction for future work.
Single locus vs. infinitesimal introgression
The exponential spread of medium-sized blocks even under infinitesimal selection, and the high variability among replicates suggest that patterns of neutral diversity (such as those associated with selective sweeps) may be very similar for an introgressing block with many weak-effect loci and a block with a single discrete locus. In both cases, a haplotype of map length will fix, where T is the time to fixation, provided the positively selected region is smaller than this. However, if a successful fragment has map length , then the region of reduced diversity might be larger (Figure 8, C and D). It remains to be established whether such a pattern has power to systematically distinguish between one selected locus vs. many, and how it might be obscured if multiple blocks are introduced.
Figure 8.
Haplotype diversity along the genome in the native population, t generations after the initial hybridization event in which a single copy of a positively selected locus (A and B), or a small selected block with map length (C and D), or a larger selected block with (E and F) is introduced into the population. The x-axis represents position along the genome, with denoting the position of the selected locus (in A and B) or the mid-point of the selected block (in C and F). The y-axis represents haplotype diversity. The light green bars in each figure show those fragments of the introduced block that have fixed; the dotted segments represent the fragments that have been lost, while the purple segments represent those fragments that are segregating at some appreciable frequency in the population. The black curves in the insets in (B and F) show how the trait value varies along the selected block (with increasing distance from the edge of the block). The two sub-figures in each row depict results from replicate simulations (corresponding to different Brownian paths). The trait value associated with the selected locus or block is in each plot; other parameters are and Each figure is obtained from individual-based simulations of populations with individuals. Haplotype diversity is measured for the discrete locus case (A and B), at in case of the short block (C and D), and at for the extended block (E and F).
When a single genome introgresses, sweeps are necessarily “hard” (Hermisson and Pennings 2017). These can be observed in individual-based simulations by tracking haplotype diversity H, measured as where N is the population size and is the frequency of haplotype i in the population (Nei and Tajima 1981). The native population is assumed to have distinct haplotypes before hybridization. Figure 8 shows how haplotype diversity changes with increasing map distance from a selected locus or block, a few hundred generations after hybridization. The discrete locus and the extended blocks are associated with the same initial trait value () and experience the same selection (). Comparable regions of reduced diversity can be observed near the discrete locus (Figure 8, A and B) as well as the short block (Figure 8, C and D), and also near introgressing fragments of the large selected block (Figure 8, E and F), making it difficult to infer the underlying genetics from these observations.
Some insight may be gained, however, by comparing introgression signatures in replicate populations. If replicates were made starting with different extended blocks drawn from the source population, there should be no concordance between regions of reduced diversity among replicates under the infinitesimal (compare Figure 8, E and F), as long as all genomic regions contribute approximately equally to the divergence between the source and recipient population. By contrast, sweep events are expected to be clustered in the same genomic regions in different replicates, when selection is concentrated at one or few loci. However, if the source population exhibits genomic islands of divergence i.e., if the average effect size of alleles, even though small, is systematically different in certain genomic regions in the source population, then again high concordance between replicates can be observed between replicates, even under the infinitesimal model. These issues will be explored in detail in future work.
Initial spread vs. long-term introgression
Our analysis of the initial spread of the introduced block and its descendants is based on the path-conditioned branching process, in which the number of offspring of different individuals is assumed to be correlated only via the Brownian path that specifies the trait values of the introgressed fragments they carry. This allows us to analyze a rather complex polygenic architecture, while still maintaining computational tractability. Interestingly, the predictions of the path-conditioned BP for the distributions of various quantities such as the block lengths and values, when averaged over different Brownian paths, are indistinguishable from the predictions of an unconditioned BP approximation that neglects correlations in trait value among different descendants of an individual. Elucidating the correspondence between the exact and approximate unconditioned BP, and exploring whether this correspondence might yield analytical predictions for signatures of sweep-like events under the infinitesimal model, remains an interesting direction for future work.
The BP framework predicts introgression dynamics in a finite population of size N over a short, initial timescale that scales as . Over long timescales, mating between descendants of the introduced genome become common, resulting in faster introgression that cannot be predicted by the BP (Figure 4). Note that recombination plays a qualitatively different role during these two phases of introgression. When the introduced block is strongly beneficial, recombination dilutes the selective advantage associated with descendant blocks in early stages of introgression (thus acting counter to selection). In later phases, recombination tends to bring together small positively selected sub-blocks (that have survived the initial phase), generating descendant individuals with multiple introgressed fragments and a strong selective advantage, thus countering Hill-Robertson interference (Hill and Robertson 1966). Ultimately, linked clusters of favorable variants fix, along with small blocks of associated genome.
Such “genomic islands,” with many linked, putative adaptive variants, have received much attention (Strasburg et al. 2012). One interpretation is that linked adaptive alleles are less prone to swamping by recurrent gene flow; genomic rearrangements that reduce recombination in regions with many such alleles are also favored by selection, thus further strengthening linkage (Yeaman and Whitlock 2011). Other explanations involve “divergence hitchhiking”—the increase in establishment probability of an adaptive mutation that is linked to adaptive variants already established in the population (Via 2012). However, theoretical analyses suggest that this is unlikely to explain most cases of clustering in the presence of recurrent gene flow (Feder and Nosil 2010; Yeaman and Whitlock 2011). Here, we show that clusters of favorable alleles may arise simply by chance sampling from a source population during a single introgression event, even when variation is uniformly spread over the genome in the source population, and when there is no swamping by continuing gene flow. Moreover, in some situations, fine-scale recombination can actually promote clustering by further separating the adaptive and maladaptive alleles within a beneficial fragment, and then bringing together various combinations of adaptive alleles.
Limits to selection
Under the infinitesimal model, any one genome can, in principle, contribute an infinite amount: if a block of length is divided into l fragments, each with variance then the sum of all positive fragments has expectation which diverges with l. Given enough time, all fragments with positive effect would be released by recombination and established by selection, resulting in an indefinite net advance under selection in an infinite population. However, in any real population of N individuals, variation will be fixed in generations. The efficiency with which selection can fix favorable variants that are embedded in a single initial genome depends on how quickly recombination can bring together those favorable fragments that survive, despite Hill-Robertson interference.
When the trait under selection is determined by an infinite number of unlinked loci (as in the standard infinitesimal model), the net advance under selection scales with the size N of the population (Robertson 1960). In our simulations of the infinitesimal model with linkage, we observe a much weaker dependence on N (see Figure 4C, where a 10-fold increase in population size causes the net advance to increase only by a factor of ). A related effect was noted by Weissman and Barton (2012)—they found that even with a constant high rate of beneficial mutations, the rate of adaptive substitution approaches a limiting value that is independent of population size and mutation rate, but is constrained only by the map length of the mutational target.
Selection on standing variation
We have considered introgression of a single block of genome into a homogeneous population. We see this as a first step toward understanding selection on standing variation. An extension of our model toward this goal would be to focus on the contribution of a single genome to the selection response of a heterogeneous population. This might be approximated by supposing that the focal genome meets random genomes, drawn from a variable population that is itself responding to selection. The net contribution of any one initial genome would be reduced by the randomness in the backgrounds it encounters, but the response of the whole population would be increased if variation were introduced from genomes rather than one. A key question is how the net advance under selection scales with N under this model.
In general, re-examining classical adaptation or introgression scenarios in the polygenic setting is becoming increasingly important in light of genome-wide association studies (GWAS) which point to the highly polygenic (and even “omnigenic”) nature of several traits (Boyle et al. 2017). These studies suggest a trait architecture in which a moderate number of strongly or moderately selected loci are embedded within a very large number of small-effect loci that are undetectable even in very high-powered GWAS, but nevertheless explain most trait heritability. This is consistent with the common observation that QTL often “break up” into multiple loci when investigated under high resolution (Flint and Mackay 2009); fine mapping of individual genes also suggests that multiple variants within each gene that contribute to trait variation (e.g., Stam and Laurie 1996). Further, the fraction of heritability that can be attributed to individual chromosomes is proportional to the length of the chromosome (Yang et al. 2011); the heritability explained by various functional gene groups has also been found to be approximately proportional to the size of the group (Boyle et al. 2017). All of this suggests a very large number of trait loci spread more or less uniformly across the genome.
A second observation concerns the large number of deleterious mutations present in the genomes of most species; these mutations have a wide range of selective effects, but with an average effect that is quite small (∼ for Drosophila, see Charlesworth (2015)). Both these lines of evidence point to the relevance of the infinitesimal model with linkage as a way of understanding polygenic evolution. This model is of course an abstraction of reality, but is arguably no less realistic than the usual assumption that the effects identified by GWAS or by QTL mapping are concentrated at single loci. Data should be tested against the alternative extremes, of a single locus vs. infinitesimal effects distributed over an extended region, rather than only against the former, as is current practice.
Acknowledgments
We thank Alison Etheridge and Sarah Penington for useful discussions.
Appendix A
Evolution of Trait Values in the Source Population Under the Infinitesimal Model with Linkage.
We describe below how the distribution of trait values in an infinite population evolves under the infinitesimal model with linkage. For simplicity, we consider a panmictic population and assume that there is no selection on the trait. Then, the frequency of diploid individuals with haplotypes associated with trait values and , is simply the product of the haploid or gametic frequencies, i.e., .
The haplotype frequencies change from one generation to the next according to:
| (A1) |
The first term on the right hand side represents the probability that there is no recombination within the genomic region contributing to the trait, so that the gamete has the same trait value as one of the haplotypes of the diploid parent. The second term describes generation of a gamete by recombination between parental haplotypes with trait values and . The map lengths of blocks inherited by the gamete from the two haplotypes are and (where is uniformly distributed in [0, ]); the additive contributions of these blocks is and respectively. The term represents the probability that given a block of map length and trait value a daughter block of length has an associated contribution [see Equation (1) in the main text].
For a population in equilibrium, we expect Approximating the equilibrium distribution by a normal distribution with mean and variance V, and substituting into Equation (A1), yields The equilibrium variance of trait values in diploid individuals is thus in the absence of selection.
If there is selection on the trait, then it is necessary to consider the evolution of diploid frequencies, since selection tends to build up correlations between the trait values associated with the two haplotypes carried by an individual. Moreover, Equation (1) in the main text does not describe inheritance of trait values when there is LD between tightly linked regions of the genome (for instance, due to stabilizing selection, see Lande 1976). Extending the infinitesimal model to a scenario with selection and linkage is an interesting direction for future work.
Appendix B
Approximate Simulation Schemes for the Infinitesimal Model with Linkage
We simulate genomes under the infinitesimal model with linkage using two different approximate simulation schemes: the discrete locus scheme and the sub-block-based scheme. In the discrete locus scheme, the Brownian path is approximated by a “staircase” with a large number of piecewise-constant segments. In practice, we assume that there is a large number of discrete loci with additive contributions uniformly spread across the introduced block.
These contributions are chosen iteratively as follows. First, the contributions of the two groups of loci are set to z and and z sampled from a normal distribution with mean and variance [see Equation (1) in the main text]. Then, each of the two groups is further divided into two and the contributions of the resultant groups of loci chosen by again sampling from a normal distribution with mean equal to half the trait value of the parent block (now consisting of loci), and variance This process is iterated R times to generate the trait values associated with finer and finer sub-divisions of the genome by conditioning on the trait value of larger sub-divisions, thus obtaining the additive contributions of each of the loci in the final iteration. We employ this iterative scheme to ensure that the always sum to some prespecified . Note that simply drawing as L independent, random variables would have generated an ensemble of paths with a distribution of trait values, rather than a fixed .
In the discrete locus scheme, recombination is implemented by uniformly sampling one of the possible crossover points between adjacent loci. The trait value associated with the descendant block is then simply the sum of the effects of all the introgressed loci that it inherits. At short times, while the typical size of descendant blocks is much larger than the spacing between loci, we expect no difference between the discrete locus scheme and the true infinitesimal model with linkage. At longer times, once recombination starts isolating individual loci, qualitatively different dynamics should emerge, since the maximum variation that can be released by recombination in the discrete locus model is limited, while this is not so for the true infinitesimal model with linkage. However, in a finite population of N individuals, there is also fixation of segments of the introduced block in generations. Thus, we expect individual loci to matter only if recombination can separate the loci within segments before they fix, i.e., if the spacing between adjacent loci (given by ) is comparable to the typical length of segments that fix. This implies that for any finite population of size N, there is a typical number of loci (which increases with the size of the population), such that various quantities of interest become independent of L for under the discrete locus scheme. This is illustrated in Figure B1b which shows how the average trait value in a population with approaches an L-independent limit with increasing L in individual-based simulations implemented using the discrete locus scheme. Since this limit depends on population size, we employ the discrete locus scheme only for individual-based simulations of finite populations.
In the sub-block-based scheme, we divide the introduced block into L sub-blocks and choose their additive contributions as in the first scheme. However, now when a portion of the parent block is transmitted to an offspring, the trait value of the descendant block is obtained by summing the contributions of all the complete sub-blocks inherited from the parent plus a random contribution ζ that corresponds to the partially inherited sub-block. If the crossover point lies within the sub-block such that the descendant inherits a fraction α of this sub-block, then ζ is drawn from a normal distribution with mean equal to α times the additive contribution of the sub-block and variance given by Thus under this approximation, the contribution of sub-blocks shorter than is uncorrelated across different individuals, which is not true for the exact model.
To test the accuracy of this approximation, we consider the introgression of a single genome (described by a particular Brownian path), and simulate it with finer and finer sub-divisions (larger and larger values of L) under the BP framework. In the example shown in Figure B1a, the number of descendants of the introduced block, conditional on survival of any part of the block, becomes independent of L beyond , suggesting that introgression dynamics is insensitive to the exact shape of the Brownian path over map scales finer than (in this example). This is consistent with the fact that introgression dynamics is typically dominated by the spread of medium-sized blocks, and not on the fine-scale variation within these. Note that if selection strength β or genic variance are low, then the typical, successful sub-blocks are shorter, and L has to be correspondingly large, for the predictions of the sub-block-based scheme to become insensitive to a further increase in L.
Appendix C
Moments of the Number of Descendants and Total Amount of Introgressed Genome Under the Unconditioned BP
For simplicity, we consider below the distribution of the number of descendants of an introduced block with initial map length y and trait value z. Recursions for the Laplace transform of this distribution can be obtained similarly to Equation (3) in the main text, and are given by:
| (C1) |
Differentiating the above equation with respect to θ and using (where is the term in the square brackets above) yields the following recursions for the first two moments of the block number distribution.
| (C2a) |
| (C2b) |
with the initial condition for all k.
The distribution of the total amount of introgressed genetic material at time t, obtained by summing over the map lengths of all descendant blocks of the introduced haplotype, can be obtained in a similar way. The distribution and the moments follow identical recursions as n, but the initial condition is now for all . As in Equation (3 )in the main text, we can numerically iterate Equations (C2a) and (C2b) by we discretize (y,z) space and replace the two-dimensional integral by a double summation.
In principle, it is also possible to compute the average (and not just the total) length of surviving blocks from the joint distribution of and n at any time t, which can be obtained by inverting the joint moment generating function but this is computationally cumbersome.
Appendix D
Effective Parameters Governing Introgression
To describe the continuous time dynamics for the number of descendants of an introduced block, we re-express Equation (C2a) in terms of and and further write y as where r is the recombination rate and L is the physical length of the block of interest. We also use the genic variance per unit physical length which is related to the genic variance per unit map length as This yields:
| (D1) |
Taking the limit and retaining the lowest order term in gives:
| (D2) |
If we now denote by α, and divide the above equation throughout by y, we obtain Equation (4) in the main text, with re-written as . Equation (4) is expressed in terms of map length y, the scaled trait value the ratio of selection to recombination strength and rescaled time
Recall that at , we have . Thus the number of descendants after an infinitesimal interval must be which is a function of θ, and but independent of y. If we now make the ansatz: then it follows from Equation (4) in the main text that is also independent of y, so that is independent of y at all later times. A similar argument can be made for the expected value of the total amount of introgressed genome, which satisfies the same equation as Equation (4) in the main text, but with the initial condition this then yields the solution Note that and here refer to the unconditional expectation values, i.e., they have not been normalized by the probability that at least some part of the introduced block survives.
We test the validity of these scaling arguments for the true model of introgression into an infinite native population (which makes no assumptions about correlations between trait values of descendants). This model involves discrete generations and does not neglect correlations between trait values of different descendants of a block (see main text). Figure D1a shows the average number of descendants of a block with map length and rescaled trait value as a function of rescaled time for various values of θ and in the true model. For each (θ, ) combination, we simulate introgression for three values of map length: (red), (green), and (black), and find that there is perfect scaling collapse of vs. rescaled time τ for blocks of different lengths, as long as z and β are varied accordingly to hold and constant. We also find excellent scaling collapse for vs. τ for different values of y (Figure D1b), in accordance with the scaling arguments above.
Note that the curve, and the curve do not coincide, although they are both characterized by the same value of This illustrates an important distinction between the infinitesimal framework and an alternative model (obtained by taking the limit of the infinitesimal model) in which offspring trait value is deterministically proportional to the length of the block it inherits from the parent (Barton 1983). In the latter model, it is the composite parameter that governs introgression dynamics.
Appendix E
Variability Between Replicates Corresponding to the Same Brownian Path
Figure 1 in the main text illustrates the variability between two replicates involving introgression of two different genomes described by distinct Brownian paths (which are drawn from the same distribution, characterized by a particular value of and ). These Brownian paths are likely to differ from each other by chance in various details, e.g., the location of the genomic fragment associated with the highest additive contribution, as well as the length and contribution of this fragment. Thus, some Brownian paths could be associated with a higher likelihood and rate of introgression, if they happen to contain a fragment that is particularly favorable.
However, there is additional variability arising from the random nature of recombination and reproduction events. This is illustrated in Figure E1, which shows results of replicate simulations for the same introduced block (corresponding to the same Brownian path). These replicates thus represent two different stochastic histories of birth and recombination events. Each column corresponds to one replicate, with the upper and lower panels depicting descendant individuals who carry some fragment of the introduced block, and generations after the initial hybridization event, respectively. Note that there is significant variability between the two replicates (columns)—the sub-blocks that survive the initial, nearly-neutral phase of the introgression process are completely different in the two cases; they are also associated with different trait values, and hence proliferate at different rates. Consequently, the number of descendant blocks at is also quite different in the two cases.
This example thus suggests that, for various parameter regimes, the stochasticity inherent in recombination and other evolutionary processes may be as (or even more) important a source of variability between replicates as the variability associated with different introduced blocks. We expect the former to be especially significant when segregating blocks are few, long, and associated with weakly nonzero effects (in which regime recombination is expected to influence dynamics more than selection). Understanding the consequences of different kinds of stochasticity during different phases of the introgression process is an interesting direction, and will be explored in more detail in a future study.
Appendix F
Introgression of Introduced Genomes with a Distribution of Trait Values
For most of the analysis, we consider introgression statistics for a fixed trait value of the introduced block. However, typically itself will be randomly distributed in the source population. For instance, in the absence of selection, the variance of trait values among blocks in a source population in LE is (Appendix A). Here, we consider introgression outcomes when the introduced genome is randomly sampled from this source population.
The main plot in Figure F1 compares the distribution of trait values of all blocks present in the source population with the distribution of trait values of those blocks that lead to “successful” introgression events, involving >100 descendant blocks (green) or >500 descendant blocks (red) in the recipient population at Unsurprisingly, blocks with higher than average trait values within the source population are more likely to initiate successful introgression events than blocks with lower trait values. Thus, the blocks that contribute most to the introgressive potential of the population are outliers with high trait values. This effect is especially marked when is low, which limits the ability of recombination to generate new variation among descendants carrying fragments of the introduced block. Then introgression is driven more by the initial selective advantage of the introduced block. This leads to a rather counter-intuitive situation where outlier genomes (with trait value much greater than the population average) are more relevant to introgression when the source population has lower genetic variability. This can be seen in Figure F1 (inset), which shows the average trait value of those blocks that initiate successful events relative to the variance of the source population from which they originate, falls with increasing map length (and hence increasing genetic variability in the source population).
Figure B1.
(A) Average number of descendants of the block (conditional on survival of some part of the block) vs. t, under the path-conditioned BP implemented using the sub-blocks based scheme. Different colors correspond to different values of L, the number of sub-blocks with prespecified trait contributions (see above). (B) Average trait value associated with individuals in the population, vs. t, in individual-based simulations of a population of size implemented using the discrete-locus scheme. Different colors correspond to different values of L, the number of uniformly-spaced loci on the introduced block. In both set of simulations, a single block ( ) is introduced at and introgresses into the recipient population under selection strength
Figure D1.
(A) Average number of descendants of an introduced block of map length and effective trait value at rescaled time τ, vs. τ for three values of map length (red), (green) and (black) and various (θ, ) combinations (specified on the plots). (B) Average total amount of introgressed genome (in units of , the map length of the selected region) vs. τ. For each (θ, ) combination, the vs. τ curves (or the vs. τ curves) corresponding to the three values of coincide completely.
Figure E1.
Snapshots of descendants of the introduced genome at (A) and (C) for a single realization of the introgression process for an initially neutral block () with map length and (B and D) show the corresponding snapshots for a second (independent) realization for introgression of the same genomic block (represented by the same Brownian path as in the case of A and C). Each horizontal line represents the genome of an individual carrying a fragment of the introduced block; the colored portion represents the introgressed fragment while the white portions represent native blocks. The trait value associated with each introgressed fragment is encoded by the color of the block (green for positive trait values and red for negative values) and can be read off from the accompanying color scale. The y-axis of each plot indexes the descendants carrying introgressed block fragments. The x-axis shows positions along the genomic region influencing trait value (here having map length ).
Figure F1.
The distribution of trait values among blocks that initiate successful introgression events, i.e., have at least 100 descendants (green) or 500 descendants (red) at is significantly shifted with respect to the original distribution of trait values in the source population (black). The introduced blocks have map length and are randomly sampled from a source population with mean trait value zero and , so that the variance of trait values of haploid genomes in the source population is The strength of selection in the recipient population is Inset: The average trait value of blocks initiating successful introgression events (i.e., having at least 100 descendants (green) or 500 descendants (red) at ) relative to the variance of trait values in the source population, falls with the map length of the block. Outlier genomes () are more important for introgression when the genomes are short (low). All predictions are obtained from the BP model.
Footnotes
Communicating editor: G. Coop
Literature Cited
- Arnold M. L., 2004. Transfer and origin of adaptations through natural hybridization: were Anderson and Stebbins right? Plant Cell 16: 562–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird S., Barton N. H., Etheridge A. M., 2003. The distribution of surviving blocks of an ancestral genome. Theor. Popul. Biol. 64: 451–471. [DOI] [PubMed] [Google Scholar]
- Barton N. H., 1983. Multilocus clines. Evolution 37: 454–471. [DOI] [PubMed] [Google Scholar]
- Barton N. H., Bengtsson B. O., 1986. The barrier to genetic exchange between hybridizing populations. Heredity 57: 357–376. [DOI] [PubMed] [Google Scholar]
- Barton N. H., Etheridge A. M., Véber A., 2017. The infinitesimal model: definition, derivation, and implications. Theor. Popul. Biol. 118: 50–73. 10.1016/j.tpb.2017.06.001 [DOI] [PubMed] [Google Scholar]
- Boyle E. A., Li Y. I., Pritchard J. K., 2017. An expanded view of complex traits: from polygenic to omnigenic. Cell 169: 1177–1186. 10.1016/j.cell.2017.05.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer M. G., 1980. The Mathematical Theory of Quantitative Genetics. Oxford University Press, Oxford. [Google Scholar]
- Charlesworth, B., 2015 Causes of natural variation in fitness: evidence from studies of Drosophila populations. Proc. Natl. Acad. Sci. USA 112: 1662–1669. (erratum: Proc. Natl. Acad. Sci. USA 112: E1049). DOI:10.1073/pnas.1423275112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eigen M., McCaskill J., Schuster P., 1988. Molecular quasi-species. J. Phys. Chem. 92: 6881–6891. [Google Scholar]
- Elyashiv E., Sattath S., Hu T. T., Strutsovsky A., McVicker G., et al. , 2016. A genomic map of the effects of linked selection in Drosophila. PLoS Genet. 12: e1006130 10.1371/journal.pgen.1006130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feder J. L., Nosil P., 2010. The efficacy of divergence hitchhiking in generating genomic islands during ecological speciation. Evolution 64: 1729–1747. 10.1111/j.1558-5646.2010.00943.x [DOI] [PubMed] [Google Scholar]
- Flint J., Mackay T. F., 2009. Genetic architecture of quantitative traits in mice, flies, and humans. Genome Res. 19: 723–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good B. H., Walczak A. M., Neher R. A., Desai M. M., 2014. Genetic diversity in the interference selection limit. PLoS Genet. 10: e1004222 10.1371/journal.pgen.1004222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris T. E., 1963. The Theory of Branching Processes. Dover Phoenix Editions, New York. [Google Scholar]
- Hedrick P. W., 2013. Adaptive introgression in animals: examples and comparison to new mutation and standing variation as sources of adaptive variation. Mol. Ecol. 22: 4606–4618. 10.1111/mec.12415 [DOI] [PubMed] [Google Scholar]
- Hermisson J., Pennings P. S., 2017. Soft sweeps and beyond: understanding the patterns and probabilities of selection footprints under rapid adaptation. Methods Ecol. Evol. 8: 700–716. [Google Scholar]
- Hill W. G., Robertson A., 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8: 269–294. [PubMed] [Google Scholar]
- Hospital F., 2005. Selection in backcross programmes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360: 1503–1511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta-Sánchez E., Jin X., Asan Z., Bianba B. M., Peter, et al. , 2014. Altitude adaptation in Tibetans caused by introgression of Denisovan-like DNA. Nature 512: 194–197. 10.1038/nature13408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R., 1976. The maintenance of genetic variability by mutation in a polygenic character with linked loci. Genet. Res. 26: 221–235. [DOI] [PubMed] [Google Scholar]
- Nei M., Tajima F., 1981. DNA polymorphism detectable by restriction endonucleases. Genetics 97: 145–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard J. K., Pickrell J. K., Coop G., 2010. The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation. Curr. Biol. 20: R208–R215. 10.1016/j.cub.2009.11.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Racimo F., Sankararaman S., Nielsen R., Huerta-Sánchez E., 2015. Evidence for archaic adaptive introgression in humans. Nat. Rev. Genet. 16: 359–371. 10.1038/nrg3936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson A., 1960. A theory of limits in artificial selection. Proc. R. Soc. Lond. B Biol. Sci. 153: 234–249. [Google Scholar]
- Robertson A., 1977. Artificial selection with a large number of linked loci, pp. 307–322 in Proceedings of the 1st International Conference on Quantitative Genetics, edited by Pollak E., Kempthorne O., Bailey T. B., Jr Iowa State University Press, Ames, IA. [Google Scholar]
- Song Y., Endepols S., Klemann N., Richter D., Matuschka F., et al. , 2011. Adaptive introgression of anticoagulant rodent poison resistance by hybridization between old world mice. Curr. Biol. 21: 1296–1301. 10.1016/j.cub.2011.06.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam L. F., Laurie C. C., 1996. Molecular dissection of a major gene effect on a quantitative trait: the level of alcohol dehydrogenase expression in Drosophila melanogaster. Genetics 144: 1559–1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strasburg J. L., Sherman N. A., Wright K. M., Moyle L. C., Willis J. H., et al. , 2012. What can patterns of differentiation across plant genomes tell us about adaptation and speciation? Philos. Trans. R. Soc. Lond. B Biol. Sci. 367: 364–373. 10.1098/rstb.2011.0199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker H., Setter D., Hermisson J., 2015. Adaptive gene introgression after secondary contact. J. Math. Biol. 70: 1523–1580. 10.1007/s00285-014-0802-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Via, S., 2012 Divergence hitchhiking and the spread of genomic isolation during ecological speciation-with-gene-flow. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367: 451–460. DOI:10.1098/rstb.2011.0260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher P. M., Haley C. S., Thompson R. D., 1996. Marker-assisted introgression in backcross breeding programs. Genetics 144: 1923–1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman D. B., Barton N. H., 2012. Limits to the rate of adaptive substitution in sexual populations. PLoS Genet. 8: e1002740 10.1371/journal.pgen.1002740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney K. D., Randell R. A., Rieseberg L. H., 2006. Adaptive introgression of herbivore resistance traits in the weedy sunflower Helianthus annuus. Am. Nat. 167: 794–807. 10.1086/504606 [DOI] [PubMed] [Google Scholar]
- Yang J., Manolio T. A., Pasquale L. R., Boerwinkle E., Caporaso N., et al. , 2011. Genome partitioning of genetic variation for complex traits using common SNPs. Nat. Genet. 43: 519–525. 10.1038/ng.823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeaman S., 2013. Genomic rearrangements and the evolution of clusters of locally adaptive loci. Proc. Natl. Acad. Sci. USA 110: E1743–E1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeaman S., Whitlock M. C., 2011. The genetic architecture of adaptation under migration-selection balance. Evolution 65: 1897–1911. 10.1111/j.1558-5646.2011.01269.x [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
FORTRAN 95 codes used to generate the simulated data can be found at https://git.ist.ac.at/himani.sachdeva/Introgression_source_codes/snippets. The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.