Developmental Bias and Evolution: A Regulatory Network Perspective

A recurrent theme in evolutionary biology is to contrast natural selection and developmental constraint – two forces pitted against each other as competing explanations for organismal form. Despite its popularity, this juxtaposition is deeply misleading....

Abstract

Phenotypic variation is generated by the processes of development, with some variants arising more readily than others—a phenomenon known as “developmental bias.” Developmental bias and natural selection have often been portrayed as alternative explanations, but this is a false dichotomy: developmental bias can evolve through natural selection, and bias and selection jointly influence phenotypic evolution. Here, we briefly review the evidence for developmental bias and illustrate how it is studied empirically. We describe recent theory on regulatory networks that explains why the influence of genetic and environmental perturbation on phenotypes is typically not uniform, and may even be biased toward adaptive phenotypic variation. We show how bias produced by developmental processes constitutes an evolving property able to impose direction on adaptive evolution and influence patterns of taxonomic and phenotypic diversity. Taking these considerations together, we argue that it is not sufficient to accommodate developmental bias into evolutionary theory merely as a constraint on evolutionary adaptation. The influence of natural selection in shaping developmental bias, and conversely, the influence of developmental bias in shaping subsequent opportunities for adaptation, requires mechanistic models of development to be expanded and incorporated into evolutionary theory. A regulatory network perspective on phenotypic evolution thus helps to integrate the generation of phenotypic variation with natural selection, leaving evolutionary biology better placed to explain how organisms adapt and diversify.

THE extraordinary diversity and adaptive fit of organisms evolving under natural selection depends fundamentally on the generation of heritable phenotypic variation. Phenotypes are the result of causal interactions at multiple levels of biological organization, including genes, cells, tissues, and organisms and their environments. Given the complexity of these interactions, it is usually not obvious how developmental and physiological systems will respond to perturbations, such as when genes mutate or environments change. Yet, without knowledge of the nature of phenotypic variability, an understanding of how and why evolution unfolds in the manner that it does is woefully incomplete. Natural selection cannot work with imaginary phenotypes, only those realized by developmental systems.

Although the diversity of life may give the impression that natural selection can produce any form, it is well-recognized and uncontroversial that not all phenotypic variants are possible or even likely to be generated (Darwin 1859; Waddington 1957; Maynard-Smith et al. 1985). The bias imposed on the distribution of phenotypic variation, arising from the structure, character, composition, or dynamics of the developmental system, relative to the assumption of isotropic variation, is known as developmental bias¹ (Maynard-Smith et al. 1985; Arthur 2004; Wilkins 2007). The concept of developmental bias² thus captures the observation that perturbation (e.g., mutation, environmental change) to biological systems will tend to produce some variants more readily, or with higher probability than others. Only at the extreme is this manifest as the complete inability to produce a trait.

The organization of a biological system is a product of its evolution. Both developmental systems that produce unbiased patterns of phenotypic variation and those that produce bias need an evolutionary explanation (Salazar-Ciudad 2006, 2008). The propensity to vary in response to particular genetic or environmental inputs can be under natural selection (e.g., McNamara et al. 2016). It is less obvious, however, if and how fitness differences can explain phenotypic bias in response to nondirected (i.e., random) genetic mutation or environments that have not been experienced in the recent evolutionary history. That phenotypic variation is unbiased has therefore probably been the default assumption in evolutionary theory. Here we explain why this assumption is likely to be unfounded. We show how mechanistic models can reveal the influence of selection in shaping developmental bias, and conversely, how developmental bias can shape subsequent evolution. This body of theory suggests that developmental bias is not only likely to be widespread, but that it may also contribute to adaptation and diversification. We end by illustrating how these predictions can be tested by combining empirical studies of developmental processes with comparative analyses of evolutionary diversification.

Evidence for Developmental Bias

In a classic discussion of developmental bias, Raup (1966) showed that only a comparably small proportion of all possible snail shell shapes was realized in nature, and suggested that this was partly explained by the mechanics of growth [see also McGhee (2007) and Brakefield (2008)]. However, it is not possible to assess the role of developmental bias solely from an absence of forms in nature since such absence is also predicted to arise if the evolutionary process has not yet had sufficient time to explore all options, or through natural selection, which restricts phenotypes to regions of phenotypic space that have adaptive value. Other approaches to identifying bias (e.g., genetic correlations between traits; Maynard-Smith et al. 1985) have also proven inconclusive, which for many years left the prevalence and significance of developmental bias difficult to ascertain.

Fortunately, recent methodological advances that afford more detailed analyses of how organisms develop are shedding light on how bias can arise and revealing its prevalence in nature (Box 1; Figure 1). For example, the regulation of the tetrapod limb creates developmental bias in the number and distribution of digits, limbs, and segments (Alberch and Gale 1985; Wake 1991), and in the proportion of skeletal parts (Sanger et al. 2011; Kavanagh et al. 2013). Interactions between the components of developmental systems also bias relationships between the size, shape, and position of structural and pigment coloration of insect wings (Brakefield and Roskam 2006; Prud’homme et al. 2006), the shape of beaks (Campas et al. 2010; Fritz et al. 2014), the positioning of cephalic horns in scarab beetles (Busey et al. 2016), and flower morphology (Wessinger and Hileman 2016).

Box 1. Methods for detecting developmental bias.

As natural selection is expected to remove variation, studies of standing phenotypic variation in a population, species, or higher taxa provides an unsatisfactory method to demonstrate bias. To establish developmental bias, researchers must study the propensity for developmental systems to vary (their variability) rather than the observed state of variation (Wagner and Altenberg 1996). Much of what we have learnt of developmental bias comes from detailed experimental studies of development that reveal causal dependencies producing correlated changes in phenotypes, sometimes allowing for the prediction of phenotypic form across multiple species. For example, decades of research have revealed how the development of the limb skeleton is regulated (Hall 2015), which makes it possible to explain and predict correlated changes in digit length and the ordered loss of digits over evolutionary time (e.g., Alberch and Gale 1985; Kavanagh et al. 2013). A more quantitative approach is to study the distribution of phenotypic variation caused by genetic or environmental perturbation. Experimental evolution (e.g., McDonald et al. 2009) and mutation accumulation lines (e.g., Houle et al. 2017) can establish if random mutation produces some phenotypes more frequently than others. Furthermore, gene-editing tools make it possible to study the effects of change to particular genes or regulatory elements (Nakamura et al. 2016). Individuals can be exposed to stress or novel environmental conditions to determine whether developmental systems produce some phenotypes more frequently than others (Badyaev 2009). Sometimes it is possible to represent developmental processes mathematically, which makes it possible to study variability in silico (Salazar-Ciudad and Jernvall 2010), and to use computational modeling to predict phenotypic variation in nature (e.g., Kavanagh et al. 2007). As illustrated in the main text, some well-understood systems have been studied from several of these perspectives.

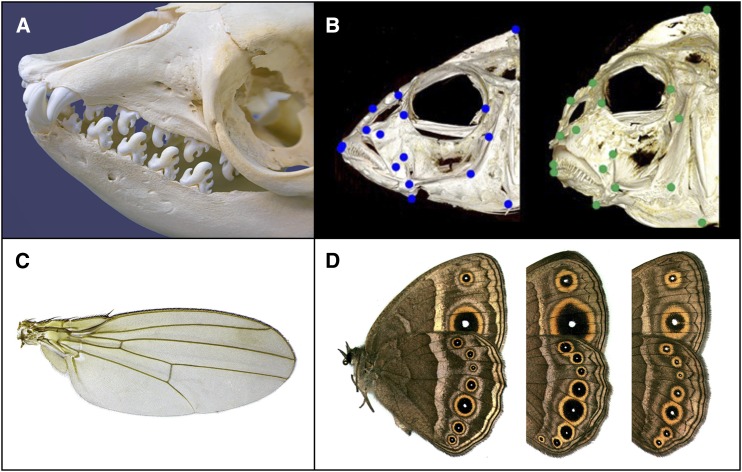
Figure 1.

Compelling examples of developmental bias and its evolutionary effect in animals. (A) By combining experiments in vivo and in vitro, comparative analyses, and mathematical modeling, researchers have shown that the evolutionary diversity in tooth morphology among mammals is shaped by the mechanism by which teeth develop. Pictured is the skull of a crabeater seal, Lobodon carcinophaga. (B) The oral and pharyngeal jaws of cichlid fishes are putative examples of how a bias caused by plasticity, itself possibly favored by selection, can feed back to facilitate adaptive divergence and convergence in independently evolving lineages. (C) In Drosophila, the phenotypic divergence between species in wing shape is aligned with the phenotypic bias associated with random mutation, one explanation for which is that developmental bias coevolves with phenotypic divergence. (D) Artificial selection on the size and color of Mycalesine butterfly eye spots demonstrates the effects of bias misaligned or aligned with the direction of selection. Photo credits: (A) Panther Media GmbH, Alamy Stock Photo; (B) Kevin Parsons; (C) Martin Hauser Phycus, CC-BY-3.0-DE; (D) Saenko et al., BMC Biology 2010 8:111, CC-BY-2.0.

Tooth morphology in mammals provides a particularly compelling example of how developmental studies can be combined with computational analyses to demonstrate bias. Salazar-Ciudad and Jernvall (2010) integrated molecular details of the gene network underlying molar development in mice with biomechanical properties of cells to build a computational model of tooth development. Their models were able to reproduce accurately variation in teeth morphology observed within species (Salazar-Ciudad and Jernvall 2010), predict morphological patterns both across species and in teeth cultivated in vitro (Kavanagh et al. 2007; Harjunmaa et al. 2014), and even retrieve ancestral character states (Harjunmaa et al. 2012).

Developmental bias can also be studied by examining how traits are affected by genetic mutation. Such studies reveal that when phenotypic effects do occur, random mutation often produces nonrandom distributions of phenotypes. For example, Braendle et al. (2010) conducted a thorough quantification of the phenotypic variability of the vulval developmental system across mutation accumulation lines of two species of Caenorhabditis nematodes. The results demonstrated that spontaneous mutations produce bias, with some phenotypic variants being common and others rare or absent. The features of the vulva that were most affected by new mutations also tended to show a greater variation in the stock population, suggesting that this bias occurs in nature. Similarly, although virtually all dimensions of the Drosophila wing are variable in nature and in mutation accumulation lines (Scharloo 1970; Mezey and Houle 2005; Houle and Fierst 2013), mutations disproportionately cause covariation among parts of the wing such that some shapes are more readily produced than others (Klingenberg and Zaklan 2000; Houle et al. 2017). In plants, chemical mutagenesis has been shown to induce phenotypic variants with a biased covariance structure between plant growth, flowering and seed set in Arabidopsis thaliana (Camara and Pigliucci 1999; Camara et al. 2000).

Although development is often buffered against environmental stress, environmental conditions can also profoundly affect phenotypic variation and covariation, and environmentally induced developmental bias is manifest in diverse taxa and contexts. For example, jaw morphology in vertebrates responds in characteristic ways to diet (e.g., Gomez-Mestre and Buchholz 2006; Young and Badyaey 2010; Young et al. 2010; Muschick et al. 2011; Scott et al. 2014). More generally, as witnessed in the house finch, stress-induced phenotypic variation can be directional, channeled by existing developmental pathways, and integrated across morphological, endocrinal, and behavioral systems (Badyaev 2005, 2009). Both genetic mutation and environmental stress contribute to the developmental bias observed in congenital abnormalities, where large and highly nonadaptive phenotypic variants have been shown to share structural regularities across distantly related species (Alberch 1989).

Developmental Bias Is More Than Constraint

To the extent that the evolutionary biology literature considers bias, these are most commonly thought to be constraints: features of organisms that hinder, or even prevent, populations from evolving adaptively (Maynard-Smith et al. 1985; Futuyma 2015). “Constraint” implies that some regions of phenotypic space that are adaptive are not populated by the phenotypic variation that arises in development. An oft-cited example is the evolution of the mammalian neck (e.g., Galis 1999). In contrast to birds and reptiles, elongation of the mammalian neck has exclusively taken place by making the vertebrae larger rather than by adding vertebrae, as seen, for instance, in long-necked plesiosaurs. Viewed from an engineering or design perspective, vertebrae number likely constrains the evolution of long, slender, and maneuverable necks in mammals. This absence of variants with additional neck vertebrae is apparently because mutations that modify the number of cervical vertebrae disrupt fundamental features of the mammalian body plan (Galis et al. 2006). The uniform selection against those variants is not itself the constraint; rather, the mammalian phenotypic space is biased in part because mammalian developmental biology struggles to produce variants with more than seven vertebrae that also preserve the remainder of the body plan. Such forms could be favored by selection, were they to appear.

While the term “developmental bias” is inclusive of developmental constraint, it goes beyond it, as do its evolutionary implications. A categorical distinction between “what is possible” (i.e., no constraints, selection has a free reign) and “what is not possible” (constraints operating) neglects that bias within the “what is possible” region can significantly shape how and why evolution unfolds the way that it does. First, developmental systems can alter the ratio or proportion of variation that occurs on one phenotypic dimension relative to another (Figure 2). Since altering the ratio of variability in different phenotypic dimensions can influence the direction of evolutionary change (Arnold et al. 2001), developmental bias will not only affect the rate or path toward an adaptive peak, but when adaptive landscapes are multipeaked, it can also change which peak is reached (Melo et al. 2016; Kounios et al. 2017). Second, developmental systems can make phenotypes develop in a correlated fashion even without reducing or increasing variability in any individual trait (Pavlicev et al. 2011). Such correlations, responsible for the functional integration of complex phenotypes, have the potential to channel phenotypic variability toward directions of high fitness (Watson and Szathmary 2016; Figure 2C).

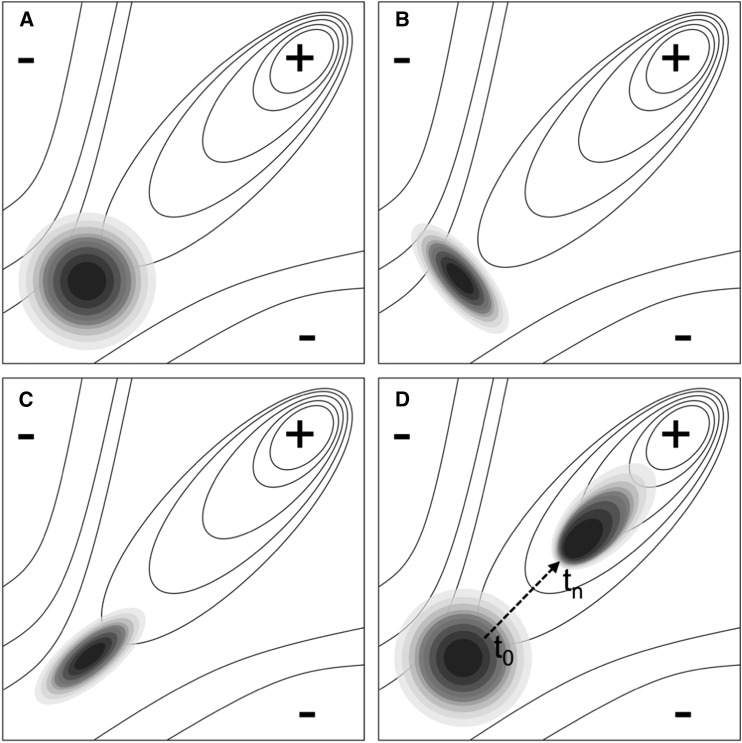
Figure 2.

Developmental bias can both constrain and facilitate adaptive evolution. (A–D) Adaptive landscapes with a ridge and a positive slope toward the top-right corner. The shading represents the distribution of evolutionarily relevant phenotypic variation introduced into the population (e.g., by mutation), with darker regions representing higher frequencies of variants. (A) The default assumption in evolutionary theory is typically that the distribution of evolutionarily relevant phenotypic variation introduced into the population is unbiased. (B) Developmental bias will constrain adaptive evolution if it limits variability in the direction of selection. (C) Developmental bias will accelerate adaptive evolution if it biases variability in dimensions aligned with the direction of selection. (D) Recent theory and empirical research described in this paper further suggests that developmental bias can itself evolve both to orient with the adaptive landscape and to increase phenotypic variability in the direction favored by past natural selection (dashed arrow represents changes in phenotypic distribution over time as the population evolves).

A well-known example is the phenotypic integration of vertebrate limbs (Hall 2015). Left and right hind limbs share developmental pathways, and mutations in a gene regulating bone growth will therefore usually affect both limbs, making them grow equally. In the course of growth, bones themselves help instruct the development of muscles, tendons, and their respective attachment sites, ensuring that mutations in genes that only directly affect skeletal growth nevertheless result in functional, well-integrated limbs. Further, bone growth responds to mechanical pressure, which helps to accommodate both genetic and environmental perturbations in ways that maintain functional integration within and between limbs. By preventing the expression of variants with longer limbs on one side of the body, or variants that have mismatches between bones, muscles, and tendons, regulation of limb development promotes variants in directions likely to be functional, even under evolutionarily novel conditions (e.g., Standen et al. 2014). This is not a special case; the dependencies between different components of development have the potential to capture and channel random mutational variation toward nonrandom, functional, integrated, phenotypes. This, in turn, can make adaptive variants more easily accessible to selection, and reduces the number of regulatory changes needed to convert developmental variation to evolutionary, adaptive changes in form and function (West-Eberhard 2003; Kirschner and Gerhart 2005; Gerhart and Kirschner 2007). This line of reasoning has been interpreted by some (e.g., Félix 2016) to imply that most mutations would produce functional phenotypes—a notion at odds with empirical observations. However, facilitated variation (Gerhart and Kirschner 2007) makes no such claim, but merely posits that the interdependencies of developmental processes increase the probability of directing the effect of mutations toward functional phenotypes able to fuel adaptive response to selection more rapidly than would otherwise be the case. Facilitated variation is entirely consistent with the empirical observation that most genetic mutations are either neutral or deleterious, and that changes in amino acids most commonly disrupt the function of proteins.

That the mechanisms of development facilitate rather than merely constrain functional integration raises the possibility that bias contributes to evolvability, by which we mean the capacity for a lineage to undergo adaptive evolution. This phenomenon is partly captured by existing theoretical models (e.g., Jones et al. 2007, 2014; Pavlicev et al. 2011). However, a general theory explaining the evolution of developmental bias and its consequences—in particular, a theory that encompasses nonlinear correlations, modularity, and other forms of functional integration that have potential to facilitate adaptation—remains to be articulated. As a consequence, examples of bias may often be perceived as special cases, idiosyncratic to specific taxa and thus interesting but of limited value for our fundamental understanding of the evolution of adaptation and diversification (Charlesworth et al. 1982; Maynard-Smith et al. 1985; Futuyma 2017).

We suggest that this conclusion is at best, premature, and almost certainly mistaken. In what follows, we explain how the study of regulatory networks is beginning to reveal the evolutionary logic of developmental bias, including facilitated variation, and their profound consequences for understanding what determines the rate and direction of the evolutionary process. This work implies that bias is likely to be the default condition, and that consideration of bias will be highly instructive in evolutionary analyses.

Evolution of Developmental Bias: A Regulatory Network Perspective

The historical treatment of bias as solely constraint and the associated focus on physical or material limits to biological form (“universal constraints,” Maynard-Smith et al. 1985) have distracted attention from how developmental biases can evolve through natural selection. That mutational bias can influence molecular evolution (e.g., Yampolsky and Stoltzfus 2001; Nei 2013; Stoltzfus and McCandlish 2017), and that selection can favor mechanisms that influence the rate at which heritable variation arises (e.g., Charlesworth 1976; Feldman and Liberman 1986; Day and Bonduriansky 2011; Geoghegan and Spencer 2012), are both well-established principles. However, understanding developmental bias requires attention not only to the frequency at which mutations arise, but also to the phenotypic properties of those variants. Most of the well-established tools of the evolutionary biologist are not well-designed to deal with the evolution of development, and shed limited light on how trait correlations originate and evolve (Rice 2004, 2008; Watson et al. 2016). Although developmental constraint has a long research tradition in evolutionary quantitative genetics [reviews in Arnold (1992), Cheverud (1996), Hansen and Houle (2008); Box 2], the reliance of quantitative genetics on linear statistical correlations means that it struggles to adequately represent variation containing gaps and some other nonlinear interactions otherwise common in development [Watson et al. 2014; but see Morrissey (2015)]. Many insights into the evolutionary causes and consequences of developmental bias therefore come from the representation of phenotypic distributions using mechanistic models, such as regulatory networks, that can capture nonlinear relationships and multimodal distributions. Below, we explain how the evolution of these networks can make nondirected genetic change or novel environments bias phenotypic variation toward functional solutions.

Box 2. Developmental bias in evolutionary quantitative genetics.

Quantitative genetics is a statistical approach to modeling phenotypic evolution. Its canonical equation is the multivariate breeder’s equation, Δz = Gβ (Falconer and Mackay 1996; Lynch 1998). This equation describes evolutionary change in a suite of traits, described as a vector of differences in trait means, Δz, as the product of a vector of selection gradients, β, and a matrix, G, whose entries are the additive genetic variances and covariances of the traits. Correlational selection has a tendency to ensure that traits that are selected together are inherited together (Lande and Arnold 1983). The coinheritance of traits at the population level is specified by their genetic covariance. As selection removes variants with low fitness, the genetic covariation in large populations will tend to be proportional to the patterns of mutational variance at pleiotropic loci and the strength of multivariate selection (Lande 1980). The genetic variance–covariance (i.e., G) is an estimate of the biasing effect on evolution of standing genetic variation (Arnold 1992). It has been suggested that the lead eigenvector of G (g_max) predicts evolutionary trajectories because genetic variances and covariances constrain possible changes and hence the response to selection (e.g., Schluter 1996). However, G is of limited value for understanding developmental bias since the same pattern of genetic covariation can arise from a variety of distributions of pleiotropy and functional epistasis (e.g., Houle 1991; Gromko 1995). G describes currently existing variation but not the propensity to generate variation (variability). A more relevant entity for understanding bias is the distribution of mutational effects, which is how new mutations enter the population (Lande 1980; Cheverud 1984). The distribution of mutational effects, which is often called the M matrix, depends on patterns of pleiotropy and epistasis (e.g., Jones et al. 2007; Chebib and Guillaume 2017). Although most quantitative genetic theory assumes that mutations have uniform effects on the phenotype (e.g., Lande 1980), both pleiotropy and epistasis are potentially evolvable features. How the elements of M evolve can be modeled if one assumes that they are underpinned by additive genetic variation (Jones et al. 2007; Pavlicev et al. 2011), or by modeling the evolution of pleiotropic loci connected by epistatic coefficients (Jones et al. 2014). A key finding of these models is that both stabilizing and directional correlational selection can result in patterns of pleiotropy and epistasis that align mutational effects with the direction of the fitness landscape [Pavlicev et al. 2011; but also see Hansen et al. (2006)]. Thus, new genetic variants may bias the phenotype in the direction favored by past selection (see Evolution of Facilitated Variation below; Figure 1, C and D).

The Phenotype as a Regulatory System

Biological processes, such as gene expression, metabolism, and signaling cascades, lend themselves well to network-based models (Kauffman 1969; Alon 2006), and a major role for regulatory changes in evolution is empirically well-supported (Prud’homme et al. 2007; Wray 2007; Wittkopp and Kalay 2012). Representation of the phenotype in terms of a network of interacting components with dynamical properties indeed has a long history, including seminal contributions by Muller (1922), Schmalhausen (1949), Waddington (1957), and Kauffman (1969). Conceptualizing phenotypes as the output of regulatory networks remains prevalent among contemporary developmental biologists (e.g., Wilkins 2005, 2007; Davidson 2006; Peter and Davidson 2015).

In computational analyses, regulatory networks are often represented by genes as nodes and the suppression or activation of other genes as edges (gene regulatory networks; Britten and Davidson 1969; Davidson 2006) (Figure 3A). The input to a node may be the presence or amount of a transcription factor that regulates gene expression and the output of a node the level of gene product. Interactions between nodes can be described using linear or nonlinear functions. The phenotype of the network is the profile of gene expression of one or more nodes, which may represent the macroscopic phenotype of interest, such as morphology or physiology. However, networks are not restricted to gene interactions. More explicit developmental models describe interactions at different levels of biological organization, such as cells and tissues (Oster and Alberch 1982; Atchley and Hall 1991; Salazar-Ciudad et al. 2003; Newman and Müller 2005), whose dynamical changes feedback on transcriptional regulation in multilayered models (von Dassow et al. 2000; Salazar-Ciudad and Jernvall 2010). One important feature of biological networks is that nodes (e.g., expression of genes) can be free to vary in their activity independently of each other, or can be connected by regulatory linkage. This allows networks to represent modularity (i.e., the extent to which different characters are developmentally integrated; Schlosser 2002), which affects the statistical correlations of characters within a population (Cheverud 1996; Melo et al. 2016).

Figure 3.

Regulatory networks, their topology, dynamics, and connectivity via mutation. (A) A regulatory network with nodes (e.g., genes) connected by regulatory interactions can be considered a genotype. Mutation to the genotype is represented by a modification in the network topology, for example, by adding or removing regulatory interactions or by modifying the interactions from suppression to activation. Pointed arrows represent activation, while those ending in perpendicular lines show suppression. (B) A regulatory network has a phase space, here represented by the concentrations of molecules encoded by the two genes. The flow of the phase space (gray arrows) describes what trajectory (black arrow) from the starting point (red circles) the system will take as it reaches equilibrium (“basin of attraction”; black circles). Which of potentially several equilibrium states is reached can depend on external conditions, such as the concentration of the activating substance (red arrow and red circles). (C) Connecting regulatory networks (A) to other regulatory networks that differ in only one regulatory change results in large “network-of-networks” or genotype networks. Real genotype networks are very large so two dimensions can only represent a small part of all possible genotypes and how they are connected by mutation. In this hypothetical example, each node represents a single regulatory network, with the color indicating its phenotype. Edges connect regulatory networks that are related by a single modification of their topologies, as represented in A. The properties of these genotype networks determine how likely it is that an alternative phenotype can be reached through mutation. The three shaded areas represent, from left to right, (i) a boundary region between two distinct phenotypes where some genotypes can produce both phenotypes; (ii) a region of genotype space where mutations (i.e., changes in topology) are phenotypically neutral; and (iii) a region where a change in topology can produce several distinct phenotypes that are not accessible from other parts of the network. (D) The regulatory network of this node in the genotype network. ‘A and B are based on representations in Jaeger and Crombach (2012) and Jaeger and Monk (2012) and C is based on representations in Wagner (2011).

In network models, “mutations” may represent changes in topology, such as the deletion or addition of a node or link, or a change of interaction from suppression to activation (Figure 3A). Networks also have dynamical properties that describe the trajectory of the inputs and outputs as the system converges (if at all) on one of possibly several steady states, or phenotypes (Figure 3B). The parameters that determine the dynamical properties of networks include initial conditions, the activating input to the nodes, and changes in the strength of interactions (Jaeger and Monk 2014), all of which may show heritable variation.

Given that there is often ample standing genetic variation in natural populations, it might seem that any bias must be transient and of little bearing on evolution (Charlesworth and Lande 1982, 2017; Coyne 2006; Futuyma 2015). Yet the amount of standing genetic variation may have little relevance for the probability that particular phenotypes will be generated. Studies of simulated and real regulatory networks demonstrate that only a small part of the phenotypic space can be reached by a given developmental system, while the remainder is inaccessible [Kauffman 1983; Borenstein and Krakauer 2008; see also Dingle et al. (2015)]. Even within accessible regions of phenotype space, changes in topology, initial conditions, or interaction strengths will not always, or even commonly, produce a smooth transition in phenotype (Kauffman 1969, 1983; Alon 2006; Jaeger and Monk 2014). Networks that differ in only a single type of interaction between two nodes, such as replacing activation with suppression, can sometimes result in a qualitative shift in phenotype. Similarly, even simple networks have multiple attractors that can lead minor differences in the dynamic parameters to have large phenotypic consequences (Figure 3B). One such example is the gap gene networks that regulate body segmentation in the early fly embryo. By simulating the biological networks in silico, Jaeger and colleagues have shown how changes in the concentration of maternally derived mRNA (i.e., initial conditions) can cause different expression profiles across the body, sometimes resulting in different segmentation phenotypes [Wotton et al. 2015; see also Clark (2017)]. Such analyses illustrate how developmental mechanisms bias phenotypes toward particular outcomes, including producing the same phenotypes under a range of different starting conditions.

From a network perspective, phenotypic evolution is typically represented by heritable changes in the topology or dynamical properties of regulatory networks in the population. An important observation is that different topologies are often functionally equivalent (Kauffman 1983; Borenstein and Krakauer 2008; Wagner 2011). Although the robustness to mutation may at first seem to limit the potential for evolution, theory suggests that it in fact increases the capacity to evolve (Fontana and Schuster 1998; Ciliberti et al. 2007; Wagner 2011). To understand how, one needs to consider two features of the space of possible regulatory networks (below we refer to topologies as “genotypes,” but emphasize that this does not imply that regulatory networks are solely represented in terms of genes).

The first is that genotypes that share the same phenotype are often topologically similar, forming a “network-of-networks” (or a “genotype network space”) where each genotype is connected to other genotypes by a single addition, deletion, or modification of one of the regulatory network components (Fontana and Schuster 1998; Wagner 2011; Figure 3C). The functional equivalence of neighboring topologies allows populations to accumulate genotypic variation through drift. The second is that regulatory networks that are topologically quite different can nevertheless share the same phenotype (Wagner 2011). However, because they are topologically different, the phenotypes of their neighbors (i.e., a network differing in only one regulatory change) may be radically different.

The fact that vast areas of the space of possible regulatory networks are phenotypically equivalent, but have different phenotypic neighbors, is important because a population that harbors many genotypes (i.e., regulatory networks) with the same phenotypes can more easily find a new phenotype through a single mutational step (Wagner 2011; Figure 3C). Since the number of neighboring genotypes with different phenotypes increases with the absolute number of neighbors, the capacity for a population to evolve new functional phenotypes should be higher if there are many phenotypically neutral neighbors than it would be if every change to a regulatory network produced a different phenotype (Wagner 2011).

Whether or not developmental bias, in the form of the phenotypic consequences of genetic perturbation, is expressed within a particular population depends on which neighboring regulatory networks can be reached through mutation. That, in turn, depends on the population’s evolutionary history. Stabilizing selection will tend to push the population to regions of genotype space where changes in topology do not affect the phenotype (Ciliberti et al. 2007; Wagner 2011), which favors regulatory networks with robust dynamical properties such as insensitivity to fluctuations in transcription factor concentrations (Jaeger and Monk 2014). In contrast, directional or disruptive selection can push the population toward regions of genotype space where small changes in regulatory network topology or its parameters are more likely to produce phenotypic effects (Kashtan et al. 2007). Theoretical analyses suggest that such differences in genotype neighborhoods are likely, and that they affect the likelihood that populations can find new high-fitness phenotypes through small changes in regulatory network topology (Psujek and Beer 2008; Payne et al. 2014). For example, a comprehensive theoretical study of three-gene circuit topologies that produce a stripe demonstrated that, of the thousands of possible circuits, each rely on one of only six mechanisms, which differ in their likelihood to reach new phenotypes through mutation (Jiménez et al. 2015). While further quantification of developmental bias across biological systems is necessary to establish how important bias is to real populations, these theoretical analyses illustrate that bias is likely to be an inherent property of evolved regulatory systems.

Evolution of Facilitated Variation

Perhaps the most surprising finding from studies of the evolution of regulatory networks is that phenotypic variability can be directed toward dimensions with high-fitness variance even when mutations are randomly distributed. For example, allowing interaction between genes controlling two traits to evolve under stabilizing or directional correlational selection causes the mutational effects (i.e., the M matrix) to become biased toward phenotypes that are aligned with the fitness landscape (Jones et al. 2007, 2014; Pavlicev et al. 2011; Watson et al. 2014). The reason is that selection strengthens the interactions between genes (i.e., epistatic effects) that produce the desired correlation among characters, while it reduces the strength of interactions among genes that produce undesired correlation. If trait correlations evolve more slowly than the quantitative traits themselves, the combination of trait values under new mutations will be biased toward those that have been favored in the past. The result of this mutational effect is an increase in the standing population genetic covariation between traits (i.e., the G matrix) in the dimension(s) aligned with past selection.

With linear interactions between traits, such developmental interactions can facilitate the production of functional phenotypes in more extreme environments because of the correlational selection in the environments to which the system has adapted (e.g., Draghi and Whitlock 2012). This can accelerate adaptive evolution, although it would not necessarily facilitate adaptation to environments that are structurally different (Kouvaris et al. 2017). To study the latter, Parter et al. (2008) modeled a combinatorial logic circuit and a secondary RNA structure using nonlinear interactions that allow small changes in genotype to produce large changes in phenotype [see also Kashtan and Alon (2005), Kashtan et al. (2007)]. When evolved under conditions where selection switched between two “goals” (i.e., target phenotypes matched to particular environments) on the order of tens of generations, the model was soon reliably able to evolve to match both goals. More importantly, the system was able to evolve adaptive phenotypes in environments that shared the same structural regularity but that had not been previously encountered (including those requiring novel combinations of subgoals). Similar results are found in gene regulatory network models evolving in fluctuating environments (Crombach and Hogeweg 2008; Draghi and Wagner 2009; Watson et al. 2014; Kouvaris et al. 2017).

At first sight, that regulatory networks evolve features that then allow them to adapt quickly to conditions that they have not previously encountered appears incompatible with the myopic vision of natural selection that rewards current and not future function (Watson and Szathmary 2016; Kounios et al. 2017). To understand these results, it is necessary to revisit some of the properties of networks described above.

First, remember that under a stabilizing selection process, the population will evolve toward regulatory networks that have a large mutational distance to other phenotypes (i.e., toward the center of the genotype network with the particular phenotype, Wagner 2011; Figure 3C). The same logic implies that switching between two environments at a frequency that enables populations to adapt but not to evolve regulatory networks that are mutationally robust, will tend to push genotypes toward a space of possible regulatory networks where the mutational distance is short between networks that are functional in environment one and networks that are functional in environment two (Kashtan et al. 2007; Wagner 2011; Figure 3C). The regulatory networks on the boundary that are performing best have some nodes or edges that have disproportionate effects on the phenotypic outcome (Parter et al. 2008).

Second, evolution in a structurally complex environment can favor regulatory networks that are modular (Lipson et al. 2002; Clune et al. 2013; Kouvaris et al. 2017). In the simulations performed by Parter et al. (2008), each goal was distinct but composed of different combinations of the same set of subgoals. Switching between two goals (each consisting of different combinations of the same subgoals) makes the network evolve modularity (Kashtan et al. 2007; Crombach and Hogeweg 2008; Clune et al. 2013; Watson et al. 2014). With a modular network topology, mutations within modules can have a relatively large but specific phenotypic effect, which enhances the possibility to acquire novel functions while reducing the pleiotropic effect of mutation on other modules. This makes it possible for regulatory networks to use their modular structure to evolve new topologies that perform well in environments that are novel, but that retain underlying features of past environments (Clune et al. 2013; Kouvaris et al. 2017).

These properties of regulatory networks evolving under natural selection suggests that evolution exploits the underlying structural regularity of the environment to produce developmental systems that retain a bias toward phenotypes evolved in the past (Lipson et al. 2002; Watson et al. 2014). As a result, evolving systems can exhibit bias toward phenotypes that are fit even in environments that have not been previously encountered, exploiting their modular structure (Parter et al. 2008; Watson and Szathmary 2016; Kouvaris et al. 2017). If future environments are structurally similar to those of the past, bias should facilitate adaptive evolution, whereas it should limit adaptation in structurally different environments.

Although most models focus on genetic change to regulatory networks, environmental perturbation may also be an important source of developmental bias, not least because organisms may be more likely to have evolved adaptive responses to environmental than genetic variation [reviewed in West-Eberhard (2003), Pfennig et al. (2010), Moczek et al. (2011), Levis and Pfennig (2016), Schneider and Meyer (2017)]. Even if environmentally induced phenotypes are not heritable, plasticity has the potential to facilitate adaptation by increasing the recurrence and fitness of functional variants, which tends to increase their likelihood of being selected and reduce the amount of genetic change needed to convert them into locally adapted phenotypes (Waddington 1957; West-Eberhard 2003; Gerhart and Kirschner 2007). Compared to regulatory networks represented by genes alone, networks with environmental dependencies have been demonstrated to evolve greater modularity, increased mutational distance to phenotypically disparate networks, and mutational variance that is exaggerated in the direction of past selection (Espinosa-Soto et al. 2011; Fierst 2011; Wagner 2011; Draghi and Whitlock 2012; van Gestel and Weissing 2016), these being features associated with enhanced evolvability. The rich literature on the effects of learning on evolution provides further insights into how plasticity contributes to bias and evolvability (Box 3).

Box 3. Learning, developmental bias, and evolvability.

As a form of adaptive plasticity that allows organisms to shift their phenotype toward the optimum, learning is inherently a source of developmental bias. Learned behavior is often the result of an exploratory search conducted over multiple trials, and this search is expanded to encompass the experiences of multiple individuals where animals learn socially. Extensive theory has demonstrated that learning has an advantageous effect on adaptation in changing environments, allowing individuals to acclimate to changes that cannot be tracked by selection of genes (Cavalli-Sforza and Feldman 1981; Boyd and Richerson 1985; Todd 1991). More contentious are the benefits of learning in stationary or slowly changing environments. Hinton and Nowlan (1987) suggested that learning could accelerate evolution in a static environment by helping genotypes to locate otherwise difficult-to-find fitness peaks. However, learning is also known to weaken selection by reducing phenotypic differences between genotypes (Anderson 1995; Ancel 2000; Frank 2011). The conflicting findings follow from different assumptions about the structure of fitness landscapes (Borenstein et al. 2006; Paenke et al. 2007; Frank 2011). The emerging consensus from theoretical analyses is that individual learning typically slows evolution in static unimodal fitness landscapes, but usually accelerates evolution in dynamic or static multimodal fitness landscapes. In the latter, the existence of multiple optima usually slows down the evolutionary process as populations become trapped on suboptimal fitness peaks. By smoothing the landscape, learning increases the likelihood of a directly increasing path of fitness to the global optimum (Borenstein et al. 2006; Mills and Watson 2006; Frank 2011). These findings parallel analyses using gene regulatory networks that, in contrast to more traditional reaction–norm modeling frameworks, also found that adaptive plasticity can reduce the likelihood of getting stuck on local fitness peaks (van Gestel and Weissing 2016; Kounios et al. 2017). More generally, diverse forms of phenotypic plasticity operate in a functionally equivalent manner to learning, by relying on a combination of exploratory and selective processes (e.g., adaptive immune system, vascular system, nervous system) (Gerhart and Kirschner 2007; Snell-Rood 2012). Such processes are thought to allow organisms to respond to evolutionarily novel environmental challenges in a manner that generates phenotypic variation aligned with functional demands. This raises the possibility that the theoretical findings concerning the developmental bias arising from learning may generalize to a broader class of adaptive plasticity.

Detecting Signatures of Developmental Bias in Phenotypic Evolution

Natural selection and developmental bias (or constraint) have often been pitted against each other as alternative explanations for phenotypic variation, but such a juxtaposition is misleading. The recognition of developmental bias does not change the status of natural selection, which remains the process by which some variants are retained and others are removed as a result of fitness differences between individuals. However, the theory reviewed above demonstrates that the phenotypic variation exposed to selection will reflect the lineage’s evolutionary history. The explanatory value of developmental bias is that it can help to explain biological features that are difficult to account for assuming that selection acts on unbiased variation. Such features include the rapid adaptation of complex phenotypes, why some lineages continue to diversify while others do not, and why some features evolve repeatedly, oftentimes using the same developmental pathways, whereas others are one-offs. Below, we briefly discuss key components of the relationship between developmental bias and evolution.

Developmental bias can influence taxonomic and phenotypic diversity

Evolutionary change in regulatory interactions may help to explain some puzzling observations with respect to the accumulation of phenotypic diversity through time (McShea 1994; Erwin 2017; Jablonski 2017). Low-dimensional regulatory networks have been found to produce higher disparity among common phenotypes than high-dimensional networks (Borenstein and Krakauer 2008), suggesting that diversification rate will be highest early in evolutionary time when regulatory networks are small. Such models predict that lineages will become increasingly clumped as evolution progresses, with the greatest divergences appearing early as higher-level taxonomic grades (Salazar-Ciudad and Jernvall 2005; Borenstein and Krakauer 2008). These predictions are consistent with the early bursts of radiation seen across several metazoan taxa, including tetrapods and arthropods (Davidson and Erwin 2006; Hughes et al. 2013; more complex patterns have also been described, e.g., Wright 2017). Preliminary studies suggest a similar pattern for some plants (Oyston et al. 2016). It has even been suggested that the rapid evolutionary diversification of body plans during the Cambrian explosion were caused by the evolution of particular gene regulatory networks (“kernels”; Davidson and Erwin 2006).

Within lineages, the evolution of novelties, such as shells, limbs, photic organs, feathers, wing patterns, or horns, is associated with rewiring existing developmental building blocks and processes into new regulatory networks. This predicts that, once they appear, diversification of novelties should proceed rapidly at first, and slow down as their regulation becomes developmentally entrenched. Consistent with this prediction, the shape of bird bills diverged rapidly during the early radiation of modern birds, and subsequent evolution of bill shapes within major bird lineages has been filling up only limited parts of morphospace (Cooney et al. 2017). Mathematical analyses of the morphospace of bird bills and experimental manipulation of bill growth indeed demonstrate that much of the observed diversity in shape can be explained by changes in only a few parameters that describe regulatory interactions among key genes (Campas et al. 2010; Mallarino et al. 2011; Fritz et al. 2014), suggesting that much of the remaining parts of morphospace is empty as a result of how bill development is regulated. The evolutionary fixation of gene regulatory networks has been applied more generally to explain why particular features of organisms are conserved and how developmental regulation channels phenotypic variation (Wagner 2014).

Developmental bias can impose directionality on evolution

Testing the prediction that divergence between lineages is shaped by the variational properties of development is challenging, and would ideally be substantiated by a detailed knowledge of developmental biology. Here, we highlight a small number of studies whose results are consistent with the theoretical prediction that the direction of phenotypic change over evolutionary time will be concordant with, and hence sometimes can be predicted by developmental bias.

Tooth morphology in mammals has both a well-understood developmental biology and a detailed record of evolutionary diversification. In the computational model of Salazar-Ciudad and Jernvall (2010), tens of parameters describing known genetic and cellular interactions were modeled, with modification of only one or a few of these accurately predicting evolutionary diversification of teeth across several groups of mammals [Salazar-Ciudad and Jernvall 2010; Harjunmaa et al. 2014; see also Kavanagh et al. (2007), Evans et al. (2016)]. These models not only support the view that the evolutionary diversity in tooth morphology among mammals is shaped by the mechanism by which teeth develop, but they also generate predictions for what developmental and genetic changes should accompany adaptive diversification of teeth. For instance, Kavanagh et al. (2007) showed that a mathematical model derived on the basis of knowledge of the mechanisms of tooth production in mice could be used to predict the relative sizes of teeth in a sample of 29 other rodent species. Herbivores tended to have more equal sized teeth and carnivores less equal, but all species were positioned along the same dimension of morphological space. Such studies raise the possibility that natural selection may only be able to move species along highly specific pathways created by the mechanisms of development.

In the absence of models that can predict patterns of variability, empiricists are often limited to comparing phenotypes within populations or species with the pattern of phenotypic diversification across species (Klingenberg 2014; Goswami et al. 2015). Although this risks confounding variation and variability (Box 1), phenotypic covariance in morphological characters in extant vertebrates has been demonstrated to be concordant with the patterns of historical diversification, including for example pharyngeal jaw morphology in cichlids (Muschick et al. 2011), beak shape in raptors (Bright et al. 2016), skull morphology in toads (Simon et al. 2016), and body shape in sticklebacks (Schluter 1996).

More robust inference is possible through complementary studies of the effects of genetic mutation. A particularly impressive study used data on wing shape for over 50,000 fruit flies to study the relationship between the phenotypic changes caused by mutation, standing genetic variation, and disparity among species (Houle et al. 2017). Despite the fact that mutations occur much more frequently than necessary to account for the phenotypic divergence between species, the phenotypic variants introduced by mutation within species parallel the phenotypic disparity between species. One interpretation of these results is that, as predicted by the regulatory network models described above, the propensity to vary in response to mutation is coevolving with the phenotypic divergence between species (Cheverud 2017). A similar study of developmental variation in the nematode vulva also found that differences between genera in the covariation among characters caused by mutation was concordant with how vulva morphology have diversified (Todd and Miller 1991; Dichtel et al. 2001; Kiontke et al. 2007; Braendle et al. 2010). The wealth of information on the developmental biology of the nematode vulva and the Drosophila wing make them outstanding cases for mechanistic models that can investigate whether the patterns of developmental bias are consistent with the mechanisms of development (Félix and Barkoulas 2012; Matamoro-Vidal et al. 2015).

Another detailed example comes from studies of the size, position, and color of eye spots in Mycalesine butterflies. A combination of artificial selection and quantification of the variation observed within and among species have revealed that characters that show little evidence for bias within species (i.e., size of different eye spots, which respond readily to selection; Beldade et al. 2002) exhibit a diversity across species that fills up a large portion of morphospace (Brakefield and Roskam 2006). Conversely, characters that show clear evidence for bias within species (i.e., eye spot color, which shows much more limited variability and fails to respond to antagonistic selection; Allen et al. 2008) show a corresponding limited diversity across the Mycalesine butterflies (Brakefield 2010). The differences in evolvability between eye spot size and coloration appear to reflect variability of the underlying developmental mechanisms. Importantly, while the majority of species fit with the trends predicted based on knowledge of developmental mechanism, certain exceptional species were found with eye spots that did not match expectations, a situation that also applies to the study of mammalian teeth. Such findings suggest that organisms may most often fall along a developmentally favored evolutionary trajectory but that developmental bias need not impose constraints that are impossible to break (Kavanagh et al. 2007; Brakefield 2010).

The potential macroevolutionary significance of developmental bias is further exemplified by hundreds of examples of repeated co-option and recruitment of the same developmental pathways into the building of analogous structures and organs in otherwise unrelated organisms [reviewed in Shubin et al. (2009) and Held (2017)]. Some of the most spectacular cases include the independent evolution of eyes across phyla (Mercader et al. 1999; Kozmik 2005; Kozmik et al. 2008), the evolution or contractile hearts in vertebrates and invertebrates (Olson 2006; Xavier-Neto et al. 2007), or the formation of outgrowths from insect legs to echinoderm tube feet or ascidian siphons (Panganiban et al. 1997; Mercader et al. 1999); in each set of cases the same set of preexisting genes, pathways, and morphogenetic processes was used to arrive at functionally highly similar outcomes. Rather than reflecting constraint, such cases are consistent with developmental systems shaping evolutionary trajectories by generating opportunities to evolve complex structures repeatedly, reliably and regardless of taxonomic context. At the same time, the number of genetic changes needed to evolve a lineage-specific eye, heart, or appendage is significantly reduced compared to a scenario requiring the de novo evolution of genes for each structure.

Nevertheless, distinguishing between bias that constrained evolution and bias that facilitated adaptation is challenging. Particularly promising examples illustrating the existence and significance of the latter are where plastic responses that help organisms cope in stressful environments become genetically accommodated (West-Eberhard 2003). Evolution via genetic accommodation of plastic responses has been demonstrated experimentally (e.g., Suzuki and Nijhout 2006), and a biasing effect of phenotypic plasticity within populations or species is known to mirror patterns of evolutionary diversification in a diversity of taxa. In both cichlids and sticklebacks, the morphology of the feeding apparatus that develop when individuals are reared on a food source to which they are not adapted resembles the morphology observed in species adapted to the same food (Wund et al. 2008; Muschick et al. 2011). This suggests that evolution has capitalized on the effects of physical stress whose functionality was ensured by channeling cellular and genetic regulatory networks in morphogenesis. Environmentally induced bias has also been suggested as a contributor to the evolution of carotenoid coloration in birds (Badyaev et al. 2017), pigmentation in water fleas (Scoville and Pfrender 2010), morphology and physiology in carnivorous toads (Gomez-Mestre and Buchholz 2006; Kulkarni et al. 2017), morphological and behavioral traits in Onthophagus dung beetles (Casasa and Moczek 2018), and sexual size dimorphism in the house finch (Badyaev 2005).

Challenges and Opportunities for Future Studies

Longstanding controversy over the roles of developmental constraints and bias in evolution reflects both conceptual and methodological challenges (e.g., Maynard-Smith et al. 1985; Amundson 2005; Salazar-Ciudad 2008). The representation of phenotypes in terms of regulatory networks resolves some of the contention as it helps to explain how evolution can give rise to developmental bias even when bias itself is not a target of selection. However, the evolutionary consequences of bias are important even if developmental bias has been favored by selection. In both cases, the propensity to vary is expected to be coevolving with the phenotypes themselves. Thus, the contributions of natural selection and developmental bias to adaptation and diversification are not easily quantified or disentangled.

One useful approach would be to identify conditions under which evolution with bias should proceed differentially from evolution in the absence of bias, or a different bias. Surprisingly few models are designed to generate such predictions explicitly (Kovaka 2017). The rapid increase in the number of studies that provide compelling empirical evidence that patterns of phenotypic diversification can be concordant with developmental bias make the development of such theory all the more relevant.

Although the patterns of temporal and extant interspecies diversity can be consistent with a contribution of developmental bias, alternative explanations must be considered. For example, selection could have produced temporal patterns of diversification from unbiased variation if the appearance of ecological niches was nonuniform and the filling of niches by divergent lineages limited the opportunity for disparity within lineages (Pie and Weitz 2005). However, the fact that ecology obviously affects rates and patterns of diversification (Schluter 2000; Rabosky 2009; Losos 2010) does not render the evolutionary effect of developmental bias unimportant or unresolvable (Brakefield 2006). If the evolutionary effect of developmental bias is persistent, phenotypic diversification into new ecological opportunities (e.g., through colonization of new environments) should remain channeled along evolutionary trajectories that are developmentally favored, be disproportionally filled by organisms with the appropriate variability, or even left unexploited. Comparisons of patterns of divergence over time between lineages or experimental populations that differ in their variability in ecologically relevant characters could therefore provide important insights. As demonstrated by analyses of mammalian teeth, a knowledge of developmental mechanisms allows a priori predictions to be made about the form of the variants most likely to be produced. Comparative phylogenetic tools could be usefully combined with this approach to ascertain whether bias was present in ancestral lineages. Such comparative statistical methods can validate, or be validated by experimental approaches to investigating bias that allow retrieval of ancestral character states (Harjunmaa et al. 2014). Studies that combine experimental work on developmental mechanisms with phylogenetic reconstructions and surveys of occupancy of morphospace may be able to reveal if developmental bias contributes to the patterns of convergence often apparent in parallel adaptive radiations, as in the anoles of Caribbean and African lake cichlids (Losos 2011; Brawand et al. 2014).

Conclusion

In a seminal contribution to the study of developmental bias, Pere Alberch (1989, p. 48) wrote: “The reason why development has not been integrated into the existing corpus of evolutionary theory is not a technical one (the ‘we do not know enough about development’ type of argument) but a philosophical one.” Our review of the above literatures suggests that, while the technical challenges are real, there is much merit to Alberch’s analysis. Habits of thought—such as that bias can be understood as constraint; that bias results primarily from physical or material limitations on form; that it is rare, exceptional, or onerous; and that it provides an alternative explanation to selection—have all hindered the integration of development and evolution. The mounting evidence that phenotypic evolution commonly involves changes in the interactions among genes, cellular components, cells, tissues, as well as organisms and their environments provides a strong impetus for evolutionary theory to address and incorporate how developmental systems acquire and control the capacity to vary, and how variability affects the rate and direction of evolution. The explanatory potential of developmental processes for evolutionary biology remains regardless of whether a given bias has itself been shaped by natural selection or emerges through other processes. Thus, it is not sufficient to accommodate developmental bias into evolutionary theory merely as a constraint on evolutionary adaptation. Knowledge of the mechanisms that produce selectable phenotypes can afford both a more detailed understanding of patterns of variation found in nature, and of the evolutionary dynamics of populations. With increasing recognition that the evolutionary process itself evolves (Watson and Szathmary 2016; Watson et al. 2016), a consideration of bias promises the resolution of longstanding puzzles within evolutionary biology (Table 1).

Table 1. Evolutionary questions that the study of developmental bias helps to answer.

Question	Answer with key reference
Why is the influence of genetic and environmental change on phenotypes not uniform?	The feedback, modular structure, and nonlinear interactions of regulatory networks allow developmental systems to exhibit both robustness (i.e., no or small phenotypic change even under large perturbation) and innovation (i.e., large yet functionally integrated phenotypic change even under small perturbation) (Wagner 2011).
How can regulatory networks facilitate the expression of functional phenotypes when populations are exposed to novel environments?	As regulatory interactions evolve, they discover underlying structural regularities of the environments to which they become adapted, including through modular structure, making it possible to reach new adaptive combinations of characters through a small number of mutations (Watson and Szathmary 2016).
Why did a great deal of morphological variation evolve early in the history of multicellular life?	Simple, low-dimensional ancestral regulatory networks will tend to produce greater disparity among the set of common phenotypes than derived high-dimensional networks because ancestral genotypes are less constrained by regulatory epistasis (Borenstein and Krakauer 2008).
Why do phenotypes occupy only a small region of possible phenotype space?	Chance and the adaptive demands of natural selection combine with regulatory epistasis in evolving networks to leave only a fraction of possible phenotypes reachable (Wagner 2011).
How can developmental processes influence the direction of phenotypic evolution?	Evolution of regulatory networks illustrate that the phenotypic variation available for natural selection will typically be biased, sometimes in a functional manner, even when mutations are randomly distributed (Watson and Szathmary 2016).
How does developmental bias contribute to evolvability?	Developmental bias increases the recurrence and fitness of new phenotypes, thereby reducing the amount of genetic change needed to convert them into adaptive phenotypes (Watson and Szathmary 2016). Developmental bias may thus increase evolvability by making it more likely that adaptive phenotypes arise.
How does developmental bias shape macro-evolutionary patterns?	Analyses of regulatory networks reveals that stabilizing selection will push evolving populations to regions of genotype space where changes in topology do not affect the phenotype (generating stasis), while disruptive selection shifts populations to regions in which rapid change can ensue (Wagner 2011).

This table provides only brief summary statements. Readers are referred to the main text for full explanations.

Footnotes

¹Our use of the term “development” is as a synonym to ontogeny, and is not intended to imply that adult forms are static; adult physiology and behavior can also generate bias. In the context of this article, “development” is best seen as a shorthand for changes that occur to individuals during their life time.

²We recognize two uses of the term “bias” in the literature, which can be summarized as “bias as process” (i.e., the developmental processes that result in biased distributions of phenotypes) and “bias as product” (i.e., the phenotypes themselves). While this duality of usage is potentially a source of confusion, in practice the intended meaning is usually clear, given the context.