Abstract
Non-human primates compare quantities in a crude manner, by approximating their values. Less is known about the mental transformations that non-humans can perform over approximate quantities, such as arithmetic transformations. There is evidence that human symbolic arithmetic has a deep psychological connection with the primitive, approximate forms of quantification of non-human animals. Here, we ask whether the subtle performance signatures that humans exhibit during symbolic arithmetic also bear a connection to primitive arithmetic. Specifically, we examined the problem size effect, the tie effect, and the practice effect -- effects which are commonly observed in children’s math performance in school. We show that, like humans, monkeys exhibited the problem size and tie effects, indicating commonalities in arithmetic algorithms with humans. Unlike humans, however, monkeys did not exhibit a practice effect. Together, these findings provide new evidence for a cognitive relation between non-symbolic and symbolic arithmetic.
Keywords: numerosity, numerical cognition, primate cognition, arithmetic
Introduction
Non-human animals cannot represent the precise value of a number because they lack the symbols needed for verbal counting. Symbols such as count words (thirteen, fourteen, fifteen, etc.) or Arabic numerals (13, 14, 15, etc.) represent numerical values precisely. Only with symbols for number is it apparent that 118 and 119 differ by the same amount as 3 and 4. Non-human animals do not have a symbolic system for representing precise numerical differences in this way. Training studies with non-human animals such as chimpanzees (Boysen & Berntson, 1989; Matsuzawa, 2009; Tomonaga, 2008) and parrots (Pepperberg, 2006) have shown that animals can learn that symbols (spoken words, numerals) represent quantitative values and they can estimate the outcomes of some arithmetic transformations of those symbols. However, even when non-human animals are successfully trained to use symbols to represent quantities, they cannot use symbols to represent precise quantities (Tomonaga, 2008). Instead of using discrete representations of numerical values, non-human animals represent numerical values approximately, which is akin to estimating (Agrillo et al., 2011; Beran, 2004; Cantlon & Brannon, 2006; Garland et al., 2012; Pepperberg, 2006; Vonk & Beran, 2012).
The main behavioral signature of the approximate number system (ANS) is the numerical ratio effect whereby the ability to psychologically discriminate numerical values depends on the ratio between the values being compared. This effect is known more broadly as Weber’s law. An implication of the numerical ratio effect is that there is noise (i.e., error) in the psychological representation of each numerical value that is proportional to its value. Hence, larger values are psychologically noisier than smaller values.
There is compelling evidence that the ANS served as an evolutionary foundation for the uniquely human ability to represent number precisely and perform symbolic arithmetic. For example, when animals and adult humans are tested in the same nonverbal numerical tasks, their performance is often indistinguishable (e.g., Cantlon & Brannon, 2006; Cantlon & Brannon, 2007; Cordes et al., 2001; Cordes et al., 2007; Beran & Beran, 2004; Beran et al., 2008; Beran et al., 2011). In a study by Cantlon & Brannon (2006), monkeys and adult humans were required to choose one of two visual arrays that contained the smaller number of elements. Humans were instructed to respond rapidly, without verbally counting the elements and monkeys were trained to do the same task through trial-and-error behavioral training. When monkeys and humans were tested on identical versions of this numerical comparison task, their patterns of performance were remarkably similar: both groups showed steady decreases in accuracy and increases in response time as numerical ratio between the stimuli approached 1. Moreover, infants and preschool children who have no formal arithmetic training can estimate the outcomes of addition and subtraction problems and, their error patterns exhibit a similar numerical ratio effect to that of non-human primates and adult humans who are prevented from verbally counting (e.g., Barth et al., 2005; Cantlon & Brannon, 2007; McCrink & Wynn, 2005). The fact that an approximate numerical ability emerges early in development and is shared by non-human species suggests that basic numerical abilities have a long evolutionary history.
More recent data support the hypothesis that the ANS is foundational for symbolic mathematics by showing a positive relation between acuity of the ANS and symbolic mathematic performance across the lifespan (Halberda et al. 2008; Hyde et al., 2014; Gilmore et al. 2010; McCrink & Wynn, 2005; Park & Brannon, 2014). Some data further suggest a causal link between non-symbolic numerical reasoning and symbolic numerical abilities (Park & Brannon, 2014). If non-symbolic numerical abilities play a causal role in symbolic numerical reasoning then some of the processes of symbolic numerical cognition may be inherited from non-symbolic numerical cognition. Thus, an understanding of non-symbolic numerical processing could be quite informative for understanding the development of symbolic mathematics in humans.
Although robust evidence indicates that non-human animals share a capacity for numerical representation and comparison with humans, less is known about the evolutionary foundations of arithmetic (but see Beran, 2004; Beran & Beran, 2004; Cantlon & Brannon, 2007; Pica et al., 2004). In particular, there are three classic psychological signatures of human arithmetic that have sometimes been described as unique to human arithmetic: the problem size effect, the tie effect, and practice effects (e.g., Ashcraft & Battaglia, 1978; Campbell, 1987; Campbell & Graham, 1985; Geary, 1996; Siegler, 1987; Zbrodoff & Logan, 2005). The problem size effect represents a systematic decline in accuracy and response time as the magnitude of the operands in an arithmetic problem increase (e.g., 5+7 is more difficult than 3+4). The tie effect represents better performance for addition problems in which the two operands are identical (e.g., 2+2 is easier than 1+3). Finally, practice effects are simply improvements in performance with repeated exposure to a given problem. Each of these effects is observed from as soon as mathematics education begins throughout adulthood. However, it is unclear whether these effects are signatures of uniquely human symbolic arithmetic or instead might be more fundamental signatures of arithmetic computation.
For three decades, the main interpretations of the problem size, practice, and tie effects have hinged on the assumption that basic arithmetic problems and outcomes are memorized in a symbolic format in humans (e.g., Ashcraft & Battaglia, 1978; Campbell, 1987; Geary, 1996; Siegler, 1987; Zbrodoff & Logan, 2005). One interpretation of the problem size effect, for example, is that it emerges from the spreading of activation in a semantic network of precisely memorized arithmetic operands and outcomes in which small numbers are represented more strongly than large numbers (e.g., Widman, Little, Geary, & Cormier, 1992). A second interpretation of the problem size effect is that children are exposed to small arithmetic problems more frequently than large problems and therefore small problems are recalled more reliably than large problems (e.g., Campbell & Graham, 1985; Hanman & Ashcraft, 1986), perhaps due to stronger associations between small problems and their outcomes (Siegler & Shrager, 1984). Similarly, the tie effect is hypothesized to emerge from less interference during memory retrieval (Campbell, 1995) or greater exposure to tie problems over development, which results in superior memorization of ties. According to these hypotheses, the problem size, practice, and tie effects would not apply to non-symbolic arithmetic because neither the ability to form precise problem-outcome associations nor the ability to retrieve precise verbal arithmetic facts occurs in the absence of a precise, language-based symbolic numerical system.
As the non-linguistic, approximate system of basic arithmetic has come into focus, alternative explanations of the problem size, practice, and tie effects have been offered that are not based in precise, language-based memorization (e.g., Campbell, 1995; Lefevre, Sadesky, & Bisanz, 1996; Zorzi, Stoianov, & Umilta, 2005). For example, one hypothesis for a non-symbolic basis of the problem-size effect is that problems with larger outcome magnitudes have more psychological overlap with adjacent outcomes than do smaller magnitudes, resulting in more errors for larger problems (Zorzi, Stoianov, & Umilta). This explanation of the problem size effect could apply to both symbolic and non-symbolic arithmetic. In terms of the tie effect, a non-symbolic hypothesis for the tie effect is that tie problems induce fewer errors due to priming of the identical addend values (Blakenberger, 2001). Priming of addends could occur with both symbolic and non-symbolic stimuli and thus the tie effect might not be unique to symbolic arithmetic. Although some proposals for a non-symbolic basis of these effects have been made, the existence of these effects has not been explored in a nonverbal animal. If these signatures of arithmetic processing originate from the fundamental structure of the computational system for arithmetic, then non-human animals could show evidence of the problem size, tie, and practice effects. The investigation of these effects in non-human animals would not only have important implications for understanding the origins of human arithmetic but also for understanding the cognitive processes underlying arithmetic.
Method
Subjects
Subjects were two adult female rhesus macaques, Feinstein and Boxer. All animal care procedures are in accordance with an IACUC protocol. Both subjects participated in prior numerical judgment experiments including numerical comparison, matching, and addition with static sets of dots (Cantlon & Brannon; 2005; Cantlon & Brannon, 2006a; Cantlon & Brannon, 2006b; Cantlon & Brannon 2007a; Cantlon & Brannon, 2007b; Jordan & Brannon, 2006). Thus, these animals had significant prior training with numerical estimation and some prior experience with addition but not subtraction.
Task
Monkeys were tested in sound-attenuated testing rooms while seated in plexi-glass primate chairs in front of a computer monitor (640×480, 30cm viewing distance, 110 pixels per degree visual angle, 60Hz). Stimuli were presented on a touch-sensitive computer screen in randomly selected locations. To begin a trial, subjects were required to press a start stimulus, a small red square presented in the bottom left corner of the screen. Following this response, a short movie was presented (Figure 1). The movie displayed a 3-D-like scene in which a set of animated red balls floated in empty black space, a green rectangular screen then emerged from the top of the screen and covered the set of floating balls. A second set of balls then floated into view from the side of the screen and moved behind the green occluder (addition problems) or a subset of the initial set of red balls flew out from behind the green occluder and off screen (subtraction problems). After viewing one of these “problems”, two static visual arrays appeared on the screen and the monkeys were required to touch the array that represented the arithmetic outcome of the problem.
Figure 1.
Example of an addition (1+1) and subtraction (4−2) trial. The problems were presented as movies wherein two sets of objects were sequentially united behind an occlude (addition) or one set of objects is displayed and then a subset of the items are removed (subtraction). Subjects were given two choices after each movie, from which to choose the correct arithmetic outcome.
Monkeys were given positive visual (light-up border) and auditory (chime) feedback for correct choices and negative visual (black screen) and auditory (warning tone) feedback for incorrect responses. Incorrect responses were also followed by a variable 2–5 second timeout period. Monkeys were rewarded with small amounts of Kool-Aid for correct responses.
Training
Throughout the addition and subtraction training period, only problems with outcomes of 2, 4 and 8 were presented. The same three values were used as distractors on each trial. The three test choice pairs (2&4, 4&8, 2&8) appeared with equal frequency in a random order and there was an equal probability that 2, 4 or 8 was the correct sum.
Both monkeys had prior experience with an addition task in which problems were presented as static arrays of dots rather than as animated arithmetic movies (Cantlon & Brannon, 2007). In the initial phase of this animated movie arithmetic experiment, monkeys were trained with familiar addition problems (1+1, 2+2, and 4+4, with the choices pairs of the values 2, 4, and 8). Monkeys required approximately 8 sessions (~1500 trials) to reach the criterion of 70% accuracy per session over at least 2 consecutive days (although overall performance was significantly above chance (>50%) from the first training session). Next, we expanded the problem set to include a greater variety of problems with the same solutions of 2, 4, or 8 (1+1, 2+2, 1+3, 3+1, 4+4, 1+7, 7+1, 2+6, and 6+2). Performance on these addition problems remained high (>70%) and so, we expanded monkeys’ training sets to include a wider variety of addition movies in which the positions and sizes of the animated balls were varied. To ensure that monkeys were competent with the animated arithmetic task, both monkeys were trained on these addition problems for over 20 sessions before we began subtraction training. During this last phase of training, one monkey (Boxer) required remedial training of approximately 30 sessions to discourage her bias to turn her head away from the movies. Note that both of these monkeys had previously performed addition with static arrays in a prior study (Cantlon & Brannon, 2007) and thus, this entire phase of training only served to facilitate the monkeys’ understanding of the animated movie addition stimuli; they were already competent at solving addition problems with static stimuli.
In the last phase of training, we introduced a set of subtraction training problems all of which had the correct outcomes of 2, 4, or 8 (4−2, 6−4, 8−6, 10−8, 12−10, 6−2, 8−4, 10−6, 12−8, 10−2, 12−5, and 14−6). Subtraction problems were randomly intermixed with addition problems in each session. Half of the trials per session were subtraction and half were addition. The total training period in this phase consisted of approximately 147 sessions of 250 trials per session over 7 months.
Testing
After training, monkeys were tested with addition and subtraction problems with the novel outcomes of 3 (1+2, 2+1, 10−7, 12−9, 11−8, 5−2, 4−1), 6 (1+5, 2+4, 3+3, 4+2, 5+1, 11−5, 10−4, and 9−3), and 12(9+3, 11+1, 10+2, 4+8, 5+7, 3+9, 14−2, 13−1). Each test problem was presented with a choice between the correct outcome versus one of all possible distractor options from the test and training outcome values (excluding the correct outcome): 2, 3, 4, 6, 8, or 12. Test problems were non-differentially reinforced such that whatever choice the monkey made, whether correct or incorrect, they were positively reinforced with juice and computer feedback. Non-differential reinforcement reinforces the animal’s initial strategy for solving the novel test problems and prevents extinction. The test problems comprised 20% of trials and were randomly mixed in with the training problems in each session. Monkeys were tested on approximately 675 test problems spread out over 18 sessions. Each test problem occurred with equal frequency.
Stimuli
The animated arithmetic problems consisted of red floating balls on a black background. There were 12 different exemplars of each of the 23 test problems. The locations and motion trajectories of the balls were varied across exemplars with the constraint that none of the balls crossed paths and that all balls moved linearly to enter or exit the screen along the horizontal axis. To control for cumulative surface area, the size of the balls held one of three values: 625, 1225, and 1849 pixels. Each addition and subtraction problem was presented with each of these element sizes so that element size could not serve as a cue to the correct outcome. These element sizes resulted in cumulative surface areas for the correct outcomes (range = 1250 to 14792 pixels) that were within the range of the cumulative surface areas for the distractors (range = 425 to 21200 pixels). This meant that the correct and incorrect choices had overlapping cumulative surface area values and thus were, on average, equally similar in cumulative surface area to the movie problem stimuli. Thus a strategy based on cumulative surface area summation or subtraction would not lead to above chance performance; since the monkeys did perform above chance, we do not further pursue the issue of a cumulative surface area confound in the results. Each movie was held constant at 1.5 seconds so that movie duration could not serve as a cue to the correct choice.
Results
Monkeys have the capacity for non-symbolic arithmetic, including addition and subtraction
Acquisition of Movie Task
Monkeys were initially trained to solve animated arithmetic problems with addition only. Both monkeys had prior experience with performing addition on static stimuli (Cantlon & Brannon, 2007) and so, this acquisition period only served to familiarize monkeys with the novelty of animated arithmetic movies. As shown in Figure 2, both monkeys’ performance remained stable at approximately 70% throughout addition training. Additionally, monkeys performed about as well on the movie addition task as on the static addition task from a previous experiment (Cantlon & Brannon, 2007). In Figure 2, each data point represents 10 sessions of approximately 250 trials each and summarizes performance across the different phases of addition training described in Methods for a constant subset of addition problems (1+1, 1+3, 2+2, 3+1, 2+4, 3+3, 4+2, 3+5, 4+4, 5+3).
Figure 2.
Performance transfer from static stimuli to the dynamic movie stimuli on the addition task. Error bars represent standard error across problems.
Subtraction Training
Once monkeys were familiarized with the animated arithmetic stimuli during the addition training phase, we trained them to perform a small set of subtraction problems. Monkeys performed significantly above chance during the first 5 sessions of subtraction training (binomial test; Boxer N = 328/486, P < 0.001 ; Feinstein N = 414/619, P < 0.001). However, their performance in this initial training phase suggested that they were using a non-arithmetic strategy. Figure 3, top panel shows monkeys’ addition and subtraction performance from the sessions where subtraction problems were first introduced. The figure shows that both monkeys performed at or below chance on subtraction problems when the correct answer was the larger numerosity (binomial test; Boxer 132/261, P = 0.45; Feinstein 121/305, P =0.99). Note that this was not true for addition problems. Thus monkeys’ early subtraction performance indicates that they initially adopted a bias to choose smaller numbers during the subtraction problems. However, as shown in Figure 3, bottom panel, that bias disappeared by the end of subtraction training for both monkeys. Figure 4 shows monkeys’ performance on each problem in the final phase of addition and subtraction movie training. Both monkeys performed significantly above chance on all problems by the end of training (Boxer all P’s < 0.02; Feinstein all P’s < 0.003).
Figure 3.
Training performance for addition and subtraction movies. Monkeys performed significantly above chance on addition trials during the initial and final stages of training. Monkeys were initially biased to choose the smaller outcome choice during subtraction training but that bias disappeared by the end of training.
Figure 4.
Monkeys performed significantly above chance on all problems for both addition and subtraction by the end of training. Each data point represents a different arithmetic problem.
Following subtraction training, monkeys were tested on a novel set of subtraction problems with the outcomes 3, 6, and 12. The purpose of this test was to determine whether monkeys were simply memorizing the outcomes of the individual arithmetic problems or whether they had learned a generalizable arithmetic rule. The novel test problems were mixed in with the familiar training problems, however, on test problems the monkeys were positively reinforced regardless of their response so that they could not learn the answers to the novel problems during testing. Figure 5, panels A and B, show each monkey’s performance on the novel test problems in red alongside their training performance in black (see also Table 1). Both monkeys performed significantly above chance on the addition and subtraction test problems overall (all P’s < .001 for both monkeys). Monkeys also performed significantly above chance on the majority of the individual arithmetic problems. The exceptions were 12−9, 10−7, 11−5, and 9−3 for Boxer and 10−7, 12−9, 11−8, and 10−4 for Feinstein (all P’s > 0.05). These patterns seem to be idiosyncratic and not to provide any evidence that monkeys used a non-arithmetic strategy to solve the problems. Figure 5C shows the outcome of control analyses that we used to determine whether the monkeys were using a non-arithmetic heuristic to solve the addition and subtraction problems. We tested whether monkeys were matching the value of the largest, first, or second addend rather than solving the arithmetic problems. The graph in Figure 5C shows the subset of addition and subtraction trials where the largest, first, or second operand was equal to the incorrect choice. Figure 5C shows that monkeys were not attempting to match a single operand since they were above chance when the largest, first, and second operands were equal to the distractor choice for both addition and subtraction operations. Monkeys’ overall performance on individual problems is presented in Table 1.
Figure 5.
Monkeys transferred from training problems (black) to novel test problems (red) for addition (filled circles) and subtraction (open circles). Each data point represents a different arithmetic problem.
Table 1.
Monkeys’ average performance on each problem of the addition and subtraction task.
| Operation | Outcome | Operand1 | Operand2 | %Correct | σ |
|---|---|---|---|---|---|
| Addition | 2 | 1 | 1 | 90% | 0.048 |
| 3 | 1 | 2 | 89% | 0.014 | |
| 3 | 2 | 1 | 88% | 0.050 | |
| 4 | 1 | 3 | 75% | 0.090 | |
| 4 | 2 | 2 | 75% | 0.092 | |
| 4 | 3 | 1 | 74% | 0.095 | |
| 6 | 1 | 5 | 78% | 0.064 | |
| 6 | 2 | 4 | 67% | 0.125 | |
| 6 | 3 | 3 | 77% | 0.044 | |
| 6 | 4 | 2 | 73% | 0.094 | |
| 6 | 5 | 1 | 73% | 0.072 | |
| 8 | 1 | 7 | 85% | 0.059 | |
| 8 | 2 | 6 | 85% | 0.050 | |
| 8 | 3 | 5 | 78% | 0.180 | |
| 8 | 4 | 4 | 83% | 0.063 | |
| 8 | 5 | 3 | 74% | 0.109 | |
| 8 | 6 | 2 | 80% | 0.039 | |
| 8 | 7 | 1 | 72% | 0.003 | |
| 12 | 3 | 9 | 98% | 0.016 | |
| 12 | 4 | 8 | 89% | 0.028 | |
| 12 | 5 | 7 | 81% | 0.138 | |
| 12 | 9 | 3 | 80% | 0.011 | |
| 12 | 10 | 2 | 87% | 0.009 | |
| 12 | 11 | 1 | 83% | 0.029 | |
| Subtraction | 2 | 4 | 2 | 75% | 0.072 |
| 2 | 6 | 4 | 58% | 0.033 | |
| 2 | 8 | 6 | 72% | 0.018 | |
| 2 | 10 | 8 | 71% | 0.070 | |
| 2 | 12 | 10 | 67% | 0.028 | |
| 3 | 4 | 1 | 88% | 0.125 | |
| 3 | 5 | 2 | 79% | 0.031 | |
| 3 | 10 | 7 | 57% | 0.016 | |
| 3 | 11 | 8 | 74% | 0.063 | |
| 3 | 12 | 9 | 64% | 0.113 | |
| 4 | 6 | 2 | 78% | 0.076 | |
| 4 | 8 | 4 | 72% | 0.021 | |
| 4 | 10 | 6 | 73% | 0.036 | |
| 4 | 12 | 8 | 68% | 0.003 | |
| 6 | 9 | 3 | 73% | 0.011 | |
| 6 | 10 | 4 | 67% | 0.000 | |
| 6 | 11 | 5 | 74% | 0.039 | |
| 8 | 10 | 2 | 85% | 0.027 | |
| 8 | 12 | 4 | 86% | 0.033 | |
| 8 | 14 | 6 | 87% | 0.037 | |
| 12 | 13 | 1 | 91% | 0.039 | |
| 12 | 14 | 2 | 86% | 0.009 |
An indication that monkeys were using a true numerical strategy to perform this task is that they both showed a ratio effect in their performance, even for problems for which their performance did not exceed chance. Figure 6 shows that the numerical ratio between the correct sum and the distractor choice influenced their accuracy for addition and subtraction. The fact that the ratio effects are parallel between addition and subtraction operations suggests that these two operations are tapping a common mechanism at the decision stage.
Figure 6.
Monkeys exhibited a ratio effect for addition and subtraction. Each data point represents a different ratio and the error bars represent standard error across different addition or subtraction problems.
Monkeys show the classic signatures of human arithmetic
As described in the introduction, there are three classic signatures of arithmetic that are observed in humans: the problem size effect, the tie effect, and the practice effect. We tested whether monkeys also exhibit these performance effects.
Problem Size Effect
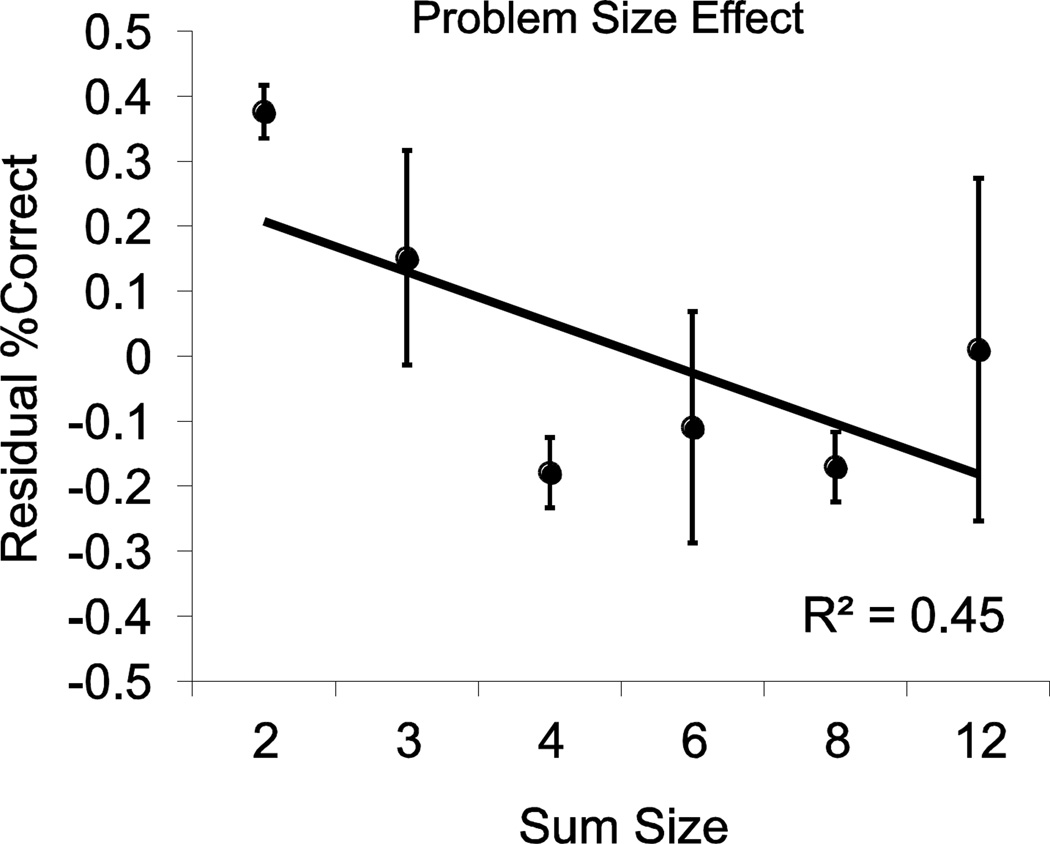
The effect of problem size on monkeys’ performance would be expected to manifest as lower performance the larger the problem size for addition. However, in our experimental design, different ratios were tested at different outcome sizes which would result in different levels of ratio-dependent difficulty at each problem size. Therefore, in order to look for a problem size effect we used a partial regression to remove the effect of ratio from monkeys’ accuracy and then tested whether the remaining variability (the residuals) showed a problem size effect. The partial correlation between problem size and accuracy, controlling for ratio, was statistically significant for each monkey (Boxer: R(585) = −0.22, P < 0.0001; Feinstein: R(562) = −0. 25, P < 0.0001). Figure 7 shows that monkeys exhibited a problem size effect in their performance that was independent of the ratio effect. That is, accuracy decreased with increasing sum size.
Figure 7.
The problem size effect. Monkeys showed a problem size effect in the residuals of their addition task accuracy after the ratio effect was regressed out. Error bars represent standard error across the different addition problems.
Tie Effect
A tie effect is defined by greater accuracy on problems with two identical addends compared to problems with two different addends. We tested whether monkeys exhibited a tie effect in their addition performance by looking at accuracy on ties versus non-ties, at equal levels of experience. Figure 8 shows monkeys’ performance on addition problems with tied addends (1+1, 2+2, 4+4) compared to non-tie problems with the same outcome values (1+3, 3+1, 2+4, 4+2, 3+5, 5+3) in blocks of 300 trials from the beginning of their training with those problems. The data show that across arithmetic training, monkeys were consistently more accurate on tie problems compared to non-ties given the same outcome values and equal levels of experience (paired t-tests; Boxer: t(10) = 2.81, P < .05; Feinstein: t(10) = 2.42, P < .05).
Figure 8.
The tie effect. Monkeys showed a tie effect with consistently better performance on problems with repeated addends (ties) than problems with the same outcome value but two different addends (non-ties). Error bars represent standard error across the different addition problems.
Practice Effect
Human children and adults show a practice effect during arithmetic learning wherein accuracy on specific problems improves with accumulated experience. We tested whether performance on a core set of problems improved for monkeys over years of experience, beginning with their 2006 performance during the static addition task from a previous study (Cantlon & Brannon, 2007) and continuing to their performance on the dynamic movie arithmetic task in the current study. The core problem set was 1+1, 1+3, 2+2, 3+1, 2+4, 3+3, 4+2, 3+5, 4+4, and 5+3. Monkeys did not show a practice effect in their performance on these problems over the course of three years, as shown in Figure 9. There was no evidence of a trend of improvement in accuracy (Boxer: R=0.27, P = 0.45; Feinstein: R=0.20, P = 0.59).
Figure 9.
No practice effect in monkeys. Monkeys did not show a trend of improvement in their performance across three years of training on the same subset of addition problems. Error bars represent standard error across the different addition problems.
Discussion
Monkeys exhibit a capacity for arithmetic that includes addition and subtraction operations. In our experiment, monkeys initially were trained on a sparse set of addition and subtraction problems. When tested with a novel set of problems (and without being conditionally reinforced for correct responses) they showed flexibility in their knowledge of arithmetic that allowed them to solve those novel problems. Additional analyses ruled out the possibility that their performance was based on a simple heuristic such as selecting the choice option closest the largest, first, or second operand. These data show that addition and subtraction operations are not unique to the human species but are instead widespread among animals like primates that possess a non-symbolic capacity for quantitative reasoning. It can be inferred from these findings that arithmetic existed before symbols in human evolution. The conclusion that arithmetic precedes symbolic representation in cognitive evolution is also supported by studies of cognitive development where young children show an intrinsic understanding of arithmetic operations before they understand the symbols that represent them in language (e.g., Gilmore et al., 2007).
Monkeys showed a problem size effect wherein performance worsened as the sums of the addition problems increased in value. This problem size effect occurred independently of ratio in monkeys’ accuracy. A possible explanation of the problem size effect in monkeys is that the process of adding two quantities together creates more noise in numerical representations than can be accounted for by the numerical ratio effect alone (Cordes et al., 2007). In a pure numerical comparison task (e.g., choose the larger value of two visual arrays), the ratio effect can be explained by the noise that arises at the point when the monkey makes a comparison between the two choice stimuli. But, unlike pure numerical comparison, addition requires that the subject represent the numerical values of each of the addends, combine those addend representations into a sum, and then (in this task) make the numerical comparison of the correct sum from the two choice stimuli. Under these circumstances, we see a problem size effect that is independent of the ratio effect in non-symbolic arithmetic. It is an open question whether a similar explanation can be extended to the problem size effect in symbolic addition in humans.
Humans are faster and more accurate at adding problems with repeated addends than problems with two different addends, even when the outcomes are the same. We observed this “tie effect” in monkeys’ addition performance. One explanation of the tie effect that could apply to both the human and monkey data is that ties have less error because there is something akin to a priming effect for two identical operands which makes the tie problems easier to compute than non-ties (Blakenberger, 2001). For example, Gallistel and Gelman (1992) argue that for tie problems the representation of a numerical value needs only to be done once because the same mental magnitude represents both operands. The redundancy in the operands in tie problems thereby reduces the noise in the computation of the sum. This explanation of the tie effect could apply to both symbolic and non-symbolic addition.
Unlike humans, monkeys did not show a practice effect in their performance over three years. The implication of this result is that when humans encode problems as linguistic symbols, they are able to store those problems as units in long-term memory. Since monkeys lack symbols for encoding problems as discrete entities, they cannot memorize arithmetic problems. Therefore, symbols might be required in order to show a practice effect in arithmetic. An open question is how the memorization process associated with the practice effect impacts the acquisition of arithmetic knowledge in humans. The ability to memorize problems appears to be critical for multiplication, for example, where problem outcomes are memorized and this type of memorization could have cascading effects for learning other types of mathematics. The uniquely human practice effect and its unique influence on human mathematics learning are still somewhat of a mystery.
In summary, we observed a capacity for addition and subtraction in non-human primates that exhibits some of the classic signatures of human arithmetic, namely the problem size and tie effects. These findings from non-human primates raise the question of whether classic signatures of human arithmetic are vestigial effects from the primitive ability to perform arithmetic without symbols rather than a consequence of mathematics instruction in school. Resolving the origins of arithmetic signatures should ultimately further our understanding of the constraints that influence children’s acquisition of mathematical concepts.
Acknowledgments
We are grateful to members of the Brannon Lab for useful discussion throughout all phases of the study, particularly Monica Carlson and Evan MacLean. This work was supported by HDR01 to EMB and a James S. McDonnell Foundation Understanding Human Cognition grant to JFC.
All procedures were approved by an institutional animal care and use board at the University of Rochester.
Footnotes
The authors declare no conflicts of interest.
References
- Ashcraft MH, Battaglia J. Cognitive arithmetic: evidence for retrieval and decision processes in mental addition. J EXP PSYCHOL LEARN. 1978;4:527–538. [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke E. Abstract number and arithmetic in preschool children. P NATL ACAD SCI USA. 2005;102:14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beran MJ. Long-term retention of the differential values of Arabic numerals by chimpanzees (Pan troglodytes) ANIM COGN. 2004;7(2):86–92. doi: 10.1007/s10071-003-0191-x. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Beran MM. Chimpanzees Remember the Results of One-by-One Addition of Food Items to Sets over Extended Time Periods. PSYCHOL SCI. 2004;15(2):94–99. doi: 10.1111/j.0963-7214.2004.01502004.x. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Johnson-Pynn JS, Ready C. Comparing children’s (Homo sapiens) and chimpanzees’ (Pan troglodytes) quantity judgments of sequentially presented sets of items. Current Zoology. 2011;57:419–428. [Google Scholar]
- Beran MJ, Evans TA, Leighty KA, Harris EH, Rice D. Summation and quantity judgments of sequentially presented sets by capuchin monkeys (Cebus apella) AM J PRIMATOL. 2008;70:191–194. doi: 10.1002/ajp.20474. [DOI] [PubMed] [Google Scholar]
- Blankenberger S. The arithmetic tie effect is mainly encoding-based. COGNITION. 2001;82:B15–B24. doi: 10.1016/s0010-0277(01)00140-8. [DOI] [PubMed] [Google Scholar]
- Boysen ST, Berntson GG. Numerical competence in a chimpanzee (Pan troglodytes) J COMP PSYCHOL. 1989;103(1):23. doi: 10.1037/0735-7036.103.1.23. [DOI] [PubMed] [Google Scholar]
- Campbell JID. The role of associative interference in learning and retrieving arithmetic facts. In: Sloboda J, Rogers D, editors. Cognitive Processes in Mathematics. Oxford, England: Oxford University Press; 1987. pp. 107–122. [Google Scholar]
- Campbell JID, Graham DJ. Mental multiplication skill: structure, process, and acquisition. CAN J PSYCHOL. 1985;39:338–366. [Google Scholar]
- Campbell JID. Mechanisms of simple addition and multiplication: A modified network-interference theory and simulation. Mathematical Cognition. 1995;1:121–164. [Google Scholar]
- Cantlon J, Brannon EM. Semantic congruity affects numerical judgments similarly in monkeys and humans. P NATL ACAD SCI USA. 2005;102(45):16507–16511. doi: 10.1073/pnas.0506463102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. PSYCHOL SCI. 2006a;17(5):401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Cantlon J, Brannon EM. The effect of heterogeneity on numerical ordering in rhesus monkeys. INFANCY. 2006b;9(2):173–189. [Google Scholar]
- Cantlon JF, Brannon EM. Basic math in monkeys and college students. PLOS BIOL. 2007a;5(12):e328. doi: 10.1371/journal.pbio.0050328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. How much does number matter to a monkey (Macaca mulatta)? J EXP PSYCHOL ANIM B. 2007b;33(1):32–41. doi: 10.1037/0097-7403.33.1.32. [DOI] [PubMed] [Google Scholar]
- Cordes S, Gelman R, Gallistel CR, Whalen J. Variability signatures distinguish verbal from nonverbal counting for both large and small numbers. PSYCHON B REV. 2001;8(4):698–707. doi: 10.3758/bf03196206. [DOI] [PubMed] [Google Scholar]
- Cordes S, Gallistel CR, Gelman R, Latham P. Nonverbal arithmetic in humans: Light from noise. PERCEPT PSYCHOPHYS. 2007;69(7):1185–1203. doi: 10.3758/bf03193955. [DOI] [PubMed] [Google Scholar]
- Garland A, Low J, Burns KC. Large quantity discrimination by North Island robins (Petroica longipes) ANIM COGN. 2012;15(6):1129–1140. doi: 10.1007/s10071-012-0537-3. [DOI] [PubMed] [Google Scholar]
- Gelman CR, Gallistel CR. Preverbal and verbal counting and computation. COGNITION. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Geary DC. The problem size effect in mental addition: Developmental and cross-national trends. Mathematical Cognition. 1996;2:63–93. [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke E. Symbolic arithmetic knowledge without instruction. NATURE. 2007;447:589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Halberda J, Mazzocco M, Feigenson L. Individual differences in nonverbal number acuity predict maths achievement. NATURE. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Hamann MS, Ashcraft MH. Textbook presentations of the basic arithmetic facts. COGNITION INSTRUCT. 1986;3:173–192. [Google Scholar]
- Hyde DC, Khanum S, Spelke ES. Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. COGNITION. 2014;131(1):92–107. doi: 10.1016/j.cognition.2013.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan K, Brannon EM. Weber’s Law influences numerical representations in rhesus macaques (Macaca mulatta) ANIM COGN. 2006;9(3):159–172. doi: 10.1007/s10071-006-0017-8. [DOI] [PubMed] [Google Scholar]
- Lefevre JA, Sadesky G, Bisanz J. Selection of procedures in mental addition: Reassessing the problem-size effect in adults. J EXP PSYCHOL LEARN. 1996;22:216–230. [Google Scholar]
- Matsuzawa T. Symbolic representation of number in chimpanzees. CURR OPIN NEUROBIOL. 2009;19(1):92–98. doi: 10.1016/j.conb.2009.04.007. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Large-number addition and subtraction by 9-month-old infants. PSYCHOL SCI. 2004;15:776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- McCrink K, Dehaene S, Dehaene-Lambertz G. Moving Along the Number Line: The Case for Operational Momentum in Nonsymbolic Arithmetic. PERCEPT PSYCHOPHYS. 2007 doi: 10.3758/bf03192949. [DOI] [PubMed] [Google Scholar]
- Park J, Brannon EM. Training the approximate number system improves math proficiency. PSYCHOL SCI. 2013;24(10):2013–2019. doi: 10.1177/0956797613482944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepperberg IM. Grey parrot (Psittacus erithacus) numerical abilities: Addition and further experiments on a zero-like concept. J COMP PSYCHOL. 2006;120(1):1–11. doi: 10.1037/0735-7036.120.1.1. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. SCIENCE. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Shrager J. Strategy choices in addition and subtraction: How do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Hillsdale, NJ: Erlbaum; 1984. pp. 229–293. [Google Scholar]
- Tomonaga M. Relative numerosity discrimination by chimpanzees (Pan troglodytes): evidence for approximate numerical representations. ANIM COGN. 2008;11(1):43–57. doi: 10.1007/s10071-007-0089-0. [DOI] [PubMed] [Google Scholar]
- Vonk J, Beran MJ. Bears ‘count’too: quantity estimation and comparison in black bears, Ursus americanus. ANIM BEHAV. 2012;84(1):231–238. doi: 10.1016/j.anbehav.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widaman KF, Little TD, Geary DC, Cormier P. Individual differences in the development of skill in mental addition: Internal and external validation of chronometric models. LEARN INDIVID DIFFER. 1992;4:167–213. [Google Scholar]
- Zbrodoff NJ, Logan GD. What everyone finds: The problem-size effect. In: Campbell JID, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 331–345. [Google Scholar]
- Zorzi M, Stoianov I, Umiltà C. Computational modeling of numerical cognition. In: Campbell J, editor. Handbook of mathematical cognition. London: Psychology Press; 2005. [Google Scholar]