Simple kinetic model of mitochondrial swelling in cardiac cells

Abstract

Mitochondria play an important role in both cell survival and cell death. In response to oxidative stress, they undergo opening of non-selective permeability transition pores (PTP) in the inner mitochondrial membrane. Sustained PTP opening triggers mitochondrial swelling due to increased colloidal osmotic pressure in the matrix accompanied by mitochondrial membrane depolarization and ATP hydrolysis. Mitochondrial swelling is the major factor leading to mitochondria-mediated cell death through both apoptosis and necrosis. Hence, precise estimation of the threshold parameters of the transition of reversible swelling to irreversible swelling is important for understanding the mechanisms of PTP-mediated cell death as well as for the development of new therapeutic approaches targeting the mitochondria under pathological conditions. In this study, we designed a simple kinetic model of the Ca²⁺-induced mitochondrial swelling that describes the mechanisms of transition from reversible to irreversible swelling in cardiac mitochondria. Values of kinetic parameters calculated using parameter estimation techniques that fit experimental data of mitochondrial swelling with minimum average differences between the experimental data and model parameters. Overall, this study provides a kinetic model verified by data simulation and model fitting that adequately describes the dynamics of mitochondrial swelling.

1 | INTRODUCTION

Mitochondria are involved in various cellular functions ranging from ATP synthesis to the crucial role in cell death. In response to various stresses such as oxidative stress, mitochondria become uncoupled and massively swollen. In 1976, Haworth and Hunter revealed that the sudden onset of inner mitochondrial membrane (IMM) permeation was due to the opening of the non-selective channels known as mitochondrial permeability transition pores (PTP) (Hunter, Haworth, & Southard, 1976). The PTP opening is induced by increased mitochondrial (matrix) Ca²⁺ $({\text{Ca}}_{\mathrm{M}}^{2+})$, reactive oxygen species (ROS) production, and ATP depletion. The molecular identity of the core pore components has not yet been established, and only cyclophilin D has been broadly accepted as a major PTP regulator (Bernardi & Di Lisa, 2015; Halestrap & Richardson, 2015).

The PTP opening can occur in low-conductance and high-conductance modes (Kwong & Molkentin, 2015; Petronilli, Penzo, Scorrano, Bernardi, & Di Lisa, 2001). The low-conductance pore opening does not induce detectable matrix swelling, and presumably accounts for Ca²⁺ efflux and regulates ${\text{Ca}}_{\mathrm{M}}^{2+}$ levels under physiological conditions (Brenner & Moulin, 2012; Petronilli et al., 1999). Mitochondrial PTP flickering at a low-conductance mode stimulates mitochondrial depolarization spikes and Ca²⁺-induced Ca²⁺ release from one mitochondrion to another, generating Ca²⁺ waves (Huser & Blatter, 1999; Ichas, Jouaville, & Mazat, 1997). Pore opening at a high-conductance induces mitochondrial swelling accompanied by depolarization of the mitochondrial membrane potential (ΔΨ_m) that stimulates ATP hydrolysis by a reverse-mode F₀F₁-ATP synthase (Bernardi & Di Lisa, 2015; Halestrap & Richardson, 2015; Javadov, Karmazyn, & Escobales, 2009). Mitochondrial swelling causes the rupture of the mitochondrial outer membrane and the release of the pro-apoptotic proteins such as cytochrome c from mitochondria into the cytosol (Petronilli et al., 2001). Sustained pore opening induced by severe pathological stimuli leads to mitochondria-mediated cell death through apoptosis or necrosis depending on cellular ATP levels (Halestrap, Clarke, & Javadov, 2004; Javadov, Jang, Parodi-Rullan, Khuchua, & Kuznetsov, 2017). Due to the heterogeneity of mitochondria, the extent of PTP opening can vary within the same cell in response to pathological stimuli. Most likely, the transition from reversible (non-pathological) to irreversible (pathological) pore opening accompanied by massive swelling plays a decisive role in cell death. Therefore, assessment of critical factors that could promote the transition of reversible to irreversible mitochondrial swelling (pore opening) is important for the timely prevention of cell death. Indeed, the PTP inhibitors cyclosporin A and sanglifehrin A do not inhibit pore opening (mitochondrial swelling) induced by high ${\text{Ca}}_{\mathrm{M}}^{2+}$ (Clarke, McStay, & Halestrap, 2002).

Kinetic analysis of the PTP opening which correlates with mitochondrial swelling can allow the development of a mathematical model that would simulate PTP opening, and predict the transition from the reversible to irreversible swelling. Different approaches have been previously applied to develop a mathematical model of Ca²⁺-induced swelling (Baranov, Stavrovskaya, Brown, Tyryshkin, & Kristal, 2008; Eisenhofer et al., 2010; Javadov, Chapa-Dubocq, & Makarov, 2017; Massari, 1996). However, these studies did not elucidate the kinetics of transition from reversible and irreversible swelling. Previous studies on the modeling analysis demonstrated that the transport of H⁺, Ca²⁺, K⁺, P_i, and oxidative substrates across the IMM involving the PTP is regulated by the total amount of Ca²⁺ in the system (Pokhilko, Ataullakhanov, & Holmuhamedov, 2006). Depending on ${\text{Ca}}_{\mathrm{M}}^{2+}$ levels, the PTP can exist in three states: (1) closed (no PTP activation), (2) reversible (periodic PTP opening and closure), and (3) permanent PTP opening. Due to the set boundaries, different values of the kinetic parameters of the ion dynamics were found for each state of mitochondria (Pokhilko et al., 2006). Therefore, it is difficult to describe ion dynamics by the same set of kinetic parameters in different mitochondrial conditions. Also, previous studies on the modeling analysis of mitochondrial swelling did not take into consideration the reversible transition state that could occur upon PTP closure (Bazil, Buzzard, & Rundell, 2010).

In the present study, we developed a kinetic model that simulates reversible (low conductance) and irreversible (high-conductance) swelling induced by a low or high Ca²⁺, respectively, in cardiac mitochondria. Our model was verified with experimental studies and adjusted to measurements for volume changes; these experiments were limited to changes in Ca²⁺. It adequately describes the dynamics of mitochondrial swelling induced by Ca²⁺, the dependence of the swelling on an initial number of mitochondria, and the mechanisms of transition from reversible to irreversible swelling.

2 | MATERIALS AND METHODS

2.1 | Animals

Adult female Sprague–Dawley rats (Charles River, Wilmington, MA) were used to isolate cardiac mitochondria. All experiments were performed by protocols that were approved by the Institutional Animal Care and Use Committee of the University of Puerto Rico Medical Sciences Campus and conformed to the National Research Council Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health (2011, Eighth Edition).

2.2 | Isolation of cardiac mitochondria

Rat ventricles were homogenized using a Polytron homogenizer in 4 ml of ice-cold sucrose buffer containing: 300 mM sucrose, 10 mM Tris–HCl, and 2 mM EGTA, and supplemented with 0.05% BSA (Jang & Javadov, 2014). The heart homogenate was then centrifuged at 2,000g for 3 min to remove cell debris. The supernatant was centrifuged at 10,000g for 6 min to precipitate mitochondria. The final pellet was washed twice by centrifugation at 10,000g for 10 min using sucrose buffer without BSA supplementation. A final mitochondria-enriched pellet was re-suspended in sucrose buffer and used for measurements of swelling. The amount of mitochondrial protein determined by the Bradford method was accepted as a mitochondrial quantity. Equal amount (50 µg) of mitochondrial protein was used for each individual measurement in all experiments.

2.3 | Measurement of mitochondrial swelling

Swelling of energized mitochondria as an indicator of PTP opening in the presence or absence of Ca²⁺ was determined by monitoring the decrease in light scattering at 525 nm as described previously (Escobales et al., 2014). Freshly isolated mitochondria were incubated at 37°C in 100 µl buffer containing 125 mM KCl, 20 mM Tris base, pH 7.4, 1 mM MgCl₂, 2 mM KH₂PO₄, 5 mM malate, 5 mM glutamate, and 1 µM EGTA. Mitochondria (50 µg) were added, and absorbance was monitored in the absence and presence of Ca²⁺ according to the protocol of experiments. Sanglifehrin A (0.5 µM), a PTP inhibitor, was added to verify PTP-dependence of mitochondrial swelling. Alamethicin (1 µM), a pore-forming antibiotic peptide, was used to permeabilize mitochondrial membranes and induce maximum (complete) mitochondrial swelling. EGTA was added in equivalent molar concentrations for sequestration of Ca²⁺.

2.4 | Computational analysis

Data were analyzed using Microsoft Excel® and MATLAB computer software programs. Absorbance simulations were approximated utilizing Runge-Kutta 4th order method adjusted to the experimental absorbance measurements, and optimization of parameters was achieved with least squared method via Microsoft solver.

3 | RESULTS

3.1 | Model development

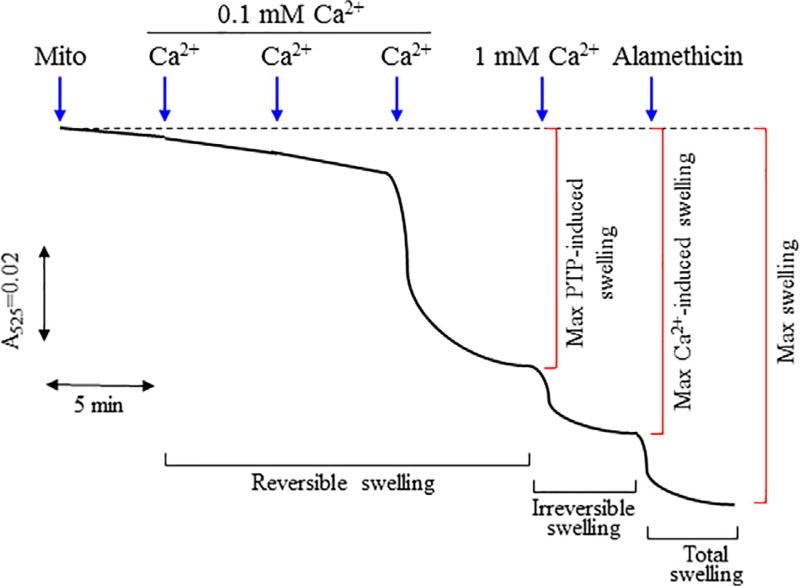
Mitochondrial swelling heavily depends on ion homeostasis within the matrix which inevitably leads to an osmotic imbalance that across the IMM. Typically, a large shift in ionic concentration may cause a colloidal osmotic pressure within the IMM that alters both the mitochondrial volume as well as the mitochondrial function. Primarily changes in concentration amongst K⁺ and Ca²⁺ have played a crucial role in provoking these ionic imbalances. In rat liver mitochondria, Ca²⁺ stimulated an energy-dependent K⁺ uptake which in turn, induced a swelling response (Halestrap, Quinlan, Whipps, & Armston, 1986). These studies suggested that Ca²⁺ influx can indirectly provoke mitochondrial swelling either through K⁺ influx or the opening of the PTP. We developed a simple kinetic model that describes Ca²⁺-induced mitochondrial swelling and transition of reversible swelling to irreversible swelling. All parameters involved in the model are listed in Table 1. Based on our experimental conditions, mitochondria undergo the following states of swelling in response to exogenous Ca²⁺ $({\text{Ca}}_{\text{ext}}^{2+})$ (Figure 1): first state, closed state of the PTP at low Ca²⁺ (up to 100 µM) when swelling is negligible; second state, open state of the PTP at medium Ca²⁺ (up to 300 µM) that induces swelling of mitochondria; third state, open state of the PTP at high Ca²⁺ (1 mM) that induces greatest Ca²⁺-induced (both PTP-dependent and PTP-independent) swelling of mitochondria; and fourth state, maximum mitochondrial swelling induced by permeabilization of the mitochondrial membranes with alamethicin.

TABLE 1.

Definition of the main parameters used in the model

${\text{Ca}}_{\mathrm{M}}^{2+}—\text{mitochondrial }(\text{matrix}){\text{ Ca}}^{2+}$

${\text{Ca}}_{\text{ext}}^{2+}—{\text{external Ca}}^{2+}$

M0—mitochondria (no Ca2+ added)

MCa—mitochondria with Ca2+

${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}—\text{mitochondria with reversible PTP}$

${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}—\text{mitochondria with irreversible PTP}$

$\text{EGTA}+{\text{Ca}}_{\text{ext}}^{2+}—{\text{Ca}}^{2+}-\text{EGTA complex}$

k0—rate constant of “zero” swelling

k1—rate constant of Ca2+ uptake

k2—rate constant of PTP-independent Ca2+ release

k3—rate constant of reversible PTP-induced Ca2+ release

k4—rate constant of reversible swelling

k5—rate constant of irreversible swelling

k6—rate constant of Ca2+ sequestration by EGTA

FIGURE 1.

Dynamics of mitochondrial swelling. Isolated cardiac mitochondria (50 µg) were incubated in the incubation buffer 100 µl buffer containing 125 mM KCl, 1 mM MgCl₂, 2 mM P_i, 5 mM malate, 5 mM glutamate, 1 µM EGTA, and 20 mM Tris base, pH 7.4. The swelling was imitated by addition of 300 µM CaCl₂ (3 times; 100 µM each 5min). The maximum Ca²⁺-induced swelling was determined after addition of 1 mM CaCl₂. In the end, alamethicin (1 µM) was added and total (Ca²⁺-dependent and Ca²⁺-independent) swelling was recorded

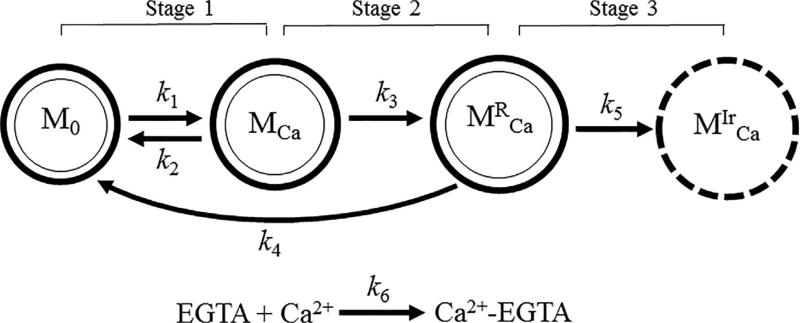
These states of the PTP were based on previously reported data (Crompton, Costi, & Hayat, 1987; He & Lemasters, 2002). Initial studies demonstrated that Ca²⁺-induced swelling of mitochondria could be reversed by EGTA, a Ca²⁺-sequestering agent (Crompton et al., 1987). Following studies revealed regulated (sensitive to cyclosporin A, a PTP inhibitor) and unregulated (insensitive to cyclosporin A) PTP opening (He & Lemasters, 2002). Figure 2 illustrates the proposed model that describes the sequence of mitochondrial swelling. According to this model, isolated mitochondria (M₀) exhibit a negligible swelling (“zero” swelling) in the absence of Ca²⁺. It can, at least partly, be explained by a deficiency of physiological environment, which maintains essential structural and functional integrity of mitochondria. Upon Ca²⁺ addition, the mitochondria may uptake and release ${\text{Ca}}_{\text{ext}}^{2+}$, increasing ${\text{Ca}}_{\mathrm{M}}^{2+}$ up to a critical pore opening threshold. Next, mitochondria containing Ca²⁺ (M_Ca) initially undergo reversible (transitional) swelling, whereby participating in the Ca²⁺ efflux. In the presence of high ${\text{Ca}}_{\text{ext}}^{2+}$, the mitochondria with transitional swelling $({\mathrm{M}}_{\text{Ca}}^{\mathrm{R}})$ is inevitably transformed into mitochondria with an irreversible swelling (inactive state) $({\mathrm{M}}_{\text{Ca}}^{\text{Ir}})$. In this stage; mitochondria are unable to uptake exogenous Ca²⁺. Mitochondrial swelling dynamics described by rate constants (k₀−k₆) can be related to the set of elementary kinetic processes:

$${\mathrm{M}}_0\stackrel{k_0}{\to }{\mathrm{M}}_{\text{Ca}}^{\mathit{\text{Ir}}}$$

$${\mathrm{M}}_0+{\text{Ca}}_{\text{ext}}^{2+}\stackrel{k_1}{\to }{\mathrm{M}}_{\text{Ca}}$$

$${\mathrm{M}}_{\text{Ca}}\stackrel{k_2}{\to }{\mathrm{M}}_0+{\text{Ca}}_{\text{ext}}^{2+}$$

$${\mathrm{M}}_{\text{Ca}}\stackrel{k_3}{\to }{\mathrm{M}}_{\text{Ca}}^R+{\text{Ca}}_{\text{ext}}^{2+}$$

$${\mathrm{M}}_{\text{Ca}}^R\stackrel{k_4}{\to }{\mathrm{M}}_0$$

$${\mathrm{M}}_{\text{Ca}}^R\stackrel{k_5}{\to }{\mathrm{M}}_{\text{Ca}}^{\mathit{\text{Ir}}}$$

$$\text{EGTA}+{\text{Ca}}_{\text{ext}}^{2+}\stackrel{k_6}{\to }[\text{EGTA}-{\text{Ca}}_{\text{ext}}^{2+}]$$

FIGURE 2.

Proposed model of mitochondrial swelling describing transitions from reversible to irreversible swelling. Definition of parameters is shown in Table 1

Upon Ca²⁺ addition, M₀ transform to M_Ca, and the rate of swelling of M₀ includes the rate constant of uptake of ${\text{Ca}}_{\text{ext}}^{2+}$ (pseudo-first order, k₁) and the rate constant of “zero” swelling (first order, k₀). The rate of swelling of M₀ is also dependent on the rate constant of ${\text{Ca}}_{\mathrm{M}}^{2+}$ release (first order, k₂) by M_Ca and the rate constant of the transition from ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to M₀ (first order, k₄). Accordingly, the rate of change in mitochondrial number is determined as follows (Figure 2, stage 1):

$$\frac{d[{\mathrm{M}}_0]}{\mathit{\text{dt}}}=-(k_1[{\text{Ca}}_{\text{ext}}^{2+}]+k_0)[{\mathrm{M}}_0]+k_2[{\mathrm{M}}_{\text{Ca}}]+k_4\left[{\mathrm{M}}_{\text{Ca}}^R\right]$$ (1)

Addition of ${\text{Ca}}_{\text{ext}}^{2+}$ affects the rate of changes in mitochondrial number in favor of M_Ca. The balance between the rates of Ca²⁺ uptake and Ca²⁺ release mechanisms are vital for regulation of the ${\text{Ca}}_{\mathrm{M}}^{2+}$. Ca²⁺ release (efflux) from the mitochondria occurs by three different mechanisms including the PTP (described by the rate constants of the first order, k₃), and two non-PTP channels (described by the rate constants of the first order, k₂): mitochondrial Na⁺/Ca²⁺ and H⁺/Ca²⁺ exchangers. Ca²⁺ enters the mitochondrial matrix via several uptake (influx) mechanisms (described by the rate constants of the second order, k₁) such as the mitochondrial calcium uniporter (MCU), rapid mode of uptake (RaM), and mitochondrial ryanodine receptors type 1 (mRyR). Given that the PTP can perform a physiological role as an additional Ca²⁺ efflux mechanism to regulate the Ca²⁺ level in the matrix, mitochondria may undergo one of two states; either they release Ca²⁺ and return to their normal functional state or enter a dysfunctional state (Kwong & Molkentin, 2015). The transition from the ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to M₀ state is a completely Ca²⁺ independent process, closure of PTP (described by the rate constants of the first order, k₄) in ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ returns (reverses) them back to M₀ due to the reversibility of swelling. Thus, the rate of changes in the M_Ca depends on the rates of the (1) transition from M_Ca to ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ (described by the rate constants of the first order k₃) and (2) bidirectional transition from M₀ to M_Ca (described by the rate constants of the second order k₁, and the first order k₂) (Figure 2, stage 2):

$$\frac{d[{\mathrm{M}}_{\text{Ca}}]}{\mathit{\text{dt}}}=k_1[{\text{Ca}}_{\text{ext}}^{2+}][{\mathrm{M}}_0]-(k_2+k_3)[{\mathrm{M}}_{\text{Ca}}]$$ (2)

The rate of changes in $[{\text{Ca}}_{\text{ext}}^{2+}]$ in the incubation medium is similar to that in M_Ca except the Ca²⁺ chelating process induced by EGTA. The rate of $\text{EGTA}-{\text{Ca}}_{\text{ext}}^{2+}$ complex formation (described by the rate constants of the second order, k₆) depends on interactions between ${\text{Ca}}_{\text{ext}}^{2+}$ and EGTA:

$$\frac{d[{\text{Ca}}_{\mathit{\text{ext}}}^{2+}]}{\mathit{\text{dt}}}=(k_2+k_3)[{\mathrm{M}}_{\text{Ca}}]-k_1[{\text{Ca}}_{\text{ext}}^{2+}][{\mathrm{M}}_0]-k_6[\text{EGTA}][{\text{Ca}}_{\text{ext}}^{2+}]$$ (3)

$$\frac{d[\text{EGTA}]}{\mathit{\text{dt}}}=-k_6[\text{EGTA}][{\text{Ca}}_{\text{ext}}^{2+}]$$ (4)

Interestingly, the change of the number of M_Ca in the absence of EGTA is the exact opposite of the rate of changes in $[{\text{Ca}}_{\text{ext}}^{2+}]$. This implies that total [Ca²⁺] $([{\text{Ca}}_{\mathrm{T}}^{2+}])$, which is the sum of $[{\text{Ca}}_{\text{ext}}^{2+}]$ and $[{\text{Ca}}_{\mathrm{M}}^{2+}]$, is constant. Accordingly,

$$[{\text{Ca}}_T^{2+}]=[{\text{Ca}}_{\mathrm{M}}]+[{\text{Ca}}_{\text{ext}}^{2+}],\text{ when}[\text{EGTA}]=0$$ (5)

Once the critical Ca²⁺ threshold has been reached, the PTP induces the M_Ca to undergo the reversible mitochondrial swelling. The latter, in turn, initiates the changes in the number of ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to increase with a Ca²⁺ release due to PTP opening (k3) or decrease by (1) reversibility of the swelling process (k4) and (2) transition to irreversible swelling (k5) produced by high $[{\text{Ca}}_{\text{ext}}^{2+}]$:

$$\frac{d[{\mathrm{M}}_{\text{Ca}}^R]}{\mathit{\text{dt}}}=k_3[{\mathrm{M}}_{\text{Ca}}]-(k_4+k_5)\left[{\mathrm{M}}_{\text{Ca}}^R\right]$$ (6)

At high $[{\text{Ca}}_{\mathrm{M}}^{2+}]$, mitochondria undergo a remodeling process, which can transform ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to ${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}$ (Figure 2, stage 3). The number of ${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}$ is primarily dependent on the rate of transition of ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to the ${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}$. The initial zero swelling rate (described by the rate constants of the first order, k₀), only observed during initial Ca²⁺-free control readings, contributes minimally and is only applied as a correction factor in the absence of Ca²⁺. With the Ca²⁺ addition, k₀ is set to a value of 0, because most of the swelling phenomenon at this point is related to Ca²⁺-induced swelling as observed in absorbance measurements. Thus

$$\frac{d\left[{\mathrm{M}}_{\text{Ca}}^{\mathit{\text{Ir}}}\right]}{\mathit{\text{dt}}}=k_0[{\mathrm{M}}_0]+k_5\left[{\mathrm{M}}_{\text{Ca}}^R\right]$$ (7)

The sum of the rates of all four mitochondrial stages (M₀, M_Ca, ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$, and ${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}$) is equal to zero. This suggests that a total number of mitochondria (M_T) in all four stages is constant and will remain the same throughout the entire swelling process:

$${[\mathrm{M}]}_T={[\mathrm{M}]}_0+[{\mathrm{M}}_{\text{Ca}}]+\left[{\mathrm{M}}_{\text{Ca}}^R\right]+\left[{\mathrm{M}}_{\text{Ca}}^{\mathit{\text{Ir}}}\right]$$ (8)

To accurately measure mitochondrial swelling dynamics via absorbance measurements, we first had to elucidate the relationship between changes in absorbance and volume. First, given that the concentration of mitochondria, temperature, and pH in our solution is constant, we could consider that the absorbance changes within the solution are directly proportional to mitochondrial morphology. Notably, the term of “absorption” is broadly used in mitochondria studies, although we do not have real absorption phenomenon by mitochondria. Instead of this, we have a light scattering effect that creates a decrease of sample light transmission spectrum. By diluting the mitochondrial matrix with Ca²⁺, the refraction coefficient of the mitochondrial sample changes. This dilution effect decreases the scattering efficiency of mitochondria that increases the light transmission properties of the sample. The effect of mitochondrial diameter on scattering efficiency should also be taken into account during detailed analysis of light scattering. However, in the present study, we did not provide a detailed analysis and discussion of this problem, and followed the conception commonly used in the literature.

The amount of light scattered by mitochondria depends on the matrix volume, where a decrease of absorption density of the mitochondrial solution is proportional to an increase of mitochondrial volume (Tedeschi & Harris, 1958). This dependence is widely used for analysis of ion transport across the IMM. Accordingly, we considered the following conditions: First, the absorbance of mitochondria in the absence of Ca²⁺ was measured as a baseline for absorbance measurements. Since the integrity of the mitochondria is maintained under these conditions, the absorbance was denoted as A_max, which is the “absorption density” of the freshly prepared mitochondria (mitochondria in the normal state are dispersed in the incubation medium used in the experiments). Second, the addition of alamethicin, a pore-forming agent, at a high concentration induces maximum (complete) swelling of mitochondria. The absorbance at the given state was presented as A_min. We used the average absorbance difference of alamethicin-induced swelling (0.07 relative absorbance units) as the value of A_max − A_min. Third, we assume that the absorption cross-section of a single mitochondrion is dependent on time (α/V(t)) during the mitochondrial swelling process, but values of mitochondrial absorbance (scattering light) are constant. Since swelling process decreases ${\text{Ca}}_{\mathrm{M}}^{2+}$ because of its release due to increased IMM permeability, absorption cross-section of such mitochondria decreases as an inverse function of mitochondrial volume. These conditions allow us to propose the following equation:

$$A(t)-A_{\text{min}}=\left(\frac{\alpha }{V(t)}\right)I{[{\mathrm{M}}_0]}_0$$

$$A_{\text{max}}-A_{\text{min}}=\left(\frac{\alpha }{V_0}\right)I{[{\mathrm{M}}_0]}_0$$

$$V(t)=V_0\left(\frac{A_{\text{max}}-A_{\text{min}}}{A(t)-A_{\text{min}}}\right)$$ (9)

where the previous propositions were satisfied due to the inverse dependency of A(t) − A_min and A_max − A_min to V(t) and V₀, respectively. We can also use another approach by introducing a time-dependent mitochondrial concentration ([M₀](t)) as an effective parameter that could take into consideration the change in cross-section of individual mitochondria. The [M₀](t) will include the sum of M₀ and M_Ca because reduction of absorbance is not observed at 100 µM of ${\text{Ca}}_{\text{ext}}^{2+}$ suggesting that the transition of M₀ to M_Ca does not affect absorbance decrease. In this case, we assume that absorption cross-section of the mitochondria is constant while effective concentration (number or density) of mitochondria is a time-dependent parameter, which describes sample absorption dynamics as follows:

$$A(t)-A_{\text{min}}=\epsilon I[{\mathrm{M}}_0](t)$$

$$\left(\frac{A(t)-A_{\text{min}}}{[{\mathrm{M}}_0](t)}\right)=\epsilon I$$

$$A_{\text{max}}-A_{\text{min}}=\mathrm{\epsilon }\mathrm{I}{[{\mathrm{M}}_0]}_0$$

$$\left(\frac{A_{\text{max}}-A_{\text{min}}}{{[{\mathrm{M}}_0]}_0}\right)=\epsilon I$$

$$[{\mathrm{M}}_0](t)={[{\mathrm{M}}_0]}_0\left(\frac{A(t)-A_{\text{min}}}{A_{\text{max}}-A_{\text{min}}}\right)$$ (10)

where ε is the effective absorption cross-section of the single M₀ mitochondria, [M₀](t) is the effective time-dependent number of mitochondria (number of mitochondria per cm³), [M₀]₀ is the initial effective number of mitochondria (when time = 0), l is the sample optical thickness (length). Since an increase in mitochondrial volume correlates well with Ca²⁺ uptake due to changes in the structural topography of mitochondria induced by swelling, the mitochondrial volume is proportional to the quotient of M_T and M₀ at a given time:

$$V(t)=V_0[{\mathrm{M}}_T]/[{\mathrm{M}}_0](t)$$ (11)

The initial (non-swollen, at rest) volume (V₀) of isolated mitochondria, which have a spherical shape with diameter d can be calculated as

$$V_0=\left(\frac{4\pi }{3}\right){\left(\frac{d}{2}\right)}^3$$ (12)

A diameter of mitochondria ranges from 0.5 to 1 µm (Santo-Domingo & Demaurex, 2010) and accordingly, we calculated the estimated initial individual mitochondrial volume (V₀) to be approximately 0.1–0.5 µm³. In our previous studies, the matrix volume determined with ³H₂O and [¹⁴C] sucrose in mitochondria isolated from control hearts was 0.67 µl and increased further to 1.21 µl per mg protein by the end of oxidative stress induced by ischemia-reperfusion (Lim et al., 2002).

3.2 | Experimental data

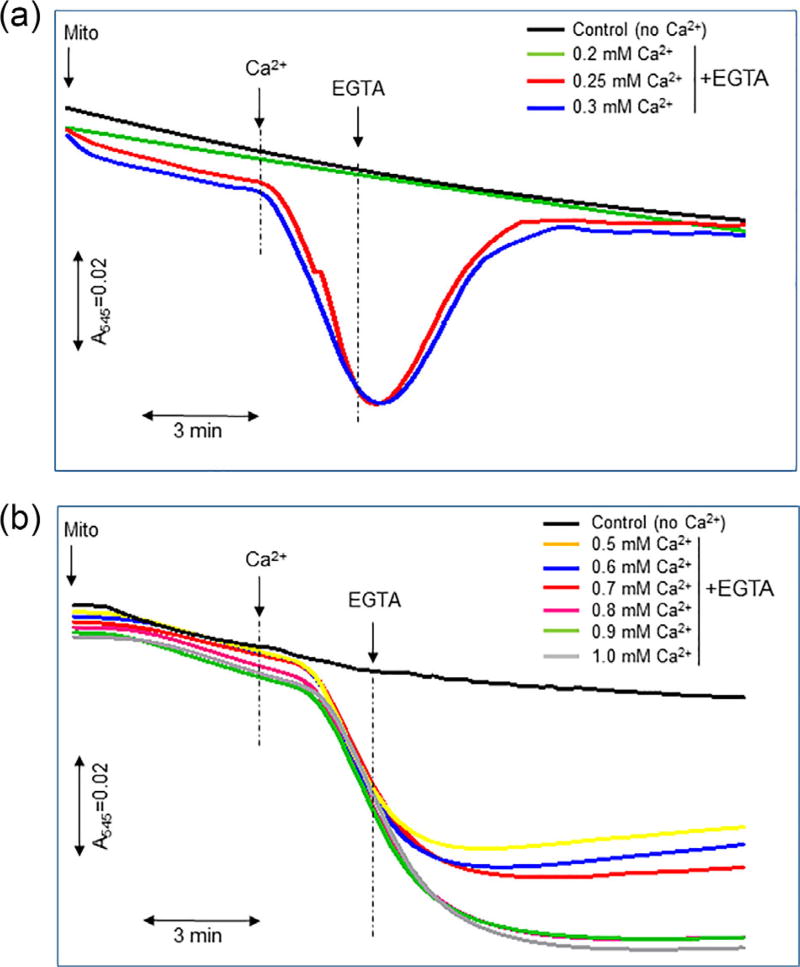
In the first set of experiments, we determined the concentration of ${\text{Ca}}_{\text{ext}}^{2+}$ that induces swelling (threshold), after which addition of extra Ca²⁺ stimulates irreversible swelling of mitochondria. Reversibility of mitochondria was assessed by addition of EGTA, which sequesters free Ca²⁺ in an equivalent ratio. Results showed that ${\text{Ca}}_{\text{ext}}^{2+}$ at a concentration up to 300 µM (6 µmol/µg mitochondrial protein) stimulates mitochondrial swelling, which is completely prevented by EGTA (Figure 3a). However, EGTA was not able to completely prevent swelling of mitochondria induced by Ca²⁺ at a concentration more than 300 µM. The effect of EGTA to prevent swelling was reduced with increasing ${\text{Ca}}_{\text{ext}}^{2+}$, and its effectiveness was insignificant at 1 mM Ca²⁺ (20 µmol Ca²⁺ per µg mitochondrial protein) (Figure 3b). Therefore, the swelling induced by 300 µM was accepted as a peak (threshold) of reversible swelling.

FIGURE 3.

Kinetics of reversible (a) and irreversible (b) swelling of mitochondria. The absorbance of mitochondria was measured in the presence of Ca²⁺ followed by addition of equivalent concentrations of EGTA. In control groups, the absorbance of mitochondria was recorded without the addition of Ca²⁺ and EGTA. Experimental conditions are the same as in Figure 1

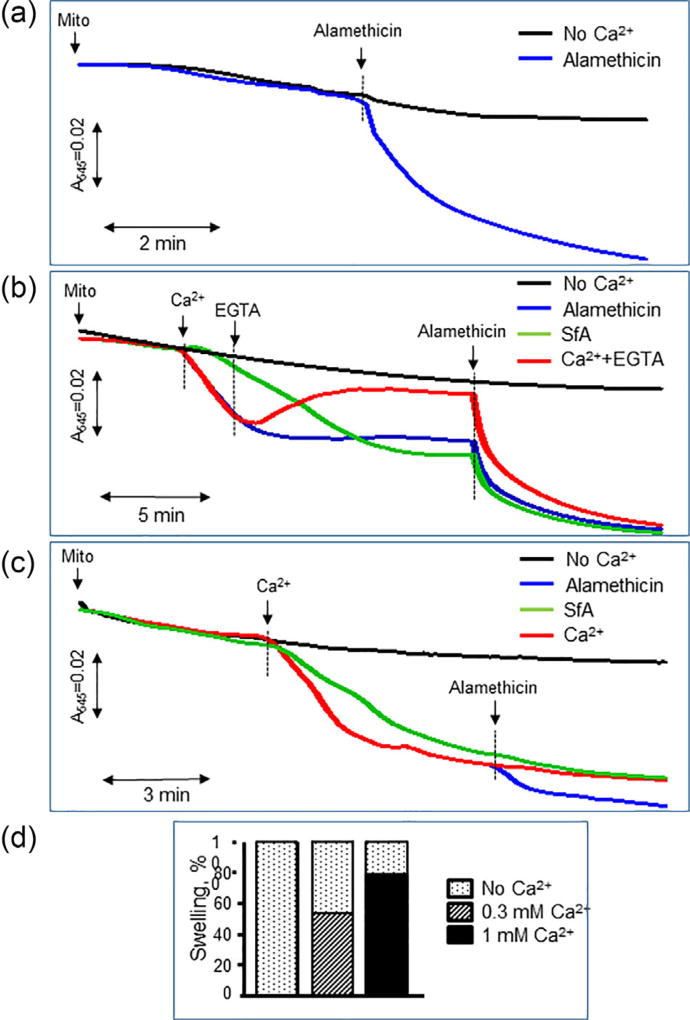
The addition of sanglifehrin A, a PTP inhibitor, significantly reduced the swelling of mitochondria induced by 300 µM Ca²⁺ but had no effect on the swelling induced by 1 mM Ca²⁺ (Figures 4b and 4c). Lack of the effects of cyclosporin A and sanglifehrin A on mitochondrial swelling at high concentration of Ca²⁺ was reported previously (Clarke et al., 2002). Ca²⁺ does not induce complete mitochondrial swelling, and therefore, we used alamethicin, a strong pore-forming agent that induces permeation in mitochondrial membranes, to ensure complete swelling for analysis of the contribution of Ca²⁺-dependent and Ca²⁺-independent mechanisms to mitochondrial swelling. We found that alamethicin induces a 45% and 20% increase of swelling, in addition to 300 µM and 1 mM Ca²⁺, respectively (Figure 4d), and these data are consistent with previous studies (Hansson et al., 2003). The differences in mitochondrial swelling between high Ca²⁺ and alamethicin were taken into consideration.

FIGURE 4.

The contribution of reversible and irreversible swelling to total swelling of mitochondria. The total swelling was measured after addition of 1 µM alamethicin in mitochondria: without addition (a), and after addition of 300 µM (b) or 1 mM (c) of CaCl₂. EGTA was added at 2 min after Ca²⁺ (b) to determine the ability of alamethicin to induce swelling in the presence of EGTA. Based on data shown in (b and c), alamethicin induced additional 45% and 20% swelling in mitochondria with reversible (0.3 mM) and irreversible (1 mM) swelling, respectively (d)

3.3 | Model simulation

Our model was numerically solved and analyzed utilizing the Runge-Kutta 4th order approximation, and the parameters were optimized with the least squared method. All measured kinetics parameters are listed in Tables 2 and 3. Since values of kinetics rate constants are dependent on experimental conditions, the parameters for the constants were extrapolated from individual experimental conditions.

TABLE 2.

Averaged and estimated kinetic rate constants of mitochondrial swelling

	No Ca2+	Ca2+									Ca2++ EGTA
	k0, min−1	k1, M−1min−1		k2, min−1	k3, min−1		k4, min−1		k5, min−1		k6, M−1min−1
Ca2+, µM	Ave & Est	Ave	Est	Both	Ave	Est	Ave	Est	Ave	Est	Ave & Est
300	(2.33 ± 0.9) × 10−2	(1.39) × 10−3	(1.31) × 10−3	0	9.00 ± 0.3	9.17	0.460 ± 0.05	0.390	0.359 ± 0.05	0.241	5.0 × 106
400	(4.28 ± 0.3)×10−2	(1.28) × 10−3	(1.14) × 10−3	0	7.93 ± 0.9	8.47	0.304 ± 0.01	0.307	0.136 ± 0.006	0.173	5.0 × 106
500	(4.74 ± 0.2)×10−2	(7.85) × 10−2	(1.00) × 10−3	0	8.42 ± 0.5	7.77	0.230 ± 0.09	0.242	(7.8 ± 2) × 10−2	0.117	5.0 × 106
600	(2.71 ± 0.4)×10−2	(7.37) × 10−2	(8.90) × 10−2	0	7.81 ± 1.0	7.07	(4.5 ± 0.3)×10−2	0.190	(4.8 ± 1) × 10−2	0.073	5.0 × 106
700	(3.10 ± 0.4)×10−2	(6.43) × 10−2	(7.95) × 10−2	0	6.69 ± 1.0	6.37	(3.0 ± 0.1)×10−2	0.145	0.992 ± 0.8	0.041	5.0 × 106
800	(3.79 ± 0.7)×10−2	(9.68) × 10−2	(7.14) × 10−2	0	4.64 ± 1.0	5.67	0.026 ± 0.04	0.107	(1.3 ± 0.9) × 10−2	0.021	5.0 × 106
900	(4.28 ± 0.9)×10−2	(6.99) × 10−2	(6.41) × 10−2	0	4.65 ± 1.0	4.97	0.095 ± 0.03	0.073	(2 ± 2) × 10−2	0.013	5.0 × 106
1,000	(4.59 ± 0.8) × 10−2	(5.69) × 10−2	(5.77) × 10−2	0	4.72 ± 1.1	4.27	(6.1 ± 0.7)×10−2	0.042	(1 ± 1) × 10−2	0.017	5.0 × 106

The kinetic parameters in the table represent data simulation values shown in Figure 6. The values of the model were first calculated by Runge-Kutta 4th order approximation and then, optimized utilizing the least squared method and Microsoft Excel solver for each condition (no Ca²⁺, Ca²⁺, and Ca²⁺+ EGTA). The average (Ave) kinetic rate constants were extrapolated from the data acquired through each individual fitting and the estimated (Est) kinetic rate constants estimated from each experiment (n = 4).

TABLE 3.

Kinetic parameters of mitochondrial swelling

Parameters	k1, M−1min−1	k3, min−1	k4, min−1	k5, min−1
αn	−612 M−1min−1	−0.007 µM−1min−1	−0.289 min−1	0.0011 µM−1min−1
Βn	4,805 M−1min−1	11.28 min−1	2.039 min−1	0.517 min−1
γn	1 µM−1	–	1 µM−1	6 × 107 µM−2min−1
R2	0.71	0.88	0.61	0.89

The parameter k₀ represents the rate constant of transition of mitochondria to M₀ (“zero” swelling) that occurs during the equilibration period in the absence of Ca²⁺ (initial, non-Ca²⁺-induced swelling). The k₀ has a relatively low average value ((3.8 ± 0.3) × 10⁻² min⁻¹), and it has been accepted as zero due to its insignificant contribution to the model. In favor of this, previous studies displayed that K⁺ influx may occur when mitochondria are added to a K⁺ based respiration buffer thus inducing a slight swelling effect (Garlid & Paucek, 2003). The validity of the model simulation data correlated well with experimental data (R² > 0.88). The rate constants k₁, k₂, k₃, and k₄ represent Ca²⁺ influx and efflux that mediate the swelling process. Synergistic effects of the Ca²⁺ uptake mechanisms through the MCU, RaM, or mRyR were only activated in the presence of ${\text{Ca}}_{\text{ext}}^{2+}$ (Santo-Domingo & Demaurex, 2010). Given that the RaM and mRyR are inhibited at high Ca²⁺ (<20 µM), the MCU is considered as the main Ca²⁺ influx mechanism under these conditions (Xu, Zhang, He, Huang, & Shao, 2016). Rate constant values were approximated from individual fittings of each experimental condition (Figure 5):

$$k_1={\alpha }_1\text{ln}({\gamma }_1[{\text{Ca}}^{2+}])+{\beta }_1$$

$$k_3={\alpha }_3[{\text{Ca}}^{2+}]+{\beta }_3$$

$$k_4={\alpha }_4\text{ln}({\gamma }_4[{\text{Ca}}^{2+}])+{\beta }_4$$

$$k_5={\gamma }_5{[{\text{Ca}}^{2+}]}^2-{\alpha }_5[{\text{Ca}}^{2+}]+{\beta }_5$$ (13)

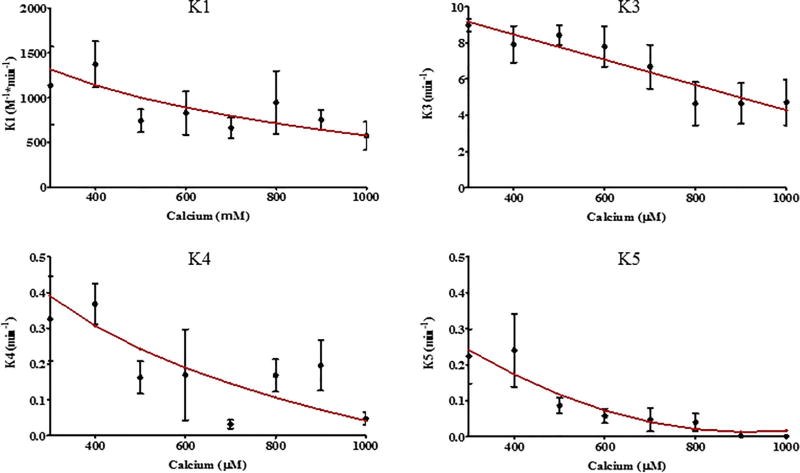
FIGURE 5.

Extrapolating kinetic rate constants. The kinetic model rate constants (k₁, k₃, k₄, and k₅) were extrapolated (red line) from the individual fitting of swelling experiments (black dot with error bars, averaged data) induced by Ca²⁺ ranging from 0.3–1 mM

The parameter values α_n, β_n, and γ_n (where n pertains to its respective rate constant k₁, k₃, k₄, and k₅) represent the constants obtained through linear regression (Table 3) for the equations of the rate constants corresponding to the changes of [Ca²⁺]. The parameter values are capable of adequately simulating Ca²⁺-induced mitochondrial swelling within the [Ca²⁺] range of 0.3–1 mM (Figure 6). The rate constant of Ca²⁺ uptake (k₁) was found to be a large value ((1.31) × 10⁻³M⁻¹ min⁻¹ at 300 µM) for energized mitochondria under all conditions, and decreases proportionally with an increase in Ca²⁺ levels ((5.77) × 10⁻²M⁻¹ min⁻¹ at 1 mM). Note, that the product of k₁ and [Ca²⁺] (shown in equation 2) make the rate of transition from M₀ to M_Ca faster for higher [Ca²⁺].

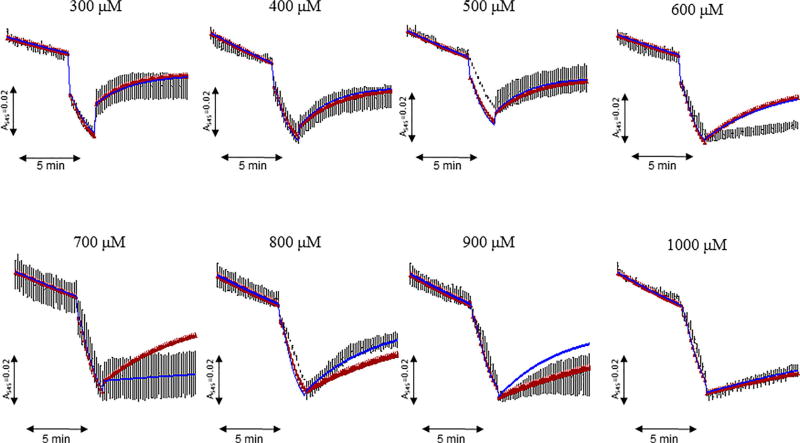
FIGURE 6.

Modeling fitting of the kinetic rate constants for reversible and irreversible swelling with experimental data. The absorbance of mitochondria was measured in the presence of 0.3–1 mM Ca²⁺ followed by addition of equivalent concentrations of EGTA. Simulation of the swelling (blue line) obtained from estimation of rate constants (shown in Figure 5) demonstrates the minimum average difference between the model, Simulation of the swelling (red line) obtained from the average of the rate constants from each Ca²⁺ group, and experimental data (black line). Each curve represents the mean of data from 4 individual experiments

After initial Ca²⁺ addition, the rate constant (k₂) for physiological Ca²⁺ efflux had a typical value of 0 min⁻¹ in the investigated Ca²⁺ range (0.3–1 mM). Typically, high levels of ${\text{Ca}}_{\text{ext}}^{2+}$ creates an enormous concentration gradient that would make Ca²⁺ efflux unfavorable. Once critical ${\text{Ca}}_{\mathrm{M}}^{2+}$ threshold is reached, the rate of transition from M_Ca to ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ (k₃) begins at a high value (9.17 min⁻¹ at 300 µM) and decreases proportionally to higher [Ca²⁺] (4.27 min⁻¹ at 1 mM). Coincidentally, the reverse transition from ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to M₀ (k₄) played a significant role of antagonizing the effects of the rate constants k₁ and k₃ at lower [Ca²⁺] (0.390 min⁻¹ at 300 µM), though the value of k₄ drops with higher [Ca²⁺] (0.042 min⁻¹ at 1 mM). It was interesting to discover that k_1–3 ceased to assist in the induction of mitochondrial swelling upon EGTA addition, this is due to the fast Ca²⁺ sequestering rate of EGTA. As [Ca²⁺] increased from 0.3 to 1 mM in experiments, the k₄ value would decrease, and the transition of ${\mathrm{M}}_{\text{Ca}}^{\mathrm{R}}$ to the ${\mathrm{M}}_{\text{Ca}}^{\text{Ir}}$ state (k₅) would appear to help prevent the reversibility of mitochondrial swelling. Surprisingly, the reduction of k₄ at higher [Ca²⁺] played a more significant role in preventing the reversibility of mitochondrial swelling than the rate constant k₅ at high [Ca²⁺] (>500 µM). This would explain why the mitochondria do not recover with EGTA addition at high (1 mM) [Ca²⁺] (Figure 6).

Similar to the previous studies (Naraghi, 1997), the rate constant (k₆), by which EGTA chelates Ca²⁺, was estimated to be 5× 10⁶ M⁻¹ min⁻¹ based on free Ca²⁺ levels in the incubation medium. This rate is so fast that ${\text{Ca}}_{\text{ext}}^{2+}$ is removed within milliseconds upon addition due to its high affinity for Ca²⁺. Therefore the final [Ca²⁺] was adjusted using Schoenmaker's EGTA-Ca calculator (Schoenmakers, Visser, Flik, & Theuvenet, 1992). As shown in Figure 5, values of kinetic parameters that were calculated using parameter estimation techniques fit experimental data for reversible and irreversible swelling with a minimum average difference between the model and the data.

4 | DISCUSSION

The kinetic model developed in this study describes the biophysical mechanisms of mitochondrial swelling in response to Ca²⁺. The proposed model explains the transition of reversible swelling to irreversible swelling in isolated cardiac mitochondria. Mitochondrial PTP opening plays both physiological and pathological role in cells. A low conductance PTP opening is involved in Ca²⁺ regulation in mitochondria where, like mitochondrial Na⁺/Ca²⁺ and H⁺/Ca²⁺ exchangers, participates in Ca²⁺ efflux (Szabo & Zoratti, 2014). PTP flickering coincides with mitochondrial membrane depolarization, ROS flashes and Ca²⁺ sparks (Zorov, Filburn, Klotz, Zweier, & Sollott, 2000) suggesting an important role of PTP in redox signaling and mitochondria-cytoplasm network. However, Ca²⁺ overload together with increases in ROS production and ATP depletion (high P_i) induce high conductance (pathological) PTP opening.

The PTP opening is involved in the pathogenesis of cardiovascular and neurodegenerative diseases, cancer, diabetes, and aging. Particularly, PTP activation plays a critical role in high energy consuming organs such as heart and brain under oxidative stress where the opening of PTPs causes mitochondria-mediated cell death through both apoptosis and necrosis (Bernardi & Di Lisa, 2015; Halestrap & Richardson, 2015; Javadov et al., 2009). PTP opening is accompanied by mitochondrial swelling which directly correlates with the extent of the mitochondrial damage. The transition between reversible and irreversible swelling is dependent on the balance between inducers and inhibitors of the PTP when shifting the PTP gating potential to higher levels can initiate pore opening whereas the PTP gating potential at a low level can induce pore closure (Petronilli, Cola, Massari, Colonna, & Bernardi, 1993). Hence, precise estimation of the threshold parameters for the transition of reversible swelling to irreversible swelling is important for understanding the mechanisms of PTP-mediated cell dysfunction as well as for the development of new therapeutic approaches targeting (inhibiting) mitochondrial swelling under pathological conditions.

Notably, PTP induction is not limited to Ca²⁺; it can be regulated by mitochondrial matrix pH where a low pH (<7.0) inhibits the opening, and high pH (>7.0) stimulates pore opening (Nicolli, Petronilli, & Bernardi, 1993). A kinetic model simulating PTP associated with mitochondrial Ca²⁺-induced Ca²⁺ release included the role of H⁺ fluxes among other parameters (Selivanov et al., 1998). The effect of mitochondrial swelling dynamics on pH can be related to a simple dilution process of H⁺ in the matrix. For example, an increase of 30% of the mitochondrial diameter, due to the swelling process, gives a dilution factor of 2.3. This dilution mechanism could significantly affect H⁺ concentration in the matrix, and thereby, control PTP opening dynamics.

Our model distinguishes reversible swelling from its irreversible state. The model displays how mitochondrial swelling effect propagates throughout the entire population eventually reaching a steady state by which nearly all mitochondria swell due to steady ${\text{Ca}}_{\text{ext}}^{2+}$. Reversibility of mitochondrial swelling may be related to the mitochondria's capacity to reestablish ionic equilibrium and ΔΨ_m with the help of the concentration shift created by the Ca²⁺ removal. The closure of the reversible PTP by Ca²⁺ sequestration demonstrates the ability of mitochondria to recover from the PTP-induced swelling that can be observed under physiological and pathological conditions. Apparently, Ca²⁺ should be present in the medium (cytoplasm) at a certain concentration to stimulate the mitochondrial Ca²⁺ uptake that occurs predominantly through the MCU. According to our estimation, the concentration of Ca²⁺ with PTP opening hardly changed in the incubation medium. Also, the rates of Ca²⁺ influx and efflux varied at different points. Immediately after Ca² ± addition, a quick Ca² ± uptake (~2–4 µM) occurred that spanned approximately 1 min, followed by a release of Ca² ± which would have persisted without EGTA intervention. The addition of EGTA resulted in some Ca² ± efflux after the saturation of EGTA; this is due to residual Ca² ± left over in the mitochondrial matrix.

Kinetic parameters of mitochondrial swelling estimated from the model fit with experimental data and high correlations between experimental and model data allow the development for the prediction of the swelling in vitro animal models of oxidative stress associated with Ca²⁺ overload. Even though the model lacks information on the contribution of distinct mechanisms to mitochondrial swelling, it provides a certain insight into a central role of Ca²⁺ kinetics in this process. Notably, spatially distinct mitochondrial populations (mitochondrial heterogeneity) have differences in metabolism associated with different Ca²⁺ retention capacity and PTP opening (Kuznetsov et al., 2006; Palmer, Tandler, & Hoppel, 1986). Further studies are necessary for modeling of swelling in different populations of mitochondria. In live cells, the mitochondrial network provides close interaction between different populations of mitochondria when PTP opening accompanied by mitochondrial depolarization initiates Ca²⁺-induced Ca²⁺ release from one mitochondrion to another that generates Ca²⁺ waves and PTP induction in new mitochondria. However, these highly regulated interactions observed in situ mitochondria are lost in isolated mitochondria which are morphologically and functionally different from those in live cells.

Nevertheless, the contributions of ${\text{Ca}}_{\text{ext}}^{2+}$ and ${\text{Ca}}_{\mathrm{M}}^{2+}$ to mitochondrial metabolism and function can be accurately investigated in isolated mitochondria. In addition to swelling, mitochondrial mass (number) can be affected differently in subcellular compartments. Intriguingly, mitochondrial biogenesis that regulates mitochondrial mass in cardiomyocytes is affected by oxidative stress during myocardial infarction and heart failure (Garnier et al., 2003; Javadov, Purdham, Zeidan, & Karmazyn, 2006). Therefore, in addition to ion transport mechanisms, mitochondrial mass and heterogeneity should be taken into consideration for development of the detailed model of swelling.

In a framework of the proposed kinetic scheme, values of parameters presented in Table 2 can be used within their defined range of original concentration of ${\text{Ca}}_{\text{ext}}^{2+}$, and in the presence/absence of EGTA. One can expect that the proposed model should describe all experimental data for a single set of values of kinetic parameters included in the model. However, it is difficult to include additional variable parameters such as ΔΨ_m to this kinetic model, even for simple heterogeneous physical and chemical processes, due to the lack of knowledge of the detailed mechanisms of Ca²⁺ transport across the IMM. It is well known that mitochondria exist as a heterogenic population within the same cell and their capability to transport Ca²⁺ varies as shown for subsarcolemmal and intermyofibrillar heart mitochondria (Lukyanenko, Chikando, & Lederer, 2009; Palmer et al., 1986). Additionally, Ca²⁺ transport is highly dependent on changes of the ΔΨ_m, which affects the ion transport rate through non-selective pores such as the PTP (Luongo et al., 2015). Therefore, the kinetic parameter values of the processes developed on the IMM surface are dramatically dependent on experimental conditions, and rate constants of kinetic schemes, in this case, are typically determined for a defined range of original experimental conditions.

In conclusion, this study provides a kinetic model verified by data simulation and model fitting that adequately describes dynamics of mitochondrial swelling. Further studies are needed to develop a multifaceted kinetic model that would provide a more accurate and precise description of the mitochondrial swelling dynamics.

5 | LIMITATIONS

The present study developed a simple kinetic model that simulates the Ca²⁺-induced mitochondrial swelling dynamics and describes the transition of reversible mitochondrial swelling to irreversible. However, this model does not take into account all influx/efflux mechanisms of Ca²⁺ transport in mitochondria. Additionally, the ΔΨ_m was not measured at different time points during the experiment. Previous studies have shown that high ${\text{Ca}}_{\mathrm{M}}^{2+}$ causes complete depolarization of the mitochondria (Bazil et al., 2010; Vergun & Reynolds, 2005), and depolarization of the ΔΨ_m have been prevented by EGTA treatment (Miyamoto, Howes, Adams, & Brown, 2005). Analysis of theΔΨ_m after Ca²⁺ insult with a delayed EGTA intervention will be performed in our future studies.

Abbreviations

ΔΨ_m

mitochondrial membrane potential

ATP

adenosine triphosphate

Caext2+

exogenous (non-mitochondrial) calcium

CaM2+

mitochondrial (matrix) calcium

EGTA

ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid

IMM

inner mitochondrial membrane

MCU

mitochondrial calcium uniporter

mRyR

mitochondrial ryanodine receptor

PTP

permeability transition pore

RaM

rapid mode of uptake

ROS

reactive oxygen species