Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jul 28.
Published in final edited form as: Phys Med Biol. 2018 Jul 19;63(14):145020. doi: 10.1088/1361-6560/aacd22

Quantifying local tumor morphological changes with Jacobian map for prediction of pathologic tumor response to chemo-radiotherapy in locally advanced esophageal cancer

Sadegh Riyahi 1, Wookjin Choi 1, Chia-Ju Liu 2, Hualiang Zhong 3, Abraham J Wu 4, James G Mechalakos 1, Wei Lu 1,*
PMCID: PMC6064042  NIHMSID: NIHMS1500715  PMID: 29911659

Abstract

We proposed a framework to detect and quantify local tumor morphological changes due to chemo-radiotherapy (CRT) using Jacobian map and to extract quantitative radiomic features from the Jacobian map to predict the pathologic tumor response in locally advanced esophageal cancer patients. In 20 patients who underwent CRT, a multi-resolution BSpline deformable registration was performed to register the follow-up (post-CRT) CT to the baseline CT image. Jacobian map (J) was computed as the determinant of the gradient of the Deformation Vector Field. Jacobian map measured the ratio of local tumor volume change where J < 1 indicated tumor shrinkage and J > 1 denoted expansion. The tumor was manually delineated and corresponding anatomical landmarks were generated on the baseline and follow-up images. Intensity, texture and geometry features were then extracted from the Jacobian map of the tumor to quantify tumor morphological changes. The importance of each Jacobian feature in predicting pathologic tumor response was evaluated by both univariate and multivariate analysis. We constructed a multivariate prediction model by using a support vector machine (SVM) classifier coupled with a least absolute shrinkage and selection operator (LASSO) for feature selection. The SVM-LASSO model was evaluated using ten-times repeated 10-fold cross-validation (10×10-fold CV). After registration, the average Target Registration Error was 4.30±1.09mm (LR:1.63mm AP:1.59mm SI:3.05mm) indicating registration error was within two voxels and close to 4mm slice thickness. Visually, Jacobian map showed smoothly-varying local shrinkage and expansion regions in a tumor. Quantitatively, the average Median Jacobian was 0.80±0.10 and 1.05±0.15 for responder and non-responder tumors, respectively. These indicated that on average responder tumors had 20% median volume shrinkage while non-responder tumors had 5% median volume expansion. In univariate analysis, Minimum Jacobian (p=0.009, AUC=0.98) and Median Jacobian (p=0.004, AUC=0.95) were the most significant predictors. The SVM-LASSO model achieved the highest accuracy when these two features were selected (Sensitivity=94.4%, Specificity=91.8%, AUC=0.94). Novel features extracted from the Jacobian map quantified local tumor morphological changes using only baseline tumor contour without post-treatment tumor segmentation. The SVM-LASSO model using Median Jacobian and Minimum Jacobian achieved high accuracy in predicting pathologic tumor response. Jacobian map showed great potential for longitudinal evaluation of tumor response.

Keywords: Deformation based morphometry, Jacobian map, Treatment Response evaluation, Esophageal cancer, Radiomics

1. Introduction

Image-based evaluation of treatment response after Chemo-radiotherapy (CRT) is important in esophageal cancer in order to make appropriate decisions about patient follow-up and the necessity for further treatment, such as surgery (Duan et al., 2014; Yamashita et al., 2014; Blazeby et al., 2000). Current standard methods to assess the therapy response via diagnostic images use either unidimensional longest diameter, i.e. Response Evaluation Criteria In Solid Tumors (RECIST), or bi-dimensional product of longest diameter and maximal perpendicular diameter of active tumor, i.e. World Health Organization (WHO) criteria (Eisenhauer et al., 2009; Sharma et al., 2012). However, utilization of these criteria in esophageal cancer is limited, mostly because cross-sectional axial measurement of heterogeneous tumor is difficult, thus yielding poor accuracy (sensitivity 57%, specificity 52%) (Kroep et al., 2003; Jones et al., 1999; Westerterp et al., 2005; Staal et al., 2010). Volumetric image analysis improved the accuracy (sensitivity 60%, specificity 73%) (van Heijl et al., 2011; Beer et al., 2006; Westerterp et al., 2005) however, one difficulty lies in the differentiation of viable tumor from normal tissues after therapy, which may lead to inaccurate tumor segmentation (Yanagawa et al., 2012; Westerterp et al., 2005; Geoffrey et al., 2011; Tang et al., 2010). For these reasons, diameter/volume-based measurements are not consistently correlated to important outcomes such as overall survival and pathologic tumor response (Kurokawa et al., 2013; Staal et al., 2010; Yanagawa et al., 2012). A method that can automatically detect the tumor location/shape after therapy and locally quantify the variations by taking voxel-by-voxel spatial distribution into account is needed (Meyer et al., 2009).

One method that measures local structural change of an object in time is Deformable Image Registration (DIR) based morphometry. Ashburner and Friston (Ashburner and Friston, 2004) classify DIR morphometric methods into three categories: Voxel-based Morphometry (VBM), Deformation-based Morphometry (DBM) and Tensor-based Morphometry (TBM). VBM measures grey level difference (i.e. subtraction map) on corresponding voxels after image registration, which is highly sensitive to image misalignment and depends on physical meaning of the voxels (Chao et al., 2010; Tan et al., 2016). DBM and TBM use the Deformation Vector Field (DVF) obtained from DIR to characterize the structural change. DBM evaluates displacement of the objects while TBM exploits the gradient of the DVF, i.e. the Jacobian matrix, to track the morphometric change (Rey et al., 2002; Sakamoto et al., 2014; Dennis et al., 2016; Ou et al., 2015). The Jacobian map obtained from the Jacobian matrix describes local volumetric shrinkage/expansion. Jacobian map has the following advantages: 1) it is invariant to linear registration misalignments (Rey et al., 2002; Sakamoto et al., 2014) 2) the estimated change can characterize voxel-by-voxel volumetric spatial distribution (Meyer et al., 2009; Sarkar et al., 2008) 3) unlike conventional tumor response (RECIST or WHO) criteria, only the Gross Tumor Volume (GTV) in the baseline image is needed to calculate the change without the necessity of tumor size measurement or delineation on the follow-up image (Thirion and Calmon, 1999; Meyer et al., 2009).

There are many studies in Magnetic Resonance Imaging (MRI) that utilize Jacobian map to evaluate volumetric change at different time points in breast cancer (Ou et al., 2015) and in normal and cancerous brain tissues (Thirion and Calmon, 1999; Fuentes et al., 2015; Hua et al., 2009; Rey et al., 2002; Dennis et al., 2016). Fuentes et al. (Fuentes et al., 2015) used Jacobian integral to measure the net volume change of an organ, for quantifying percentage of atrophy and dilation in cerebral and ventricle volumes as a response to therapy in irradiated whole-brain tissue in MRI images. They compared Jacobian integral with automatic segmentation and showed that the two methods had small differences in calculating volume change. In Computed Tomography (CT), Jacobian map is mostly exploited to evaluate lung tissue function e.g. to visualize lung volumetric shrinkage/expansion and to estimate ventilation (Michalski et al., 2017; Cao et al., 2013; Christensen et al., 2007; Reinhardt et al., 2008). Additionally, some efforts attempted to analyze correlation between Jacobians and radiation dose (Niedzielski et al., 2017; Ding et al., 2010) and to detect radiation-induced lung diseases (Diot et al., 2015). Sarkar et al. (Sarkar et al., 2008) compared Jacobian integral and subtraction map (Pre-CT - linearly aligned Post-CT) with manual segmentation in interval CT scans of liver cancer. In 4 subjects, they showed that Jacobian method is segmentation-free and the estimated change had better agreement with manual segmentation compared to subtraction map. Sakamoto et al. (Sakamoto et al., 2014) also calculated Jacobian map to visually identify temporal changes of pulmonary nodules in serial lung CT images. They showed that combination of Jacobian and subtraction map could be practical for a comprehensive visualization of temporal change, especially when nodules emerge or disappear. Few works using Jacobian map have been performed to assess the voxel-wise tumor change and to the best of our knowledge none of them quantified the Jacobian map features to evaluate their correlation with histopathologic response.

In this work, we developed a framework to extract novel morphometric features from the Jacobian map. The purpose of this study is to (1) detect and quantify voxel-wise structural change in tumor between baseline and follow-up CT images using Jacobian map and (2) extract quantitative radiomic Jacobian features from the Jacobian map to predict the pathologic tumor response in locally advanced esophageal cancer patients.

2. Materials and Method

The main flowchart of our framework is presented in Figure 1. Image registration and Jacobian map calculation were performed using Elastix and ITK toolbox (Klein et al., 2010; Shamonin et al., 2013; Ibanez et al., 2003) and statistical analysis was implemented in RStudio (RStudio, 2015).

Figure 1.

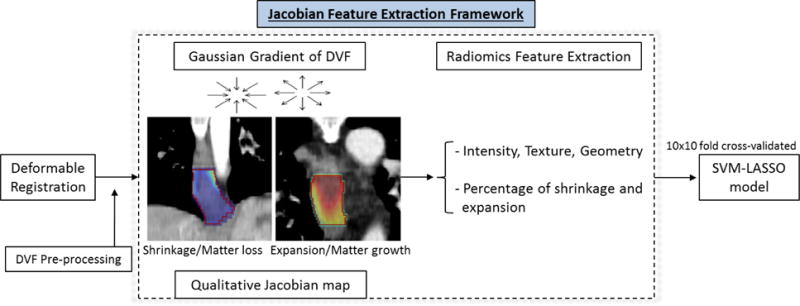
Figure 1

Open in a new tab

Main framework for Jacobian feature extraction.

2.1. Patient and Image dataset

This retrospective study included 20 patients with esophageal cancer who were treated with trimodal therapy from 2006 to 2009 and underwent pre- and post-CRT PET/CT imaging at University of Maryland Medical Center. Pre-CRT imaging was performed at 3~5 weeks before CRT and post-CRT imaging was performed at 4~6 weeks after completion of CRT but before surgery. Surgical resection (Ivor–Lewis, transhiatal, or 3-field esophagectomy) was performed 1–7 weeks after post-CRT PET/CT imaging. Resolution for CT images was 0.98 × 0.98 × 4 mm3. A physician manually delineated a baseline GTV and a follow-up GTV on the pre-CRT and post-CRT PET/CT respectively. The GTV were delineated according to both abnormal esophagus wall thickening on CT and increased FDG uptake on PET. Furthermore, the physician manually placed 16~20 corresponding anatomical landmarks on each image. The landmarks were placed on anatomical structures which are less affected by imaging orientation, such as vessel bifurcation, retroperitoneal organs or calcification spots on bones and vessels. Resected surgical specimens were evaluated by a pathologist and categorized into two groups: 9 responders (pathologic complete response or microscopic residual disease) and 11 non-responders (gross residual disease). For more details about the patient cohort please refer to Tan et al (Tan et al., 2013).

2.2. Image registration

The purpose of image registration is to find the optimized transformation T that spatially maps the corresponding points between baseline and follow-up images. We performed registration in a cropped region 5cm (AP/LR/IS) surrounding the GTV. We first linearly registered follow-up CT to baseline CT images to roughly align the global structures. A multi-resolution BSpline deformable registration was then performed at four resolutions 128, 64, 32 and 16 mm. Displacement between the corresponding points is denoted by a discrete Deformation Vector Field i.e. u→(x,y,z)=T(x,y,z)−(x,y,z), where T(x, y, z) represents the transformed point of (x, y, z). An Adaptive Stochastic Gradient Descent optimizer with pixel level step size was used to minimize a cost function (Equation 1) to obtain the transformation (T) between baseline (Ib) and follow-up (If) images:

C(T,Ib°If)=Csim+αCReg (1)

where Csim was a similarity metric, Creg was a regularization term, and α was a weight that balanced the two terms. We used Sum of Square Difference (SSD) as Csim (Hill et al.) and bending energy of transformation (Equation 2) as Creg (Riyahi-Alam et al., 2014):

CReg=Ebending=∬∫(∂2T∂x2)2+(∂2T∂y2)2+(∂2T∂z2)2+(∂2T∂x∂y)2+(∂2T∂x∂z)2+(∂2T∂y∂z)2 (2)

This function penalized discontinuity in DVF such as folding/tearing, but had no impact on sink (converging) and source (diverging) vectors which we intended to preserve. Converging vectors create a sink point that is mapped to many points in its vicinity and represents a morphological shrinkage. On the other hand, diverging vectors create a source point that represents a morphological expansion. Usually 0 ≤ α ≤ 1.0 (Kanai et al., 2014; Shusharina and Sharp, 2012) and in this study α was experimentally set to 0.1.

To evaluate the registration accuracy, we first visually assessed the alignment of the two images. Then we computed the Target Registration Error (TRE) and Dice Similarity Coefficient (DSC) between baseline landmarks/contours and the transformed follow-up landmarks/contours. We also used percentage of negative determinant of Jacobians and Inverse Consistency Error (ICE) to assess the plausibility and smoothness of the transformation, respectively. Moreover, we compared BSpline SSD to two other registration methods: i) BSpline transformation with Mutual Information (MI) similarity metric (Qiao et al., 2015) and ii) non-diffeomorphic Demons method (Thirion, 1998). We used the same multi-resolution BSpline grid configuration, regularization α and number of iterations for MI metric with Limited Memory Broyden–Fletcher–Goldfarb–Shanno (LMBFGS) Quasi Newton optimization function (Qiao et al., 2015). Number of joint histogram bins was set to 64. For Demons, three levels of registrations with 100 iterations were performed where DVF in each iteration was regularized in an elastic manner using Gaussian smoothing function (∂=2).

2.3. Computing Jacobian Map from the deformation vector field (DVF)

As a preprocessing step, the DVF was smoothed using an Anisotropic Diffusion Filter (Ibanez et al., 2003) to remove the noise while preserving the high frequency structures. A 3×3 Jacobian matrix j and its determinant J were calculated from the DVF u→ at a voxel (Chung et al., 2001):

j(u)=∂ux∂x∂ux∂y∂ux∂z∂uy∂x∂uy∂y∂uy∂z∂uz∂x∂uz∂y∂uz∂z (3)
J(u)=Det(j(u))

j is the first derivative of the DVF and encodes the local stretching, shearing and rotation. These were calculated at every voxel to produce a map of J, which was termed Jacobian map. The Jacobian map indicates the volumetric ratio of an object g before and after the transformation (Equation 4):

J(g)=Volume(g′)Volume(g){J>1volumeexpansionJ=1novolumechangeJ<1volumeshrinkage (4)

where g′ = T(g). J > 1 means local volume expansion, J < 1 means shrinkage and J = 1 denotes no local volume change (Chung et al., 2001). Net volume change of g can be computed using Jacobian integral as (mean J − 1) × initial volume (Fuentes et al., 2015).

Figure 2 presents a conceptual illustration of Jacobian map using a synthetic sphere that simulates tumor shrinkage/expansion.

Figure 2.

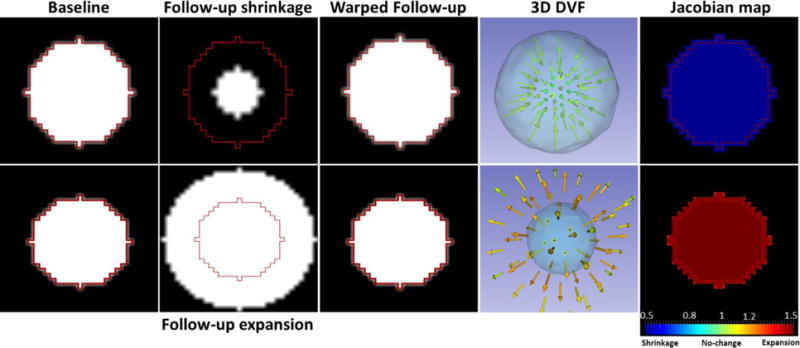
Figure 2

Open in a new tab

Conceptual illustration of Jacobian map. Red contour simulates GTV in the baseline image. Top row: smaller follow-up sphere illustrates shrinkage of a tumor. The DVF converge towards the tumor center (sink) resulting in a Jacobian map with shrinkage (blue). Bottom row: larger follow-up sphere simulates expansion of a tumor resulting in a diverging DVF (source) and a Jacobian map with expansion (red).

2.4. Radiomic Features for Prediction of Tumor Response

Quantitative image features or “radiomics” have shown a significant role in prediction of therapy response (Lambin et al., 2012; Zhang et al., 2014). We extracted 664 features in total (Supplemental Table 5) including both baseline and follow-up PET/CT features (n=378), their changes (n=189) and features from the Jacobian map (n=97) using the Insight Segmentation and Registration Toolkit (Ibanez et al., 2003). These radiomic features quantified the intensity, texture and geometry (Haralick et al., 1973; Galloway, 1975; Xiaoou, 1998) of a tumor in the baseline and follow-up PET/CT images along with their changes, and in the Jacobian map. Intensity features quantify the level and distribution of intensity and Jacobian values. Shape features describe geometric characteristics (e.g., shape and size) of a tumor. Texture features quantify the spatial patterns of tissue density, such as homogeneity, coarseness, and correlation of intensity by using Gray-level co-occurrence matrix (GLCM) (Haralick et al., 1973) and gray-level run-length matrix (GLRM) (Galloway, 1975; Tang, 1998). The average value of each texture feature was computed over all 13 directions to obtain rotationally invariant features. Some features were also extracted on the slice with the largest area (2D features). Since each voxel in the Jacobian map represents local volumetric shrinkage/expansion, the Jacobian features quantified the distribution and spatial patterns of volumetric shrinkage/expansion within the tumor.

The importance of radiomic features as well as patient’s clinical and demographic parameters (Tan et al., 2013) in predicting pathologic tumor response was evaluated by both univariate and multivariate analysis. In univariate analysis, p-value and Area Under the Receiver Operating Characteristic Curve (AUC) for each feature was calculated using Wilcoxon rank sum test. P-values were adjusted using Bonferroni correction, because we tested multiple features (n=664) for one single outcome (Pagano and Gauvreau, 2000). In multi-variate analysis, firstly distinctive features were identified by using a pair-wise correlation cutoff (r=>0.85). Only independent features and representative features, which had the smallest mean absolute correlation were kept for subsequent analysis. A linear Support Vector Machine (SVM) model was then constructed coupled with a Least Absolute Shrinkage and Selection Operator (LASSO) feature selection. All distinctive features were fed to the SVM classifier in a manner of a 10-fold cross-validation (CV). Within each fold CV of the model building process, LASSO was applied to automatically select the ten most important distinctive features by using another (inner loop) 10-fold CV. We repeated the outer-loop 10-fold CV ten times to obtain the model accuracy (10×10-fold CV). RStudio software (RStudio, 2015) was used for construction of the prediction model.

3. Results

3.1. Registration Accuracy

After registration, warped CTs were visually checked and they were well aligned to the baseline CTs. Quantitatively, average percentage of negative J in GTV was 0% and was less than 1% in the cropped image for all the registrations. Negative J indicates folding/tearing vectors and thus smoothness of transformation is not guaranteed. Average TRE (LR, AP, SI, 3D), ICE and DSC for each registration is shown in Supplemental Table 1 and Supplemental Figure 1. The BSpline SSD registration achieved the best TRE (4.30±1.09mm) and DSC (0.66±0.11). TRE in LR and AP were within 2 voxels and TRE in SI was within the slice thickness (4mm) for all registrations. BSpline SSD had slightly lower ICE (2.77±1.33 vs. 3.04±1.95) than BSpline MI. Demons achieved the lowest ICE (1.48±0.49 mm) mainly due to the Gaussian regularization of DVF that was applied in each iteration to avoid negative Jacobian. This led to an over-smoothed DVF that could not accurately capture the shrinkage/expansion in tumor and showed poor performance in detecting the corresponding anatomical landmarks and hence larger TRE.

3.2. Tumor growth/shrinkage measured using Jacobian map

An Example Responder case

Figure 3 shows a responder tumor with its DVF and Jacobian map. Esophageal wall thinning/shrinkage was visible in the follow-up image (white arrows). Tumor shrinkage was illustrated by DVF overlaid on the baseline image that shows vectors are converging from right to left in axial view and from the boundary toward the center of GTV (red contour) in sagittal view. Converging vectors generated a sink point in the middle of GTV where Jacobians were much smaller than 1 (dark blue) indicating large shrinkages. Quantitatively, majority of voxels (97.48%) were shrinking with average Jacobian of 0.66±0.13, indicating overall a 34% shrinkage in the tumor volume.

Figure 3.

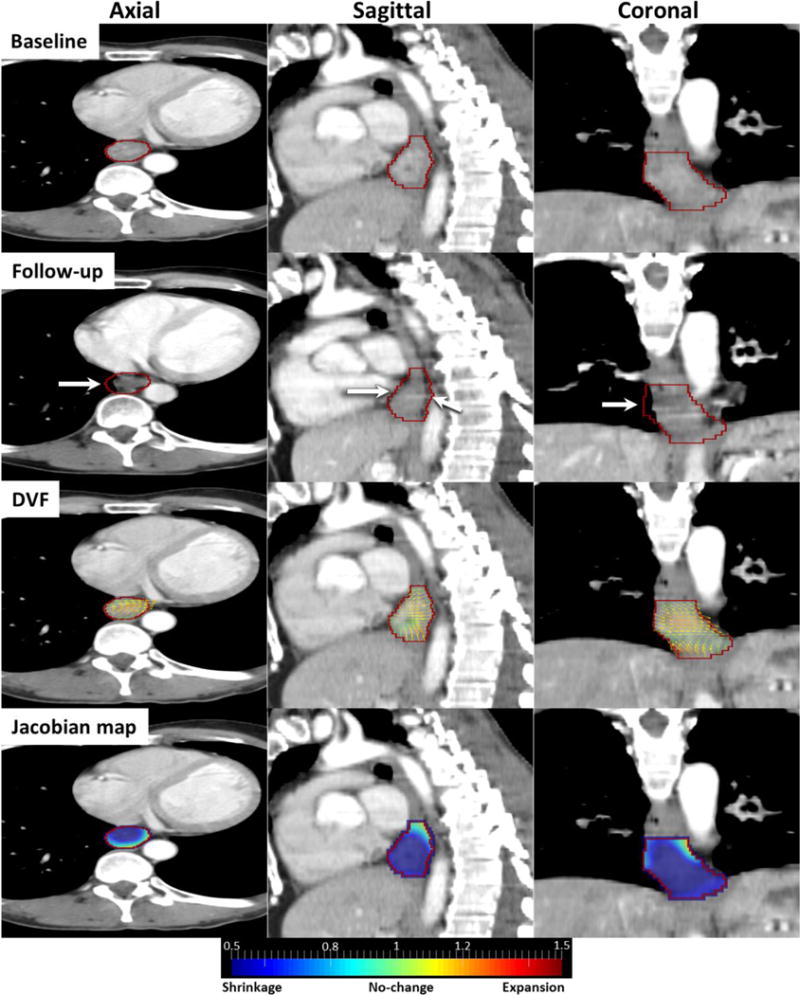
Figure 3

Open in a new tab

Responder case: Baseline, follow-up, DVF and Jacobian images in axial, sagittal and coronal views. Red contour is GTV and white arrows indicate shrinking esophageal wall.

An Example Non-responder case

Figure 4 shows a non-responder tumor with its DVF and Jacobian map. In the follow-up image, a large expansion appeared on the right distal side of esophageal wall (white arrows). DVF overlaid on the baseline image illustrates that vectors are diverging toward the right distal side of GTV (red contour) where Jacobians were much larger than 1 (dark red), indicating large expansions. In this case, majority of voxels (97.24%) were expanding with Jacobian greater than 1. The mean Jacobian was 1.29±0.17, indicating overall a 29% expansion in the tumor volume.

Figure 4.

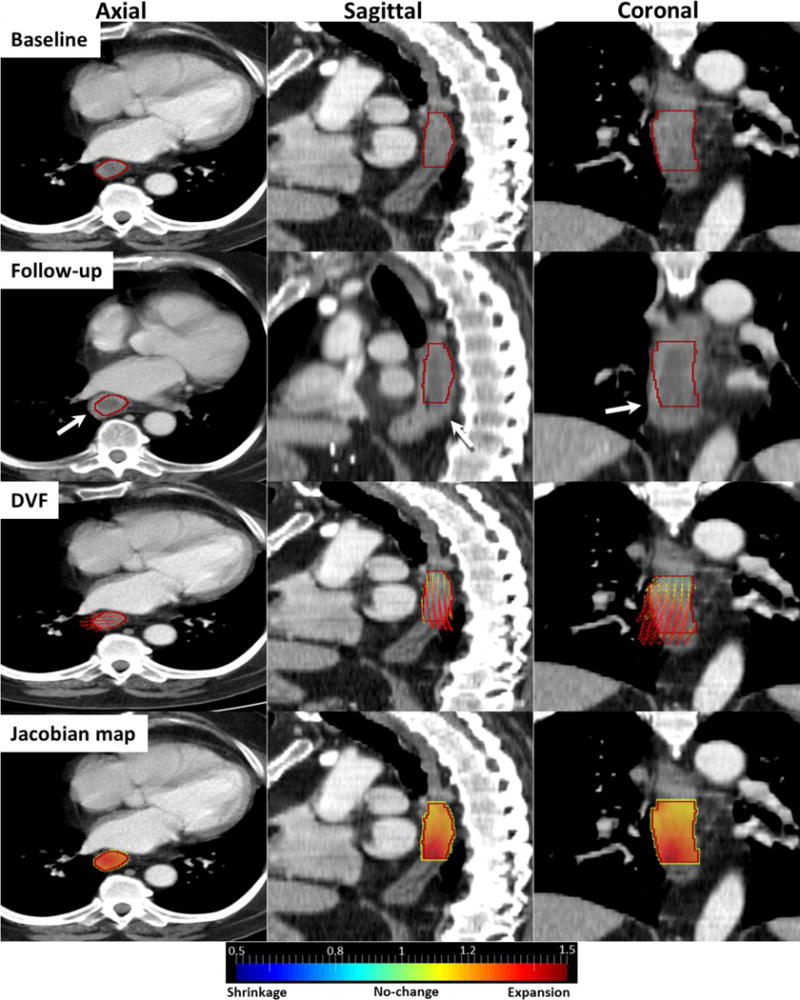
Figure 4

Open in a new tab

Non-Responder case: Baseline, follow-up, DVF and Jacobian images in axial, sagittal and coronal views. Red contour is GTV and white arrows indicate expanding esophageal wall.

3.3. Univariate analysis of PET/CT and Jacobian Features for Pathologic Tumor Response Prediction

Table 1 lists the p-value, AUC and correlation to responders for all significant features (p<0.05 after Bonferroni correction) in univariate analysis. The Minimum Jacobian and Median Jacobian inside the tumor were the only two significant features with high AUCs of 0.98 and 0.95 respectively. Figure 5 shows that both features can differentiate responders from non-responders very well. None PET/CT features was significant after Bonferroni correction. The average Median Jacobian for responders was 0.80±0.10 indicating 20% median shrinkage in tumor volume. In contrast, the average Median Jacobian for non-responders was 1.05±0.15 indicating 5% median expansion in tumor volume. Both features had negative correlation to responders, suggesting that responder tumors tended to have lower Jacobians, i.e. greater volumetric shrinkage. The Median Jacobian and Minimum Jacobian features were independent (r=0.51).

Table 1.

The P-value, AUC and correlation to responders for all significant features in univariate analysis.

Features P-value AUC Correlation to responders
Minimum Jacobian 0.009 0.98 −0.79
Median Jacobian 0.046 0.95 −0.72
Open in a new tab

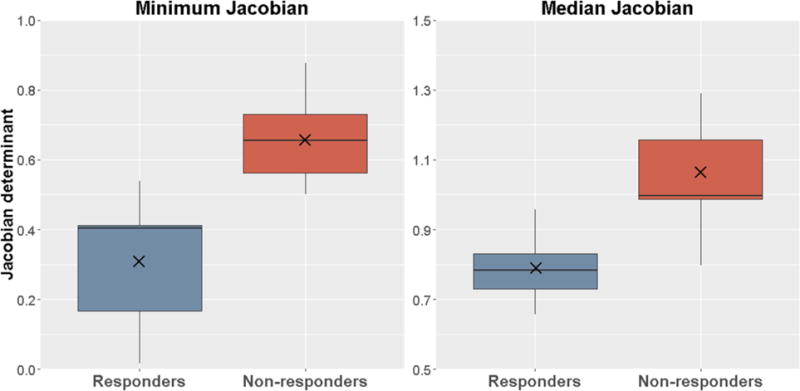
Figure 5.

Figure 5

Open in a new tab

Box plots of the Median Jacobian and Minimum Jacobian features inside the tumor. × indicates average value.

3.4. Multi-variate analysis of PET/CT and Jacobian Features for Pathologic Tumor Response Prediction

Using Jacobian features only, the SVM-LASSO model achieved the highest accuracy when two features -Median and Minimum Jacobian were selected into the SVM classifier (Table 2). Median and Minimum Jacobian were selected as the first feature 6 and 94 times, respectively. They were selected as the second feature 94 and 6 times, respectively. Therefore, the two features were always selected into the best SVM classifier. The best single-feature model achieved 78±0.08% accuracy (0.77±0.08 AUC). When adding the second feature in the model, the prediction accuracy was improved to 94.0±0.03% (0.94±0.03 AUC). However, the performance was worsened when adding more than two features. Using PET/CT features only, the model achieved its highest accuracy with three features. Mean of Inertia in follow-up PET and standard deviation (SD) of Inertia in baseline CT were selected as the first two features (Accuracy 51.5±0.06%). When the third feature – SD of Short Run High Gray Level (SD SRHG) in follow-up PET was added, the accuracy increased to 82.0±0.05%. Lastly using both PET/CT and Jacobian features, the best model was the same as that using Jacobian features only. The same two features (Median and Minimum Jacobian) were selected into the best model and it achieved the same accuracy. Mean of Short Run Emphasis and Mean of Inertia in follow-up PET were selected as the third and fourth feature but they did not improve the accuracy. This indicated that PET/CT features were not significant against Jacobian features in predicting pathologic tumor response.

Table 2.

Prediction performance of PET/CT and Jacobian features using SVM-LASSO model.

Data Features Sensitivity (%) Specificity (%) Accuracy (%) AUC
Jacobian Median Jacobian 94.4±0.05 91.8±0.03 94.0±0.03 0.94±0.03
Minimum Jacobian
PET/CT Follow-up PET Mean Inertia 80.0±0.09 83.6±0.07 82.0±0.05 0.82±0.05
Baseline CT SD Inertia
Follow-up PET SD SRHG
PET/CT and Jacobian Median Jacobian 94.4±0.08 91.8±0.06 94.0±0.05 0.94±0.05
Minimum Jacobian
Open in a new tab

Median Jacobian measured the median tumor shrinkage/expansion. It was more robust than mean Jacobian since it was not affected by outlier Jacobians from inaccurate registration. Minimum Jacobian measured the greatest shrinkage within the tumor. The smaller the Median or Minimum Jacobian, the greater was the volumetric shrinkage. Figure 6 shows a scatter plot of the Median and Minimum Jacobian and the classification line by the SVM-LASSO model that clearly separates responders from non-responders. In general, responders had lower Median and Minimum Jacobians, i.e., larger tumor shrinkage, compared to non-responders. Clearly when combining the two features in the classifier, the prediction accuracy was improved over that of each feature.

Figure 6.

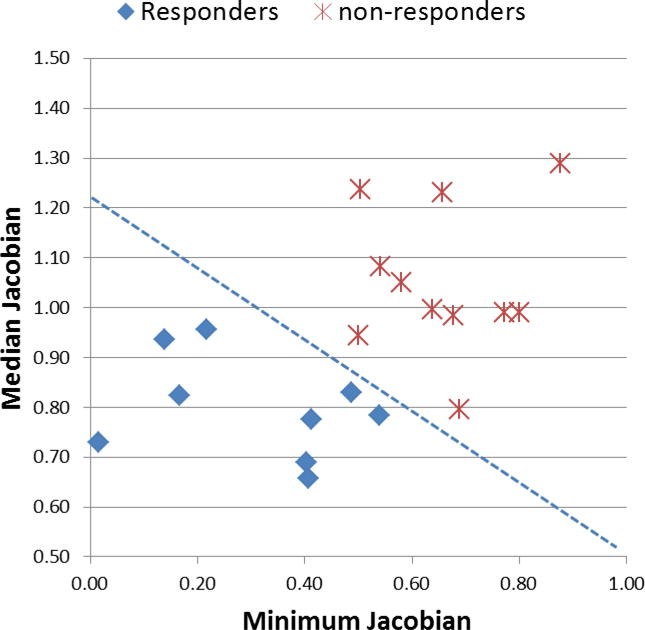
Figure 6

Open in a new tab

Scatter plot of the Median and Minimum Jacobian and the classification line by the SVM-LASSO model.

4. Discussion

4.1. Comparison with studies using conventional response measurements in CT

Table 3 summarizes a few studies that used global changes in tumor volume or diameter measured in CT for the prediction of pathologic tumor response in esophageal cancer. Although the reported changes and accuracies were not consistent, van Heijl et al. (van Heijl et al., 2011), Jones et al. (Jones et al., 1999) and Griffith et al. (Griffith et al., 1999) concluded that neither change in tumor volume nor diameter was associated with pathologic tumor response. However, Beer et al. (Beer et al., 2006) reported that change in tumor volume was associated with pathological tumor response (p=0.04) while change in diameter was not (p=0.37).

Table 3.

Comparison with studies using CT for esophageal cancer response evaluation. Negative sign (−) indicates shrinkage.

Study Patient number Follow-up CT Change in tu mor volume Sensitivity Specificity AUC p Response criteria
Responders Non-responders
Jones et al. (Jones et al., 1999) 50 4-5 w post-Chemo −11.6% (tumor length)
−33.3% (esophageal wall thickness)		 65% 33% – 0.22 AJCCa
van Heijl et al. (van Heijl et al., 2011) 39 14 d during CRT 12% 22% 19% 92% 0.63 0.18 Mandardb
Beer et al. (Beer et al., 2006) 21 14 d during Chemo −24% −16% 100% 53% 0.73 0.04 Mandardb
Griffith et al. (Griffith et al., 1999) 45 6 d (1-17d) post-CRT ~−55% ~−35% – – – 0.58 Mandardb
Conventional volume change+ 20 4-6 w post-CRT −33% −36% 64% 67% 0.58 0.6 Mandardb
Jacobian map −20% 5% 94.4% 91.8% 0.94 0.0002
Open in a new tab
a

American Joint Committee on Cancer (Edge and Compton, 2010).

+

Current study.

Due to differences in therapy, tumor histology, time of follow-up CT, and definition of response, it was impossible to fairly compare the proposed Jacobian method to other studies. Nevertheless, Jacobian method achieved a very high accuracy of AUC 0.94 mainly due to the following reasons: 1) In this study, both pathologic complete response and microscopic residual disease were considered as responders because they are associated with similar rates of survival (Mandard et al., 1994; Koshy et al., 2011) and this classification led to a balanced dataset. Van Heijl (van Heijl et al., 2011) used the same classification while all other studies considered only pathologic complete response as responders, which was more challenge to predict particularly in an imbalanced dataset (much fewer responders than non-responders). 2) it measured local tumor volumetric change rather than global tumor volume change (Meyer et al., 2009). 3) it only required baseline tumor contour without the need of post-treatment tumor segmentation, which is associated with higher uncertainty. 4) it used a multivariate machine learning model (SVM-LASSO) that selected two important features from 664 features. Other studies used only one feature – change in tumor volume or diameter. 5) thinner CT slice (4mm) was used while thicker CT slice was used in some of the other studies – Griffith (Griffith et al., 1999) (8mm) and Jones (Jones et al., 1999) (10mm), which led to inaccuracy in the measurement of tumor volume. In contrast to other studies that reported tumor shrinkage, van Heijl reported tumor expansion in both responders and non-responders (van Heijl et al., 2011), This was likely due to inflammatory response to radiation in Mid-treatment (14 d) of CRT (van Heijl et al., 2011).

In this study, Spearman correlation (ρ) and percentage of difference between volume change calculated by BSpline SSD Jacobian method and manual segmentation was 0.63 and 24%, respectively. Supplemental Table 1 shows very similar results for BSpline MI and Demons registrations. The main reason for this large difference was that the post-treatment manual contour was drawn using both PET and CT images where metabolic tumor volume change was also taken into account. However, Jacobian map was calculated only on CT where anatomic change was smaller. Therefore, computed tumor change using Jacobian map was much smaller than conventional volume change measured by manual contouring.

4.2. Comparison with studies using Jacobian integral

Sarkar (Sarkar et al., 2008) (1 synthetic, 3 clinical cases) used Jacobian integral to measure net volume change of lesions in CT liver cancer in a small number of cases and compared it to manual segmentation where average volume difference was as small as 2.86cm3. Fuentes (Fuentes et al., 2015) (15 cases) reported 2.8% difference in cerebral shrinkage and 1% difference in ventricle increase between Jacobian integral and automatic segmentation. They evaluated the brain tumor change in MRI images using a diffeomorphic image registration where the differentiation of viable tumor and the surrounding normal tissue are thought to be more trivial compared to esophageal tumor in CT images.

In studies by Sarkar (Sarkar et al., 2008) and Fuentes (Fuentes et al., 2015), Jacobian integral was the only feature calculated. The main novelty of our work was that we quantified the Jacobian map with quantitative radiomic features and we integrated these features in a multi-variate model (SVM-LASSO) to evaluate their association with pathologic response. As a result, combination of Median and Minimum Jacobian features showed potential for an accurate response evaluator.

4.3. Influence of registration parameters on Jacobian map

The accuracy of Jacobian map depends on the accuracy of the image registration. We experimentally chose an optimal set of registration parameters that reduced the percentage of negative Jacobians and ICE while TRE was within 2 voxel resolution. The weight (α) of the regularization term and the BSpline grid size were the most sensitive parameters. Larger α over-regularized or over-smoothed the DVF so that sink/source was lost in the Jacobian map. On the other hand, smaller α led to a distorted alignment. Smaller BSpline grid size increased the accuracy of alignment but also captured noises and produced undesired irregular deformations such as folding, tearing and vorticity. We experimentally chose α = 0.1 and multi-resolution BSpline grid size of 128, 64, 32 to 16 mm, which worked for small to relatively large deformations.

However, the optimal set of parameters failed for 5 cases with large non-correspondence between baseline and follow-up CT scans. Figure 7 shows one non-responder case whose baseline CT contained a large air cavity inside the GTV (Fig. 7a), which was filled in the follow-up CT (Fig. 7b). Using the default registration parameters, we obtained a shrinking Jacobian map (Fig. 7e) as consequence of DVF converging toward the center of tumor (Fig. 7c). The Median and Minimum Jacobian were 0.79 and 0.23 respectively that led to misclassification of this case as a responder. Because of the severe violation of the correspondence assumption for a deformable image registration algorithm, the registration was not accurate. In this case, the soft tissues is attempting to fill the air cavity and thus the DVF is pointing towards a sink caused by the air cavity, producing a Jacobian map that reflecting untruthful tumor shrinkage. To resolve this issue, we first masked the air cavity (with a threshold of −150HU) out from both baseline and follow-up CTs, so that non-corresponding points were excluded from the registration. This removes the untruthful sink in the DVF (Fig. 7d). Then, we experimentally set α = 0.5 to make the DVF smoother and set the finest BSpline grid size = 22mm to take more global deformations into account. These resulted in a reasonably smooth DVF (Fig. 7d) and overall no-change Jacobian map with Median and Minimum Jacobian of 0.98 and 0.63 respectively (Fig. 7f) that led to correct classification of this case as a non-responder.

Figure 7.

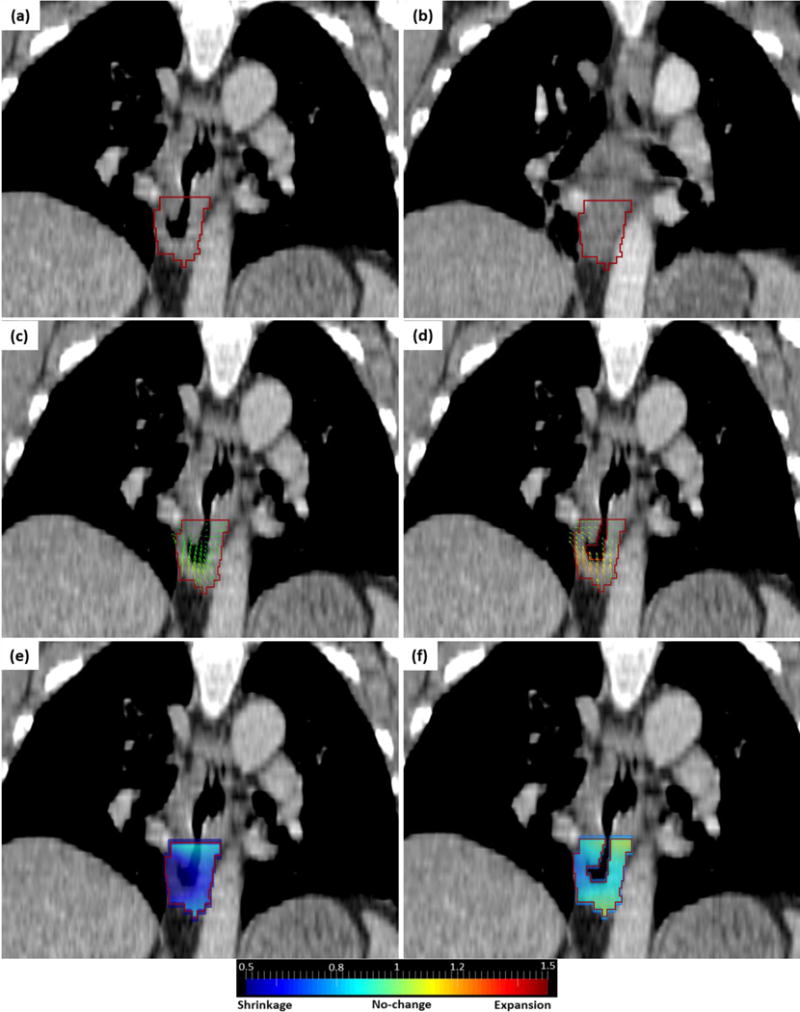
Figure 7

Open in a new tab

(a) baseline CT containing air cavity in GTV (red contour). (b) follow-up CT filled with soft tissue. (c) DVF using default registration parameters. (d) DVF using masked optimized registration. (e) Jacobian map using default registration parameters. (f) Jacobian map using masked optimized registration.

Anisotropic CT voxel size may affect the registration result due to lower resolution in SI component (Ashburner and Friston, 2004). However, its impact on the estimation of the DVF and the Jacobian map was minimal if the registration is accurate and performed with a set of optimized parameters.

Finally, no texture features were significant in Jacobian map for predicting the tumor pathological response, mainly because Jacobian map computed volumetric change in CT images and change in CT texture feature has been proved to be less predictive in esophageal cancer (Westerterp et al., 2005; van Rossum et al., 2016; Tan et al., 2013; Zhang et al., 2014). Instead, PET texture features have shown better prediction value (Tan et al., 2013). Moreover, Median and Minimum Jacobian represented local tumor volume change and shrinkage which expected to be more correlated to tumor response than the texture features.

4.4. Robustness Analysis

As an external validation of SVM-LASSO model and Jacobian features, we dilated and eroded the baseline tumor GTV by 2mm respectively to mimic the uncertainty in tumor contour delineation. We then computed the two features (Median and Minimum Jacobian) from the dilated/eroded Jacobian map and fed them to the SVM-LASSO model in 3.4 for response prediction. For agreement in feature values, we examined Bland-Altman plots (Bland and Altman, 2007) (Supplemental Figure 2) and calculated the intra-class correlation coefficient (ICC) (Parmar et al., 2014) among the original and dilated/eroded GTVs (Supplemental Table 3). The Bland-Altman plots showed that the mean differences (bias) were close to zero and the 95% limits of agreement were small. The bias of Median Jacobian was almost zero for both dilated and eroded GTVs. The bias of Minimum Jacobian was slightly lower than zero suggesting greater maximum tumor shrinkage for dilated GTV, but slightly higher than zero suggesting smaller maximum tumor shrinkage for eroded GTV. The ICCs were 0.98 for Median and 0.95 for Minimum Jacobian, suggesting high agreement. The prediction accuracy increased by 1% for dilated GTV and decreased by 4% for eroded GTV (Supplemental Table 4). In summary, the prediction accuracy was similar and the proposed method showed consistent results across dilated/eroded contours.

4.5. Limitations

One limitation of Jacobian map was that it can’t affirm that the measured shrinkage/expansion was indeed due to tumor volume shrinkage/expansion, i.e., tumor response to therapy. The measured shrinkage/expansion could have been the results of daily anatomy variations (e.g., esophageal lumen filling) or of radiation-induced normal tissue inflammation. This limitation was generally seen in tumor response measurements based on anatomic imaging.

Another limitation was that this was a retrospective analysis of a small patient cohort (n=20). Although we used 10-fold cross-validations to avoid potential overfitting, the predictive accuracy and stability of the model should be validated in a larger and independent patient cohort.

4.6. Future Work

We observed much larger metabolic tumor volume change in PET than the measured volumetric change in CT. Furthermore, the metabolic tumor volume change is more likely due to tumor response to therapy than due to daily anatomy variations. Therefore, we plan to calculate Jacobian map from the blended PET/CT images to quantify the metabolic tumor volume change.

5. Conclusion

Novel features extracted from the Jacobian map quantified local tumor morphological changes using only baseline tumor contour without post-treatment tumor segmentation. The SVM-LASSO model using Median and Minimum Jacobian features achieved high accuracy in predicting pathologic tumor response. Jacobian map showed great potential for longitudinal evaluation of tumor response.

Supplementary Material

PMBaacd22_supplementarymaterial.pdf

Acknowledgments

This work was supported in part by the NIH/NCI Grant No. R01 CA172638 and the NIH/NCI Cancer Center Support Grant P30 CA008748.

Footnotes

The authors have no relevant conflicts of interest to disclose.

References

  1. Ashburner J, Friston KJ. Human Brain Function. Academic Press; 2004. [Google Scholar]
  2. Beer AJ, Wieder HA, Lordick F, Ott K, Fischer M, Becker K, Stollfuss J, Rummeny EJ. Adenocarcinomas of esophagogastric junction: multi-detector row CT to evaluate early response to neoadjuvant chemotherapy. Radiology. 2006;239:472–80. doi: 10.1148/radiol.2391050043. [DOI] [PubMed] [Google Scholar]
  3. Bland JM, Altman DG. Agreement between methods of measurement with multiple observations per individual. J Biopharm Stat. 2007;17:571–82. doi: 10.1080/10543400701329422. [DOI] [PubMed] [Google Scholar]
  4. Blazeby JM, Farndon JR, Donovan J, Alderson D. A prospective longitudinal study examining the quality of life of patients with esophageal carcinoma. Cancer. 2000;88:1781–7. [PubMed] [Google Scholar]
  5. Cao K, Ding K, Amelon RE, Du K. 4D modeling and Estimation of Respiratory Motion for Radiation Therapy. Springer: Biological and Medical Physics and Biomedical Engineering; 2013. [Google Scholar]
  6. Chao M, Xie Y, Moros EG, Le Qt, Xing L. Image-based modeling of tumor shrinkage in head and neck radiation therapy. Med Phys. 2010;37:2351–8. doi: 10.1118/1.3399872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Christensen GE, Song JH, Lu W, El Naqa I, Low DA. Tracking lung tissue motion and expansion/compression with inverse consistent image registration and spirometry. Medical Physics. 2007;34:2155–63. doi: 10.1118/1.2731029. [DOI] [PubMed] [Google Scholar]
  8. Chung MK, Worsley KJ, Paus T, Cherif C, Collins DL, Giedd JN, Rapoport JL, Evans AC. A Unified Statistical Approach to Deformation-Based Morphometry. NeuroImage. 2001;14:595–606. doi: 10.1006/nimg.2001.0862. [DOI] [PubMed] [Google Scholar]
  9. Dennis EL, Hua X, Villalon-Reina J, Moran LM, Kernan C, Babikian T, Mink R, Babbitt C, Johnson J, Giza CC, Thompson PM, Asarnow RF. Tensor-Based Morphometry Reveals Volumetric Deficits in Moderate Severe Pediatric Traumatic Brain Injury. J Neurotrauma. 2016;33:840–52. doi: 10.1089/neu.2015.4012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ding K, Bayouth JE, Buatti JM, Christensen GE, Reinhardt JM. 4DCT based measurement of changes in pulmonary function following a course of radiation therapy. Medical Physics. 2010;37:1261–72. doi: 10.1118/1.3312210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Diot Q, Kavanagh B, Vinogradskiy Y, Garg K, Gaspar L, Miften M. Lung deformations and radiation-induced regional lung collapse in patients treated with stereotactic body radiation therapy. Medical Physics. 2015;42:6477–87. doi: 10.1118/1.4932624. [DOI] [PubMed] [Google Scholar]
  12. Duan XF, Tang P, Yu ZT. Neoadjuvant chemoradiotherapy for resectable esophageal cancer: an in-depth study of randomized controlled trials and literature review. Cancer Biol Med. 2014;11:191–201. doi: 10.7497/j.issn.2095-3941.2014.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Edge SB, Compton CC. The American Joint Committee on Cancer: the 7th Edition of the AJCC Cancer Staging Manual and the Future of TNM. Annals of Surgical Oncology. 2010;17:1471–4. doi: 10.1245/s10434-010-0985-4. [DOI] [PubMed] [Google Scholar]
  14. Eisenhauer EA, Therasse P, Bogaerts J, Schwartz LH, Sargent D, Ford R, Dancey J, Arbuck S, Gwyther S, Mooney M, Rubinstein L, Shankar L, Dodd L, Kaplan R, Lacombe D, Verweij J. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1) Eur J Cancer. 2009;45:228–47. doi: 10.1016/j.ejca.2008.10.026. [DOI] [PubMed] [Google Scholar]
  15. Fuentes D, Contreras J, Yu J, He R, Castillo E, Castillo R, Guerrero T. Morphometry-based measurements of the structural response to whole-brain radiation. Int J Comput Assist Radiol Surg. 2015;10:393–401. doi: 10.1007/s11548-014-1128-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Galloway MM. Texture analysis using gray level run lengths. Computer Graphics and Image Processing. 1975;4:172–9. [Google Scholar]
  17. Geoffrey RO, Binsheng Z, Camelia SS, Michelle SG, Leonard PJ, Robert AL, Pingzhen G, Mark GK, Lawrence HS, Gregory JR. Variability of Lung Tumor Measurements on Repeat Computed Tomography Scans Taken Within 15 Minutes. Journal of Clinical Oncology. 2011;29:3114–9. doi: 10.1200/JCO.2010.33.7071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Griffith JF, Chan AC, Chow LT, Leung SF, Lam YH, Liang EY, Chung SC, Metreweli C. Assessing chemotherapy response of squamous cell oesophageal carcinoma with spiral CT. Br J Radiol. 1999;72:678–84. doi: 10.1259/bjr.72.859.10624325. [DOI] [PubMed] [Google Scholar]
  19. Haralick RM, Shanmugam K, Dinstein I. Textural Features for Image Classification. IEEE Transactions on Systems, Man, and Cybernetics. 1973;SMC-3:610–21. [Google Scholar]
  20. Hill DL, Batchelor PG, Holden M, Hawkes DJ. Medical image registration. Phys Med Biol. 2001;46:R1–45. doi: 10.1088/0031-9155/46/3/201. [DOI] [PubMed] [Google Scholar]
  21. Hua X, Leow AD, Levitt JG, Caplan R, Thompson PM, Toga AW. Detecting Brain Growth Patterns in Normal Children using Tensor-Based Morphometry. Human brain mapping. 2009;30:209–19. doi: 10.1002/hbm.20498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ibanez L, Schroeder W, Ng L. The ITK software guide. Insight Toolkit Kitware, Inc; 2003. [Google Scholar]
  23. Jones DR, Parker LA, Jr, Detterbeck FC, Egan TM. Inadequacy of computed tomography in assessing patients with esophageal carcinoma after induction chemoradiotherapy. Cancer. 1999;85:1026–32. doi: 10.1002/(sici)1097-0142(19990301)85:5<1026::aid-cncr3>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
  24. Kanai T, Kadoya N, Ito K, Onozato Y, Cho SY, Kishi K, Dobashi S, Umezawa R, Matsushita H, Takeda K, Jingu K. Evaluation of accuracy of B-spline transformation-based deformable image registration with different parameter settings for thoracic images. J Radiat Res. 2014;55:1163–70. doi: 10.1093/jrr/rru062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging. 2010;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
  26. Koshy M, Greenwald BD, Hausner P, Krasna MJ, Horiba N, Battafarano RJ, Burrows W, Suntharalingam M. Outcomes After Trimodality Therapy for Esophageal Cancer: The Impact of Histology on Failure Patterns. American Journal of Clinical Oncology. 2011;34:259–64. doi: 10.1097/COC.0b013e3181e841ce. [DOI] [PubMed] [Google Scholar]
  27. Kroep JR, Van Groeningen CJ, Cuesta MA, Craanen ME, Hoekstra OS, Comans EFI, Bloemena E, Hoekstra CJ, Golding RP, Twisk JWR, Peters GJ, Pinedo HM, Lammertsma AA. Positron Emission Tomography Using 2-Deoxy-2-[18F]-Fluoro-D-Glucose for Response Monitoring in Locally Advanced Gastroesophageal Cancer; A Comparison of Different Analytical Methods. Molecular Imaging and Biology. 2003;5:337–46. doi: 10.1016/j.mibio.2003.09.007. [DOI] [PubMed] [Google Scholar]
  28. Kurokawa Y, Shibata T, Ando N, Seki S, Mukaida H, Fukuda H. Which is the Optimal Response Criteria for Evaluating Preoperative Treatment in Esophageal Cancer: RECIST or Histology? Annals of Surgical Oncology. 2013;20:3009–14. doi: 10.1245/s10434-013-2946-1. [DOI] [PubMed] [Google Scholar]
  29. Lambin P, Rios-Velazquez E, Leijenaar R, Carvalho S, van Stiphout RGPM, Granton P, Zegers CML, Gillies R, Boellard R, Dekker A, Aerts HJWL. Radiomics: Extracting more information from medical images using advanced feature analysis. European journal of cancer (Oxford, England: 1990) 2012;48:441–6. doi: 10.1016/j.ejca.2011.11.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mandard AM, Dalibard F, Mandard JC, Marnay J, Henry-Amar M, Petiot JF, Roussel A, Jacob JH, Segol P, Samama G, Ollivier JM, Bonvalot S, Gignoux M. Pathologic assessment of tumor regression after preoperative chemoradiotherapy of esophageal carcinoma. Clinicopathologic correlations. Cancer. 1994;73:2680–6. doi: 10.1002/1097-0142(19940601)73:11<2680::aid-cncr2820731105>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
  31. Meyer CR, Armato SG, Fenimore CP, McLennan G, Bidaut LM, Barboriak DP, Gavrielides MA, Jackson EF, McNitt-Gray MF, Kinahan PE, Petrick N, Zhao B. Quantitative imaging to assess tumor response to therapy: common themes of measurement, truth data, and error sources. Transl Oncol. 2009;2:198–210. doi: 10.1593/tlo.09208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Michalski D, Huq MS, Bednarz G, Heron DE. The use of strain tensor to estimate thoracic tumors deformation. Medical Physics. 2017;41 doi: 10.1118/1.4884222. [DOI] [PubMed] [Google Scholar]
  33. Niedzielski J, Yang J, Zhang L, Martel M, Briere T, Gomez D, Court L. Development and QA of a Novel Framework to Quantify Normal Tissue Toxicity Using the Jacobian Map. Medical Physics. 2017;40:454–5. [Google Scholar]
  34. Ou Y, Weinstein SP, Conant EF, Englander S, Da X, Gaonkar B, Hsieh MK, Rosen M, DeMichele A, Davatzikos C, Kontos D. Deformable registration for quantifying longitudinal tumor changes during neoadjuvant chemotherapy. Magn Reson Med. 2015;73:2343–56. doi: 10.1002/mrm.25368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pagano M, Gauvreau K. Principles of biostatistics. Duxbury; 2000. [Google Scholar]
  36. Parmar C, Rios Velazquez E, Leijenaar R, Jermoumi M, Carvalho S, Mak RH, Mitra S, Shankar BU, Kikinis R, Haibe-Kains B, Lambin P, Aerts HJ. Robust Radiomics feature quantification using semiautomatic volumetric segmentation. PLoS ONE. 2014;9:e102107. doi: 10.1371/journal.pone.0102107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Qiao Y, Sun Z, Lelieveldt BPF, Staring M. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Springer International Publishing; 2015. pp. 297–304. Cham. vol Series. [Google Scholar]
  38. Reinhardt JM, Ding K, Cao K, Christensen GE, Hoffman EA, Bodas SV. Registration-based estimates of local lung tissue expansion compared to xenon-CT measures of specific ventilation. Med Image Anal. 2008;12:752–63. doi: 10.1016/j.media.2008.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rey D, Subsol G, Delingette H, Ayache N. Automatic detection and segmentation of evolving processes in 3D medical images: Application to multiple sclerosis. Med Image Anal. 2002;6:163–79. doi: 10.1016/s1361-8415(02)00056-7. [DOI] [PubMed] [Google Scholar]
  40. Riyahi-Alam S, Peroni M, Baroni G, Riboldi M. Regularization in deformable registration of biomedical images based on divergence and curl operators. Methods Inf Med. 2014;53:21–8. doi: 10.3414/ME12-01-0109. [DOI] [PubMed] [Google Scholar]
  41. RStudio T. RStudio: Integrated Development Environment for R. Boston, MA: RStudio, Inc; 2015. [Google Scholar]
  42. Sakamoto R, Mori S, Miller MI, Okada T, Togashi K. Detection of time-varying structures by large deformation diffeomorphic metric mapping to aid reading of high-resolution CT images of the lung. PLoS ONE. 2014;9:e85580. doi: 10.1371/journal.pone.0085580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sarkar S, Narayanan R, Park H, Ma B, Bland P H and Meyer C R 2008), vol. Series)
  44. Shamonin DP, Bron EE, Lelieveldt BP, Smits M, Klein S, Staring M. Fast parallel image registration on CPU and GPU for diagnostic classification of Alzheimer’s disease. Front Neuroinform. 2013;7:50. doi: 10.3389/fninf.2013.00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sharma MR, Maitland ML, Ratain MJ. RECIST: no longer the sharpest tool in the oncology clinical trials toolbox—point. Cancer Res. 2012;72:5145–9. doi: 10.1158/0008-5472.CAN-12-0058. discussion 50. [DOI] [PubMed] [Google Scholar]
  46. Shusharina N, Sharp G. Analytic regularization for landmark-based image registration. Phys Med Biol. 2012;57:1477–98. doi: 10.1088/0031-9155/57/6/1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Staal EFC, Van Velthuysen MF, Aleman BM, Cats A, JW VS. Pathological assessment of tumor response after neoadjuvant chemoradiotherapy for esophageal cancer. 2010 Gastrointestinal Cancers Symposium 2010 [Google Scholar]
  48. Tan M, Li Z, Qiu Y, McMeekin SD, Thai TC, Ding K, Moore KN, Liu H, Zheng B. A New Approach to Evaluate Drug Treatment Response of Ovarian Cancer Patients Based on Deformable Image Registration. IEEE Trans Med Imaging. 2016;35:316–25. doi: 10.1109/TMI.2015.2473823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tan S, Kligerman S, Chen W, Lu M, Kim G, Feigenberg S, D’Souza WD, Suntharalingam M, Lu W. Spatial-temporal [(1)(8)F]FDG-PET features for predicting pathologic response of esophageal cancer to neoadjuvant chemoradiation therapy. Int J Radiat Oncol Biol Phys. 2013;85:1375–82. doi: 10.1016/j.ijrobp.2012.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tang H, Foster NR, Grothey A, Ansell SM, Goldberg RM, Sargent DJ. Comparison of error rates in single-arm versus randomized phase II cancer clinical trials. J Clin Oncol. 2010;28:1936–41. doi: 10.1200/JCO.2009.25.5489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tang X. Texture information in run-length matrices. IEEE Trans Image Process. 1998;7:1602–9. doi: 10.1109/83.725367. [DOI] [PubMed] [Google Scholar]
  52. Thirion JP. Image matching as a diffusion process: an analogy with Maxwell’s demons. Med Image Anal. 1998;2:243–60. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
  53. Thirion JP, Calmon G. Deformation analysis to detect and quantify active lesions in three-dimensional medical image sequences. IEEE Trans Med Imaging. 1999;18:429–41. doi: 10.1109/42.774170. [DOI] [PubMed] [Google Scholar]
  54. van Heijl M, Phoa SS, van Berge Henegouwen MI, Omloo JM, Mearadji BM, Sloof GW, Bossuyt PM, Hulshof MC, Richel DJ, Bergman JJ, Ten Kate FJ, Stoker J, van Lanschot JJ. Accuracy and reproducibility of 3D-CT measurements for early response assessment of chemoradiotherapy in patients with oesophageal cancer. Eur J Surg Oncol. 2011;37:1064–71. doi: 10.1016/j.ejso.2011.09.004. [DOI] [PubMed] [Google Scholar]
  55. van Rossum PS, Xu C, Fried DV, Goense L, Court LE, Lin SH. The emerging field of radiomics in esophageal cancer: current evidence and future potential. Translational Cancer Research. 2016;5:410–23. doi: 10.21037/tcr.2016.06.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Westerterp M, van Westreenen HL, Reitsma JB, Hoekstra OS, Stoker J, Fockens P, Jager PL, Van Eck-Smit BL, Plukker JT, van Lanschot JJ, Sloof GW. Esophageal cancer: CT, endoscopic US, and FDG PET for assessment of response to neoadjuvant therapy–systematic review. Radiology. 2005;236:841–51. doi: 10.1148/radiol.2363041042. [DOI] [PubMed] [Google Scholar]
  57. Xiaoou T. Texture information in run-length matrices. IEEE Transactions on Image Processing. 1998;7:1602–9. doi: 10.1109/83.725367. [DOI] [PubMed] [Google Scholar]
  58. Yamashita H, Omori M, Okuma K, Kobayashi R, Igaki H, Nakagawa K. Longitudinal Assessments of Quality of Life and Late Toxicities Before and After Definitive Chemoradiation for Esophageal Cancer. Japanese Journal of Clinical Oncology. 2014;44:78–84. doi: 10.1093/jjco/hyt170. [DOI] [PubMed] [Google Scholar]
  59. Yanagawa M, Tatsumi M, Miyata H, Morii E, Tomiyama N, Watabe T, Isohashi K, Kato H, Shimosegawa E, Yamasaki M, Mori M, Doki Y, Hatazawa J. Evaluation of response to neoadjuvant chemotherapy for esophageal cancer: PET response criteria in solid tumors versus response evaluation criteria in solid tumors. J Nucl Med. 2012;53:872–80. doi: 10.2967/jnumed.111.098699. [DOI] [PubMed] [Google Scholar]
  60. Zhang H, Tan S, Chen W, Kligerman S, Kim G, D’Souza WD, Suntharalingam M, Lu W. Modeling Pathologic Response of Esophageal Cancer to Chemoradiotherapy Using Spatial-Temporal (18)F-FDG PET Features, Clinical Parameters, and Demographics. International journal of radiation oncology, biology, physics. 2014;88 doi: 10.1016/j.ijrobp.2013.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

PMBaacd22_supplementarymaterial.pdf
NIHMS1500715-supplement-PMBaacd22_supplementarymaterial_pdf.pdf (653.9KB, pdf)

RESOURCES