Abstract
Fiber ball imaging (FBI) provides a means of calculating the fiber orientation density function (fODF) in white matter from diffusion MRI (dMRI) data obtained over a spherical shell with a b-value of about 4000 s/mm2 or higher. By supplementing this FBI-derived fODF with dMRI data acquired for two lower b-value shells, it is shown that several microstructural parameters may be estimated, including the axonal water fraction (AWF) and the intrinsic intra-axonal diffusivity. This fiber ball white matter (FBWM) modeling method is demonstrated for dMRI data acquired from healthy volunteers, and the results are compared with those of the white matter tract integrity (WMTI) method. Both the AWF and the intra-axonal diffusivity obtained with FBWM are found to be significantly larger than for WMTI, with the FBWM values for the intra-axonal diffusivity being more consistent with recent results obtained using isotropic diffusion weighting. An important practical advantage of FBWM is that the only nonlinear fitting required is the minimization of a cost function with just a single free parameter, which facilitates the implementation of efficient and robust numerical routines.
Keywords: fiber ball, white matter tract integrity, axonal water fraction, intra-axonal diffusivity, diffusion MRI, brain microstructure
1. Introduction
Diffusion MRI (dMRI) is widely applied as a tool for investigating brain microstructure in vivo (Le Bihan and Johansen-Berg, 2012). However, determining specific microstructural properties from measured dMRI data is challenging due to the intricacies of water diffusion within the complex cytoarchitecture of brain tissue (Le Bihan and Iima, 2015). This has led to an assortment of “tissue modeling” methods being proposed for dMRI, which are still being actively developed and evaluated (Alexander et al., 2017; Ferizi et al., 2014; Jelescu and Budde, 2017; Novikov et al., 2016; Panagiotaki et al., 2012; Reisert et al., 2017; Yablonskiy and Sukstanskii, 2010).
A common difficulty associated with dMRI tissue models is managing the multiple local optima that often arise in nonlinear fitting algorithms with several free parameters, which adds to numerical computation times and may increase sensitivity to noise and imaging artifacts (Harms et al., 2017; Jelescu et al., 2016a; Novikov et al., 2016; Novikov et al., 2018). In addition, estimating certain microstructural parameters with good accuracy and precision has proven problematic. This is notably true for the intrinsic intra-axonal diffusivity (Da), with predictions from different approaches varying by over a factor of two (Jelescu et al., 2016a; Novikov et al., 2018; Jensen et al., 2017). Here we present a dMRI modeling method based on fiber ball imaging (FBI) (Jensen et al., 2016) intended to ameliorate these issues.
FBI is closely related to q-ball imaging (Tuch, 2004) and yields estimates for the fiber orientation density function (fODF) in white matter from high angular resolution diffusion imaging (HARDI) data, by employing b-values typically in the range of 4000 to 6000 s/mm2 (Jensen et al., 2016; McKinnon et al., 2017). It can also be used to calculate several microstructural properties associated with axonal fiber bundles. An advantage of FBI is that the core post-processing step is a straightforward linear transformation of the dMRI signal data that avoids the complications of nonlinear fitting.
In this study, we demonstrate how to augment FBI with lower b-value dMRI data in order to estimate several additional parameters, including Da, the mean extra-axonal diffusivity ( ), and the axonal water fraction (AWF). While determining these extra quantities does require nonlinear fitting, the proposed algorithm involves the minimization of a cost function having only a single free parameter. This allows the global optimum to be found robustly and efficiently.
This approach differs markedly from the conventional tactic of directly fitting the signal model corresponding to the assumed microstructural framework (i.e., the tissue model) to dMRI signal data, which typically leads to a cost function with multiple adjustable parameters and the aforementioned computational challenges. Instead, we regard the outputs of the FBI analysis as fixed inputs upon which the cost function is built. Similarly, we also use the diffusion tensor, obtained by standard means from the lower b-value dMRI data, as a fixed input. In this way, the number of free parameters that need to be determined by nonlinear optimization is reduced to one, resulting in a relatively simple numerical procedure.
A principal motivation for this fiber ball white matter (FBWM) modeling approach is to improve upon the white matter tract integrity (WMTI) method (Fieremans et al., 2011; Jelescu et al., 2016b), which yields predictions for the same basic physical quantities. An advantage of WMTI is its simple computational algorithm that uses only comparatively low b-value dMRI data. However, WMTI assumes all axons within any given voxel to be aligned in approximately the same direction, which may be a significant source of error particularly in crossing fiber regions. The FBWM approach overcomes this limitation by employing the measured fODF from FBI rather than presuming a specific geometrical arrangement for the axons. In order to investigate the extent to which FBWM and WMTI lead to different predictions, we utilize experimental results obtained from three healthy volunteers.
2. Theory
2.1. Signal Model
We assume the intra-axonal and extra-axonal spaces can be treated as separate compartments, which requires the intra-axonal water exchange time to be large in comparison to the diffusion time for the dMRI sequence. Although this exchange rate is not known with high precision, it has been estimated to be on the order of seconds (Nilsson et al., 2013), which is indeed long relative to typical dMRI diffusion times. In addition, we neglect the dMRI signal from myelin water. Myelin water has a T2 of about 10–20 ms (MacKay and Laule, 2016), so the myelin water signal will be suppressed by over a factor of 100 for typical clinical scanner dMRI echo times of about 100 ms.
For the intra-axonal space, we idealize axons as thin, straight cylinders, which implies an intra-axonal dMRI signal of the form
| (1) |
where f is the AWF, S0 is the signal without diffusion weighting, b is the b-value for the dMRI sequence, n is the diffusion encoding direction unit vector, and F(u) is the fODF as a function of a unit vector u that indicates the axon orientation. The integral in Eq. (1) is taken over all possible axon orientations, and the fODF is normalized so that
| (2) |
This corresponds to the widely used “stick” model for axons (Behrens et al., 2003, Ferizi et al., 2014; Kaden et al., 2016; Kroenke et al., 2004; Jespersen et al., 2007; Jespersen et al., 2010; Novikov et al., 2016; Panagiotaki et al., 2012; Yablonskiy and Sukstanskii, 2010; Veraart et al., 2016a; Veraart et al., 2017; Zhang et al., 2012), and it is also employed in FBI (Jensen et al., 2016). However, here we adopt a different normalization for the fODF than used in our previous work (Jensen et al., 2016), as this is more convenient for our proposed FBWM modeling approach.
For the extra-axonal space, we treat water diffusion as Gaussian so that the signal in a diffusion encoding direction n is given by
| (3) |
where De is the extra-axonal diffusion tensor. This same model has been utilized by Jespersen and coworkers (Jespersen et al., 2010) and should be appropriate for b-values small enough so that the intrinsic kurtosis of the extra-axonal space can be neglected. As we shall argue, for FBWM the details of the extra-axonal signal at high b-values should be relatively unimportant, since the intra-axonal signal is then much larger and dominates the full signal, which is simply the sum of Sa and Se.
2.2. Fiber ball imaging
FBI requires HARDI data for a single spherical b-value shell with a large number of uniformly distributed diffusion encoding directions. The chosen b-value, bFBI, should be high enough to strongly suppress the dMRI signal from the extra-axonal space, but not so big as to induce a significant noise bias. In practice, bFBI would usually be in the range of 4000–6000 s/mm2, depending on scanner performance and the desired spatial resolution (Jensen et al., 2016; McKinnon et al., 2017).
From the HARDI data, one can construct a spherical harmonic expansion for the dMRI signal on the b-value shell as
| (4) |
where S(b,n) is the signal magnitude as a function of the b-value and the diffusion encoding direction, are the expansion coefficients, are the spherical harmonics, and (θ, φ) are the spherical angles corresponding to n. In Equation (4), we assume the convention (Jackson, 1975)
| (5) |
where
| (6) |
is the associated Legendre function. The expansion coefficients for odd l may be set to zero, since reflection symmetry implies S (b, −n) = S (b, n).
The central result of FBI is then that the fODF is approximately given by (Jensen et al., 2016)
| (7) |
where
| (8) |
with being a Legendre polynomial and
| (9) |
In Eq. (8), D0 represents an upper bound on Da, which would usually be chosen as either infinity or as the free water diffusivity at body temperature of about 3.0 µm2/ms (Holz et al., 2000), while in Eq. (9), 1F1 is the confluent hypergeometric function and Γ is the Gamma function. One may verify that Eq. (7) is normalized in accord with Eq. (2). For D0 = ∞, Eq. (8) simplifies to
| (10) |
since g2l(∞) = 1. In this case, the fODF is proportional to the inverse Funk transform (Bailey et al., 2003) of the dMRI signal for the b = bFBI HARDI shell. In practice, the difference between using a D0 of infinity or 3.0 µm2/ms is typically small, with the fODF being slightly sharper with D0 = 3.0 µm2/ms. In general, this parameter becomes more irrelevant as bFBI is increased (Jensen et al., 2016).
From Eq. (7), one may show that the diffusion tensor for the intra-axonal compartment, within the stick model approximation, is
| (11) |
with
| (12) |
Observe that tr(A) =1. The tensor A is guaranteed to be real, since as follows from the requirement that the fODF be real. Even though Da is not known a priori, Eqs. (11) and (12) are sufficient to calculate the fractional anisotropy (FA) for the intra-axonal space, as well as other related dimensionless properties of Da. More explicitly, this FA for the axons (FAA) is given by
| (13) |
The derivations of Eqs. (11)–(13) are discussed in the Appendix. FBI also estimates the parameter as (Jensen et al., 2016)
| (14) |
The FAA is simply related to the axonal dispersion metric by , which may be used to calculate a characteristic dispersion angle for the fODF (Novikov et al., 2018; Veraart et al., 2017).
2.3. Expressions for intra-axonal and extra-axonal signals in terms of AWF
By combining Eqs. (1) and (7), one can show that the spherical harmonic expansion for intra-axonal signal may be expressed as (Jensen et al., 2016)
| (15) |
A notable feature of the spherical harmonic expansion in Eq. (15) is that the only unknown parameter is f, as all the other quantities are determined by FBI. This contrasts with several other white matter modeling approaches that utilize multiple free parameters in order to represent the intra-axonal signal (Jespersen et al., 2007; Jespersen et al., 2010; Novikov et al., 2016; Veraart et al., 2017; Zhang et al., 2012). Consistency of Eqs. (4), (14), and (15) requires that
| (16) |
where erf indicates the error function; this approximation holds to better than 0.1% provided bFBI Da > 5.5.
Now let us assume that, in addition to the HARDI b-value shell acquired for FBI, one also obtains low b-value data sufficient for estimating the total diffusion tensor, D, as is conventionally done with either diffusion tensor imaging (DTI) (Basser and Jones, 2002) or diffusional kurtosis imaging (DKI) (Jensen and Helpern, 2010). The diffusion tensor for the extra-axonal space, De, is related to D and Da by
| (17) |
which implies
| (18) |
With the help of Eq. (11) and the definition of ζ, this leads to
| (19) |
Except for the AWF, all the quantities on the right-hand side of Eq. (19) can be directly calculated from either FBI or low b-value dMRI data. For fitting purposes, we can therefore regard De as only a function of f. This also applies to the extra-axonal signal of Eq. (3), which is determined by De and f.
2.4. Cost function
The dMRI signal for the full FBWM model is
| (20) |
As we have seen, both Sa and Se can be thought of as functions of the AWF, given the information provided by FBI and the total diffusion tensor. Therefore, we may consider the total signal Smod to also be a function of the AWF.
In order to determine the AWF, we introduce the cost function
| (21) |
where Sexp (b, n) is the magnitude of the measured dMRI signal as a function of b-value and diffusion encoding direction, M is the number of b-value shells, Ni is the number of diffusion encoding directions for the ith shell, bi is the b-value for the ith shell, and ni,j is the jth diffusion encoding direction for the ith shell. Normally, one would set bM = bFBI. This cost function represents a weighted root-mean-square difference between the model and experimental signals divided by the signal for b = 0, with the weight factors depending on the number of directions for each shell. The “best” estimate for the AWF is then defined as the value of f that minimizes C.
By construction, we expect the model and experimental signals to agree fairly well for both low and high b-values, even if f is only roughly correct. Thus in order to predict the AWF with useful precision, shells having intermediate b-values should be included in Eq. (21). By intermediate, we mean b-values larger than the range for which the signal’s b-value dependence is primarily governed by the total diffusion tensor (as assumed for DTI), but smaller than the b-values for which the intra-axonal signal predominates (as assumed for FBI). In brain, we expect such intermediate b-values to be roughly 2000 to 3000 s/mm2, corresponding to the smallest b-values with readily apparent non-Gaussian diffusion effects in the dMRI signal (Clark and Le Bihan, 2000; Jensen and Helpern, 2010). A minimal FBWM imaging protocol would, therefore, have three nonzero b-value shells, with low, medium, and large b-values.
2.5. Microstructural parameters
Once the AWF has been determined by minimizing C, then several other microstructural parameters are easily calculated. In particular, the intrinsic intra-axonal diffusivity can be found from
| (22) |
which follows directly from the definition of ζ, and the mean extra-axonal diffusivity is given by
| (23) |
where D̅ = tr(D) / 3 is the mean diffusivity (MD), which follows from Eq. (19). If the eigenvalues of De are λe,1 ≥ λe,2 ≥ λe,3, then one can also estimate the axial extra-axonal diffusivity as
| (24) |
and the radial extra-axonal diffusivity as
| (25) |
3. Methods
3.1. Imaging
Diffusion weighted imaging (DWI) data were acquired for three healthy volunteers on a 3T Prisma MRI scanner (Siemens Healthcare, Erlangen, Germany) under a protocol approved by the Medical University of South Carolina institutional review board. Using a twice-refocused echo planar imaging pulse sequence to minimize eddy current distortion (Reese et al., 2003), 42 axial brain slices with 3.0 mm slice thickness and no interslice gap were obtained. The b-values were 0, 1000, 2000, and 6000 s/mm2. For the b=1000 and 2000 s/mm2 shells, 30 vendor-supplied diffusion encoding directions were employed, while 256 diffusion encoding directions were acquired for the b =6000 s/mm2 (HARDI) shell. For the b= 0 images, 25 separate signal excitations were utilized for each slice. The HARDI shell had a large number of directions since these data were applied in estimating the spherical harmonic expansion of Eq. (4). The echo time was 98 ms, the repetition time was 5100 ms, the field of view was 222×222 mm2, and the acquisition matrix was 74×74, resulting in isotropic voxels with dimensions of 3×3×3 mm3. The data were acquired with an in-plane parallel imaging factor of 2 and a multiband acceleration factor of 2, using a bandwidth of 1438 Hz/pixel. Partial Fourier encoding was not employed. This entire DWI scan protocol was then repeated, in the same scan session, in order to allow the reproducibility of our parameter estimates to be tested. The combined scan time for both runs was 59 min 20 s.
For anatomical reference, T1-weighted (MPRAGE) images were also acquired with isotropic 1×1×1 mm3 voxels for 192 slices. The echo time was 2.26 ms, the inversion time was 900 ms, the repetition time was 2300 ms, and the total scan time was 5 min 21 s.
3.2. Data analysis
All DWI data were denoised using a principal components analysis approach (Veraart et al., 2016b), and the method of moments (Gudbjartsson and Patz, 1995) was applied to reduce noise bias. Subsequently, a Gibbs ringing correction was employed (Kellner et al., 2015), and all DWI images were co-registered to correct for any subject motion.
The DWI images for b =0, 1000 and 2000 s/mm2 were used to calculate the diffusion tensor with Diffusional Kurtosis Estimator (https://www.nitrc.org/projects/dke/) in order to estimate the total diffusion tensor D on a voxel-by-voxel basis (Tabesh et al., 2011). This DKI-based approach was employed instead of DTI in order to improve the accuracy of the tensor calculation (Veraart et al., 2011). The spherical harmonic coefficients of Eq. (4) were determined with linear least squares from the b=0 and HARDI data. For our main results, all harmonics up to degree l =6 were kept in Eq. (4), but we also considered other maximum degrees in auxiliary calculations aimed at investigating the impact of this cutoff. The spherical harmonic coefficients for the fODF of Eq. (8) were calculated with D0 = 3.0 µm2/ms, and the microstructural parameter ζ was obtained from Eq. (14).
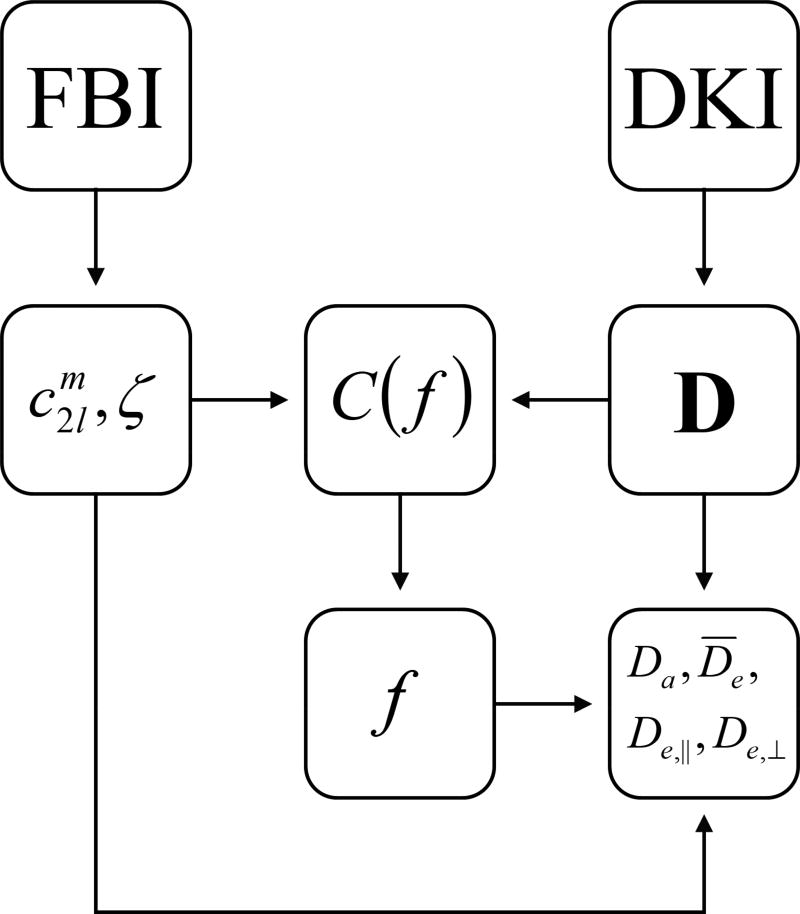
In order to estimate the AWF, the cost function C of Eq. (21) was evaluated in each voxel for 100 equally spaced points between f = 0 and f = 1. For our DWI protocol, we have M = 3, N1 = N2 = 30, N3 = 256, b1 = 1000 s/mm2, b2 = 2000 s/mm2, and b3 = bFBI = 6000 s/mm2. For each value of f, the eigenvalues of De were calculated with the help of Eq. (18). If any of these eigenvalues were less than zero for a particular f, then that value of the AWF was excluded as being unphysical. The optimal AWF was taken as the f value that minimized C, among all those that were not excluded. From the optimal AWF, parametric maps of Da, D̅e, De,‖, and De,⊥ were obtained by using Eqs. (22)–(25). A flow chart outlining the FBWM data analysis procedure is shown in Fig. 1. To process a full whole brain dataset for one subject required about 12.5 min on an iMac computer with a 4 GHz Intel Core i7 CPU.
Figure 1.
Flow chart showing the data analysis pipeline for FBWM. The parameters and ζ are determined with FBI, while the total diffusion tensor D is found with DKI. The cost function C(f) is then constructed from , ζ, and D. By minimizing C(f), one obtains a best estimate for the AWF. Finally, the AWF, together with the FBI and DKI results, is used to calculate the additional microstructural parameters of Da, , De,‖, and De,⊥.
For comparison, the DWI data for b=0, 1000 and 2000 s/mm2 were used with Diffusional Kurtosis Estimator to obtain standard DKI maps of MD, FA, mean kurtosis (MK), axial diffusivity (D‖), and radial diffusivity (D⊥). These same data were also applied to determine ζ, f, Da, D̅e, De,‖, and De,⊥ following the WMTI procedure of Fieremans and coworkers (Fieremans et al., 2011). The parametric maps for all diffusion measures were skull-stripped, and a white matter mask was defined as all brain voxels with MK ≥ 1.0 (Yang et al., 2013). The white matter mask was based on MK rather than FA, since the FA can be low in white matter regions with extensive fiber crossing.
To test reproducibility, the two scans for each subject were analyzed independently. The absolute percent difference between the parameter values from Run 1 and Run 2 were then calculated for each white matter voxel. From the full set of these voxels, median absolute percent differences were found for each of the three subjects. We used the median rather than the average difference in order to reduce the effect of outliers, as may arise from imaging artifacts and co-registration errors. In calculating overall means for the various estimated diffusion parameters, all the white matter voxels from both runs were pooled for each subject, with standard deviations being used to indicate the spread in values.
Finally, to compare the FBI and FBWM predictions to those obtained with WMTI, average values were calculated for each parameter by binning all white matter voxels for all three subjects according to FA, with a bin size of 0.1. Even though the application of the WMTI is only recommended for voxels with FA values larger than 0.3 to 0.4 (Fieremans et al., 2011; Jensen et al. 2017), we determined all measures for FA values ranging from 0.15 to 0.75 for the sake of completeness. The validity of the FBI and FBWM estimates is not expected to depend significantly on FA.
3.3. Numerical Simulations
In order to investigate the effect of signal noise on our parameter estimates, we conducted numerical simulations by adding varying amounts of Rician noise to a “ground truth” dataset constructed from our signal model with the model parameters set to those estimated for one of our in vivo scans (Subject 1, Run 1). Using a signal-to-noise ratio (SNR) ratio of 50, we also numerically tested the impact of employing different numbers of diffusion encoding directions (30, 64, 128, 256) for the b =6000 s/mm2 HARDI shell, while keeping the number of directions for b =1000 and 2000 s/mm2 fixed at 30. In performing the simulations, we utilized the same data analysis pipeline as for the in vivo data, except that co-registration was not performed (since there was no motion to correct) and denoising was skipped in a subset of the simulations in order to demonstrate the effect of this processing step.
4. Results
4.1. In vivo
Our denoising algorithm (Veraart et al., 2016b) generated voxelwise noise maps, which were used to estimate the average SNR in white matter. For the b=0 images, the average SNR over all scans was 59 ± 9, while for the b=6000 s/mm2 images, the average SNR was 15 ± 5. This latter number was obtained by first averaging the b=6000 s/mm2 images over all of the diffusion encoding directions prior to dividing by the noise.
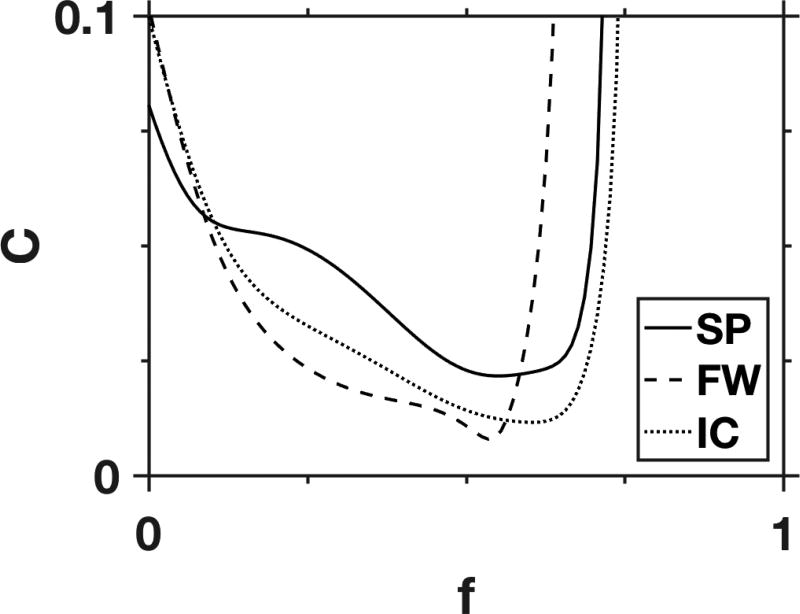
Representative examples of the cost function C of Eq. (21) are shown in Fig. 2, for three different white matter voxels. In most cases, the cost function has a quasi-parabolic shape with a minimum skewed toward higher AWF values. Only 10.4% of white matter voxels had multiple local minima out of a total of 16,184 for all three subjects. In any case, finding the global minima was not problematic due to our exhaustive grid search strategy.
Figure 2.
Representative FBWM cost functions for three individual voxels from the splenium of the corpus callosum (SP), frontal white matter (FW), and the internal capsule (IC). The only adjustable parameter in the cost function is the AWF, since all other quantities are fixed with information supplied by DKI and FBI. For most white matter voxels, the cost function has a single local minimum, as illustrated here.
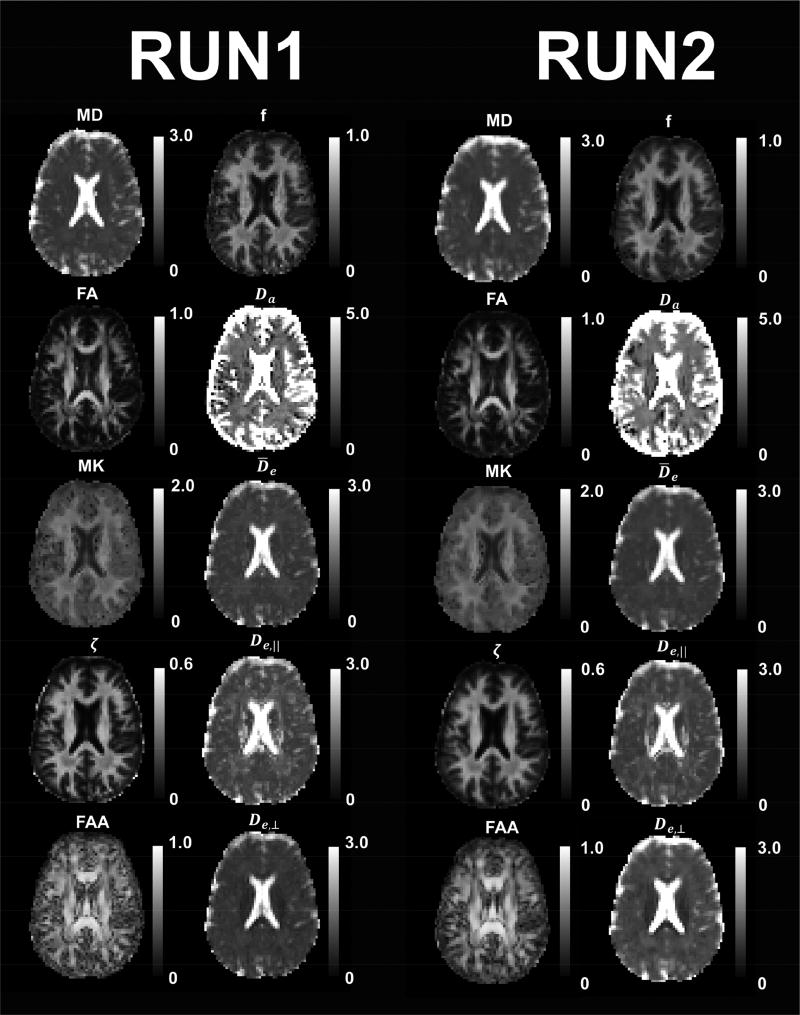
Parametric maps of selected diffusion parameters for one anatomical slice from Subject 1 are given in Fig. 3. The Run 1 and Run 2 maps are derived from independent datasets obtained during a single scan session. The similarity of the corresponding FBWM metrics within white matter regions demonstrates the minimal effect of signal noise (after denoising) on the reproducibility of the method. Outside of white matter, both the FBI and FBWM values have no clear physical meanings, even though our post-processing algorithms generate results for all voxels.
Figure 3.
Parametric maps for selected diffusion measures from a single anatomical slice for Subject 1. Two independent datasets (Runs 1 and 2) were acquired within a single scan session in order to test reproducibility. The parameters in Columns 1 and 3 were calculated with DKI (MD, FA, MK) and FBI (ζ, FAA), while the parameters in Columns 2 and 4 were calculated with FBWM. The corresponding maps for Run 1 and Run 2 are fairly similar for all metrics, indicating that they are not overly sensitive to signal noise. The calibration bars for the diffusivities (MD, Da, , De,‖, De,⊥) are in units of µm2/ms, and the calibration bar for ζ is in units of ms1/2/ µm, while all other quantities (FA, MK, FAA, f) are dimensionless. The FBI and FBWM results are only meaningful in white matter regions.
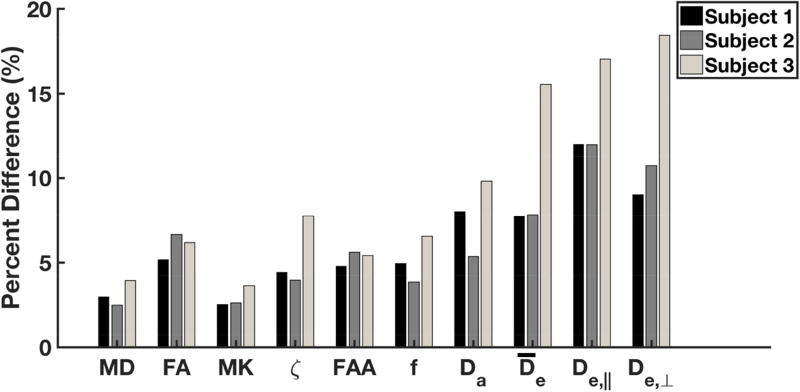
The absolute percent differences of all white matter voxels from each subject, for the same set of diffusion parameters as in Fig. 3, are plotted in Fig. 4. For Subjects 1 and 2, the voxelwise reproducibility is about 10% or better for all the FBWM measures. For Subject 3, the FBWM measures have a reproducibility of about 20% or better. The axial extra-axonal diffusivity, De,‖, has the highest degree of variability for Subjects 1 and 2, while De,⊥ has the highest variability for Subject 3.
Figure 4.
Median absolute percent difference between Runs 1 and 2 for selected diffusion measures in white matter. These were calculated for all three subjects on a voxelwise basis by using all voxels considered as white matter (i.e., MK ≥ 1). In most cases, the percent difference is about 10% or less. However, the extra-axonal diffusivites ( , De,‖, De,⊥) differed by up to 20% for Subject 3. All quantities were obtained with either DKI (MD, FA, MK), FBI (ζ, FAA), or FBWM (f, Da, , De,‖, De,⊥).
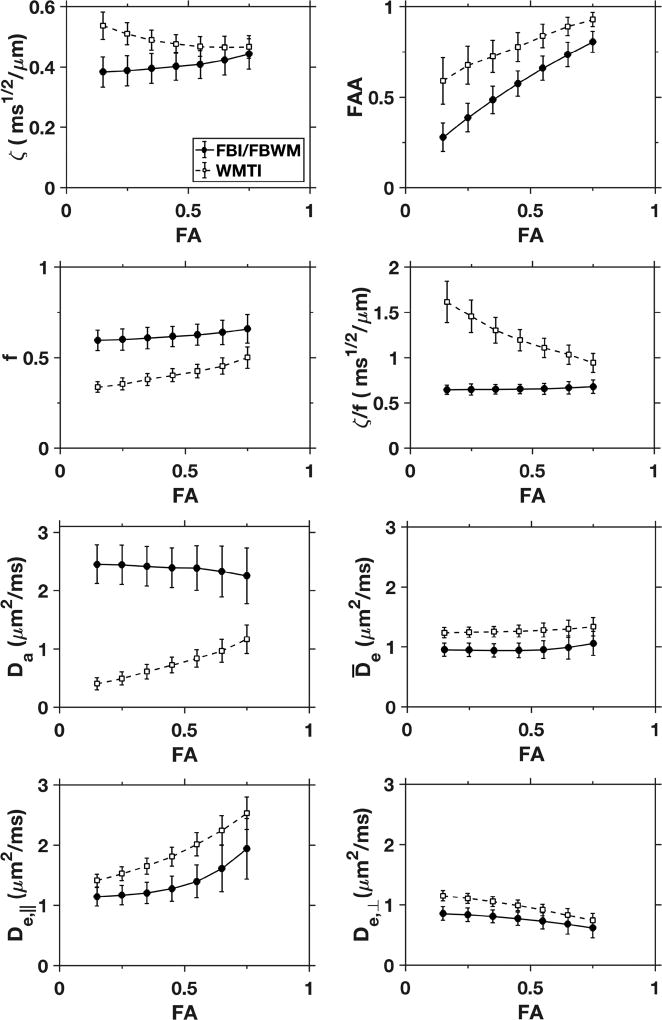
In Fig. 5, FBI, FBWM, and WMTI parameter estimates are plotted as functions of the FA. The ζ values are relatively close for both FBI and WMTI, especially at higher FA, which confirms the findings of a prior study (Jensen et al., 2017). In addition, the FBWM and WMTI averages for D̅e and De,⊥ are comparable. For FAA, f, and De,‖, WMTI shows similar trends as FBI/FBWM, but the numerical values are quite different. Importantly, the estimates for f found with FBWM are higher than the WMTI values by about 20% or more. Even more striking, Da as predicted with FBWM is over twice that from WMTI for all FA values. This discrepancy is a manifestation of the well-known difficulty associated with estimating Da accurately (Jelescu et al., 2016a; Novikov et al., 2018). Finally, Fig. 5 also shows that the ratio ζ / f for FBI/FBWM (but not for WMTI) to be nearly constant across the full range of FA, with tight error bars. This suggests a high correlation between ζ and f, as estimated with FBI/FBWM, and indeed their voxelwise Pearson correlation coefficient is r = 0.78.
Figure 5.
Selected diffusion measures versus FA. All white matter voxels for all three subjects and both imaging runs were pooled. The solid data points are averages calculated with either FBI (ζ, FAA) or FBWM (f, ζ / f, Da, , De,‖, De,⊥), while the open data points are all averages calculated with WMTI. The error bars indicate standard deviations. For the FBI/FBWM parameters, Da, , and ζ / f vary little with FA, but an FA dependence is discernible for the other metrics. The WMTI averages are relatively close to the FBI/FBWM values for ζ, , and De,⊥, at least for FA > 0.5 where the assumptions underlying WMTI are better justified. Otherwise substantial differences are apparent. In particular, the WMTI estimates for Da are much smaller than the FBWM estimates over the full range of FA.
Average values for the DKI-, FBI-, and FBWM-derived measures over all white matter voxels (both runs) for each of the three subjects are listed in Table 1. All the parameters are relatively consistent across subjects. For the FBWM-derived metrics, the coefficients of variation range from 0.08 for the AWF in Subject 1 to 0.27 for the axial extra-axonal diffusivity in Subject 3. Note that the axial diffusivity, D‖, obtained from the diffusion tensor is very similar to the axial extra-axonal diffusivity but that the radial diffusivity, D⊥, from the diffusion tensor is smaller than the radial extra-axonal diffusivity.
Table 1.
Mean values (± std. dev.) of diffusion parameters in white matter as estimated with DKI, FBI, and FBWM.
| Parameter | Subject 1 | Subject 2 | Subject 3 |
|---|---|---|---|
| MD [µm2/ms]* | 0.85 ± 0.06 | 0.87 ± 0.08 | 0.85 ± 0.08 |
| FA* | 0.46 ± 0.14 | 0.44 ± 0.14 | 0.46 ± 0.14 |
| MK* | 1.09 ± 0.06 | 1.14 ± 0.08 | 1.13 ± 0.08 |
| D‖ * | 1.31 ± 0.21 | 1.32 ± 0.23 | 1.32 ± 0.26 |
| D⊥ * | 0.62 ± 0.10 | 0.64 ± 0.12 | 0.61 ± 0.11 |
| ζ [ms1/2/ µm]† | 0.40 ± 0.04 | 0.40 ± 0.05 | 0.42 ± 0.05 |
| FAA† | 0.57 ± 0.14 | 0.56± 0.14 | 0.58 ± 0.15 |
| f ‡ | 0.60 ± 0.05 | 0.63 ± 0.06 | 0.62 ± 0.07 |
| Da [µm2/ms] ‡ | 2.36 ± 0.31 | 2.50 ± 0.35 | 2.23 ± 0.40 |
| D̄e [µm2/ms] ‡ | 0.95 ± 0.09 | 0.93 ± 0.13 | 1.02 ± 0.18 |
| De,‖ [µm2/ms] ‡ | 1.31 ± 0.26 | 1.29 ± 0.32 | 1.46 ± 0.39 |
| De,⊥ [µm2/ms] ‡ | 0.76 ± 0.11 | 0.75 ± 0.14 | 0.80 ± 0.16 |
Estimated with DKI.
Estimated with FBI.
Estimated with FBWM.
In our model, the principal eigenvectors for the total diffusion tensor D and the extra-axonal diffusion tensor De need not be parallel, although on physical grounds one might expect them to be approximately parallel in most white matter voxels. For our data the average absolute angle between the two eigenvectors was 21° ± 21°. Moreover, for about 14% of the white matter voxels, the angle exceeded 45°.
The above FBWM results were calculated by including all spherical harmonics in Eq. (4) up to and including the degree l = 6. In order to investigate how varying this maximum degree affects the number of local minima, we also calculated the percentage of white matter voxels, across all subjects, with more than one local minima for maximum degrees of l = 2, 4, and 8, obtaining 45.3%, 13.6%, and 9.6%, respectively. This should be compared to the 10.4% for l = 6, as previously stated. Thus increasing the degree cutoff tends to reduce the number of voxels with multiple local minima.
4.2. Simulations
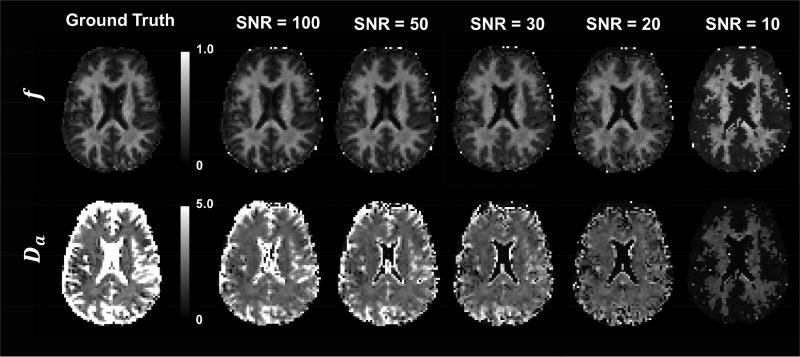
Ground truth maps of a single anatomical slice for the parameters f and Da are given in Fig. 6 together with the corresponding maps determined with FBWM using different simulated noise levels. The full brain slice is shown, even though FBWM is only expected to yield meaningful results for white matter. Within white matter regions, the FBWM estimates agree fairly well with the ground truth values for SNR of 20 and above, but large discrepancies are apparent for SNR = 10. Here the SNR is defined with respect to the b=0 images.
Figure 6.
Numerical simulations of the effect of signal noise on parametric maps of the AWF and the intrinsic intra-axonal diffusivity for a single anatomical slice. The ground truth data are based on the signal model of Eq. (20) together with the FBWM fits for Subject 1 (same slice as in Fig. 3). Rician noise was added to create SNR values ranging from 10 to 100 (defined with respect to the b = 0 images), and the simulated data were processed according to our standard analysis pipeline. In white matter regions, where the FBWM approach is expected to apply, the parameter values are fairly insensitive to the added noise, for SNR values of 20 and above. The calibration bar for Da is in units of µm2/ms, while that for f is dimensionless.
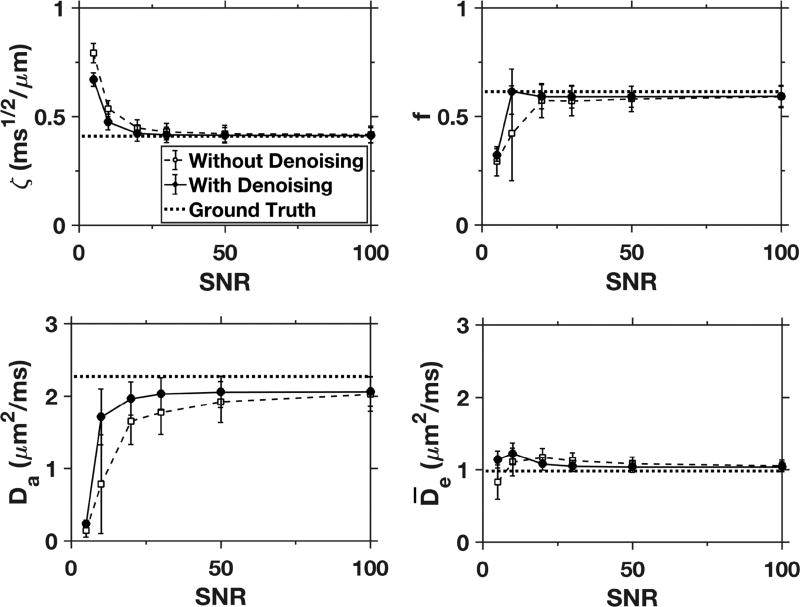
Mean values for ζ, f, Da, and from the simulations are plotted in Fig. 7 as a function of the SNR. The estimates are averages over all 4608 white matter voxels in our simulated dataset. The solid line shows the results for our full analysis pipeline, while the dashed line shows the effect of skipping the denoising step. With denoising, the parameter estimates are close to the ground truth values when the SNR is 20 or higher, but without denoising larger errors are apparent especially for Da. The small underestimation of Da at an SNR of 100 is primarily due to systematic errors in the calculation of the diffusion tensor from DKI, which propagate into the cost function.
Figure 7.
Mean values of ζ, f, Da, and over all white matter voxels for simulated data with varying amounts of added noise (solid data points). The ground truth values are indicated by the dotted lines, and the open data points give the simulated results with the denoising step omitted from the processing pipeline. The error bars indicate standard deviations. With denoising, the FBI/FBWM estimates agree well with the ground truth values for SNRs of 20 and above. Without denoising, both accuracy and precision are noticeably reduced, particularly for Da.
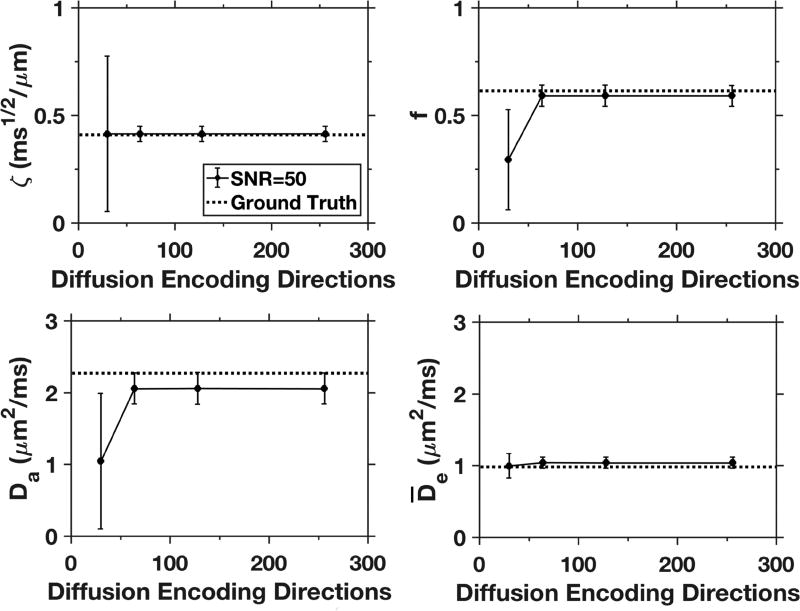
Simulated results (with denoising) using different numbers of diffusion encoding directions for the HARDI shell are given in Fig. 8. Little difference in the parameter mean values and standard deviations are seen with 64, 128, or 256 directions, but both f and Da are significantly underestimated when only 30 directions are employed.
Figure 8.
Results for selected diffusion measures from simulations with varying numbers of diffusion coding directions (30, 64, 128, 256) for the b = 6000 µm2/ms HARDI shell. The data points reflect average values over all white matter voxels from the simulated dataset, and error bars indicate standard deviations. The SNR is fixed at 50, which is comparable to that of our experiments, and the number of directions is set to 30 for both the b =1000 and b = 2000 µm2/ms shells. The parameter estimates are all similar for 64 directions and above, but are much less accurate for f and Da when only 30 directions are used for the HARDI shell.
5. Discussion
A premise underlying FBI is that the dMRI signal in white matter is predominately due to intra-axonal water for high b-values, as is strongly supported by the observed decrease of the direction-averaged signal as for large diffusion weightings (McKinnon et al. 2017; Veraart et al., 2016a). Furthermore, this drop-off is a signature of diffusion restricted within thin cylindrical pores, which presumably correspond to axons. These facts allow the fODF to be estimated in a simple manner, along with the microstructural parameter (Jensen et al., 2016).
For low b-values, the dMRI signal is well-described by the total diffusion tensor D, which is easily estimated with either DTI or DKI. Knowledge of D, the fODF, ζ, and f are sufficient to calculate both the intra-axonal and extra-axonal diffusion tensors via Eqs. (11), (12), and (19). Of these quantities, f is the only one of the inputs not determined by the combination of FBI and DTI/DKI. Thus one additional condition is needed in order to find the AWF and thereby independently characterize the intra-axonal and extra-axonal diffusion environments.
Here we have estimated f by requiring the model dMRI signal of Eq. (20) to match the measured dMRI signal as closely as possible through minimization of the cost function of Eq. (21). As formulated, this is a one-dimensional optimization problem that is straightforward to solve numerically, in contrast to some alternative approaches (Harms et al., 2017; Jelescu et al., 2016a; Novikov et al., 2018). Moreover, we find empirically that the cost function has a single minimum for most white matter voxels so that potential issues arising from multiple local minima should be minor. From the optimal f, we are then able to calculate the intra-axonal and extra-axonal diffusion tensors, along with a variety of associated diffusion parameters (see Fig. 3). A crucial distinction between the FBWM optimization and alternative diffusion modeling approaches that also employ a spherical harmonic expansion of the dMRI signal (Jespersen et al., 2007; Jespersen et al., 2010; Novikov et al., 2016; Veraart et al., 2017) is that, for the alternatives, the number of free parameters increases with the number of harmonics used, while for FBWM there is always a single free parameter regardless of the number of harmonics. The reason for this is that FBWM uses the harmonic expansion coefficients determined with FBI rather than treating them as fitting parameters.
Our results suggest that harmonics at least up to a degree of about 6 should be kept for numerical calculations, since the occurrence of voxels with multiple local minima increases substantially as the maximum degree is reduced below this, raising concerns regarding unphysical solutions (Harms et al., 2017; Jelescu et al., 2016a; Novikov et al., 2016; Novikov et al., 2018). However, including harmonics with very high degrees may not be beneficial as these are likely dominated by signal noise.
The model for the full dMRI signal is the sum of the intra-axonal and extra-axonal signal models. The intra-axonal signal model of Eq. (15) follows directly from the theory for FBI. There is, however, no similar basis for the extra-axonal signal model. For our cost function, we have adopted the simplest possibility of regarding water diffusion in the extra-axonal space as Gaussian, which leads to Eq. (3). It has been argued that treating the extra-axonal space as Gaussian is overly simplistic (Kaden et al., 2016), but we hypothesize that this may be adequate for b-values of 2000 s/mm2 or less, as would be the case if the kurtosis of the extra-axonal space were not too large. Furthermore, for our high b-value shell of 6000 s/mm2, the form of the extra-axonal signal should be irrelevant, since the dMRI signal in white matter is expected to mainly arise from intra-axonal water. Thus, Eq. (3) may be appropriate for our dataset, even if it is less accurate than some other models for intermediate b-values. Indeed, a possible advantage of our method could be a relative insensitivity to the details of the extra-axonal signal model, although further work would be necessary to confirm this.
In this initial study, we have applied our FBWM method to estimate several different microstructural parameters for characterizing diffusion in white matter using data from three healthy volunteers. Most of these parameters have a high degree of reproducibility, as demonstrated by Figs. 3 and 4. Their values are all within physically plausible ranges, although we have no ground truth for comparison. Alternative approaches have yielded variable results, particularly for the intra-axonal diffusivity, which seems to be especially difficult to estimate accurately (Jelescu et al., 2016a; Novikov et al., 2018). Nonetheless, our results are fairly similar to those from the recently proposed spherical mean technique (Kaden et al., 2016), from b-value scaling (Veraart et al., 2016a), and from TE dependent diffusion imaging (Veraart et al., 2017), even while these methods employ more complex numerical fitting schemes than used here. More specifically, we find a mean value from FBWM for the intra-axonal diffusivity of 2.46 ± 0.20 µm2/ms. This is also quite close to the value of 2.25 ± 0.03 µm2/ms recently reported by Dhital and coworkers (Dhital et al., 2017b) based on multiple diffusion encoding dMRI and a novel analysis method. The discrepancy between these two results could either be caused by intersubject differences or by systematic errors in the respective estimation methods. It would be of interest to gather data with both techniques on the same subjects to better assess their concordance.
Another interesting observation is that the AWF and the microstructural parameter ζ are strongly correlated, indicating that the regional variation in ζ is mainly driven by differences in the AWF rather than in the intra-axonal diffusivity. This fact can be helpful for interpreting FBI results when full FBWM modeling is not available.
A principal motivation for this work is to improve upon the WMTI method, which also uses DKI data. Our basic rationale is that FBI can supply the fODF and thus eliminate the need to assume, as with WMTI, that all axons are approximately aligned in a single direction. In this way, meaningful parameter estimates can be obtained for the entire white matter instead of just a small subset of voxels in which the axons may be regarded as largely unidirectional. Moreover, fixing the parameter ζ with FBI provides an additional constraint that may improve accuracy and precision. Our results show that WMTI and FBWM give similar results for ζ in high FA regions, as previously reported (Jensen et al., 2017), but the WMTI estimates of both f and Da are substantially lower in comparison to those from FBWM. We speculate that the FBWM values are more accurate, since the FBWM prediction for Da is closer to several recent estimates obtained with a variety of techniques, as mentioned above. In addition, experiments employing isotropic diffusion weighting (Dhital et al., 2017a) and in fixed spinal cord (Jespersen et al., 2017) both indicate that Da > De,‖, which is consistent with our FBWM results but not with WMTI.
Our experimental data were acquired with 3 mm isotropic voxels and an average SNR of about 59. However, our numerical simulations (Figs. 6 and 7) suggest that an SNR as low as 20 may be adequate as long as denoising is included as part of the post-processing analysis pipeline. Thus higher resolution maps may be attainable with FBWM. In addition, our numerical simulations (Fig. 8) indicate that as few as 64 diffusion encoding directions could be sufficient for the HARDI shell, which would sharply reduce the dMRI data acquisition time for FBWM to about 12 min from the 30 min of our experimental protocol with 256 HARDI directions. However, actual experiments should be conducted to verify this.
There are two important limitations of our proposed FBWM method. First, it only applies to white matter, since the direction-averaged dMRI signal in gray matter does not obey the scaling behavior for large diffusion weightings, as required for FBI (McKinnon et al., 2017). This contrasts with several other previously proposed dMRI tissue models that are intended to apply to both gray and white matter (Jespersen et al. 2010, Zhang et al., 2012, Kaden et al., 2016). Second, the effect of different T2 values for the intra-axonal and extra-axonal spaces is not accounted for in FBWM. As a consequence, the estimated AWF may be T2-weighted. In particular, Veraart and coworkers (Veraart et al., 2017) have recently argued that the T2 of intra-axonal water may be substantially longer than for extra-axonal water. FBWM might therefore overestimate f, depending somewhat on TE.
The primary goals of this paper have been to describe the FBWM approach in detail and to give some preliminary results for healthy human brain. Further work is needed in at least three directions. First, the imaging protocol should be optimized in order to reduce the acquisition time. Specifically, the 256 directions used for the b=6000 s/mm2 HARDI shell could likely be reduced, as our numerical simulations suggest, with minimal impact on the parameter estimates. Second, the predictions of FBWM should be more rigorously validated by comparison with histology and other dMRI methods. Advanced dMRI techniques that employ nonstandard pulse sequences with complex gradient wave forms seem especially promising in this regard, as they can potentially estimate diffusion parameters with fewer modeling assumptions and thereby yield more reliable results (Dhital et al., 2017a; Dhital et al., 2017b; Shemesh et al., 2010; Topgaard 2017; Westin et al., 2016). Finally, the relative strengths and weaknesses of FBWM in comparison to the several related alternatives (e.g., Jespersen et al., 2017; Reisert et al., 2017) should be more thoroughly investigated. Here we have mainly compared FBWM to WMTI and argued that FBWM is both more comprehensive and more accurate.
6. Conclusion
By combining FBI with low to intermediate b-value dMRI data, FBWM provides estimates for multiple biophysical parameters that characterize tissue microstructure in white matter. FBI is used to determine the orientation of the axonal fibers, while the low/intermediate b-value dMRI data are employed to find the total diffusion tensor of the system. From these two inputs, a cost function is constructed with the AWF as the sole free parameter. The minimum of this cost function gives the optimal AWF, from which several other microstructural parameters may be calculated. A key advantage of FBWM is the simplicity of cost function, which facilitates efficient and robust numerical algorithms. The predictions of FBWM differ substantially from those of the WMTI approach, particularly for the intrinsic intra-axonal diffusivity, and are in better agreement with results from some alternative methods.
Acknowledgments
This work was supported in part by National Institutes of Health research grant T32GM008716 (to P. Halushka) and T32DC0014435 (to J. Dubno) and by the Litwin Foundation (to J.A.H.). We are grateful to Hunter Moss for technical assistance.
Abbreviations
- AWF
axonal water fraction
- DKI
diffusional kurtosis imaging
- dMRI
diffusion MRI
- DTI
diffusion tensor imaging
- DWI
diffusion weighted imaging
- FA
fractional anisotropy
- FAA
fractional anisotropy axonal
- FBI
fiber ball imaging
- FBWM
fiber ball white matter
- fODF
fiber orientation density function
- HARDI
high angular resolution diffusion imaging
- MD
mean diffusivity
- MK
mean kurtosis
- WMTI
white matter tract integrity
Appendix
Here we sketch the derivations of Eqs. (11) through (13). The diffusion tensor for the intra-axonal space may be expressed as
| (A1) |
where Daxon (u) is the diffusion tensor for an individual axon oriented in a direction u. If axons are idealized as thin, straight cylinders (i.e., a stick model), we then have
| (A2) |
where (θ, φ) are the spherical angles for u. From Eqs. (7), (A1) and (A2), one sees that
| (A3) |
The spherical integrals in Eq. (A3) may be evaluated with the help of Eqs. (5) and (6), which leads directly to Eqs. (11) and (12). All the needed integrals correspond to elementary trigonometric forms, with those for l > 1 yielding zero.
In order to derive Eq. (13), we exploit the fact that the FAA is given by
| (A4) |
where I indicates the identity matrix, tr(…) indicates the trace, and ‖…‖ indicates the Frobenius norm (Basser and Pierpaoli, 1996; Glenn et al., 2015). By applying Eq. (A4) to Eq. (12), one finds the result of Eq. (13).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander DC, Dyrby TB, Nilsson M, Zhang H. Imaging brain microstructure with diffusion MRI: practicality and applications. NMR Biomed. 2017 doi: 10.1002/nbm.3841. [DOI] [PubMed] [Google Scholar]
- Bailey TN, Eastwood MG, Gover R, Mason LJ. Complex analysis and the Funk transform. J. Korean Math. Sociol. 2003;40:577–593. [Google Scholar]
- Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis - a technical review. NMR Biomed. 2002;15:456–67. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of magnetic resonance. J. Magn. Reson. B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen H. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med. 2003;50:1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- Clark CA, Le Bihan D. Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn. Reson. Med. 2000;44:852–859. doi: 10.1002/1522-2594(200012)44:6<852::aid-mrm5>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- Dhital B, Kellner E, Kiselev VG, Reisert M. The absence of restricted water pool in brain white matter. Neuroimage. 2017a doi: 10.1016/j.neuroimage.2017.10.051. [DOI] [PubMed] [Google Scholar]
- Dhital B, Reisert M, Kellner E, Kiselev VG. Intra-axonal diffusivity in brain white matter. arXiv:1712.04565 [physics.bio-ph] 2017b doi: 10.1016/j.neuroimage.2019.01.015. [DOI] [PubMed] [Google Scholar]
- Ferizi U, Schneider T, Panagiotaki E, Nedjati-Gilani G, Zhang H, Wheeler-Kingshott CA, Alexander DC. A ranking of diffusion MRI compartment models with in vivo human brain data. Magn. Reson. Med. 2014;72:1785–1792. doi: 10.1002/mrm.25080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011;58:177–188. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glenn GR, Helpern JA, Tabesh A, Jensen JH. Quantitative assessment of diffusional kurtosis anisotropy. NMR in Biomed. 2015;28:448–459. doi: 10.1002/nbm.3271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995;34:910–914. doi: 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harms RL, Fritz FJ, Tobisch A, Goebel R, Roebroeck A. Robust and fast nonlinear optimization of diffusion MRI microstructure models. Neuroimage. 2017;155:82–96. doi: 10.1016/j.neuroimage.2017.04.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holz M, Heil SR, Sacco A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys. Chem. Chem. Phys. 2000;2:4740–4742. [Google Scholar]
- Jackson JD. Classical Electrodynamics. second. Wiley; New York: 1975. [Google Scholar]
- Jelescu IO, Budde MD. Design and validation of diffusion MRI models of white matter. Front. Phys. 2017;5:61. doi: 10.3389/fphy.2017.00061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Veraart J, Fieremans E, Novikov DS. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. 2016a;29:33–47. doi: 10.1002/nbm.3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Zurek M, Winters KV, Veraart J, Rajaratnam A, Kim NS, Babb JS, Shepherd TM, Novikov DS, Kim SG, Fieremans E. In vivo quantification of demyelination and recovery using compartment-specific diffusion MRI metrics validated by electron microscopy. Neuroimage. 2016b;132:104–114. doi: 10.1016/j.neuroimage.2016.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Glenn GR, Helpern JA. Fiber ball imaging. Neuroimage. 2016;124:824–833. doi: 10.1016/j.neuroimage.2015.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710. doi: 10.1002/nbm.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, McKinnon ET, Glenn GR, Helpern JA. Evaluating kurtosis-based diffusion MRI tissue models for white matter with fiber ball imaging. NMR Biomed. 2017;30:e3689. doi: 10.1002/nbm.3689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen SN, Bjarkam CR, Nyengaard JR, Chakravarty MM, Hansen B, Vosegaard T, Østergaard L, Yablonskiy D, Nielsen NC, Vestergaard-Poulsen P. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage. 2010;49:205–216. doi: 10.1016/j.neuroimage.2009.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage. 2007;34:1473–1486. doi: 10.1016/j.neuroimage.2006.10.037. [DOI] [PubMed] [Google Scholar]
- Jespersen SN, Olesen JL, Hansen B, Shemesh N. Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC. Multi-compartment microscopic diffusion imaging. Neuroimage. 2016;139:346–359. doi: 10.1016/j.neuroimage.2016.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med. 2016;76:1574–1581. doi: 10.1002/mrm.26054. [DOI] [PubMed] [Google Scholar]
- Kroenke CD, Ackerman JJ, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn. Reson. Med. 2004;52:1052–1059. doi: 10.1002/mrm.20260. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Iima M. Diffusion magnetic resonance imaging: what water tells us about biological tissues. PLoS Biol. 2015;13:e1002203. doi: 10.1371/journal.pbio.1002246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bihan D, Johansen-Berg H. Diffusion MRI at 25: exploring brain tissue structure and function. Neuroimage. 2012;61:324–341. doi: 10.1016/j.neuroimage.2011.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKay AL, Laule C. Magnetic resonance of myelin water: an in vivo marker for myelin. Brain Plasticity. 2016;2:71–91. doi: 10.3233/BPL-160033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinnon ET, Jensen JH, Glenn GR, Helpern JA. Dependence on b-value of the direction-averaged diffusion-weighted imaging signal in brain. Magn. Reson. Imaging. 2017;36:121–127. doi: 10.1016/j.mri.2016.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magn. Reson. Med. 2013;69:1572–1580. doi: 10.1002/mrm.24395. [DOI] [PubMed] [Google Scholar]
- Novikov DS, Jespersen SN, Kiselev VG, Fieremans E. Quantifying brain microstructure with diffusion MRI: theory and parameter estimation. arXiv:1612.02059 [physics.bio-ph] 2016 doi: 10.1002/nbm.3998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage. 2018 doi: 10.1016/j.neuroimage.2018.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage. 2012;59:2241–2254. doi: 10.1016/j.neuroimage.2011.09.081. [DOI] [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn. Reson. Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. Neuroimage. 2017;147:964–975. doi: 10.1016/j.neuroimage.2016.09.058. [DOI] [PubMed] [Google Scholar]
- Shemesh N, Özarslan E, Komlosh ME, Basser PJ, Cohen Y. From single-pulsed field gradient to double-pulsed field gradient MR: gleaning new microstructural information and developing new forms of contrast in MRI. NMR Biomed. 2010;23:757–780. doi: 10.1002/nbm.1550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabesh A, Jensen JH, Ardekani BA, Helpern JA. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn. Reson. Med. 2011;65:823–836. doi: 10.1002/mrm.22655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Topgaard D. Multidimensional diffusion MRI. J. Magn. Reson. 2017;275:98–113. doi: 10.1016/j.jmr.2016.12.007. [DOI] [PubMed] [Google Scholar]
- Tuch DS. Q-ball imaging. Magn. Reson. Med. 2004;2004(52):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Veraart J, Fieremans E, Novikov DS. Universal power-law scaling of water diffusion in human brain defines what we see with MRI. arXiv:1609.09145 [physics.bio-ph] 2016a [Google Scholar]
- Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage. 2016b;142:394–406. doi: 10.1016/j.neuroimage.2016.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Poot DH, Van Hecke W, Blockx I, Van der Linden A, Verhoye M, Sijbers J. More accurate estimation of diffusion tensor parameters using diffusion kurtosis imaging. Magn. Reson. Med. 2011;65:138–145. doi: 10.1002/mrm.22603. [DOI] [PubMed] [Google Scholar]
- Westin CF, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell LJ, Kubicki M, Topgaard D, Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage. 2016;135:345–362. doi: 10.1016/j.neuroimage.2016.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA, Sukstanskii AL. Theoretical models of the diffusion weighted MR signal. NMR Biomed. 2010;23:661–681. doi: 10.1002/nbm.1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AW, Jensen JH, Hu CC, Tabesh A, Falangola MF, Helpern JA. Effect of cerebral spinal fluid suppression for diffusional kurtosis imaging. J. Magn. Reson. Imaging. 2013;37:365–371. doi: 10.1002/jmri.23840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012:61,1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]