An Algorithm Based on Deep Learning for Predicting In‐Hospital Cardiac Arrest

Abstract

Background

In‐hospital cardiac arrest is a major burden to public health, which affects patient safety. Although traditional track‐and‐trigger systems are used to predict cardiac arrest early, they have limitations, with low sensitivity and high false‐alarm rates. We propose a deep learning–based early warning system that shows higher performance than the existing track‐and‐trigger systems.

Methods and Results

This retrospective cohort study reviewed patients who were admitted to 2 hospitals from June 2010 to July 2017. A total of 52 131 patients were included. Specifically, a recurrent neural network was trained using data from June 2010 to January 2017. The result was tested using the data from February to July 2017. The primary outcome was cardiac arrest, and the secondary outcome was death without attempted resuscitation. As comparative measures, we used the area under the receiver operating characteristic curve (AUROC), the area under the precision–recall curve (AUPRC), and the net reclassification index. Furthermore, we evaluated sensitivity while varying the number of alarms. The deep learning–based early warning system (AUROC: 0.850; AUPRC: 0.044) significantly outperformed a modified early warning score (AUROC: 0.603; AUPRC: 0.003), a random forest algorithm (AUROC: 0.780; AUPRC: 0.014), and logistic regression (AUROC: 0.613; AUPRC: 0.007). Furthermore, the deep learning–based early warning system reduced the number of alarms by 82.2%, 13.5%, and 42.1% compared with the modified early warning system, random forest, and logistic regression, respectively, at the same sensitivity.

Conclusions

An algorithm based on deep learning had high sensitivity and a low false‐alarm rate for detection of patients with cardiac arrest in the multicenter study.

Clinical Perspective

What Is New?

• We developed a deep learning–based early warning system (DEWS).

• The DEWS found >50% of patients with in‐hospital cardiac arrest 14 hours before the event. This means that the medical staff would have enough time to intervene.

• The DEWS had high sensitivity with a low false‐alarm rate for detection of patients with in‐hospital cardiac arrest in the multicenter study. Compared with a modified early warning system, the DEWS achieved up to 24.3% higher sensitivity and reduced alarms by 41.6%.

What Are the Clinical Implications?

• The rapid response team needs an accurate track‐and‐trigger system to prevent in‐hospital cardiac arrest.

• With the DEWS, the rapid response team can find patients with cardiac arrest faster and more accurately than with the current system.

• The DEWS is easy to apply in various hospital environments because it uses only 4 vital signs.

Introduction

In‐hospital cardiac arrest is a major burden to public health, which affects patient safety.1, 2, 3 More than a half of cardiac arrests result from respiratory failure or hypovolemic shock, and 80% of patients with cardiac arrest show signs of deterioration in the 8 hours before cardiac arrest.4, 5, 6, 7, 8, 9 However, 209 000 in‐hospital cardiac arrests occur in the United States each year, and the survival discharge rate for patients with cardiac arrest is <20% worldwide.10, 11 Rapid response systems (RRSs) have been introduced in many hospitals to detect cardiac arrest using the track‐and‐trigger system (TTS).12, 13

Two types of TTS are used in RRSs. For the single‐parameter TTS (SPTTS), cardiac arrest is predicted if any single vital sign (eg, heart rate [HR], blood pressure) is out of the normal range.14 The aggregated weighted TTS calculates a weighted score for each vital sign and then finds patients with cardiac arrest based on the sum of these scores.15 The modified early warning score (MEWS) is one of the most widely used approaches among all aggregated weighted TTSs (Table 1)16; however, traditional TTSs including MEWS have limitations, with low sensitivity or high false‐alarm rates.14, 15, 17 Sensitivity and false‐alarm rate interact: Increased sensitivity creates higher false‐alarm rates and vice versa.

Table 1.

Modified Early Warning Score

Score	3	2	1	0	1	2	3
SBP, mm Hg	≤70	71–80	81–100	101–199	…	≥200	…
HR, beats/min	…	≤40	41–50	51–100	101–110	111–129	≥130
RR, breaths/min	…	≤8	…	9–14	15–20	21–29	≥30
BT, °C	…	≤35	…	35.1–38.4	…	≥38.5	…
Mental status	…	…	…	Alert	Reacting to voice	Reacting to pain	Unresponsive

BT indicates body temperature; HR, heart rate; RR, respiratory rate; SBP, systolic blood pressure.

Current RRSs suffer from low sensitivity or a high false‐alarm rate. An RRS was used for only 30% of patients before unplanned intensive care unit admission and was not used for 22.8% of patients, even if they met the criteria.18, 19 Consequently, most previous studies focused on improving sensitivity.20, 21 Nevertheless, number of false alarms is also an important criteria when evaluating TTSs. Whenever alarms sound, medical staffs need to intervene and reverify the alarms in real time for RRSs. False alarms waste the time of medical staff and increase operating costs for RRSs; therefore, the false‐alarm rate is a key factor in making the RRS practical.

A practical TTS should satisfy 2 criteria simultaneously: high sensitivity and low false‐alarm rate. We developed a deep learning–based early warning system (DEWS) that satisfies both. Deep learning approaches have recently achieved state‐of‐the‐art performance in several domains such as computer vision and speech.22, 23, 24 An advantage of deep learning is the ability to learn features automatically from given data.25 Our DEWS extracts the useful features from the vital signs (eg, HR and blood pressure) and learns the relationship with the cardiac arrest. To the best of our knowledge, this study is the first to predict cardiac arrest using deep learning.

Methods

The data, analytic methods, and study materials will not be made available to other researchers for purposes of reproducing the results or replicating the procedure.

We performed a multicenter retrospective cohort study in 2 hospitals. The study population consisted of all patients admitted to 2 hospitals over 91 months. The characteristics of the 2 hospitals are different (hospital A is a cardiovascular teaching hospital, and hospital B is a community general hospital), as shown in Table 2. We excluded patients who were admitted or discharged outside the study period and patients who underwent cardiac arrest or death within 30 minutes after admission. The institutional review boards of Sejong General Hospital and Mediplex Sejong Hospital approved this study (2017‐452, 2017‐004) and granted waivers of informed consent based on general impracticability and minimal harm. Patient information was anonymized and deidentified before the analysis.

Table 2.

Characteristics of Study Population

Characteristic	Model Derivation	Test for Model Comparison
	Hospital A	Hospital A	Hospital B
Study period	Jun 2010–Jan 2017	Feb–Jul 2017	Mar–Jul 2017
Total patients, n	46 725	3634	1772
Input vectors, n	2 769 324	152 587	60 782
Patients with in‐hospital cardiac arrest, n	396	19	4
Input vectors, n	10 772	352	82
Patients with death without attempted resuscitation, n	770	25	19
Input vectors, n	28 208	801	446
Age, y, mean±SD	56.7±23.3	58.2±21.7	58.1±17.2
Male sex, n (%)	24 171 (51.7)	1878 (51.7)	829 (46.8)
Maximum DEWS score, mean±SD
Nonevent	16.3±28.4	9.2±20.9	6.6±17.5
Cardiac arrest	89.0±21.0	60.6±35.7	67.2±38.3
Death without attempted resuscitation	97.9±7.9	84.5±27.8	81.1±18.5
Hospital type	Cardiovascular teaching hospital		Community general hospital
Number of beds	310	310	172

DEWS indicates deep learning–based early warning system.

The hospital A data were split by date into a derivation set (June 2010–July 2016) and a validation set (August 2016–January 2017). The derivation and validation sets were used to develop the DEWS and to determine the parameters of the DEWS, respectively. We evaluated the accuracy of the DEWS using hospital A data (February 2017–July 2017), which were not used for model derivation. Furthermore, we used hospital B data (March 2017–July 2017) to verify that the DEWS was applicable across centers.

The primary outcome was cardiac arrest, and the secondary outcome was death without attempted resuscitation. For cardiac arrest, we used only the first cardiac arrest if cardiac arrest occurred several times during a patient's length of stay. We reviewed electronic health records to identify the exact time of each outcome.

We used only 4 vital signs as predictor variables: systolic blood pressure, HR, respiratory rate, and body temperature (BT). These vital signs are associated with adverse clinical outcomes and are measured periodically and frequently.6, 16, 26 Furthermore, they are objective values that are barely affected by medical staff measuring them.27 We defined the input vector as the predictor variables observed at the same time, and each input vector consisted of 4 vital signs: systolic blood pressure, HR, respiratory rate, and BT. The vital signs of the general ward patient were measured at least 3 times per day manually by the medical staff. In contrast, the vital signs of intensive care unit patients were measured every 10 minutes automatically by monitoring devices, and the medical staff verified that measurements were correct. Because human errors could exist in the electronic health records, we excluded systolic blood pressure, HR, respiratory rate, and BT values that were outside the ranges of 30 to 300 mm Hg, 10 to 300 beats/min, 3 to 60 breaths/min, and 30 to 45°C, respectively.

The objective of this study was to predict whether an input vector belonged within the prediction time window. The prediction time window was defined as the interval from 0.5 to 24 hours before the outcomes.28, 29 It is important to note that the prediction unit was not the patient but the input vector. For a patient with outcomes, if the input vector belonged to the prediction window, it was labeled as event (eg, an alarm sounded); otherwise, it was labeled as a nonevent. For a patient without outcomes, all input vectors were labeled as nonevents. For example, when a patient was hospitalized and vital signs were measured 8 times, the model predicted an event or a nonevent 8 times.

When an alarm was set off in the clinical environment, medical staff examined and observed the patient for a few hours and ignored the alarm during the examination. To make our experiments like the clinical environment, we regarded the alarms in the window (1 hour) to 1 alarm. If a vital sign data was missing, the most recent value was used. If no value was available, the median value was used.

The DEWS used time series data as an input. Given the input, the DEWS evaluated the risk score using all input vectors measured during the 8 hours. For example, when calculating the risk score of an input vector measured at 11 am, DEWS used all input vectors measured from 3 am to 11 am, as shown in Figure 1. The DEWS calculated the risk score, which ranged from 0 (nonevent) to 100 (event), every time the input vector was measured.

Figure 1.

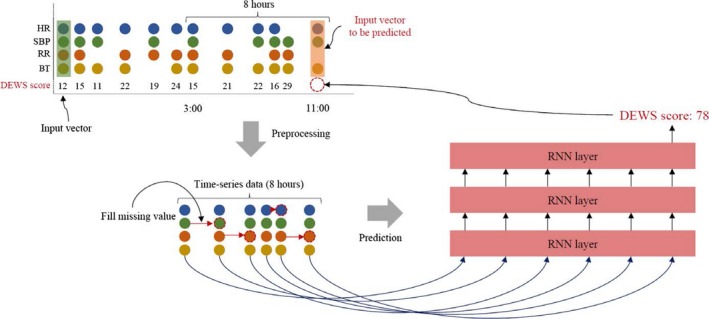
The process of the DEWS. DEWS indicates deep learning–based early warning system; HR, heart rate; RNN, recurrent neural network; RR, respiratory rate; SBP, systolic blood pressure; BT, body temperature.

The DEWS consisted of 3 recurrent neural network layers with long short‐term memory unit which deal with the time‐series data well.30 The recurrent neural network is a neural network with loops, allowing it to process sequential data such as electronic health records. In Figure 2, a loop allows previous information to influence the present task. This is similar to referring to a patient's past information when medical staff checks a patient's condition. The recurrent neural network, however, has a problem called “long‐term dependency.”25 As the length of sequential data increases, the information that is important early is hard to reach until the end. The long short‐term memory unit is designed to avoid long‐term dependency via gates that can keep the information in early. The output of the k‐th long short‐term memory unit at a time t is ${\mathrm{h}}_{\mathrm{t}}^{\mathrm{i}}$, which is passed on to the next time t+1. The calculation is as follows:

$${\mathrm{h}}_{\mathrm{t}}^{\mathrm{k}}={\mathrm{o}}_{\mathrm{t}}^{\mathrm{i}}\text{tanh}\left({\mathrm{c}}_{\mathrm{t}}^{\mathrm{k}}\right)$$

$${\mathrm{o}}_{\mathrm{t}}^{\mathrm{k}}=\mathrm{\sigma }{\left({\mathrm{W}}_{\mathrm{o}}{\mathrm{x}}_{\mathrm{t}}+{\mathrm{U}}_{\mathrm{o}}{\mathrm{h}}_{\mathrm{t}-1}+{\mathrm{b}}_{\mathrm{o}}\right)}^{\mathrm{k}}$$

$${\mathrm{c}}_{\mathrm{t}}^{\mathrm{k}}={\mathrm{f}}_{\mathrm{t}}^{\mathrm{k}}{\mathrm{c}}_{\mathrm{t}-1}^{\mathrm{k}}+{\mathrm{i}}_{\mathrm{t}}^{\mathrm{k}}{\tilde{\mathrm{c}}}_{\mathrm{t}}^{\mathrm{k}}$$

$${\tilde{\mathrm{c}}}_{\mathrm{t}}^{\mathrm{k}}=\text{tanh}{({\mathrm{W}}_{\mathrm{c}}{\mathrm{x}}_{\mathrm{t}}+{\mathrm{U}}_{\mathrm{c}}{\mathrm{h}}_{\mathrm{t}-1}+{\mathrm{b}}_{\mathrm{c}})}^{\mathrm{k}}$$

$${\mathrm{f}}_{\mathrm{t}}^{\mathrm{k}}=\mathrm{\sigma }{({\mathrm{W}}_{\mathrm{f}}{\mathrm{x}}_{\mathrm{t}}+{\mathrm{U}}_{\mathrm{f}}{\mathrm{h}}_{\mathrm{t}-1}+{\mathrm{b}}_{\mathrm{f}})}^{\mathrm{k}}$$

$${\mathrm{i}}_{\mathrm{t}}^{\mathrm{k}}=\mathrm{\sigma }{({\mathrm{W}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{t}}+{\mathrm{U}}_{\mathrm{i}}{\mathrm{h}}_{\mathrm{t}-1}+{\mathrm{b}}_{\mathrm{i}})}^{\mathrm{k}}$$

where W, U, and b are input weights, recurrent weights, and biases, respectively, into the long short‐term memory unit. The input, output, and “forget” gates are denoted by i, o, and f, respectively, whereas the memory cell is denoted by c. The σ is a logistic sigmoid function. The input and forget gates determine whether or not to forget the previous information and to keep the current information, respectively. The output gate adjusts the current information, and the memory cell has the previous and current memory contents.

Figure 2.

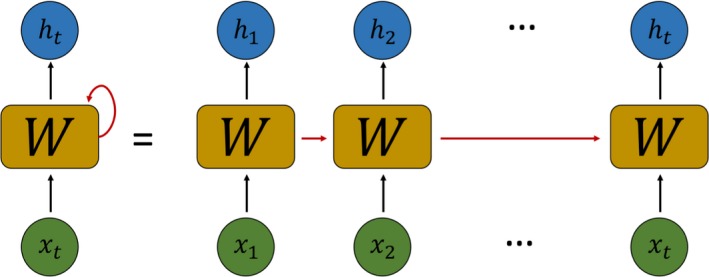
The architecture of the recurrent neural network. ^X _t and ^h _t indicate input and output at time t; W, weights.

We used the Adam optimizer with the default parameters and a binary‐cross entropy as a loss function.31 To validate our model, we used the hyperparameters of the model with the best performance on 10% of the data from the derivation data during the training process.

We compared the performance of the DEWS, the MEWS, SPTTS, logistic regression, and random forest. The details of SPTTS are shown in Table 3. In the previous studies, logistic regression and random forest were the most commonly used machine‐learning methods and showed better performance than traditional TTSs.32, 33 We used the area under the receiver operating characteristic curve (AUROC) and the area under the precision–recall curve (AUPRC) to measure the performance of the model. AUROC is one of the most used metrics and shows sensitivity against 1−specificity. Compared with AUROC, AUPRC is suitable for verifying false‐alarm rates with varying sensitivity and shows precision (ie, 1−false‐alarm rate) against recall (ie, sensitivity).34, 35

Table 3.

Single‐Parameter Track‐and‐Trigger System^a

Parameter	Value
SBP, mm Hg	≤85
HR, beats/min	≤50 or ≥130
RR, breaths/min	≤8 or ≥25
BT, °C	≤35 or ≥39
Mental status (AVPU)	V, P, U

^aIf >1 parameter is positive, activate rapid response team.

Another important criterion to evaluate TTSs is the number of alarms. As the number of alarms increases, the operating costs for RRSs also increases because of medical‐staff expenses; therefore, we evaluated sensitivity against mean alarm count per hour per patient (MACHP). For example, 0.02 MACHP means that if there are 1000 patients in the hospital, the number of alarms is 20 times an hour. It is easy to know the effect of the TTS (ie, sensitivity and the number of alarms) when applied to RRSs because MACHP normalizes the number of alarms.

We also evaluated positive predictive value $\left(\right.\text{PPV}=\frac{\text{True positive}}{\text{True positive}+\text{False positive}}\left)\right.$, negative predictive value $\left(\right.\text{NPV}=\frac{\text{True negative}}{\text{True negative}+\text{False negative}}\left)\right.$, net reclassification index, and F‐measure $\left(\right.2\times \frac{\text{precision}\times \text{recall}}{\text{precision}+\text{recall}}\left)\right.$. Net reclassification index is used to compare the improvement in prediction performance gained.35, 36 The comparison is performed at the same sensitivity because the results of these metrics are different depending on sensitivity. We compared the DEWS and the MEWS at 3 sensitivities according to the cutoff score. The cutoff scores for the MEWS that were most commonly used were 3, 4, and 5.37, 38 The comparison of the DEWS and SPTTS was performed at 1 sensitivity, as SPTTS has only one sensitivity. We also compared DEWS with logistic regression and random forest at 75% sensitivity, in accordance with the previous study.32

Results

A total of 56 076 patients were admitted during the study period. We excluded 448 patients who were admitted or discharged outside the study period and 3497 patients who experienced an event or were discharged within 30 minutes after admission. The study population consisted of 52 131 patients, of which 1233 patients underwent cardiac arrest or death without attempted resuscitation. The DEWS was developed using 2 769 324 input vectors from 46 725 patients of Hospital A, and a test was performed using 213 369 input vectors for a total of 5406 patients (Figure 3).

Figure 3.

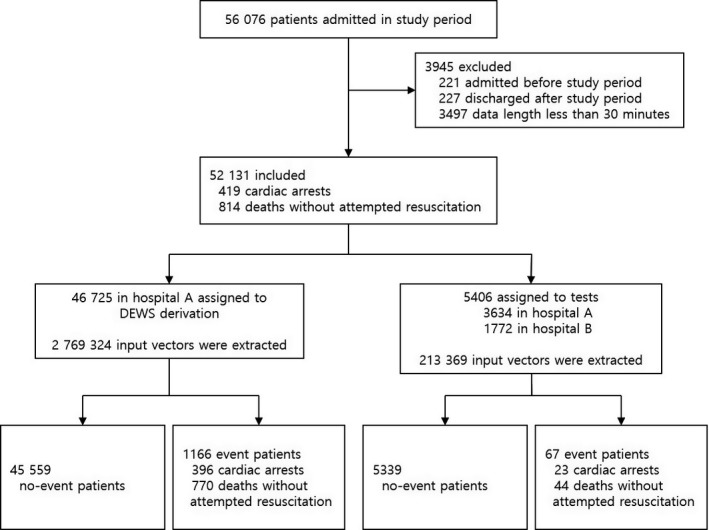
Study flow chart. DEWS indicates deep learning–based early warning system.

As shown in Figure 4, the DEWS (AUROC: 0.850; AUPRC: 0.044) significantly outperformed the MEWS (AUROC: 0.603; AUPRC: 0.003), random forest (AUROC: 0.780; AUPRC: 0.014), and logistic regression (AUROC: 0.613; AUPRC: 0.007) for 352 input vectors labeled cardiac arrest in hospital A. We also validated that the DEWS is applicable across centers by measuring AUROC and AUPRC for 88 input vectors labeled cardiac arrest in hospital B. Note that hospital B is unrelated to hospital A, and the data collected from hospital B were not used for model derivation. The DEWS was the most accurate among all methods, as shown in Figure 4.

Figure 4.

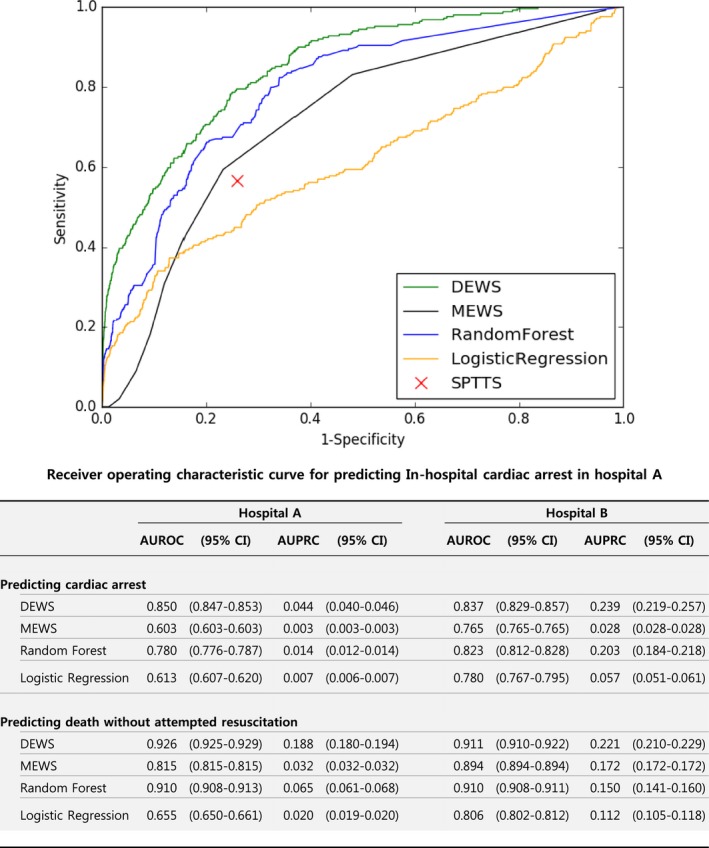
Accuracy for predicting in‐hospital cardiac arrest and death without attempted resuscitation. AUPRC indicates area under the precision–recall curve; AUROC, area under the receiver operating characteristic curve; CI, confidence interval; DEWS, deep learning–based early warning system; MEWS, modified early warning score; SPTTS, single‐parameter track‐and‐trigger system.

In the following set of experiments, we used the combined data from hospitals A and B. We also evaluated specificity, positive predictive value, negative predictive value, net reclassification index, F‐measure, and MACHP with the same sensitivity (Table 4). Negative predictive values were all high because labels of input vectors were mostly nonevent. Conversely, DEWS was the most consistently accurate of all metrics. Compared with the widely used MEWS ≥5, the DEWS achieved 8.7%, 484.0%, and 466.9% higher specificity, positive predictive value, and F‐measure, respectively, and reduced MACHP by 82.2%. Compared with random forest, which showed the best performance in the previous study, the DEWS also achieved 10.1%, 30.6%, and 30.5% higher specificity, positive predictive value, and F‐measure, respectively, and reduced MACHP by 13.5%.32

Table 4.

Comparison of Accuracy of In‐Hospital Cardiac Arrest Prediction Model With Same Sensitivity Point

TTS	Sensitivity	Specificity	PPV	NPV	F‐Measure	MACHP	NRI (95% CI)
MEWS ≥3	63.0	79.9	0.5	99.9	1.0	0.293
DEWS ≥7.1	63.0	87.0	0.8	99.9	1.5	0.199	0.071 (0.061–0.082)
MEWS ≥4	49.3	86.8	0.6	99.9	1.2	0.198
DEWS ≥18.2	49.3	94.6	1.4	99.9	2.8	0.084	0.078 (0.067–0.089)
MEWS ≥5	37.3	90.6	0.6	99.9	1.3	0.143
DEWS ≥52.8	37.3	98.4	3.7	99.9	7.1	0.025	0.079 (0.068–0.090)
SPTTS	60.7	77.0	0.4	99.9	0.8	0.334
DEWS ≥8.0	60.7	88.3	0.8	99.9	1.6	0.180	0.151 (0.138–0.163)
Random forest	75.3	69.9	0.4	99.9	0.8	0.409
DEWS ≥3.0	75.3	77.0	0.5	99.9	1.0	0.354	0.071 (0.060–0.082)
Logistic regression	76.3	34.6	0.2	99.9	0.4	0.622
DEWS ≥2.9	75.7	76.5	0.5	99.9	1.0	0.360	0.413 (0.399–0.427)

CI indicates confidence interval; DEWS, deep learning–based early warning system score; MACHP, mean alarm count per hour per patient; MEWS, modified early warning score; NPV, negative predictive value; NRI, net reclassification index; PPV, positive predictive value; SPTTS, single‐parameter track‐and‐trigger system; TTS, track‐and‐trigger system.

The main goal of this study was to develop a TTS with high sensitivity and a low false‐alarm rate. We estimated sensitivity with varying MACHP, as shown in Figure 5. The DEWS, MEWS, random forest, and logistic regression showed 42.7%, 4.0%, 26.7%, and 25.0% sensitivity, respectively, at 0.04 MACHP.

Figure 5.

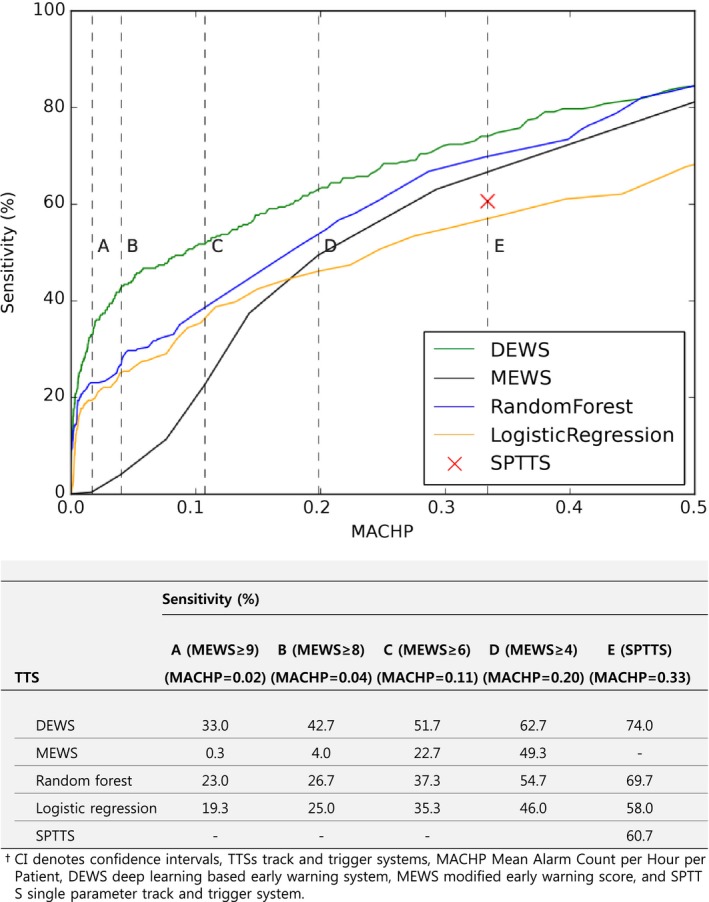
Sensitivity according to MACHP for predicting in‐hospital cardiac arrest. DEWS indicates deep learning–based early warning system; MACHP, mean alarm count per hour per patient; MEWS, modified early warning score; SPTTS, single‐parameter track‐and‐trigger system; TTS, track‐and‐trigger system.

Discussion

In this study, the DEWS predicted cardiac arrest and death without attempted resuscitation better than a MEWS, SPTTS, logistic regression, and random forest in all metrics. In particular, the DEWS showed higher sensitivity with fewer alarms than other TTSs. This result demonstrates that the DEWS is applicable to RRSs. The performance of the DEWS was also verified through the multicenter study. The reasons for the high performance of the DEWS are as follows. First, the DEWS finds the relationship between vital signs, unlike MEWS and SPTTS. For example, although HR is high, it is interpreted differently depending on BT. Second, one of the most important advantages of the deep learning model compared with logistic regression and random forest is feature learning. In this study, feature learning is applied to find useful features to predict the risk score from vital signs.25 Using a large amount of data, the deep learning model automatically learns features or representations needed for given tasks such as classification and detection. This is why deep learning shows better results than traditional machine learning.39, 40, 41

Class imbalance is one of the most significant problems in machine learning. When the data are very imbalanced, the trained model tends to perform poorly on minority class (ie, low sensitivity). Unfortunately, this often occurs in medical data sets because most data are nonevents. To mitigate this problem, we adjusted the ratio of nonevent/event data in a training process by copying the data labeled as events. Although this solution is simple, it provides high sensitivity (before 21%, after 63%).

We evaluated accuracy according to MACHP for similarity to the clinical environment. The MACHPs for a MEWS ≥5 and SPTTS were 0.143, and 0.334; this means that for a hospital with 1000 beds, there are 143 and 334 alarms, respectively, every hour (Table 4)—too many for an RRS to handle. Considering limited resources for an RRS, if the MACHP is set to 0.04, as in Figure 4, sensitivity of the DEWS and the MEWS is 42.7% and 4.0%, respectively. This is why the existing TTSs were not successfully applied to RRSs in some hospitals and is consistent with previous studies.17, 42

The risk (ie, score) of cardiac arrest and death without attempted resuscitation predicted by the DEWS increased from 24 hours ago (Figure 6). The DEWS found >50% of patients with cardiac arrest 14 hours before the event (death without attempted resuscitation 24 hours before the event). This result means that the medical staff could have enough time to intervene when using the DEWS. In addition, the DEWS found 78% of cardiac arrests 30 minutes before the event. Even in situations in which it was too late to prevent cardiac arrest, it is important for the rapid response team to have the information before cardiac arrest occurs; the faster that cardiopulmonary resuscitation is conducted after cardiac arrest, the greater the chance that the patient will survive. The survival rate decreases by 10% per minute before cardiopulmonary resuscitation. Consequently, the DEWS can reduce the number of preventable deaths in hospitals and help more patients survive.

Figure 6.

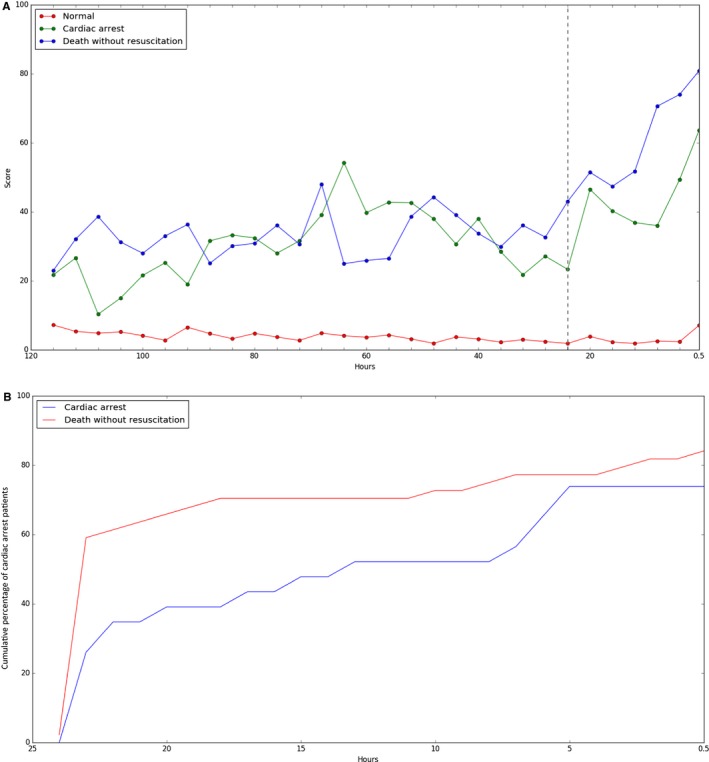
Trend of the DEWS score. A, The change in the mean of the DEWS scores over time as a group of patients. B, Cumulative percentage of cardiac arrest patients on detection time before event. We used the DEWS with sensitivity 70% for this plot. DEWS indicates deep learning–based early warning system.

A multicenter study is not supposed to use a variety of different hospital data but rather was used to separate the test and derivation sets independently. For example, instead of mixing data from 2 hospitals to separate test and derivation data, data from 1 hospital were used for model derivation and data from the other hospital were used only for test purposes. In this respect, the result is not guaranteed in other hospitals because the model memorizes the characteristics of the derivation set. Wolpert explains the “No Free Lunch” theorem: If optimized in one situation, an algorithm cannot produce good results in other situations.43 To overcome this issue, we experimented in 2 ways. The derivation set (June 2010–January 2017) and the test set (February–July 2017) were completely exclusive. We also used the data collected from hospital B only for test purposes.

Previous studies attempted to predict deterioration using machine learning. Churpek et al confirmed that logistic regression and random forest outperformed a MEWS.32 Pirrachio et al developed the “Super ICU Learner Algorithm (SICULA)” using a combination of multiple machine learning methods for patients in intensive care units.44 Although machine learning outperformed the existing TTSs, they used more variables. To show the effect of deep learning, we used fewer variables than a MEWS. The DEWS and random forest were more accurate than the MEWS, but logistic regression was less accurate than the MEWS. The DEWS, which uses fewer variables, has the advantage of being applicable to various hospital environments and devices (eg, wearable device). To validate the effect of the DEWS in a clinical environment, we are planning a multicenter prospective study. Furthermore, we are developing DEWS+ using more variables (eg, clinical note and laboratory data) to improve accuracy.

Our study has 2 limitations. First, deep learning is known as a “black box” because it is used to find the relationship between the given data and a result, not to create a rule based on knowledge. When alarms sound, the medical staff does not know what immediate action to take until team members check the patient. If the medical staff immediately knows the likely reason for the alarm, team members can take care of the patient promptly by considering the likely reason. Interpretable deep learning has been studied recently and is our next area of focus for research.45, 46 The interpretation of the DEWS can help medical staff reduce decision time. Second, we consider only the first cardiac arrest in the patient's length of stay, although second and third cardiac arrests are also significant. Nevertheless, the first cardiac arrest is the highest priority because medical staffs focus on patients after cardiac arrest.

The DEWS is not interpretable but assists the medical staff as a screening tool. Because it reduces the number of alarms and increases accuracy at the same time, the medical staff could have enough time to reverify every alarm. Furthermore, staff can intuitively guess the reason for the prediction because fewer variables are used in the DEWS than in a MEWS, which is based on medical knowledge.

Conclusion

An algorithm based on deep learning had high sensitivity and a low false‐alarm rate for detection of patients with cardiac arrest in a multicenter study. In addition, the DEWS was developed with only 4 vital signs: systolic blood pressure, HR, respiratory rate, and BT. Consequently, it is easy to apply in various hospital environments and offers potentially greater accuracy by using additional information.

Disclosures

None.

(J Am Heart Assoc. 2018;7:e008678 DOI: 10.1161/JAHA.118.008678.)