Solute movement in the t-tubule system of rabbit and mouse cardiomyocytes

Significance

Microscopic invaginations of the surface membrane, called t-tubules, carry electrical and chemical signals into cardiomyocytes. Previous studies have found slow rates of solute exchange inside t-tubules and have suggested that diffusion may be highly restricted. By combining fluorescent tracer measurements and detailed computational modeling, we show that small solutes ($\le$1 kDa) appear to move almost freely within t-tubules and most of the ∼5–16× slowing in exchange rate, compared with free diffusion, arises from t-tubule geometry effects. Larger solutes (>4 kDa) show restricted access into t-tubules, and species-dependent entry may also be impeded by differences in t-tubule mouth configuration. Our data and analyses provide a new pathway to understanding how disease-induced t-tubule derangement may contribute to altered cellular function.

Abstract

Cardiac transverse (t-) tubules carry both electrical excitation and solutes toward the cell center but their ability to transport small molecules is unclear. While fluorescence recovery after photobleaching (FRAP) can provide an approach to measure local solute movement, extraction of diffusion coefficients is confounded by cell and illumination beam geometries. In this study, we use measured cellular geometry and detailed computer modeling to derive the apparent diffusion coefficient of a 1-kDa solute inside the t-tubular system of rabbit and mouse ventricular cardiomyocytes. This approach shows that diffusion within individual t-tubules is more rapid than previously reported. T-tubule tortuosity, varicosities, and the presence of longitudinal elements combine to substantially reduce the apparent rate of solute movement. In steady state, large (>4 kDa) solutes did not freely fill the t-tubule lumen of both species and <50% of the t-tubule volume was available to solutes >70 kDa. Detailed model fitting of FRAP data suggests that solute diffusion is additionally restricted at the t-tubular entrance and this effect was larger in mouse than in rabbit. The possible structural basis of this effect was investigated using electron microscopy and tomography. Near the cell surface, mouse t-tubules are more tortuous and filled with an electron-dense ground substance, previously identified as glycocalyx and a polyanionic mesh. Solute movement in the t-tubule network of rabbit and mouse appears to be explained by their different geometric properties, which impacts the use of these species for understanding t-tubule function and the consequences of changes associated with t-tubule disease.

Cardiac contraction depends on the efficient and coordinated propagation of action potentials across all cells in the heart. At the level of individual ventricular cardiomyocytes, uniform contraction is enabled by rapid action potential propagation throughout the entire cell volume via invaginations of the surface membrane called t-tubules (1, 2). T-tubules also permit additional signaling functions because they reduce the average distance from the cytosol to the extracellular space and thereby provide a conduit for solute exchange. This is especially important for the various channels, transporters, and receptors that are preferentially located within the t-tubular network (3). Previous studies have suggested that solute movement in the t-tubular system may be restricted; the exchange of K⁺ may be ∼4.5 times slower (4), and Ca²⁺ ∼8 times slower (5), than expected for free diffusion. It has also been suggested that solute movement in the murine t-system may be further impeded by an unidentified diffusion barrier (6). A recent study using fluorescence recovery after photobleaching (FRAP) of a 3-kDa solute in rat cardiomyocytes suggested that t-tubular diffusion was ∼22 times slower than free diffusion (7). However, this large decrease in solute movement has been questioned (8) and another study using local superfusion did not find such slow rates of solute exchange (9). The latter study suggested that local t-tubule constrictions and dilations are key determinants of solute movement, even though the diameter of rodent t-tubules (∼250 nm; ref. 10) is far larger than the molecular dimensions of typical solutes. Moreover, while optical methods such as FRAP can provide a means to probing the movement of labeled solutes, interpretation of fluorescence time course is complicated by the (often ill-defined) relationship between the illumination profile of the microscope system and the test object (11, 12).

Further complexity may arise from differences in the geometric organization of the t-tubule system between species. By using a combination of numerical and optical techniques we have examined how test solutes enter and diffuse within the t-tubule system of rabbit and mouse ventricular cardiomyocytes. Far from being a simple tubular network, we find evidence for molecular weight (MW)-sensitive effects on solute penetration, which differ between the species studied. These results have potentially important implications for interpretation of data regarding the functional role of the t-tubular system in health and disease and highlight the consequences of species differences in common animal cardiac models.

Results

Steady-State Solute Penetration into the T-Tubule Network.

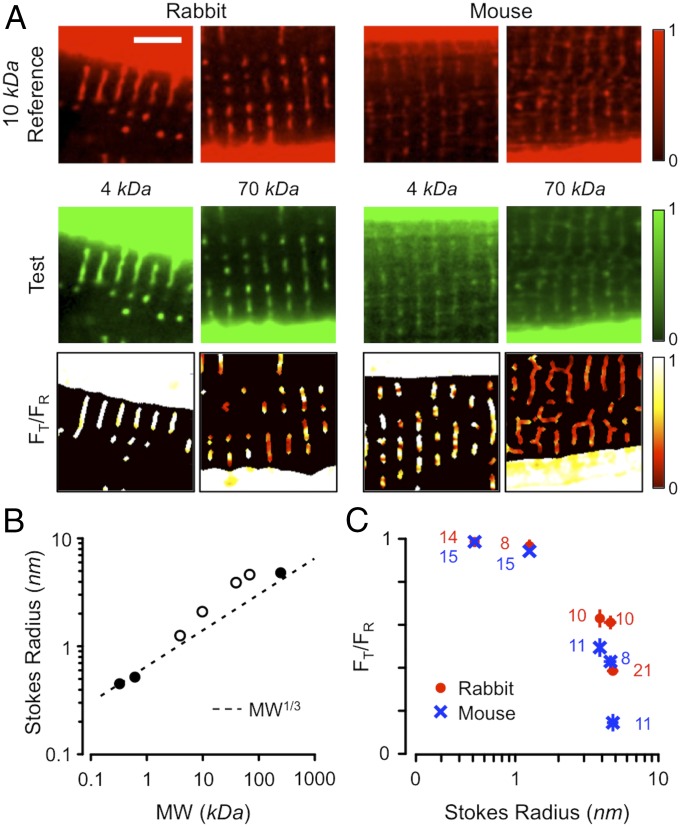
Solutes in the extracellular space should equilibrate throughout t-tubule if they have free access and Stokes radii smaller than the radius of the t-tubule lumen. This prediction was tested by immersing rabbit and mouse ventricular cardiomyocytes in fluorescent solutes with MWs varying from 0.6 to 240 kDa for >10 min. Fig. 1 shows images of rabbit (Fig. 1A, Left) and mouse (Fig. 1A, Right) cardiomyocytes incubated in a reference 10-kDa dextran-rhodamine B (Fig. 1A, Top) and 4- or 70-kDa test dextran-fluorescein solution (Fig. 1A, Middle). By normalizing the fluorescence signals to the bathing fluorescence and calculating the test to reference fluorescence ratio (F_T/F_R), the relative ability of the test solutes to penetrate the t-tubules can be determined (Fig. 1A, Bottom). It is apparent that, in steady state, the low-MW probe had greater penetrance in both species. Since steady-state differences in penetrance would not be expected for molecules much smaller than the tubule diameter, we measured the effective Stokes radii of our probes using fluorescence correlation spectroscopy (FCS). Our FCS measurements (Fig. 1B; see also SI Appendix, Fig. S1) showed that the Stokes radii of the test solutes were in reasonable agreement with that expected from MW^1/3 (dashed line), although the dextran probes (open symbols) were larger than predicted from this relationship, a result that may be explained by their branching structure (13). The measured Stokes radii from our FCS experiments were consistent with those in other reports (e.g., refs. 14 and 15). The dependence of F_T/F_R on Stokes radius (Fig. 1C) showed that solutes with Stokes radii >1 nm had reduced penetrance into the t-tubules. For example, for the ∼5-nm probe, steady-state penetration was reduced ∼2.5-fold in rabbit and ∼10-fold in mouse. Since t-tubule radii are on average ∼180 nm in rabbit and ∼85 nm in mouse (16), the clear reduction in penetrance was unexpected and, intriguingly, penetrance was greater in rabbit t-tubules than in mouse t-tubules.

Fig. 1.

Steady-state solute penetrance of t-tubules in rabbit and mouse ventricular cardiomyocytes. (A) Fluorescence images of rabbit (Left) and mouse (Right) cardiomyocytes bathed in a 10-kDa rhodamine B-linked dextran reference dye (Top) and 4- or 70-kDa fluorescein-linked dextran test dyes (Middle). Cells were incubated for >10 min to reach steady state. The test-to-reference ratio (F_T/F_R) images are shown (Bottom) (color table at the right). (Scale bar for all panels: 5 μm.) (B) Stokes radii of the test solutes, as measured with FCS, and compared with MW^1/3. Error bars for three to six determinations were generally smaller than the symbol size. Open symbols indicate dextran-based probes. (C) Dependence of F_T/F_R from rabbit (red circles) and mouse (blue crosses) on the measured Stokes radius. Numbers of independent determinations are indicated beside each data point.

Simulating FRAP in a Superfused Myocyte.

The rate of solute exchange between the t-tubule lumen and the bulk extracellular space can be probed using FRAP (7, 17). However, interpretation of FRAP data is complicated by the interaction of the illumination cone with sample geometry, a problem previously noted in analysis of FRAP time course in membrane diffusion experiments (e.g., ref. 18). Since bleaching in the bath outside the cell alters the solute source concentration, a recent study used local superfusion with the fluorescent solute to limit this effect (7).

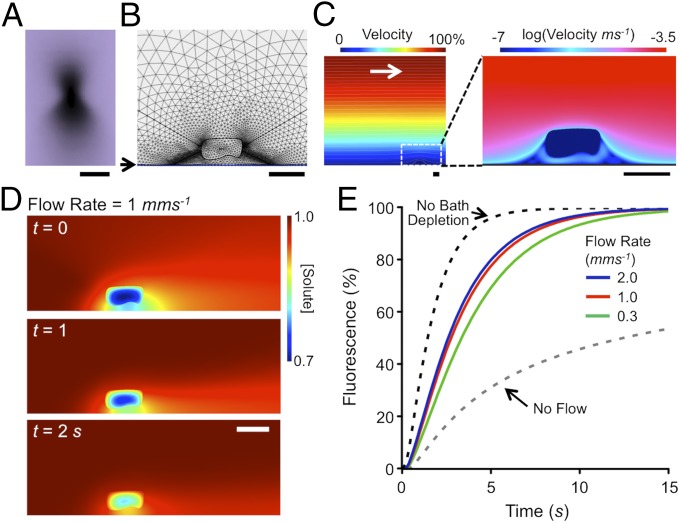
To examine the efficacy of this approach, we carried out computer simulations of FRAP in a flowing solute, incorporating cell geometry and microscope illumination profile (Fig. 2A). We solved the incompressible flow Navier–Stokes equations with reaction–diffusion in a nonlinear finite difference scheme using unstructured triangular and rectangular meshes (in COMSOL). This mesh is illustrated for a part of the computational volume in Fig. 2B and the general equations were

$$\rho \left(\frac{\partial \overrightarrow{\mathit{v}}}{\partial t}+\overrightarrow{\mathit{v}}\cdot \nabla \overrightarrow{\mathit{v}}\right)=-\nabla P+\mu {\nabla }^2\overrightarrow{\mathit{v}};\nabla \cdot \overrightarrow{\mathit{v}}=0;\hspace{0.17em}\frac{\partial C}{\partial t}+\overrightarrow{\mathit{v}}\cdot \nabla C=D{\nabla }^{2}C-\overrightarrow{I}\left(t\right)C,$$

where $\overrightarrow{\mathit{v}}$ is the velocity field, P pressure, C the concentration of fluorophore, µ the viscosity and ρ the density of water, D the local diffusion coefficient, and $\overrightarrow{I}\left(t\right)$ the laser bleaching rate (due to the illumination field and laser intensity). For efficiency, the problem was split into three regions: the bath where $\overrightarrow{I}\left(t\right)$ was always zero (i.e., outside the illumination cone), the extracellular illumination cone, and the myocyte as shown in Fig. 2B with continuity across these regions. Once steady state was achieved in the velocity field, $\overrightarrow{I}\left(t\right)$ was increased within the illumination cone to cause a bleaching rate that matched experimental data. After typical bleach durations (2–5 s), $\overrightarrow{I}\left(t\right)$ was then (re)set to zero to allow FRAP to occur. These calculations showed that the cell and the coverslip (on which the cell lies) profoundly change the solute exchange time course and FRAP. As shown in Fig. 2C, while the bulk solution had a parabolic velocity profile above the coverslip (as expected), the solvent flow velocity at the level of the cell (∼10 µm above the coverslip) was reduced to ∼16% of the average flow velocity. It is also clear from the streamlines that there are points of stagnation around the cell as well as boundary layer effects (which are accentuated by proximity to the coverslip) which reduce the rate of solute exchange and thereby alter the time course of FRAP within the cell.

Fig. 2.

Effect of bath superfusion on FRAP. (A) Photobleaching profile (x–z) from a 1.2 N.A. water immersion objective. (Scale bar: 5 μm.) (B) A part of the computational space showing position of cell above coverslip (at arrow) and limits of the FRAP illumination cone (produced by the objective N.A.) as well as the nonlinear mesh used for solving equations. (C) Calculation of local flow velocity above coverslip. Color scale at the top shows fraction of bulk flow velocity (2 mm⋅s⁻¹). A magnified region (white dashed box) surrounding the model is shown (Right) with flow velocities displayed on a log scale from 0.3 mm⋅s⁻¹ to 0.1 μm⋅s⁻¹ with colors as indicated at the top. (D) Simulation of FRAP at a bulk superfusion flow rate of 1 mm⋅s⁻¹ after the end of a 5-s bleach period (t = 0), and at t = 1 and t = 2 s. Diffusion coefficient of solute was assumed to be 1.45 × 10⁻¹⁰ m²⋅s⁻¹ for a 3-kDa dextran with diffusion inside the cell reduced by a factor of 22 (7). (Scale bars in B–D: 20 μm.) (E) FRAP inside the modeled cell at varying superfusion flow rates, from 0 to 2 mm⋅s⁻¹, as well as with no extracellular depletion effects.

The latter point is illustrated in Fig. 2D for a realistic transverse bulk solution flow rate of 1 mms⁻¹, with free (D) and apparent t-tubular (D_app) diffusion coefficients of 145 and 6.5 μm²/s, respectively (7). Immediately after the bleaching period (t = 0) and during FRAP at 1 s and 2 s, the solute gradients in the bath are still present and affect the resulting FRAP time course within the cell (Fig. 2E and Movie S3). It is notable that the simulated FRAP half-time (3.2 s) is almost the same as the 3.4 s reported by Scardigli et al. (7) for a 3-kDa dextran. These simulations also show that the FRAP time course is highly dependent on solute flow rate (and local cell geometry). Thus, while superfusion can help alleviate the no-flow induced slowing of FRAP (Fig. 2E), the rate of recovery will always be reduced by flow stagnation and unstirred layer effects.

FRAP in Rabbit and Mouse Ventricular T-Tubules.

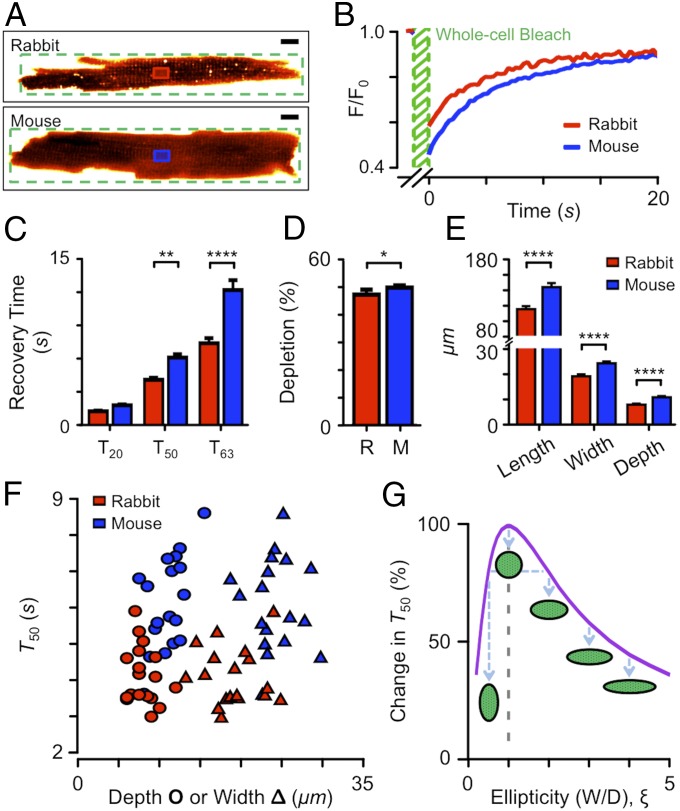
Paradoxically, uncertainties in local flow effects can be removed by having no flow and solving a simpler reaction–diffusion problem without Navier–Stokes (i.e., $\overrightarrow{\nu }=0)$. With this approach, we measured FRAP time course in cardiomyocytes from rabbit and mouse ventricles (Fig. 3A) using a 1-kDa probe to avoid the fluorescent probe penetration problem described above. In the exemplar traces shown in Fig. 3B, the half-time of FRAP was ∼5 s in rabbit and ∼6 s in mouse. This is faster than expected from the no-flow simulation shown in Fig. 2E after accounting for the difference in Stokes radius of the different solutes (Fig. 1B), suggesting that a t-tubular diffusion coefficient of 6.5 μm²⋅s⁻¹ (7) is likely to be too low.

Fig. 3.

Kinetics of solute entry into t-tubules examined by FRAP with no solute flow. (A) Exemplar fluorescence images of rabbit and mouse cardiomyocytes in the ∼1-kDa test solute. The FRAP bleach region (green) and region of interest where recovery was tracked (red for rabbit, blue for mouse) are shown. (Scale bars: 10 μm.) (B) FRAP time course for a rabbit (red) and mouse (blue) cardiomyocytes. (C) Time for 20%, 50%, and 63% recovery. **P < 0.01; ****P < 0.001, two-way ANOVA with Bonferroni post hoc analysis. (D) Depth of photobleaching during FRAP. *P < 0.05, Mann–Whitney U test. (E) Length, width, and depth of cardiomyocytes used for FRAP. ****P < 0.001, for rabbit vs. mouse Mann–Whitney U test. (F) FRAP T₅₀ as a function of cell depth (circles) or width (triangles) as measured from confocal z-sections. For C–F, red indicates rabbit (n = 18) and blue mouse (n = 18) cardiomyocytes. (G) Calculated change in T₅₀ as a function of cell cross-section ellipticity (width/depth; illustrated by cartoons). Note that cells do not always orient conveniently on the coverslip so that both cell width (in x–y) and cell depth (in z) need to be measured.

There were systematic differences in FRAP time constants (Fig. 3C), with the rabbit cardiomyocytes generally exchanging solute more quickly. If solute exchange within the rabbit t-system is faster than in mouse (as simple interpretation of these data suggests), then the extent of depletion during the bleaching phase of FRAP should be reduced, and this was indeed the case (Fig. 3D).

Effect of Cell Size and Ellipticity.

For diffusion problems within a scalable isomorphic geometry, the time taken for solute movement is proportional to the square of the geometry scale (19) and therefore cell size will play an important role in the measured time course of FRAP. In these experiments, rabbit cells (n = 18) were generally smaller than mouse cells (n = 18) in length (115.0 ± 3.8 vs. 143.5 ± 5.2 μm, P = 0.002), width (19.1 ± 0.8 vs. 24.2 ± 0.7 μm, P < 0.0001), and depth (8.0 ± 0.4 vs. 10.9 ± 0.5 μm, P < 0.0001) (Fig. 3E). Fig. 3F shows that for a given cell width (or depth) FRAP was generally slower in mouse than in rabbit. A part of the variance in FRAP time course between cells is also due to the noncircular cell cross-sections (note the separation between cell width and depth data points in Fig. 3F). Diffusion in elliptical cells can be calculated using a doubly infinite series of exponentials (20) but, given the computational model described above, it was simpler to solve the diffusion equations for elliptical cylinders numerically. Fig. 3G shows that as cell cross-section ellipticity ($\xi$, here defined as cell width/depth) deviates from 1.0, the apparent FRAP half-time will decrease. Thus, for the range of ellipticity measured for rabbit ($\xi$ = 1.4–4.1, $\overline{\xi }$ = 2.50 ± 0.18, n = 18) and mouse ($\xi$ = 1.5–3.4, $\overline{\xi }$ = 2.27 ± 0.1, n = 18) cells, D_app would be overestimated by up to 2.3 times if a circular myocyte cross-section is assumed.

T-Tubule Tortuosity.

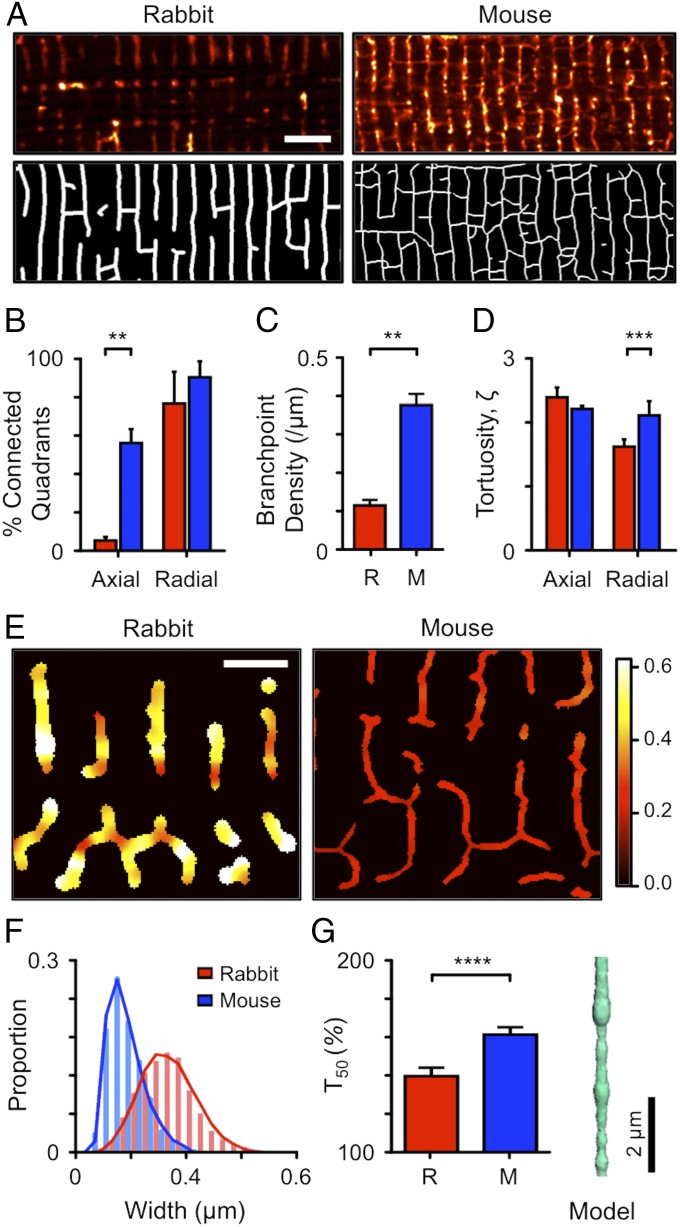
The tortuosity ($\zeta )$ of the t-system (21) will also contribute to a reduction in D_app inside the t-system, but this has only been measured (to our knowledge) for human myocytes in a thin (2.2 μm) sample by serial block face scanning EM (22). We therefore calculated the t-tubule connectivity and tortuosity from confocal images of the t-tubule system (Fig. 4A, Top) which were skeletonized (Fig. 4A, Bottom) and processed by the new TauFactor algorithm (23) in 6- by 6-μm quadrants. The low density of axial tubules in rabbit ventricular cells, compared with mouse, is shown by the low proportion of image quadrants that were internally connected (Fig. 4B) and reduced branch-point density in this species (Fig. 4C). Fig. 4D shows that tortuosity also differed between species, with mouse t-tubules ($\overline{\zeta }=$ 2.04 ± 0.22, n = 41) being ∼1.4 times as tortuous as rabbit t-tubules ($\overline{\zeta }=$ 1.47 ± 0.12, n = 20; P < 0.01). This increased tortuosity will decrease D_app within the t-system of mice (compared with rabbits) by a factor of ∼1.4² and thereby significantly increase the time for penetrating solutes to equilibrate across the cell.

Fig. 4.

T-tubule morphology in rabbit and mouse ventricular cardiomyocytes. (A) Confocal images of rabbit (Left) and mouse (Right) t-tubules labeled with di-8-ANEPPS (Top) and corresponding binary images (Bottom). For illustrative purposes, the rabbit and mouse t-tubule diameters are set to their means of 360 and 170 nm (respectively) (16). (Scale bar: 5 μm.) (B) Proportion of 6- × 6-μm quadrants that are internally connected in the directions shown for rabbit (n = 20 quadrants, 6 cells) and mouse (n = 48 quadrants, 5 cells; **P < 0.01, two-way ANOVA with Bonferroni post hoc analysis). (C) Branch-point density of t-tubule network. **P < 0.01, Mann–Whitney U test. (D) Tortuosity (ζ) of quadrants calculated by TauFactor (23). ***P < 0.005, two-way ANOVA with Bonferroni post hoc test. (E) Local variations in t-tubule width measured using a shape-based analysis method (16). The colors indicate the local width in micrometers with the width color scale at the right. (Scale bar: 2 µm.) (F) Distribution of t-tubule widths in living rabbit (n = 11) and mouse (n = 12) cardiomyocytes (total t-tubule length analyzed was ∼1 mm). The continuous curve was randomly sampled for simulations. (G) Effect of t-tubule varicosities in rabbit (n = 50 simulations) and mouse (n = 50 simulations) on time for 50% solute exchange compared with a circular cylinder of the same length and mean diameter. ****P < 0.001, Mann–Whitney U test. The inset at the right shows an exemplar simulation model used in calculations.

T-Tubule Varicosities.

T-tubules do not have constant cross-sections but can vary locally in diameter by a factor of more than 2 (10, 16, 24). Such local varicosities (or constrictions) can reduce the apparent rate of diffusion below that expected for simple diffusion in radial tubes with constant cross-section (9). We have recently developed an optical method for estimating the local t-tubule diameter by simultaneously labeling t-tubule membranes and lumens with two fluorescent probes (16). The results of such analyses are illustrated in Fig. 4E, with histograms of t-tubule diameters in rabbit and mouse summarized in Fig. 4F. To estimate the effect of these variations in t-tubule diameter on solute exchange, we constructed linearized t-tubule models with the same distribution of diameters. The results of 100 simulations are shown in Fig. 4G, with an exemplar t-tubule geometry provided as an inset. This analysis revealed that variations in t-tubule diameter can reduce D_app by a factor of 1.32 ± 0.04 (n = 50) and 1.49 ± 0.03 (n = 50) in rabbit and mouse, respectively.

Computational Analysis of FRAP to Obtain D_app.

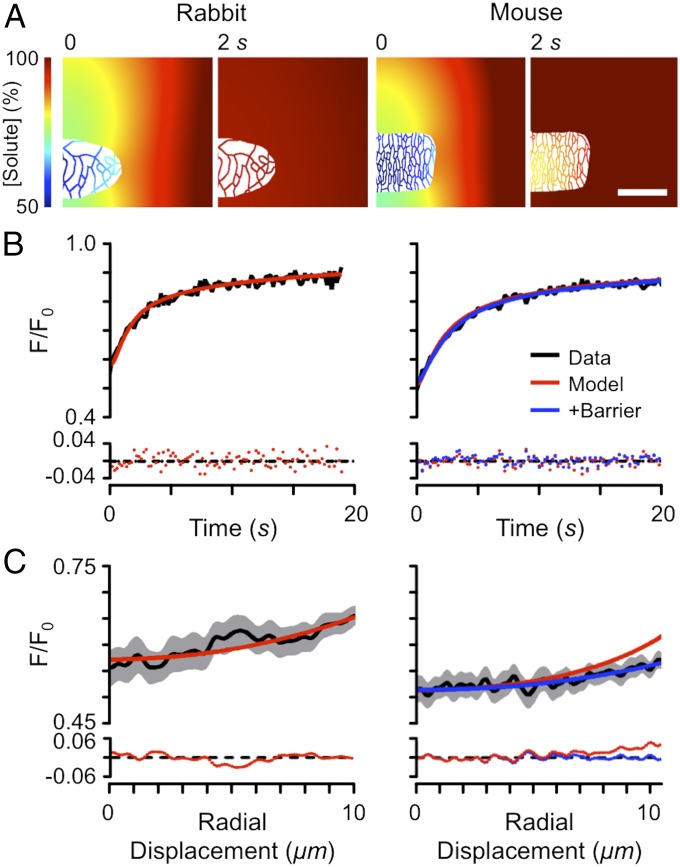
To examine the extent to which the above factors could explain the D_app observed during FRAP, we carried out detailed modeling of FRAP using measured cell and illumination geometries (Fig. 5A). Fig. 5B shows the fit of simulated FRAP time course to experimental data and illustrates that the model is able to adequately explain the time course of FRAP. While the model fits to rabbit data generally showed no systematic residuals, fitting mouse data proved more problematic, particularly in the radial profile of fluorescence, as shown in Fig. 5C. The flatter radial profile seen in the mouse indicates that there might be a barrier to diffusion near the cell surface and, as shown in Fig. 5C, Right, adding a thin region of reduced diffusion near the outer cell surface markedly improved the fit to the observed fluorescence profile. On average, D_app inside the t-tubule lumen was 52 ± 14 (n = 5) µm²⋅s⁻¹ and 23 ± 6 (n = 5) µm²⋅s⁻¹ in rabbit and mouse, respectively, which is ∼5–12× slower than free diffusion but significantly faster than the 22–35× reduction in free diffusion recently reported for mouse and rat cardiomyocytes (7, 9). Importantly, our measured reduction in apparent diffusion coefficient is compatible with the 8× reduction in free diffusion of K⁺ estimated electrophysiologically (5).

Fig. 5.

Computational modeling of FRAP in rabbit (Left) and mouse (Right) cardiomyocytes, incorporating measured cell dimensions, t-tubule distribution, and illumination geometry. (A) Solute concentration at t = 0 and 2 s after photobleaching. (Scale bar: 20 μm.) (B) FRAP time course with model fit and residual errors (Bottom). (C) Spatial fluorescence profiles at t = 0 s, corresponding model fits and residual errors (Bottom). For B and C, red lines show model fits when t-tubule D_app was uniform across the cell. Blue lines show fits incorporating a thin (0.2 μm) region of slowed diffusion (reduced to 1.5% of the free t-tubule diffusion coefficient) at the t-tubule mouth.

Cellular Origins of a Functional Near-Surface Barrier in Mouse.

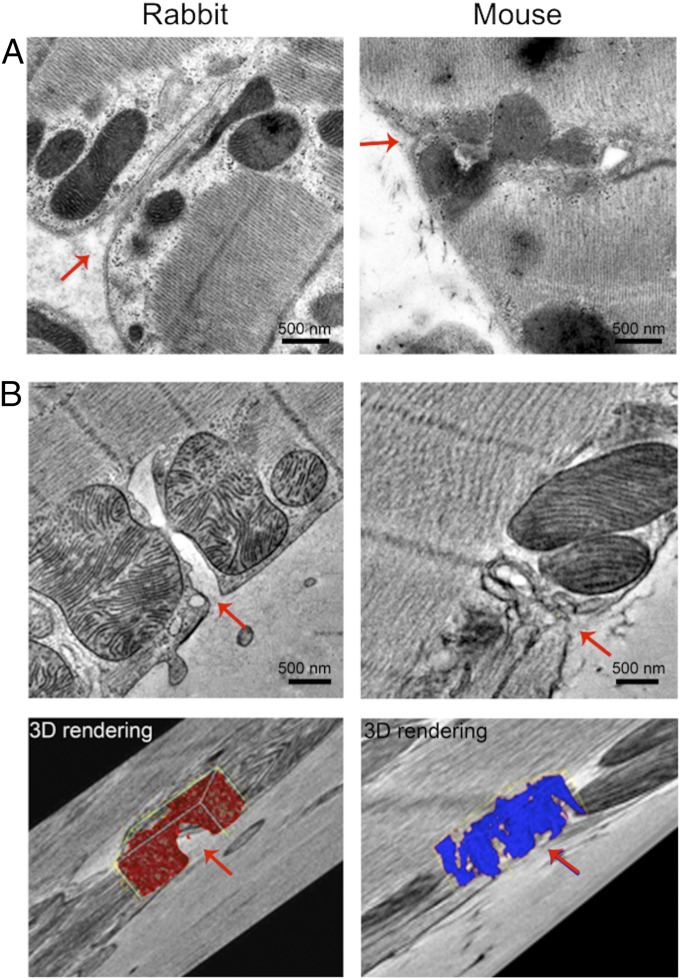
To investigate the possible physical origin of the reduced penetrance near the surface of mouse cardiomyocytes, we used EM and tomography to compare peripheral t-tubule lumens of cardiomyocytes from mouse and rabbit. As shown in Fig. 6A in thin sections, rabbit t-tubule mouths appear quite open and generally continuous with an approximately linear t-tubule lumen near the cell outer surface. Closer inspection revealed ground substance within the mouth and body of the t-tubule, consistent with the presence of a polyanionic mesh within the t-tubule lumen (25). In contrast, mouse t-tubules showed marked tortuosity and, near the cell surface, their lumen was often indistinct and hard to follow. To overcome the problem of following such complex structures in thin sections, we used electron tomography of thicker sections (∼400 nm, voxel size ∼1.0 nm³) (Fig. 6B), which showed that, in rabbit, the t-tubules join the cell surface without any apparent constrictions, unlike in mouse. The ground substance (as identified by computer thresholding) appeared to only partially occlude the t-tubule mouth in rabbit, but in mouse the ground substance appeared as a more extensive barrier (see 3D rendering in Fig. 6B). This structural difference may explain both the reduced penetrance of higher-MW solutes and the surface barrier implied by our FRAP simulations.

Fig. 6.

Electron microscopy and tomography of rabbit (Left) and mouse (Right) cardiomyocyte t-tubule at the cell surface. (A) Electron micrographs of t-tubule entrances (indicated by red arrows). Note the basement membrane and fuzzy ground substance. (B) Electron tomograms of t-tubule entrances with corresponding 3D reconstructions of the ground substance. Note that for rabbit (red) the ground substance appears to leave a visible lumen (red arrow, Bottom), while in mouse (blue) the ground substance appears more uniform across the entire width of the lumen.

Discussion

In this study, we show both steady-state and kinetic differences in the rate of solute movement within the t-tubular systems of rabbits and mice. These differences are dependent on the MW of diffusing particles, with pronounced differences being seen in dextrans having a MW >1 kDa. In mouse, the greater reduction in steady-state penetrance of higher-MW substances may be related to the greater degree of access restriction and the presence of more ground substance (26) in the mouth regions of the t-system. The efficiency of this functional barrier would also be enhanced by the generally smaller diameter of mouse t-tubules compared with rabbit t-tubules (16). Computer simulations showed that this barrier reduces internal radial gradients of solute by slowing solute exchange with the bulk extracellular space.

Once this barrier is passed, diffusion inside rabbit and mouse t-tubular systems proceeds similarly. The time course of equilibration for a given solute in a myocyte is then affected by (i) cell radius and ellipticity and (ii) t-tubule geometric effects including tortuosity, local varicosities/constrictions, longitudinal t-tubule connections, and possible wall effects (discussed below). A key question is: To what extent do each of the latter factors determine solute movement?

The effect of cell width on the rate of solute movement has been appreciated since the time of A. V. Hill (27), and diffusion time is proportional to the radius² for a circular cell cross-section. Although the assumption of circular cross-section leads to relatively simple diffusion equations, we found that the cell width-to-depth ratio ranged from 1.4 to 4.1, in accordance with the earlier measurements of Satoh et al. (28). This suggests that a cardiomyocyte cross-section may be better approximated by an ellipse. Ellipticity causes the net direction of diffusion to change from purely radial (in the case of a circular cylinder) to more nearly parallel (flat sheet) in a highly elliptical body and this can speed recovery by up to ∼50% (Fig. 3G). We avoided the uncertainty in ellipticity by measuring actual cell cross-sections and incorporating that data in the models. Physiologically, having a more elliptical cross-section carries the benefit of speeding diffusion for a given cross-sectional area as well as potentially improving packing within the tissue.

T-tubules do not run in straight lines but wrap irregularly around bundles of myofilaments (29). This causes an increase in the path length (the tortuosity) for diffusion inside t-tubules and increases diffusion time with the square of the tortuosity. Tortuosity has been previously estimated to be ∼1.04 in human (22), ∼2 in rat (10), and ∼2.8 (5) in guinea pig. However, quantitative evaluation of tortuosity is complicated by uncertainties in where the centerline of a complex thin t-tubule should lie, and by the fact that t-tubules themselves are not simple cylindrical structures (as often assumed). It is difficult to follow t-tubules for large distances in thin EM sections and we suggest that this may explain the very low tortuosity reported for human (22) when confocal images appear to show greater tortuosity (see ref. 30).

Perhaps paradoxically, the presence of longitudinal (or axial) t-tubules also slows the rate of radial diffusion (9). This occurs because the longitudinal t-tubules act as a sink for the radially diffusing solute, so that their effect depends not only on their relative volume but also on their distribution (SI Appendix, Fig. S2). To our knowledge, the impact of this factor has not been previously quantified, although the presence of extensive axial components in ventricular t-tubules has been known from early EM (31, 32) and later confocal imaging studies (ref. 10 and as shown here). Since longitudinal t-tubules do not form a regular structure (cf. Fig. 4A), analytical solutions to the problem do not exist, so, again, we simulated their effect (SI Appendix, Fig. S2) using confocal image data (Fig. 4A) which confirmed that radial solute movement is significantly reduced (up to ∼1.8-fold) by the presence of connected longitudinal tubules (Fig. 7). This reduction is somewhat larger than recently suggested (9) and could be even larger in atrial cells, compared with ventricular cardiomyocytes, as they have a larger ratio of longitudinal to transversal t-tubular elements (33).

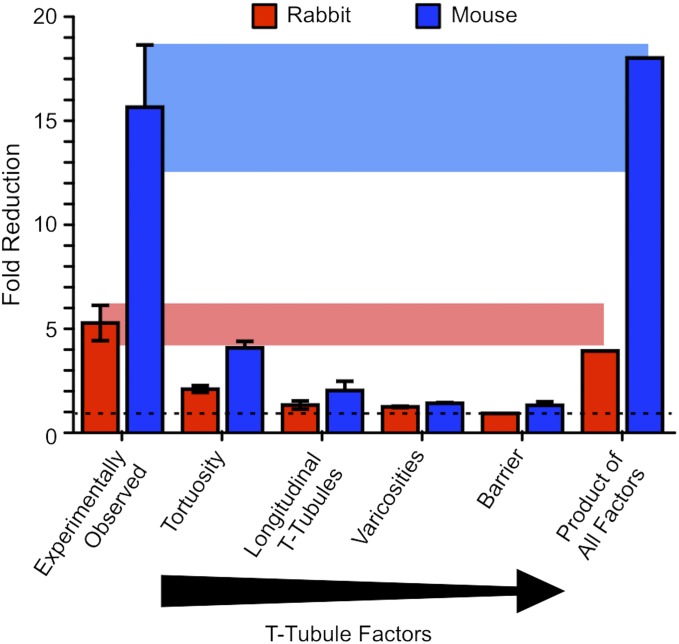
Fig. 7.

Relative contribution of t-tubule geometric factors on solute movement within the t-tubule system for rabbit (red bars) and mouse (blue bars) ventricular cardiomyocytes. Bars show fold reduction in D_app (from left to right) as calculated from FRAP experiments in rabbit (n = 5) and mouse (n = 5) cardiomyocytes and reduction explainable by (i) an increase in path length due to tortuosity, (ii) the contribution from longitudinal t-tubules, (iii) variations in tubule width (varicosities), and (iv) a thin barrier of slowed diffusion in the t-tubule entrances near the cell surface. The rightmost set of bars show the product of these four t-tubule geometric factors, representing their combined effect. The shaded areas link the observed values (leftmost set of bars) to the product of factors to indicate their similarity.

Recently, it has been suggested that local varicosities, rather than tortuosity, along mouse t-tubules may be responsible for most of the observed slowing in solute movement (9). However, our analysis of measured t-tubule geometry shows that tortuosity has a somewhat larger effect than varicosities on solute exchange time (Fig. 7). The net effect of these t-tubule geometric factors is to reduce the rate of solute movement by a factor of ∼4 in rabbit and ∼18 in mouse (Fig. 7). This appears to be sufficient to explain most of the experimentally observed reduction in t-tubule solute transport and removes the need to invoke a large reduction in the local free diffusion coefficient.

The presence of the glycocalyx (34) at the cell surface reduces the effective diameter of a t-tubule, and the basement membrane and ground substance within the t-tubule will impede the free diffusion of ions (35) and the solute probes used here. In rat ventricular myocytes, the ground substance within the t-tubule prevents particles larger than 11 nm from entering (35), which appears consistent with the presence of a polyanionic mesh within the t-tubule lumen (25). We cannot directly measure the reduction in t-tubule movement that might arise from the glycocalyx, but we note that a reduction of effective t-tubule radius by 50 nm (34) would produce a solute surface drag effect (36) which will only reduce the diffusion coefficient of 1-nm particles by ∼10% in a 100-nm-radius t-tubule. We therefore suggest that the glyocalyx and mesh-like ground substance within the t-tubule may be sufficient to explain any residual reduction in free diffusion that might remain unexplained by the above geometric factors.

Previous work has shown that as human heart failure progresses t-tubules can dilate, create more varicosities, and become more tortuous, creating microstructural changes that are highly correlated with the contractile deficit (37). In light of results shown here, the relative impact of these changes can be assessed (Fig. 7) to understand how t-tubule disease processes will affect the diffusion of solutes into, and out of, the cardiomyocyte.

Methods

Myocyte Preparation.

All procedures carried full ethical approval from the Animal Welfare and Ethical Review Body (AWERB) of the University of Bristol and complied with relevant UK legislation and were in accord with the Guide for the Care and Use of Laboratory Animals (38). Ventricular cardiomyocytes were enzymatically isolated from the hearts of male mice (C57BL/6, 25 g) or rabbits (New Zealand White, 2.5 kg), as described previously (39, 40). Further details can be found in SI Appendix.

EM and Analysis.

T-tubule structure was examined using EM after high-pressure freezing (41) and freeze substitution (1% osmium tetroxide and 0.1% uranyl acetate in acetone). Sections were cut and stained with uranyl acetate and lead citrate and coated with 15-nm colloidal gold particles. Ultrathin (80 nm) sections were analyzed using a 100-kV Tecnai 12 transmission electron microscope (FEI Co.) fitted with a TVIPS F214 digital camera. Thick sections (380 nm) were analyzed using a 200-kV Tecnai T20 transmission electron microscope fitted with an Eagle 4k × 4k camera (FEI Co.). For the latter, images in a double-tilt series (with 90° sample rotation in between two series) were collected between ±70° using the Saxton tilt increment scheme (42). Tilt series were aligned, reconstructed, and combined using IMOD software (43, 44).

Confocal Microscopy and Analysis.

Functional studies were performed using a laser-scanning confocal system (LSM 880; Carl Zeiss). Cells were allowed to settle in a chamber with an uncoated glass coverslip bottom and imaged with the confocal pinhole set to 1 Airy unit, and with a 40 × 1.2 N.A. water immersion objective. Data were obtained at 12-bit depth, with voxel size set at 0.12 μm in plane (x–y) and 0.3 μm along the optical axis (z). Analysis of confocal image stacks was achieved using custom and in-built routines in MATLAB (R2016a; MathWorks Inc.).

FCS.

Direct measurement of the (average) hydrodynamic radius of the solutes was performed using FCS. Fluorescence intensity of the probe solutions was measured with the confocal pinhole set to 0.7 Airy units. The solution was diluted to achieve ∼10 average particles within the confocal volume. The autocorrelation of the fluorescence fluctuations was calculated for each of 30 sweeps, averaged, and the resulting correlogram fitted with

$$G\left(\tau \right)=1+G_t\left(\tau \right)\cdot G_d\left(\tau \right),$$

where

$$G_t\left(\tau \right)=1+\frac{T_t\cdot e^{\raisebox{1ex}{$-\tau $}\!\left/ \!\raisebox{-1ex}{$T_t$}\right.}}{1-T_t}$$

and

$$G_d\left(\tau \right)=\frac{\varphi }{1+{\left(\frac{\tau }{{\tau }_d}\right)}^{\alpha }+{\left(1+{\left(\frac{\tau }{{\tau }_d}\right)}^{\alpha }\cdot \frac{1}{S^2}\right)}^{0.5}}.$$

The second equation reflects the presence of a fluorescence triplet state, and the third equation is the diffusive term. Exemplar correlograms are shown in SI Appendix, Fig. S1.

T-Tubule Penetrance at Steady State.

Since the ability of molecules to enter the t-system should depend on tubule and molecule size, isolated cardiomyocytes were superfused with solutions containing solutes of increasing MW. As a positive control and reference, 0.4 mM of 10-kDa rhodamine B dextran (Life Technologies) was applied to each cell. The test compounds used were fluorescein-dextran 0.2–0.4 mmol⋅L⁻¹ solutions of 3- to 70-kDa average MW (Life Technologies) or calcein (623 Da; Sigma-Aldrich). All solutions were applied to the cells for ∼10 min before imaging. Fluorescein was excited at 488 nm and emission recorded from 493 to 553 nm; rhodamine B was excited at 543 nm and emission recorded from 553 to 700 nm.

A t-tubule skeleton was created from the reference dye signal to define points for t-tubule and cytosol measurements. For both dyes, the local cytosol fluorescence intensity was subtracted from the t-tubule signal and then normalized to the signal in the bath outside the cell. The signal from the test dye was then divided by that of the reference dye to give a signal (R_TT) that depended only on local test dye penetrance (compared with rhodamine B) since the local volume of the t-tubule was cancelled by the division.

Diffusion Within the T-Tubule Network.

The rate of diffusion within the t-tubular network was assessed using FRAP. The extracellular space and t-tubule lumen were labeled by adding 0.2 mmol⋅L⁻¹ Fluo-4 pentapotassium salt (927 Da; Life Technologies) to the perfusion bath and allowed to equilibrate for ∼10 min. Cell regions were typically bleached at 100% laser power for 3 s, which was sufficient to bleach ∼50% of the initial fluorescence. The time course of recovery was quantified by fitting FRAP traces with a double-exponential function and evaluating the fit for the time to recover by 20% (T₂₀), 50% (T₅₀), and 63% (T₆₃).

Computational Analysis of FRAP.

To analyze the FRAP signal, a computer model was constructed in the COMSOL Multiphysics modeling system. The model included the measured illumination cone of the microscope and cell width and depth derived from confocal images of the cell. The focal position and height of the cell above the coverslip were also measured and incorporated into the model. The model consisted of ∼16,000 unstructured elements and the finite difference scheme for local diffusion during simulated FRAP experiments could be solved in ∼10 min on a quad core Intel i7 processor laptop computer. The coverslip surface (cs) formed a thin “no-slip” boundary where ${\overrightarrow{v}}_{cs}=\nabla {\overrightarrow{v}}_{cs}=0$ and calculations (and meshing) near this boundary layer were aided by adding a local rectangular mesh. The solution to the diffusion equation within the cell gave results that were equivalent to using orthogonal elliptical coordinates (45) for numbers of elements exceeding 100 (not shown). The effect of cell ellipticity (ξ, defined as the measured cell width/cell depth) on apparent D_app shown in Fig. 3G was examined by adjusting model cell width and depth for a constant cell cross-sectional area and solving the diffusion equation with COMSOL:

$$\frac{\partial C}{\partial t}=D{\nabla }^{2}C\hspace{0.17em};\text{with Dirichlet boundary}\hspace{0.17em}C\left(x,y\right)=k\hspace{0.17em}\forall \left(\text{x},\text{y}\right)\in \partial \Omega .$$

Varicosities along a t-tubule were reproduced in silico by random (Gaussian-distributed) assignment of widths sampled from live-cell data obtained from rabbit and mouse (Fig. 4 F and G). The rate of diffusion along such a tubule was then compared with a circular cylinder of equal length (10 µm).

Data Presentation.

Where appropriate, mean data are presented with error bars representing one SEM. Statistical testing was performed using Mann–Whitney U test or two-way ANOVA tests as appropriate, where P < 0.05 was taken as the limit for statistical significance.