Picture perception reveals mental geometry of 3D scene inferences

Significance

We show that, in both 3D scene understanding and picture perception, observers mentally apply projective geometry to retinal images. Reliance on the same geometrical function is revealed by the surprisingly close agreement between observers in making judgments of 3D object poses. These judgments are in accordance with that predicted by a back-projection from retinal orientations to 3D poses, but are distorted by a bias to see poses as closer to fronto-parallel. Reliance on retinal images explains distortions in perceptions of real scenes, and invariance in pictures, including the classical conundrum of why certain image features always point at the observer regardless of viewpoint. These results have implications for investigating 3D scene inferences in biological systems, and designing machine vision systems.

Abstract

Pose estimation of objects in real scenes is critically important for biological and machine visual systems, but little is known of how humans infer 3D poses from 2D retinal images. We show unexpectedly remarkable agreement in the 3D poses different observers estimate from pictures. We further show that all observers apply the same inferential rule from all viewpoints, utilizing the geometrically derived back-transform from retinal images to actual 3D scenes. Pose estimations are altered by a fronto-parallel bias, and by image distortions that appear to tilt the ground plane. We used pictures of single sticks or pairs of joined sticks taken from different camera angles. Observers viewed these from five directions, and matched the perceived pose of each stick by rotating an arrow on a horizontal touchscreen. The projection of each 3D stick to the 2D picture, and then onto the retina, is described by an invertible trigonometric expression. The inverted expression yields the back-projection for each object pose, camera elevation, and observer viewpoint. We show that a model that uses the back-projection, modulated by just two free parameters, explains 560 pose estimates per observer. By considering changes in retinal image orientations due to position and elevation of limbs, the model also explains perceived limb poses in a complex scene of two bodies lying on the ground. The inferential rules simply explain both perceptual invariance and dramatic distortions in poses of real and pictured objects, and show the benefits of incorporating projective geometry of light into mental inferences about 3D scenes.

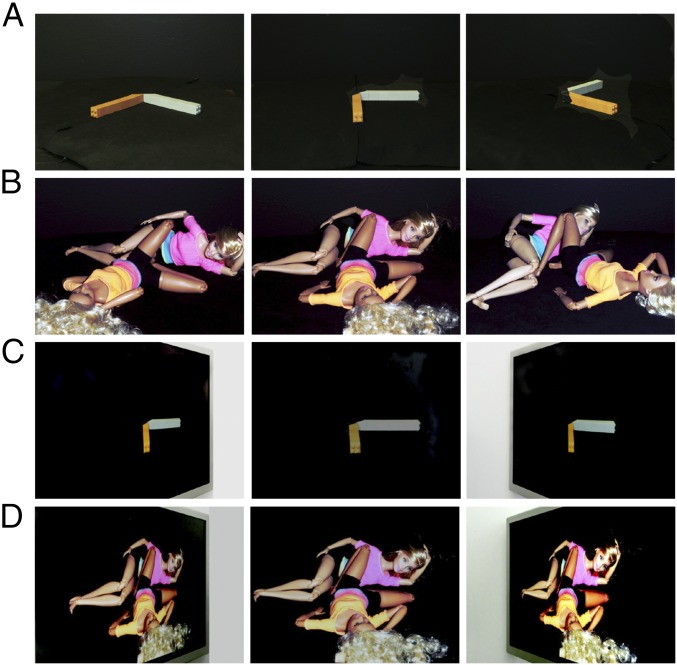
The three panels in Fig. 1A, show one pair of connected sticks lying on the ground, pictured from different camera positions. The angle between the perceived poses of the two sticks changes from obtuse (Fig. 1A, Left) to approximately orthogonal (Fig. 1A, Center) to acute (Fig. 1A, Right), illustrating striking variations in perception of a fixed 3D scene across viewpoints. Fig. 1B shows two dolls lying on the ground, pictured from different camera positions. The perceived angle between the two bodies changes from obtuse (Fig. 1B, Left) to approximately orthogonal (Fig. 1B, Right). The situation seems quite different when a picture of the 3D scene in Fig. 1A, Center is viewed from different angles in Fig. 1C. The entire scene seemingly rotates with the viewpoint, so that perceived poses are almost invariant with regard to the observer, e.g., the brown stick points to the observer regardless of screen slant. Similarly, in Fig. 1D, the doll in front always points toward the observer, even when the viewpoint shifts by 120°. The tableau in Fig. 1D was based on a painting by Phillip Pearlstein that appears to change a lot with viewpoint. It has the virtue of examining pose estimation of human-like limbs located in many positions in the scene, some flat on the ground, whereas others could be elevated on one side or float above the ground. As opposed to relative poses, relative sizes of body parts change more in oblique views of the 2D picture than of the 3D scene. Interestingly, extremely oblique views of the pictures appear as if the scene tilts toward the observer. We present quantification of these observations, and show that a single model explains both perceptual invariance (1–4) and dramatic distortions (5–9) of pose estimation in different views of 3D scenes and their pictures.

Fig. 1.

Perceptual distortions in a 3D scene and 2D images of the scene. (A) Different camera views of one scene of two sticks connected at a right angle. (B) Different camera views of the same scene of two bodies lying together. (C) Different observer views of the central image in A. (D) Different observer views of the center image from B.

Results

Geometry of Pose Estimation in 3D Scenes.

For a camera elevation of ${\varphi }_C$, a stick lying at the center of the ground plane with a pose angle of ${\mathrm{\Omega }}_T$ uniquely projects to the orientation, ${\theta }_S$, on the picture plane (SI Appendix, Fig. S1A; derivation in SI Appendix, Supplemental Methods),

$${\theta }_S=\mathrm{atan}\left(\tan \left({\mathrm{\Omega }}_T\right)\sin \left({\varphi }_C\right)\right).$$ [1]

Seen fronto-parallel to the picture plane (observer viewing angle ${\varphi }_V=0$), the orientation on the retina ${\theta }_R={\theta }_S$. As shown by the graph of equation 1 in SI Appendix, Fig. S1A, sticks pointing directly at or away from the observer along the line of sight (${\mathrm{\Omega }}_T=$ 90° or 270°) always project to vertical (${\theta }_R=$ 90° or 270°) in the retinal plane, while sticks parallel to the observer project to horizontal in the retinal plane. For intermediate pose angles, there is a periodic modulation around the unit diagonal. If observers can assume that the imaged stick is lying on the ground in one piece (10), they can use the back-projection of Eq. 1 to estimate the physical 3D pose from the retinal orientation,

$${\mathrm{\Omega }}_T=\mathrm{atan}\left(\tan \left({\theta }_R\right)/\sin \left({\varphi }_c\right)\right).$$ [2]

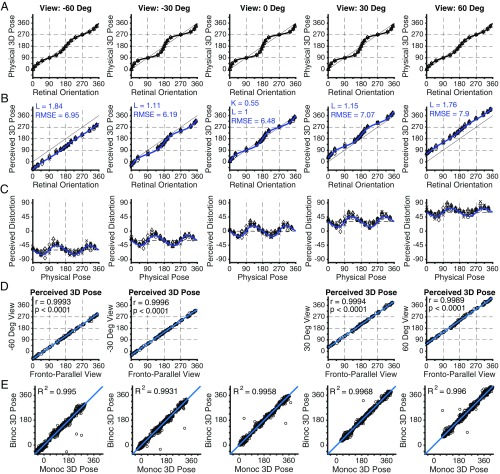
Fig. 2A, center column (View 0 Deg) shows the back-projection curve for physical 3D poses against their 2D retinal orientation.

Fig. 2.

Perceived 3D poses from retinal projections. Perceived poses of sticks. Columns represent different observer viewpoints. (A) The back-projection from the 2D retinal orientation of each stick to the true 3D physical pose on the ground plane. Curves show the continuous back-projection function. (B) Perceived 3D pose against retinal orientation, averaged across eight observers. Each observer made seven judgments for each physical pose, represented by different symbols (o, single stick; x, each of acute angle paired sticks; ∆, each of right angle paired sticks; ◊ , each of obtuse angle paired sticks), binocularly and monocularly. Curves represent the best-fitting model based on the back-projection. The fronto-parallel bias as estimated from the fronto-parallel viewing condition (View 0 Deg column) is reported as K. The multiplying parameter on the camera elevation at each viewpoint is reported as L. The RMSE is given for each viewing condition. (C) Perceived distortion (perceived pose minus physical pose) is plotted against the physical 3D pose. Curves represent the distortion predicted from the best fit of the model shown above. (D) Perceived 3D pose at each viewing angle is plotted versus perceived 3D pose from the fronto-parallel viewing condition. The blue line is the line of unit slope shifted so that the y intercept is equal to the viewing angle. The correlation is reported as r. (E) Binocular 3D pose percept plotted against monocular 3D pose percept. Blue line is the line of unity. Fit of the line of unity is shown as R².

To study how humans estimate 3D poses, we used sticks lying on the ground at 16 equally spaced poses, either alone or joined to another stick at an angle of 45°, 90°, or 135°. Observers viewed images of the scene from in front of a monitor, consistent with camera distance (11), recreating a monocular view of the 3D scene through a clear window. They estimated the 3D pose of each stick relative to themselves by adjusting a clock hand on a horizontal touchscreen to be parallel to the stick’s perceived pose (SI Appendix, Fig. S1C). Perceived 3D poses are plotted in Fig. 2B, View 0 Deg column against the 2D retinal orientations of each stick, averaged across eight observers. Each observer ran binocular and monocular viewing conditions, and the results were combined because they were very similar (Fig. 2E). Perceived poses fall on a function of retinal 2D orientation similar to the geometrical back-transform, but the modulation around the diagonal is shallower. Poses pointing directly toward or away from the observer were correctly perceived, as were those parallel to the observer. The shallowness of the function arises from oblique poses being perceived as being closer to fronto-parallel than veridical. This can be seen in Fig. 2C, View 0 Deg column, which shows the veridical pose subtracted from the perceived pose as a function of the physical 3D pose. Negative distortions for physical poses between 0° and 90° indicate shifts toward 0°, and positive distortions for physical poses between 90° and 180° indicate shifts toward 180°. The View 0 Deg column of SI Appendix, Fig. S2 shows perceived poses as functions of retinal orientations for eight observers, some of whom had no psychophysical experience, and the agreement across observers is astounding for a complex visual task.

The similarity between perceived poses and the back-projection function suggests that the perceived pose is estimated by the visual system using a hardwired or learned version of the geometric back-projection, but is modified by a fronto-parallel bias. We model this bias with a multiplicative parameter, K, so the perceived orientation, ${\mathrm{\Omega }}_P$, is given by

$${\Omega }_P=\mathrm{atan}\left(\text{K}\cdot \tan \left({\theta }_R\right)/\sin \left({\varphi }_c\right)\right).$$ [3]

The best fit of this model, with K as the only free parameter, is shown in Fig. 2B, View 0 Deg column. The fit is excellent with a root mean square error (RMSE) of 6.5°. Similarly excellent fits obtained to individual observers’ results are shown in SI Appendix, Fig. S2 (View 0 Deg column). The images in this experiment can be considered as either sticks of 16 different poses from the same camera view or a stick of one pose from 16 different camera viewpoints, because both produce the same retinal images. The predicted distortions in Fig. 2C, View 0 Deg column, can be quite large, in accordance with the dramatically different percepts across viewing angles in Fig. 1A. The model’s fit demonstrates that these distortions are consistent with a bias toward the fronto-parallel (see Discussion).

Geometry of 3D Pose Estimation from 2D Pictures.

Artists have long known how to distort sculpture and paintings for eccentric viewpoints, elevations, and distances, e.g., Michelangelo’s David (1501–1505) and Mantegna’s Lamentation (1475–1485), and many theoretical and empirical analyses of invariances and distortions in picture perception have been published (4, 5, 7–9, 12, 13). Our hypothesis in this study is that 3D poses in pictures are perceived based on the same back-projections identified above for actual 3D scenes. We test this hypothesis with oblique views (${\varphi }_V$) of pictures where 2D orientations in the retinal image can differ from those in the picture, leading to a projection function which is reduced in amplitude of modulation around the diagonal (SI Appendix, Fig. S1B),

$${\theta }_R=\mathrm{atan}\left(\tan \left({\mathrm{\Omega }}_T\right)\cdot (\sin \left({\varphi }_c\right)/\cos \left({\varphi }_v\right))\right).$$ [4]

Inverting gives the back projection

$${\Omega }_T=\mathrm{atan}\left(\tan \left({\theta }_R\right)\cdot (\cos \left({\varphi }_v\right)/\sin \left({\varphi }_c\right))\right).$$ [5]

The main experiment was a randomized block design for observations from the frontal and four oblique viewpoints (SI Appendix, Fig. S1D). Fig. 2A shows the back-projection for the five observer viewpoints with the 3D poses defined relative to the fixed position of the monitor. Since vertical and horizontal lines on the monitor project to vertical and horizontal retinal images in all five viewpoints, elements that are vertical or horizontal in the retinal plane back-project to poses that are oriented perpendicular to or parallel to the monitor, respectively. The predicted amplitude of modulation is smaller in the more oblique back-projections, indicating a more linear relationship between retinal orientation and physical pose.

Since sticks pointing at the monitor have vertical projections on the retina for all five viewpoints (e.g., invariant 2D orientation of brown stick in the three screen slants in Fig. 1C), if our hypothesis is correct that observers use the same back-projection rule for pictures as they do for 3D scenes, they will interpret a vertical image orientation as arising from a stick pointing at them, as opposed to perpendicular to the screen (the two are the same only in fronto-parallel viewing). In fact, they will perceive the whole scene as rotated toward them. From the perceived 3D poses plotted against retinal orientations (Fig. 2B), it is evident that, when the viewpoint is oblique, the whole set of measurements shifts up or down by the viewing angle, consistent with a perceived rotation supporting our hypothesis. In addition, the amplitude of modulation around the diagonal becomes smaller with more oblique viewing. The empirical function is shallower than the back-projection for every viewpoint, suggesting that perceived poses are all subject to a fronto-parallel bias (Fig. 2C).

To quantitatively test our hypothesis about 3D poses perceived in pictures, we used the best-fitting model for 3D scene viewing (Eq. 3 with K at the value that best accounted for the fronto-parallel bias). We added a fixed constant, ${\varphi }_V$, to predict that the perceived rotation of the scene will be equal to the observer viewpoint angle. We add just one free parameter, L, which multiplies ${\varphi }_C$ to allow for the observation that the ground plane seems to tilt toward the observer in oblique viewing conditions,

$${\Omega }_P=\text{atan}\left(K_0\cdot \text{tan}\left({\theta }_R\right)/\sin \left(L{\varphi }_c\right)\right)+{\varphi }_v.$$ [6]

The fits of this one parameter model to the average results are as good as the fits to the fronto-parallel condition, with similar RMS errors between 6.45° and 7.54°. The best-fitting values for L gave estimated camera elevations of 27.66°, 16.58°, 15.00°, 17.29°, and 26.42° for the viewing angles −60°, −30°, 0°, +30°, and +60°, respectively. The main deviations from the physical camera elevation of 15.00° are for the most oblique viewpoints. In oblique viewing conditions, the retinal projection is a vertically stretched and horizontally compressed image of the scene, causing the percept of a ground plane tilted down toward the observer (14).

The fits to each observer’s results are also excellent (SI Appendix, Fig. S2). To quantify agreements across observers, we correlated each pose setting for all pairs of observers for each viewpoint. The average correlation was 0.9934 with an SD of 0.0037. This remarkable agreement, plus the excellent fit of the model to the perceived poses (Fig. 2B and SI Appendix, Fig. S2), and to the deviations from veridical (Fig. 2C), shows that all observers use the same back-projection rule from retinal orientations to estimate poses from pictures as from 3D scenes, with the same fronto-parallel bias.

The conclusion that observers are using the same back-projection function to infer 3D poses from retinal images irrespective of viewpoint is buttressed by plotting perceived poses from oblique viewpoints versus perceived poses from the frontal viewpoint (Fig. 2D), where all of the points fall almost perfectly on the line of unit positive slope, passing through the viewpoint angle on the ordinate. Given that 3D scene understanding has been important for millions of years, and pictures are probably no more than 35,000 y old, it is not surprising that strategies for estimating 3D poses are used when inferring poses from pictures.

Control for Frame Effects.

Our hypothesis implies that observers use retinal projections in picture viewing, without considering the slant of the picture. A qualitatively different hypothesis would be that observers estimate the slant of the screen and apply the correct back-projection for that slant (Eq. 5). This hypothesis predicts that perceived poses should vary around the unit diagonal, similar to the back-projection functions in Fig. 2A. The systematic shifts in Fig. 2B that are equal to the viewing angle reflect the perceived rotation of the scene, and refute this hypothesis. In the following control experiment, we rule out all models that assume estimated screen slant.

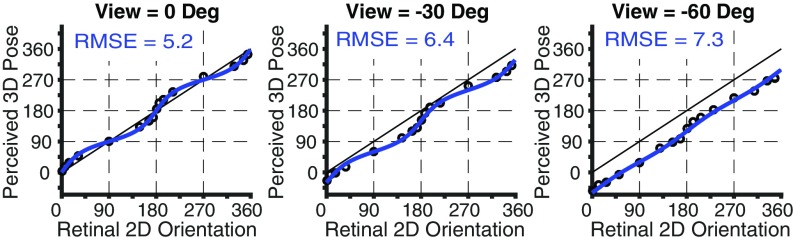
We knew that observers were not using binocular disparity as an additional cue, because monocular and binocular results were almost identical (Fig. 2E). We tested whether observers were using the slant of the image estimated from the monitor frame, by asking observers to view the single-stick images through a funnel so that the frame was not visible. We ran observers in blocks where the display screen was slanted by 0°, 30°, or 60°. The results of these conditions were fit very well by the same parameters that fit the same viewpoints in the main experiment, for the average (Fig. 3) and for individual observers (SI Appendix, Fig. S3), showing that observers used the same information in both experiments. Since the background was uniformly dark, it is unlikely that it provided any significant accommodation or luminance cues to distance. Since slant could not be estimated from the frame of the monitor in the control experiment, it follows that visibility of the frame had no effect on the main results.

Fig. 3.

The 3D pose estimates without screen slant information. Shown are perceived poses of single sticks seen with monitor frame occluded in three monitor slants (0°, −30°, −60°), averaged across five observers. The curve represents the best model fitted to the main experiment for these three viewpoints (Fig. 2B).

Three-Dimensional Pose Estimation in Complex Scenes.

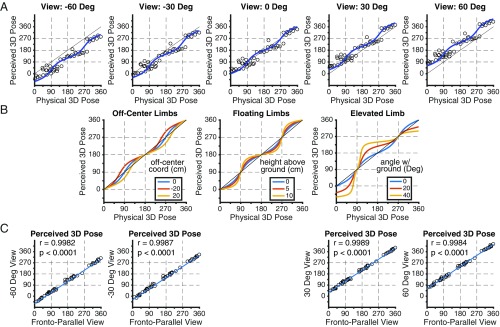
Geometric projection is more complicated in the doll configurations in Fig. 1, because, unlike the sticks, most limbs are translated away from the center of the 3D scene, and a few have an elevation angle to the ground plane, or float over it. After estimating the best-fitting model for pose estimation of sticks, we tested it on pose percepts of 250 (10 limbs × 5 camera angles × 5 observer viewpoints) limbs of the dolls without clothes, so that cloth folds and textures did not bias the estimation. The perceived 3D limb poses averaged across observers, plotted against physical poses (Fig. 4A), are overlaid by the best-fitting models from Fig. 1B. This model captures the general form of the results, but there are systematic deviations, because the back-projection was calculated for centered sticks lying on the ground plane. If a limb is situated off-center, has an elevation, is floating above the ground-plane, or some combination, this can alter the retinal orientation of the limb’s image ${\theta }_R$, even for fronto-parallel viewing, as seen by comparing Eqs. 7–9 to Eq. 1,

Fig. 4.

Perceived pose in complex 3D scenes. Shown are perceived poses of 10 limbs at five different camera angles from the 3D doll scene for different observer viewpoints. (A) Perceived 3D poses of limbs averaged across seven observers as a function of physical 3D pose. Curves represent the best-fitting model from Fig. 2B. (B) Predicted perceived 3D pose as a function of physical 3D pose if observers used the original back-projection on retinal orientations altered by limbs shifted from the center (Left), floating above the ground (Center), or elevated from the ground (Right). Each plot has three curves showing three different displacements, heights, or elevations. (C) Perceived 3D pose at each viewing angle is plotted versus perceived 3D pose from the fronto-parallel viewing condition. The blue line is the line of unit slope shifted so that the y intercept is equal to the viewing angle. The correlation is reported as r.

For a limb on the ground plane extending from $(X_0,Z_0)$, where the origin is at the center of the camera’s line of sight, and $d_C$ is the distance from the camera,

$${\theta }_R=\mathrm{atan}(\tan \left({\mathrm{\Omega }}_T\right)\cdot \sin \left({\varphi }_C\right)\cdot d_c/\left(d_c+\cos \left({\varphi }_C\right)\cdot (Z_0-\tan \left({\mathrm{\Omega }}_T\right)\cdot X_0))\right).$$ [7]

For a limb with elevation angle ${\varphi }_E$ with the ground plane,

$${\theta }_R=\mathrm{atan}(\tan \left({\mathrm{\Omega }}_T\right)\cdot \sin \left({\varphi }_C\right)-\tan \left({\varphi }_E\right)\cdot \cos \left({\varphi }_C\right)).$$ [8]

For a limb floating $H$ units above the ground plane,

$${\theta }_R=\mathrm{atan}\left(\tan \left({\mathrm{\Omega }}_T\right)\cdot \left(\sin \left({\varphi }_C\right)-\left(H/d_C\right)\right)\right).$$ [9]

Based on these equations, Fig. 4B shows the predicted perceived poses as a function of physical pose, if an observer is assumed to use the same back-projection as in Fig. 1B but on the altered retinal orientations. For off-center limbs, the prediction is that there will be a large variation in perception of 90° physical poses but not of 180° poses, and the deviations in Fig. 4A correspond to the fact that almost all limbs in Fig. 1 are placed off-center. A couple of limbs each are seen as floating, and they should show deviations at oblique poses. If limbs around 180° physical poses were elevated at one end, they would be predicted to vary in perceived poses, but this does not occur in the results. The similarities between deviations across viewing angle in Fig. 4A suggest that observers use the same back-projection irrespective of viewing angle, and this is strongly supported by the almost perfect correlation of perceived poses between oblique and frontal views (Fig. 4C). Note that, by assuming all limbs are lying centered on the ground, a visual system simplifies the back-projection condition to a 2D to 2D mapping which is 1 to 1. The errors caused by this simplification may cost less than the benefits of a powerful geometric strategy to do the complex task of estimating limb poses on a 3D horizontal plane from a vertical image. Results for individual observers (SI Appendix, Fig. S4) reveal the strong agreement across observers even for these complex stimuli. To quantify agreements across observers, we correlated each limb’s pose setting for all pairs of observers for each viewpoint. The average correlation was 0.9840 with a SD of 0.0101. This remarkable agreement indicates that the deviations from each observer’s back-projection model are not random but systematically due to every observer using the same inferential strategy, so that the analyses for the averaged results also explain the deviations for individual observers.

Discussion

Projective geometry is the geometry of light (15), and, given the selective advantage conferred by perception at a distance provided by vision, it would not be surprising if, over millions of years of evolution, brains have learned to exploit knowledge of projective geometry. Our results that observers use a geometrical back-projection show that this knowledge can be intricate and accurate. We modeled only for objects lying centered on the ground, but the deviations for the limbs from the model for the sticks suggest that pose estimation for noncentered objects not lying on the ground partially or completely may use the same back-projection from retinal orientations. In real 3D viewing, head and eye movements can center selected elements of a scene along the line of sight. The remarkable similarity in pose judgments across observers indicates that the accessed geometrical knowledge is common between all observers, whether innate or learned. Another visual capacity that suggests accurate knowledge of projective geometry is shape from texture, where 3D shapes are inferred from the orientation flows created by perspective projection (16, 17). On the other hand, perceived shape and relative size distortions of dolls (Fig. 1), buildings (18, 19), and planar shapes (12) suggest that embodied knowledge of light projection is incomplete (20) and sometimes combined with shape priors (18, 19). Questions about the innateness of geometry have been addressed by Plato (21), Berkeley (22), Kant (23), von Helmholtz (24), and Dewey (25), and questions about whether abstract geometry comes from visual observations have been addressed by Poincaré (15), Einstein (26), and others. Measurements such as pose estimation, extended to other object shapes and locations, may help address such long-standing issues.

The fronto-parallel bias we find is curious, but has been reported previously for slant of planar surfaces (27) and tilt of oblique objects in natural scenes (28). Could it be based on adaptation to orientation statistics of natural scenes? Measured statistics of orientations in pictures of naturalistic scenes (29–31) show the highest frequency for horizontal orientations. From the projection functions in SI Appendix, Fig. S1, one could reason back to relative frequencies of 3D orientations, and suggest a prior probability for shifting perceived poses toward the fronto-parallel. In addition, a bias toward seeing horizontal 2D orientations (32) could arise from anisotropy in populations of cortical orientation selective cells that are largest in number and most sharply tuned for horizontal orientations (29, 33). Finally, if the visual system treats pictures as containing zero stereo disparity, then minimizing perceived depth between neighboring points on the same surface would create a fronto-parallel bias. The same could be true of monocular viewing or at distances that don’t allow for binocular disparity.

There have been too many mathematical and experimental treatments of picture perception to address comprehensively, so we reconsider just a few recent developments in light of our results. Erkelens (27) found that perceived slants of surfaces simulated as rectangular grids in perspective projection corresponded closely to the visual stimulus, and attributed the results to the idea that “observers perceive a particular interpretation of the proximal stimulus namely the linear-perspective-hypothesized grid at the virtual slant and not the depicted grid at the slant of the physical surface.” There was an underestimation of slant similar to the fronto-parallel bias in our results. In relying on internalized rules of perspective geometry, this proposal is somewhat similar to ours, but our idea of using back-projections from retinal images per se simplifies explanations. For example, the “following” behavior of fingers pointing out of the picture, studied by Koenderink et al. (8), is explained in terms of highly slanted surfaces, such as the left and right sides of a finger, being perceived as almost independent of the slant of the screen, whereas we explain it simply as due to back-projections of vertical retinal orientations that stay invariant with observer translations or viewpoints. In addition, our model has the virtue of not requiring observers to estimate converging lines or vanishing points. Vishwanath et al. (4) had observers estimate aspect ratios of objects. Our model is formulated only for object poses, but the same projective geometry methods can be used to formulate back-projection models for object sizes along different axes. Informally, the body parts in Fig. 1 B and D appear distorted in size and aspect ratio, in proportion to the retinal projections, so it is likely that a back-projection model could provide a good explanation for perceived distortions in object shapes. Similar to ref. 27, we did not find any contribution of screen-related cues or binocular disparity, which is very different from the claim that object shape “invariance is achieved through an estimate of local surface orientation, not from geometric information in the picture” (4). This difference could be due to the different tasks or, as has been attributed by ref. 27, to the data being “averaged over randomly selected depicted slants, a procedure that, as the analyses of this study show, leads to unpredictable results.”

To sum up, we show that percepts of 3D poses, in real scenes, can be explained by the hypothesis that observers use a geometric back-projection from retinal images. We then provide critical support for this hypothesis by showing that it also explains pose perception in oblique views of pictures, including the illusory rotation of the picture with viewpoint (2, 6–8, 34). Our simple explanation in terms of retinal image orientations obviates the need for more complicated considerations that have been raised for this phenomenon, which is often found in posters and paintings.

Materials and Methods

We created five 3D scenes, four with sticks and one with two dolls. The stick scenes had either a single brown stick lying flat on the ground plane or a brown stick joined to a gray stick at the center of the scene at a 45°, 90°, or 135° angle. The two dolls were placed at an angle to each other, with limbs bent at different angles (Fig. 1). The scenes were photographed with a Casio Exilim HS EX-ZR300 (sensor: 1/2.3″; diagonal: 7.87 mm; width: 6.3 mm; height: 4.72 mm; distance: 0.62 m; zoom: 64 mm; focal length: 11.17; elevation: 15°). Different views of the 3D scene were acquired by rotating a pedestal under the objects. For the sticks, the pedestal was rotated 16 times by 22.5° for views spanning 360°. For the dolls, camera viewpoints were restricted to a range across which limbs were not occluded, i.e. −40°, −20°, +20°, and +40° around the original setup. The ground plane was completely dark like the surround, so was not visible in the images (Fig. 1).

In the main experiment, stick images were displayed on a 55″ Panasonic TC-55CX800U LED monitor. Chairs were set up at five viewing locations 2.4 m from the screen [calculated according to Cooper et al. (11)]: 0° (fronto-parallel to the screen), and −60°, −30°, +30°, and +60° from fronto-parallel (SI Appendix, Fig. S1D). Observers ran the main experiment once binocularly, and once monocularly with one eye patched. On each trial image, the test stick was designated by color (brown or gray), and the observer was instructed to judge its 3D pose using its medial axis, relative to themselves. Observers recorded their judgment by rotating a vector in a clock face on a horizontal touchscreen to be parallel to, and point in the same direction as, the designated stick in the 3D scene. The response touchscreen plane was placed parallel to the ground plane of the 3D scene, and, for reference, the axis formed by the observer’s line of sight to the center of the monitor and the axis perpendicular to it were inscribed in the circle around which the vector was rotated. Observers viewed the touchscreen at an elevation of 70° to 90°, leading to almost no distortion of vector orientation in retinal image (SI Appendix, Fig. S1C). Subjects had unlimited time to set their response using fingers and buttons. The experiment was blocked by the five viewing locations, ordered randomly, and images were displayed in random order. Eight observers completed the main experiment with the stick scenes. The procedures for the complex scene measurements were exactly the same, except that the relevant limb on each trial was specified by a brief small red dot. Five previous and two new observers completed the complex scene experiment.

In the experiment to control for the visibility of the monitor frame, the images were displayed on a 23″ Sony SDM-P232W TFT LCD Monitor in a dark room, 0.88 m from the observer [Cooper et al. (11)]. A long funnel ran through a box such that, when the observer looked through the small end of the funnel with one eye, they could see the display but not its frame. The experiment was blocked by the monitor slanted fronto-parallel to the observer, or rotated 30° or 60°. The control experiment used only the single-stick images.

The alignment of the response screen elicited responses where the 90° to 270° axis pointed to the observer. For data analyses, comparisons across observer locations, and comparisons to the original 3D scene, responses were transformed to the real 3D scene coordinates (the 0° to 180° axis parallel to the picture plane, 90° to 270° axis perpendicular to the picture plane, with 90 pointing “out of” the picture). The stimulus display, response paradigm, and data analyses utilized Matlab and routines in PsychToolbox. All parameter fits in the model were computed via the Levenberg–Marquardt nonlinear least squares algorithm.

The experiments in the paper were approved by the IRB at State University of New York Optometry, and observers gave written informed consent.