Significance
River discharge exerts an important influence on coastal ocean circulation but has been overlooked as a driver of historical coastal sea-level change and future coastal flood risk. We explore the relation between observed river discharge and sea level on the United States Atlantic and Gulf coasts over interannual and longer periods. We formulate a theory that predicts the observed correspondence between river discharge and sea level, demonstrating a causal relation between the two variables. Our results highlight a significant but overlooked driver of coastal sea level, indicating the need for (1) improved resolution in remote sensing and modeling of the coastal zone and (2) inclusion of realistic river runoff variability in climate models.
Keywords: coastal sea level, coastal river plumes, coastal flood risk, climate modeling, physical oceanography
Abstract
Identifying physical processes responsible for historical coastal sea-level changes is important for anticipating future impacts. Recent studies sought to understand the drivers of interannual to multidecadal sea-level changes on the United States Atlantic and Gulf coasts. Ocean dynamics, terrestrial water storage, vertical land motion, and melting of land ice were highlighted as important mechanisms of sea-level change along this densely populated coast on these time scales. While known to exert an important control on coastal ocean circulation, variable river discharge has been absent from recent discussions of drivers of sea-level change. We update calculations from the 1970s, comparing annual river-discharge and coastal sea-level data along the Gulf of Maine, Mid-Atlantic Bight, South Atlantic Bight, and Gulf of Mexico during 1910–2017. We show that river-discharge and sea-level changes are significantly correlated (), such that sea level rises between 0.01 and 0.08 cm for a 1 annual river-discharge increase, depending on region. We formulate a theory that describes the relation between river-discharge and halosteric sea-level changes (i.e., changes in sea level related to salinity) as a function of river discharge, Earth’s rotation, and density stratification. This theory correctly predicts the order of observed increment sea-level change per unit river-discharge anomaly, suggesting a causal relation. Our results have implications for remote sensing, climate modeling, interpreting Common Era proxy sea-level reconstructions, and projecting coastal flood risk.
Predicting regional sea-level changes and their coastal impacts is a grand challenge in climate research (1). To improve projections of future sea-level changes, it is important to understand the physical process responsible for past coastal sea-level changes in historical observations and proxy reconstructions. The tide-gauge record on the United States Atlantic and Gulf coasts has received considerable attention in this regard. Partly motivated by projections of rapid future sea-level rise along parts of this coastline (2, 3) and observations suggesting that this region is a hotspot of ongoing regional sea-level acceleration (4, 5), recent studies explored myriad processes influencing Atlantic and Gulf coast sea level over interannual to multidecadal time scales, including changes in the overturning circulation, Gulf Stream, Sverdrup transport, remotely generated planetary waves, alongshore winds, barometric pressure, groundwater extraction, dam retention, vertical land motion, and melting of land-based ice (6–14).
Conspicuously absent from these discussions is consideration of variable river discharge into the coastal ocean and its impact on sea level at interannual and longer time scales. More generally, global ocean circulation models often omit boundary forcing by year-to-year changes in river discharge (15). Despite being an important driver of circulation in the coastal ocean (16–24), river discharge is often overlooked as a driver of sea-level change. Coastal currents and river plumes can be strongly trapped to the coast, making such features difficult to observe with conventional satellite altimetry and difficult to resolve in global models. The extent to which coastal sea level as observed by tide gauges reflects the influence of river discharge thus remains to be rigorously determined.
In 1971, Meade and Emery (25) compared annual river-discharge and sea-level data over the Gulf of Maine, Mid- and South Atlantic Bights, and Gulf of Mexico during 1931–1969. Using linear regression and correlation analysis, they suggested that river discharge explained 20% to 31% of detrended annual sea-level variance, such that sea level rose between 0.01 and 0.05 cm for a 1 increase in annual river discharge, depending on region. Meade and Emery (25) reasoned that the sea-level rise per unit river-discharge increase was inversely related to total discharge but unrelated to the discharge per unit length of coastline. While these conclusions suggest that recent studies of United States Atlantic and Gulf coast sea level (and global ocean models more generally) are overlooking a potentially important driver of coastal sea-level change, many questions remain open. Meade and Emery (25) alluded to rapid dynamic adjustment and horizontally uniform spreading of fresh water over the shelf in their interpretation of the observed relations between river discharge and sea level along the coast. However, they provided no formal physical framework within which to interpret their mainly statistical findings, so it remains to be determined whether their results reflect correlation or causation. In the years since Meade and Emery (25), many have studied mixing and transport in buoyant coastal river plumes and developed theories for the dominant mechanisms (16–24). However, these theoretical developments have not been applied to the problem of the relation between coastal sea level and river discharge. Moreover, the availability of additional data since 1969 gives an opportunity to see whether the results of Meade and Emery (25) hold over longer and more recent time periods.
These considerations motivate us to pose the following interrelated questions: (1) Do the general results of Meade and Emery (25) hold for longer and more recent time periods? (2) Does river discharge exert a significant causal influence on coastal sea-level variability? (3) What processes mediate the relation between river discharge and sea level at the coast? We revisit the analysis of Meade and Emery (25), reconsidering the relation between river discharge and sea level along the United States Atlantic and Gulf coasts on interannual and longer time scales based on updated datasets. We then evaluate whether these relations are correlational or causal, assessing whether the observed correspondence between river discharge and sea level is consistent with expectations from simple theories for transport in coastal river plumes. Our results highlight a significant, but overlooked, driver of coastal sea-level change (which we expect to be important also in other locations along the global coastal ocean), with implications for observing systems, climate modeling, interpreting Common Era proxy sea-level reconstructions, and projecting future coastal flood risk.
Observations
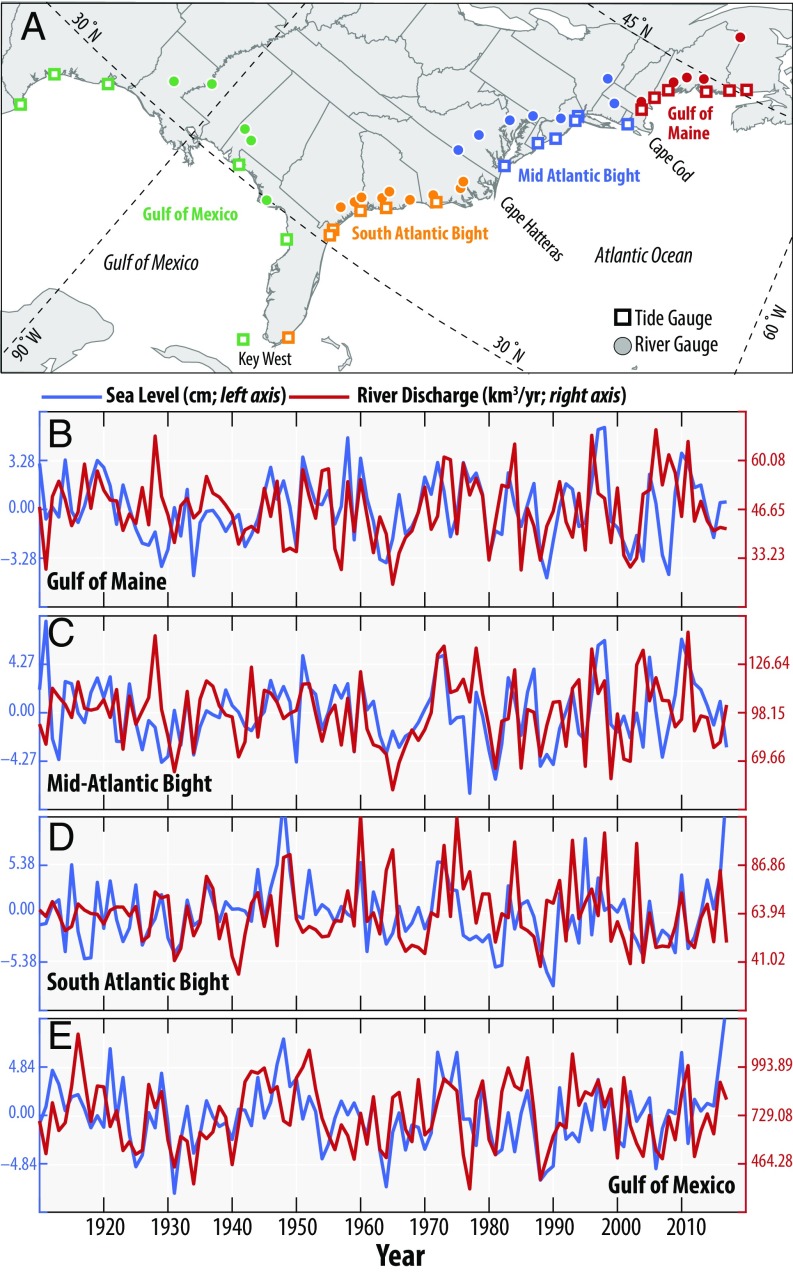
We use observations to examine the relation between river discharge and coastal sea level, following methods described earlier by Meade and Emery (25). The analysis is based on relative sea level from the Permanent Service for Mean Sea Level (PSMSL) Revised Local Reference (RLR) database (26) and river discharge from the United States Geological Survey (USGS) on the United States Atlantic and Gulf coasts during 1910–2017 (Fig. 1A). This period is nearly three times as long as that considered by Meade and Emery (25). The sea-level records constitute 2,050 gauge years of data from 24 tide gauges at locations mostly along open-ocean boundaries. Given our focus on nonlocal sea-level behavior in the far-field downstream of river mouths (see Theory), we exclude sea-level records from locations within bays or estuaries. We consider more tide gauges than Meade and Emery (25) to reduce the impact of local processes on regional averages (see next paragraph). Discharge time series for 26 rivers were compiled based on 9,893 station-years of discharge data from 250 river stations. These 26 rivers are the same ones considered by Meade and Emery (25). See SI Appendix for more details on the data.
Fig. 1.
Observations of coastal sea-level and river-discharge variations. (A) Locations of 26 river stations (circles) and 24 tide gauges (squares) on the Gulf of Maine (red), Mid-Atlantic Bight (blue), South Atlantic Bight (yellow), and Gulf of Mexico (green) used here. See SI Appendix, Tables S1–S3 for more details on the data sites. Subsequent panels show detrended annual water-year averages of integrated river discharge (red) and averaged sea level (blue) over the (B) Gulf of Maine, (C) Mid-Atlantic Bight, (D) South Atlantic Bight, and (E) Gulf of Mexico versus water year. Time series have been adjusted for large-scale climate modes as explained in the text and SI Appendix.
To study fluctuations on interannual and longer time scales, we compute detrended annual water-year averages of both sea level and river discharge. To investigate large-scale regional behavior, we follow Meade and Emery (25) and average the sea-level records and sum the observed river-discharge time series over four separate regions: Gulf of Maine, Mid-Atlantic Bight, South Atlantic Bight, and Gulf of Mexico (Fig. 1A). These regions are demarcated by Cape Cod, Cape Hatteras, and Key West. To distinguish correlation from causation, we use multiple linear regression to remove contributions from large-scale modes of climate variation known to impact regional sea level (8, 9, 27, 28). See SI Appendix for more details on the regional time series and adjustment for climate variability.
The regional river-discharge and sea-level series are shown alongside one another in Fig. 1 B–E. While the magnitude and timing of river-discharge and sea-level changes can vary substantially between regions, river-discharge and sea-level time series within any given region show synchronous behavior. Coastal sea level generally rises over years of anomalously high river discharge and falls during years of lower than normal river discharge. There are multiyear periods of persistently positive river-discharge and sea-level anomalies in the Gulf of Mexico during the late 1940s and early 1970s, along with periods of negative anomalies along this coastline during the early 1930s and early 1960s (Fig. 1E). Also apparent are contemporaneous decadal increases in river discharge and sea level from the early 1960s to the early 1970s in the Mid-Atlantic Bight and Gulf of Maine (Fig. 1 B and C), as well as strongly correlated interannual fluctuations in these two variables over the South Atlantic Bight during the mid-1920s through the mid-1930s (Fig. 1D). However, some exceptions are evident. During the late 1920s, sea level fell along the Mid-Atlantic Bight and Gulf of Maine despite increased river discharge (Fig. 1 B and C), demonstrating that regional river-discharge and sea-level behaviors are not always synchronous.
Correlations between regional river discharge and coastal sea level are statistically significant (), with Pearson correlation coefficients ranging from 0.24 (South Atlantic Bight) to 0.39 (Gulf of Mexico). This suggests that river discharge could explain 6% to 15% of the detrended annual sea-level variance during 1910–2017, depending on region. These findings are consistent with results from Meade and Emery (25) in that significant correlations between river discharge and sea level are found for each region. However, these correlation coefficients are smaller than those found by Meade and Emery (25), perhaps due to the longer data records studied here, or potential nonstationarity in the relation between river discharge and sea level. The correlation coefficient between river discharge and sea level over the South Atlantic Bight is significantly stronger () during 1910–1963 (0.47) compared with 1964–2017 (0.12), demonstrating that the correspondence between these two variables can be time sensitive. For context, ref. 29 found that local atmospheric pressure effects explain 10% to 15% of the variance in detrended annual sea-level records along the global coastal ocean during the 20th century, meaning that variable river discharge could be as important a driver of year-to-year coastal sea-level variations as other processes more commonly discussed in the literature and regularly corrected for in tide-gauge data analyses.
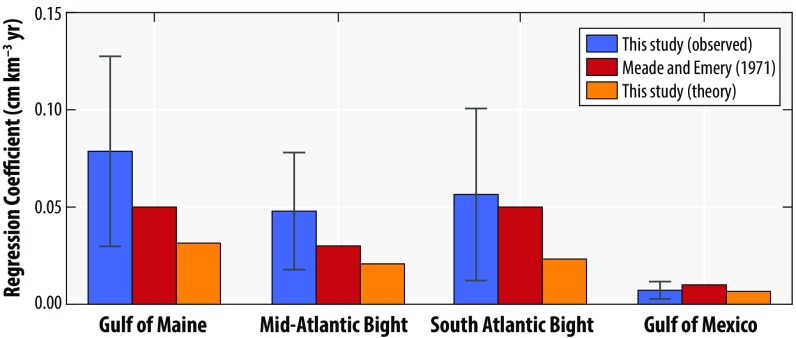
Using ordinary linear regression, we compute best estimates for the unit sea-level change per annual river discharge of 0.077 cmy for Gulf of Maine, 0.048 cmy for the Mid-Atlantic Bight, 0.056 cmy for the South Atlantic Bight, and 0.007 cmy for the Gulf of Mexico (Fig. 2). As in Meade and Emery (25), there is no obvious relation between these values and the river discharge per unit length of coastline, but regression coefficients are larger for regions with smaller river discharge. The estimated uncertainties on our regression coefficients overlap with the values given in Meade and Emery (25) (Fig. 2), demonstrating that their basic results hold more generally for longer and more recent time periods.
Fig. 2.
Bar plot showing, for each region, the regression coefficient observed over 1910–2017 between river discharge and sea level (blue), the corresponding value reported by Meade and Emery (25) (red), and the theoretical value computed based on Eq. 6 (yellow). Whiskers on blue bars indicate the 95% confidence interval estimated on the data values using Monte Carlo simulation and Fourier phase scrambling as described in SI Appendix.
Theory
To provide a framework within which to interpret the observations (Figs. 1 and 2) and determine whether relations between river discharge and coastal sea level reflect correlation or causation, we extend theories previously developed for alongshore transport in the far field of a coastal river plume (18, 24). We imagine a rate of fresh river water discharged into an otherwise quiescent salty coastal ocean (SI Appendix, Fig. S1). Upon entering the coastal ocean, the plume of fresh river water is subject to intense mixing, such that ambient salty ocean water is entrained into the plume. Due to its buoyancy, along with the effects of centripetal acceleration and planetary rotation, this less dense mixture of fresh river water and entrained salty ocean water will sit “above” and shoreward of the more dense “pure” salty ocean water, turning to the right (left) in the northern (southern) hemisphere in the sense of coastal Kelvin waves. Trapped to the coast, this buoyant flow establishes an offshore density gradient in thermal-wind balance with an alongshore coastal current. On account of the density contrast, this lens of fresher water along the coast is thicker than would be an equivalent mass of pure salty ocean water, effecting a halosteric sea-level anomaly.
To formulate a theory for this coastal halosteric sea-level anomaly, we consider a control volume bounded by the ocean surface, the layer interface, the river mouth, and a depth-offshore transect across the alongshore current downstream of the river mouth (SI Appendix, Fig. S1). Similar to past studies, we assume (i) volume, salt, and far-field offshore momentum fields are in steady state; (ii) alongshore volume transport balances the volumetric rates of river discharge and ambient-water entrainment; (iii) salt entrained into the plume in the near- and midfield is balanced by alongshore salt transport in the far field by the coastal current; (iv) the alongshore flow in the far field is linear, with horizontal scales large enough that geostrophic and hydrostatic balances apply; (v) ocean mass equivalent to the river discharge is displaced and redistributed evenly over the global ocean, such that related changes in bottom pressure contribute negligibly to local changes in sea level at the coast; and (vi) there is no flow along the ocean bottom. Further discussion of these assumptions is given in SI Appendix.
The equations for conservation of volume, salt, and far-field offshore momentum are
| [1] |
| [2] |
| [3] |
Here is alongshore volume transport, is volumetric river-discharge rate, is rate of entrainment, is salinity of the ambient coastal ocean, is salinity difference between buoyant waters flowing along shore and ambient coastal-ocean waters, is Coriolis parameter, is alongshore velocity, is thickness of the buoyant upper layer, is offshore coordinate, and is reduced gravity, where is gravitational acceleration, is anomalous density due to the offshore salinity gradient, and is ambient background ocean-water density.
These equations are manipulated (see SI Appendix) to give an expression for upper layer thickness at the coast as a function of river discharge :
| [4] |
By virtue of the hydrostatic relation, the coastal layer-thickness anomaly corresponds to an anomalous coastal sea level ,
| [5] |
where we have used the fact that , with the haline contraction coefficient. Differentiating Equation 5 with respect to gives the increment sea-level change per unit river-discharge change,
| [6] |
which can be directly compared with our previous results based on linear regression of the observations.
Application of Theory to Observations
The form of Eq. 6 is consistent with basic results here and in Meade and Emery (25). That is, there is no functional dependence on coastline length, and varies with the inverse (square root) of , such that larger regression coefficients are anticipated for regions with smaller river discharge and vice versa. To determine more rigorously whether this theory is consistent with observed relations between river discharge and sea level (Figs. 1 and 2), we compare estimates of determined empirically from ordinary linear regression of the data to those predicted by Eq. 6. We use observed values (Fig. 1), values computed based on the average latitudes of the tide gauges for a region, a standard value of m, and representative values of practical salinity units (PSUs) and .
We compute theoretical values of 0.031 cmy for the Gulf of Maine, 0.021 cmy for the Mid-Atlantic Bight, 0.023 cmy for the South Atlantic Bight, and 0.007 cmy for the Gulf of Mexico (Fig. 2). For the Gulf of Mexico, theoretical and observational values are very similar, whereas for other regions, theoretical values are smaller than the corresponding best estimates from observations (Fig. 2). However, for all regions, theoretical and observational values are of the same order of magnitude, and theoretical values are within the estimated observational uncertainties (Fig. 2). This suggests that observed relations between river discharge and coastal sea level are causal and interpretable in terms of basic physical principles (i.e., salt and volume conservation, geostrophic and hydrostatic balances).
However, the fact that the theoretical regression coefficients consistently underestimate observed best estimates hints that additional considerations are needed to fully understand the data. One possibility is that, while we used linear regression to adjust for large-scale climate processes (see SI Appendix), other more local factors that are correlated with river discharge could also be at play. Downwelling-favorable alongshore winds coinciding with anomalously strong river discharge would effect depth-dependent Ekman transports and enhanced coastal trapping of the buoyant outflow, leading to higher coastal sea-level anomalies than would have occurred otherwise (20, 22). Also, we adopted the coastal demarcations of Meade and Emery (25), assuming that these regions are distinct and no communication takes place between them. The observed spatial cross-covariance structure between river-discharge time series (SI Appendix, Fig. S2) shows that these regions generally correspond to areas of coherent river-discharge fluctuation. However, instances of significant correlation between rivers from different regions are also seen. Future studies could consider alternative delineations to determine their influence on the relation between river discharge and sea level. Additional factors ignored here—such as background flows, upstream boundary conditions, groundwater discharge, incomplete data records, and the detailed distribution of rivers within any given region—could also play a role. In any case, the general correspondence between theory and data suggests that Eq. 6 encapsulates the most basic and important physical controls (discharge, rotation, and stratification) mediating the relation between annual river-discharge and sea-level anomalies at the coast.
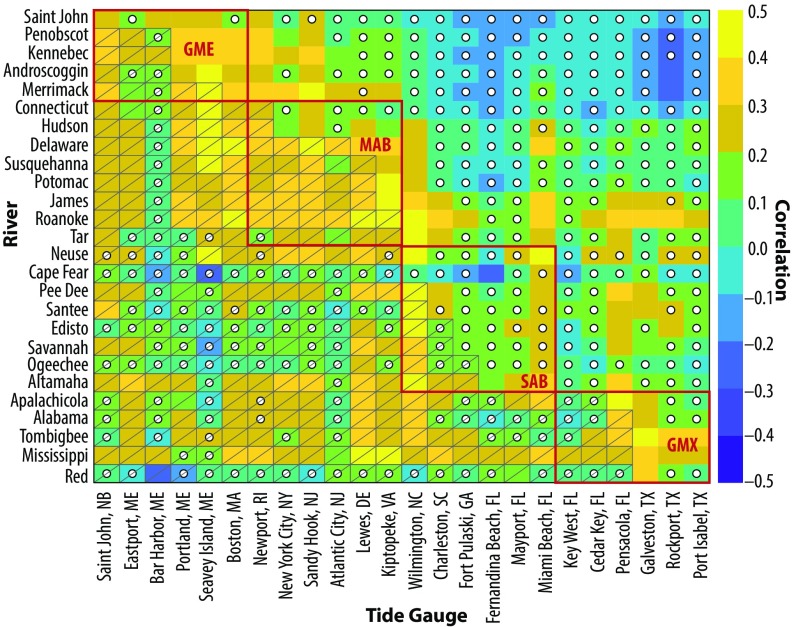
To suggest in more detail the influence of particular rivers on sea level at specific coastal locations, we compare individual river-discharge and sea-level records. Fig. 3 shows a matrix of correlation coefficients between all possible pairs of river-discharge and sea-level time series. The correlation between river discharge and downstream sea level tends to decrease with increasing separation. For most river-discharge records, downstream tide gauges closer to the river are usually more strongly and significantly correlated with the discharge time series than are tide gauges farther away down the coast. Discharge from the Potomac River is significantly correlated with sea level at the two closest downstream tide-gauge stations at Kiptopeke Beach and Charleston but not significantly correlated with any other downstream sea-level records. However, this general pattern is not universal, and some rivers are exceptions to this rule. The Ogeechee River does not show significant correlation with any downstream tide gauges. It should be noted that this river has relatively small discharge, and its signal in the tide-gauge data could be overcome by the noise due to other local forcing factors.
Fig. 3.
Color shading shows correlation coefficients between all possible pairs of river discharge and sea level. All time series have been adjusted for large-scale climate modes as with the regional time series and described in SI Appendix. White dots indicate values not statistically significant at the level. Grid cells without hatching are downstream sea-level sites, whereas hatched cells indicate upstream tide-gauge sites. Red boxes encapsulate groups of river stations and tide gauges within the same coastal region: GME (Gulf of Maine), MAB (Mid-Atlantic Bight), SAB (South Atlantic Bight), and GMX (Gulf of Mexico).
There are also some interesting, statistically significant correlations between river-discharge records and sea level at upstream tide gauges. Discharge from rivers within Chesapeake Bay (Susquehanna, Potomac, James, Roanoke) are significantly correlated with sea level at sites upstream along the New England coast (Portland, Seavey Island, Boston, Newport). Similarly, there are instances of more remote significant correlations, such as between discharge from the Roanoke River (in Virginia along the Atlantic coast) and sea level at Pensacola, Galveston, Rockport, and Port Isabel (in Florida and Texas along the Gulf coast). It is unlikely that these upstream and remote correlations indicate causation. Rather, they probably reflect underlying correlation between river flows within the same large-scale drainage basins (SI Appendix, Fig. S2). For instance, the correlation between outflows from the Roanoke and Apalachicola Rivers is 0.53 (SI Appendix, Fig. S2), and the latter river is immediately upstream of the four Florida and Texas tide gauges just mentioned.
Discussion
We investigated the relation between river discharge and sea level along the United States Atlantic and Gulf coasts on interannual and longer time scales during 1910–2017. We updated earlier calculations made by Meade and Emery (25) for 1931–1969, demonstrating that their results hold for longer and more recent time periods, and also addressed some outstanding issues prompted by that earlier analysis. We showed that river discharge can be a significant causal driver of year-to-year coastal sea-level changes and argued that observed correspondences between the two variables are roughly consistent, to order of magnitude, with expectations from theories for alongshore transport downstream of coastal river plumes (18, 24). While its relation to coastal sea level is statistically significant, river discharge explains only a portion of the overall variance in the tide-gauge records. This is unsurprising, given the myriad other processes that influence sea level along this coastline (6–14). Our results thus complement previous sea-level studies, adding to our understanding of the complex and multifaceted nature of sea-level variation along this densely populated coastline.
Although we focused on a particular coastline, our theory is sufficiently general that it should apply to other global coastal ocean locations as well. Applied to the world’s 25 largest rivers by annual mean discharge (30), Eq. 5 predicts that river discharge can raise the background mean downstream coastal sea level by cm and can force interannual sea-level variations of cm (SI Appendix, Fig. S3). The theory should be useful in studies of other areas where river runoff may be an important driver of coastal sea level (31).
Our results have important implications for monitoring coastal-zone changes from space (32). A useful order-of-magnitude length scale characterizing the coastal trapping and offshore decay of these sea-level signals is the baroclinic Rossby deformation radius , which, by virtue of Eq. 4, can be expressed:
| [7] |
Using the parameter values above and river-discharge data for the United States Atlantic and Gulf coasts, we find that baroclinic Rossby deformation radii are km. (This argument ignores the influence of shallow bathymetry. If, as in the case of the Mississippi River, coastal-ocean depths are shallower than the layer depth predicted by Eq. 4, which is typically of order 1 to 10 m, offshore length scales of the coastal sea-level anomaly will be broader than (18, 19).) This suggests that coastal sea-level anomalies caused by river discharge may not be captured by conventional satellite-altimetry data products, which have poor resolution within 10 to 20 km of the coast, due to uncertainties in correction algorithms and contamination of the satellite footprint (33). This could partly explain the poor correspondence between interannual sea level from tide gauges and satellite altimetry observed in some coastal regions (34). These results underscore the crucial importance of ongoing coastal-altimetry data reprocessing efforts (35) and future high-resolution satellite-altimetry missions (36) for monitoring the coastal ocean to provide empirical linkages between the terrestrial and marine realms.
Our findings show that the influence of river discharge on coastal sea level can be regional and nonlocal, extending downstream along the coast for hundreds of kilometers (23) (Fig. 3). This has important implications for the interpretation of tide-gauge records in the context of ocean-circulation and climate studies. Previous authors interpret low-frequency sea-level variations from tide-gauge records in terms of fluctuations in large-scale ocean circulation (28, 37–40). Our findings suggest that such interpretations should be made carefully, such that sea-level time series from locations downstream of major rivers should be used with caution in this context. This point raises interesting questions, which should be taken up in later studies. For example, what is the ultimate fate of buoyant coastal outflows, and how far down the coast can their influence be observed? Relatedly, note that we focused on coastal sea level along open-ocean boundaries and in the far-field downstream of rivers. We did not consider sea level at more near- or midfield sites within bays, estuaries, or river mouths. Since many populous United States cities are situated directly on major rivers (e.g., Philadelphia, Baltimore, Washington, DC), future efforts are needed to understand the relation between river discharge and sea level in this latter case, since the basic dynamical balances (e.g., hydraulic control, gradient-wind balance) are expected to be distinct from those considered here (24).
These results have clear implications for modeling and projection. To accurately simulate future discharge-driven sea-level changes and their coastal impacts, climate models would need to transfer accurately projected precipitation changes over a drainage basin to the coastal ocean and use sufficiently high spatial resolution over the ocean to resolve the attendant dynamical response. Most Coupled Model Intercomparison Project Phase 5 (CMIP5) models use horizontal ocean resolutions on the order of to 100 km (41), which is too coarse to resolve discharge-driven coastal sea-level changes. Thus, regional-scale flood risk in a given year may not be accurately represented in these projections. It will take another decade of model development before state-of-the-art global climate models have sufficiently high horizontal resolution to resolve the first baroclinic Rossby radius over most of the shallow ( m) global ocean (42). This suggests that alternative means of incorporating the discharge effects into model projections (e.g., improved parameterization schemes for impacts at the coast) warrant further attention. Such efforts will be crucial in light of projected future intensification of the hydrological cycle. For example, discharge of the Mississippi River is projected to increase by 11% to 60% over the coming century (43). Eq. 5 suggests that this increase in discharge would cause a background mean coastal sea-level rise downstream of the Mississippi River of 0.5 to 2.6 cm. Such considerations should be factored into centennial coastal sea-level projections at local to regional spatial scales.
Finally, these results have potential implications for interpretation of proxy relative sea-level reconstructions. Derived from cm-thick salt-marsh sediment samples, Common Era proxy sea-level reconstructions are inherently time averaged. Depending on background rates of glacial isostatic adjustment, the temporal averaging implicit in a sediment sample can vary, for example, from y in Florida (44) to y in southern New Jersey (45). To evaluate whether proxy-relative sea-level reconstructions are influenced by river discharge, we extended our analysis by averaging the data over different multiyear time periods (SI Appendix, Fig. S4). The correlation between river discharge and sea level generally decreases and becomes statistically insignificant for time scales to 10 y on the Atlantic coast and y along the Gulf Coast (SI Appendix, Fig. S4). While this finding could imply that river discharge is not an important contributor to the decadal and longer sea-level variations reflected in proxy reconstructions, it could also reflect the relative shortness of the data records given the time scales relevant to paleo problems. Also possibly important in this context are the broader distances over which advection by the alongshore flow can act on increasingly long time scales. Model studies would therefore be informative in these regards. If river discharge exerts an appreciable control on sea level at decadal and longer time scales, its influence on proxy reconstructions would be regional in scale (i.e., not restricted to sites in or very close to estuaries but also present at far-field sites along the open coast), as evidenced by the spatial scales of correlation seen in the instrumental record.
Supplementary Material
Acknowledgments
C.G.P. and R.M.P. acknowledge support from NASA Contract NNH16CT01C (which also supported C.M.L.), NASA Jet Propulsion Laboratory Subcontract 1569246, and National Science Foundation Award 1558966. C.G.P. also acknowledges support from The Investment in Science Fund at Woods Hole Oceanographic Institution. A.C.K. and S.E.E. acknowledge NSF Awards OCE-1458921 and OCE-1458903, respectively. This is a contribution to the International Geoscience Programme Project 639 “sea-level change from minutes to millennia” and PALSEA 2 (paleo constraints on sea level rise 2).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1805428115/-/DCSupplemental.
References
- 1.World Climate Research Programme 2017. WCRP, 2017. WCRP grand challenge: Regional sea level change and coastal impacts, science and implementation plan (International CLIVAR Project Office, Qingdao, China), Version 1.0.
- 2.Landerer FW, Jungclaus JH, Marotzke J. Regional dynamic and steric sea level change in response to the IPCC-A1B scenario. J Phys Oceanogr. 2007;37:296–312. [Google Scholar]
- 3.Yin J, Schlesinger ME, Stouffer RJ. Model projections of rapid sea-level rise on the northeast coast of the United States. Nat Geosci. 2009;2:262–266. [Google Scholar]
- 4.Sallenger AH, Doran KS, Howd PA. Hotspot of accelerated sea-level rise on the Atlantic coast of North America. Nat Clim Change. 2012;2:884–888. [Google Scholar]
- 5.Valle-Levinson A, Dutton A, Martin JB. Spatial and temporal variability of sea-level rise hotspots over the eastern United States. Geophys Res Lett. 2017;44:7876–7882. [Google Scholar]
- 6.Bingham RJ, Hughes CW. Signature of the Atlantic meridional overturning circulation in sea level along the east coast of North America. Geophys Res Lett. 2009;36:L02603. [Google Scholar]
- 7.Kopp RE. Does the mid-Atlantic United States sea level acceleration hot spot reflect ocean dynamic variability? Geophys Res Lett. 2013;40:3981–3985. [Google Scholar]
- 8.Andres M, Gawarkiewicz GG, Toole JM. Interannual sea level variability in the western North Atlantic: Regional forcing and remote response. Geophys Res Lett. 2013;40:5915–5919. [Google Scholar]
- 9.Calafat FM, Chambers DP. Quantifying recent acceleration in sea level unrelated to internal climate variability. Geophys Res Lett. 2013;40:3661–3666. [Google Scholar]
- 10.Thompson PR, Mitchum GT. Coherent sea level variability on the North Atlantic western boundary. J Geophys Res Oceans. 2014;119:5676–5689. [Google Scholar]
- 11.Piecuch CG, Ponte RM. Inverted barometer contributions to recent sea level changes along the northeast coast of North America. Geophys Res Lett. 2015;42:5918–5925. [Google Scholar]
- 12.Piecuch CG, Dangendorf S, Ponte RM, Marcos M. Annual sea level changes on the North American northeast coast: Influence of local winds and barotropic motions. J Clim1. 2016;29:4801–4816. [Google Scholar]
- 13.Davis JL, Vinogradova NT. Causes of accelerating sea level on the Atlantic and Gulf coasts of North America. Geophys Res Lett. 2017;44:5133–5141. doi: 10.1002/2017GL072845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Frederikse T, Simon K, Katsman CA, Riva R. The sea-level budget along the Northwest Atlantic coast: GIA, mass changes, and large-scale ocean dynamics. J Geophys Res Oceans. 2017;122:5486–5501. [Google Scholar]
- 15.Chepurin GA, Carton JA, Leuliette E. Sea level in ocean reanalyses and tide gauges. J Geophys Res Oceans. 2014;119:147–155. [Google Scholar]
- 16.Chapman DC, Lentz SJ. Trapping of a coastal density front by the bottom boundary layer. J Phys Oceanogr. 1994;24:1464–1479. [Google Scholar]
- 17.Kourafalou VK, Oey L-Y, Wang JD, Lee TN. The fate of river discharge on the continental shelf. 1. Modeling the river plume and the inner shelf coastal current. J Geophys Res. 1996;101:3415–3434. [Google Scholar]
- 18.Yankovsky AE, Chapman DC. A simple theory for the fate of buoyant coastal discharges. J Phys Oceanogr. 1997;27:1386–1401. [Google Scholar]
- 19.Lentz SJ, Helfrich KR. Buoyant gravity currents along a sloping bottom in a rotating fluid. J Fluid Mech. 2002;464:251–278. [Google Scholar]
- 20.Fong DA, Geyer WR. Response of a river plume during an upwelling favorable wind event. J Geophys Res. 2001;106:1067–1084. [Google Scholar]
- 21.Fong DA, Geyer WR. The alongshore transport of freshwater in a surface-trapped river plume. J Phys Oceanogr. 2002;32:957–972. [Google Scholar]
- 22.Whitney MM, Garvine GW. Wind influence on a coastal buoyant outflow. J Geophys Res. 2005;110:C03014. [Google Scholar]
- 23.Chant RJ, et al. Bulge formation of a buoyant river outflow. J Geophys Res. 2008;113:C01017. [Google Scholar]
- 24.Horner-Devine AR, Hetland RD, MacDonald DG. Mixing and transport in coastal river plumes. Annu Rev Fluid Mech. 2015;47:569–594. [Google Scholar]
- 25.Meade RH, Emery KO. Sea level as affected by river runoff, Eastern United States. Science. 1971;173:425–428. doi: 10.1126/science.173.3995.425. [DOI] [PubMed] [Google Scholar]
- 26.Holgate SJ. Coauthors New data systems and products at the permanent service for mean sea level. J Coastal Res. 2013;288:493–504. [Google Scholar]
- 27.Hamlington BD, et al. The effect of the El Niño-Southern oscillation on U.S. regional and coastal sea level. J Geophys Res. 2015;120:3970–3986. [Google Scholar]
- 28.McCarthy GD, Haigh ID, Hirschi JJ-M, Grist JP, Smeed DA. Ocean impact on decadal Atlantic climate variability revealed by sea-level observations. Nature. 2015;521:508–510. doi: 10.1038/nature14491. [DOI] [PubMed] [Google Scholar]
- 29.Piecuch CG, Thompson PR, Donohue KA. Air pressure effects on sea level changes during the twentieth century. J Geophys Res. 2016;121:7917–7930. [Google Scholar]
- 30.Dai A. 2016. Historical and future changes in streamflow and continental runoff. Terrestrial Water Cycle and Climate Change: Natural and Human-Induced Impacts, Geophysical Monograph (American Geophysical Union, Washington DC), Vol 221, 1st Ed, pp 17–38.
- 31.Emery KO, Aubrey DG. Sea Levels, Land Levels, and Tide Gauges. Springer; New York: 1991. pp. 45–46. [Google Scholar]
- 32.Cazenave A, Le Cozannet G, Benveniste J, Woodworth PL, Champollion N. 2017 Monitoring coastal zone changes from space, Eos, 98. [Google Scholar]
- 33.Vignudelli S, Kostianoy A, Cipollini P, Benveniste J. Coastal Altimetry. Springer; Berlin: 2011. p. 565. [Google Scholar]
- 34.Vinogradov SV, Ponte RM. Low-frequency variability in coastal sea level from tide gauges and altimetry. J Geophys Res. 2011;116:C07006. [Google Scholar]
- 35.Passaro M, Cipollini P, Benveniste J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J Geophys Res Oceans. 2015;120:3061–3078. [Google Scholar]
- 36.Dufau C, Orsztynowicz M, DIbarboure G, Morrow R, Le Traon P-Y. Mesoscale resolution capability of altimetry: Present and future. J Geophys Res Oceans. 2016;121:4910–4927. [Google Scholar]
- 37.Enfield DB, Allen JS. On the structure and dynamics of monthly mean sea level anomalies along the pacific coast of North and South America. J Phys Oceanogr. 1980;10:557–578. [Google Scholar]
- 38.Chelton DB, Davis RE. Monthly mean sea-level variability along the west coast of North America. J Phys Oceanogr. 1982;12:757–784. [Google Scholar]
- 39.Chelton DB, Enfield DB. Ocean signals in tide gauge records. J Geophys Res. 1986;91:9081–9098. [Google Scholar]
- 40.Miller L, Douglas BC. Gyre-scale atmospheric pressure variations and their relation to 19th and 20th century sea level rise. Geophys Res Lett. 2007;34:L16602. [Google Scholar]
- 41.Taylor KE, Stouffer RJ, Meehl GA. An overview of CMIP5 and the experimental design. Bull Amer Meteorol Soc. 2012;93:485–498. [Google Scholar]
- 42.Holt J, et al. Prospects for improving the representation of coastal and shelf seas in global ocean models. Geosci Model Dev. 2017;10:499–523. [Google Scholar]
- 43.Tao B, et al. Increasing Mississippi river discharge throughout the 21st century influenced by changes in climate, land use, and atmospheric . Geophys Res Lett. 2014;41:4978–4986. [Google Scholar]
- 44.Gerlach MJ, et al. Reconstructing common era relative sea-level change on the Gulf coast of Florida. Mar Geol. 2017;390:254–269. [Google Scholar]
- 45.Kemp AC, et al. Sea-level change during the last 2500 years in New Jersey, USA. Quat Sci Rev. 2013;81:90–104. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.