A Comparison of Three Liquid Chromatography (LC) Retention Time Prediction Models

Abstract

High-resolution mass spectrometry (HRMS) data has revolutionized the identification of environmental contaminants through non-targeted analysis (NTA). However, chemical identification remains challenging due to the vast number of unknown molecular features typically observed in environmental samples. Advanced data processing techniques are required to improve chemical identification workflows. The ideal workflow brings together a variety of data and tools to increase the certainty of identification. One such tool is chromatographic retention time (RT) prediction, which can be used to reduce the number of possible suspect chemicals within an observed RT window. This paper compares the relative predictive ability and applicability to NTA workflows of three RT prediction models: (1) a logP (octanol-water partition coefficient)-based model using EPI Suite^TM logP predictions; (2) a commercially available ACD/ChromGenius model; and, (3) a newly developed Quantitative Structure Retention Relationship model called OPERA-RT. Models were developed using the same training set of 78 compounds with experimental RT data and evaluated for external predictivity on an identical test set of 19 compounds. Both the ACD/ChromGenius and OPERA-RT models outperformed the EPI Suite^TM logP-based RT model (R²=0.81–0.92, 0.86–0.83, 0.66–0.69 for training-test sets, respectively). Further, both OPERA-RT and ACD/ChromGenius predicted 95% of RTs within a ± 15% chromatographic time window of experimental RTs. Based on these results, we simulated an NTA workflow with a ten-fold larger list of candidate structures generated for formulae of the known test set chemicals using the U.S. EPA’s CompTox Chemistry Dashboard (https://comptox.epa.gov/dashboard), RTs for all candidates were predicted using both ACD/ChromGenius and OPERA-RT, and RT screening windows were assessed for their ability to filter out unlikely candidate chemicals and enhance potential identification. Compared to ACD/ChromGenius, OPERA-RT screened out a greater percentage of candidate structures within a 3-minute RT window (60% vs. 40%) but retained fewer of the known chemicals (42% vs. 83%). By several metrics, the OPERA-RT model, generated as a proof-of-concept using a limited set of open source data, performed as well as the commercial tool ACD/ChromGenius when constrained to the same small training and test sets. As the availability of RT data increases, we expect the OPERA-RT model’s predictive ability will increase.

Graphical abstract

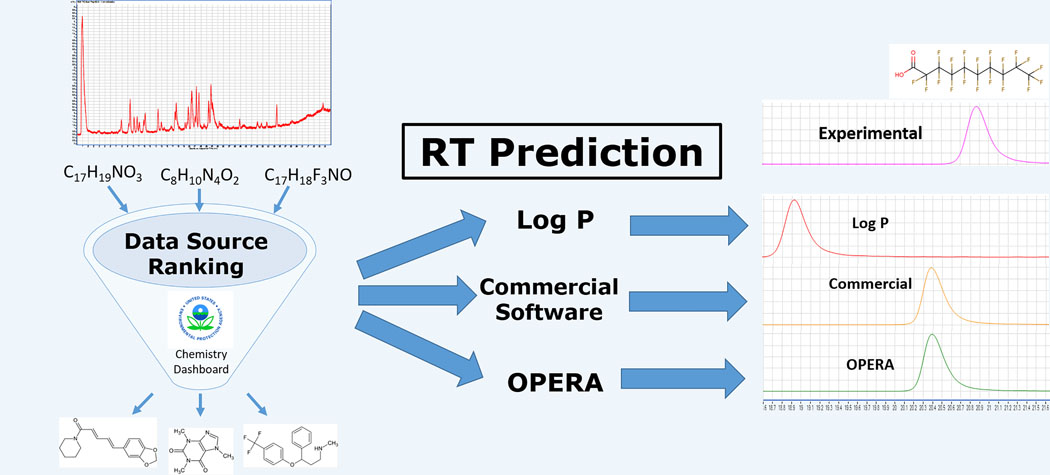
INTRODUCTION

High-resolution mass spectrometry (HRMS) and its coupling to gas chromatography (GC) and liquid chromatography (LC) systems have revolutionized processes used to identify environmental contaminants [1–5]. High mass accuracy and sensitivity in HRMS instruments routinely allow observation of thousands of chemical features (defined by an accurate monoisotopic mass, retention time, abundance, and related isotopes) in environmental samples [1–5]. However, data processing and chemical characterization remain challenging despite recent developments [6, 7]. Chemical reference standards and their associated spectral data allow structure confirmation of observed features, but reference standards rarely are available for thousands of observed features in non-targeted analysis (NTA) and suspect screening analysis (SSA). Therefore, research consortia around the world have begun to develop workflows to effectively identify unknown chemicals in environmental samples with increasing degrees of certainty [5, 8, 9]. Identifying unknowns through data source ranking has become a fixture in many workflows [10, 11]. The growth and availability of spectral libraries such as MassBank [12], improvements to in silico fragmentation resources [13], and the CompTox Chemistry Dashboard [14, 15] have all increased probable structure identification from HRMS data [16].

Effective NTA workflows combine multiple tools and types of information for chemical identification, including data source ranking, comparison between empirical and reference (or theoretical) spectra, and chromatographic retention time (RT) prediction [13, 17]. However, many RT prediction tools and models, when integrated into NTA workflows, have been used with varying degrees of success [16–22], and it is difficult to determine their performance in isolation. Comparing RT prediction tools should improve NTA workflows by characterizing their performance in context.

Although RTs can vary considerably between analytical columns, mobile phases, and instrumentation, RT information has proven useful in identifying some chemical unknowns [13, 18]. Comparing predicted RTs to experimental RTs of unknowns provides data on how to focus subsequent investigation efforts on only those features observed within specified RT windows and can provide weighted evidence toward tentative chemical identification if RTs align. RTs are directly related to chemical structure and have been predicted using a variety of physicochemical properties with varying degrees of complexity [19–21]. Simple RT prediction models based on octanol-water partition coefficients (logP) have been commonly used and can provide a reasonably good prediction (coefficient of determination R₂ = 0.60 to 0.70) [17, 19, 22], although the reliability of the logP data is critical to model performance and resulting prediction accuracy. Bade et al [19] reported very little difference between using experimental and predicted logP values when estimating RT, but indicated a preference for predicted logP data based on broader availability.

Multivariate Quantitative Structure-Retention Relationship (QSRR) methods for RT prediction are more complex than logP-based RT models and have been increasingly used in recent years [20, 21, 23, 24]. Descriptors such as logP, the pH-dependent partition coefficient logD, molecular mass, polarity, and Linear Solvation Energy Relationship (LSER) [25] have been incorporated into workflows to complement identification strategies. QSRR methods have predicted 95% of RTs within a 2-minute RT window of an 18-minute chromatographic run (or ±11% of the total run time) for ~600 chemicals [18] and have yielded R² values for predicted versus experimental RTs consistently exceeding 0.80 [21, 24]. Artificial neural networks (ANN) [18, 20, 24], k-nearest neighbor clustering [21], partial least squares regression (PLS) [26–28], and support vector machine learning (SVM) approaches have recently been used to develop descriptor-based models for RT prediction [21]. Finally, commercial chromatography-specific software solutions providing RT prediction are available (such as http://www.acdlabs.com/products/com_iden/meth_dev/lc_sim/ and http://molnar-institute.com/drylab/) and can be used to support NTA. ACD/ChromGenius (Advanced Chemistry Development, Inc., Toronto, Canada) is one such commercial software tool. ACD/ChromGenius has been minimally described in the literature but is a comprehensive tool capable of providing analysts with RT prediction information for use in structure identification.

The focus of some recent environmental non-targeted analytical chemistry efforts has shifted towards more polar emerging contaminants due to their ubiquity in the environment [17, 24, 29], leading to the development of LC-based targeted and NTA methods and related data processing tools. GC-based systems have established retention indices and RT databases (such as the National Institute of Standards and Technology [NIST] database [30]) to improve identification in NTA, but LC systems are lacking. Therefore, LC-based RT prediction models require development and validation for ultimate inclusion in structural identification workflows. The purpose of this research was to compare performance across three RT prediction tools, including a new in-house QSRR model, and to evaluate impact of these models on overall NTA workflow performance. Three RT prediction models were compared for relative predictive ability and applicability to NTA workflows using 97 chemicals observed using high-performance liquid chromatography (HPLC)-time of flight (TOF)/MS instrumentation: (1) a logP-based RT model using EPI Suite^TM property predictions; (2) an ACD/ChromGenius model; and (3) an in-house QSRR model called OPERA-RT. OPERA-RT was structured similarly to physical and chemical property prediction models [31] and in this work was applied to RT as a proof-of-concept. To our knowledge, this research represents the first time that three RT models such as these have been explicitly compared using data from the same sets of chemicals.

METHODS

HPLC Retention Time Data Acquisition

Retention time data for 97 unique chemicals were used for this investigation. The data were acquired via analysis of 10 individual standards and three mixtures of the remaining 87 standards. The full results set for the 97 chemicals was separated into a training set of 78 chemicals (~80%) and a test set of 19 chemicals (~20%). The ten chemicals analyzed as individual standards were split proportionally between the test and training sets and comprised ~10% of each list. Supplemental Table S1 lists all 97 chemicals, with annotations indicating if each chemical was analyzed individually or in a mixture and included in the training or test set (Supplemental File S1 provides structures in SDF format).

RTs were acquired using an Agilent 1100 series HPLC interfaced with a 6210 series accurate-mass LC-TOF/MS system (Agilent Technologies, Palo Alto, CA) fitted with an electrospray ionization source. Chromatographic separation was accomplished using an Eclipse Plus C8 column (2.1 × 50 mm, 3.5 μm; Agilent Technologies) following previously published methods [1]. The flow rate was set to 0.2 mL/min and the column was kept at 30 °C. Mobile phase A consisted of ammonium formate buffer (0.4 mM) and DI water:methanol (95:5 v/v), and B consisted of ammonium formate (0.4 mM) and methanol:DI water (95:5 v/v). Separation occurred using a gradient method as follows: 0–25 min linear gradient from 75:25 A:B to 15:85 A:B; 25–40 min linear gradient from 15:85 A:B to 100% B; 40–50 hold at 100% B. Molecular features were acquired between 0 and 45 min.

Model Descriptions

LogP-based model

The logP-based RT prediction model was developed following previously published methods [17, 19]. Predicted logP values were used to develop the RT prediction model. To select the better logP-based RT model for comparison with the ACD/ChromGenius and OPERA-RT models, three sources of predicted logP were used: EPI Suite^TM (KOWWIN) [32], ACD/Labs, and OPERA (OPEn saR App) [33]. EPI Suite^TM KOWWIN uses a fragment contribution method, and ACD/Labs primarily uses the principle of isolating carbons [34]. OPERA is a suite of QSAR models used to predict physicochemical and environmental fate properties [31]. OPERA model predictions of logP, referred to as OPERA logP, are based on k-nearest neighbors (kNN) classification of molecular descriptors. OPERA logP is distinct from OPERA-RT, the model used to predict RT.

Experimental RT values were regressed on logP estimates from all three sources for the training set chemicals (n = 78). The resulting linear regression equations were then used to predict RTs for chemicals in the training and test sets. Results of the logP-based prediction models were evaluated, and the best model was chosen for further comparison to the ACD/ChromGenius and OPERA-RT models.

ACD/ChromGenius

ACD/ChromGenius was developed by ACD/Labs to predict RTs and inform chromatographic method development based on structural information for chemical compounds of interest [35]. The software bases RT prediction on a proprietary algorithm using a number of physicochemical parameters, including logP, logD, molecular weight, molecular volume, polar surface area, and other molecular properties. Algorithm criteria were selected to maximize model performance (see Supplementary Figures S1 through S6), and structure similarity searching based on structure fingerprints was performed to narrow the prediction database. Supplementary Figure S3 illustrates the parameter options selected during model generation [36]. The software incorporates a knowledgebase of chemical structures and RTs used to develop RT prediction models and can simulate different separation methods available in the knowledgebase. Different chromatographic methods can be ranked according to suitability (optimal separation of chemicals, gradient parameters, length of chromatographic run, etc.) and displayed with a simulated chromatogram and a table of predicted RTs. The software also has a training mode where a user can input a data set of chemical structures, experimental RTs, and chromatographic method parameters, which then are used to build an RT prediction model. Applications of the ACD/ChromGenius model for GC methods are reported in the literature [36].

For the current application, chromatographic method parameters (see “Retention Time Data Acquisition” above), the training set of structures (n = 78), and experimental RTs were loaded into the software. The software’s prediction algorithms then used chemical structures and their associated ACD-predicted physicochemical properties to build unique prediction equations. Algorithm criteria and model parameters were selected to minimize prediction error (see Supplementary Figures S1 through S6). Predicted RTs were ultimately exported from the results screen within the software.

OPERA-RT model

The OPERA-RT model was generated using methods similar to the generation of property prediction model [31]. First, molecular descriptors of the chemicals were calculated. PaDEL, a free and open-source software for molecular descriptor calculation [37] was used to calculate constitutional indices, ring descriptors, topological indices, functional group counts, atom-centered fragments, atom-type E-state indices, and two-dimensional (2D) atom pair descriptors based on the molecular topology of the chemicals. After removing variables (descriptors) with constant, near-constant, and missing values, descriptor pairwise correlation was checked with a fixed threshold of 95% to avoid multicollinearity [38, 39].

Seven-hundred sixty descriptors remained for variable selection to identify the most predictive descriptors. This identification was performed using genetic algorithms (GA) [40, 41]. These nature-inspired machine-learning algorithms start from an initial random population of chromosomes. Each chromosome is a binary string (genes) that represents the presence or absence of the initial variables (descriptors) in a model. Afterwards, an evolution process is simulated and new chromosomes are obtained by coupling the chromosomes of the initial population with genetic-like operations (crossover and mutation). The evolution process is driven by maximizing a defined fitness function for 100 generations, and the whole process is repeated for 100 runs using the following parameters: cross-over rate=0.5, mutation rate=0.01, population size=30. The ultimate output is an optimal number of the most relevant descriptors and the appropriate model parameters.

The predictive squared correlation coefficient Q², representing the predictive ability calculated in five-fold cross-validation, was used to evaluate fitness (Equation 1). This parameter has been calculated using various formulas in the literature [42–44]. In this work, the following formula was used:

$$Q^2=1-\frac{{\displaystyle {\sum }_{i=1}^{n_{EXT}}{\left(y_i-{\widehat{y}}_i\right)}^2/n_{EXT}}}{{\displaystyle {\sum }_{i=1}^{n_{TR}}{\left(y_i-\overline{y}\right)}^2/n_{TR}}}$$ (1)

where n_EXT is number of test compounds and n_TR is the number of training compounds, ŷ_i and y_i are the estimated and observed responses, respectively, and ȳ is the mean. GAs were coupled to partial least squares (PLS) to calibrate the models. PLS is a fitting technique that finds fundamental relationships between the matrix of descriptors (X) and the response (Y) using latent variables (LV), which are orthogonal and explain the maximum variance in the Y space [45].

The GAs provided a set of optimal models that were compared to minimize the number of used descriptors and the number of LVs for PLS models. The model with the best compromise between these criteria was selected. The applicability domain (AD) of the best model was investigated using the leverage approach, with a threshold of three times the average of leverages from the matrix of the used descriptor values of the training set [46]. All calculations were performed in MATLAB 8.2 [47].

Criteria Used to Evaluate RT Models

A variety of metrics have been used in the literature to compare and evaluate RT prediction model performance [18, 19, 21, 48]. For this application, the relative predictive ability and performance of all three models (log P, OPERA-RT, and ACD/ChromGenius) were evaluated using criteria and statistics common to QSAR modelling [21, 42–44, 49] as well as more specific criteria relevant to the analytical chemistry and chromatography community [18, 19]. All of the following statistics were calculated using R Computing Software (Version 3.3.2) [50].

• •
  The coefficient of determination (R₂) between predicted and experimental RTs, was calculated as follows (Equation 2):

  $$R^2=1-\frac{RSS}{TSS}=1-\frac{{\displaystyle {\sum }_{i=1}^{n_{TR}}{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^{n_{TR}}{\left(y_i-\overline{y}\right)}^2}}$$ (2)

  where ŷ_i and y_i are the estimated and observed responses, respectively, ȳ is the mean, RSS is the residual sum of squares, TSS is the total sum of squares, and n_TR is the number of training compounds.

• •
  The root mean squared error (RMSE) between predicted and experimental RTs for the training and test sets, calculated as (Equation 3):

  $$RMSE=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{n}}$$ (3)

  where ŷ_i and y_i are the estimated and observed responses, respectively.

• •Absolute mean error of experimental versus predicted RT for both sets, in minutes.
• •The number of chemicals whose predicted RT fell within specific RT windows of accuracy, relative to the total chromatographic run time.

RT Prediction for Structure Identification

To explore the capabilities of the two best-performing models discussed in this paper, ACD/ChromGenius and OPERA-RT, further analysis was conducted on the test set chemicals. Mimicking an NTA-type workflow, molecular formulae of the test set chemicals were searched in the CompTox Chemistry Dashboard [12], and the top 10 candidate chemical results for each formula, as determined by data source ranking [13], were compiled. RTs of all the chemicals in the resulting list of candidate structures were predicted using the ACD/ChromGenius and OPERA-RT models. Predicted RTs were then evaluated relative to the experimental RT of the known test set chemicals by calculating RT error as the difference between the experimental RT of the known test set chemical and the predicted RT of the candidate chemicals from the search results list (see Supplemental Table S5). Then, three RT screening windows were applied to evaluate the efficacy of each prediction model: ±5, ±3, and ±2 minutes. Results were reported as the percentage of known test set chemicals retained within each screening window (i.e. true positives) and the percentage of total results screened out per formula search, indicating selectivity.

RESULTS AND DISCUSSION

Chemical Sets

Experimental RTs of the training set compounds ranged from 1.1 to 40.8 min, and logP values ranged from −0.4 to 9.5. RTs of the test set compounds ranged from 1.7 to 29.4 min and covered a logP range of −0.04 to 9.6 (see Supplemental Tables S1 through S3).

Evaluation of logP-Based Models

To select the best logP-based RT model for comparison, three sources of predicted logP were used: EPI Suite^TM, ACD/Labs, and OPERA. The three sources of predicted logP were evaluated separately and a single model was chosen on the basis of predictive performance of the corresponding RT models on the training and test sets (see Supplemental Table S3). Based on R² and RMSE statistics, the EPI Suite^TM logP-based model performed similarly to OPERA logP on the training set and outperformed OPERA logP on the test set. As a result, the EPI Suite^TM logP-based model was selected for further comparison and evaluation.

Model Performance

A number of models resulted from the GA-PLS machine learning run on PaDEL descriptors. Among these, the optimal OPERA-RT model offered a compromise between model complexity and predictivity. The selected OPERA-RT model included seven descriptors that were projected orthogonally into three latent variables corresponding to the first three significant principal components (see Supplemental Table S2). Most of the best performing models included the seven selected descriptors. Other models were generated that present higher predictive ability but for a higher number of descriptors.

Table 1 shows the prediction summary statistics of the EPI Suite^TM logP-based, ACD/ChromGenius, and OPERA-RT models. For the training set compounds, R², RMSE, and absolute-mean-error values between the predicted and experimental RTs indicate that the OPERA-RT model performed better than the ACD/ChromGenius model, which performed better than the logP-based model. For the test set compounds, the ACD/ChromGenius model performed better than the OPERA-RT model, which performed better than the EPI Suite^TM logP-based model. On the combined sets (n=97), based on RMSE, R², and absolute mean error, the OPERA-RT and ACD/ChromGenius models performed similarly and outperformed the EPI Suite^TM logP-based model.

Table 1.

Summary model performance statistics of all three models

	EPI Suite™ logP	ACD/ChromGenius	OPERA-RT
Training Set (n = 78)
R2	0.66	0.81	0.86
RMSE (min)	5.58	4.18	3.56
Absolute Mean Error (min)	4.71	3.25	2.88
Test Set (n = 19)
R2	0.69	0.92	0.83
RMSE (min)	5.14	2.66	3.86
Absolute Mean Error (min)	4.41	2.36	3.28
Combined Set (n = 97)
R2	0.66	0.83	0.86
RMSE (min)	5.50	3.93	3.60
Absolute Mean Error (min)	4.65	3.03	2.93

R² = coefficient of determination, RMSE = root mean squared error

Figure 1 shows predicted versus experimental RTs and RT error versus experimental RT for the three models. Training and test sets are combined. Prediction errors throughout the chromatographic run time were lowest for the ACD/ChromGenius and OPERA-RT models and greatest for the EPI Suite^TM logP-based model (Figure 1). Additionally, the OPERA-RT model performed more consistently across the full range of RTs than the ACD/ChromGenius model, despite similar R² values (see Figure 1). The EPI Suite^TM logP-based model used for this research performed similarly to previous logP-based RT prediction models. Bade et al [20] reported an R² of 0.67 and an RMSE of 2.19 min (or 12.2% of total run time) based on a training set of ~600 compounds, and others have reported similar R² values ranging from 0.6 to 0.7 [17] on ~90 compounds. The EPI Suite^TM logP-based RT model did not perform as well as the QSRR models but it performed as well as other previously reported RT prediction models built on logP values. Accessibility to predicted logP data and consistent performance across laboratory groups based on literature data indicates that logP can be used to predict LC RTs across research groups with some reliability.

Figure 1.

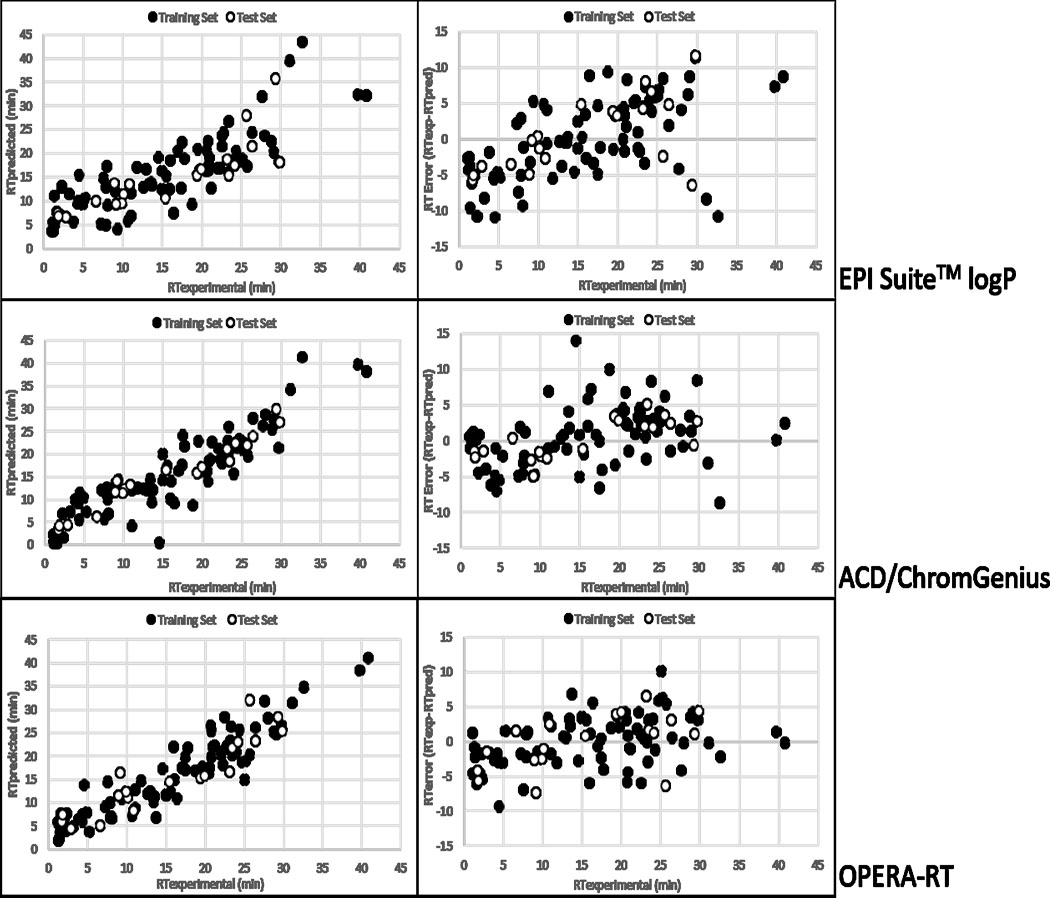
Predicted versus experimental RTs (left column) and RT error versus RT (right column) for EPI Suite^TM logP-based (top), ACD/ChromGenius (middle), and OPERA-RT (bottom) models. Training and test sets are combined.

Both the ACD/ChromGenius and OPERA-RT models performed similarly to other models using QSRR methods. ANN modelling of RT has yielded R² values of 0.86 to 0.90 [18] and absolute RT errors of approximately 5% of the total chromatographic run time [20]. The ACD/ChromGenius and OPERA-RT models performed within the ranges of previous ANN models based on model performance statistics (see Table 1; 5% of the total run time in this research is 2.25 min). Additionally, previously reported ANN models had substantially larger training sets (~1000 compounds), which likely improved model performance relative to smaller training sets [24]. The ACD/ChromGenius and OPERA-RT models were outperformed only by the best models described in Aalizadeh et. al. [21], where several linear and non-linear models were developed. R² values between the predicted and experimental RTs reported in Aalizadeh et al ranged from 0.82 to 0.98 for the training set and 0.78 to 0.85 for the test set [21].

Finally, some similarly structured PLS models for RT prediction outperformed the models described herein, but these PLS models were built on specific training sets (less than 15 chemicals) of structurally similar chemicals within the same class (steroids [26] and chalcones [27]). Another recent kernel-based PLS model for RT prediction ( R² = 0.86) performed similar to the OPERA-RT model but was generated on a training set of ~1000 compounds [28]. Therefore, with respect to standard model performance statistics, both the ACD/ChromGenius and OPERA-RT models perform similarly to many other QSRR models, and logP-based models are outperformed by the more complex QSRR models.

Chromatographic Windows

There are multiple approaches for using RT predictions as part of NTA workflows. One approach uses prediction windows to determine if estimated RTs for candidate compounds fall within a predetermined range of the experimental RTs of unknowns. Researchers have applied this approach using time windows around experimental RTs based on minutes throughout the chromatographic run [18, 19]. However, use of fractional windows (such as 1/10th or 10% of the total run time) allows the use of a common rule across multiple methods, whereas a straight time window is specific to a particular method (for example, ± 10% of a 20-min run yields a window of ± 2 min).

Table 2 shows the number of predicted RTs in both the training and test sets that fell within ± 5, 10, 15, and 20% time windows (as percentage of the total chromatographic run time) of the experimental RTs (or ± 2.25, 4.5, 6.75, and 9 min, respectively) calculated for each model. For the EPI Suite^TM logP-based model, 90% of the predicted RTs fell within a ± 20% time window of the experimental RTs, and both the ACD/ChromGenius and OPERA-RT models predicted 97% of the RTs within the same window. The OPERA-RT model predicted 81% (63 out of 78) of the training set to be within the ±10% window, while the ACD/ChromGenius model predicted 72% (56 out of 78) of the training set to be within the same window. For the test set, the ACD/ChromGenius and OPERA-RT models predicted nearly 100% of RTs to be within the ± 15% window, while the logP-based model predicted 89% of the test set to be within the ±15% window. At smaller RT windows, the ACD/ChromGenius and OPERA-RT models performed similarly across both sets and outperformed the EPI Suite^TM logP-based model.

Table 2.

Number of predicted RTs from each model reported within a RT window, as a % of the total chromatographic run time. Total run time is 45 min.

	Number of predicted RTs found within window of experimental      RTs
RT window (± % of total 45-min run, ± min)	EPI SuiteTM logP	ACD/ChromGenius	OPERA-RT
Training Set (n = 78)
± 5%  (2.25 min)	19	36	36
± 10% (4.50 min)	39	56	63
± 15% (6.75 min)	59	70	74
± 20% (9.00 min)	70	76	76
Test Set (n = 19)
± 5%  (2.25 min)	3	9	7
± 10% (4.50 min)	10	17	15
± 15% (6.75 min)	17	19	18
± 20% (9.00 min)	18	19	19

The logP-based model in this research performed similarly to other logP-based models in studies where chromatographic RT prediction windows were considered as a decision criterion [19]. At approximately the same percentage of the total run time (± 20%), Bade et al [19] reported that 92% of the compounds in the study set were within the defined range, versus 89% of the training set and 95% of the test set reported here. For ANN-based models predicting RTs on the same chemical set, Bade et al [18] reported that 95% of predicted RTs were within a window set at 16% of the total run time. In this research, the OPERA-RT model predicted more than 95% of both the training and test sets within 15% of the run time, while the ACD/ChromGenius model predicted more than 95% of the test set only within the same error range. These results indicate that the OPERA-RT and ACD/ChromGenius models outperformed logP-based models (this research and [20]) and performed as well as another QSRR model built on a larger training set [18].

Applying defined windows to evaluate RT predictions enables the analyst to view the likelihood that prediction models can aid more comprehensive NTA workflows. Accurate RT prediction within a selective time window (the smallest window in which the prediction RT falls) could allow the screening out of unlikely chemicals based on RT. Both the ACD/ChromGenius and OPERA-RT models performed similarly to other previously reported QSRR models, indicating that both models may enhance processes for assigning candidate structures to unknown features as a part of larger workflows.

RT Prediction for Structure Identification

Identifying observed chemical features in NTA and SSA applications requires cohesive workflows that bring together a variety of data sources, in silico tools, and software applications. Applying RT prediction models to identification workflows can improve chemical identification by reducing potential candidates or ranking potential candidates by RT feasibility [5, 13].

The two best models in this research, ACD/ChromGenius and OPERA-RT, were further evaluated in a mimicked NTA workflow. As expected and shown in Table 3, in both models, tighter RT windows increased the number of search results screened out. However, as tighter RT windows were applied, known chemicals were more likely to fall outside the RT screening windows, especially at the smallest windows that approached the prediction error of the models. At a conservative RT window of ± 5 min (or 11% of the total run time), the ACD/ChromGenius model screened out about 20% of the search results while keeping 18 of the 19 chemicals in the test set (Table 3 shows selected chemicals only). The OPERA-RT model also screened out about 20% of the search results and kept 17 of the 19 chemicals at RT window of ± 5 min.

Table 3.

Selected chemicals and screening results based on RT windows applied to RT predictions for the OPERA-RT and ACD/ChromGenius models. The percentage of search results screened out based on each formula search are presented along with whether or not the known chemical was kept within the RT window (Y/N). Only those chemicals with 10 candidate chemical results (see RT Prediction for Structure Identification) are included below for accurate representation of percentages (n=12). Total chromatographic run time was 45 minutes.

	% of Search Results Screened Out and Whether the Known Chemical was Kept
Test Set Chemical	±5 min	±3 min	±2 min
OPERA-RT
Carbofuran	10% - Y	20% - Y	40% - Y
Tetradecanoic acid, 2,3-   dihydroxypropyl ester	60% - Y	90% - N	90% - N
Piperine	90% - Y	100% - N	100% - N
Corticosterone	10% - Y	40% - Y	50% - Y
Rofecoxib	10% - Y	70% - N	80% - N
1,2-Benzisothiazolin-3-one	0% - Y	40% - Y	60% - Y
N-Dodecanoyl-N-methylglycine	0% - Y	60% - N	80% - N
Nootkatone	80% - N	90% - N	90% - N
6-Propyl-2-thiouracil	0% - Y	60% - N	80% - N
Bisphenol F	0% - Y	10% - Y	20% - N
6-Hydroxychlorzoxazone	70% - Y	100% - N	100% - N
4'-Hydroxydiclofenac	40% - Y	60% - Y	90% - Y
Median percentage screened -total knowns kept	10% - 11	60% - 5	80% - 4
ACD/ChromGenius
Carbofuran	10% - Y	20% - Y	40% - N
Tetradecanoic acid, 2,3-   dihydroxypropyl ester	50% - Y	70% - Y	100% - N
Piperine	70% - Y	80% - N	80% - N
Corticosterone	40% - Y	40% - Y	90% - Y
Rofecoxib	60% - Y	90% - N	90% - N
1,2-Benzisothiazolin-3-one	20% - Y	20% - Y	30% - Y
N-Dodecanoyl-N-methylglycine	10% - Y	40% - Y	70% - N
Nootkatone	0% -Y	30% -Y	40% -N
6-Propyl-2-thiouracil	0% - Y	3% - Y	60% - Y
Bisphenol F	20% - Y	20% - Y	70% - N
6-Hydroxychlorzoxazone	0% - Y	90% - Y	100% - N
4'-Hydroxydiclofenac	40% - Y	50% - Y	80% - N
Median percentage screened -total knowns kept	20% - 12	40% - 10	75% - 3

The search results summarized in Table 3 were pre-screened by the number of data sources, therefore the number of screened chemicals reported should not be considered comprehensive. When a full search results list is used, it is probable that a greater number of candidate chemicals would be screened out. It is imperative to find a balance between screening out potential false positives from search results while not eliminating true positives. To exclude no true positives (i.e. the known test set chemical), the RT window for screening results in the ACD/ChromGenius model would need to be 5.06 min and in the OPERA-RT model 6.5 minutes. The ACD/ChromGenius model achieved slightly greater specificity than the OPERA-RT model in this NTA scenario, but both models performed similarly.

RT prediction has value in identification workflows but must be applied with caution. Further, RT prediction alone is not sufficient for identification in NTA scenarios, and, as previous research shows [5, 17–18], should be combined with other metrics and metadata to improve identification. For future applications, it is recommended that the RT prediction models used in this research be conservatively applied (with RT windows at or exceeding ± 5 min) to tentative chemical lists after initial identification methods in order to preserve true positives.

Several tools incorporate RT prediction into structural identification workflows. Recent additions to MetFrag [51] and FOR-IDENT [9] enable users to incorporate or predict RTs and to use RT likelihood as part of weighting-based identification schemes. Other simulators (both open and software-based) achieve predictions based on pre-built training sets and chromatography conditions. Incorporating RT prediction into identification workflows will improve processes, but difficulties arise when RT prediction models cover small applicability domains or apply only to one LC setup as is the case in most prediction models. Large multi-laboratory collaborations and trials can assist in the development of global RT prediction models for use as cross-laboratory workflows [5, 52, 53].

Challenges

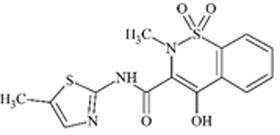
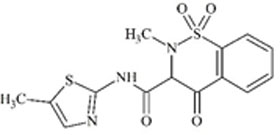
Understanding the challenges and limitations within each RT prediction model and identifying solutions can improve overall model performance. One potential cause of errors in RT prediction may occur when tautomers have not been correctly identified and differentiated using mass spectrometry. Tautomers for a particular chemical of interest may have different RTs or may be predicted to have different RTs if their physicochemical properties differ sufficiently. RTs of five chemical compounds within the combined chemical set that could display tautomerization were observed further. Predicted RTs of tautomers generally varied by 3 min or less than the original, but predicted RTs of one pair of tautomers were substantially further apart as shown in Table 4.

Table 4.

Experimental and predicted RTs of two training set chemicals and their respective tautomeric forms. DTXSID is the unique chemical identifier of the DSSTox Database underlying the CompTox Chemistry Dashboard (https://comptox.epa.gov/dashboard/).

	Experimental RT	ACD/ChromGenius RT	OPERA-RT RT	EPISuite logP RT
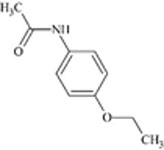	4.9	9.3	7.8	9.6
DTXSID1021116
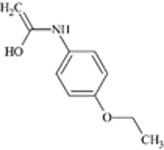		8.0	9.3	9.6
	7.5	5.5	9.7	14.9
DTXSID1020803
		12.9	6.6	11.9

For these two chemicals, the original structural representation included in the training set was predicted with greater accuracy by the ACD/ChromGenius model (Table 4, top structure in each section). However, RT predictions across tautomers showed substantial changes in RT. For a tautomer of the chemical meloxicam (DTXSID1020803, Table 4, bottom), the ACD/ChromGenius model predicted an RT ~7 min different than the original structure of meloxicam and OPERA-RT predicted an RT ~3 min different. This indicates the effect structural representation can have on RT predictions. In this instance, the OPERA-RT predicted RT of the meloxicam tautomer was closer to the experimental RT than the predicted RT of meloxicam. RT changes of this magnitude could negatively impact structure elucidation in NTA as well as model performance.

Charged species, specific classes of chemical compounds and method parameters, also may result in greater errors in RT prediction. For example, two of the five worst predictions of the OPERA-RT model were for parabens (heptylparaben and propylparaben). However, both the EPI Suite logP-based and ACD/ChromGenius models accurately predicted the RTs of these compounds. The ACD/ChromGenius model performed poorly on several late-eluting compounds (8:2/10:2 diPAP, 1-dodecanamine, etc.; experimental RT exceeding 23 min), whereas the OPERA-RT model performed well on these compounds (absolute RT errors of less than 3.5 min). Three of the worst predictions made by the logP-based model were for chemical compounds whose logP values ranged from approximately 4 to 7, indicating that overestimation is likely as logP values increase. Further deviations occur where errors to repeating structural units are present, such as increasing chain length perfluorinated substances. Charged species and ionizable chemicals can present problems when performing HPLC due to interactions with both the stationary and mobile phases, especially as pH changes within the mobile phase. All charged species within the combined training and test sets were observed for differences in RTs based on neutralization, if possible. The neutralized structures differed in predicted RT by less than 0.75 min from the original, charged structure, indicating that charge had little effect on RT prediction for the tested sets and models. Finally, expanding the chemical set used in this research could increase the chemical space, reduce RT error, and increase applicability.

Future Work

The U.S. EPA and many others are conducting collaborative work to address challenges in NTA, develop open workflows, and provide open data for the analytical chemistry community. Open tools that offer performance comparable to commercial tools would greatly benefit the analytical chemistry community as open tools are free, easily accessible, shareable, and customizable. The descriptors used to generate the OPERA-RT model are available for public use through the OPERA standalone app (https://github.com/kmansouri/OPERA.git), and RT data is available from the National Center for Computational Toxicology (NCCT) Figshare account (https://figshare.com/projects/NCCT_Presentations/22852). We note that the OPERA-RT algorithm in its present application is very constrained (with one chromatographic method and a constrained dataset of only 97 chemicals). OPERA-RT does not offer some of the benefits of the commercial tool ACD/ChromGenius, which has an intuitive user interface, an underpinning of multiple physicochemical prediction algorithms, and a knowledgebase containing training sets aggregated across multiple methods. However, OPERA-RT is easily accessible, free, and customizable and additional resources will improve the OPERA-RT model through the inclusion of more experimental data across different chromatographic methods to improve the model’s predictivity and widen the applicability domain for subsequent applications on large sets of heterogeneous chemicals.

Additional work will further incorporate data from a collaborative NTA trial to work towards a global RT prediction system [53]. Future implementation of the OPERA-RT model [54] and associated data through the U.S. EPA’s CompTox Chemistry Dashboard [15] will allow analysts to incorporate the OPERA-RT model in chemical identification workflows in NTA.

CONCLUSIONS

Incorporating RT prediction into NTA and SSA workflows has been shown to improve the identification of unknowns for environmental and exposure analysis [4,5,15,18,22]. This paper compared three RT prediction models on the same set of 97 chemicals to assess the viability of a new, in-house QSRR-based RT prediction model (OPERA-RT) relative to a well-documented logP-based model and the ACD/ChromGenius model. For all statistics reported in this research, both the ACD/ChromGenius and OPERA-RT models outperformed the simple EPI Suite logP-RT prediction model. The ACD/ChromGenius and OPERA-RT models performed similarly, and depending on the metric of interest, one model may perform better than the other. However, the OPERA-RT has benefits that the ACD/ChromGenius model cannot provide (such as open access and availability), while the latter may be more accessible to users with commercial or vendor solutions.

All the models described in this paper were developed based on a small dataset and can only be expected to cover a narrow applicability domain. Greater coverage of RT data and the chemical space may increase predictive ability and widen the applicability domain. The OPERA-RT model still is in development and was created here as a proof-of-concept, with goals to expand and improve it. Based on its performance relative to a commercial software solution and its open accessibility, the OPERA-RT model is worth improving and exploring for future applications.