Biophysics of membrane curvature remodeling at molecular and mesoscopic lengthscales

Abstract

At the micron scale, where cell organelles display an amazing complexity in their shape and organization, the physical properties of a biological membrane can be better-understood using continuum models subject to thermal (stochastic) undulations. Yet, the chief orchestrators of these complex and intriguing shapes are a specialized class of membrane associating often peripheral proteins called curvature remodeling proteins (CRPs) that operate at the molecular level through specific protein-lipid interactions. We review multiscale methodologies to model these systems at the molecular as well as at the mesoscopic and cellular scales, and also present a free energy perspective of membrane remodeling through the organization and assembly of CRPs. We discuss the morphological space of nearly planar to highly curved membranes, methods to include thermal fluctuations, and review studies that model such proteins as curvature fields to describe the emergent curved morphologies. We also discuss several mesoscale models applied to a variety of cellular processes, where the phenomenological parameters (such as curvature field strength) are often mapped to models of real systems based on molecular simulations. Much insight can be gained from the calculation of free energies of membranes states with protein fields, which enable accurate mapping of the state and parameter values at which the membrane undergoes morphological transformations such as vesiculation or tubulation. By tuning the strength, anisotropy, and spatial organization of the curvature-field, one can generate a rich array of membrane morphologies that are highly relevant to shapes of several cellular organelles. We review applications of these models to budding of vesicles commonly seen in cellular signaling and trafficking processes such as clathrin mediated endocytosis, sorting by the ESCRT protein complexes, and cellular exocytosis regulated by the exocyst complex. We discuss future prospects where such models can be combined with other models for cytoskeletal assembly, and discuss their role in understanding the effects of cell membrane tension and the mechanics of the extracellular microenvironment on cellular processes.

1. Introduction

For over a century, researchers both in the physical and biological sciences have pondered over the question of ‘how a cell gets its shape?’ The initial interests in cell shapes were mainly due to its use as a taxonomical classifier. However, research over the past decades have uncovered a deeper tie between cell shape and function which makes the question highly relevant to our quest to engineer cells [1, 2]. The shape of a cell and its organelles is primarily determined by the morphology of the cell membrane, which is constituted of lipids, proteins and sugars that are organized as a bilayer [3]. The composition of these individual components varies across cells and cell-organelles and has a direct correlation with their structure and function.

The shape of a cell membrane is modulated either by changes in its environmental variables, such as pressure and temperature, or due to its interactions with other cellular components such as individual proteins, the cytoskeleton, extracellular matrix, other cells in the tissue, and also due to its interaction with foreign particles such as a virus. The assembly, organization and shapes of fluid membranes have been reported in the literature using both theoretical [4–13] and computational methods [14–24] and a number of excellent reviews [25–35] have been written on this topic. The interactions of vesicular membranes with external components such as polymers and nano-sized particles and the resulting changes in membrane morphologies have also been reported [36–44].

In the past decade and a half, there has been a significant focus on membrane associated proteins and their role in reshaping cell membranes [45–50]. A special class of membrane associated proteins that spontaneously deform cell membranes are of importance in a number of cellular processes and these proteins are generally called curvature remodeling proteins (CRPs). Notable examples of CRPs include dynamin [51–55], cavaeolin [56], clathrin [57], reticulon [58], synuclein [59], apolipoprotein [59], endosomal sorting complexes required for transport (ESCRT) [60–62], and proteins whose membrane facing region is constituted of either a Bin/amphiphysin/Rvs (BAR) domain [63–69], an epsin N-terminal homology (ENTH) domain [70–72], or an Exo70 domain [73]. Each of these proteins associate differently with lipid membranes and induce curvatures of varying degrees and directions. Despite these differences in the underlying chemistry, do the curvature induction by CRPs follow a minimal set of physical principles? This question will be the focus of this review. We will focus on the thermodynamics of membrane deformation induced by the organization and assembly of CRPs at the molecular (<100 nm), mesoscopic (100 nm–1 μm) and cellular length-scales (>1 μm).

2. Membrane remodeling at the molecular scale

Treating protein-induced morphological changes in cell membranes in complete detail requires both a nanoscale description of a heterogeneous material—the protein interacting with individual lipids—as well as a continuum description of membrane shape and fluctuations at the mesoscale. Since the problem is inherently a multi-scale one, even the simplest mesoscale model for protein-mediated membrane shapes requires an approximation of all of the chemical interactions at the protein-membrane interface. Contemporary molecular investigations of this interface yield a wide variety of structural and energetic information about specific membrane-protein interactions, while a survey of the literature suggests several common features of this interface which must be captured in the corresponding continuum models so that they remain faithful to the underlying physics and chemistry.

Specific CRPs have been identified as early as the 1990s in microscopy images of dynamin and ENTH domain, both of which are known to stabilize elongated tubular structures in lipid membranes [70, 78]. To set the nomenclature, let us consider a CRP (or a cluster of CRPs) attached to the intracellular (i.e. the cytoplasmic) side of a cell membrane. We denote the CRP to induce a positive curvature when the induced membrane deformations grow into the intracellular side, and induce a negative curvature when the deformations grow into the extracellular side. The direction of the induced curvature depends on a number of factors including the intrinsic curvature of the CRP, the location of its lipid binding motifs, the distribution of lipids in the cell membrane, and the lateral interactions between CRPs.

Molecular models to explicitly study the protein-lipid interactions at lengthscales large enough to detect morphological changes have only become tractable in the last decade and figure 1 shows representative snapshots from various works, along these lines, published in the literature. The first explicit molecular models of CRPs began with the investigation of the BAR domain, which is known to facilitate vesicle budding and stabilization of the vesicle neck. The first study of this domain to use molecular dynamics (MD) found that membrane complied with the banana-shaped surface of the protein to generate curvature [75] in agreement with the crystal structure and liposome binding assays [63]. The resulting molecular view of this interaction suggested that a BAR domain can induce or comply to a range of curvatures depending on its orientation, and that particular positively-charged residues in the membrane facing domain were necessary to bend the bilayer. A follow-up study tested the influence of the amphipathic helices found in the protein N-BAR, a BAR domain containing an N-terminal amphipathic helix [79]. Larger-scale simulations of N-BAR bolstered the support for the view that the orientation of the N-BAR domain could change with curvature, finding that the N-BAR domains achieved a specific twist when binding to tubule-like structures [80]. An MD study of another BAR domain member (F-BAR) identified a similar ‘induced fit’ between the protein and bilayer, noting that the flexural rigidity of the protein must oppose the bending rigidity of the membrane, and that the balance of these forces is necessary to explain the protein-decorated tubules observed via electron microscopy (EM) [81]. MD simulations of I-BAR, whose curvature directionality is opposite to that of the N-/F-BAR domains, show that it induces and stabilizes membrane curvature through the formation of salt bridges with the lipids [82]. These studies highlight the four properties that bear most heavily on the resulting protein-decorated structures: (1) the protein-bilayer interface, (2) the organization of the protein-protein lattice, (3) the conformational changes within the protein, and (4) the bending modulus of the bilayer. Each of these questions can be addressed by specific molecular models, however no single model can reveal the general features of CRPs since they must necessarily choose specific proteins to study, at a specific concentration, on a particular membrane structure. In that sense, many of these studies contribute a single point on a metaphorphical phase diagram of membrane morphologies. Since the measurement of a single value for (mean) curvature often serves as a taxonomic classifier for many features, it is useful to review the many ways in which these models measure curvature.

Figure 1.

Molecular models to study and quantify protein-induced curvature in lipid membranes. (A) Molecular dynamics flexible fitting simulation of a light harvesting protein. Reprinted from [74], Copyright 2009, with permission from Biophysical Society. (B) Atomistic simulation of an N-BAR dimer. Reproduced with permission from [75]. (C) Profile view of the protein α-synuclein attached to a bilayer. Reprinted from [76], Copyright 2016, with permission from Elsevier. (D) Coarse-grained molecular dynamics simulation of 48 α-synuclein molecules forming a tubule on a bilayer containing 85 000 lipids. Reprinted from [76], Copyright 2016, with permission from Elsevier. (E) A coarse-grained molecular dynamics simulation of 8 ENTH domains anchored to a lipid bilayer. Reproduced with permission from [77]. (F) A coarse-grained molecular dynamics simulation of the Exo70 dimer generating negative curvature in the lipid membrane. Reprinted from [73], Copyright 2013, with permission from Elsevier.

There are two general methods for measuring membrane curvature from a molecular simulation: either via geometry, by measuring the structure of the bilayer surface, or via mechanics, by measuring the forces across it. Curvature typically refers to the mean curvature, which is a strictly geometric quantity which can only be defined on a twice-differentiable surface. Since the bilayer is a rugged object, especially at the scale of individual lipids, the choice of this surface requires an abstract representation of the coordinates observed in a molecular simulation.

The simplest way to infer curvature is to measure the deflection of a tensionless, planar bilayer in the normal direction since the peaks and valleys of a curved bilayer create local extrema in curvature as well. Several studies have used this method to qualitatively describe how bound proteins alter the average height/deflection of a free bilayer [76, 77, 83–85]. Using bilayer deflection as a proxy for curvature introduces the first of several challenges for understanding protein-mediated membrane sculpting: are proteins sensing or creating curvature? That is, proteins which lack the capacity to bend the bilayer may simply prefer particular curvature developed by undulations in a naturally fluctuating membrane bilayer. The studies which use deflection as a proxy for curvature typically address this question by comparing the protein-influenced membrane shapes to the equilibrium structures of a free bilayer (i.e. a flat surface in a planar simulation), or by comparing their simulations to experiments which provide a negative control or comparison to a membrane which has not been remodeled.

It is possible to measure curvature with more precision by approximating the bilayer midplane and then computing the curvature of the resulting surface. This can even be done in one dimension for proteins which induce anisotropic curvature by simply fitting the bilayer shape to a cylinder in one direction and then computing its radius. For instance, the intrinsic curvature of light harvesting proteins has been computed by measuring protein tilt and spacing angles [86] or by fitting a smooth surface with uniform principal radii of curvature [74]. The first solved BAR domain structure led many researchers to intuit the preferred curvature from its most likely membrane-contacting face, with some researchers even performing docking to a vesicle to demonstrate this feature [87]. Other models of BAR domains, ENTH domains, α-synuclein, and Exo70 have led to measurements of the mean curvature induced by a protein by fitting bilayer structures to higher resolution surfaces, with locally varying radii of curvature, yielding curvature estimates in the range of 0.006–0.074 nm⁻¹ [73, 74, 75, 79–81, 84, 86, 88]. These studies implicitly smooth the nanoscale ruggedness of the bilayer when fitting their structures, however it is also posssible to use spectral filters to accomplish this [89, 90].

The ambiguity in representing a bilayer as a 2D surface raises the second major challenge to quantifying protein-induced membrane curvature: we expect the deformations induced by proteins and other inclusions to be heterogeneous. Treating the curvature with the typical ‘dimple shape’ — that is, a maximum curvature induced near the protein which decays away from it—is a necessary consequence of measuring curvature on a small planar bilayer which satisfies periodic boundary conditions and hence forbids a non-uniform curvature unless it is identically zero. The planar topology of the simulation may constrain the observable deformations, but the protein may also induce a heterogeneous deformation. It is likely that CRPs with various remodeling capacities can create a heterogeneous field on highly curved surfaces as well, particularly since these proteins have structures that suggest that particular residues account for disproportionate amounts of the protein adhesion energy, and that multiple mechanisms, including electrostatics and amphipathic wedging, may contribute to the binding.

The third challenge concerns the question of dynamics. The geometric methods for measuring curvature described above sometimes rely on an average ‘snapshot’ of the bilayer structure to compute curvature. Even those that characterize the instantaneous bilayer shapes do not usually formally account for the variation in bilayer shapes. Some studies which use the deflection measurement [85] or geometry method [79] compare their observed geometries to that of a protein-free bilayer in order to attribute an enhanced structure to the membrane-protein complex. However comparatively few studies directly study the undulations as such. Simulations of the protein α-synuclein show qualitatively that bilayer fluctuations are enhanced in the presence of the protein [91]. Mesoscale models described in the following section 3, including work by Tourdot et al [92], propose a method for measuring the degree to which curvature couples to the underlying thermal undulations. This theory has been recently applied to simulations of ENTH domain to identify a cooperative curvature-undulation coupling effect whereby increased surface coverage of the protein leads to stronger curvatures [77]. Nevertheless, explicit connections between dynamic membrane remodeling typically study the rearrangement of proteins on curved surfaces without explicitly accounting for their membrane remodeling propensities.

Finite-size effects pose the fourth challenge for using computer simulations to measure CRP-induced membrane curvature; these effects are important even if we study CRPs whose interactions are strong enough to significantly reshape the bilayer surface. It should be noted that the curvature measured from simulations of small 20–50 nm bilayers has a slightly different meaning compared to that measured from membrane structures viewed in microscopy images, notwithstanding the accuracy of the underlying model. The enforced periodicity or the so-called the finite-size effect of the simulation can influence the measured curvature in three distinct ways:

1. Finite-sized membranes do not support long-wavelength undulations: It is well-known that enforcing periodic boundary conditions only allows for membrane undulations that can ‘fit’ inside the box while those that are larger than the box size are ignored [93]. Therefore, any curvature contribution from these longer modes are effectively suppressed. The omission of long modes is not unique to molecular simulations, since continuum models also lack undulations beyond the size of their simulation box or frame.

2. Finite-size effect alters diffusion: The boundary conditions applied to a simulation box can influence density fluctuations in the fluid, leading to altered diffusion of the fluid implicitly confined between periodic images of the bilayer [94]. The altered hydrodynamics of the fluid also affects diffusion of objects embedded within the bilayer, resulting in either an under- or over-estimation of the lateral diffusion rate, depending on the amount of fluid between the bilayer images [95, 96].

3. Finite-size influences lateral organization of CRPs: Simulations with small membrane dimensions may prevent the self-association of many proteins into enriched or depleted domains. Insofar as a large bilayer offers opportunities for more large-scale rearrangements and morphology changes, then smaller simulations may provide conflicting results. For example, the curvature of BAR domains on large but broken tubule shapes is smaller (30 nm radius) [80, 87] than an earlier estimate of curvature on a small, planar bilayer (6.7 nm radius) [75]. The broken tubule has the benefit of size and high density but lacks tension in the direction along which it is broken. Simulations of CRPs have likewise observed that membrane undulations can mediate long-ranged interactions between proteins [77].

The most obvious way to overcome the finite size problem is to make bigger simulations which nevertheless contain the relevant physics. Larger, typically coarse-grained investigations of proteins generate the obvious problem of controlling membrane shape, since these proteins either sense or generate their own curvature. As a result, larger models, many of which reach the mesoscale, include complex topologies including buds, vesicles, and tubules. We should note that there are opportunities for pursuing finite-size scaling theories to describe the asymptotic behavior of finite-size effects versus system size.

The fifth challenge as in any molecular dynamics simulation is that the results of a MD calculation strongly depend on the force-field used to parameterize the interactions between the various molecular entities. For example, electrostatic interactions have been shown to play a major role in governing the dynamics and organization at the bilayer-protein-solvent interface. It was recently shown that the coarse-grained dielectric constant used in early investigations of BAR domains (e.g. [80, 113]) may overestimate the electrostatic interactions between the protein and the lipids, and that these interactions may be more effectively screened by water molecules at the interface [114]. Parameterizing electrostatic interactions is particularly difficult in coarse-grained models which necessarily reduce the interaction strengths between coarser particles and cannot model the effects of a single water molecule. The challenge in generating accurate atomistic and coarse-grained force fields is common to all molecular simulations, however the question of accurately recapitulating the electrostatic environment and the hydrophobic interactions between the proteins and lipids is particularly important to predicting curvature.

The largest simulations of membrane-protein systems either target a particular CRP or attempt to include generic features of all CRPs. Simulations of large tubules and vesicles show that ENTH domains are more disordered on spherical structures and suggest that the formation of tubules in vitro depend on reaching a sufficient concentration of locally-ordered domains [97]. Large simulations of α-synuclein have generated budding tubules in massive coarse-grained simulations [90]. Large simulations of vesicles coated with N-BAR domains have been compared to atomic force microscopy images of these proteins on supported lipid membranes [98]. These examples are constructed to directly match simulations with microscopy experiments. However, more general models of curved caps and capsids have yielded models of vesicle budding which show that curvature-mediated protein attractions can be driven by non-specific actions [39] and that general features of transmembrane proteins, particularly the shape and hydrophobic mismatch of the inserted domains, may determine the nature of protein association in simulations of vesicles [99]. Both general and specific models of such large, protein-mediated structures have the benefit of validating molecular models with microscopy images, however these models are typically used to reveal the mechanism of protein organization on a highly curved surface, not necessarily to measure the degree to which these proteins actively sculpt the bilayer.

The construction of larger simulations with alternate topologies is born of the necessity to more accurately scale the protein-membrane interaction to larger systems with biologically relevant topologies, however they have added benefit of demonstrating curvature sensing in silico. Several CRPs including BAR and ENTH domains are sensitive to the curvature of membranes adhered to wavy substrates [100]. The large-scale ENTH domain simulations show that they adjust their local order to match the anisotropy of their substrates [97] while simulations performed on buckled bilayers demonstrate that amphipathic helices can sense curvature and lipid packing defects [101, 102].

Rather than measuring the shape of the bilayer, it is also possible to measure local, 3D stresses from a molecular simulation in order to measure the spontaneous curvature induced by the action of CRPs. The local pressure tensor P(r) can be used to compute the lateral pressure profile as $\mathrm{\sum }(z)=\frac{1}{2}({\mathbf{P}}_{xx}+{\mathbf{P}}_{yy})-{\mathbf{P}}_{zz}$ and the integral of its first moment along the bilayer normal z between z₁ and z₂, relative to the bilayer midplane z₀, gives the intrinsic or spontaneous curvature $C_0\text{via}\kappa C_0={\int }_{z_1}^{z_2}(z-z_0)\mathrm{\sum }(z)\mathrm{d}z$ [103]. This method has been used to study voltage-gated channels in molecular dynamics simulations [104] but is equally relevant to CRPs and the question of bilayer curvature in general. However, calculations of pressure tensors in a MD or CGMD simulation remains a challenge due to the large fluctuations in its components over the course of a 100 ns run [88]. To minimize noise and increase signal, this method is most effective when measuring the curvature of lipids or any uniformly-distributed species which modulates curvature. Calculation of the stress profile from atomistic simulations yields a spontaneous curvature which is in good agreement with experiments that measure the intrinsic curvature lipids from the geometry of inverted lipid tubules in the inverse hexagonal phase [105]. Differences in lipid density across monolayers and the addition of adsorbing particles also induce curvature in a uniform way and hence produce measurable changes in the spontaneous curvature according to the lateral pressure profile measured from dissipative particle dynamics (DPD) simulations [106]. Simulations of α-synuclein on vesicles show that it qualitatively alters the lateral pressure profile compared to a free vesicle [91].

The hypothesis that some proteins sense lipid packing defects and consequently the intrinsic curvature of a buckled bilayer point towards the importance of understanding the precise boundary conditions imposed by a protein on the surrounding lipids. Features of this boundary have been addressed in both theory [107, 108] and tentatively in some MD simulations [99]. Model membranes with rich, asymmetric compositions suggest that curvature correlates with the clustering of particular lipids [109]. This effect highlights the possible feedback between curvature-sensitive proteins and lipids, in which altered distributions of either can stabilize and enhance stronger folds in the membrane.

The uniform curvature fields which can be resolved from the lateral pressure profile are unlikely to be biologically representative given the fairly uneven binding energy imparted by the rugged face of membrane-bound proteins and plaques. Their specific chemical moieties may help to create the rich set of protein-membrane binding strengths in biological context, but pose a problem for quantifying the protein-induced deformation field, because they ensure that this field is highly heterogeneous. Even if it were not heterogeneous, the induced deformation field is nevertheless likely to be concentration-and composition-dependent. Preliminary evidence suggests that even a single protein domain can induce curvature cooperatively [77], while most of the molecular studies cited above provide evidence that both specific and non-specific protein-protein interactions are relevant to the mechanisms of curvature sensing. Therefore, molecular crowding may affect the function of CRPs. Recent experiments have shown that green fluorescent protein (GFP), which has no role in membrane sculpting processes, can bend the bilayer at sufficiently large surface coverage [110]. This has bolstered support for the hypothesis that so-called ‘protein crowding’ can induce shape change. Recent methods for measuring curvature via GUV shape stability show that CRPs such as the endophilin BAR domain generate curvature at lower densities than GFP [111], confirming that not all proteins are equally capable of remodeling the bilayer. Nevertheless, crowding between CRPs and many other proteins in vivo is a necessary feature of any model for protein-mediated shape changes.

Even though it is difficult to directly estimate the curvature field strength of a CRP experimentally, in some cases, one can impose some bounds on the values. If we assume that the curvature induced in the membrane is fully derived by CRP interaction with the membrane, the enthalpy of binding of the protein with the membrane can be the upper-bound for the curvature energy. The latter can be measured using isothermal titration calorimetry or similar methods. Alternatively, experimental estimates of off-rates of CRPs from single molecule experimental measurements can be used to derive a free energy of binding by assuming that the on-rate is diffusion limited, and a procedure similar to above can be used to constrain the curvature parameters. Also, the radius of curvature of the membrane under high concentration of the CRPs can be determined using electron microscopy and this measurement can also be used to constrain the curvature parameters. These approaches have been described in [88, 112].

3. Membrane remodeling at the mesoscale

In vitro experiments of protein-membrane systems along with crystallographic analysis of protein structures have clearly established that curvature inducing proteins preferentially localize to regions on the cell membrane that match their intrinsic (natural) curvatures. For instance, dynamin, BAR, N-BAR, and F-BAR domains whose membrane facing interfaces have a pronounced positive curvature, are preferentially recruited to tubular membranes, endocytic vesicles. Similarly, I-BAR (inverted-BAR) and Exo70 domains, whose membrane facing interfaces have a negative curvature, preferentially localize to caveolae pits and invaginations. A curvature remodeling protein is both a curvature inducer, in that it deforms the membrane in its vicinity, and a curvature sensor, in that it diffuses to a pre-deformed region on the membrane that matches its intrinsic curvature. As a result, the assembly of proteins on a membrane surface is driven jointly by both the curvature-inducing and curvature-sensing properties of the protein.

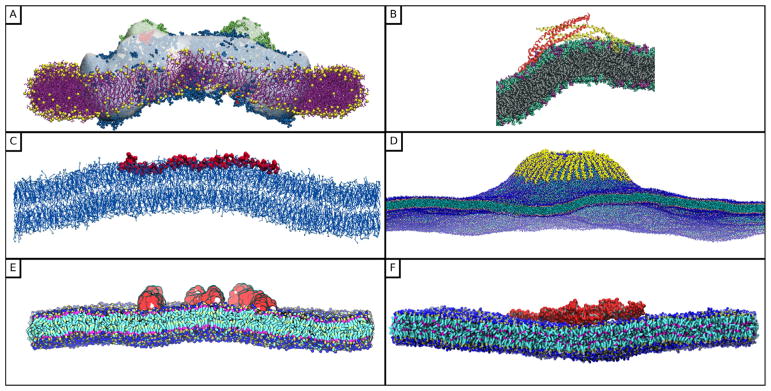
The assembly of CRPs at physiologically relevant concentrations and the resulting membrane morphologies at the length scale of cytoskeletal assembly (~50–500 nm) is extremely important for cell functions such as signaling and motility. This mesoscopic scale is not directly accessible to experiments and hence the sensitivity of indirect methods used to access this scale is low especially at low protein concentrations. However, mesoscopic protein-membrane systems are well suited for investigations through computer simulations which yield deeper insights into the function. As discussed in section 2, this approach has been previously used by a number of groups to understand the interplay between the lateral organization of proteins and the mesoscale morphologies of lipid bilayer membranes. Snapshots of protein-remodeled membrane structures from some of these works are displayed in figure 2. Methods based on all-atom (AA) and coarse grained (CG) molecular dynamics simulations explicitly account for the proteins and their interactions with the lipid membrane as is shown in panels (A)–(E) in figure 2. Here, it may be seen that a planar bilayer membrane spontaneously deforms to a curved morphology due to its interactions with CRPs, and here the average deformed shape of the membrane is shown as solid lines. A major requirement for generation of membrane curvature in the AA and CG models shown in panels (A), (B) and (D) in figure 2 is that the proteins were required to be arranged in an oriented configuration. In the ultra CG models shown in figures 2(C) and (E) the membrane-mediated interactions drive the proteins to aggregate into such oriented configurations and induce membrane curvature in a cooperative manner. Detailed reports on this topic may be found in [31, 68, 118–121], as well as the discussion in section 2. As noted earlier, membrane interactions with mesoscale objects can also induce spontaneous deformation which are important in a number of biophysical processes. For example, membrane curvature induced by viral capsid proteins and glycoproteins govern the assembly and budding of viruses [122–124], specific receptor-ligand interactions of functionalized particles determine binding avidity [125], and non-specific interaction of nanoparticles drive membrane tubulation [13, 40, 126].

Figure 2.

Equilibrium morphologies of a patch of a lipid bilayer due to the assembly of CRPs on bilayer patches with lengths between 50–500 nm. (A) all-atom (AA) and coarse-grained (CG) simulations of membrane remodeling by BAR domains by Arkhipov et al [113, 115] (reprinted from [113], Copyright 2008, with permission from Biophysical Society), (B) AA simulation of the assembly of N-BAR helix on lipid membranes by Blood et al [79] (reprinted from [79], Copyright 2008, with permission from Biophysical Society), (C) CG simulations of the effect of curvature remodeling capsids by Reynwar et al [39] (reprinted by permission from Macmillan Publishers Ltd: Nature [39], Copyright 2007), (D) CG simulation of tubule formation by BAR domains by Yin et al [80] (reprinted from [80], Copyright 2009, with permission from Elsevier), (E) ultra CG simulations of BAR domain assembly by Noguchi [116] (reproduced from [116], CC BY 4.0), and (F) field theoretic simulations of membrane tubulation by the action of protein curvature field by Tourdot et al [117] (reprinted figure with permission from [117], Copyright 2014 by the American Physical Society). The solid lines in panels (A) and (B) denote the average curvature of the deformed membrane bilayer, and AA and CG refer to all-atom and coarse-grained molecular dynamics, respectively.

In the following, we will therefore focus on a complementary strategy to study membrane-protein systems at larger length (and time) scales. The most popular and explored is an elasticity-based approach, in which the membrane is modeled as a thin elastic sheet of nearly constant area and its morphology is governed by the Canham–Helfrich energy functional for lipid membranes [127, 128]:

$${\mathcal{H}}_{\text{el}}=\frac{\kappa }{2}\int {(2H-H_0)}^2\mathrm{d}A+\sigma \int \mathrm{d}A.$$ (1)

κ and σ are the bending rigidity and surface tension of the bilayer membrane, H the mean curvature, and the integral is carried over the surface of the membrane. The effect of the curvature-inducing proteins is accounted for in the model through the spontaneous curvature field H₀, which stabilizes positive curvature in the membrane for H₀ > 0 and vice versa. Equation (1) can be studied analytically and numerically using a variety of techniques (see [33] for a review) including a popular method termed the Dynamically Triangulated Monte Carlo (DTMC) [5, 6, 129] technique which provides an excellent framework to simulate membranes in the presence of thermal fluctuations and fluidity. The simulations methods are described in [92, 117] in which the spontaneous curvature of the protein is represented as a Gaussian function. In this representation, the curvature induced at location x′ due to a protein at location x is given by H₀(x, x′) = C₀ exp(−|x − x′|²/(2ε²)). Here C₀ is the maximum curvature induced by the protein, whose measurement was the topic of our discussions in section 2, and ε is the root mean square distance over which the protein induces non-zero curvature in the cell membrane. A snapshot of the continuum membrane simulated using the DTMC technique is shown in figure 2(F); here the bright spots represent the protein-induced curvature field. It can also be seen from figure 2(F) that multiple curvature fields aggregate to generate a tubular protrusion in the cell membrane. The curvature field associated with a protein is parameterized either from experimental data [88] or through molecular simulations [77, 88], as described in section 2.

In figure 3(A) are depicted representative morphologies of a membrane patch for three different values of n_P (the number of protein curvature fields on the membrane surface) taken to be n_P = 4, 12 and 18; these configurations were obtained using the DTMC approach for a membrane with κ = 10 k_BT and σ = 0, and protein fields with $C_0=0.8a_0^{-1}$ and ${\epsilon }^2=2.3a_0^2$. Here a₀ ≈ 10 nm is a characteristic length scale that denotes the size of the mesh in the triangulated surface, for more details see [33]. The morphology of the membrane surface and the degree of curvature are determined collectively by n_P, C₀, κ, σ, and T. Specifically, with respect to the effect of n_P, at low values of n_P, the membrane remains nearly planar, while at higher values of n_P, the model supports tubulation.

Figure 3.

(A) Equilibrium configurations of a membrane patch, with κ = 10 k_BT, σ = 0, $C_0=0.8a_0^{-1},{\epsilon }^2=2.3a_0^2$, for number of protein fields n_P = 4, 12 and 18. Tubular protrusions are stabilized on the membrane surface for n_P ≥ 12. (B) P(H), the distribution of mean curvature H for the membrane surfaces displayed in panel (A).

P(H), the distribution of the membrane mean curvature H, shown in figure 3(B), can also be used to identify morphological transitions in membranes, such as the planar to tubular transition shown in panel (A). P(H) for n_P = 0, 4, 12, and 18 are shown in panel (B), in which the distribution for n_P = 0 follows a Boltzmann distribution P(H) ∝ exp(−βℋ_elas), as expected. As n_P increases the average distribution starts to deviate from that for n_P = 0 and the presence of tubular protrusions, due to curvature induction by the proteins, is marked by a pronounced peak at H ≈ C₀. This bimodal distribution indicative of a tubulation transition is readily seen in figure 3(B) for n_P = 12 and 18. The analysis of the membrane morphologies and the associated measures have clearly shown how proteins act in a cooperative fashion and drive local shape changes in cell membranes. As a result, we expect that a threshold density of proteins (or minimum n_P per unit membrane area) is required to elicit a tubulation transition.

The effect of protein density on membrane conformations was previously studied by Leibler [130] using a mean-field model for elastic energy of the membrane where the presence of the CRPs was included by introducing a density field ϕ. By including a coupling between the field ϕ and the curvature, the total free energy of the membrane in terms of the height fluctuation h(x, y), measured with respect to the x-y plane, was written as:

$${\mathcal{H}}_{h\varphi }=\frac{1}{2}\int \mathrm{d}x\mathrm{d}y\{\kappa [{({\nabla }^{2}h)}^2-C_0\varphi {\nabla }^{2}h]+\sigma {(\nabla h)}^2+a{\varphi }^2+b{(\nabla \varphi )}^2\}.$$ (2)

Here, a and b are constants controlling the density field fluctuations of the CRP and C₀ is its intrinsic curvature. By performing a linear stability analysis of the Hessian of ℋ_hϕ, the onset of instability in a sinusoidally modulated height fluctuation (i.e. a Fourier mode) relates the spontaneous curvature C₀ to κ and σ as: $\sqrt{a\kappa }+\sqrt{b\sigma }=\mid \kappa C_0\mid$. This theory is an instability theory rather than a thermodynamic one and also ignores the role of membrane thermal fluctuations, whose effects are quite significant. Only a free energy landscape can ascertain the precise thresholds and the nature of these morphological transitions, which we discuss next.

3.1. Methods to delineate thermodynamic free energy landscapes for protein-induced remodeling of membranes

The deformation energy landscape for protein induced remodeling of cell membranes can be computed using a variety of techniques such as Widom Insertion [131], Thermodynamic Integration [132] and Bennett acceptance ratio scheme [133], all of which yield similar results [117]. The statistical mechanics underlying these methods may be found in [132, 134]. Umbrella sampling combined with Weighted Histogram Analysis method [135] have also been used to study morphological transitions in cell membranes [136–138] using both MD and DTMC techniques.

It is instructive to summarize the Widom ghost particle insertion technique [131, 132] adapted for the insertion of curvature fields on a triangulated membrane to systematically compute the excess chemical potential as a function of n_P. As we discuss below, this exercise provides mechanistic insight linking the recruitment of CRPs to the state of the membrane, namely the tension it is under, or the amount of its excess area.

The total chemical potential μ is defined as the free energy cost to add the n_P + 1th protein onto a membrane surface containing n_P proteins. It is constituted of an ideal part μ^id(ρ), that only depends on the protein density ρ, and a configurational or excess part μ^ex, that only depends on the interactions, and in our case, those between the protein and the membrane. Thus, the total chemical potential is μ = μ^id + μ^ex. The configurational part of μ, also called the excess chemical potential, is an excellent thermodynamic measure to quantify the curvature contribution of CRPs to the free energy. μ^ex is calculated in the DTMC simulations using the standard procedures prescribed for molecular simulations [132]:

$${\mu }^{\text{ex}}(n_P)=-k_{\mathrm{B}}Tln\int {\langle exp(-\beta \mathrm{\Delta }{\mathcal{H}}_{\text{elas}})\rangle }_{n_P}{P}_{\text{uniform}}(x_{n_P+1})\mathrm{d}{x}_{n_P+1},$$ (3)

were Δℋ_elas = ℋ_elas(n_P + 1)−ℋ_elas(n_P) is the change in the elastic energy (equation (1)) upon addition of the ghost n_P + 1th curvature field onto a membrane surface containing n_P curvature fields. The average is computed by sampling the n_P + 1th field at position x_nP+1 over random configurations drawn from a uniform distribution on the membrane. The membrane itself is evolved through ℋ_elas(n_P); therefore, the 〈·〉_nP denotes an ensemble average defined with respect to the n_P fields. A similar approach can be used to compute the spatially inhomogeneous excess chemical potentials at defined regions on the cell membrane. For instance, one can compute the excess chemical potential ${\mu }_{\mathrm{P}}^{\text{ex}}(n_P)$ and ${\mu }_{\mathrm{T}}^{\text{ex}}(n_P)$ to distinguish the affinity of the protein field for planar regions P on the membrane, where H < H^*, compared to that for tubular protrusions T, where H ≥ H^*. The value of H^* can be defined based on the P(H) distribution in figure 3; for example H^* = 0.5 separates unimodal distributions for n_P < 12 from bimodal distributions (showing protrusions) for n_P > 12. Excess chemical potentials computed by choosing the location of insertion x_nP+1 in regions where H < H^* yields ${\mu }_{\mathrm{P}}^{\text{ex}}(n_P)$ and x_nP+1 in regions where H > H^* yields ${\mu }_{\mathrm{T}}^{\text{ex}}(n_P)$.

3.2. Membrane tubulation is marked by a sharp transition in the chemical potential

Tubular protrusions start to spontaneously emerge from the planar membrane surface when n_P is greater than a critical value, and a representative configuration of a fully grown tubular protrusion is shown in the top panel of figure 4(A) for a membrane with κ = 20 k_BT, σ = 0, $C_0=0.8a_0^{-1}$ and ${\epsilon }^2=2.3a_0^2$. Such tubular transitions have previously been reported in experiments of model membrane systems interacting with CRPs. In the lower panel of figure 4(A) we display a micrograph from the work of Shi and Baumgart [139], where the circular region denotes a giant unilamellar vesicle (GUV) laden with proteins and the arrow denotes a tubular protrusion, similar to that seen in our model. The corresponding values of the the bulk chemical potential μ^ex as a function of the protein number n_P is shown in figure 4(B).

Figure 4.

(A) Membrane tubes seen in the DTMC simulations and in experiments by Shi and Baumgart [139]. (B) The bulk excess chemical potential μ^ex, excess chemical potentials in the planar and tubular regions ${\mu }_{\mathrm{P}}^{\text{ex}}$ and ${\mu }_{\mathrm{T}}^{\text{ex}}$, respectively, are shown as a function of the protein number n_P. The protein field exhibits curvature sensing behavior for n_P < 9, beyond which it exhibits curvature inducing behavior. Data shown for a membrane with κ = 20 k_BT, σ = 0, $C_0=0.8a_0^{-1}$ and ${\epsilon }^2=2.3a_0^2$ . (C) Comparison of bulk chemical potential μ^ex for a membrane with increasing membrane tension; the horizontal arrows denote the point of planar to tubular transition for each system.

At small values of n_P, μ^ex increases linearly with increasing n_P. This regime can be rationalized by noting that each added n_P + 1th curvature field experiences a membrane environment under the average influence of the previous n_P fields. Following Tourdot [117], we can write in the meanfield limit the chemical potential when n_P proteins are on the membrane as:

$${\mu }_P^{\text{ex}}(n_P)=-k_{\mathrm{B}}Tln\langle exp\left(-\frac{\kappa }{2k_{\mathrm{B}}T}\int \mathrm{d}A[-4\overline{H}{H}_0+H_0^2]\right)\rangle .$$ (4)

Here, H₀ is the spontaneous curvature of one (i.e. the n_P + 1th) CRP field and $2\overline{H}=2H-\langle {\mathrm{\sum }}_{i=1}^{n_P}{H}_0(i)\rangle$ is the difference between mean curvature and average spontaneous curvature due to n_P CRP fields. Using the cumulant expansion [117], the above expression can be expressed as:

$$exp\left(\frac{{\mu }_P^{\text{ex}}(N)}{k_{\mathrm{B}}T}\right)=exp\left(\frac{\kappa }{2k_{\mathrm{B}}T}\int H_0^2\mathrm{d}A\right)\times {\left[1+\left(\frac{2\kappa }{k_{\mathrm{B}}T}\right)\langle \int \overline{H}{H}_0\mathrm{d}A\rangle +\frac{1}{2!}{\left(\frac{2\kappa }{k_{\mathrm{B}}T}\right)}^2\langle {\left(\int \overline{H}{H}_0\mathrm{d}A\right)}^2\rangle +\cdots \right]}^{-1}.$$ (5)

The increase in chemical potential with increasing n_P in figure 4 indicates that the finite temperature corrections due to the thermal undulations of the membrane has a significant contribution. In the mean-field approximation, the increase in n_P has an effect of increasing 〈H〉, as evident from the P(H) distributions in figure 3; consequently this results in a decrease in 〈H̄〉. Hence, the increase in μ^ex with increasing n_P is a reflection the second term of the cumulant expansion, which actually decreases with increasing 〈H̄〉; however, it should be noted that the cumulant expansion is a slowly converging series, wherein up to 15 terms need to be considered [117]. We note that while equation (5) describes a mean-field treatment, figure 4 does not invoke the mean-field approximation and in that sense is an exact (albeit numerically evaluated) result for μ^ex(n_P). Still, the mean-field picture of the membrane protein interactions described above is a good description of the curvature sensing behavior of the CRP, which is demonstrated experimentally by measuring protein localization to predeformed regions on the cell membrane [69, 102, 140–144].

We note that both the mean-field theory and the exact calculations highlight the importance of thermal fluctuations in defining the chemical potentials of CRPs. In this curvature-sensing regime, one can describe the coupling between induced curvature and undulations which also depends on the state of the membrane. Rewriting equation (1) for a planar membrane (i.e. when H₀ = 0, and assuming small slopes in height deflections, h(x, y), where the height of the midplane of the membrane is represented as a function on the reference x-y plane), it is straightforward to show that the magnitude of an undulation mode with wavenumber q is |h_q|² = k_BT [A_p(κq⁴ + σq²)]⁻¹ [25]. Here, h_q is the 2D Fourier transform of h(x, y) and A_p is the projected area that represents the area of the reference plane. Similarly, for non-zero H₀, we can write [117],

$$\langle {\mathcal{H}}_{\text{el}}\rangle =k_{\mathrm{B}}T=A_p\{\kappa [q^4\langle h_q^2\rangle +q^2\langle h_q{h}_{0,q}\rangle +q^2\langle h_{0,q}{h}_q\rangle +\langle h_{0,q}^2\rangle ]+\sigma q^2\langle h_q^2\rangle \},$$ (6)

where h_0,q is the Fourier transform of the protein curvature field H₀. The curvature-undulation coupling represented by equation (6) formally describes how the curvature field influences the undulation spectrum, and also establishes an entropic coupling between curvature and tension that is long ranged, i.e. in the range of the undulation wave-length, in contrast to that of the curvature field itself, which may be short-ranged. In fact, as discussed in section 2, this relationship was utilized by Bradley and Radhakrishnan [77] to infer a curvature-field from the undulation spectra of the CGMD simulation data. Together, the discussion above provides a comprehensive picture of how the recruitment of CRPs can be influenced by thermal undulations, membrane excess area, and membrane tension.

For $n_P>n_P^{\ast }$, μ^ex deviates from the linear scaling regime and shows a sharp transition to a negative value, as is displayed in figure 4(B). Membrane configurations in this regime show pronounced tubular protrusions, with a large number of protein curvature fields localized to these highly curved regions, as is seen in figure 4(A). This is indicative of the cooperative and curvature inducing behavior of the protein curvature field. In figure 4(B), we have also shown ${\mu }_P^{\text{ex}}$ and ${\mu }_T^{\text{ex}}$, the excess chemical potentials for a protein curvature field to migrate to planar and tubular regions on the membrane, respectively. It may be seen that in the absence of any morphological transitions (i.e. for $n_P<n_P^{\ast }$) the bulk chemical potential closely follows that for the planar region ( ${\mu }^{\text{ex}}~{\mu }_P^{\text{ex}}$) while for $n_P>n_P^{\ast }$ it is slaved to that for the tubular region ( ${\mu }^{\text{ex}}~{\mu }_T^{\text{ex}}$). The fact that μ^ex < 0 for $n_P>n_P^{\ast }$ implies that a protein in the bulk solution would preferentially migrate to regions on the membrane surface that already contain an assembly of proteins with $n_P>n_P^{\ast }$. The nature of the transition from planar to tubular states is akin to a micellar transition as described in detail by Tourdot et al [117]. In this regard, $n_P^{\ast }$ can be considered analogous to a critical micelle concentration, which in general is a function of the state of the membrane, namely its value of σ and A^ex. This trend is illustrated in figure 4.

3.3. Critical tension at tubulation and comparison to experiments

The importance of membrane tension on the tubulation transition in membranes has been demonstrated in a number of experiments [139, 145, 146]. The thermodynamic free energy landscape for protein remodeling have direct correlation with such experiments. In the micrograph shown in figure 4(A) σ, the surface tension of the membrane, is controlled by applying a suction pressure using a micropipette, which is shown as a cylinder on the top right. Shi and Baumgart have recently reported a phase diagram for membrane tubulation by N-BAR domain and have shown its dependence on the surface tension and surface concentration of the N-BAR domains [139]. A computational analogue of this experiment is shown in figure 4(C) where we display the bulk excess chemical potential μ^ex as a function of n_P for membranes with five different surface tensions; the model explores varying surface tension σ by controlling the excess area in the membrane as described in [117]. The value of $n_P^{\ast }$ (the critical number for tubulation) increases with increasing surface tension as is shown by the positions of the vertical arrows in figure 4(C). A comparison of the experimentally measured values of σ^* [139] to that estimated using the model is shown in figure 5 and found to be in excellent agreement.

Figure 5.

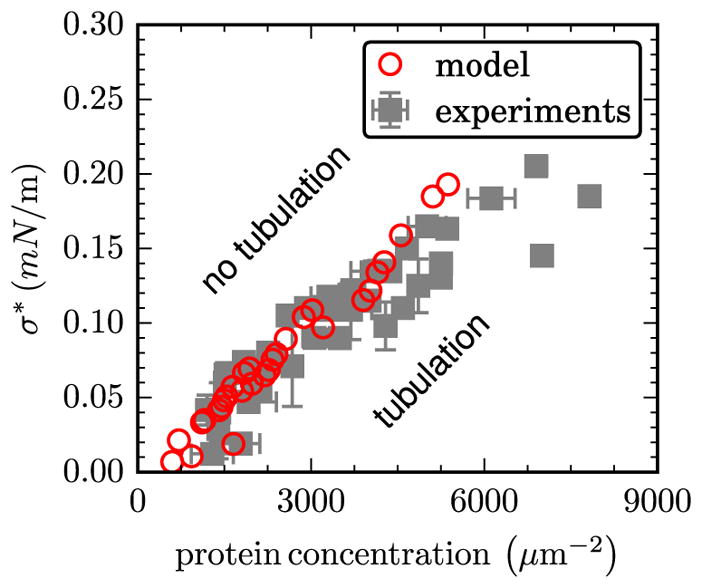
A comparison of the experimentally measured critical tension at tubulation σ^* to that predicted computationally. Data shown as a function of the surface concentration of N-BAR domains.

4. Membrane remodeling at the cellular scale

Protein-induced curvature remodeling of whole vesicles have been investigated by a number of groups. Interactions between curvature inducing domains⁴ on a whole-cell membrane has been extensively studied using mesoscopic particle methods such as the EM [15–17], EM2 [68, 147–151] and the MesM-P model [152] of Voth et al, DPD models of Laradji et al [14, 153, 154] the meshless membrane model of Noguchi [116, 155], and the two-component CGMD model of Lykotrafitis et al [156–158]. Alternatively, continuum isotropic elasticity models have also been used to computationally examine the interactions between curvature inducing domains on cell membranes [159–163]. These studies cover a large number of protein domains that include the BAR family, ENTH, and Shiga toxins. Ramakrishnan et al [164–168] have explored the anisotropic elasticity based nematic membrane model to study protein-induced shape changes in vesicular membranes. In the anisotropic elasticity model, the protein is represented as an in-plane nematic field whose local orientation is denoted n̂. The presence of such in-plane fields have been previously considered in the study of orientational order in lipid membranes that arise due to the presence of anisotropic phospholipids [169–171], and lipid tilt and chirality [172–174]. Orientational order in the in-plane nematic field endows the membrane with interesting properties and morphologies [175–181] since the presence of such an order implicitly couples the membrane curvature to the nematic orientation. The nematic ordering interaction, to the lowest order, is described by the well known Frank’s free energy for nematics [182]:

$${\mathcal{H}}_{\text{nem}}=\int \mathrm{d}A\{\frac{K_1}{2}{({\mathcal{D}}_i{\widehat{n}}^i)}^2+\frac{K_3}{2}{({\mathcal{D}}_i{\widehat{n}}_{\perp }^i)}^2\},$$ (7)

where 𝒟 denotes the covariant derivative that contains information about the membrane curvature, which leads to the implicit coupling mentioned above. K₁ and K₃ are the elastic constants that govern the splay and bend modes of the nematic field. In practice, we use the Lebwohl–Lasher model [183] which is the one constant approximation of equation (7). The explicit interactions of the nematic field (i.e. the protein) with the membrane is modeled as an anisotropic elastic energy given by Frank and Kardar [184]:

$${\mathcal{H}}_{\text{anis}}(C_{\Vert }^0,C_{\perp }^0)=\int \mathrm{d}A\left\{\frac{{\kappa }_{\Vert }}{2}{\left(C_{\Vert }-C_{\Vert }^0\right)}^2+\frac{{\kappa }_{\perp }}{2}{(C_{\perp }-C_{\perp }^0)}^2\right\}.$$ (8)

Here, κ_|| and κ_⊥ are the energy costs for the membrane to bend locally, $C_{\Vert }^0$ and $C_{\perp }^0$ are the spontaneous curvatures induced by the protein field, and C_|| and C_⊥ are the membrane curvatures along directions parallel and perpendicular to n̂. The equilibrium conformations of the vesicular membrane is determined by a number of parameters that include: (i) the bending rigidity, (ii) the directional spontaneous curvatures $C_{\Vert }^0$ and $C_{\perp }^0$, (iii) composition of the nematic field ϕ, (iv) directional rigidities κ_|| and κ_⊥, and (v) the strength of orientational interactions between the in-plane field. These configurations are obtained through the DTMC technique, details of which may be found in [33, 164].

Membrane conformations in the continuum-based and particle- based models

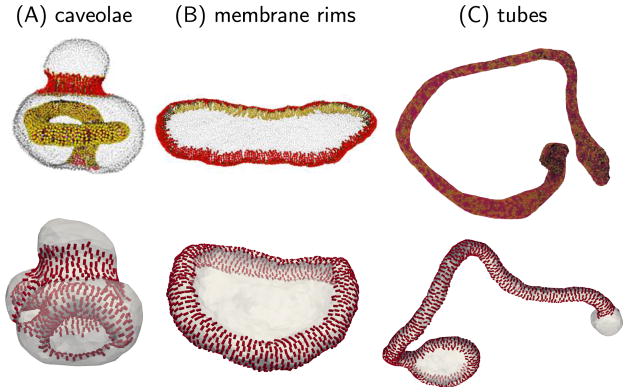
The anisotropic nature of protein-membrane interactions yields a rich conformational space for the membrane, compared to that obtained using isotropic elasticity models. For example, it was previously shown that physiologically relevant shapes, such as spheres, disks, rims, tubes, and caveolae can be stabilized solely by changing the value of the directional spontaneous curvature $C_{\Vert }^0$ [166, 167]. The membrane shapes obtained using the nematic membrane model are consistent with those obtained using molecular dynamics of particle based models for protein-membrane interactions refered to at the start of this section. This comparison is displayed in figure 6, where membrane configurations obtained from the particle-based models are shown in the top panels and those obtained from Monte Carlo simulations of the nematic membrane model are shown in the lower panels. The caveolae and rim like organization in the top panels of figures 6(A) and (B), respectively, are results from the meshless membrane model of Noguchi [116, 155], and the tubular membrane shown in figure 6(C) is from the EM2 model of Voth et al [148].

Figure 6.

Comparisons of protein remodeled membrane structures obtained using the mesoscopic particle models, by Noguchi [116] (top panels in (A) and (B) reproduced from [116], CC BY 4.0) and Ayton et al [148] (top panel in (C) reprinted from [148], Copyright 2009, with permission from Biophysical Society), with that from the nematic membrane model (bottom panels).

4.1. Method of thermodynamic integration to compute free energy landscapes

There are striking similarities both in the shape of the membrane and in the organization of the proteins (or protein curvature fields in the case of the nematic membrane model), as is evident from figure 6. While the importance of protein assembly and organization on membrane remodeling are both readily observed, the thermodynamic stabilities of the ensuing states have not been investigated in detail.

In the following, we will describe a thermodynamic free energy perspective of protein-induced remodeling of cell membrane using the nematic membrane model. We construct the free energy landscape for the nematic-membrane using the method of thermodynamic integration, in which we couple the anisotropic energy in equation (8) to a Kirkwood coupling parameter 0 ≤ λ ≤ 1 as:

$${\mathcal{H}}_{\text{anis}}(\lambda )=(1-\lambda ){\mathcal{H}}_{\text{anis}}(C_{\Vert ,\text{ref}}^0)+\lambda {\mathcal{H}}_{\text{anis}}(C_{\Vert }^0),$$ (9)

where $C_{\Vert }^0$ and $C_{\Vert ,\text{ref}}^0$ are the target and reference values of the directional spontaneous curvature. Here, for simplicity, we have ignored contributions from n̂ along its perpendicular direction by setting κ_⊥ = 0. The free energy of the nematic membrane in a state with directional spontaneous curvature $C_{\Vert }^0$, relative to its corresponding state with curvature $C_{\Vert ,\text{ref}}^0$, is then given by:

$$\mathrm{\Delta }\mathcal{F}(C_{\Vert ,\text{ref}}^0,C_{\Vert }^0)=\int \langle \frac{\mathrm{d}{\mathcal{H}}_{\text{anis}}(\lambda )}{\mathrm{d}\lambda }\rangle \mathrm{d}\lambda .$$ (10)

4.2. Free energy landscape as a function of directional spontaneous curvature

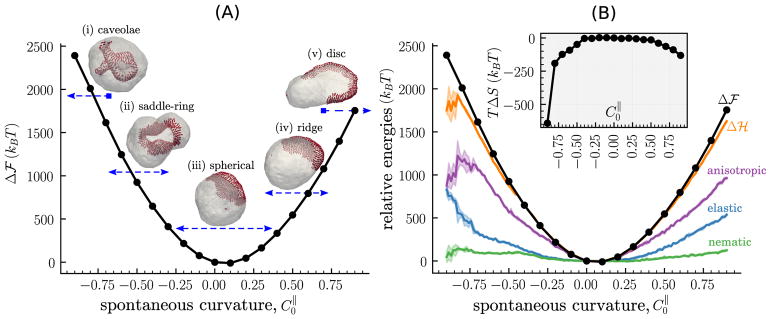
The relative free energy Δℱ as a function of $C_{\Vert }^0$ for a nematic membrane with ϕ = 0.25, κ_|| = 5 k_BT and κ = 10 k_BT is displayed in figure 7; here the reference curvature is taken to be $C_{\Vert ,\text{ref}}^0=0.0$. This corresponds to five distinct classes of membrane morphologies for $C_{\Vert }^0$ in the range −0.9 to 0.9; representative snapshot of these morphologies for $C_{\Vert }^0=-0.9$, −0.6, 0.0, 0.6 and 0.9 are also shown alongside in figure 7(A). At large negative curvatures (e.g. $C_{\Vert }^0=-0.9$) the region of the cell membrane containing the protein field invaginates into the cytoplasmic side of the vesicular membrane, consistent with our discussions in figure 6. However, the invaginated region in figures 7(A(i)) has a rim like structure compared to the tubular invaginations shown in figure 6(A). With increasing $C_{\Vert }^0$ the equilibrium shape of the membrane is remodeled to accommodate the assembly of the protein field into a saddle-ring ( $-0.6<C_{\Vert }^0<-0.3$), a circular domain ( $-0.3<C_{\Vert }^0<0.3$), a ridge ( $0.3<C_{\Vert }^0<0.7$) and a disc ( $C_{\Vert }^0>0.7$), as shown in figures 7(A(i)–(v)). It should be noted that these membrane morphologies are highly sensitive to the concentration of the protein assemblies and their interactions with the cell membrane, and this is shown later.

Figure 7.

(A) The relative free energy Δℱ, as a function of the directional spontaneous curvature $C_{\Vert }^0$ for a nematic membrane with κ = 10 k_BT, κ_|| = 5 k_BT, and ϕ = 0.25. Images marked (i)–(v) are representative snapshots of the membrane configuration at $C_{\Vert }^0=-0.9$, −0.6, 0.0, 0.6 and 0.9; the arrows underneath each image represent the range of $C_{\Vert }^0$ over which the corresponding configuration is stable. (B) The main panel shows the relative internal energies denoted nematic (equation (7)), elastic (equation (1)), and anisotropic (equation (8)), and their sum is denoted by Δℋ. The entropic contribution to the free energy TΔS is shown in the inset.

The transition between the five distinct morphological states of the nematic membrane for ϕ = 0.25 is continuous, as is evidenced by the smooth harmonic profile of the relative free energy Δℱ shown in figure 7(A). Despite the symmetry of equation (8) with respect to $C_{\Vert }^0$, the calculations show that there is a pronounced asymmetry in the values of Δℱ. We find $\mathrm{\Delta }\mathcal{F}(C_{\Vert }^0)<\mathrm{\Delta }\mathcal{F}(-C_{\Vert }^0)$ for all values of $C_{\Vert }^0>0$, and this asymmetry is primarily attributed to the finite positive curvature of a spherical vesicle even in its undeformed equilibrium state, thereby pointing to the importance of background membrane curvature in the recruitment and assembly of CRPs.

In figure 7(B) is depicted Δℱ for the nematic membrane alongside its three relative internal energies, namely elastic, nematic, and anisotropic. As for Δℱ, we compute the relative internal energies with respect to the membrane state with $C_{\Vert }^0=0$. All internal energies increase with an increase in both | $C_{\Vert }^0$| and also as a function of the coupling parameter λ; the latter has been shown explicitly in [185]. The dominant contribution is from equation (8), the anisotropic elastic energy, which is explicitly coupled to $C_{\Vert }^0$. In contrast, equations (1) and (7), the elastic and nematic energies, respectively, which are only implicitly related to $C_{\Vert }^0$, also start to increase at large values of | $C_{\Vert }^0$| and this is a signature of membrane morphological transition into highly curved shapes.

The sum of the three internal energy contributions, denoted by Δℋ, is also shown in figure 7(B). It is related to the relative free energy as Δℱ = Δℋ − TΔS, where ΔS denotes the change in the entropy with respect to the reference state. For small values of | $C_{\Vert }^0$|, the relative free energy of the nematic membrane is indistinguishable from its internal energy (i.e. Δℱ = Δℋ) as is shown in figure 7(B) for directional curvatures in the range $-0.4<C_{\Vert }^0<0.4$. However, at large values of | $C_{\Vert }^0$|, the relative free energy deviates significantly from its internal energy such that Δℱ > Δℋ pointing to the importance of entropic contributions in this regime. This contribution is quantified in the inset to figure 7(B) where we have displayed the energy TΔS as a function of $C_{\Vert }^0$. The calculations show that the entropy of highly deformed nematic membrane (for larger values of | $C_{\Vert }^0$|) is lower compared to that with quasi-spherical shapes (for lower values of | $C_{\Vert }^0$|). This is counterintuitive since highly deformed membrane shapes are known to have a higher entropy.

The loss in entropy may be understood by noting that the total entropy of a nematic membrane is given by S = S₁ + S₂ + S₃, where the three additive contributions are due to (i) the morphology of the membrane, (ii) the orientation of the nematic field, and, (iii) the lateral organization of the nematic field, respectively. At smaller values of | $C_{\Vert }^0$| the S₂ and S₃ terms are higher since the director of the oriented nematic field can be along any direction on the membrane surface, and similarly the nematic field can assemble at any spatial location on the membrane thereby maximizing the diffusion of the nematic cluster. However, at large values of | $C_{\Vert }^0$| the nematic field deforms the membrane surface leading to reduced diffusion of the nematic cluster (this reduction has been previously noted for scalar fields [186, 187]), and preferentially orients either along the direction of maximum curvature (for $C_{\Vert }^0>0$) or minimum curvature (for $C_{\Vert }^0<0$) [166] thereby reducing the degrees of freedom for the director. As a result, we observe an overall reduction in the total entropy of the nematic membrane, despite an increase in the S₁ term, as is shown in figure 7(B). Here, we find TΔS ~ −600 k_BT for $C_{\Vert }^0=-0.9$ and TΔS ~ −150 k_BT for $C_{\Vert }^0=0.9$ and this is significant since it is 10%–30% of the total internal energy required for membrane deformation.

4.3. Free energy as a function of the membrane bending rigidity κ

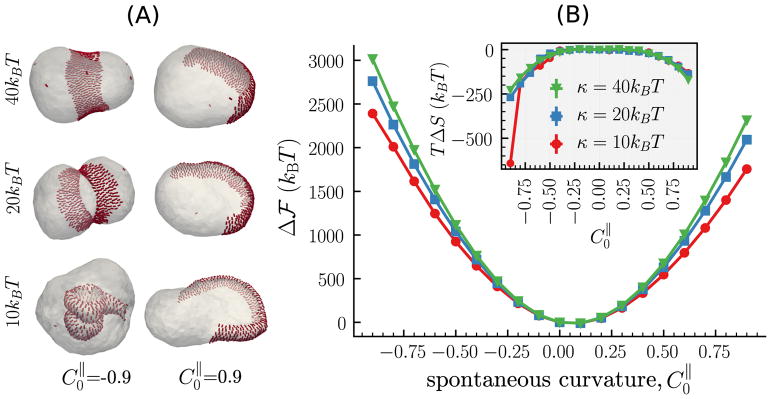
Variation in the physical and chemical microenvironment of a cell membrane, by modulation in factors such as the lipid composition and asymmetry, the aqueous environment, the surface charge density, and the local curvature of the cell membrane, not only affects its chemical interaction with a curvature remodeling protein but also modulates its bending rigidity κ [188–193]. The implicit change in membrane bending rigidity alters the curvature remodeling properties of an assembly of proteins. Field theoretic models are well suited to investigate the effect of κ on the free energy landscape for membrane deformation. In figure 8 we compare the relative free energies and representative morphologies, computed using the anisotropic model, for cell membranes with κ = 10, 20, and 40 k_BT, protein concentration ϕ = 0.25, and directional rigidities κ_|| = 5 k_BT and κ_⊥ = 0.

Figure 8.

The relative free energy, for a nematic membrane with κ = 10, 20 and 40 k_BT, as a function of its directional spontaneous curvature $C_0^{\Vert }$. κ_|| = 5 k_BT, and ϕ = 0.25 for all three cases. The representative snapshots correspond to membrane configuration obtained at $C_0^{\Vert }=-0.9$ (left panel) and 0.9 (right panel).

The effect of κ on the equilibrium membrane morphologies is readily visible in figure 8(A), where we show snapshots of the membrane for protein assemblies with $C_{\Vert }^0=-0.9$ (left panel) and $C_{\Vert }^0=0.9$ (right panel). As expected, a given protein assembly deforms membranes with lower bending rigidities into highly complex shapes, such as the caveolae and disc seen in figure 8(A) for κ = 10 k_BT, while it prefers to stabilize quasispherical shapes for membranes high bending rigidities. This feature is also seen in the relative free energy for deformation shown in the main panel of figure 8(B), where we find $\mathrm{\Delta }\mathcal{F}(C_{\Vert }^0)$ to increase with increasing κ for all values of $\mid C_{\Vert }^0\mid >0.25$. The entropic contributions shown in the inset to figure 8(B) primarily depends on the morphology of the cell membrane, and the lateral organization and orientation of the nematic field, as noted in our earlier discussions. Consistent with this fact, we only observe a significant deviation in the energy TΔS for κ = 10 k_BT and $C_{\Vert }^0=-0.9$, the only parameter for which the membrane deforms into a highly-curved caveolae like structure.

4.4. Effect of protein concentration on remodeling of cell membranes

Membrane associated proteins are constantly subject to changes in their expression levels, which together with the chemical potential for protein association dictate the number of proteins recruited to the membrane. In this section, we will discuss the role of protein concentration ϕ on the assembly and organization of proteins and the ensuing morphological changes in the cell membrane.

The equilibrium conformations of a cell membrane as a function of its protein concentration is displayed in figure 9(A) for five different values of ϕ = 0.1, 0.25, 0.5, 0.75, and, 1.0. The left and right panels correspond to proteins with spontaneous curvatures $C_{\Vert }^0=-0.9$ and $C_{\Vert }^0=0.9$, respectively, and these correspond to the limit of maximum negative and positive curvatures used in our model. The negatively curving protein assembly ( $C_{\Vert }^0=-0.9$) drives the membrane into caveolae like structures, even at very low concentrations as is shown for ϕ = 0.1 in figure 9(A), and the number of such invaginations increases with increasing ϕ. The positively curving protein assembly ( $C_{\Vert }^0=0.9$) drives a series of morphological transitions as a function of ϕ, which in figure 9(A) corresponds to quasi-spherical (ϕ = 0.0) → rims (0.0 < ϕ < 0.4) → discs (0.4 < ϕ < 0.6) → tube with disc caps (0.6 < ϕ < 0.9) → tube with spherical caps ϕ ≥ 0.9).

Figure 9.

(A) Representative snapshots for nematic membranes with protein concentrations ϕ = 0.1, 0.25, 0.5, 0.75, and 1.0 are shown for directional spontaneous curvatures $C_{\Vert }^0=-0.9$ (left panel) and $C_{\Vert }^0=0.9$ (right panel). (B) The main panel shows the relative free energies for the five protein concentrations as a function of $C_{\Vert }^0$, while the inset shows the corresponding entropic contributions. Data corresponds to a membrane with κ = 10 k_BT, κ_|| = 5 k_BT, κ_⊥ = 0, and ε_LL = 3 k_BT.

The relative free energy of the nematic membrane as a function of $C_{\Vert }^0$ for the five different protein concentrations is shown in figure 9(B). As before, Δℱ for all values of ϕ follows an asymmetric harmonic profile and increases with increasing ϕ, for all values of $C_{\Vert }^0$. The entropic contribution to the free energy TΔS, shown in the inset to figure 9(B), also decreases with ϕ for all values of $C_{\Vert }^0$.

5. Applications and future outlook

Formation of membrane signalosomes (i.e. signaling complexes that are central to intracellular trafficking) are often followed by recruitment and reorganization of actin filaments providing the force required for multiple biological processes [2]. Most of these processes are coupled with the deformation of the cell membrane. Examples of such membrane-cytoskeleton- coupled processes include: the formation of filopodia, lamellipodia and podosomes for cell movement or cancer-cell invasion; endocytosis, phagocytosis, exocytosis and various membrane-trafficking and recycling events on the plasma membrane and the endosome. While the driving forces for the assembly of these functional signaling complexes are not precisely understood, it is appreciated that the assembly itself requires an elaborate and delicate orchestration of multiple proteins and lipids in precise spatial patterns and temporal sequence. Can the models discussed in this review provide insight into the regulation of such signaling and trafficking at the cellular scale? Although the treatment of larger length-scale processes in models at a sub-cellular scale necessitates additional approximations and gross reductionism, such models provide a unique opportunity to connect with cellular experiments. We discuss below, specific applications and future outlook of models presented in this review, as they pertain to invaginations of plasma membranes in the nucleation of invadopodia during cell migration, budding of vesicles in the plasma membrane during clathrin-mediated endocytosis (CME), and budding of vesicles in the endosomes due to membrane constriction by ESCRT proteins.

5.1. Invaginations of lipid membranes due to Exo70 of the exocyst complex

Zhao et al [73] have described the application of the anisotropic curvature model to the specific cellular process of exocytosis. Their model included a vesicular membrane decorated with different concentrations (surface coverages) of curvature fields (denoting Exo70 protein dimers), with coverage ranging from 20% to 100%. The bending rigidity κ was set to 20 k_BT (typical value for cell membranes), where T = 300 K is the ambient temperature. In the simulations, they explored a range of ε_LL values 1 to 5 k_BT to account for the interaction of Exo70 with the membrane, and chose κ_|| = 5 k_BT and vary $C_0^{\Vert }$ in the range $-0.5a_0^{-1}$ to $-1.0a_0^{-1}$. The values of κ_⊥ and $C_0^{\perp }$ were both set to zero. Using the model parameters, it was shown that the simulations studies reproduced the experimentally observed spontaneous tubulation into the interior side of a giant unilamellar vesicle. To establish consistency with the chosen parameters, the study also reported the curvature field induced by an Exo70 dimer using the CGMD framework showing Exo70 dimers inducing negative curvature on a bilayer membrane, whose radius of curvature matched the curvature strength needed for tubulation in the mesoscale model [73]. Interestingly, the study also reported that overexpressing Exo70 in cells led to an increase in cell protrusions and causing the cell migration program to activate.

5.2. Budding of vesicles in CME

Several studies have explored the role of cooperative proteinprotein and protein-membrane interactions in the ubiquitous endocytic pathway in mammalian cells, namely the CME, isotropic curvature field model. In the model for CME, the epsins bind to the lattice of a growing clathrin coat through the interaction of the CLAP domain of epsin with the clathrin triskelion. This way, multiple epsins localized spatially and orientationally templated on the clathrin coat collectively play the role of a curvature inducing capsid. In addition, epsin serves as an adapter in binding the clathrin coat to the membrane through the interaction of its ENTH domain with the phosphotidylinositol (4,5) bisphosphate (PI(4,5)P2 or PIP2) molecules on the membrane. By employing the Helfrich methodology outlined above, Liu et al [194], Agrawal et al [114], Ramanan et al [195], and Hassinger et al [196] have addressed how the shapes and energetics of vesicular-bud formation in a planar membrane is stabilized by presence of the epsin/clathrin assembly. Tourdot et al [88, 160] used a free energy approach to evaluate the free energy of bud formation for different areas of the clathrin coat and discussed how the critical coat area needed for vesiculation depends on the state of the membrane, (namely the bending modulus and the membrane excess area). This study also highlighted the need for computing free energies (and including thermal undulations) to which the neck formation is quite sensitive. These studies have also collectively helped link the model predictions with specific perturbation experiments involving endocytosis in yeast and mammalian cells.

5.3. Budding of vesicles due to membrane constriction by ESCRT proteins

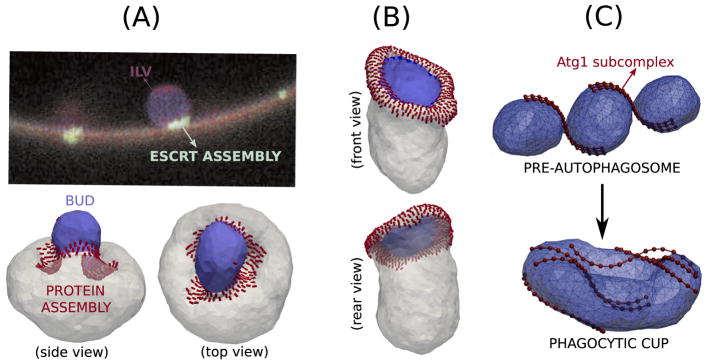
The ESCRT are a family of cytosolic proteins, which are known be involved in membrane budding and also in endosomal sorting. In vitro, it has been shown that ESCRT proteins acting on the outer surface can generate membrane buds that grow into the interior side of a giant unilamellar vesicle. The mechanism of bud formation and the form of the curvature field induced by an ESCRT protein has not been well understood. In experiments, it has been observed that the ESCRT proteins are localized to the neck region of the budded vesicle; in figure 10(A), green regions represent the ESCRT proteins in the experimental data taken from Hurley and Hanson [61]. While the endocytosis models described above have shown that bud formation requires the presence of an induced curvature field in the budding region, the absence of the ESCRT proteins on the surface of the bud in the experiment rules out such a mechanism for ESCRT-induced budding. Using the anisotropic curvature model in section 3 and localizing the protein curvature field to an annular region we demonstrate a novel phenomenon where a positively curved vesicular bud is formed due to the constrictive action of negatively curving proteins, in a region around it, and vice versa. The positively curved bud stabilized for $C_0^{\Vert }=-0.6a_0^{-1}$ and the vesicle budding into the membrane seen at $C_0^{\Vert }=0.6a_0^{-1}$ are shown respectively in panels (A, B) of figure 10. The annulus like arrangement of the curvature field does not occur below a lower threshold while it prefers to segregate to a single patch when the surface coverage exceeds an upper threshold. A detailed quantitative analysis of the thermodynamic stability of the annular distribution of the curvature field as described by the free energy methods in section 4.1 can then be directly related to experiments and be useful in predicting the concentration of the curvature remodeling members of the ESCRT family around the neck of the budding vesicle. The problem of ESCRT-mediated budding has been theoretically studied using the tools of continuum membrane mechanics (see equations (1) and (2)) [197, 198]. Here, the proteins were modeled as a density field and their lateral organization was controlled by their phase separation kinetics in the background of the lipid field. These studies also clearly demonstrate the novel phenomenon of neck constricted budding and show features similar to that seen in figures 10(A) and (B).

Figure 10.

(A) Fluorescence image of intraluminal vesicle (ILV) showing the membrane in red and the location of ESCRT proteins in green. Image reprinted by permission from Macmillan Publishers Ltd: Nature Reviews Molecular Cell Biology [61], Copyright 2010. ((A) and (B)) Simulation results showing the novel phenomenon of budding by constriction positively curved bud generated by negatively curved proteins and negatively curved bud from proteins inducing positive curvature. The protein field does not localize the area of the bud. (C) Image (reproduced from [137], CC BY 4.0) showing the role of Atg proteins (shown as beads) in stabilizing membrane morphologies that resemble cells undergoing autophagy.

Bahrami et al [137] recently used a multiscale approach combining CGMD simulations with DTMC simulations (and free energy calculations) to study the role of Atg1 complexes in the formation of the phagocytic cup. They investigated the role of the intrinsic curvature of the S-shaped Atg1 subcomplex Atg17-Atg31-Atg29 in remodeling the pearl-on-string shaped preautophagosomal membrane into a cup shaped double membrane exhibited by cells undergoing autophagy. In their study, they explicitly showed that the interaction of the membrane with wild type Atg1 dimers was essential to overcome the large free energy barrier between the two structures (see figure 10(C)).

5.4. Future outlook

A definitive understanding of the interplay between protein binding/migration and membrane curvature evolution is emerging but remains incomplete. The mechanisms that underpin such behavior are hugely important in intracellular assembly and stability of organelles (which often sustain extreme curvatures) and in intracellular transport and sorting of proteins and cargo. Though aspects of these fundamental processes are well-characterized from a molecular biology perspective, especially in the domain of protein-protein interactions and increasingly in the area of protein localization, several open questions remain which are fundamental to a complete understanding of the underlying mechanisms in these fundamental (‘unit’) cellular process from a biophysical and thermodynamic perspective, which have been addressed in this review. The two main messages of this review are to highlight how molecular interactions between the protein and the lipids at the molecular scale directly determine the morphology of cellular membranes at the micron scale primarily by setting up curvature fields; and that the determination and characterization of these fields and how they interact with a dynamically changing membrane curvature morphology is quantified and interpreted based on the free energy landscape.

We would like to comment on the context of the approximations of the methods we have discussed. The CGMD models have near molecular resolution, but the model-parameters are subject to approximations. At the continuum level, the approximations do not consider interlayer-friction and hydro-dynamics (see references within [33]), explicit electrostatics, and membrane lipid heterogeneity. Despite such simplifications, following the success of the studies discussed, we may dare to explore more complex and more challenging unsolved mechanisms in cellular biophysics of trafficking and signaling. For example, the structural basis for a variety of membrane binding by PH, PX, FYVE, ENTH, BAR and other domains is well studied [199, 200], and provides a rich set context and opportunity for the multiscale modeling methodology we have presented to connect to specific pathways these proteins are involved in. Moreover, several of the CRPs feedback to the cytoskeletal pathways via direct or indirect recruitment of adaptors regulating actin assembly/disassembly [2]. Future work can focus on the effect of the cytoskeletal interactions, in particular, the roles of membrane, and frame tensions in regulating cellular processes and some promising headway in this direction has been reported in recent studies [125, 138, 201]. Another intriguing possibility suggested by the results we have discussed is that the recruitment of CRPs can be dependent on the membrane tension, which in turn is influenced by the cytoskeletal or cortical tension. This is explicitly shown in figure 4 where the chemical potential of a CRP in a planar membrane is tension dependent. It is also inferred from the curvature undulation coupling studies discussed in section 3.2, by recognizing that tension and curvature are coupled via equation (6). More generally, increase in tension inhibits the ability of the CRPs to effect a protrusion transition at a fixed/given density/expression of CRPs. Furthermore, given that most CRPs are also part of various signal transduction pathways, the scenario described above implies how curvature of cell membranes can control cellular signaling. If the CRPs themselves serve as signaling mediators, then such signals are inhibited by an increasing tension, thereby providing possible mechanisms for mechanosensitivity in cells as speculated by Weiner et al [202].