Abstract
A superbubble is a type of directed acyclic subgraph with single distinct source and sink vertices. In genome assembly and genetics, the possible paths through a superbubble can be considered to represent the set of possible sequences at a location in a genome. Bidirected and biedged graphs are a generalization of digraphs that are increasingly being used to more fully represent genome assembly and variation problems. In this study, we define snarls and ultrabubbles, generalizations of superbubbles for bidirected and biedged graphs, and give an efficient algorithm for the detection of these more general structures. Key to this algorithm is the cactus graph, which, we show, encodes the nested decomposition of a graph into snarls and ultrabubbles within its structure. We propose and demonstrate empirically that this decomposition on bidirected and biedged graphs solves a fundamental problem by defining genetic sites for any collection of genomic variations, including complex structural variations, without need for any single reference genome coordinate system. Further, the nesting of the decomposition gives a natural way to describe and model variations contained within large variations, a case not currently dealt with by existing formats [e.g., variant cell format (VCF)].
Keywords: : genome assembly, genome graphs, genomic variation, sequence analysis, variant discovery
1. Introduction
Graphs are used extensively in biological sequence analysis, where they are often used to represent uncertainty about, or ensembles of, potential nucleotide sequences. Several subtypes have become especially prominent for sequence representation, in particular the de Bruijn graph (de Bruijn, 1946; Pevzner et al., 2001), the string graph (Myers, 2005), the breakpoint graph (Pevzner, 2000; Alekseyev and Pevzner, 2009), and the bidirected graph (aka sequence graph; Edmonds and Johnson, 1970; Medvedev and Brudno, 2009).
In the context of de novo sequence assembly, several characteristic types of subgraph are recognized, in particular the bubble (Zerbino and Birney, 2008), a pair of paths that start and end at common source and sink nodes but are otherwise disjoint. In the context of sequence analysis, a bubble can represent a potential sequencing error or a genetic variation within a set of homologous molecules. An efficient algorithm for bubble detection was proposed by Birmelé et al. (2012).
A generalization of the notion of a bubble, the superbubble is a more complex subgraph type in which a set of (not necessarily disjoint) paths start and end at common source and sink nodes. This problem was initially proposed by Onodera et al. (2013), who gave a quadratic solution. Brankovic et al. (2015) recently provided a linear time algorithm for superbubbles on directed acyclic graphs (DAGs). This result, when paired with a previous linear time transformation of the problem of superbubbles on directed graphs to superbubbles on DAGs (Sung et al., 2015), yields a linear cost solution for computing superbubbles on digraphs. For a review of superbubbles and their use in sequence analysis, refer Iliopoulos et al. (2016). In this article, we generalize the idea of superbubble to the more general case of a bidirected graph, connect a slight generalization of the superbubble, which we call the ultrabubble, and show how it relates to the decomposition of the graph into 2- and 3-edge connected (2-EC and 3-EC) components.
2. Methods
2.1. Directed, bidirected, and biedged graphs
A bidirected graph
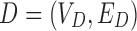 is a graph in which each endpoint of every edge has an independent orientation (denoted either “left” or “right”), indicating whether the endpoint is incident with the left or right side of the given vertex. The sides of D are, therefore, the set
is a graph in which each endpoint of every edge has an independent orientation (denoted either “left” or “right”), indicating whether the endpoint is incident with the left or right side of the given vertex. The sides of D are, therefore, the set 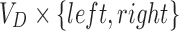 , and each edge in ED is a pair set of two sides (Fig. 1). We say for all
, and each edge in ED is a pair set of two sides (Fig. 1). We say for all 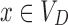 ,
, 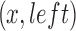 and
and 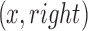 are opposite sides.
are opposite sides.
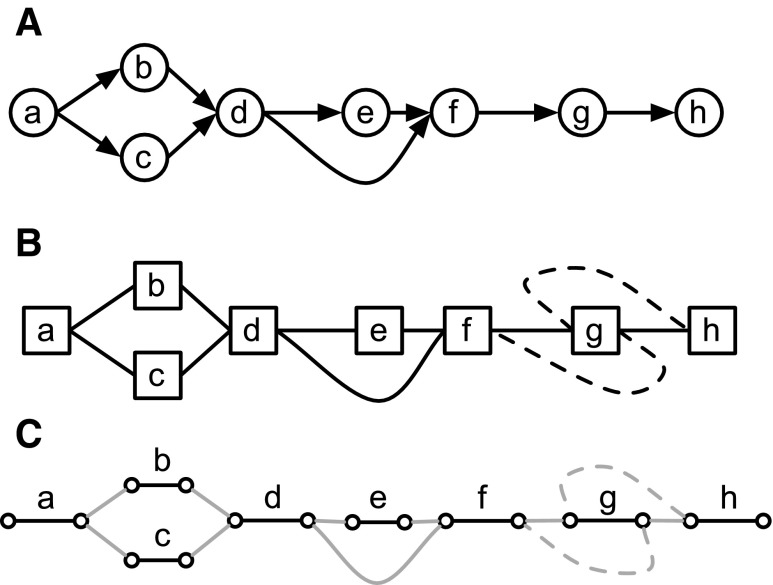
FIG. 1.
(A) A digraph. (B) A bidirected graph. Each node is drawn as a box, and the orientation for each edge endpoint is indicated by the connection to either the left or right side of the node. The graph excluding the dotted edges is the equivalent bidirected graph for the digraph in (A); the dotted edges encode an inversion that cannot be expressed in the digraph representation. (C) A biedged graph equivalent to the bidirected graph shown in (B).
Any digraph is a special case of a bidirected graph in which each edge connects a left and a right side (by convention, we here consider the right side to be the outgoing side and the left side the incoming side, so that the conversion from a digraph to a bidirected graph is determined; Fig. 1).
A biedged graph is a graph with two types of edges: black edges and gray edges, such that each vertex is incident with at most one black edge (Fig. 1C).
For any bidirected graph D, there exists an equivalent biedged graph 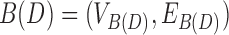 , where:
, where:
•
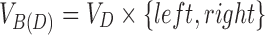 , the sides of VD,
, the sides of VD,•
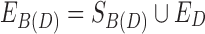 , where ED are the gray edges,
, where ED are the gray edges,• and
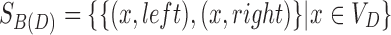 are the black edges.
are the black edges.
For a vertex 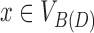 , we use the notation
, we use the notation 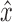 to denote its opposite side.
to denote its opposite side.
Clearly, the bidirected and biedged representations are essentially equivalent, and the choice to use either one is largely a stylistic consideration. For the remainder of this article, we will mostly use the biedged representation. As any digraph is a special case of a bidirected graph and any bidirected graph has an equivalent biedged graph, so any digraph has an equivalent biedged graph.
2.2. Directed walks on biedged and bidirected graphs
A directed walk on a bidirected graph is a walk that at each visited vertex exits the opposite side to that which it enters. On a biedged graph, a directed walk is equivalent to a walk that alternates between black and gray edges. A directed cycle is a closed directed walk that starts and ends either on the same side (e.g., a self-loop edge) or on opposites sides of a vertex (in which case the start and end is arbitrary due to symmetry). A bidirected or biedged graph is acyclic if it contains no directed cycles.
These definitions are a generalization of a directed walk on a digraph. In a bidirected representation of a digraph, all edges in a directed walk are left-to-right or all are right-to-left. A directed walk on a general bidirected (or biedged) graph can mix these two types and additionally include edges that do not alternate the orientation of their endpoints (e.g., left-right, right-right, and left-left edges).
Given these generalizing relationships, clearly a digraph D is acyclic if B(D) is acyclic. Note that any acyclic biedged graph can also be converted into an equivalent DAG:
Lemma 1. For any acyclic biedged graph B(D), there exists an isomorphic biedged graph B(D) such that D is a DAG.
Proof. For each connected component in B(D), use a depth first search (DFS) beginning at side x to label the sides either “red” or “white”: If x is not already labeled, then label x red and 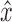 white. For each gray edge incident with
white. For each gray edge incident with 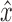 , if the connected side is not labeled, label the connected side red and continue recursively via DFS. In this way, all the sides in the connected component containing x will be labeled in a single DFS. If during the recursion the connected side encountered is already labeled, then it must be labeled red, else there would exist a directed cycle, a contradiction. Use the labeling to create B(D), isomorphic to B(D) but replacing the orientation of the sides so that each side labeled white is a left side and each side labeled red is a right side. All edges in B(D) connect a left and a right side.
, if the connected side is not labeled, label the connected side red and continue recursively via DFS. In this way, all the sides in the connected component containing x will be labeled in a single DFS. If during the recursion the connected side encountered is already labeled, then it must be labeled red, else there would exist a directed cycle, a contradiction. Use the labeling to create B(D), isomorphic to B(D) but replacing the orientation of the sides so that each side labeled white is a left side and each side labeled red is a right side. All edges in B(D) connect a left and a right side.
2.3. Superbubbles, snarls, and ultrabubbles
Repeating the definition from Onodera et al. (2013), any pair of distinct vertices 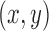 in a digraph D is called a superbubble (Fig. 2A) if:
in a digraph D is called a superbubble (Fig. 2A) if:
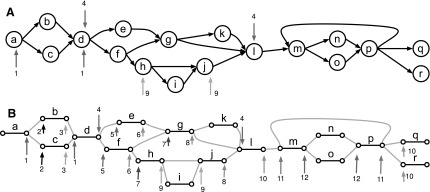
FIG. 2.
(A) Superbubbles in a digraph. The superbubbles are indicated by pairs of numbered arrows, numbered consistently with (B). (B) A biedged graph representation of the digraph in (A). The snarls are illustrated by numbered arrows; the ultrabubbles are those numbered 1, 4, 9, and 12. Note, a side incident with a black bridge edge may be in multiple snarls (see snarls numbered 10).
• reachability: y is reachable from x.
• matching: The set of vertices, X, reachable from x without passing through y is equal to the set of vertices from which y is reachable without passing through x (passing through here means to enter and then exit a vertex on the path).
• acyclicity: The subgraph induced by X is acyclic.
• minimality: No vertex in X other than y forms a pair with x that satisfies the criteria previously defined, and similarly for y.
We call the subgraph induced by X the superbubble subgraph.
To generalize superbubbles for biedged graphs, we introduce the notion of a snarl, a minimal subgraph in a biedged graph whose vertices are at most 2-black-edge-connected (2-BEC) to the remainder of the graph (two vertices in a biedged graph are k-BEC if it takes the deletion of at least k black edges to disconnect them). In a biedged graph B(D), a pair set of distinct, non-opposite vertices 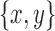 are a snarl (Fig. 2B) if:
are a snarl (Fig. 2B) if:
• separable: The removal of the black edges incident with x and y disconnects the graph, creating a separated component X containing x and y and not
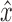 and
and 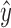 .
.• minimality: No pair of opposites
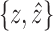 in X exists such that
in X exists such that 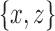 and
and 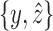 fulfills the criteria described earlier.
fulfills the criteria described earlier.
We call a vertex not incident with a gray edge a tip (Zerbino and Birney, 2008). In a biedged graph B(D), a snarl is an ultrabubble if its separated component is acyclic and contains no tips.
The following shows that a superbubble in a digraph is an ultrabubble in the equivalent biedged graph.
Lemma 2. For any superbubble (x, y) in a digraph D, the pair set 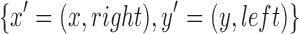 is an ultrabubble in B(D).
is an ultrabubble in B(D).
Proof. Let d and e be the black edges incident with 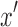 and
and 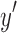 , respectively, and let X be the superbubble subgraph of
, respectively, and let X be the superbubble subgraph of 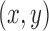 .
.
We start by proving that 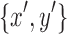 satisfies the separable criteria. As y is reachable from x by definition, there exists a directed path in B(D) between
satisfies the separable criteria. As y is reachable from x by definition, there exists a directed path in B(D) between 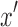 (the right side of x) and
(the right side of x) and 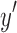 (the left side of y) that excludes d and e. After the deletion of these black edges,
(the left side of y) that excludes d and e. After the deletion of these black edges, 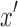 and
and 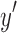 , therefore, remain connected. If the separable criteria are not satisfied, the deletion of d and e must, therefore, not disconnect
, therefore, remain connected. If the separable criteria are not satisfied, the deletion of d and e must, therefore, not disconnect 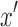 and
and 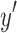 from either or both
from either or both 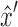 and
and 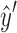 , without loss of generality assume
, without loss of generality assume 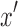 (and therefore
(and therefore 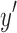 ) remains connected to
) remains connected to 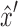 .
.
If 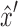 is on a directed walk from
is on a directed walk from 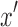 that excludes d, then the addition of d to this walk defines a directed cycle in B(D). As all nodes reachable from x are in the separated component X, the existence of this cycle in B(D) implies the existence of a corresponding directed cycle in X, a contradiction.
that excludes d, then the addition of d to this walk defines a directed cycle in B(D). As all nodes reachable from x are in the separated component X, the existence of this cycle in B(D) implies the existence of a corresponding directed cycle in X, a contradiction.
If there exists a non-directed walk from 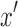 to
to  , then let
, then let 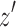 be the last node on the walk from
be the last node on the walk from 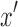 such that the subwalk between
such that the subwalk between 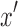 and
and 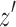 is a directed walk. By definition, there exists a directed walk from
is a directed walk. By definition, there exists a directed walk from 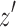 to
to 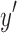 . The next node on the walk from
. The next node on the walk from 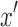 to
to 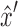 after
after 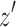 is, by definition, not reachable from
is, by definition, not reachable from 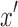 but
but 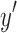 must be reachable from this node. This implies a contradiction of the matching criteria for the corresponding nodes in X.
must be reachable from this node. This implies a contradiction of the matching criteria for the corresponding nodes in X.
We have, therefore, established that 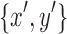 fulfills the separable criteria. We have already established that if a digraph is acyclic, its equivalent biedged graph is acyclic, therefore the separated component of
fulfills the separable criteria. We have already established that if a digraph is acyclic, its equivalent biedged graph is acyclic, therefore the separated component of 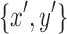 is acyclic. As every node in X is reachable from both x and on a path from y, the separated component clearly contains no tips.
is acyclic. As every node in X is reachable from both x and on a path from y, the separated component clearly contains no tips.
It remains to prove that 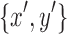 fulfills the minimality criteria. If
fulfills the minimality criteria. If 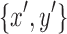 do not satisfy the minimality criteria without loss of generality, there exists a node
do not satisfy the minimality criteria without loss of generality, there exists a node 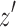 in the separated component of
in the separated component of 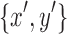 such that
such that 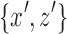 are separable. It follows that all directed paths from
are separable. It follows that all directed paths from 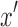 to
to 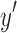 that exclude d and e visit
that exclude d and e visit 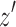 , and for the node z in D contained in
, and for the node z in D contained in 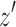 ,
, 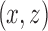 fulfills (clearly) all the superbubble criteria, a contradiction.
fulfills (clearly) all the superbubble criteria, a contradiction.
2.4. Cactus graphs
A cactus graph is a graph in which any two vertices are at most 2-EC (Harary and Uhlenbeck, 1953). In a cactus graph, each edge is part of at most one simple cycle, and, therefore, any two simple cycles intersect at most one vertex.
For a graph 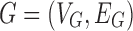 , let
, let 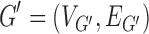 be a multigraph created by merging subsets of the vertices, such that:
be a multigraph created by merging subsets of the vertices, such that:
•
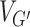 is a partition of VG,
is a partition of VG,•
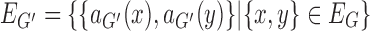 is a multiset,
is a multiset,
where 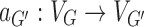 is a graph homomorphism that maps each vertex in VG to the set in
is a graph homomorphism that maps each vertex in VG to the set in 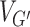 that contains it.
that contains it.
Merging all equivalence classes of 3-EC vertices in a graph results in a cactus graph (Paten et al., 2011).
For a biedged graph B(D), let C(D) be the cactus graph created by first contracting all the gray edges in B(D); then for each equivalence class of 3-EC vertices in the resulting graph merging together the vertices within the equivalence class (Fig. 3A–C). As with 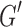 and G,
and G, 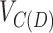 is a partition of the vertices of
is a partition of the vertices of 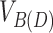 , and
, and 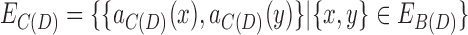 is a multiset.
is a multiset.
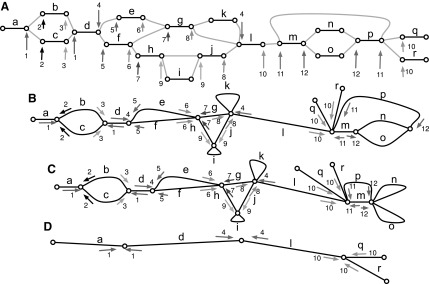
FIG. 3.
(A) A biedged graph B(D) with the snarls indicated by pairs of numbered arrows. (B) The graph in (A) after contracting the gray edges. (C) The cactus graph C(D) for B(D), constructed by merging the vertices in each 3-EC in (B). (D) The bridge forest D(D), constructed by contracting the edges in simple cycles in (C). 3-EC, 3-edge connected.
For a vertex 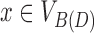 , we call
, we call 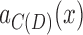 its projection in C(D). Similarly for a set of vertices
its projection in C(D). Similarly for a set of vertices 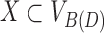 , we call
, we call 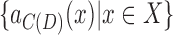 the projection of X in C(D). Let
the projection of X in C(D). Let 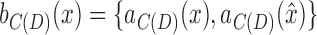 , which is the projection of the black edge incident with x in C(D).
, which is the projection of the black edge incident with x in C(D).
Appendix 1 gives lemmas that make explicit the relationship between the edge connectivity of vertices in B(D) and C(D), and that we use to prove the relationship between the snarls of B(D) and C(D).
2.5. Snarls and cacti
A pair set of distinct vertices 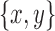 in B(D) are a chain pair if they project to the same vertex in C(D) and their incident black edges project to the same simple cycle in C(D) (e.g., pairs of arrows in simple cycles in Fig. 3C). A cyclic sequence of chain pairs within the same simple cycle in C(D) and ordered according to the ordering of this simple cycle is a (cyclic) chain. Contiguous chain pairs in a chain share two opposite sides of a black edge in B(D).
in B(D) are a chain pair if they project to the same vertex in C(D) and their incident black edges project to the same simple cycle in C(D) (e.g., pairs of arrows in simple cycles in Fig. 3C). A cyclic sequence of chain pairs within the same simple cycle in C(D) and ordered according to the ordering of this simple cycle is a (cyclic) chain. Contiguous chain pairs in a chain share two opposite sides of a black edge in B(D).
For a cactus graph C(D), the graph D(D) resulting from contracting all the edges in simple cycles in C(D) is a called a bridge forest (Fig. 3D).
A pair set of distinct vertices 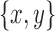 in B(D) are a bridge pair if they project to the same vertex in D(D) and both their incident black edges are bridges (e.g., pairs of arrows numbered 1 and 2 in Fig. 3D). A maximum sequence of bridge pairs within D(D) connected by incident nodes with degree 2 is an (acyclic) chain. As with chain pairs, contiguous bridge pairs in a chain share two opposite sides of a black (bridge) edge in B(D).
in B(D) are a bridge pair if they project to the same vertex in D(D) and both their incident black edges are bridges (e.g., pairs of arrows numbered 1 and 2 in Fig. 3D). A maximum sequence of bridge pairs within D(D) connected by incident nodes with degree 2 is an (acyclic) chain. As with chain pairs, contiguous bridge pairs in a chain share two opposite sides of a black (bridge) edge in B(D).
Theorem 1. The set of snarls in B(D) is equal to the union of chain pairs and bridge pairs.
Proof. Follows from Lemmas 10 and 11 given in Appendix 2.
Given Theorem 1 to calculate the set of snarls for a given biedged graph, it is sufficient to calculate the cactus graph to give the set of snarls that map to chain pairs and the bridge forest to calculate the set of snarls that map to bridge pairs. Constructing a cactus graph of the type described for a biedged graph is linear in the size of the biedged graph [using the algorithm described in Paten et al. (2011)], and clearly the cost of then calculating the bridge forest from the cactus graph is similarly linear. The number of chain pairs is clearly linear in the size of the biedged graph; however, the number of bridge pairs is potentially quadratic in the number of bridge pairs, so enumerating these latter snarls has potentially worst case quadratic cost in terms of the size of the biedged graph. Next, we consider ways to prune the set of snarls by using their natural nesting relationships to create a hierarchy of snarls that is at most linear in the size of the biedged graph.
2.6. Compatible snarl families
One particularly attractive feature of superbubbles is that they have nested containment relationships. That is, superbubbles have subgraphs that are either strictly nested or disjoint. Accordingly, a digraph is partitioned into a set of top-level superbubble subgraphs and other graph members not contained in a superbubble subgraph, and each top-level superbubble component then contains one or more child superbubbles, forming a tree structure. The situation is more complex for snarls. The separated component of snarls can overlap (Fig. 4) such that each partially contains the other. To create a properly nested hierarchy of snarls, it is, therefore, necessary to exclude some snarls.
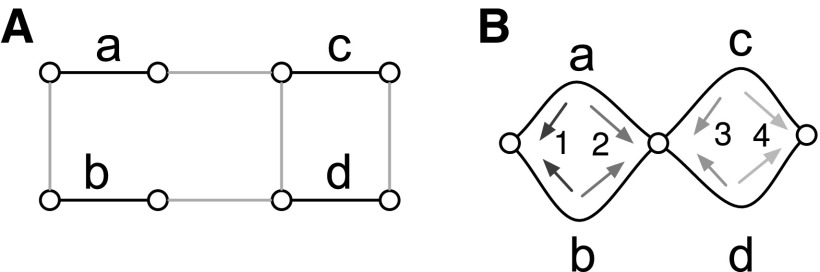
FIG. 4.
Overlapping snarls. (A) A bidirected graph, its corresponding (B) cactus graph. The snarl numbered 2 contains the snarl numbered 4; similarly, the snarl numbered 3 contains the snarl numbered 1. The snarls numbered 2 and 3 overlap.
We will call a family of snarls compatible if all pairs of distinct snarls in the family have snarl subgraphs that are either disjoint or nested. A compatible family of snarls has a nesting structure that is a forest, similar to superbubbles. The following theorem provides a sufficient condition for constructing such a family in many bidirected graphs.
Theorem 2. In a connected biedged graph with at least one black bridge edge, the family of snarls whose subgraphs have no black bridge edges is compatible.
In addition, the next theorem shows that this family of snarls is a generalization of ultrabubbles.
Theorem 3. No ultrabubble contains a black bridge edge in its subgraph.
Proofs of these theorems are included in Appendix 3.
The bridge edge condition can also be used to construct a compatible family of snarls in a graph with no black bridge edges. To do so, we break one black edge into two tips. Each of these tips is then a bridge edge, so the family of snarls we construct from the modified graph is compatible. However, the family of snarls we obtain will depend on our choice of a black edge to break. Heuristically, an edge corresponding to a highly conserved genomic element should be chosen, since by construction it will not occur in any snarl's subgraph.
Given a snarl decomposition, the following algorithm will filter them down to the compatible family we have described:
• Iterate over the black bridge edges of the graph [i.e., the edges of D(D)].
• For a bridge edge
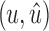 , if either u or
, if either u or 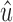 is the boundary of a snarl, mark that snarl as not containing
is the boundary of a snarl, mark that snarl as not containing  .
.• Initialize a queue with u and
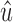 , and traverse outward in breadth-first order, ignoring restrictions on directed biedged walks.
, and traverse outward in breadth-first order, ignoring restrictions on directed biedged walks.• On reaching a node x that is a boundary for a snarl
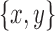 , if y,
, if y, 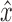 , or
, or 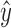 has not been traversed, mark the snarl as containing
has not been traversed, mark the snarl as containing 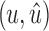 .
.• On reaching a node
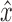 whose opposite is boundary for a snarl
whose opposite is boundary for a snarl 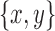 , if
, if 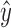 , x, or y has not been traversed, mark the snarl as not containing
, x, or y has not been traversed, mark the snarl as not containing 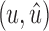 .
.• After completing every traversal, retain only snarls that were never marked as containing a black bridge edge.
The validity of this algorithm is proved by Lemma 21. Naively, this algorithm requires 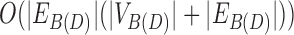 time for the traversals, and
time for the traversals, and 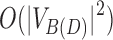 to mark all snarls. However, we can implement optimizations that improve on this behavior. First, we can also stop the breadth first search (BFS) traversals whenever they encounter a bridge edge. Lemmas 22 and 23 demonstrate that the portion of the BFS traversal after a bridge edge is redundant. This reduces the time required for the traversal to
to mark all snarls. However, we can implement optimizations that improve on this behavior. First, we can also stop the breadth first search (BFS) traversals whenever they encounter a bridge edge. Lemmas 22 and 23 demonstrate that the portion of the BFS traversal after a bridge edge is redundant. This reduces the time required for the traversal to 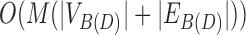 , where
, where 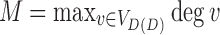 . In general,
. In general, 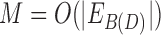 , so this does not improve over the worst case asymptotic bound. However, in many practical cases, M is approximately constant.
, so this does not improve over the worst case asymptotic bound. However, in many practical cases, M is approximately constant.
We can also reduce the total number of snarls we need to filter by neglecting to produce some snarls a priori. The quadratic bound on the number snarls is due to the fact that there is a bridge pair for all pairs of edges incident on a node in D(D). However, Lemma 17 shows that none of these bridge pairs will pass the filter. Accordingly, we can reduce the set of snarls we consider to only chain pairs and bridge pairs that project to nodes of degree 2 in D(D), which we call simple bridge pairs. This reduces the total number of snarls to 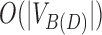 .
.
2.7. Ultrabubbles and cacti
Given Theorem 1, to determine the ultrabubbles in B(D), it is sufficient to check for each chain and bridge pair if the separated component is acyclic and contains no tips.
Using Theorem 3, we can restrict the search to snarls whose separated component does not contain a black bridge edge. This implies that we need only consider bridge pairs whose projection in D(D) is a node whose degree is two, and we call such bridge pairs simple. The number of simple bridge pairs must be less than the cardinality of D(D), and therefore the total number of chain pairs and simple bridge pairs is less than or equal to 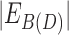 . Using D(D) and C(D), which both can be constructed in
. Using D(D) and C(D), which both can be constructed in 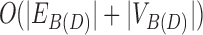 time, we can clearly enumerate the set of simple chain pairs and bridge pairs in
time, we can clearly enumerate the set of simple chain pairs and bridge pairs in 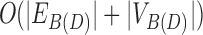 time.
time.
A simple algorithm to find the set of ultrabubbles enumerates all chain pairs and simple bridge pairs and checks for each the acyclicity and tipless requirement by using a DFS, and is therefore worst case 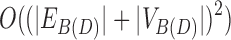 time.
time.
3. Results
We implemented algorithms to create the cactus graph and bridge forest for an arbitrary bidirected graph in the vg software package (http://github.com/vgteam/vg), where these structures are used to decompose graphs into sites for variant calling.
Families of compatible snarls are created by picking the longest path in the bridge graph of simple bridge pairs, making this the top-level chain. The subset of ultrabubbles can also be computed by running vg stats -u.
In this study, we present the results of running this decomposition on a graph for human chromosome 1 constructed from the (∼6.5 million) variant calls from phase 3 of the 1000 Genomes Project (Consortium et al., 2015). The graph contained 19,917,881 nodes and 26,782,661 edges, and the runtime was 23 minutes by using a maximum of 49G RAM on a single 2.27 GHz Intel Xeon core (4 minutes and 30G of RAM were spent loading the graph into memory, a process that can be made an order of magnitude more efficient by switching the implementation to use xg, vg's succinct representation).
Table 1 shows the relative proportion of each of these structures. The first three rows describe the top-level ultrabubble decomposition, which covers exactly every base in the input graph. The second three rows display the same statistics but for structures that are entirely contained within top-level ultrabubbles or snarls. The remaining rows describe the third and deepest nesting level, which is contained within second-level ultrabubbles or snarls. Every base within the graph is part of either a top-level chain, ultrabubble, or snarl in this decomposition.
Table 1.
Coverage Statistics for the Ultrabubble Decomposition of the Human Chromosome 1 Variant Graph
| Structure | Nesting level | Count | Coverage (bp) | Coverage (pct) |
|---|---|---|---|---|
| Chains | Top | 1 | 221,715,143 | 86.60 |
| Ultrabubbles | Top | 5,554,903 | 12,539,619 | 4.90 |
| Snarls | Top | 75 | 21,775,387 | 8.50 |
| Chains | Second | 919 | 20,594,450 | 8.04 |
| Ultrabubbles | Second | 533,252 | 1,199,777 | 0.47 |
| Snarls | Second | 0 | 0 | 0 |
| Chains | Third | 67 | 495 | 0.00 |
| Ultrabubbles | Third | 694 | 1623 | 0.00 |
| Snarls | Third | 0 | 0 | 0 |
bp, base pairs; pct, percent.
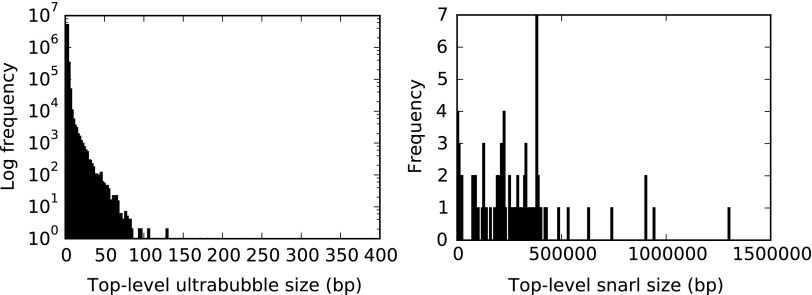
Figure 5 shows the size distribution of the top-level ultrabubble and snarl sizes. All but 22 top-level ultrabubbles (totaling 3251 bases) are 100 bases long or shorter. If we consider such sites “easy” to call, along with top-level chains, then we can assign roughly 91.5% of chromosome 1 into this category. Figure 6 displays three examples of such small ultrabubbles. The remaining 9.5% of cases are found in a small number of relatively large snarls.
FIG. 5.
Histograms of top-level ultrabubble and snarl sizes in number of bases, as found in the 1000 Genomes graph for chromosome 1.
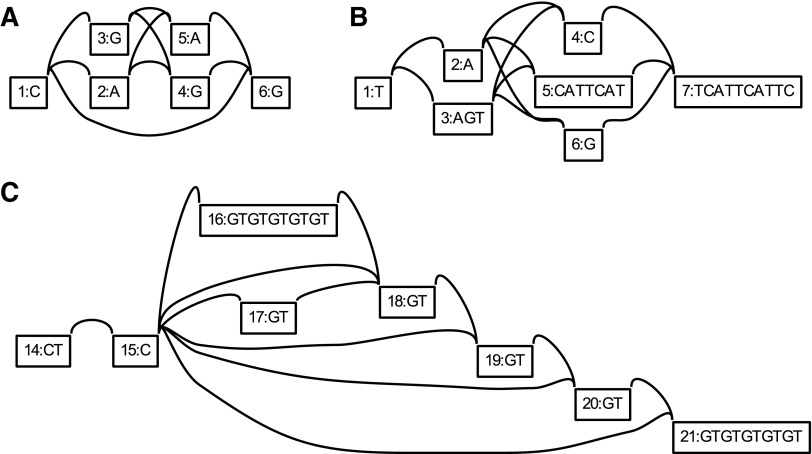
FIG. 6.
Ultrabubbles found in the 1000 Genomes-derived graph for chromosome 1. (A) Two adjacent SNPs inside a deletion (chr1:209,887,366). (B) A more complex combination of SNP and indel events (chr1:237,977,845). (C) Copy number changes in a GT repeat (chr1:1,200,943). SNP, single nucleotide polymorphism.
4. Discussion and Conclusion
We have presented a partial decomposition of a bidirected graph into a set of nested snarls and ultrabubbles. We believe this solves an important problem in using graphs for representing arbitrary genetic variations by defining a decomposition that determines sites and alleles.
As the decomposition is only partial, not all elements in a graph will necessarily fit into one of the ultrabubbles. However, we demonstrate that for an existing large library of variation (1000 Genomes), the large majority of sites are either invariant or described by simple, top-level ultrabubbles.
For bases outside of these easy sites, it is possible to imagine further subclassification. For example, classifying snarls that contain tips but are acyclic might define a useful class of subgraph that is common in some subproblems (e.g., sequence assembly). Some structures representing dense or overlapping collections of sequence polymorphisms, insertions, and deletions cannot be fully described by using nested ultrabubbles. We have previously shown that a generalization of the separability criterion for ultrabubbles can describe sites in these cases (Rosen et al., 2017). Similarly, characteristic structures representing genomic phenomena, such as inversions and translocations, are imaginable. Beyond our initial investigation, a more thorough evaluation of how much of a graph fits within a snarl, ultrabubble, or one of these more complex structures would be a useful exercise. We propose that the compatible family of snarls we constructed provides one path forward in this endeavor.
We can also envision that the nesting structure of snarls could play a powerful role in decomposing genotyping problems. Nested graph structures often arise from nested indels and substitutions.
In the context of assembly, various error correction algorithms have been proposed to remove graph elements and reduce the complexity of the graph. This increases the fraction of the graph that is contained within an ultrabubble structure. We foresee the cactus graph structure providing a useful basis for exploring such algorithms.
5. Appendix
5.1. Appendix 1
Lemma 3. A pair of vertices x, y are in the same component of B(D) if their projections are in the same component of C(D).
Proof. IF: Follows given that, by definition, no pair of vertices not connected in B(D) project to the same vertex in C(D). ONLY IF: Follows given that 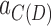 is a graph homomorphism from B(D) to C(D) and graph homomorphisms preverse connectedness.
is a graph homomorphism from B(D) to C(D) and graph homomorphisms preverse connectedness.
Lemma 4. For a subset of edges 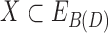 , if the removal of the projection of X disconnects C(D), then the removal of X disconnects B(D).
, if the removal of the projection of X disconnects C(D), then the removal of X disconnects B(D).
Proof. Follows given that graph homomorphisms preverse connectedness.
Lemma 5. The vertices in C(D) are the equivalence classes of 3-BEC in B(D).
Proof. Each pair of vertices B(D) that project to the same vertex in C(D) are either/or-both connected by a path of gray edges (and hence 3-BEC) or connected by at least three black-edge-disjoint paths (using Menger's theorem).
Lemma 6. A black edge in B(D) is a bridge edge if its projection in C(D) is a bridge edge.
Proof. Let 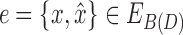 .
.
ONLY IF: Suppose e is a bridge. As e is a bridge, the vertices X reachable from x without visiting 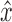 are black-edge connected only by e to the vertices
are black-edge connected only by e to the vertices 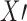 reachable from
reachable from 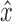 without visiting x. Given Lemma 5, it follows that the projection of X and the projection of
without visiting x. Given Lemma 5, it follows that the projection of X and the projection of 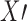 are disjoint, therefore the projection of e is a bridge.
are disjoint, therefore the projection of e is a bridge.
IF: Suppose e is not a bridge but its projection is. By definition, there exists a path in 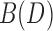 from x to
from x to 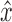 that does not include e. As
that does not include e. As 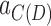 is a homomorphism, the projection of that path connects
is a homomorphism, the projection of that path connects 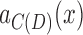 and
and 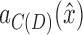 without traversing
without traversing 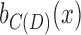 , implying that it is not a bridge, a contradiction.
, implying that it is not a bridge, a contradiction.
Lemma 7. A maximal set of vertices in C(D) is 2-EC if the union of its members is a 2-BEC equivalence class of vertices in B(D).
Proof. Delete the black bridge edges in B(D) and the bridge edges in C(D) to create 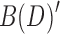 and
and 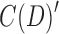 , respectively. Each component is
, respectively. Each component is 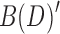 is, by definition, 2-BEC, and similarly each component in
is, by definition, 2-BEC, and similarly each component in 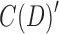 is 2-EC. The proof follows from Lemmas 3 and 6, by showing there exists a bijection between components in
is 2-EC. The proof follows from Lemmas 3 and 6, by showing there exists a bijection between components in 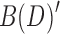 and
and 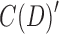 such that for each component X in
such that for each component X in 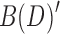 all the vertices in X project to vertices in the same component in
all the vertices in X project to vertices in the same component in 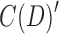 .
.
A cut pair is a pair of edges whose deletion disconnects the graph.
Lemma 8. A pair of edges in a 2-EC component of a cactus graph is a cut pair if both edges are contained within the same simple cycle.
Proof. By definition, a 2-EC component of a cactus graph is a set of simple cycles connected by articulation (cut) vertices. It is easily verified that such a graph is and can only be disconnected by a pair of edges if they occur within one such simple cycle.
Lemma 9. A pair of black edges 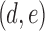 in a 2-BEC component X of B(D) is a cut pair if its projection is a cut pair in C(D).
in a 2-BEC component X of B(D) is a cut pair if its projection is a cut pair in C(D).
Proof. Let 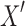 be a vertex-induced subgraph of the projection of X. By Lemma 7,
be a vertex-induced subgraph of the projection of X. By Lemma 7, 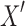 is a 2-EC component in C(D).
is a 2-EC component in C(D).
IF: If the deletion of the projection of d and e disconnects 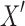 , then, using Lemma 4, the deletion of d and e disconnects X.
, then, using Lemma 4, the deletion of d and e disconnects X.
ONLY IF: If the projections of d and e are not a cut pair, by the definition of a cactus graph and Lemma 8, the projections of d and e in 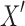 are each members of two distinct simple cycles. If the projection of d (similarly e) were a self-loop, then its endpoints are 3-BEC, implying that after the deletion of d and e its endpoints remain connected. This is impossible if the deletions of d and e disconnect the 2-EC component, hence each simple cycle containing the projection of d or e has length >1. For any pair of distinct vertices x, y in B(D) that project to the same vertex in C(D), there exists a path in B(D) that connects them that excludes their incident black edges, because by Lemma 5 they are 3-BEC, and are therefore connected either by a path of gray edges or by Menger's theorem, connected by at least three edge disjoint paths containing black edges. From this observation, it is easily verified that the endpoints of d (and similarly e) must be connected by a path Y in B(D) that includes the black edges that project to the simple cycle containing d, in the order of the cycle, and that excludes both d and e. This implies that the endpoints of d (similarly e) remain connected after the deletion of d and e, contradicting the claim that they are a cut pair.
are each members of two distinct simple cycles. If the projection of d (similarly e) were a self-loop, then its endpoints are 3-BEC, implying that after the deletion of d and e its endpoints remain connected. This is impossible if the deletions of d and e disconnect the 2-EC component, hence each simple cycle containing the projection of d or e has length >1. For any pair of distinct vertices x, y in B(D) that project to the same vertex in C(D), there exists a path in B(D) that connects them that excludes their incident black edges, because by Lemma 5 they are 3-BEC, and are therefore connected either by a path of gray edges or by Menger's theorem, connected by at least three edge disjoint paths containing black edges. From this observation, it is easily verified that the endpoints of d (and similarly e) must be connected by a path Y in B(D) that includes the black edges that project to the simple cycle containing d, in the order of the cycle, and that excludes both d and e. This implies that the endpoints of d (similarly e) remain connected after the deletion of d and e, contradicting the claim that they are a cut pair.
5.2. Appendix 2
Lemma 10. Each snarl 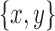 in B(D) is either a chain pair or a bridge pair.
in B(D) is either a chain pair or a bridge pair.
Proof. Using Lemma 3, both x and y must project to a vertex in the same component of C(D) as they are connected in B(D).
Let d and e be the black edges incident with x and y, respectively. If d is a bridge, then e must be a bridge, or else, by definition, e connects two vertices in a 2-EC component X, the removal of d and e cannot therefore disconnect X, and therefore y and 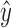 , violating the snarl separation criteria. Using Lemma 6, in this case the projections of d and e must, therefore, also be bridges. If both d and e are bridge edges but x and y do not project to the same vertex in D(D) (and are, therefore, not a bridge pair), there exists an intermediate bridge edge
, violating the snarl separation criteria. Using Lemma 6, in this case the projections of d and e must, therefore, also be bridges. If both d and e are bridge edges but x and y do not project to the same vertex in D(D) (and are, therefore, not a bridge pair), there exists an intermediate bridge edge 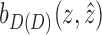 on the path between
on the path between 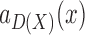 and
and 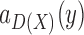 . The deletion d, e and
. The deletion d, e and 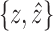 for B(D) disconnects B(D) into distinct components: One contains x and z, one contains
for B(D) disconnects B(D) into distinct components: One contains x and z, one contains 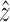 and y, one contains
and y, one contains 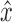 , and one contains
, and one contains 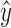 . This implies that
. This implies that 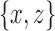 and
and 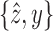 each fulfill the separation criteria, contradicting the minimality of
each fulfill the separation criteria, contradicting the minimality of 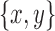 .
.
If d and e are not bridges, both must be in the same 2-BEC component or contradict the separation criteria, by the same reasoning as earlier. In this case, Lemma 7 implies that both d and e must project edges in the same 2-EC component in C(D). Lemmas 8 and 9 further imply that they must project to edges in the same simple cycle. If x and y do not project to the same vertex in C(D) (and are, therefore, not a chain pair), then there exists an intermediate black edge 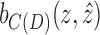 on the path between
on the path between 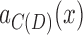 and
and 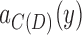 that excludes
that excludes  and
and 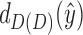 . As with the case that both d and e were bridge edges, this similarly contradicts the minimality of
. As with the case that both d and e were bridge edges, this similarly contradicts the minimality of 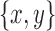 .
.
Lemma 11. Each chain pair or bridge pair 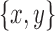 in B(D) is a snarl.
in B(D) is a snarl.
Proof. Lemmas 4 and 8 imply that 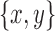 meet the separation criteria. It remains to prove that
meet the separation criteria. It remains to prove that 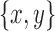 is minimal. If
is minimal. If 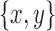 is not minimal, then there must exist an intermediate edge
is not minimal, then there must exist an intermediate edge 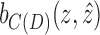 on a path between
on a path between 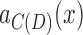 and
and 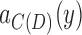 that excludes
that excludes 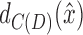 and
and 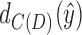 , and that, using Lemma 10, forms chain or bridge pairs with
, and that, using Lemma 10, forms chain or bridge pairs with 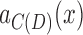 and
and 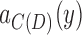 . As
. As 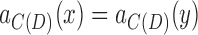 if
if 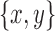 is a chain pair, or
is a chain pair, or 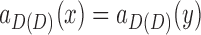 if
if 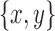 is a bridge pair, this is clearly impossible.
is a bridge pair, this is clearly impossible.
5.3. Appendix 3
In this section, we prove Theorems 2 and 3, which characterize a sufficient condition to produce a family of compatible snarls. We begin with two useful lemmas.
Lemma 12. Let 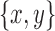 be a snarl with snarl subgraph X. If u is a node in X and v is a node that is not in X, then any path from u to v includes the black edge incident on x or the black edge incident on y.
be a snarl with snarl subgraph X. If u is a node in X and v is a node that is not in X, then any path from u to v includes the black edge incident on x or the black edge incident on y.
Proof. Suppose a path exists that does not include either of the black edges incident on x and on y. Then u is not disconnected from v after deleting these edges, which contradicts the separability of 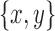 .
.
Lemma 13. Let 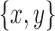 be a snarl with subgraph X. Then there exists a path from u to either x or y that includes neither the black edge incident on x nor the black edge incident on y if u is in X.
be a snarl with subgraph X. Then there exists a path from u to either x or y that includes neither the black edge incident on x nor the black edge incident on y if u is in X.
Proof. First assume u is in X. Some path exists from u to either x or y, else u is not in the same connected component as x and y. Consider the shortest such path. Without loss of generality, assume this path is between u and x. Suppose the black edge incident on x or the black edge incident on y occurs somewhere along the path. Without loss of generality, assume it is the black edge incident on x. By Lemma 1, x or y must occur in the prefix of the path between u and 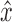 . This implies that the path was not the shortest, which is a contradiction. Therefore, there exists a path from u that contains neither the black edge incident on x nor the black edge incident on y.
. This implies that the path was not the shortest, which is a contradiction. Therefore, there exists a path from u that contains neither the black edge incident on x nor the black edge incident on y.
Next assume without loss of generality that a path exists from u to x that includes neither the black edge incident on x nor the black edge incident on y. This path is preserved after removing these two edges. This implies that u is in the same connected component as x (and hence also y) in the resulting graph, so u is in X.
Let 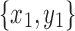 and
and 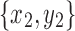 be two snarls with snarl subgraphs X1 and X2 respectively. We will say that
be two snarls with snarl subgraphs X1 and X2 respectively. We will say that 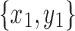 splits
splits
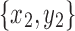 if either a) x2 is in X1 but y2 is not in X1 or b) y2 is in X1 but x2 is not in X1. This condition clearly violates compatibility.
if either a) x2 is in X1 but y2 is not in X1 or b) y2 is in X1 but x2 is not in X1. This condition clearly violates compatibility.
Lemma 14. Let 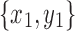 and
and 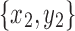 be snarls with snarl subgraphs X1 and X2. If
be snarls with snarl subgraphs X1 and X2. If 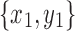 splits
splits 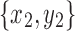 , then x1 and y1 are in X2.
, then x1 and y1 are in X2.
Proof. We will proceed by showing that all other cases lead to contradictions. Without loss of generality, assume x2 is in X1 and y2 is not in X1.
Case I: x1 and y1 are not in X2
Consider the set of paths from x2 to y2 that do not pass through 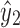 or
or 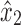 . This set is nonempty, else X2 is disconnected. By Lemma 12, any such path must include x1 or y1, which would imply that x1 is in X2 or y1 is in X2, respectively, by Lemma 13. This violates the assumption of the case, so this case is contradictory.
. This set is nonempty, else X2 is disconnected. By Lemma 12, any such path must include x1 or y1, which would imply that x1 is in X2 or y1 is in X2, respectively, by Lemma 13. This violates the assumption of the case, so this case is contradictory.
Case II: x1 is in X2, and y1 is not in X2
Any path from x1 to y1 that does not include the black edges incident on x and y cannot include y2, else y2 is in X1 by Lemma 13. Therefore, it must contain the black edge incident on x2 by Lemma 12. Without loss of generality, this implies that 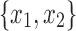 and
and 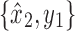 are separable, which violates the minimality of
are separable, which violates the minimality of 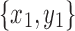 . Thus, this case is contradictory as well.
. Thus, this case is contradictory as well.
Case III: y1 is in X2, and x1 is not in X2
Same as Case II.
This proves the lemma.
Lemma 15. Let 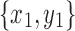 and
and 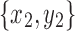 be snarls with snarl subgraphs X1 and X2. If
be snarls with snarl subgraphs X1 and X2. If 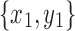 splits
splits 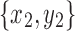 , then X1 contains a black bridge edge.
, then X1 contains a black bridge edge.
Proof. Without loss of generality, assume x2 is in X1 and y2 is not in X1. Then, there exists at least one path from 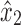 to either x1 or y1, else X1 is disconnected. By Lemma 14, x1 and y1 are in X2, so all such paths must include the black edge incident on x2 or the black edge incident on y2 by Lemma 12. Since y2 is not in X1, all paths from x1 or y1 to
to either x1 or y1, else X1 is disconnected. By Lemma 14, x1 and y1 are in X2, so all such paths must include the black edge incident on x2 or the black edge incident on y2 by Lemma 12. Since y2 is not in X1, all paths from x1 or y1 to 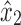 in X1 must include the black edge incident on x2. Therefore, the black edge incident on x2 is a bridge edge by Menger's theorem.
in X1 must include the black edge incident on x2. Therefore, the black edge incident on x2 is a bridge edge by Menger's theorem.
There are also cases that violate compatibility without splitting a snarl. The following lemmas characterize these cases.
Lemma 16. Let 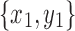 and
and 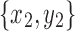 be snarls with distinct boundaries in a connected graph
be snarls with distinct boundaries in a connected graph 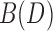 whose snarl subgraphs are X1 and X2. If x1 and y1 are in X2, and x2 and y2 are in X1, then
whose snarl subgraphs are X1 and X2. If x1 and y1 are in X2, and x2 and y2 are in X1, then 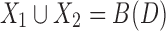 .
.
Proof. Let u be an arbitrary node that is not in X1 be arbitrary. There exists at least one path from u to a node in X1, else B(D) is not connected. Let p1 be the shortest such path. Clearly, no node from X1 occurs in p1 except at its terminus. In particular, p1 does not contain either 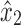 or
or 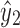 . By Lemma 12, p1 includes x1 or y1, so one of these must be the terminal node. Without loss of generality, assume it is x1. Since x1 is in X2, there also exists a path p2 from
. By Lemma 12, p1 includes x1 or y1, so one of these must be the terminal node. Without loss of generality, assume it is x1. Since x1 is in X2, there also exists a path p2 from 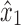 to either x2 or y2 that does not include
to either x2 or y2 that does not include 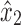 or
or 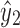 by Lemma 13. Note that
by Lemma 13. Note that 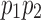 is a path from u to either x2 or y2 that does not include the black edges incident on x2 and y2. Thus, u is in X2 by Lemma 13. This implies
is a path from u to either x2 or y2 that does not include the black edges incident on x2 and y2. Thus, u is in X2 by Lemma 13. This implies 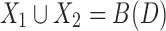 .
.
Lemma 17. Let 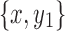 and
and 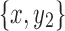 be snarls with snarl subgraphs X1 and X2. If
be snarls with snarl subgraphs X1 and X2. If 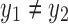 , then both X1 and X2 contain a black bridge edge.
, then both X1 and X2 contain a black bridge edge.
Proof. Suppose y2 is not in X1. Then, all paths from y2 to x must include the black edge incident on x or the black edge incident on y1 by Lemma 12. There exists at least one path between x and y2 in X2, which cannot include the black edge incident on x. Therefore, all paths between y2 and x must include the black edge incident on y1. This implies without loss of generality that 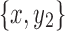 and
and 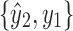 are separable, which violates the minimality of
are separable, which violates the minimality of 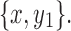 Thus, y2 is in X1. Note that the black edge incident on x is not in X1. Therefore, removing the black edge incident on y2 from X1 disconnects x from
Thus, y2 is in X1. Note that the black edge incident on x is not in X1. Therefore, removing the black edge incident on y2 from X1 disconnects x from 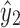 because of the separability of
because of the separability of 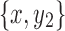 . Thus, the black edge incident on y2 is a bridge edge in X1. Similarly, the black edge incident on y1 is a bridge edge in X2.
. Thus, the black edge incident on y2 is a bridge edge in X1. Similarly, the black edge incident on y1 is a bridge edge in X2.
Finally, we establish the relationship between pairs of snarls that allow for compatibility.
Lemma 18. Let 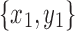 and
and 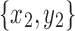 be snarls with snarl subgraphs X1 and X2. If both x2 and y2 are in X1, and both x1 and y1 are not in X2, then
be snarls with snarl subgraphs X1 and X2. If both x2 and y2 are in X1, and both x1 and y1 are not in X2, then 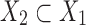 .
.
Proof. Let u be an arbitrary node in X2. There exists a path p1 from u to x1 or y1 that consists of only nodes in X2, else X2 is not connected. In particular, 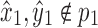 , else x1 or y1 would be in X2. There also exists a path p2 from x2 to x1 that includes neither
, else x1 or y1 would be in X2. There also exists a path p2 from x2 to x1 that includes neither 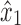 nor
nor 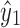 by Lemma 13. The path
by Lemma 13. The path 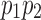 connects u to x1 and includes neither
connects u to x1 and includes neither 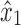 nor
nor 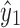 . Thus, u is in X1 by Lemma 13.
. Thus, u is in X1 by Lemma 13.
Lemma 19. Let 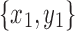 and
and 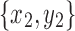 be snarls with snarl subgraphs X1 and X2. If x2 and y2 are not in X1, and x1 and y1 are not in X2, then X1 and X2 are disjoint.
be snarls with snarl subgraphs X1 and X2. If x2 and y2 are not in X1, and x1 and y1 are not in X2, then X1 and X2 are disjoint.
Proof. Let u be an arbitrary node in X1, and let p be any path from u to x2 or y2. By Lemma 12, p includes x1 or y1. Thus, by Lemma 12, p includes 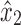 or
or 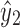 . Since p was chosen arbitrarily, this implies u is not in X2 by Lemma 13. Therefore, X1 and X2 are disjoint.
. Since p was chosen arbitrarily, this implies u is not in X2 by Lemma 13. Therefore, X1 and X2 are disjoint.
Taken together, these results yield the sufficient condition for compatibility that we set out to prove.
Theorem 4. In a connected biedged graph with at least one black bridge edge, the family of snarls whose subgraphs have no black bridge edges is compatible.
Proof. Let 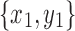 and
and 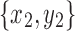 be arbitrary snarls with snarl subgraphs X1 and X2 such that neither subgraph contains a black bridge edge. By Lemma 15, neither snarl splits the other. By Lemma 17, the two snarls cannot share a boundary node. Therefore, we also cannot have both x1 and y1 in X2, and x2 and y2 in X1, else either X1 or X2 must contain the graph's black bridge edge by Lemma 16. This leaves three cases:
be arbitrary snarls with snarl subgraphs X1 and X2 such that neither subgraph contains a black bridge edge. By Lemma 15, neither snarl splits the other. By Lemma 17, the two snarls cannot share a boundary node. Therefore, we also cannot have both x1 and y1 in X2, and x2 and y2 in X1, else either X1 or X2 must contain the graph's black bridge edge by Lemma 16. This leaves three cases:
1. x1 and y1 are in X2, and x2 and y2 are not in X1
2. x1 and y1 are not in X2, and x2 and y2 are in X1
3. x1 and y1 are not in X2, and x2 and y2 are not in X1
In the first two cases, one subgraph is nested in the other by Lemma 18. In the last case, the subgraphs are disjoint by Lemma 19. Therefore, 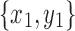 and
and 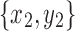 are compatible.
are compatible.
We will now move on to proving that ultrabubbles are included in the family of snarls with no black bridge edges.
Lemma 20. Let u be a terminal of a black bridge edge whose removal separates a graph B(D) into connected components B1 and B2 with u in B1 and 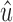 in B2. Then, all snarls
in B2. Then, all snarls 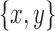 have either both x and y in B1 or both x and y in B2.
have either both x and y in B1 or both x and y in B2.
Proof. Suppose without loss of generality that x is in B1 and y is in B2. All paths between x and y include the black edge incident on u. Therefore, 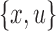 and
and 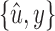 are separable. This contradicts the minimality of
are separable. This contradicts the minimality of 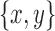 .
.
Theorem 3. No ultrabubble contains a black bridge edge in its subgraph.
Proof. Let 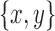 be an ultrabubble with subgraph X. Suppose X contains a black bridge edge with terminals u and
be an ultrabubble with subgraph X. Suppose X contains a black bridge edge with terminals u and 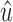 . Removing this edge separates X into connected components X1 and X2 with u in X1 and
. Removing this edge separates X into connected components X1 and X2 with u in X1 and 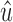 in X2. By Lemma 20, we may assume without loss of generality that x and y are in X1.
in X2. By Lemma 20, we may assume without loss of generality that x and y are in X1.
Since 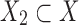 , there are no cyclic walks in X2. Moreover, there is at least one edge in X2, else the black bridge edge is a tip. Let w be the longest biedged walk starting from
, there are no cyclic walks in X2. Moreover, there is at least one edge in X2, else the black bridge edge is a tip. Let w be the longest biedged walk starting from 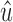 in X2. This walk must exist, since walks of unbounded length could only exist if there is a cyclic biedged walk. Moreover, w is not empty since X2 contains at least one edge.
in X2. This walk must exist, since walks of unbounded length could only exist if there is a cyclic biedged walk. Moreover, w is not empty since X2 contains at least one edge.
Suppose the final edge in w is gray. Since x and y are not in X2, one endpoint of this gray edge must have no black edge incident on it in the full graph, else w could be lengthened. This violates the definition of a bidirected graph. Therefore, the final edge in w must be black. However, this implies that one endpoint of this black edge has no gray edges incident on it, else w could be lengthened. That is, the black edge is a tip, which contradicts the definition of ultrabubble. Therefore, X does not contain a black bridge edge.
Lemma 21. Let 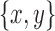 be a snarl with subgraph X. Further, let u be any node, and let p be the shortest path from u to either x or y and q be the shortest path from u to either
be a snarl with subgraph X. Further, let u be any node, and let p be the shortest path from u to either x or y and q be the shortest path from u to either 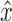 or
or 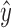 . If u is in X, then
. If u is in X, then 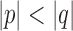 , and if u is not in X, then
, and if u is not in X, then 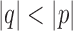 .
.
Proof. First assume that u is in X. Then, q contains x or y by Lemma 12. The subpath up to this point is a path between u and either x or y that is strictly shorter than q. Therefore, 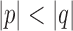 . Similarly, if u is in X, then
. Similarly, if u is in X, then 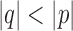 .
.
Lemma 22. Let 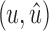 be a black bridge edge that separates a graph
be a black bridge edge that separates a graph 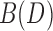 into connected components B1 and B2 with u in B1 and
into connected components B1 and B2 with u in B1 and 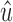 in B2. Further, let
in B2. Further, let 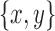 be a snarl subgraph X such that (1) x is in B2 and (2)
be a snarl subgraph X such that (1) x is in B2 and (2) 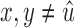 . Then, X contains
. Then, X contains 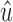 if X contains w.
if X contains w.
Proof. By Lemma 20, y is in B2 as well as x. Note that if 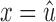 or
or 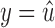 , then the claim is verified trivially, so we may focus on the case where
, then the claim is verified trivially, so we may focus on the case where 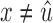 and
and 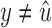 . In this case, the black edges
. In this case, the black edges 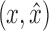 and
and 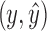 must be in B2.
must be in B2.
First, assume 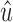 is in X. There exists a path p1 from w to u in B1. Note that this implies that p1 contains neither
is in X. There exists a path p1 from w to u in B1. Note that this implies that p1 contains neither 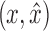 nor
nor 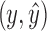 . There also exists a path p2 from
. There also exists a path p2 from 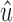 to x or y that includes neither
to x or y that includes neither 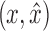 nor
nor 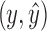 by Lemma 13. Thus,
by Lemma 13. Thus, 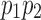 is a path from w to x or y that includes neither
is a path from w to x or y that includes neither 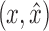 nor
nor 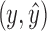 , which implies that w is in X by Lemma 13.
, which implies that w is in X by Lemma 13.
Next, assume w is in X. There exists a path p from w to x or y that includes neither 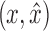 nor
nor 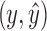 by Lemma 13. Since x and y are in B2, this path must include
by Lemma 13. Since x and y are in B2, this path must include 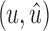 , which means that it includes a subpath from
, which means that it includes a subpath from 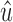 to x or y. Therefore,
to x or y. Therefore, 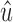 is in X by Lemma 13.
is in X by Lemma 13.
Lemma 23. Let 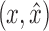 be a black bridge edge whose removal separates a graph B(D) into connected components B1 and B2 with x in B1 and
be a black bridge edge whose removal separates a graph B(D) into connected components B1 and B2 with x in B1 and 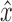 in B2. If
in B2. If 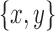 is a snarl with subgraph X, then
is a snarl with subgraph X, then 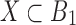 .
.
Proof. X consists of only nodes that can be reached from x without crossing 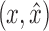 by Lemma 13. Therefore,
by Lemma 13. Therefore, 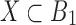 .
.
Acknowledgments
This work was supported by the National Human Genome Research Institute of the National Institutes of Health under Award Number 5U54HG007990 and grants from the W.M. Keck Foundation and the Simons Foundation. This work benefited from numerous conversations with David Haussler and Daniel Zerbino.
Author Disclosure Statement
No competing financial interests exist.
References
- 1000 Genomes Project Consortium, Auton A., Brooks L.D., et al. 2015. A global reference for human genetic variation. Nature. 526, 68–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alekseyev M.A., and Pevzner P.A. 2009. Breakpoint graphs and ancestral genome reconstructions. Genome Res. 19, 943–957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birmelé E., Crescenzi P., Ferreira R., et al. 2012. Efficient bubble enumeration in directed graphs, 118–129. In Calderón-Benavides L., González-Caro C., Chávez E., et al., eds. String Processing and Information Retrieval: 19th International Symposium, SPIRE 2012, Cartagena de Indias, Colombia, October21–25, 2012 Springer: Berlin, Heidelberg [Google Scholar]
- Brankovic L., Iliopoulos C.S., Kundu R., et al. 2015. Linear-time superbubble identification algorithm for genome assembly. Theor. Comput. Sci. 609, 374–383 [Google Scholar]
- de Bruijn N.G. 1946. A combinatorial problem. Proceedings of the Section of Sciences of the Koninklijke Nederlandse Akademie van Wetenschappen te Amsterdam 49, 758–764 [Google Scholar]
- Edmonds J., and Johnson E.L. 1970. Matching: A Well-Solved Class of Integer Linear Programs, 27–30. Springer: Berlin, Heidelberg [Google Scholar]
- Harary F., and Uhlenbeck G.E. 1953. On the number of Husimi trees: I. Proc. Natl. Acad. Sci. USA. 39, 315–322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iliopoulos C.S., Kundu R., Mohamed M., et al. 2016. Popping Superbubbles and Discovering Clumps: Recent Developments in Biological Sequence Analysis, 3–14. Springer International Publishing, Cham [Google Scholar]
- Medvedev P., and Brudno M. 2009. Maximum likelihood genome assembly. J. Comput. Boil. 16, 1101–1116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers E.W. 2005. The fragment assembly string graph. Bioinformatics. 21(Suppl 2), ii79–ii85 [DOI] [PubMed] [Google Scholar]
- Onodera T., Sadakane K., and Shibuya T. 2013. Detecting superbubbles in assembly graphs, 338–348. In Algorithms in Bioinformatics. Eds: Darling A., and Stoye J. Springer: Berlin, Heidelberg [Google Scholar]
- Paten B., Diekhans M., Earl D., et al. 2011. Cactus graphs for genome comparisons. J. Comput. Biol. 18, 469–481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pevzner P. 2000. Computational Molecular Biology: An Algorithmic Approach. MIT Press: Cambridge, MA [Google Scholar]
- Pevzner P.A., Tang H., and Waterman M.S. 2001. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. USA. 98, 9748–9753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen Y., Eizenga J., and Paten B. 2017. Describing the Local Structure of Sequence Graphs, 24–46. Springer International Publishing, Cham [Google Scholar]
- Sung W.-K., Sadakane K., Shibuya T., et al. 2015. An O(m log m)-time algorithm for detecting superbubbles. IEEE/ACM Trans. Comput. Biol. Bioinform. 12, 770–777 [DOI] [PubMed] [Google Scholar]
- Zerbino D.R., and Birney E. 2008. Velvet: Algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 18, 821–829 [DOI] [PMC free article] [PubMed] [Google Scholar]