Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Jul 9;3(7):7555–7566. doi: 10.1021/acsomega.8b00721

A Comparative Study of Modern Homology Modeling Algorithms for Rhodopsin Structure Prediction

Dmitrii M Nikolaev †, Andrey A Shtyrov †, Maxim S Panov ‡, Adeel Jamal §, Oleg B Chakchir †, Vladimir A Kochemirovsky ‡, Massimo Olivucci ∥, Mikhail N Ryazantsev ‡,⊥,*
PMCID: PMC6068592  PMID: 30087916

Abstract

graphic file with name ao-2018-00721z_0004.jpg

Rhodopsins are seven α-helical membrane proteins that are of great importance in chemistry, biology, and modern biotechnology. Any in silico study on rhodopsin properties and functioning requires a high-quality three-dimensional structure. Due to particular difficulties with obtaining membrane protein structures from the experiment, in silico prediction of the three-dimensional rhodopsin structure based only on its primary sequence is an especially important task. For the last few years, significant progress was made in the field of protein structure prediction, especially for methods based on comparative modeling. However, the majority of this progress was made for soluble proteins and further investigations are needed to achieve similar progress for membrane proteins. In this paper, we evaluate the performance of modern protein structure prediction methodologies (implemented in the Medeller, I-TASSER, and Rosetta packages) for their ability to predict rhodopsin structures. Three widely used methodologies were considered: two general methodologies that are commonly applied to soluble proteins and a methodology that uses constraints that are specific for membrane proteins. The test pool consisted of 36 target-template pairs with different sequence similarities that was constructed on the basis of 24 experimental rhodopsin structures taken from the RCSB database. As a result, we showed that all three considered methodologies allow obtaining rhodopsin structures with the quality that is close to the crystallographic one (root mean square deviation (RMSD) of the predicted structure from the corresponding X-ray structure up to 1.5 Å) if the target-template sequence identity is higher than 40%. Moreover, all considered methodologies provided structures of average quality (RMSD < 4.0 Å) if the target-template sequence identity is higher than 20%. Such structures can be subsequently used for further investigation of molecular mechanisms of protein functioning and for the development of modern protein-based biotechnologies.

Introduction

Obtaining a three-dimensional protein structure is one of the central tasks of structural biology. Modern diffraction and NMR methodologies allow acquiring structures of quality that varies from average to high. However, experimental approaches are not quick and cheap, and even though the number of experimentally obtained structures is constantly increasing, they are limited. The lack of experimental structures is especially true for membrane proteins, for which crystallization is challenging. These difficulties call for the development of reliable computational structure prediction methods (for review, see refs (1−6)). In general, three different approaches exist: ab initio modeling, threading, and homology modeling. In the first method, ab initio modeling, the structure is predicted based on physical principles.7 Even though this approach is the most general, it is not widely applicable because of its low accuracy and significant computational resources that are required to investigate the extensive conformational space of protein. Thus, up to now, only the structures of small proteins have been successfully predicted using this approach.8 The second approach, threading, is based on two principles: (1) close primary sequences fold into similar structures9,10 and (2) the number of possible structural folds of proteins is finite,11 which means that even nonhomologous proteins can have similar structures. In this approach the amino acid sequence of the target protein is “threaded” onto the structure of a suitable template, then local structure rearrangement and optimization are performed.12,13 Threading is usually not used per se, but it is combined with other computational techniques.4 In the third and most successful method, homology (or comparative) modeling, the structure of the protein is built based on the three-dimensional structure of an evolutionally close template protein.14 Close homologues can be used as the “starting approximation” for further refinement and model prediction.

The pipeline of homology modeling is usually divided into four steps: (1) finding the best template; (2) target-template sequence alignment; (3) structure building; and (4) model evaluation. Many statistically-driven and physically-driven alignment algorithms have been proposed to increase the target-template alignment quality.15,16

For the structure building step, three following approaches are mostly used: rigid-body reassembly, fragment matching, and satisfaction of spatial restraints. In the rigid-body reassembly, the parts of the template that are similar to the parts of the target protein are exerted and assembled in a proper order.4 In the segment matching approach, Cα atoms of the shared (from alignment) residues consist of the framework that is subsequently gradually complemented with suitable fragments taken from the database.17 In the satisfaction of spatial restraints approach, two types of geometrical restraints are simultaneously introduced: template-derived and stereochemical database-derived.18,19 More specifically, the first approximation of the target structure is initially obtained by some approximate method. Then the target structure is reorganized by the minimization of violations of all restraints.

Modern homology modeling algorithms adopt a combination of structure building approaches.4 To evaluate the quality/limits of such structure prediction protocols, different benchmark tests and competitions are made.20−22 The major competitions in this field are critical assessment of protein structure prediction (CASP)23−25 and continuous automated model evaluation (CAMEO).26 However, these benchmarks have been mainly developed for soluble proteins. Indeed, the evaluation of homology modeling of membrane proteins, which are the class of proteins of interest here, have not been extensively developed. A straightforward approach to membrane protein structure prediction is to transfer methodologies that have been developed for soluble proteins without changes. This approach has to be validated by extensive benchmarks. On the other hand, methods taking into account the specific membrane protein features are emerging and they also have to be tested.27,28

In the present study, we performed a benchmark investigation of several modern protein structure prediction methodologies (both developed for soluble proteins and membrane-specific protocols). As the test pool, we chose proteins from the rhodopsin family.29 Rhodopsins are widely spread in nature and are of vital importance for modern technologies such as optogenetics,30 live cell imaging,31 and for the development of new biological photoswitches.32,33 Computational chemistry can help in the development of these fields by providing rhodopsin models capable of predicting specific properties or functions. For instance, quantum mechanics/molecular mechanics (QM/MM) models have the capacity to simulate spectroscopic and reactivity properties.34−37 For this reason, there is presently an interest in the automatic construction of rhodopsin QM/MM models. One of these methodologies (automatic rhodopsin modeling, ARM) has been recently reported in the literature by one of the authors.38 However, an automatic generation requires high-quality three-dimensional structures as an input. Consequently, given the limited number of experimentally determined structures available for such family (only 23 crystallographic and 1 NMR unique structures), homology modeling techniques become extremely important for developing these types of technologies.

As reported below, we investigated several modern homology modeling approaches. Accordingly, the present report begins by evaluating the impact of different algorithms for protein sequence alignment (step 2 in the homology model building pipeline) on the quality of the final model. Then we continue by evaluating the performance of three structure building algorithms implemented in the Medeller, I-TASSER, and Rosetta packages (step 3 in the same pipeline). For globular proteins, Modeller,19 I-TASSER, and Rosetta demonstrated excellent performance in CASP or CAMEO competitions. Therefore, for our tests we choose Medeller (that is a membrane-oriented analogue of the approach implemented in Modeller), I-TASSER, and Rosetta with membrane-specific terms included in the force field.

To unambiguously evaluate the quality of the final homology models, we decided to produce homology models of rhodopsins whose structure has been determined experimentally. In this way, we could compare the resulting model with the corresponding experimental structure using common metrics, such as the root mean square deviation (RMSD) and global distance test-high accuracy (GDT-HA). Furthermore, to further evaluate the quality of modeling from an atomistic point of view, we carry out a comparative analysis of the conformation of the amino acid side chains forming the rhodopsin active site. Accordingly, we form pairs of experimental structures and use one member of the pair as the template and the other member as a target and vice versa. Thus, for each pair we test two generated homology models. As we detail below, during the present study we predicted 252 homology models for cases when target-template sequence identity ranged from 15 to 92%. The results show that the right choice of template and methodology allows constructing structures of rhodopsins with quality close to the crystallographic one.

Methods

All experimental protein structures studied in this work were taken from the RCSB database.39

Alignment

Three algorithms of pairwise sequence alignment of target and template (1–3, below) and two algorithms of multiple sequence alignment (4, 5) were tested:

  • 1.

    The algorithm combines the environment-specific substitution matrices and gap penalties with evolutionary information. The protein transmembrane (TM) region is predicted from the template structure by taking into account solvent accessibility, S–S bonds, and hydrogen bonds for each residue. This algorithm is implemented in the MP-T program.40,41

  • 2.

    The algorithm exploits the Needleman–Wunsch scheme42 supplemented with specific membrane protein information in the form of hydrophobicity profiles and template structure topology. This algorithm is implemented in the AlignMe suite.43,44

  • 3.

    The algorithm combines evolutionary information about the target and the template proteins in the form of sequence profiles45 and uses information on the template secondary structure and hydrophobicity predictions (based on the Needleman–Wunsch algorithm). This alignment is implemented in the MUSTER program.46

  • 4.

    The algorithm is based on an application of hidden Markov models47 and does not use any specific membrane protein information. This algorithm is implemented in the Clustal Omega program.48

  • 5.

    The algorithm is based on the classical progressive alignment protocol49 and uses extra information about the topology and location of the transmembrane region in proteins. This algorithm is implemented in the PralineTM program.50

Structure Building

Three algorithms of structure building were tested:

  • 1.

    The algorithm builds the structure under the guidance of artificial constraints. The central part of the template transmembrane region is considered highly conserved and it is used as the model core. Then the residues are added one by one under specific rules which have the form of membrane-specific substitution scores.28,51 The flexible regions are built by a segment matching approach—the fitting fragments are chosen from the database of crystallographic structures and the energy is minimized after the insertion.52,53 This method is implemented in the Medeller program.

  • 2.

    The algorithm uses a combination of different approaches. The framework is built by a rigid-body reassembly approach; the remaining parts are built ab initio. Two rounds of replica-exchange Monte Carlo modeling54−56 are performed for the initial model under the guidance of knowledge-based energy function combined with spatial constraints and the term considering the hydrogen bond network. The models from the first round are clustered and the second round starts from the centroid models of each cluster. This algorithm is implemented in the I-TASSER suite.57,58

  • 3.

    Also, this algorithm uses the combination of different approaches. The framework is built by a rigid-body reassembly approach; the remaining parts are built ab initio. Two rounds of Monte Carlo modeling are performed for the initial model under the guidance of a physically realistic energy function combined with spatial constraints. The second round starts from the lowest-energy model from the first round. For membrane proteins, the physically realistic part of energy function changes to favor the membrane nature. The algorithm is implemented in the Rosetta suite.59,60

Results and Discussion

Clustering of Rhodopsins with Known Three-Dimensional Structures

We analyzed the RCSB database39 and found 24 unique rhodopsin structures (not including mutants, photocycle intermediates, anion-free halorhodopsins, and halorhodopsins with anions different from Cl–). If the database contains several structures for the same protein, the structures of the highest quality (Jan, 2017) were used. To cluster these proteins, we examined all protein pairs. Two proteins were considered to belong to the same cluster if the value of their sequence identity was higher than 40% (the sequence identity between two proteins is defined as the percentage of identical amino acids in the corresponding pairwise sequence alignment). Since the identity may critically depend on the sequence alignment, we tested the MP-T, AlignMe, and MUSTER algorithms to align each pair. Because all algorithms gave similar sequence identity values, we used the results of AlignMe in the clustering procedure.

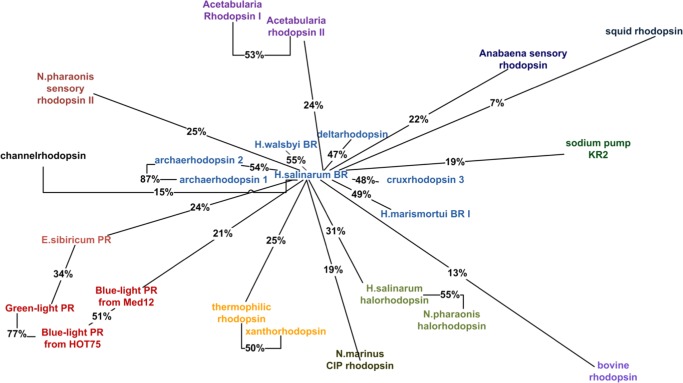
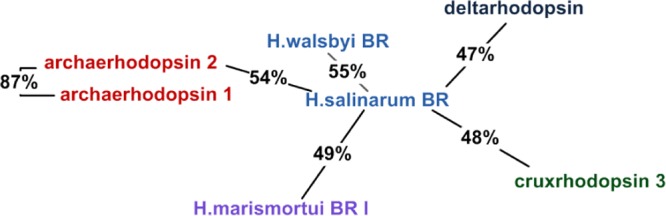
We chose bacteriorhodopsin from Halobacterium salinarum as the reference protein for starting the clustering. The resulting bacteriorhodopsin cluster contains seven structures. Then we constructed other cluster by examining the sequence identity using reference rhodopsins not included in the bacteriorhodopsin cluster. In this way we generated 13 clusters in total. To label each cluster and define its distance from the bacteriorhodopsin cluster, we selected the cluster member with the largest identity with respect to H. salinarum bacteriorhodopsin. The resulting clusters and their distances are color-coded (the members of each cluster are marked with the same color) in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Rhodopsin clusters considered in the present work. The connection between names used and RCSB codes is given in the Supporting Information.

Construction of the Set of Target-Template Pairs

To define a representative set of target-template rhodopsin pairs we started with the assumption that the best pairs are found within clusters. Accordingly, we used the following strategy. From the two largest clusters, the bacteriorhodopsin cluster and the proteorhodopsin cluster, we chose three pairs and two pairs, respectively (see Table 1). Note that since our main goal was to obtain pairs with different levels of sequence identity and since within the bacteriorhodopsin cluster the possible pairs display only slightly different identities (excluding the pair archaerhodopsin 1 + archaerhodopsin 2), we decided to choose 3 pairs out of 21. For the same reason, for the proteorhodopsin cluster, we chose two pairs out of three. Three clusters contain two rhodopsins each giving three more target-template pairs. The remaining eight clusters contain only a single rhodopsin and, therefore, these rhodopsins had to be paired with rhodopsins from different clusters.

Table 1. Target-Template Rhodopsin Pairs Considered in Our Study.

target rhodopsin template rhodopsin sequence identity (%)
H. salinarum BR Haloquadratum walsbyi BR 55
archaerhodopsin 1 archaerhodopsin 2 84
H. salinarum BR archaerhodopsin 2 54
green-light PR blue-light PR from HOT75 77
blue-light PR from Med12 blue-light PR from HOT75 57
thermophilic rhodopsin xanthorhodopsin 53
H. salinarum halorhodopsin Natronomonas pharaonis halorhodopsin 55
Acetabularia rhodopsin I Acetabularia rhodopsin II 55
H. salinarum BR Acetabularia rhodopsin II 19
H. salinarum BR N. pharaonis sensory rhodopsin II 28
H. salinarum BR Anabaena sensory rhodopsin 27
H. salinarum BR sodium pump KR2 19
H. salinarum BR thermophilic rhodopsin 24
H. salinarum BR blue-light PR from HOT75 25
H. salinarum BR Euastrum sibiricum PR 26
H. salinarum BR Nemotelus marinus CIP rhodopsin 20
H. salinarum BR H. salinarum halorhodopsin 31
H. salinarum BR channel rhodopsin 15
Open in a new tab

In addition to the pairs above, we also considered 10 extra pairs formed by H. salinarum bacteriorhodopsin and one representative rhodopsin from each of the remaining clusters featuring a sequence identity higher than 15%. Note that even though the homology modeling is usually performed for cases when sequence identity is higher than 30%, we decided to investigate the “gray zone” from 30 to 15% of sequence identity to see how modern homology modeling algorithms work in these cases. In conclusion, our investigation is focused on a set of 18 target-template pairs.

Comparison of Different Methodologies

As mentioned above, we compared the impact of three different sequence alignment algorithms on the quality of the predicted models. The following are the algorithms implemented in the program packages MP-T, AlignMe, and MUSTER. Then the aligned sequences were used to investigate the performance of three homology modeling strategies implemented in the Medeller, RosettaCM, and I-TASSER programs (see details in the Methods section).

The performance of each methodology was assessed as follows: the predicted models with Cα-RMSD > 4 Å or with GDT-HA < 45% from the corresponding experimental structure were considered a failure (these failed structures will be analyzed later in this section). For the rest of the predicted models, we performed statistical analysis on both the entire protein and the transmembrane (TM) region (i.e., ignoring the outer parts in this last case). The results are given in Table 2 and 3, Figures 2–4.

Table 2. Average Quality of the 16 Predicted Structures for Cases When Target-Template Sequence Identity was Higher Than 40% (Intracluster Structures)a.

homology modeling algorithm Cα-RMSD, Å GDT-HA, % Cα-RMSD, Å (TM part) GDT-HA, % (TM part)
I-TASSER (MP-T align.) 1.350 (0.584–2.422) 75.60 (59.26–90.81) 1.137 (0.551–2.059) 76.80 (59.73–91.82)
I-TASSER (AlignMe align.) 1.342 (0.779–2.061) 75.97 (62.11–88.32) 1.206 (0.568–1.977) 77.06 (63.25–89.53)
I-TASSER (MUSTER align.) 1.440 (0.958–2.293) 72.67 (56.47–83.05)    
Medeller (MP-T align.) 2.234 (0.680–4.000) 80.52 (70.92–86.75) 0.938 (0.639–1.702) 83.24 (72.03–88.49)
Medeller (AlignMe align.) 2.154 (0.769–4.657) 80.52 (70.12–85.46) 1.079 (0.674–1.736) 82.73 (71.21–88.07)
RosettaCM (MP-T align.) 1.901 (0.979–3.048) 63.52 (52.41–73.61) 1.571 (0.974–2.783) 65.78 (52.41–73.95)
RosettaCM (AlignMe align.) 2.054 (1.199–3.787) 63.87 (54.38–73.03) 1.752 (1.085–3.702) 65.04 (53.89–74.89)
Open in a new tab
a

The range of the corresponding values is given in brackets.

Table 3. Average Quality of All 36 Predicted Models (Excluding the Failed Ones) Considered in the Present Worka.

homology modeling algorithm Cα-RMSD, Å GDT-HA, % Cα-RMSD, Å (TM part) GDT-HA, % (TM part) number of failed structures
I-TASSER (MP-T align.) 2.042 (0.584–3.731) 66.54 (49.89–90.81) 1.806 (0.551–3.529) 68.78 (54.30–91.82) 6
I-TASSER (AlignMe align.) 1.990 (0.779–3.896) 68.78 (52.20–88.32) 1.839 (0.568–3.754) 70.20 (54.41–89.53) 7
I-TASSER (MUSTER align.) 2.055 (0.958–3.816) 66.07 (49.12–83.05)     5
Medeller (MP-T align.) 2.483 (0.680–4.000) 70.20 (50.70–86.75) 1.663 (0.639–3.688) 72.85 (53.35–88.49) 7
Medeller (AlignMe align.) 2.429 (0.769–4.657) 70.30 (48.06–85.46) 1.714 (0.674–3.754) 72.74 (51.94–88.07) 8
RosettaCM (MP-T align.) 2.493 (0.979–3.943) 60.39 (49.67–73.61) 2.121 (0.974–3.782) 62.35 (50.89–73.95) 10
RosettaCM (AlignMe align.) 2.586 (1.199–3.952) 59.72 (48.25–73.03) 2.292 (1.085–3.783) 60.82 (45.48–74.89) 11
Open in a new tab
a

The range of the corresponding values is given in brackets.

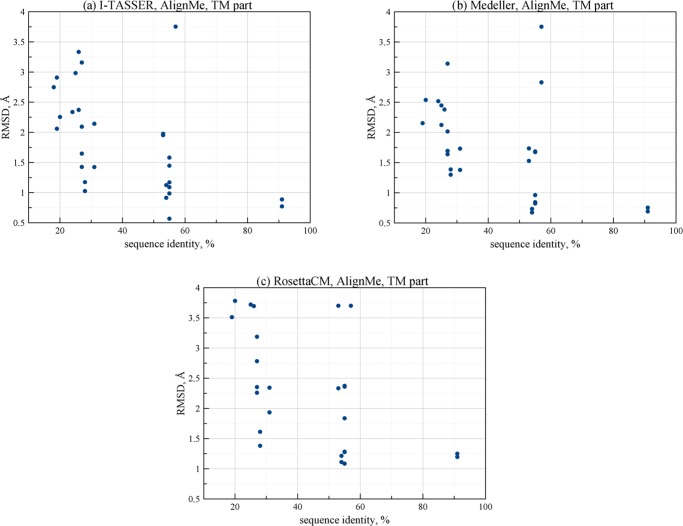
Figure 2.

Figure 2

Open in a new tab

Dependence of Cα-RMSD of predicted models TM part on the target-template sequence identity for different algorithms of homology modeling with AlignMe alignment provided.

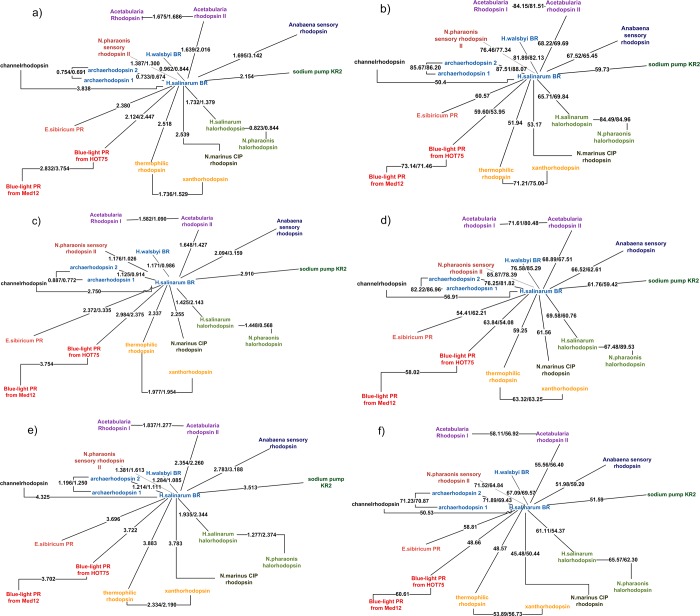
Figure 4.

Figure 4

Open in a new tab

Clustering pictures of the rhodopsins considered in the present work based on the quality of homology modeling predictions. For each pair of proteins, A and B, the three-dimensional model of A was predicted based on the crystallographic structure of B (AB value) and vice versa (BA value). The AB/BA values are given along each connecting line. For each prediction the average quality determines the reported distance between proteins. The different panels refer to different method/scoring combinations: (a) Medeller/Cα-RMSD; (b) Medeller/GDT-HA; (c) I-TASSER/Cα-RMSD; (d) I-TASSER/GDT-HA; (e) RosettaCM/Cα-RMSD; and (f) RosettaCM/GDT-HA. In all cases the AlignMe alignment results were provided.

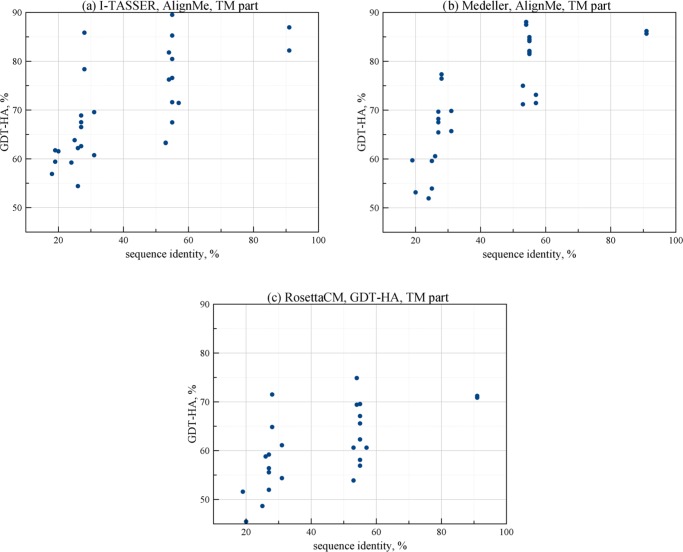
The performance of the three structure building algorithms in combination with different sequence alignment methodologies was compared. In Table 2, statistical analysis of the data obtained for cases where the target and template proteins were from the same cluster is represented (16 models from 8 target-template pairs). The table shows that all methods provide average Cα-RMSD values less than 2.5 Å and average GDT-HA values higher than 60% with the best values being less than 1.5 Å for RMSD and more than 75% for GDT-HA respectively. For the TM regions these values are only slightly higher, which means that the flexible parts are also accurately packed in these cases. Table 3 presents statistical analysis of all successful models. It shows that when the cases with a target-template sequence identity lower than 40% are included, the average RMSD and GDT-HA values do not get significantly worse. It is still possible to predict structures with RMSD around 2 Å.

In Figures 2 and 3, the dependence of the model quality on the target-template pair sequence identity is analyzed for different structure building algorithms. The results show similar trends for all three algorithms for both Cα-RMSD (Figure 2) and GDT-HA (Figure 3) metrics. The quality gradually falls for template-target pairs with less than 55% sequence identity. However, it can still be quite high up to 20% sequence identity. These findings are in accordance with previous studies that considered the comparative modeling of G protein-coupled receptors (GPCRs).61−63 In Figure 4, this dependence is also visualized by clustering. In this clustering, the distance between each pair of proteins (say A and B) is higher when the structure building algorithm produces models of target A based on template B and vice versa, of lower quality. We made such clustering based on Cα-RMSD (Figure 4, panels a, c, e) and GDT-HA (Figure 4, panels b, d, f) metrics for each algorithm with the AlignMe alignment. For cases when one of the predicted models in the pair (e.g., target A with template B) was considered as a failure, only a single successful result (e.g., the corresponding target B with template A) was used for clustering, because we did not include the second value in statistical analysis. In other cases, the two values were averaged to provide the distance values. For cases when none of the pair members was successful, the best of the two values was used. The analysis of these results shows that the resulting clustering only slightly differ from the clustering based on the sequence identities (Figure 1). Also, the obtained clusters are similar to each other. On average, the structure building methodologies considered in our study provide models of similar quality without notable pitfalls even in the low sequence identity region.

Figure 3.

Figure 3

Open in a new tab

Dependence of GDT-HA of predicted models TM part on the target-template sequence identity for different algorithms of homology modeling with AlignMe alignment provided.

The results show that Medeller sometimes poorly predicts the flexible regions (not in the TM part). For example, the Cα-RMSD of halorhodopsin from the N. pharaonis model (3a7k), predicted using the structure of halorhodopsin from H. salinarum as a template, equals 4.657 Å. However, the RMSD for the TM part of the same model is only 0.844 Å. Another example is the case of the H. salinarum BR model predicted based on the structure of archaerhodopsin 2 (Cα-RMSD was 3.393 for the full protein and 0.654 for the TM part).

We can see that Medeller produces models with comparatively low Cα-RMSD values for the TM part even when the target-template pair sequence identity is very low. In fact, this trend is similar for all algorithms. In general, the results show that for cases when the target-template sequence identity is higher than 40%, it is possible to predict structures with average Cα-RMSD values lower than 1.5 Å and average GDT-HA values higher than 75%. The quality of structures drops gradually in the region of sequence identity values between 50 and 55%.

Our analysis reveals that the best choice of structure building method depends on whether or not tails and loops are essential for the model. When considering the alignment provided by AlignMe, Medeller gives the best results for the TM part. For cases when conformation of flexible regions matter, the best choice is I-TASSER.

To evaluate how well the “protein function” may be represented by the selected structure building methods, we performed a visual investigation of the amino acid side-chains forming the rhodopsin active site (Figure 5). This corresponds to the cavity hosting one isomer of the protonated Schiff base of retinal (i.e., of the rhodopsin chromophore). The results show that while Medeller reproduces this functionally important part of the protein, I-TASSER and RosettaCM gave several side-chains orientated towards the cavity center, leading to steric clashes upon chromophore insertion. This result is expected since Medeller uses strong geometrical constraints during the construction of the transmembrane region. These constraints, mostly taken from the template, allow a “memory” effect reproducing the cavity structure of the template and, therefore, the “presence” of the chromophore itself. On the other hand, I-TASSER and RosettaCM algorithms are not subjected to constrains during the energy minimization of side-chains. Thus, during structure building, since the information about the retinal chromophore is lost (i.e., the cavity is hollow), the most energetically favorable orientation for the cavity side-chains is towards the center of the cavity making the prediction of the cavity structure problematic/nonrealistic. Further development of I-TASSER and RosettaCM allowing the inclusion of cofactors shall improve the quality of the predicted structures in this region. As an example, in Figure 5, we compared the retinal-binding pockets of archaerhodopsin 2 model predicted with all three structure building methods using the crystallographic structure of H. salinarum BR as the template (sequence identity 55%).

Figure 5.

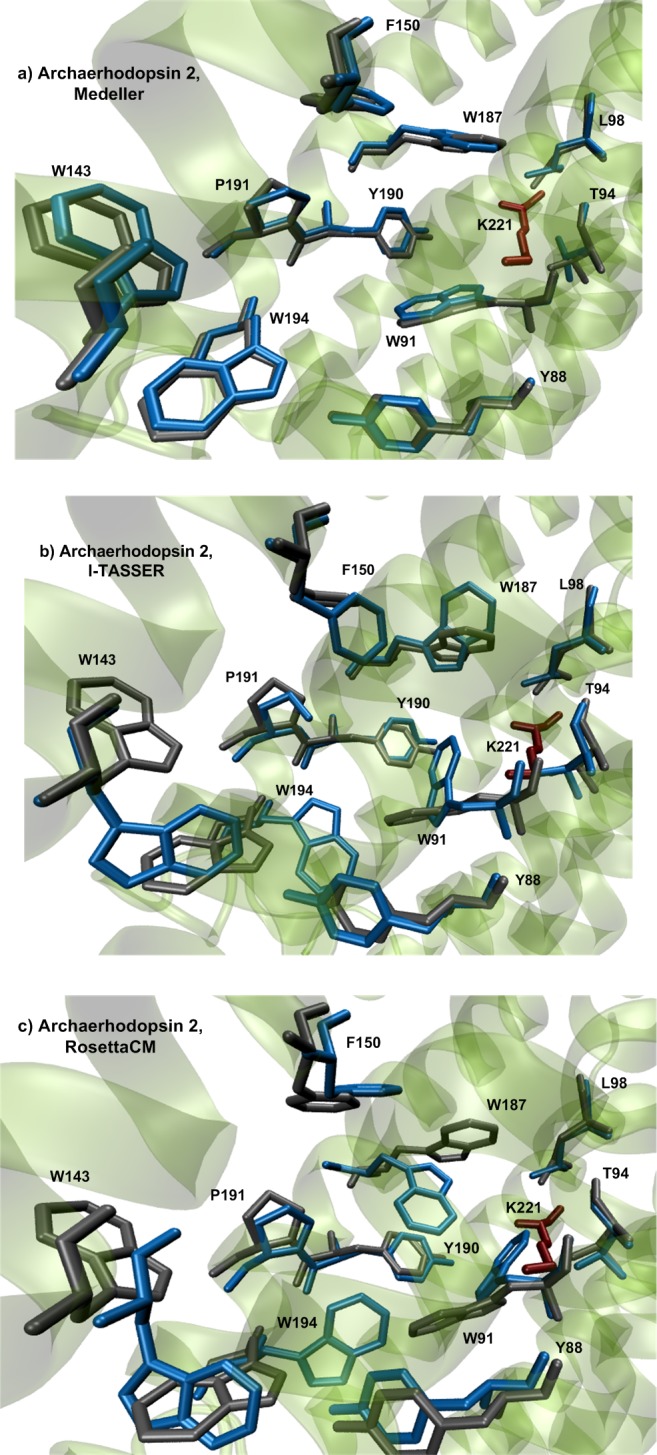
Figure 5

Open in a new tab

Visualization of amino acid side-chains forming the active site of archaerhodopsin 2 in models produced by different algorithms of homology modeling: (a) Medeller; (b) I-TASSER; and (c) RosettaCM with AlignMe alignment. The crystallographic structure of H. salinarum BR (sequence identity 55%) was taken as the template. The side chains of the predicted model are blue, the side chains of the crystallographic structure are gray.

To assess how these differences in the side-chain orientations affect the quality of models with the inserted chromophore, we added retinal into these models and performed a short geometrical optimization at the molecular mechanics level in the Charmm27 force field.64 To insert the retinal chromophore we superimposed the template crystallographic structure containing retinal on the target model. Because the retinal-binding pockets share very similar conformations among homologous rhodopsins, the superposition was accurate. We could then extract the coordinates of retinal from the superimposed template structure and move them into the target structure. Retinal insertion in I-TASSER models and Rosetta models revealed several steric claches of the retinal with surrounding amino acids. These clashes were eliminated by subsequent geometry optimization . The insertion of the retinal in Medeller models did not encounter any considerable clashes with amino acids of the retinal pocket. In other words, even though the conformation of several amino acid side-chains surrounding the chromophore was wrong in the predicted models, the subsequent insertion of retinal and geometry optimization corrected most problems (Figure 6).

Figure 6.

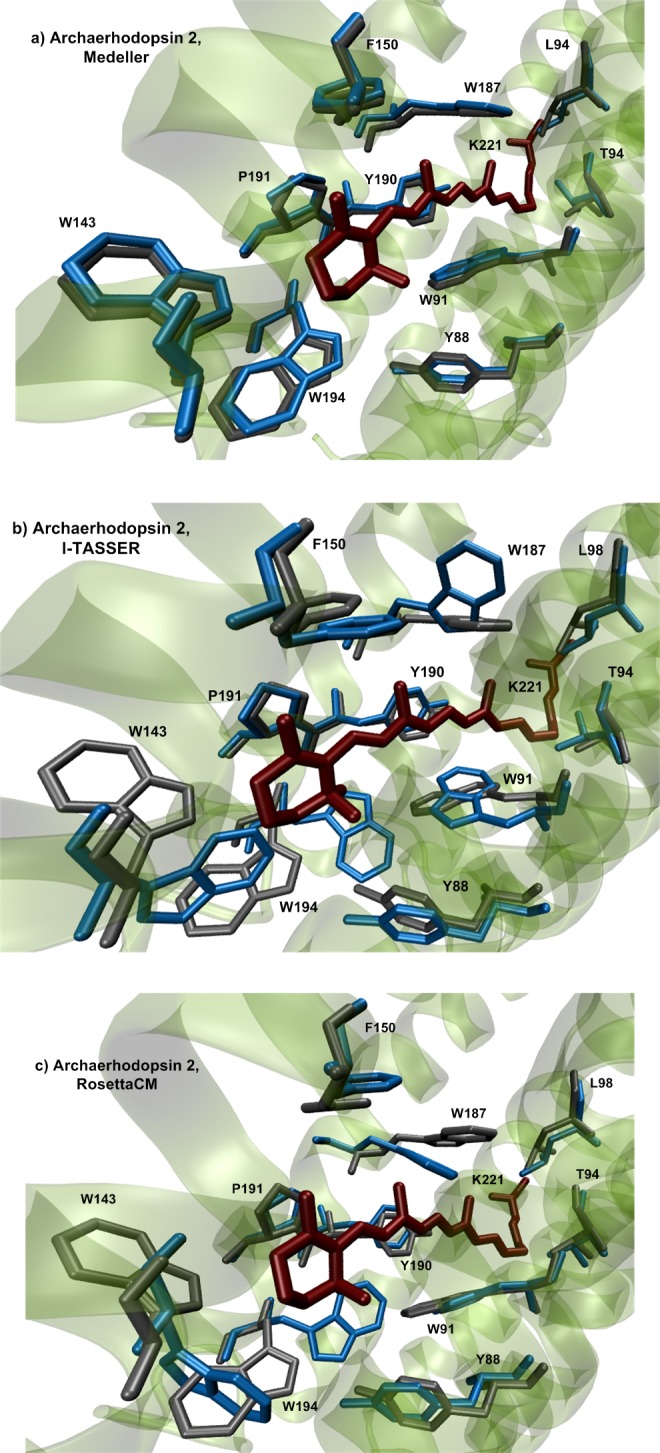
Figure 6

Open in a new tab

Visualization of amino acid side-chains forming the active site of archaerhodopsin 2 in models produced by different structure building algorithms: (a) Medeller; (b) I-TASSER; and (c) RosettaCM with AlignMe alignment after the retinal insertion and short geometry optimization. The crystallographic structure of H. salinarum BR (sequence identity 55%) was taken as the template. The side chains of the predicted model are blue, the side chains of the crystallographic structure are gray.

Also, as it was demonstrated in our recent work,65 an advantage of I-TASSER models was detected when the structure of a archaerhodopsin 3, was predicted. While Medeller predicted seven TM helices and a long tail at the end of the seventh helix, I-TASSER predicted a half helix and a short tail instead. Even though archaerhodopsin 3 does not have an experimental structure, the I-TASSER model seems more realistic.

The analysis of failed models shows that low quality predictions occurred when the target-template sequence identity was low and, mostly, when the target sequence was longer than the template sequence. The example of the failed models are chanelrhodopsin (294 residues) and thermophilic rhodopsin (251 residues) based on H. salinarum BR (227 residues), sequence identities 15 and 24% respectively. Also, the prediction of the KR sodium pump (273 residues) based on H. salinarum BR (227 residues), sequence identity 19%, did not fail only for the I-TASSER modeling with AlignMe and MUSTER alignment. The prediction of blue-light PR from HOT75 (232 residues) based on H. salinarum BR (227 residues), sequence identity 25%, did not fail only for Medeller models with AlignMe alignment. In several cases, the reverse structure prediction also gave unsatisfying results. Finally, models from the pair green-light PR + blue-light PR from HOT75 failed in all cases despite the fact that these two proteins were from the same cluster. This problem may be related to the quality of experimental structure of the green-light PR, which was obtained using the NMR method rather than crystallography.

Modeling with Multiple Templates

We also tested the possibility of improving the quality of structure predictions by using more than one template. For this purpose, we used the RosettaCM algorithm and two algorithms for multiple sequence alignment: ClustalO and PralineTM. The resulting structures were compared with the best models, predicted by RosettaCM and other algorithms using a single template (Table 4).

Table 4. Results of Structure Prediction with Multiple Templates Performed by RosettaCM Algorithma.

structure templates alignment method Cα-RMSD GDT-HA
1m0l, best RosettaCM 3wqj MP-T 1.615 71.15
1m0l, lowest RMSD 3wqj, I-TASSER MUSTER 1.108 77.31
1m0l, highest GDT-HA 3wqj, Medeller AlignMe 2.865 85.46
1m0l, 3 templates 4qi1, 3wqj, 1uaz ClustalO 1.149 73.78
1m0l, 3 templates 4pxk, 4fbz, 4jr8 ClustalO 1.508 62.43
1m0l, 6 templates BR cluster ClustalO 1.249 70.59
1m0l, 9 templates seq. id. ≥ 29% ClustalO 1.375 69.60
1m0l, 3 templates 4qi1, 3wqj, 1uaz PralineTM 1.950 67.50
1m0l, 3 templates 4pxk, 4fbz, 4jr8 PralineTM 1.780 68.50
1m0l, 6 templates BR cluster PralineTM 1.574 65.53
1m0l, 9 templates seq. id. ≥ 29% PralineTM 1.348 73.24
3wqj, best RosettaCM 1uaz MP-T 0.979 73.61
3wqj, lowest RMSD 1uaz, Medeller MP-T 0.680 86.75
3wqj, highest GDT-HA 1uaz, Medeller MP-T 0.680 86.75
3wqj, 3 templates 1uaz, 1m0l, 4qi1 ClustalO 1.235 68.80
3wqj, 6 templates bacteriorhodopsin cluster ClustalO 1.924 64.32
3wqj, 3 templates 1uaz, 1m0l, 4qi1 PralineTM 1.504 60.79
3wqj, 6 templates BR cluster PralineTM 2.530 65.06
3ug9, best RosettaCM 1m0l MP-T 4.216 35.96
3ug9, lowest RMSD 1m0l, RosettaCM MP-T 4.280 35.96
3ug9, highest GDT-HA 1m0l, Medeller AlignMe 4.731 42.23
3ug9, 5 templates seq. id. ≥ 20% ClustalO 13.514 31.28
3ug9, 5 templates seq. id. ≥ 20% PralineTM 5.357 38.19
1e12, best RosettaCM 3a7k AlignMe 1.466 65.48
1e12, lowest RMSD 3a7k, Medeller AlignMe 1.097 83.89
1e12, highest GDT-HA 3a7k, Medeller MP-T 1.117 84.10
1e12, 6 templates seq. id. ≥ 30% ClustalO 2.260 61.40
1e12, 6 templates seq. id. ≥ 30% PralineTM 2.664 59.21
Open in a new tab
a

The results are compared with the best models for the same proteins produced by the RosettaCM algorithm based on the single template and with models with lowest Cα-RMSD values and GDT-HA values obtained in the current work.

The results show that for all cases except one, the use of several templates decreased the model quality. This conclusion is in agreement with the results reported by other investigators.20,28

Conclusions

We have reported on the study of the quality of predicted three-dimensional rhodopsin structures using different homology modeling protocols. More specifically, we benchmarked different homology modeling protocols on two levels: the sequence alignment and the structure building. The quality of the predicted models was then evaluated by comparison with the known crystallographic structures. In total, we predicted 252 structures for cases where the target-template pair sequence identity ranged from 15 to 92%.

There are several conclusions that can be made from our investigation.

  • 1.

    The quality of models predicted by all homology modeling methodologies tested in our study gradually falls in the region between 50 and 55% of target-template sequence identity. On the other hand, we found that models of good quality, especially in the TM region, can be generated even in the 20–40% region of target-template sequence identity. These findings were earlier reported for the homology modeling of GPCRs.61−63

  • 2.

    Medeller protocol sometimes poorly predicts the flexible regions of rhodopsins. However, the TM part of models produced by Medeller was of high quality even when the target-template sequence identity was very low.

  • 3.

    The choice of the homology modeling methodology depends on the requirements for loops and tails. If the quality of flexible regions is important, Medeller protocol with AlignMe alignment should be used. Otherwise, I-TASSER protocol with the same alignment protocol should be used.

  • 4.

    The rhodopsin active sites are predicted correctly with all three model building algorithms. However, in the case of models predicted by Rosetta or I-TASSER protocols additional geometrical optimization is required after the chromophore insertion to remove the occurrence of steric clashes.

  • 5.

    Using multiple templates did not lead to the increase of the model quality. This finding is in agreement with the results reported in other works.20,28

Generally, the results show that up to date the right choice of template and methodology makes possible the prediction of rhodopsin models with a quality close to that of the experimental structure, which was earlier claimed only for globular proteins.6,19 Specifically, for high target-template similarity (>40%) it is possible to predict structures with an average Cα-RMSD less than 1.5 Å and with an average GDT-HA more than 75% with respect to the experimental reference. Moreover, it is possible to obtain models with average RMSD around 2 Å and GDT-HA values higher than 65% even for target-template pairs with much lower sequence identities (up to 15%), but in this region one has to consider each case individually.

The results of our work can be used for the computer-aided engineering of rhodopsin proteins with possible applications in fields such as optogenetics and molecular imaging techniques. Indeed, the ability to predict a high-quality three-dimensional rhodopsin structures is an essential step for the computational investigation of their spectroscopic and photochemical functions. For example, the homology modeling is an important step towards a more effective automatic construction of QM/MM models (e.g., as a recently proposed ARM protocol).36 Thus, the selection of effective homology modeling methods together with the further development of suitable QM/MM methods can facilitate, via rational design or random mutation methods, the achievement of new rhodopsin-based tools for the mentioned technologies. Moreover, the results of our benchmark may be extended to other classes of membrane proteins, such as GPCRs, which are also extensively studied nowadays.66,67

Acknowledgments

This work was supported by the Russian Foundation for Basic Research (grant numbers 15-29-03872 ofi_m and 16-04-00494 A) and by the program No. 32 of the Basic Research of Presidium RAS “Nanostructures: physics, chemistry, biology, basics of technology”. D.M.N., A.A.S., and M.N.R. thank the Skolkovo Foundation (grant agreement for Russian educational and scientific organization No. 7 dd 19.12.2017) and the Skolkovo Institute of Science and Technology (General agreement No. 3663-MRA dd 25.12.2017) for financial support. The research was carried out using equipment of the shared research facilities of HPC computing resources at the Lomonosov Moscow State University. The research was carried out using computational resources provided by Resource Center “Computer Center of SPbU”.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b00721.

  • Correspondence between rhodopsin names and their RCSB codes, analysis of all predicted rhodopsin models (PDF)

  • The PDB archive of all constructed models (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao8b00721_si_001.pdf (361.8KB, pdf)
ao8b00721_si_002.zip (12.6MB, zip)

References

  1. Khan F. I.; Wei D.-Q.; Gu K.-R.; Hassan M. I.; Tabrez S. Current updates on computer aided protein modeling and designing. Int. J. Biol. Macromol. 2016, 85, 48–62. 10.1016/j.ijbiomac.2015.12.072. [DOI] [PubMed] [Google Scholar]
  2. Ginalski K. Comparative modeling for protein structure prediction. Curr. Opin. Struct. Biol. 2006, 16, 172–177. 10.1016/j.sbi.2006.02.003. [DOI] [PubMed] [Google Scholar]
  3. Eswar N.; Webb B.; Marti-Renom M. A.; Madhusudhan M. S.; Eramian D.; Shen M.-y.; Pieper U.; Sali A.. Comparative Protein Structure Modeling Using MODELLER. In Current Protocols in Protein Science; John Wiley & Sons, Inc., 2001. [Google Scholar]
  4. Dorn M.; e Silva M. B.; Buriol L. S.; Lamb L. C. Three-dimensional protein structure prediction: Methods and computational strategies. Comput. Biol. Chem. 2014, 53, 251–276. 10.1016/j.compbiolchem.2014.10.001. [DOI] [PubMed] [Google Scholar]
  5. Floudas C.; Fung H.; McAllister S.; Mönnigmann M.; Rajgaria R. Advances in protein structure prediction and de novo protein design: A review. Chem. Eng. Sci. 2006, 61, 966–988. 10.1016/j.ces.2005.04.009. [DOI] [Google Scholar]
  6. Zhang Y. Protein structure prediction: when is it useful?. Curr. Opin. Struct. Biol. 2009, 19, 145–155. 10.1016/j.sbi.2009.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lee J.; Wu S.; Zhang Y.. Ab Initio Protein Structure Prediction. In From Protein Structure to Function with Bioinformatics; Rigden D. J., Ed.; Springer: Dordrecht, Netherlands, 2009; pp 3–25. [Google Scholar]
  8. Wu S.; Skolnick J.; Zhang Y. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol. 2007, 5, 17. 10.1186/1741-7007-5-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chothia C.; Lesk A. M. The relation between the divergence of sequence and structure in proteins. EMBO J. 1986, 5, 823–826. 10.1002/j.1460-2075.1986.tb04288.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Lesk A. M.; Chothia C. H. The Response of Protein Structures to Amino-Acid Sequence Changes. Philos. Trans. R. Soc., A 1986, 317, 345–356. 10.1098/rsta.1986.0044. [DOI] [Google Scholar]
  11. Govindarajan S.; Recabarren R.; Goldstein R. A. Estimating the total number of protein folds. Proteins 1999, 35, 408–414. . [DOI] [PubMed] [Google Scholar]
  12. Russell R. B.; Saqi M.; Bates P. A.; Sayle R. A.; Sternberg M. Recognition of analogous and homologous protein folds--assessment of prediction success and associated alignment accuracy using empirical substitution matrices. Protein Eng. 1998, 11, 1–9. 10.1093/protein/11.1.1. [DOI] [PubMed] [Google Scholar]
  13. Rayan A.; Siew N.; Cherno-Schwartz S.; Matzner Y.; Bautsch W.; Goldblum A. A novel computational method for predicting the transmembrane structure of G-protein coupled receptors: application to human C5aR and C3aR. Recept. Channels 2000, 7, 121–137. [PubMed] [Google Scholar]
  14. Sánchez R.; Šali A. Advances in comparative protein-structure modelling. Curr. Opin. Struct. Biol. 1997, 7, 206–214. 10.1016/S0959-440X(97)80027-9. [DOI] [PubMed] [Google Scholar]
  15. Daugelaite J.; O’Driscoll A.; Sleator R. D. An overview of multiple sequence alignments and cloud computing in bioinformatics. ISRN Biomath. 2013, 615630 10.1155/2013/615630. [DOI] [Google Scholar]
  16. Lambert C.; Campenhout J.; DeBolle X.; Depiereux E. Review of common sequence alignment methods: clues to enhance reliability. Curr. Genomics 2003, 4, 131–146. 10.2174/1389202033350038. [DOI] [Google Scholar]
  17. Levitt M. Accurate modeling of protein conformation by automatic segment matching. J. Mol. Biol. 1992, 226, 507–533. 10.1016/0022-2836(92)90964-L. [DOI] [PubMed] [Google Scholar]
  18. Šali A.; Blundell T. L. Comparative Protein Modelling by Satisfaction of Spatial Restraints. J. Mol. Biol. 1993, 234, 779–815. 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
  19. Webb B.; Sali A. Comparative Protein Structure Modeling Using MODELLER. Curr. Protoc. Bioinformatics 2014, 47, 5.6.1–5.6.32. 10.1002/0471250953.bi0506s47. [DOI] [PubMed] [Google Scholar]
  20. Larsson P.; Wallner B.; Lindahl E.; Elofsson A. Using multiple templates to improve quality of homology models in automated homology modeling. Protein Sci. 2008, 17, 990–1002. 10.1110/ps.073344908. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wallner B.; Elofsson A. All are not equal: a benchmark of different homology modeling programs. Protein Sci. 2005, 14, 1315–1327. 10.1110/ps.041253405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Zhang Y. Progress and challenges in protein structure prediction. Curr. Opin. Struct. Biol. 2008, 18, 342–348. 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Moult J.; Fidelis K.; Kryshtafovych A.; Rost B.; Tramontano A. Critical assessment of methods of protein structure prediction—Round VIII. Proteins 2009, 77, 1–4. 10.1002/prot.22589. [DOI] [PubMed] [Google Scholar]
  24. Kryshtafovych A.; Fidelis K.; Moult J. CASP9 results compared to those of previous CASP experiments. Proteins 2011, 79, 196–207. 10.1002/prot.23182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kryshtafovych A.; Fidelis K.; Moult J. CASP10 results compared to those of previous CASP experiments. Proteins 2014, 82, 164–174. 10.1002/prot.24448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Haas J.; Roth S.; Arnold K.; Kiefer F.; Schmidt T.; Bordoli L.; Schwede T. The Protein Model Portal—a comprehensive resource for protein structure and model information. Database 2013, bat031 10.1093/database/bat031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Leman J. K.; Ulmschneider M. B.; Gray J. J. Computational modeling of membrane proteins. Proteins 2015, 83, 1–24. 10.1002/prot.24703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kelm S.; Shi J.; Deane C. M. MEDELLER: homology-based coordinate generation for membrane proteins. Bioinformatics 2010, 26, 2833–2840. 10.1093/bioinformatics/btq554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ernst O. P.; Lodowski D. T.; Elstner M.; Hegemann P.; Brown L. S.; Kandori H. Microbial and Animal Rhodopsins: Structures, Functions, and Molecular Mechanisms. Chem. Rev. 2014, 114, 126–163. 10.1021/cr4003769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Deisseroth K. Optogenetics. Nat. Methods 2011, 8, 26–29. 10.1038/nmeth.f.324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kralj J. M.; Douglass A. D.; Hochbaum D. R.; Maclaurin D.; Cohen A. E. Optical recording of action potentials in mammalian neurons using a microbial rhodopsin. Nat. Methods 2012, 9, 90–95. 10.1038/nmeth.1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Martínez-López D.; Blanco-Lomas M.; Campos P. J.; Sampedro D. Visible light sensitized isomerization of rhodopsin-based molecular switches. Tetrahedron Lett. 2015, 56, 1991–1993. 10.1016/j.tetlet.2015.02.115. [DOI] [Google Scholar]
  33. Blanco-Lomas M.; Campos P. J.; Sampedro D. Synthesis and Photoisomerization of Rhodopsin-Based Molecular Switches. Eur. J. Org. Chem. 2012, 2012, 6328–6334. 10.1002/ejoc.201200870. [DOI] [Google Scholar]
  34. Ryazantsev M. N.; Altun A.; Morokuma K. Color Tuning in Rhodopsins: The Origin of the Spectral Shift between the Chloride-Bound and Anion-Free Forms of Halorhodopsin. J. Am. Chem. Soc. 2012, 134, 5520–5523. 10.1021/ja3009117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schapiro I.; Ryazantsev M. N.; Ding W. J.; Huntress M. M.; Melaccio F.; Andruniow T.; Olivucci M. Computational photobiology and beyond. Aust. J. Chem. 2010, 63, 413–429. 10.1071/CH09563. [DOI] [Google Scholar]
  36. El-Khoury P. Z.; Tarnovsky A. N.; Schapiro I.; Ryazantsev M. N.; Olivucci M. Structure of the Photochemical Reaction Path Populated via Promotion of CF2I2 into Its First Excited State. J. Phys. Chem. A 2009, 113, 10767–10771. 10.1021/jp902873h. [DOI] [PubMed] [Google Scholar]
  37. Sumita M.; Ryazantsev M. N.; Saito K. Acceleration of the Z to E photoisomerization of penta-2, 4-dieniminium by hydrogen out-of-plane motion: theoretical study on a model system of retinal protonated Schiff base. Phys. Chem. Chem. Phys. 2009, 11, 6406–6414. 10.1039/b900882a. [DOI] [PubMed] [Google Scholar]
  38. Melaccio F.; del Carmen Marín M.; Valentini A.; Montisci F.; Rinaldi S.; Cherubini M.; Yang X.; Kato Y.; Stenrup M.; Orozco-Gonzalez Y.; Ferré N.; Luk H. L.; Kandori H.; Olivucci M. Toward Automatic Rhodopsin Modeling as a Tool for High-Throughput Computational Photobiology. J. Chem. Theory Comput. 2016, 12, 6020–6034. 10.1021/acs.jctc.6b00367. [DOI] [PubMed] [Google Scholar]
  39. Westbrook J.; Feng Z.; Chen L.; Yang H.; Berman H. M. The Protein Data Bank and structural genomics. Nucleic Acids Res. 2003, 31, 489–491. 10.1093/nar/gkg068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Hill J. R.; Deane C. M. MP-T: improving membrane protein alignment for structure prediction. Bioinformatics 2013, 29, 54–61. 10.1093/bioinformatics/bts640. [DOI] [PubMed] [Google Scholar]
  41. Kelm S.; Shi J.; Deane C. M. iMembrane: homology-based membrane-insertion of proteins. Bioinformatics 2009, 25, 1086–1088. 10.1093/bioinformatics/btp102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Needleman S. B.; Wunsch C. D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
  43. Stamm M.; Staritzbichler R.; Khafizov K.; Forrest L. R. Alignment of Helical Membrane Protein Sequences Using AlignMe. PLoS One 2013, 8, e57731 10.1371/journal.pone.0057731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Stamm M.; Staritzbichler R.; Khafizov K.; Forrest L. R. AlignMe—a membrane protein sequence alignment web server. Nucleic Acids Res. 2014, 42, W246–W251. 10.1093/nar/gku291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Marti-Renom M. A.; Madhusudhan M.; Sali A. Alignment of protein sequences by their profiles. Protein Sci. 2004, 13, 1071–1087. 10.1110/ps.03379804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wu S.; Zhang Y. MUSTER: Improving protein sequence profile–profile alignments by using multiple sources of structure information. Proteins 2008, 72, 547–556. 10.1002/prot.21945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Eddy S. R. Profile hidden Markov models. Bioinformatics 1998, 14, 755–763. 10.1093/bioinformatics/14.9.755. [DOI] [PubMed] [Google Scholar]
  48. Sievers F.; Wilm A.; Dineen D.; Gibson T. J.; Karplus K.; Li W.; Lopez R.; McWilliam H.; Remmert M.; Söding J.; Thompson J. D.; Higgins D. G. Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Mol. Syst. Biol. 2011, 7, 539 10.1038/msb.2011.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Heringa J. Local weighting schemes for protein multiple sequence alignment. Comput. Chem. 2002, 26, 459–477. 10.1016/S0097-8485(02)00008-6. [DOI] [PubMed] [Google Scholar]
  50. Pirovano W.; Feenstra K. A.; Heringa J. PRALINE: a strategy for improved multiple alignment of transmembrane proteins. Bioinformatics 2008, 24, 492–497. 10.1093/bioinformatics/btm636. [DOI] [PubMed] [Google Scholar]
  51. Ebejer J.-P.; Hill J. R.; Kelm S.; Shi J.; Deane C. M. Memoir: template-based structure prediction for membrane proteins. Nucleic Acids Res. 2013, 41, W379–W383. 10.1093/nar/gkt331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Choi Y.; Deane C. M. FREAD revisited: accurate loop structure prediction using a database search algorithm. Proteins 2010, 78, 1431–1440. 10.1002/prot.22658. [DOI] [PubMed] [Google Scholar]
  53. Fiser A.; Do R. K. G.; Šali A. Modeling of loops in protein structures. Protein Sci. 2000, 9, 1753–1773. 10.1110/ps.9.9.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Thachuk C.; Shmygelska A.; Hoos H. H. A replica exchange Monte Carlo algorithm for protein folding in the HP model. BMC Bioinf. 2007, 8, 342 10.1186/1471-2105-8-342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Metropolis N.; Ulam S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. 10.1080/01621459.1949.10483310. [DOI] [PubMed] [Google Scholar]
  56. Hansmann U. H.; Okamoto Y. New Monte Carlo algorithms for protein folding. Curr. Opin. Struct. Biol. 1999, 9, 177–183. 10.1016/S0959-440X(99)80025-6. [DOI] [PubMed] [Google Scholar]
  57. Xu D.; Zhang J.; Roy A.; Zhang Y. Automated protein structure modeling in CASP9 by I-TASSER pipeline combined with QUARK-based ab initio folding and FG-MD-based structure refinement. Proteins 2011, 79, 147–160. 10.1002/prot.23111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Yang J.; Yan R.; Roy A.; Xu D.; Poisson J.; Zhang Y. The I-TASSER Suite: protein structure and function prediction. Nat. Methods 2015, 12, 7–8. 10.1038/nmeth.3213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Leaver-Fay A.; Tyka M.; Lewis S. M.; Lange O. F.; Thompson J.; Jacak R.; Kaufman K.; Renfrew P. D.; Smith C. A.; Sheffler W.; et al. ROSETTA3: an object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011, 487, 545. 10.1016/B978-0-12-381270-4.00019-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Song Y.; DiMaio F.; Wang R. Y.-R.; Kim D.; Miles C.; Brunette T. J.; Thompson J.; Baker D. High-Resolution Comparative Modeling with RosettaCM. Structure 2013, 21, 1735–1742. 10.1016/j.str.2013.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Rayan A. New vistas in GPCR 3D structure prediction. J. Mol. Model. 2010, 16, 183–191. 10.1007/s00894-009-0533-y. [DOI] [PubMed] [Google Scholar]
  62. Shahaf N.; Pappalardo M.; Basile L.; Guccione S.; Rayan A. How to Choose the Suitable Template for Homology Modelling of GPCRs: 5-HT7 Receptor as a Test Case. Mol. Inf. 2016, 35, 414–423. 10.1002/minf.201501029. [DOI] [PubMed] [Google Scholar]
  63. Pappalardo M.; Rayan M.; Abu-Lafi S.; Leonardi M. E.; Milardi D.; Guccione S.; Rayan A. Homology-based Modeling of Rhodopsin-like Family Members in the Inactive State: Structural Analysis and Deduction of Tips for Modeling and Optimization. Mol. Inf. 2017, 36, 1700014 10.1002/minf.201700014. [DOI] [PubMed] [Google Scholar]
  64. MacKerell A. D. Jr.; Bashford D.; Bellott M.; Dunbrack R. L. Jr.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  65. Nikolaev D. M.; Emelyanov A.; Boitsov V. M.; Panov M. S.; Ryazantsev M. N. A voltage-dependent fluorescent indicator for optogenetic applications, archaerhodopsin-3: Structure and optical properties from in silico modeling. F1000Research 2017, 33 10.12688/f1000research.10541.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Heifetz A.; James T.; Morao I.; Bodkin M. J.; Biggin P. C. Guiding lead optimization with GPCR structure modeling and molecular dynamics. Curr. Opin. Pharmacol. 2016, 30, 14–21. 10.1016/j.coph.2016.06.004. [DOI] [PubMed] [Google Scholar]
  67. Yang J.; Jang R.; Zhang Y.; Shen H.-B. High-accuracy prediction of transmembrane inter-helix contacts and application to GPCR 3D structure modeling. Bioinformatics 2013, 2579–2587. 10.1093/bioinformatics/btt440. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao8b00721_si_001.pdf (361.8KB, pdf)
ao8b00721_si_002.zip (12.6MB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES