Investigating Risk Adjustment Methods for Health Care Provider Profiling When Observations are Scarce or Events Rare

Abstract

Background:

When profiling health care providers, adjustment for case-mix is essential. However, conventional risk adjustment methods may perform poorly, especially when provider volumes are small or events rare. Propensity score (PS) methods, commonly used in observational studies of binary treatments, have been shown to perform well when the amount of observations and/or events are low and can be extended to a multiple provider setting. The objective of this study was to evaluate the performance of different risk adjustment methods when profiling multiple health care providers that perform highly protocolized procedures, such as coronary artery bypass grafting.

Methods:

In a simulation study, provider effects estimated using PS adjustment, PS weighting, PS matching, and multivariable logistic regression were compared in terms of bias, coverage and mean squared error (MSE) when varying the event rate, sample size, provider volumes, and number of providers. An empirical example from the field of cardiac surgery was used to demonstrate the different methods.

Results:

Overall, PS adjustment, PS weighting, and logistic regression resulted in provider effects with low amounts of bias and good coverage. The PS matching and PS weighting with trimming led to biased effects and high MSE across several scenarios. Moreover, PS matching is not practical to implement when the number of providers surpasses three.

Conclusions:

None of the PS methods clearly outperformed logistic regression, except when sample sizes were relatively small. Propensity score matching performed worse than the other PS methods considered.

Introduction

Health care providers, whether individual physicians or health care centers, are increasingly being monitored or profiled on their quality of care.^1,2 Despite its over-simplistic interpretation of quality of care, mortality is a frequently used outcome measure^3,4 and is used in the widely implemented Hospital Standardized Mortality Ratio model.⁵ An essential step when profiling providers is the adjustment for case-mix, often called risk adjustment.¹

Provider profiling using traditional regression-based risk adjustment has been shown to lead to inconsistent results that are highly dependent on the specific statistical model chosen.^6–8 In addition, these methods may perform poorly when low-volume providers are included or outcomes are rare, leading to an inability to detect poor performing providers in such scenarios.^9,10 As high patient volume has been associated with better patient outcomes,^11,12 it is especially crucial to monitor the quality of care of low-volume providers. Currently, providers that do not reach a certain volume threshold are often omitted from analyses and comparisons.¹⁰

An alternative to standard regression models when adjusting for covariates in observational studies is propensity score (PS) analysis. When considering dichotomous treatments, PS analysis may outperform standard multivariable analysis,^13–15 especially when dealing with a large number of covariates or few events per covariate.^16,17 Even though several different PS methods have been extended for multiple treatment comparisons (see Linden et al¹⁸ for a comparison), these methods have barely been considered in a provider profiling setting.¹⁹

The objective of this study was to assess the performance of PS methods (notably PS adjustment, PS weighting, and PS matching) for risk adjustment in studies of multiple providers. A simulation study was performed to investigate the effect of sample size, event rate, and provider volume on the risk adjustment performance of PS methods and conventional fixed-effects logistic regression when profiling 3 providers. Subsequently, the suitability of using these PS methods in a more realistic provider profiling setting was explored by considering scenarios with up to 20 providers. Finally, different risk adjustment methods were illustrated in an empirical example from the field of cardiac surgery.

Risk Adjustment Methods

Fixed-effects logistic regression

Traditionally, multivariable regression models have been used to adjust provider effects for possible case-mix variables. The inclusion of providers as random or fixed effects in the logistic regression model is largely dependent on the goal of provider profiling.^20,21 In this article, a fixed-effects logistic regression model was chosen for both the data generation model and analysis model as the aim was to make direct comparisons between only a few provider effects. In addition, only patient-level case-mix variables were included, reducing the necessity of a hierarchical model. Given the theoretical differences between fixed- and random-effects models, it was deemed inappropriate and unfair to analyze data generated under a fixed-effects model with a random-effects risk adjustment method.

PS models

In 1983, Rosenbaum and Rubin introduced the PS as “the conditional probability of assignment to a particular treatment given a vector of observed covariates”²² and demonstrated that adjustment using these scores was sufficient to remove bias due to observed covariates if the assumptions of exchangeability and positivity hold. In health care provider profiling, the treatment is not a medical intervention but the provider attended by the patient. When comparing 2 providers, the PS can be estimated using a binary logistic regression model where the provider indicator is regressed on the observed case-mix variables. The fitted values of this model, the PSs, can then be used for stratification, covariate adjustment, inverse probability weighting, or matching. PS weighting, PS matching, and to a lesser extent PS adjustment have been shown to lead to a better balance of case-mix between providers and less biased effect estimates when compared with PS stratification.^14,23 PS stratification will therefore not be considered in this article.

Generalized PS models

The PS methods can be extended to a multiple provider setting using the generalized PS (gPS) described by Imbens²⁴ as the conditional probability of attending a particular provider given case-mix variables.²⁵ The gPS of each provider can be estimated using multinomial logistic regression including all relevant observed case-mix variables. The application of the aforementioned risk adjustment methods will be described for a setting with 3 providers, yet naturally extends to situations with more than 3 providers. For gPS adjustment, the outcome is regressed on 2 dummy variables of the provider indicator, 2 of the estimated gPSs, and possible interactions. This allows the estimation of the conditional provider effect (for further details, see the following implementations: Spreeuwenberg et al²⁶; Feng et al²⁷). For gPS weighting, the sample is reweighted by the inverse gPS of the provider actually attended. The outcome is then regressed on 2 dummy variables of the provider indicator to estimate the marginal provider effect.²⁷ Extreme weights may be trimmed to help reduce the influence of outliers and model misspecification in certain situations but can also decrease the amount of risk adjustment.²⁸ For gPS matching, the average provider effect of the matched set can be estimated after selecting individuals from each provider based on the overlap of the gPSs, also known as the common support region.²⁹ Although gPS matching will not necessarily use the same target population as the above-mentioned methods to estimate the provider effect, the estimated average provider effects are comparable if interaction effects are absent (ie, the average provider effect is then equal to the average provider effect on those attending the provider). For the remainder of this article, the standard multivariable logistic regression method will be referred to as LR, gPS adjustment as PS_C, gPS weighting as PS_W, gPS weighting with trimming as PS_WT, and gPS matching as PS_M. The performance of all these methods was assessed using a simulation study.

Simulation Study

A Monte Carlo simulation study was performed using R (v3.1.2)³⁰ to assess the influence of sample size, event rate, provider volume, and number of providers on the performance of the PS methods and LR. The first 3 factors were varied in a limited provider profiling setting with only 3 providers. Even though such a situation is rarely encountered in practice, it is analogous to the 3 treatment settings for which the studied methods have been extended previously and allow for a detailed assessment of performance. Subsequently, the suitability and performance of the studied methods in settings with up to 20 providers was explored. Using a simulation study, estimated provider effects of each method could be compared with their true (marginal or conditional) effects. The simulation study was conducted in a controlled setting with properly specified regression models, no interaction terms, and equal coefficients for all included case-mix variables. This ensured comparability of the causal effects estimated by each method.

Data generation

The data generation procedure described in this section was written for a 3-provider setting, yet naturally extends to situations with more than 3 providers.

Ten case-mix variables (Z₁, . . ., Z₁₀) were generated from a multivariate standard normal distribution with correlations either all equal to 0 or 0.1. These variables were then included as covariates in a multinomial logistic regression model to assign each patient to 1 of 3 centers (A, B, or C) within provider indicator X, where center B acted as the reference category. The coefficients of the case-mix variables for center A and C, β_j1, . . ., β_j10, were set equal to 1/10, where k = {A,C}, j ∈ k. The following formula was used to generate probabilities for categories A and C of the provider indicator X:

$${\pi }_j=\frac{e^{{\alpha }_j+{\beta }_{j1}{Z}_1+\cdots +{\beta }_{j10}{Z}_{10}}}{1+{\displaystyle {\sum }_k{e}^{{\alpha }_k+{\beta }_{k1}{Z}_1+\cdots +{\beta }_{k10}{Z}_{10}}}}$$ (1)

Given that center B was the reference category, ${\pi }_B=1-({\pi }_A+{\pi }_C)$. As the total sample size (N) was fixed, the intercepts of the multinomial model (α_A and α_C) shown in equation (1) could be manipulated to determine the size of each provider (N_j). A fixed-effects logistic regression model was used to generate the dichotomous outcome variable (Y). Providers A and C (provider B acted as reference) were included in the model as dummy variables (X_A and X_C) with relative coefficients (β_A and β_C) of −0.5 and 0.5, respectively. Thus, irrespective of patient characteristics, the estimated odds of mortality for a patient attending provider A or C were e^−0.5 = 0.61 and e^0.5 = 1.65 times the estimated odds for a patient attending provider B. In scenarios with more than 3 providers, provider A acted as reference with the remaining providers having relative coefficients between −1 and 1 assigned at equidistant intervals based on the number of providers. Z₁, . . ., Z₁₀ were included with β_Z1, . . ., β_Z10 = 1/10:

$$logit\left[P\left(Y=1\right)\right]=\alpha +{\beta }_A{X}_A+{\beta }_C{X}_C+{\beta }_{Z1}{Z}_1+\cdots +{\beta }_{Z10}{X}_{Z10}$$ (2)

Due to this data-generating model, the case-mix variables acted as confounders of the provider-outcome relation. No interaction terms were included in the model. The provider effects were therefore assumed constant over the different levels of the case-mix variables. On average, the unadjusted estimates of β_A and β_C were found to be −0.40 and 0.60, respectively, across simulations.

A total of 16 scenarios were investigated in which the number of providers, the total sample size over all providers, provider volumes, and the event rate were separately manipulated (see Table 1). Varying the total event rate was achieved by manipulating the intercept (α) of the logistic model (equation (2)), whereas the intercepts of the multinomial model (α_A and α_C in equation (1)) were manipulated to determine the distribution of the sample size over the providers. Each scenario was simulated 2000 times. Scenarios 1 through 12 were repeated with a correlation of 0.1 between all case-mix variables. This correlation coefficient is frequently encountered between baseline variables in observational studies.³¹

Table 1.

For each scenario, the number of providers, total sample size over all providers (N), sample size distribution and total event rate was fixed.

Scenario	No. of providers	N	Sample size distribution	Total event rate, %
1	3	500	NA = NB = NC	10
2	3	1000	NA = NB = NC	10
3	3	2000	NA = NB = NC	10
4	3	5000	NA = NB = NC	10
5	3	10 000	NA = NB = NC	10
6	3	10 000	NA = NB = NC	28
7	3	10 000	NA = NB = NC	13
8	3	10 000	NA = NB = NC	02
9	3	10 000	NA = NB = NC	01
10	3	10 000	NA = NC = 800	10
11	3	10 000	NA = NC = 2500	10
12	3	10 000	NA = NC = 4600	10
13	5	15 000	NA = . . . = NE	10
14	10	30 000	NA = . . . = NJ	10
15	15	45 000	NA = . . . = NO	10
16	20	60 000	NA = . . . = NT	10

Methods

This section describes how the methods, which were described above, were applied in the 3-provider setting (scenarios 1-12). For scenarios 13 to 16, PS_M was not applied due to both logistical and computational challenges that arise when trying to find suitable matches for more than 3 groups. For LR, Y was regressed on 2 dummy variables for X (X_A and X_C) and all 10 case-mix variables (Z₁, . . ., Z₁₀) just as in equation (2). The svyglm function of the survey package (v3.30)³² was used to estimate the model coefficients and the corresponding standard errors (using Taylor series linearization). For all methods except PS_W, the weight of each individual was set to 1. To alleviate potential problems with separation in the most extreme scenarios of scenarios 1 to 12, results of LR were compared with Firth’s bias reduced logistic regression³³ (applied using the logistf package [v1.21]³⁴).

For the PS methods, gPSs were first estimated from the data by fitting a multinomial regression model using the function multinom of the nnet package (v7.3)³⁵ and extracting each patients’ fitted values for all categories of X. For PS_C, a logistic regression model was fitted with 2 dummy variables for X (X_A and X_C) and 2 gPSs (gPS_A and gPS_B). For PS_W, the gPSs were first used to calculate a weight for each patient. A patient’s weight was equal to the inverse of the gPS of the provider actually attended. A weighted logistic regression analysis was performed as in LR, except with only the 2 dummy variables representing X. For PS_WT, the highest 2% of weights were trimmed to the 98th percentile.²⁸ The determination of the optimal trimming threshold was beyond the scope of this study. For PS_M, a 1:1:1 matching without replacement strategy was used where the gPS_A and gPS_B values of all individuals were divided into equal-sized bins. The bin width was equal to 0.2 times the pooled standard deviation of the logit of the gPS_A and gPS_B values, based on the caliper width advised by Wang et al.³⁶ A matched set consisted of one random individual from each category of X that fell within the same bin. The amount of individuals in the matched set was therefore always smaller than the original sample and depended on the overlap of the PS distributions in the 3 groups. The data set containing all matched sets was then analyzed using marginal logistic regression with only the 2 dummy variables of X included in the model. All models used in each method were properly specified as all case-mix variables used to generate the data were also included in the analysis. Investigations into the consequences of model misspecification are discussed elsewhere.^37,38

Reference values

When determining the reference values to compare the provider effect estimates (B_j) with, it is important to consider the different types of effects each method estimates. LR and PS_C both estimate a provider effect conditional on either the observed case-mix variables or a summary in the form of gPSs. The reference provider effects (β_j) were therefore set equal to the conditional effects used in the data-generating model. Thus, for a 3-provider setting, β_A = −0.5 and β_C = 0.5, whereas for a 5-provider setting, β_A = −1, β_C = −0.33, β_D = 0.33, and β_E = 1. PS_W and PS_WT both estimate a marginal provider effect. As this effect is influenced by the event rate, different reference values were used for scenarios 5 through 9. The reference values were determined by taking the mean over 100 samples of 10⁶ patients generated for each event rate with β_j1, . . ., β_j10 = 0. The effect of the case-mix variables on X was thus removed and a marginal logistic regression model was fit using X_A and X_C. A similar procedure was used to determine the marginal reference values for scenarios 13 through 16. For PS_M, the analysis did not take into account the matched nature of the data set as suggested by Sjölander and Greenland.³⁹

Performance measures

For each scenario, the bias, coverage, and mean squared error (MSE) of the estimated provider effects were assessed over 2000 simulations. The bias is equal to the difference between the average estimated provider effect over all simulations and the reference value. The coverage is equal to the proportion of times that the reference value falls within the 95% confidence interval (CI) constructed around the estimated provider effect over all simulations. To provide a measure of the uncertainty in the results of the simulations, note that in case the true coverage is 95%, the coverage based on 2000 simulation runs is expected to lie between 94% and 96% in 95% of the simulations. To confirm that the standard errors of the provider effects were being properly estimated for each method in each scenario, the ratio of the average standard error of B_j over the standard deviation of the 2000 estimates of B_j was also examined. A ratio of 1 indicates that these values are identical. The MSE is equal to the sum of the average squared standard error of the provider effect over all simulations and the square of the bias.

Results

For scenarios 1 to 12, there were no meaningful differences in the performance of methods when the correlation between the case-mix variables was 0 or 0.1. The figures discussed in this section thus assumed a correlation of 0. Furthermore, Firth’s bias reduced logistic regression gave practically identical results to LR. As such, the former method is not further discussed.

Total sample size

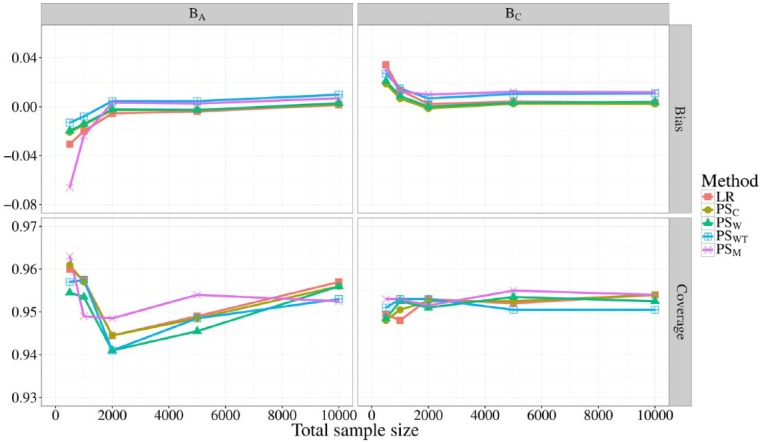
In Figure 1, the bias and coverage (of the 95% CI) of B_A and B_C are shown for all 5 methods at different total sample sizes, corresponding to scenarios 1 through 5. When the total sample size was at least 2000, LR, PS_C, and PS_W gave unbiased estimates of B_A and B_C, whereas PS_M and PS_WT consistently slightly overestimated B_A and B_C. For lower sample sizes, all methods underestimated B_A and overestimated B_C, which was in the same direction as the reference value. PS_M and LR showed the most bias when the total sample size was only 500, with biases of about −0.065 (13% of β_A) and −0.030 (6% of β_A) for B_A and 0.035 (7% of β_C) and 0.030 (6% of β_C) for B_C. Coverage of the 95% CI of B_C fluctuated closely about 0.95 for all methods and sample sizes. Coverage of B_A was more variable with LR, PS_C, and PS_M showing very slight overcoverage when the sample size was 500.

Figure 1.

Bias (top) and coverage of the 95% confidence interval (bottom) of B_A and B_C for different total sample sizes. The sample sizes were evenly distributed over providers with a fixed event rate of 10%. Different line colors represent the different risk adjustment methods used.

Total event rate

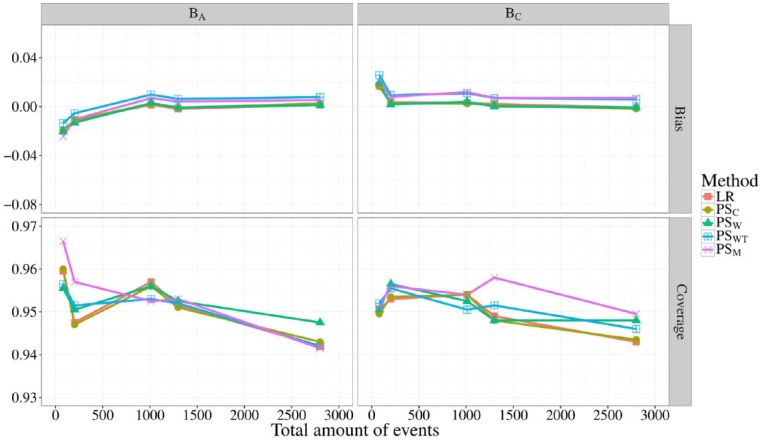
In Figure 2, the bias and coverage of B_A and B_C are shown for all 5 methods at different event rates, corresponding to scenarios 5 through 9. As the total sample size was kept constant at 10 000, the most extreme scenario (9) had an average of 100 total events per simulated data set. Only when the total amount of events decreased below 200, did all methods show slight bias, never exceeding an absolute bias of 0.03. Coverage probabilities of all methods fluctuated between 0.94 and 0.96 and were similar for both B_A and B_C at all event rates, with only PS_M straying beyond 0.96 when the total amount of events was 100.

Figure 2.

Bias (top) and coverage of the 95% confidence interval (bottom) of B_A and B_C for differing total amounts of events. The total sample size was fixed to 10 000 and distributed evenly over the providers. Different line colors represent the different risk adjustment methods used.

Sample size distribution

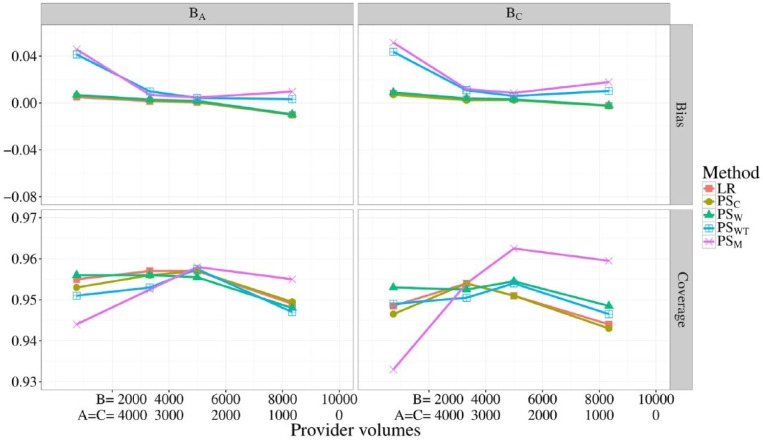
In Figure 3, the bias and coverage of B_A and B_C are shown for all 5 methods at different provider volumes, corresponding to scenarios 5, and 10 through 12. Note that for all scenarios, the total sample size was 10 000 and the volumes of providers A and B were kept equal. Provider volumes seemed to have no meaningful effect on the bias or coverage of B_A and B_C when using LR, PS_C, or PS_W. When using, PS_M or PS_WT, however, the absolute bias exceeded 0.04 for both provider effects when provider B had only 7% of the total sample size. Although PS_WT demonstrated good coverage for both provider effects, PS_M showed both undercoverage and overcoverage for B_C when the volume of provider B was low and high, respectively.

Figure 3.

Bias (top) and coverage of the 95% confidence interval (bottom) of B_A and B_C for differing provider volumes. The total sample size was fixed to 10 000. Different line colors represent the different risk adjustment methods used.

Number of providers

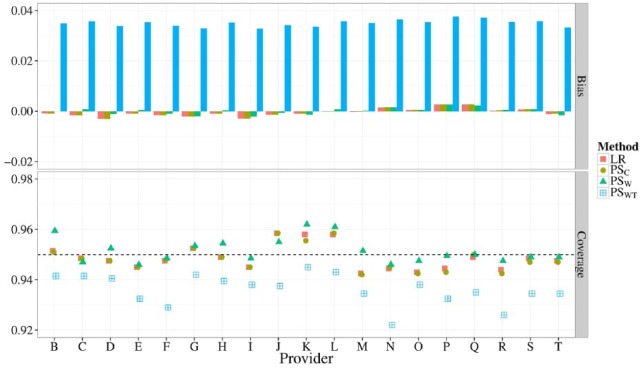
In Figure 4, the bias and coverage of 20 provider effects (corresponding to 16) is shown when using LR, PS_C, PS_W, or PS_WT for risk adjustment. Similar figures comparing 5, 10, or 15 providers (corresponding to scenarios 13 through 15) are shown in the Appendix (Supplemental Figures 1 to 3). The absolute bias of LR, PS_C, and PS_W never exceeded 0.005 for all estimated provider effects as the number of providers increased from 5 to 20. For PS_WT, however, the overall bias of the provider effects increased as the number of providers increased, culminating in biases of about 0.04 for many provider effects when profiling 20 providers. Coverage probabilities of provider effects fluctuated closely about 0.95 for all methods when considering 5 providers. When profiling 20 providers, however, PS_WT lead to undercoverage (below 0.94) for most provider effects.

Figure 4.

Bias (top) and coverage of the 95% confidence interval (bottom) of 19 estimated provider effects when using different risk adjustment methods. All provider volumes were fixed to 3000 with a total event rate of 10%.

Standard error estimation and MSE

Ratios of the average estimated standard errors over the standard deviation of provider effects fluctuated closely about 1 in almost all situations. Only when applying PS_M with a sample size of 500, did this ratio drop below 0.7 for B_A indicating that the average standard error was an underestimation of the actual variation in provider effects simulated. As expected, the MSE generally declined as the total sample size or amount of events increased. Although most methods had an almost identical MSE under all conditions, PS_M consistently scored higher, especially when the total sample size decreased to 500. Figures for these outcome measures can be found in the Appendix (Supplemental Figures 4 to 10).

Empirical Example—Profiling Cardiac Surgery Centers

Open heart surgery is a field that has been subject to many developments in risk-adjusted mortality models for quality control in the past decades.^40,41 Although many have disputed the legitimacy of mortality as a proxy for quality,^42–44 mortality is considered appropriate when profiling procedures such as coronary artery bypass grafting (CABG).^40,41,45 A selection of anonymized data from the Adult Cardiac Surgery Database provided by the Netherlands Association of Cardio-Thoracic Surgery (NVT; www.nvtnet.nl) was used to illustrate the statistical methods evaluated above when profiling multiple centers. This database is similar to databases in other countries, such as the Society of Thoracic Surgeons Adult Cardiac Surgery Database (STS-ACSD) maintained in the United States which has also been used for recent provider profiling investigations.⁴¹

Data

The Adult Cardiac Surgery Database of the NVT contains patient and intervention characteristics of all cardiac surgery performed in 16 centers in the Netherlands as of January 1, 2007. This data set has previously been described and used by Siregar et al^46,47 for benchmarking. In the current study, all patients, from all 16 centers, who underwent isolated CABG with an intervention date between January 1, 2007, and December 31, 2009, were included in the cohort. Case-mix variables were selected based on the EuroSCORE prediction model. Dichotomous case-mix variables with an overall prevalence below 5% were excluded from the analysis. In-hospital mortality was used as the dichotomous mortality indicator. As a result, the final data set included 8 case-mix variables (age [centered], sex, chronic pulmonary disease, extracardiac arteriopathy, unstable angina, LV dysfunction moderate, recent myocardial infarction, and emergency intervention), 1 mortality indicator, and 1 anonymized center indicator (with centers labeled A through P). This data set contained 25 114 patients with an average center mortality rate of 1.4%, ranging from 0.7% to 2.3%.

Comparison of risk adjustment methods

Although the performance of the different risk adjustment methods could be compared in the simulation study described earlier, this is not possible in an empirical data set as the true center effects are unknown. Nevertheless, the consequences of using different risk adjustment methods can be illustrated by ranking centers based on their standardized mortality ratio (SMR). This ratio is calculated by dividing the observed by the expected mortality. Expected mortality rates were calculated using the case-mix variables mentioned above. After fitting the different risk adjustment models on the full data set, the predicted probability of mortality was extracted for the patients attending each center. To mimic a situation with smaller provider volumes or more frequent monitoring, the same procedure was applied to a selection of the total data set only including information from the year 2008. Note that PS_M was not included as a risk adjustment method due to logistical issues that arise when dealing with more than 3 centers.

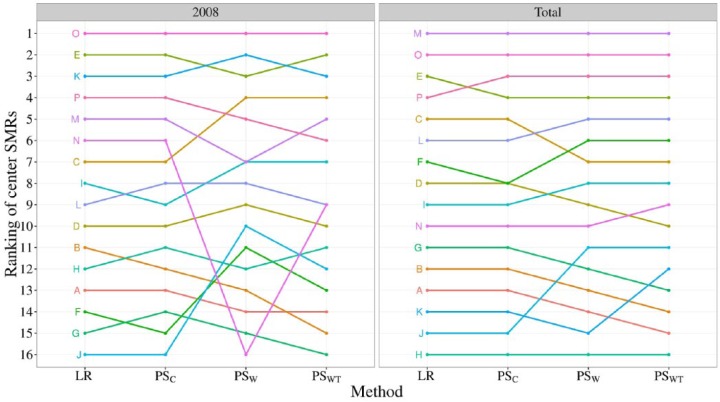
Results

In Figure 5, the SMRs for all 16 centers are ranked for the year 2008 as well as the years 2007 through 2009 combined. In the total data set, all methods showed slight differences in the rankings of the centers. This disagreement increased in the reduced data set as the uncertainty around the SMRs became much larger due to the smaller center volumes. The similarity in rankings of LR and PS_C in both panes echoes the similar performance observed in the simulation study. The marginal methods (PS_W and PS_WT) led to quite different conclusions, especially in the lower ranked centers.

Figure 5.

Ranking of SMRs of all 16 centers for the total data set and for 2008 separately. A rank of 1 is given to the center with the lowest SMR. SMR indicates standardized mortality ratio.

Discussion

Key findings

Our simulation study, in which risk adjustment methods for provider profiling were compared, showed that of the 4 PS methods considered, PS adjustment and PS weighting performed best. Both showed similar or slightly less absolute bias as compared with conventional logistic regression across all scenarios of the simulation study. The PS matching clearly performed worse in terms of bias and coverage than the other methods when the number of observations decreased. Furthermore, PS matching and PS weighting with trimming were the only methods strongly affected by the distribution of volume across providers. When the number of providers to be profiled increased beyond 3, PS weighting was the only method that led to increasingly biased provider effect estimates.

Relation to previous work

In line with Spreeuwenberg et al,²⁶ PS adjustment consistently showed similar performance to logistic regression. Also, PS adjustment as well as PS weighting suffered, albeit slightly, in performance when sample sizes were low, which was suggested before by Feng et al.²⁷ The PS weighting with trimming did not improve on the performance of untrimmed weighting. This may be due to the fact that only one trimming threshold was investigated. However, the arduous task of determining the trimming threshold that has the optimal variance-bias trade-off was beyond the scope of this study. Other alternatives to enhance PS weighting include using stabilized weights.⁴⁸

These findings contrasted those of simulation studies comparing PS methods with conventional regression analysis in settings with 2 exposure levels (eg, providers) in which observations or events were rare. In our study, none of the PS methods clearly outperformed logistic regression.^13,15 Furthermore, PS matching performed slightly worse than all other methods, especially when the total sample size was very low.¹⁴ This is most likely due to the added complexity of applying PS methods in settings with multiple providers, as studies are yet to find noteworthy performance improvements of different PS methods over conventional regression analyses when comparing multiple treatment options.^25–27,29

PS matching

The performance of PS matching was likely influenced by the specific matching procedure applied, as earlier simulation studies have shown that risk adjustment performance can depend highly on the specific matching algorithm used.¹⁰ As the matching procedure was developed for quick application in a simulation study and ease of use, it failed to locally minimize distances between potential matches. This could have led to the occasionally biased estimates and the consistently higher MSE, which were not found by Rassen et al²⁹ when using a computationally more intensive matching algorithm that did implement local minimization.

Strengths and limitations

A strength of our simulation study is that the scenarios investigated were chosen to reflect realistic situations that may be encountered in practice. As such, more extreme scenarios with smaller total sample sizes or lower event rates were deemed unnecessary. However, an obvious limitation of this simulation study was that most scenarios are still a simplification of reality, in which often more than 20 providers are profiled. Nevertheless, the studied scenarios allowed for a fair technical comparison of PS methods and multivariable regression in a provider profiling context. Scenarios 13 to 16 suggest that most PS methods can also be applied in settings with more providers, yet further investigation into the practical consequences (eg, in terms of outlier detection rates) of using these methods in settings with many providers or when there are unobserved case-mix differences is required.

Unobserved case-mix

In all simulations that were performed, all relevant case-mix variables were observed and appropriately included in the model (either the PS model or the outcome regression model). All methods used the same amount of case-mix information and all models were correctly specified. Although the performance of the methods differs for relatively small samples, it may not come as a surprise that for relatively large samples the different methods yield similar results. However, in the presence of nonignorable, yet unobserved, differences in case-mix across providers, the different methods may yield biased results, also in relatively large samples. The question whether the methods are differentially affected by unobserved case-mix was beyond the scope of this study.

Directions for future research

The PS methods investigated in this article are the ones most commonly encountered in the literature and easiest to apply. There are, however, alternative and more complex methods that may be used for risk adjustment. First of all, the gPSs can also be estimated using machine learning procedures such as generalized boosted models.⁴⁹ These methods are able to estimate larger numbers of gPSs with higher accuracy than conventional multinomial regression models but are computationally more intensive and therefore not included in the simulation study. There are also alternative ways to use the estimated gPSs. One such example is marginal mean weighting through stratification, which computes weights based on stratified PSs and has recently been suggested as a suitable risk adjustment method.⁵⁰ To limit the scope of this study, these methods were not considered. Further research is required into these alternative gPS estimation and risk adjustment methods to determine whether they are better than the risk adjustment methods presented in this study.

Recommendations

Inherent advantages of PS methods compared with covariate adjustment to correct for differences in case-mix have been described before.¹⁴ The PS methods separate the design from the analysis of a study, allowing the assessment of balance and overlap of case-mix variables across different providers; an assessment that can be performed independent of the outcome variable. Furthermore, once balance is achieved, eg, through PS matching, it becomes relatively easy to study multiple outcomes. However, due to unfamiliarity with the methods, application of PS methods may be more prone to error compared with more traditional covariate adjustment through regression analysis. Considering the similarity in performance between PS methods and covariate adjustment through logistic regression that we observed in our simulations, neither of the methods can be clearly recommended instead of the others.

Conclusions

None of the PS methods clearly outperformed logistic regression, except for relatively small sample sizes. The PS matching performed slightly worse than all other methods, especially when the total sample size was very low.