Competing Effects of Indirect Protection and Clustering on the Power of Cluster-Randomized Controlled Vaccine Trials

Abstract

Power considerations for trials evaluating vaccines against infectious diseases are complicated by indirect protective effects of vaccination. While cluster-randomized controlled trials (cRCTs) are less statistically efficient than individually randomized controlled trials (iRCTs), a cRCT’s ability to measure direct and indirect vaccine effects may mitigate the loss of efficiency due to clustering. Within cRCTs, the number and size of clusters affects 3 determinants of power: the effect size being measured, disease incidence, and intracluster correlation. We simulated trials conducted in a collection of small communities to assess how indirect protection and clustering affected the power of cRCTs and iRCTs during an emerging epidemic. Across diverse parameters, we found that within the same trial population, cRCTs were never more powerful than iRCTs, although the difference can be small. We also identified 2 effects that attenuated the loss of cRCT power traditionally associated with increased cluster size. First, if enrollment of fewer, larger clusters was performed to achieve higher vaccine coverage within vaccinated communities, this increased the effect to be measured and, consequently, power. Second, the greater rate of imported transmission in larger communities may increase the attack rate and similarly mitigate loss of power relative to a trial in many, smaller communities.

Cluster-randomized controlled trials (cRCTs) have become an increasingly common method for evaluating interventions for infectious diseases, including vaccines. Compared with individually randomized controlled trials (iRCTs), cRCTs may offer logistical, operational, and acceptability advantages (1), and they allow the measurement of direct and indirect effects of vaccination, which are often relevant for policy-makers (2). The statistical theory of cRCT design has largely focused on the effect of clustering, commonly measured by intracluster correlation, on power (3–5). Intracluster correlation arises because outcomes of members of the same cluster are more similar than those from different clusters. Therefore, increasing the number of individuals within a cluster provides less information than would adding the same number of individuals in a new cluster.

When the trial outcome is an infectious disease, correlation arises also because each case in a cluster can transmit infection to other cluster members. Thus, trials of vaccines against infectious diseases exhibit a more complicated relationship between statistical power and sample size than is seen in trials for noninfectious outcomes (6, 7); in particular, the total or overall vaccine effect measured by a cRCT is generally larger than the direct effect measured by an iRCT. In principle, this increased effect size in a cRCT might partially or fully offset the loss of power due to within-cluster correlation. Understanding these complexities can aid in vaccine trial design for emerging epidemics. While an important consideration in any clinical trial, maximizing efficiency is particularly crucial in trials during infectious disease emergencies such as the 2014–2016 Ebola epidemic, where evaluation of experimental vaccines is especially urgent and where limited available vaccine doses and/or changing disease incidence may constrain trial design (8).

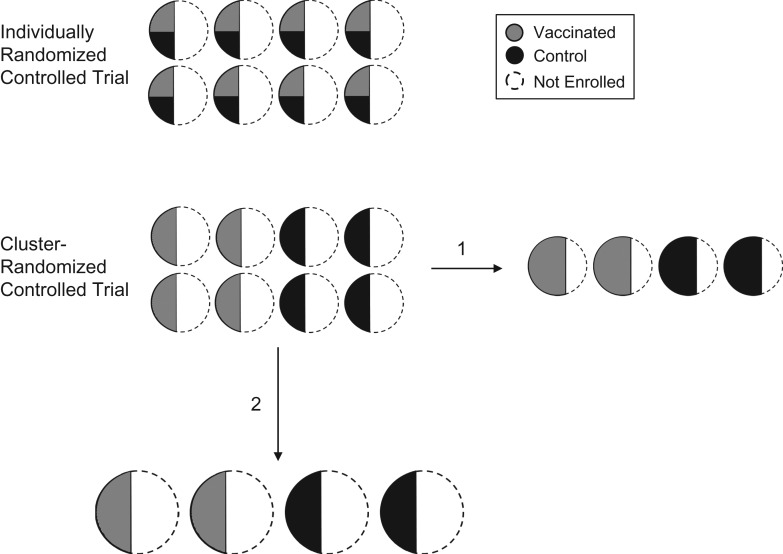
In the present study, we first compared the power of an iRCT with that of a cRCT in the same population across a broad range of realistic parameters, taking into account that the cRCT is generally measuring a larger effect size. We hypothesized that, when R₀ is slightly above 1, a cRCT may have greater power to detect total vaccine effects than an iRCT would have to detect direct effects. Our justification was 2-fold. First, a vaccine’s total effect is greater than its direct effect and thus more easily detected. Second, when an iRCT is conducted within numerous small communities, the indirect effects of vaccination may reduce incidence among control participants sufficiently to erode the trial’s power (6). In a second analysis, we restricted our attention to cRCTs and considered 2 decisions an investigator must navigate when balancing the number of clusters with the size of a cluster, for a given trial population size (Figure 1). Throughout we distinguished between communities that are targeted for enrollment and clusters that comprise the individuals enrolled. When study clusters are sampled from communities, the first decision (enrollment proportion) concerns whether to enroll a larger proportion of each community from fewer communities, or to enroll a smaller proportion from a larger number of communities, fixing community size. The second decision (community size) concerns whether to recruit clusters from a smaller number of large communities or recruit from a larger number of small communities, fixing enrollment proportion.

Figure 1.

Schematic of an example of an individually randomized controlled trial (iRCT) and a cluster-randomized controlled trial (cRCT). Study clusters (solid outline) are enrolled from communities (circles). In the iRCT, individuals within each cluster are randomized to a vaccine (gray) or control (black) group. In the cRCT, half the clusters are randomized to vaccination and half to control. In the cRCT design, fixing the number of individuals enrolled, there are 2 ways to balance cluster size and number of clusters in the trial: 1) fixing the community size: vary the enrollment proportion and the number of communities enrolled; and 2) fixing the enrollment proportion: vary the community size and number of communities.

With regard to enrollment proportion, recruiting a higher proportion of each community leads to higher vaccine coverage in communities receiving vaccination and thus more indirect protection to the community members. The greater overall protection may lead to increased power. With regard to community size, larger communities may experience an increased rate of introduction into the community if, for example, disease importations are proportional to the number of travelers to and from the community, which likely scales with community size. Both the increased indirect protection and the increased importation rate may increase power because they increase the effect size and the average number of cases in the trial population, respectively. These effects may thus partially counterbalance the loss of power that is known to accompany having fewer, larger clusters. We used a transmission model of an emerging directly transmitted infection (such as Ebola virus disease) to assess the contribution of these effects to the relative power of iRCTs and cRCTs.

METHODS

Theoretical analysis

We first explored the plausibility that cRCTs might be more efficient than iRCTs by using theoretical final size equations to calculate the expected outbreak probability and attack rate in clusters, varying enrollment proportion, R₀, and vaccine efficacy (see Web Appendix 1 for details, available at https://academic.oup.com/aje). While this analysis provided some insight into the trade-off between indirect effects and clustering, we conducted the following simulation-based analyses to more realistically account for how epidemic stochasticity may increase variability between communities.

Simulated population structure

We considered a population divided into 2 distinct groups: a main population in which a major epidemic is progressing, and a smaller population made up of multiple small communities from which the trial population is enrolled. The communities are represented with a stochastic block network model (9), in which contacts between individuals within the same block are far more common than those between blocks. This assumption is essential; it increases the strength of indirect effects within clusters relative to scenarios in which there is more between-cluster transmission (10). A connection between individuals in the network represents a single infectious contact per day, and we assume that the number of contacts per individual (degree) is Poisson-distributed.

Transmission models

To balance realism with computational feasibility, we relied on distinct transmission models for the main population and for the communities, using a deterministic compartmental model and a stochastic compartmental model, respectively.

Both models use a susceptible-exposed-infectious-removed compartmental structure. We assumed that infections are introduced into communities via transmission from the main population, and the daily hazard of infection for an individual is proportional to the prevalence of infection in the main population. The community-level rate of disease importation (“importation rate”) is defined as the number of cases per year arising solely as a function of these external transmission events. We assumed that the importation rate varies with the size of the community. In particular, larger communities experience more disease importation events, with community importation rate M_i increasing with $\sqrt{N_i}$, where N_i is the size of the ith community (11). See Web Appendix 1 for more details on importation rate and disease natural history.

Vaccine trial design

For both designs, the specified number of communities are enrolled on a fixed calendar day with a target proportion of community members enrolled at random from the susceptible and exposed individuals therein, forming that community’s study cluster. In the iRCT, half the individuals in each study cluster are randomized to vaccination with the other half to placebo control. In the cRCT all individuals in half the study clusters are assigned to vaccination, while those in the other half are assigned to placebo control. In this design, all enrolled individuals in clusters assigned to vaccination are vaccinated.

Statistical analysis

Statistical analysis of the trial was based on time to symptom onset, with individuals censored after a fixed time. For the iRCT, a Cox proportional hazards (PH) analysis was performed to estimate the direct effect of the vaccine, stratifying by community (12). We defined statistical significance at the α = 5% level using a 2-tailed Wald test, and for each combination of parameters we simulated 500 trials, estimating the power as the proportion of trials that reject the null hypothesis of no vaccine effect, which accounts for different estimands used by different designs. We calculated the median vaccine effect estimate across the simulated vaccine effect estimates. To estimate the type I error of each design, we repeated the above process with the true vaccine efficacy set to 0. To measure the magnitude of clustering in the cRCT, we report the design effect, defined as $\mathrm{design}\mathrm{effect}=1+\mathrm{\rho }(m-1)$, where ρ is the intracluster correlation coefficient (ICC) calculated using the method in Shoukri et al. (13), which is likely an underestimate of the ICC for time-to-event data (14), and m is the average size of a study cluster. The design effect increases with ICC, as subjects in the same cluster are more similar, and with the size of each cluster, as there are fewer, larger groups of similar individuals. The ICC is a measure of between-cluster variance relative to total variance in the outcome: If between-cluster variance is large relative to within-cluster variance, the ICC is large and individuals in the same cluster provide little information relative to individuals in different clusters.

In this cRCT design, a Cox PH model estimates the total effect of vaccination. To ensure we used a cRCT analysis that maintains nominal type I error when comparing cRCT power with that of an iRCT, we first compared type I error between several methods to account for clustering when determining statistical significance within the cRCT design: namely, a Cox PH model with Gaussian- or gamma-distributed shared frailty, and a Cox PH model with robust standard error estimate. We excluded from analysis individuals who developed symptoms within 10 days after vaccination (the average incubation/latent period) to avoid diluting the vaccine effect by analyzing infections that preceded vaccination. All simulations were performed in R (R Foundation for Statistical Computing, Vienna, Austria) (15), and code that can be used to generate the data presented in this study is available on Github (16).

Choice of parameters

Table 1 shows the parameters used in the model, their meanings, values under baseline assumptions, range explored (where applicable), and references or justifications.

Table 1.

Model Parameter Names, Meanings, Values, Ranges Considered, and References or Justifications, Used for an Analysis Comparing Cluster-Randomized Controlled Trials With Individually Randomized Controlled Trials, 2018

Parameter	Meaning	Value	Range Considered	Reference or Justification
R0	Average number of secondary infections generated by an infected individual		0.6–3	Wide range spanning most emerging infectious diseases. Calculated for network models using Meyers et al. (26).
Mean (latent)	Mean latent period length (days)	9.7		(27)
SD (latent)	SD of latent period length (days)	5.5		(27)
Mean (infectious)	Mean infectious period length (days)	5.0		Time to hospitalization (27).
SD (infectious)	SD of infectious period length (days)	4.7		(27)
VE	Individual vaccine efficacy	0.6	0.4–0.8	Baseline assumption.
Ni	Size of community i	100	50–200	Assumption that some unit of this size exists in the population.
Mi	Importation rate into communities	$\begin{array}{c}0.0025\sqrt{N_i}\\ \text{cases}/\text{year}\end{array}$	$\begin{array}{c}0.0125-0.05\sqrt{N_i}\\ \text{cases}/\text{year}\hfill \end{array}$	Based on a calculation for measles (11), with the magnitude of the rate chosen so that there are on average 0.5 importations into a community of size 100 over a 2-year epidemic.
Within-community degree	Average total number of contacts of an individual within the same community	14.85	14.83–14.85	Based on “Ebola, ça suffit!” trial (24) (ring size of 90, <20% of which were primary contacts).
Between-community degree	Average total number of contacts of an individual from outside their community	0	0–0.02	Assumption that communities are disconnected, to minimize spillover effect. A range was explored to represent 1 or 2 contacts outside each community.
Trial size	Average number of individuals enrolled	4,000		Assumption to achieve reasonable power for chosen parameters.
Trial start day	First day of enrollment, vaccination, and start of follow-up, relative to the first day of the epidemic in the main population	150	100–250	Assumed the trial starts before the peak of the epidemic in the main population and that the trial team is ready to go when epidemic starts.
Trial length	Length of follow-up after trial start (days)	140	70–210	Assumption to achieve reasonable power for chosen parameters.

Abbreviations: SD, standard deviation; VE, vaccine efficacy.

RESULTS

Comparison of iRCT and cRCT

In our theoretical analysis based on final size calculations, we found support for our initial hypothesis that cRCTs could be more efficient than iRCTs: When R₀ in vaccinated clusters in the cRCT is just above 1, the measured total effect is close to 1, which increases power; on the other hand, indirect effects in the iRCT drive down the incidence of disease among controls, undermining its power. Increasing enrollment proportion increased power of the cRCT relative to the iRCT, and there were parameter ranges for which the cRCT was more powerful than the iRCT. For example, with communities of size 100 and enrollment proportion 60%, we estimated that a cRCT would be more efficient than an iRCT when R₀ was close to 1.6 and vaccine efficacy was between 50% and 60% (see Web Figure 1).

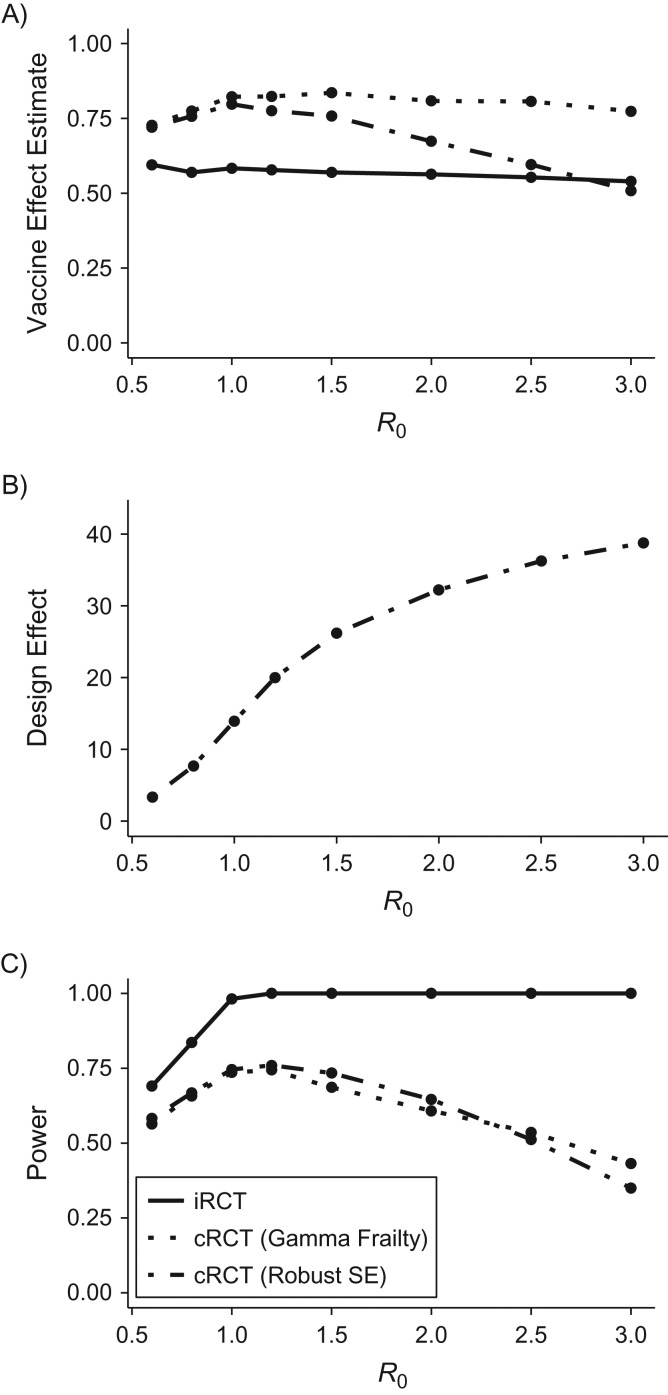
However, our simulation model revealed that, across a broad range of parameters—including population structure, trial design, and vaccine efficacy parameters—iRCTs were always were more powerful than cRCTs in the same population, despite the larger effect size being measured in cRCTs. The discrepancy between the models arises because theoretical calculations underestimate the average cumulative incidence, as well as the variability in transmission across clusters, when R₀ is close to 1. Figure 2 illustrates the power of simulated iRCT and cRCT designs versus R₀, and highlights 2 findings. First, the cRCT generally yields greater effect-size estimates than the iRCT does, because it measures the total vaccine effect rather than solely direct effects (Figure 2A). Second, the design effect is large and increases with increasing R₀ (Figure 2B), because large R₀ leads to more outbreaks within communities, which increases between-cluster variance and thus the ICC (see Web Figure 2). Therefore, the power that the cRCT gains by measuring a larger effect is more than compensated by loss of efficiency due to within-cluster correlation. These 2 points explain why cRCT power first increases and then decreases with increasing R₀. As R₀ increases past a certain threshold, the effect of clustering begins to dominate the effect of increased incidence in the study population, and the trial loses rather than gains power from the increased transmission.

Figure 2.

Comparison of vaccine effect estimates and power of individually randomized controlled trials (iRCTs) and cluster-randomized controlled trials (cRCTs), showing vaccine effect estimates (A), design effect (B), and power (C), analyzed using either a shared gamma-frailty model or a Cox proportional hazards model with robust standard error (SE) estimates. The data are simulated. The incidence rate of importations into an average community is 0.5 cases/year, the vaccine efficacy is 60%, and other parameters are the baseline values listed in Table 1.

As hypothesized, we found that there was reduced incidence among controls in the iRCT compared with those in the cRCT due to indirect protection from vaccinated individuals (17), although this did not significantly affect the power of iRCTs in our simulations. This is likely because vaccine coverage was low in the iRCT (a maximum of 50% of individuals within clusters are vaccinated) such that there is still sufficient transmission among control participants to evaluate the vaccine, in part because importation events from the main population occur even in the presence of herd immunity.

The above results focus on the gamma-frailty model for analyzing the cRCT. We found that the estimated vaccine effect from a Cox PH model with robust standard errors decreased drastically as R₀ increased. This occurred because the effect estimate from the robust standard errors model is not stratified by cluster, and it is thus biased by heterogeneity in hazard of infection caused by stochastic variation in outbreak size (12). The gamma-frailty model can account for this heterogeneity and performed better, yielding both type I error rates below 5% and unbiased estimates of total vaccine effects for many of the parameter combinations. Still, when R₀ was sufficiently small, the gamma-frailty model of cRCT designs did exhibit slightly elevated type I error (17) due to the sporadic and heterogeneous nature of outbreaks in the communities.

Figure 2 shows that the power of the cRCT is strongly affected by the design effect (Figure 2C), and that the difference in power between the cRCT and iRCT is smaller when there is low R₀. This observation held when other parameters were varied, including trial start day (relative to epidemic onset), vaccine efficacy, importation rate, and population structure. In the setting of low R₀, epidemics will die out stochastically in most clusters experiencing at least 1 case importation. The cluster-level attack rates are thus close to zero, and the between-cluster variance is small (17).

Varying community enrollment proportion in a cRCT

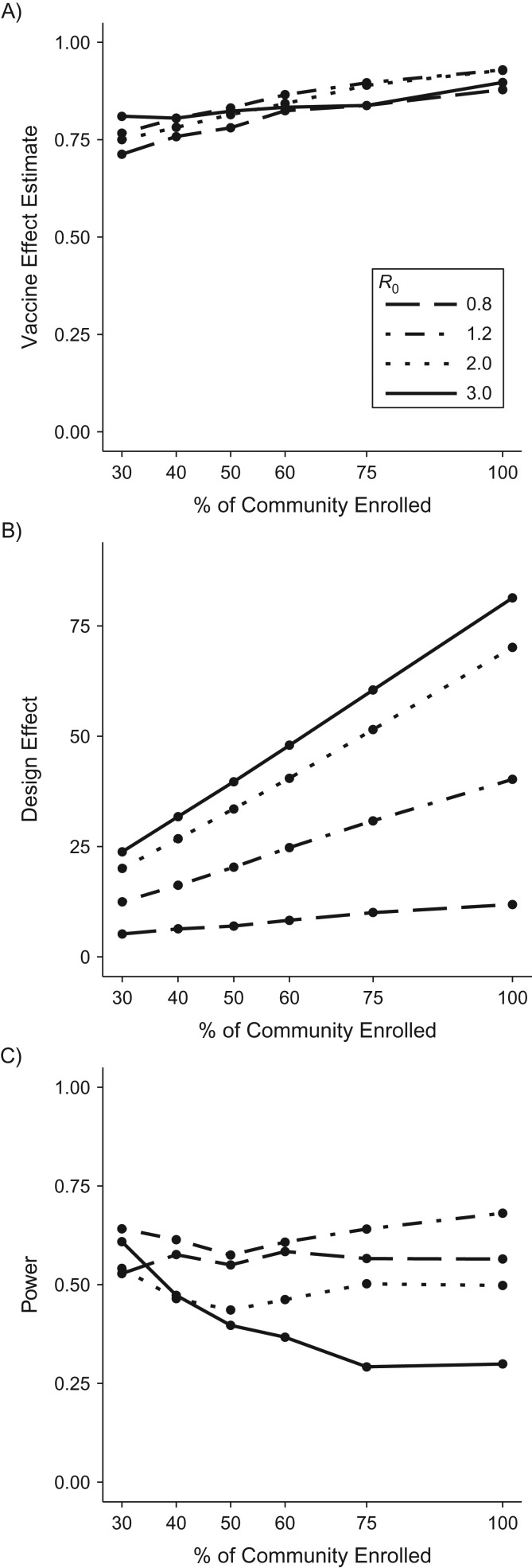
Restricting attention to cRCTs, Figure 3 displays the vaccine effect estimate (Figure 3A), design effect (Figure 3B), and power (Figure 3C) for a cRCT across varying community enrollment proportions (holding community sizes constant, but varying number of communities). As expected, the estimate of total vaccine effect increases with increasing proportion enrolled because it increases vaccine coverage and, consequently, the indirect effects in vaccinated clusters. However, the increased effect size is counterbalanced by increases in the design effect (driven by larger clusters). Thus, for all values of R₀ displayed, except the highest considered (R₀ = 3), there is no clear trend in power with the community enrollment proportion. For R₀ = 3, the simulations follow the trend generally expected for cRCTs, in which the use of more, smaller clusters increases trial power.

Figure 3.

Relationship between power and community enrollment proportion for a cluster-randomized controlled trial (cRCT), using simulated data. Vaccine effect estimates (A), design effect (B), and power (C) from a cRCT versus the percentage of individuals enrolled from each community, with total sample size held constant and assuming a vaccine efficacy of 60%.

Varying size of enrolled communities in a cRCT

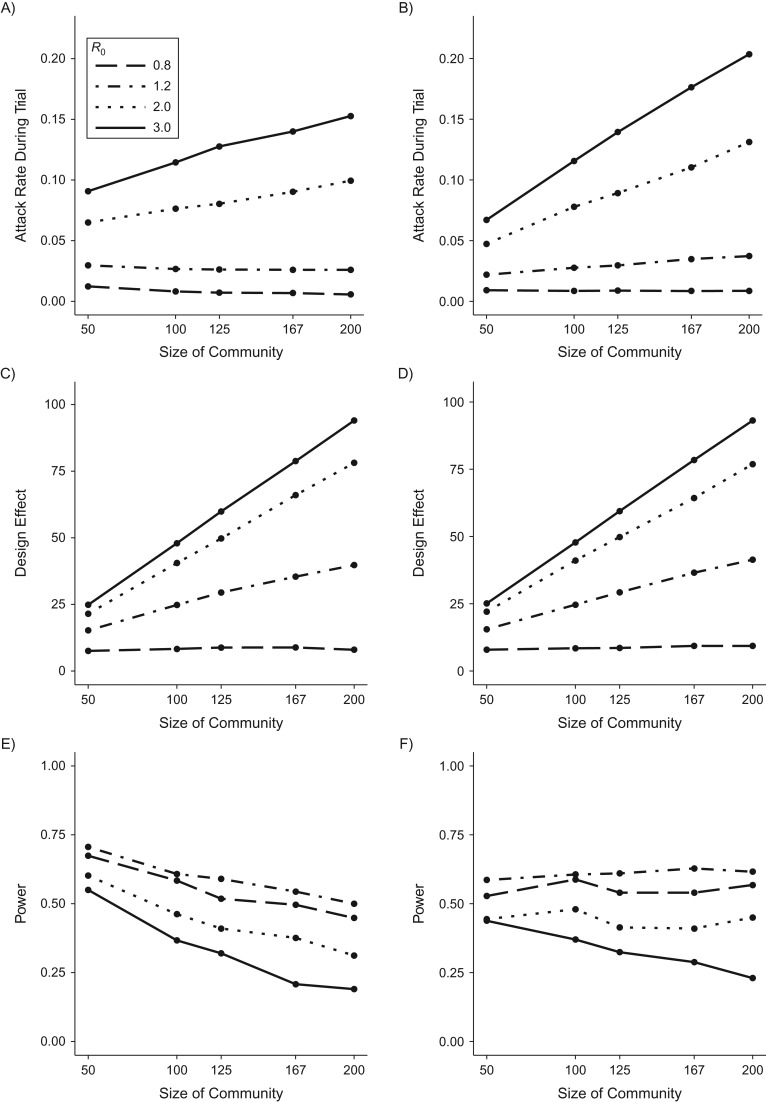
Figure 4 displays the attack rate in the study population (Figure 4A), design effect (Figure 4C), and power (Figure 4E) for a cRCT with varying size of enrolled communities, holding the proportion of communities enrolled and the total number of trial participants constant. The attack rate in the trial population is determined by the product of: 1) the average proportion of a community infected given an outbreak in that community (final size); and 2) the proportion of communities that experience an outbreak. When R₀ > 1, the final size is the same regardless of community size because we assume frequency-dependent transmission (18). However, if importation rate increases with community size, then the grouping of individuals into fewer large communities makes each community more likely to receive at least 1 importation, increasing the proportion of communities that experience an outbreak. In effect, letting each importation be shared across more individuals increases the probability that any trial participant lives somewhere that experiences an importation and, thus, an outbreak. The magnitude of the increase in attack rate with fewer large communities depends on how importation rate scales with community size. In this case, assuming sublinear increase in importation rate, the increased attack rate with fewer, larger communities is not large enough to offset the greater design effect and thus power decreases when increasing community size and decreasing community number.

Figure 4.

Relationship between power and size of enrolled communities for a cluster-randomized controlled trial (cRCT), using simulated data. Attack rates in the trial population (A and B), design effects (C and D), and power (E and F) for cluster-randomized vaccine efficacy trials versus the size of the communities recruited, with total sample size held constant. In the left-hand column, community case importation rate is proportional to the square root of community size, and in the right-hand column it is proportional to the community size. All results shown here assume 60% community enrollment.

If community importation rate scales linearly with community size, there is an even greater increase in attack rate when there are fewer, larger communities (Figure 4B), relative to the analysis above. In this case, even though the design effect increases with community size (Figure 4D), the higher attack rate offsets the increased design effect, and power does not change appreciably with size of enrolled communities when transmission is moderate (Figure 4F).

Analysis methods for a cRCT

In answering our primary research questions, we explored a range of analysis methods for the cRCT. We found that a Cox PH model with Gaussian-distributed frailty had significantly elevated type I error (17). Fortunately, 2 common approaches to analyzing clustered survival data—a Cox PH model with gamma-distributed frailty or robust standard error estimation—were the best methods in terms of power and validity. The robust standard error analysis has higher power than the gamma-frailty model when transmission is low. However, the model does not account for heterogeneity in hazard rates in its estimate of the vaccine effect, leading to a downward bias that is particularly apparent when R₀ is high, as seen in Figure 2. The gamma-frailty model is not susceptible to this bias.

DISCUSSION

Traditional comparisons of cRCTs versus iRCTs that focus on within-cluster correlation and the design effect should also consider other ways in which the unit of randomization affects power in randomized controlled trials. Although an iRCT and a cRCT answer different research questions (measuring direct and total effects, respectively), a positive finding for either could arguably lead to the same policy outcome, especially during an epidemic (19). For example, the recombinant vesicular stomatitis virus (rVSV)–Zaire ebolavirus vaccine was approved for use in the Democratic Republic of Congo in 2017 based on the findings of “Ebola, ça suffit!,” a cRCT (20). We have shown that a cRCT’s ability to measure both indirect and direct effects can partially compensate for the loss of power due to clustering. Theoretical calculations suggest that cRCTs may exhibit greater statistical efficiency than iRCTs in some low-R₀ scenarios. However, simulations that more realistically capture stochasticity in transmission suggest that iRCTs remain more powerful than cRCTs conducted in the same trial population. In low-transmission settings, the difference in power between them may be small, although for R₀ values lower than those considered here, a risk-prioritized design (such as ring vaccination) would be preferable, and these results should be examined separately in this context.

The above comparisons between cRCTs and iRCTs can be extended to examine cRCTs of different cluster sizes (which is particularly apparent once noting that an iRCT can be considered a cRCT with cluster size of 1). For instance, within cRCT designs, enrolling more individuals from the same cluster is generally less statistically efficient than enrolling individuals in a new cluster. Previous work has argued that the ICC often decreases with cluster size, mitigating some loss of efficiency with larger clusters (10), and demonstrated how cross-contamination may increase when cRCTs are run in clusters of fewer individuals, reducing the effect to be estimated and thus power. Cross-contamination occurs either via transmission between intervention and control clusters or inadvertent receipt of intervention by control clusters, both of which are less likely when clusters are separated in space (21) or are sufficiently large that they are less affected by external populations (10).

Here we showed that, even in the absence of cross-contamination, indirect effects in themselves can mitigate the loss of efficiency caused by the increasing design effect associated with fewer, larger clusters. To our knowledge, this fact has been alluded to but the effect on power has never been quantified (22, 23). Another counterintuitive finding arises from the fact that, because larger communities experience a greater influx of transmission imported from elsewhere, enrolling fewer but larger communities may yield a greater attack rate, and thereby partly or fully compensate for the loss in power due to the design effect. This result is dependent on the relationship between case importation rate and community size. Consequently, this will differ according to disease and population setting and may be true only in scenarios in which a pathogen is not endemic to trial communities and the probability of pathogen introduction into a community is relatively low.

Our findings highlighted the importance of adequately accounting for heterogeneity between study clusters while maintaining the nominal false-positive rate and maximizing power. We limited the methods to those widely used and found that a Cox PH model with gamma-distributed frailty performs best overall, although when R₀ is low, a Cox PH model with robust standard errors may be superior.

The results presented here are part of a body of work demonstrating the utility of simulation when considering the design of vaccine trials for infectious diseases (7). It is only by including transmission dynamics in models that we are able to quantify the relative strength of clustering and indirect protection in affecting trial power. The present study is intended to explore these effects more generally, but we expect our findings to be relevant to investigators considering cRCT design, whether or not they develop a full-fledged trial simulation study during the planning phase. Theoretical work on trial design can help prepare stakeholders to rapidly design trials in the face of unexpected epidemics of emerging pathogens. However, it is important to note that sample size is only one of many factors that must be taken into consideration when planning a vaccine trial. Considerations of logistics, cost, ethics, acceptability, or the particular research question of interest may, in certain contexts, hold priority.

There are at least 2 sources of intracluster correlation in a cRCT for an infectious disease: transmission between individuals within a cluster and the shared characteristics of individuals within a cluster. When R₀ is large enough, any outbreak that takes off will infect many individuals in a community, so all clusters will have an attack rate close to either 0% or 100%. In such cases, there is very little within-cluster variance, and the total variance comprises chiefly between-cluster variance, leading to ICCs approaching 1. Clustering due to shared characteristics can arise for many reasons (e.g., within-community similarities in behavior, health, or proximity to source populations). Intracluster correlation, whether due to transmission or to shared characteristics in clusters, increases the design effect. Given these different sources of clustering, and the fact that we observed ICCs ranging from 0.05 to 0.8 in our simulations, it is critically important that ICCs are reported by study investigators when presenting the results of a cRCT because this may aid in planning for future trials (24).

Our analysis neglects some aspects of a realistic population in which a trial is conducted. For example, we do not consider the second source of clustering described above (i.e., shared characteristics). More broadly, modeled individuals do not vary in characteristics other than degree and the community to which they belong, whereas real populations would vary in age structure, proximity to the epicenter of the epidemic, and other variables that would predict disease incidence. By ignoring these characteristics, we underestimate the extent of clustering in a cRCT and overstate its power. This makes more robust our conclusion that the iRCT is always more powerful than the cRCT in the situations considered.

We have conceptualized the population structure as being a number of small groups separated in space so that there is minimal transmission between communities; in reality, population structure is likely to be less distinct. We have not considered permanent or temporary migration, or secondary structure within communities (i.e., households). Moreover, real-life degree distributions have a heavier tail (due to superspreading (25)) than considered here, although a sensitivity analysis showed that our results are robust to this assumption (17).

We found that the general principle that enrollment of fewer, larger clusters leads to decreased power is strongly dependent on the relationship between community size and rate of importation. Our base assumption, that importation frequency is proportional to the square root of community size, is based on a finding for measles (11). For other diseases, the community-level importation rate may be independent of community size, in which case the increased design effect would entirely dictate the loss of power as community size increases. Our conclusions should thus be considered in the context of each specific disease and population.

The indirect effect of vaccination should be considered along with clustering in calculating the power of a cluster-randomized trial and in comparing different trial designs for interventions against infectious diseases. Using simulation, we show that it does not always increase power to enroll more, smaller clusters into a cRCT when doing so is associated with reduced indirect protection to vaccinated individuals or importation of infection into the study population. Still, while cRCTs measure a greater vaccine effect than iRCTs, we found that iRCTs are generally more powerful, though their power may be comparable in low-transmission settings.

Abbreviations

cRCT

cluster-randomized controlled trial

ICC

intracluster correlation coefficient

iRCT

individually randomized controlled trial

PH

proportional hazards