Seeing number using texture: How summary statistics account for reductions in perceived numerosity in the visual periphery

Abstract

Peripheral visual perception is characterized by reduced information about appearance due to constraints on how image structure is represented. In particular, visual crowding (poorer recognition of peripheral targets when presented among flankers) is a consequence of excessive integration in the visual periphery. The basic phenomenology of visual crowding and a number of other tasks have been successfully accounted for by a summary-statistic model of pooling, suggesting that texture-like processing is a useful model of how information is reduced in peripheral vision. Here, I attempt to extend the scope of this model by examining a recently reported property of peripheral vision: reduced perceived numerosity in the periphery. I demonstrate that a summary-statistic model of peripheral appearance accounts for reduced numerosity in peripherally-viewed arrays of randomly placed dots, but does not account for observed effects of dot clustering within such arrays. The model thus offers a limited account of how numerosity is perceived in the visual periphery. I also demonstrate, however, that the model predicts that numerosity estimation is sensitive to element shape, which represents a novel prediction regarding the phenomenology of peripheral numerosity perception. In closing, I discuss possible ways to extend the model to account for a broader range of behavior and also the potential for using the model to make further predictions regarding how number is perceived in untested scenarios in peripheral vision.

Introduction

Peripheral vision is subject to lossy encoding such that substantial information content is not available to observers. Basic examples of how information is lost due to the constraints imposed by visual physiology are the reductions in acuity and color sensitivity in peripheral vision. Peripheral visual acuity is poor largely due to changes in photoreceptor size as eccentricity increases (Virsu & Rovamo, 1979) and similarly, peripheral color sensitivity is reduced as a direct result of the decreasing proportion of cones vs. rods as retinal eccentricity increases (Martin et al., 2001).

Beyond these initial limitations, there are downstream constraints on peripheral vision that further limit the fidelity of the visual system’s representation of visual structure. In particular, the phenomenology of visual crowding (Whitney & Levi, 2011) is an important example of how perception is limited by processes that further reduce representational fidelity in peripheral vision. Visual crowding refers to deficits in peripheral target recognition induced by neighboring flanking items. Crowding does not impair target detection, which differentiates crowding from masking (Pelli, Palomares, & Majaj, 2004), and observers’ ability to identify isolated peripheral targets rules out accounts based on visual acuity in the periphery. Crowding thus results from additional constraints on visual processing that limit representational fidelity. Understanding the nature of these constraints and determining how they limit visual processing in computational terms is an ongoing enterprise. There are a range of factors that alter crowding strength, and the effects of manipulating flanker/target similarity (Bernard & Chung, 2011), the geometric arrangement of flankers relative to targets (Manassi, Sayim & Herzog, 2012), and other spatial and temporal factors that influence performance (Kooi et al., 1994), all offer important constraints on the computational mechanisms that lead to crowding, and by extension, may also govern a wide range of phenomena observed in peripheral vision (Rosenholtz, 2011). Here, I consider how these mechanisms may govern the perception of numerosity in peripheral vision using a recent model of peripheral visual function to explain recent empirical data.

A key issue in understanding how peripheral vision works is characterizing the nature of integration in peripheral vision. A fundamental assumption of most descriptions of crowding and related phenomena is that image structure is somehow pooled over increasingly large chunks of the visual field as eccentricity increases. In the context of crowding, the size of the regions in which crowding occurs scales with eccentricity (Pellu & Tillman, 2008; Rosen, Charkravarti & Pelli, 2014), a relationship that is referred to as Bouma’s Law (Bouma, 1973). This is a quantitative description of where information is pooled, but it does not tell us how information is pooled. Subjectively, peripherally-viewed image features often appear jumbled or mixed together, but what is the nature of that jumbling and mixing? What processes lead to a description of image structure such that visual features appear to be re-arranged and combined in strange ways? One proposal is that image structure may be represented by summary statistics that describe visual features using distributional information (e.g. texture descriptors), leading to a histogram-like representation of appearance that is sufficient to capture some aspects of what objects or targets are present in a peripheral region, but that lacks joint encoding of form and location. In general, models based on summary statistics record some information about what features were present in a stimulus, but tend to lack information about where those features were and how they co-occurred spatially with other features. Initially, summary-statistic models of crowding used very simple distributional measurements to account for behavior. For example, Parkes et al. (2001) suggested that stimulus averaging within a crowded array could explain observers’ responses in an orientation discrimination task. Rather than representing each item in a crowded array, their proposal was that observers were subject to compulsory averaging of the orientations in the stimulus and made responses based on that average. While adequate for simple scenarios (e.g oriented bars) it is difficult to understand exactly what averaging would mean for an array of complex objects (Wallace & Tjan, 2011). Recently, texture-based summary-statistic models that address this issue have been applied to a range of problem domains. Such models rely on texture features to describe image structure and are applicable to arbitrary image inputs. Also, using models that support texture synthesis makes it possible to test model predictions behaviorally using “mongrel” images that reflect the image constraints imposed by the statistical descriptors imposed by the model. If the model captures the information loss imposed by peripheral vision, then performance with original images presented in the periphery should match performance with mongrels. In several recent reports, performance with mongrels generated using the Portilla-Simoncelli texture synthesis algorithm (Portilla & Simoncelli, 2000) does correlate significantly with performance in peripheral tasks, suggesting this is a useful model of peripheral encoding. For example, Balas, Nakano & Rosenholtz (2009) demonstrated that mongrels could account for performance across a range of visual crowding tasks. Visual search performance, which depends on observers’ ability to identify candidate target locations in the periphery, is also accounted for by mongrels that reflect local summary statistics (Rosenholtz et al., 2012). More broadly, the texture statistics in the Portilla-Simoncelli model may be a good approximation of mid-level computations that are carried out in area V2 (Freeman et al. 2013) that are used to encode scene structure across the visual field (Freeman & Simoncelli, 2011). This particular set of summary statistics is thus a promising candidate model of peripheral visual function that may explain performance in many tasks.

In the present study I have applied the model to numerosity perception in the visual periphery, which is an interesting problem domain for several reasons. Perceived numerosity in large arrays of items appears to depend upon texture-like properties of the array including density and local area computations (Durgin, 2008; Raphael, Dillenburger, & Morgan, 2013), suggesting that texture features may be appropriate descriptors of array appearance. Though numerosity judgments are not necessarily texture-based in all settings (Mandler & Schebo, 1982; Palomares et al., 2011), texture representations do appear to be employed for numerosity judgments as a function of stimulus features like array density. For example, Anobile, Cicchini & Burr (2014) demonstrated that when element density is relatively low, numerosity discrimination thresholds have a constant Weber fraction (linear increases as a function of numerosity). However, when density is comparatively high, numerosity discrimination thresholds increase according to a square-root law, which suggests a different, texture-like, mechanism for low vs. high-density arrays.

Perceived numerosity has also been shown to change as a function of peripheral viewing in ways that are consistent with visual crowding. The aforementioned transition between linear vs. square-root threshold increases as a function of numerosity occurs at different dot densities as a function of eccentricity, for example, such that texture mechanisms appear to be utilized at lower densities in the periphery (Anobile et al., 2015). This dependence on eccentricity is consistent with the impact of visual crowding on other tasks, and the square-root dependence between discrimination thresholds and numerosity further supports the use of texture descriptors as a tool for understanding peripheral numerosity in particular. Moreover, there are further unique features of how number is perceived in the periphery that are intriguing targets for a model of peripheral vision. Specifically, Valsecchi, Toscani, & Gegenfurtner (2013) showed that the numerosity of peripherally-viewed arrays of dot is reduced relative to numerosity perceived in the fovea. They reported that numerosity was reduced by approximately 60–80% depending on the specific stimulus configuration and eccentricity used in their experiments, suggesting that the appearance code that supports peripheral visual processing represents the array in such a way that number is consistently reduced. By manipulating various stimulus properties including the minimum distance between elements, the authors demonstrated that visual crowding may drive this effect. Given the success of explaining visual crowding via specific summary statistics and the evidence indicating that crowding contributes to behavioral performance in peripheral numerosity perception, I therefore chose to investigate whether the Portilla-Simoncelli texture statistics could account for the reduction in perceived numerosity reported by Valsecchi, Toscani, & Gegenfurtner.

Specifically, I focused on examining whether parameter values that were sufficient to explain observers’ performance in previously reported visual crowding tasks (Balas, Nakano & Rosenholtz, 2009) yielded numerosity underestimates when the model was presented with arrays similar to those used in Valsecchi et al. (2013). In particular, I chose to examine whether the model could account for the amount of underestimation when randomly-placed dots were presented to observers in the periphery and also whether the model would exhibit similar sensitivity to varying inter-dot distance. Overall, these simulations reveal that decreased numerosity emerges naturally from the model in all conditions. However, while the quantitative fit is good when randomly-placed dots are used as target stimuli, the model does not exhibit sensitivity to inter-dot distance that is consistent with human performance. Despite this shortcoming, I also demonstrate that the model exhibits sensitivity to element shape, which represents a novel prediction regarding peripheral numerosity perception that remains to be tested in human participants. These particular summary statistics thus offer limited explanatory power for understanding peripheral numerosity perception, which constrains the scope of this model of peripheral vision. Nonetheless, I argue that the model may still suggest interesting directions for future research and also discuss principled extensions of the model that may reveal critical properties of peripheral vision that must be adequately characterized to increase the generality of summary-statistic models of the periphery.

Methods

In the simulations I report here, my aim was to examine three distinct aspects of peripheral numerosity perception, two of which were reported by Valsecchi et al. (2013) and a third scenario that has not been tested psychophysically. With regard to the former, I carried out simulations to determine: (1) If peripheral numerosity would be underestimated in “mongrel” images created using the Portilla-Simoncelli algorithm, and (2) If varying the minimum inter-dot distance between elements in a peripherally-viewed array would affect underestimation in mongrel images. With regard to the latter, I carried out additional simulations to determine if changing element shape (dots vs. crosses/circles, e.g.) led to changes in numerosity underestimation. In general, the model supports quantitative measurement of the amount of underestimation, allowing direct comparison between human observers and the model.

Creating dot arrays

To generate the arrays that mongrel images would be based on, each simulation began by plotting randomly-placed elements using basic graphing routines in Matlab. To examine peripheral numerosity subject to random element placement (Exp. 1), element positions were sampled from a regular grid spanning 0–255 units in both the x and y-axes, with element centers spaced 10 units apart (to eliminate overlap) within a bounding frame 10 units wide (to eliminate elements being cut off during plotting). Each dot was then randomly perturbed horizontally and vertically by sampling x and y displacements independently from a normal distribution with zero mean and a standard deviation of 2 units. To examine the impact of clustering (varying inter-element distance) on peripheral numerosity (Exp. 2), element positions were sampled according to a satellite algorithm (Allik & Tuulmets, 1991) that guarantees that each newly-sampled element is positioned within some fixed distance from a previously plotted element. Finally, to examine the potential effects of element shape on numerosity perception (Exp. 3), the markers used to plot randomly selected points could either be dots (closed circles), crosses, or naughts (open circles). In all cases, the Matlab plot depicting all of the dots was resized (if necessary) to 256×256 pixels before texture analysis and synthesis.

Synthesizing “mongrels” from dot arrays

To create a mongrel from each simulated dot array, I applied the Portilla-Simoncelli texture synthesis algorithm to each image. This involves first using analysis routines to describe the target image using a set of joint wavelet statistics. The analysis algorithm includes free parameters that specify the number of spatial scales (N_sc) used to compute wavelet coefficients, the number of orientation bands (N_or) used to describe image structure, and the size of the spatial neighborhood (N_neigh) over which local correlations are computed. I chose these parameter values to match those reported in Balas, Nakano, & Rosenholtz (2009) to test the hypothesis that values that proved adequate for accounting for visual crowding may also account for numerosity underestimation in the periphery (N_sc=4, N_or=4, N_neigh=9). Following texture analysis, synthesis proceeded by generating a random starting image and adjusting this image iteratively until it matched the target image’s statistics (Figure 1).

Figure 1.

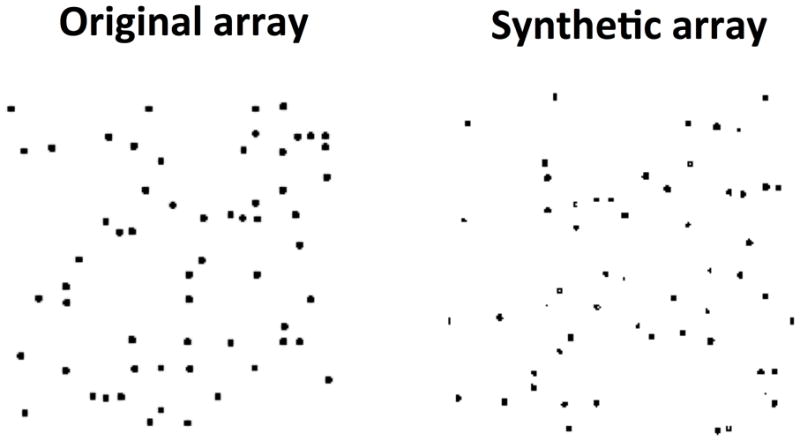
An example of an original dot array and a synthetic array created from this parent image. These images have been processed per the description in the text, which includes resizing of the original array and thresholding of both the original and synthetic arrays to yield a binary image.

Counting dots in original and synthetic arrays

To objectively measure numerosity in each dot array, I applied morphological operators to thresholded versions of the original and synthetic arrays generated for each simulated trial. The synthetic arrays were histogram-matched to the parent image used to generate them, and an intensity threshold was applied to both images to convert them to binary images. Both images consistently had bimodal intensity histograms with narrow peaks centered near intensity values of 2 (near-black) and 200 (near-white), making it possible to impose a threshold in between these values without concern that the outcome depended critically on the exact intensity threshold used. Next, I applied Matlab functions for labeling contiguous regions to obtain the size of each black region in both the original and synthetic image. Each original and synthetic array was thus described in terms of the number of segmented regions in the thresholded image. Regions in the synthetic array were only counted if they were at least as large as the smallest region in the original array. In keeping with the original report by Valsecchi et al., I expressed model performance using the ratio of dot numerosity in the synthetic image relative to its parent. Perfect performance would yield a ratio of 1, while overestimates would be larger and underestimates smaller than this. For each combination of stimulus parameters (target numerosity, clustering conditions) I conducted 50 simulations to obtain mean underestimation ratios and bootstrap estimates of 95% confidence intervals.

Results

To summarize the results of the model, I briefly describe the parameters that were allowed to vary across the three experimental scenarios I considered here and report underestimation ratios for all conditions as compared to the results reported in Valsecchi et al. (2013).

Experiment 1 – Random Dot Placement

In these simulations, target numerosity was either 30, 60 or 90 dots and elements were randomly positioned in the original arrays. Dot size was set to a Matlab marker size of 18 units. The observed underestimation ratios for each target numerosity (with 95% confidence intervals are listed in Table 1.

Table 1.

Mean underestimation ratios for dots as a function of target numerosity. Values in brackets represent 95% confidence intervals of the mean.

	Mean underestimation ratio
30 dots	85.2% [82%–88%]
60 dots	85.4% [83%–87%]
90 dots	86.0% [84%–87%]

These ratios exhibit the stability across target numerosities reported in Valsecchi et al. (2013) and are quantitatively a good fit to their results from the 12-degree eccentricity condition in their Exp. 1 (These means vary between 79%-85% across the same target numerosities).

Experiment 2 – Clustering

In these simulations, target numerosity was either 20, 40, or 60 dots. For each target numerosity, the minimum allowed inter-dot distance was controlled via “Satellite” sampling to yield “small”, “medium” and “large” clustering. In Table 2, I have listed the mean underestimation ratio for each condition along with 95% confidence intervals. At best, the model exhibits only a mild sensitivity to clustering (an increase of approximately 5% between the small and large clustering conditions), which is far smaller than the approximately 30% difference reported in Valsecchi et al.’s Exp. 2. Clustering thus matters somewhat to the model, but not nearly as much as it matters to human observers.

Table 2.

Mean underestimation ratios as a function of inter-element distance (clustering) and target numerosity. Values in brackets represent 95% confidence intervals of the mean.

	20 elements	40 elements	60 elements
Small	80.2% [75%–86%]	81.0% [79%–83%]	84.4% [82%–87%]
Medium	84.6% [72%–99%]	83.3% [77%–87%]	83.0% [80%–85%]
Large	86.4% [84%–89%]	86.5% [82%–88%]	86.5% [85%–89%]

Experiment 3 – Element Shape

In these final simulations using Portilla-Simoncelli mongrels (which have not been tested psychophysically), target numerosity was either 40 or 60 elements. For each numerosity, target shape was either dots (closed circles) 18 units in size, crosses that were 8 units in size, or naughts (open circles) that were also 8 units in size. The marker size of naughts and crosses was selected so that element size in the original arrays would be matched when naughts and crosses were drawn with a line of sufficient thickness to guarantee that elements in the original images were counted correctly using our morphological operators. The mean underestimation ratio for each condition with associated 95% confidence intervals is listed in Table 3. At both target numerosities, underestimation varies with shape: crosses lead to greater underestimation than dots, and naughts lead to even greater underestimation.

Table 3.

Mean underestimation ratios as a function of element shape and target numerosity. Values in brackets represent 95% confidence intervals of the mean.

	40 elements	60 elements
Dots	85.3% [84%–86%]	85.9% [84%–87%]
Crosses	76.8% [73%–78%]	78.0% [75%–80%]
Naughts	66.8% [64%–70%]	66.6% [65%–68%]

Image blur as an alternate model of peripheral numerosity

Finally, to assess whether or not increased image blur in peripheral vision could also account for the results, I carried out additional simulations in which I generated “blur mongrels” made by convolving the original dot arrays with Gaussian filters with increasingly large spatial kernels. In these simulations, I observed a clear effect of target numerosity on the underestimation ratio – for numerosities of 30 or 60 dots, even severe blur tended to yield underestimation ratios of approximately 90%, while the same amount of blur applied to an array of 90 dots yielded a much larger underestimation ratio of approximately 15–20%. These effects were further exacerbated when clustered dots were used, since small inter-dot distance could lead to arrays that were dramatically underestimated due to the vast majority of dots being blurred together. This discrepancy between an extreme effect of target numerosity on “blur mongrels” and the lack of such an effect in human observers suggests that reduced numerosity is likely not the result of blur, which is consistent with arguments made in prior reports.

Discussion

These simulations demonstrate that some (but not all) aspects of peripheral numerosity perception emerge naturally from a summary-statistic model of peripheral vision. This is consistent with an emerging computational description of peripheral vision in terms of the constraints imposed by a texture-like statistical code for appearance (Rosenholtz, 2011) and also with the proposal that perceived numerosity depends on crowding and texture statistics in some settings. The model is limited in scope, however. While performance when dots are placed randomly is quantitatively good, it fails to reproduce the phenomenology associated with dot clustering. This latter outcome complicates matters a good deal, because the psychophysical impact of clustering (and related results concerning element density) is an important piece of supporting evidence for the putative relationships being explored here between peripheral vision, visual crowding, texture representations, and numerosity perception. I conclude by discussing the implications of the limited success of the model first, then consider how the model may be extended in a principled fashion to account for a broader range of data.

To speak first of what the model can do, like prior reports describing correspondences between summary-statistic codes for appearance and the perception of peripheral targets, I find that the basic phenomenology of a task that depends on peripheral vision is a natural consequence of using texture features to describe discrete objects: Mongrels underestimate numerosity. Critically, the observation that the same parameter values that predict visual crowding performance across a range of conditions also account for perceived numerosity in arrays of randomly-placed dots (Exp. 1) suggests that at least in some cases, numerosity judgments are affected by the information lost due to the imposition of an image-based texture representation of image structure. An advantage of this model is that it requires neither an explicit description of items in an array in terms of their position or “occupancy” (Allik & Tuulmets, 1991), nor does it depend on special computations that capture numerosity/density (Dakin et al., 2011). Instead, the model depends on a general texture-based description of appearance that can be applied to arbitrary inputs. This does not preclude specific mechanisms for number processing that operate at later stages of visual cognition, but does offer a means of accounting for some properties of number perception in terms of lower-level processes. This model also succeeds where some simpler ones fail: Estimating numerosity after blurring dot arrays has a tendency to lead either to catastrophic amounts of underestimation as clustering or target numerosity increases, or to lead to very little underestimation at all.

But what to make of the failure to reproduce the effects of clustering? This obviously signals that this model (which has been successful in many domains) fails to capture some feature of peripheral vision or numerical cognition. That the model has such a limit is not surprising and delineating the boundaries of the model’s ability to account for behavior is an important step towards developing better theories of peripheral vision. Though mongrel-like images of natural scenes have been described as metameric stimuli that make it possible to assay specific stages of processing along the ventral visual stream (Freeman & Simoncelli, 2011), it is also the case that adult observers are quite sensitive to discrepancies between natural images and synthetic images made from them (Balas, 2006; Wallis, Bethge & Wichmann, 2016). Portilla-Simoncelli mongrels are thus known to not capture all the information observers have access to in peripheral vision, and here we are likely seeing a consequence of that imperfect representation. Applying full-field texture synthesis with multiple, overlapping pooling regions (per Freeman & Simoncelli, 2011) may be one way to extend the scope of the current model in a principled fashion, and perhaps this may account for a wider range of phenomena in this domain. Alternatively, it may also be necessary to include a wider class of texture descriptors (center-surround descriptors, e.g.) to arrive at a more expressive vocabulary for peripheral image structure. Of course, it may also be the case that there are simply other mechanisms at work here, and this is as far as summary statistics will take us in terms of understanding how numerosity is perceived.

With regard to this latter possibility, however, I want to emphasize the novel results included here regarding the impact of shape on underestimation. To my knowledge, this outcome has not been observed experimentally and contradicts the overall characterization of number perception as being sufficiently abstract to be robust to manipulations of element shape or orientation. While the current model clearly has limits, its moderate success also argues for its utility as a means of generating novel hypotheses regarding peripheral vision. My results suggest in part that we need a better model of the periphery to account for some of the ways people perceive number, but they also suggest that we can potentially learn more about how peripheral vision in general (and number perception in particular) works by querying appearance-based models like this one. I conclude therefore, that while summary-statistic representations of the periphery cannot currently get us all the way towards a comprehensive account of peripheral numerosity, they offer enough explanatory power to be an important platform for further exploration of peripheral visual function.