Progression from latent infection to active disease in dynamic tuberculosis transmission models: a systematic review of the validity of modelling assumptions

Abstract

Mathematical modelling is commonly used to evaluate infectious disease control policy and is influential in shaping policy and budgets. Mathematical models necessarily make assumptions about disease natural history and, if these assumptions are not valid, the results of these studies can be biased. We did a systematic review of published tuberculosis transmission models to assess the validity of assumptions about progression to active disease after initial infection (PROSPERO ID CRD42016030009). We searched PubMed, Web of Science, Embase, Biosis, and Cochrane Library, and included studies from the earliest available date (Jan 1, 1962) to Aug 31, 2017. We identified 312 studies that met inclusion criteria. Predicted tuberculosis incidence varied widely across studies for each risk factor investigated. For population groups with no individual risk factors, annual incidence varied by several orders of magnitude, and 20-year cumulative incidence ranged from close to 0% to 100%. A substantial proportion of modelled results were inconsistent with empirical evidence: for 10-year cumulative incidence, 40% of modelled results were more than double or less than half the empirical estimates. These results demonstrate substantial disagreement between modelling studies on a central feature of tuberculosis natural history. Greater attention to reproducing known features of epidemiology would strengthen future tuberculosis modelling studies, and readers of modelling studies are recommended to assess how well those studies demonstrate their validity.

Introduction

Latent infection is a defining feature of tuberculosis epidemiology. On infection with Mycobacterium tuberculosis, approximately 5% of otherwise healthy adults will develop active disease within 2 years (so-called fast progressors).^1,2 Individuals who do not have rapid progression are classified as having slow-progressing latent tuberculosis infection. With latent infection, individuals experience no adverse health effects and will not transmit M tuberculosis, but they face an ongoing risk of developing active tuberculosis through reactivation. For individuals with long-established infection, the annual risk of active tuberculosis is low; empirical estimates are on the order of 10–20 per 100 000 individuals.³ However, as a result of high prevalence of latent tuberculosis infection in many settings,⁴ reactivation can represent a substantial proportion of incident tuberculosis cases, or even the majority of such cases in settings in which transmission has been in sustained decline.⁵ The risk of progressing to active disease also varies by individual characteristics, with infants,⁶ individuals with advanced HIV infection,^7,8 and individuals with other conditions that affect immune function^9–12 having elevated progression risks.

Since tuberculosis interventions can prevent transmission, they generate benefits beyond the individuals receiving the intervention. Furthermore, the potential delay between infection and disease means that the consequences of improved control can be spread over many years. For these reasons, it is difficult for empirical tuberculosis policy evaluations to capture all effects, and studies that forecast future disease trends or compare competing disease control policies commonly estimate results using dynamic transmission models. These models represent the mechanisms of transmission, natural history, and health system interactions that generate tuberculosis outcomes.^13,14 Despite more than a century of epidemiological research into tuberculosis, concrete evidence for these underlying processes is imperfect,¹⁵ and studies have taken various approaches for constructing and parameterising transmission models. This variation can be consequential: in a modelling collaboration examining the post-2015 End TB Strategy,¹⁶ variation in epidemiological assumptions was identified as a cause of the wide range of estimates produced for the health impact¹⁷ and cost-effectiveness¹⁸ of expanded tuberculosis control. Several reviews^13,14,19 have described standard tuberculosis modelling approaches, and methodological studies^20–25 have examined specific modelling approaches. However, little systematic investigation has been done of assumptions made by published tuberculosis models. If these assumptions are not valid, the results of these studies could be biased.

To assess the validity of assumptions about progression to active disease after initial infection, we did a systematic review of published studies using dynamic tuberculosis transmission models. We describe how these studies modelled progression from initial infection to active disease, and the implications of these assumptions for predicted tuberculosis outcomes. We compare model predictions with empirical data^26–28 and discuss the consequences for future modelling studies.

Methods

Search strategy and selection criteria

We identified eligible studies by searching PubMed, Web of Science, Embase, Biosis, and Cochrane Library. We also searched a publication database compiled by the TB Modelling and Analysis Consortium,²⁹ reference lists of eligible publications, several non-indexed journals, and the personal databases of the authors to identify publications not included in the electronic search (appendix p 2). We collected studies from the earliest available date (Jan 1, 1962) to Aug 31, 2017. We included published studies using transmission dynamic models of tuberculosis in human populations to describe tuberculosis epidemiology or to evaluate competing policy options. We excluded analyses in which the force of infection was not modelled (ie, were not transmission dynamic models) and studies that provided insufficient information to describe the model structure representing progression to active disease after initial infection, the associated parameter values, and the population group (or groups) represented by the model, such that we could not reconstruct this part of the model. We also excluded non-English language studies and unpublished reports. As one intent of this Review is to describe the quality of assumptions made by modelling studies, we did not exclude studies on the basis of quality criteria. The quality of studies was judged by their ability to reproduce empirical data, and these findings are reported in the results section. No additional quality assessment was done. We followed Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines³⁰ and registered our protocol with PROSPERO (CRD42016030009).

Identification of studies

Titles and abstracts of collected studies were screened by one of two reviewers (EW and MB) to remove studies not meeting the inclusion criteria that could be judged on the basis of the title and abstract alone (eg, non-English language studies and non-transmission dynamic models). We retrieved the full texts for the remaining articles. Articles were assessed independently by two of five reviewers (ANS, EW, DC, KG, and MB) to confirm that they met inclusion criteria. Disagreements were resolved by discussion between the two reviewers.

Extraction

For each study, we extracted bibliographic information as well as information on the study setting and how the model stratified the population by tuberculosis progression risk. For each of these model strata, we extracted data on model structure and parameter values describing tuberculosis progression. We also extracted the citations provided for parameter values. We did not extract information on tuberculosis progression risks after reinfection in previously exposed individuals, for whom risks of primary progressive tuberculosis are lower than for unexposed individuals.³¹

We developed a typology of model structures and categorised models according to this typology (figure 1). In cases in which several different parameterisations were provided for the same population group, we used the values provided for the main analysis. If a study provided a point estimate as well as upper and lower bounds, we extracted the point estimate, and if a study only provided upper and lower bounds, we took the arithmetic mean of these values. For each paper, extraction was undertaken independently by two of five reviewers (ANS, EW, DC, KG, and MB). When extracted values differed between reviewers, the article was reviewed by an additional reviewer (NAM), and disagreements were resolved through discussion between the two reviewers and NAM.

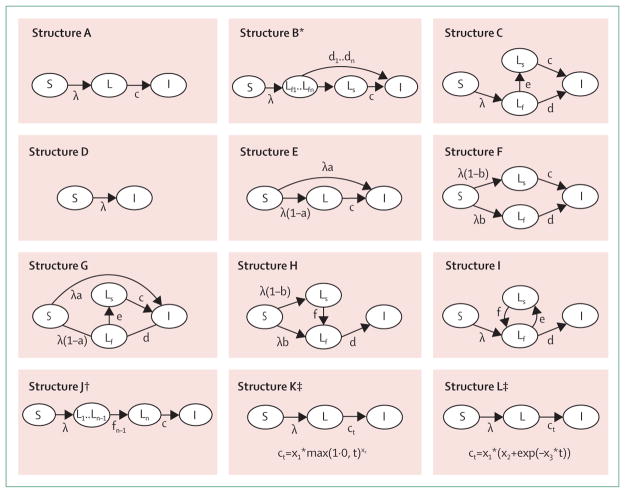
Figure 1. Classification of model types and transition probabilities.

Some model structures are special cases of other structures. For example, structures A and C are special cases of structures E and G, with parameter “a” set to zero. S=susceptible compartment (not infected with tuberculosis and not previously exposed). λ =force of infection for Mycobacterium tuberculosis. L=latent M tuberculosis infection compartment. c=rate of progression to active tuberculosis for individuals in the latent compartment or slow latent compartment. I=active tuberculosis disease compartment. L_s=slow latent M tuberculosis infection compartment. L_f=fast latent M tuberculosis infection compartment. f=rate of transition to the fast latent compartment for individuals in the slow latent compartment. d=rate of progression to active tuberculosis for individuals in the fast latent compartment. e=rate of transition to the slow latent compartment for individuals in the fast latent compartment. a=probability of immediate progression to active tuberculosis compartment, for individuals in susceptible compartment who are infected with M tuberculosis. b=probability of progression to fast latent compartment, for individuals in susceptible compartment who are infected with M tuberculosis. *Structure B involves a set of tunnel states for recent latent infection (L_f1..L_fn), whereby individuals not progressing to active tuberculosis transition deterministically to next tunnel state (n+1) at each time step. Each of these compartments has a different progression risk (d₁..d_n). †Structure J involves a sequence of latent compartments (L₁..L_n), with individuals only transitioning to the active tuberculosis compartment from the final compartment. ‡Structures K and L involve a single latent compartment, with the rate of transition to active tuberculosis calculated as a function of time since infection. Both of these structures were implemented using individual-based models, allowing time since infection to be tracked at the individual level.

Descriptive statistics

We calculated statistics to describe the distribution of studies according to publication year, setting, model structure, and population groups represented by model strata. We also identified the most commonly cited sources for model parameters.

Quantitative comparison of model predictions

We recreated the formulae of each model determining the risk of active tuberculosis for an individual initially infected with M tuberculosis, matching the model structures shown in figure 1. Using these formulae, and the parameter values extracted for each study and population group, we estimated the annual incidence of tuberculosis after initial infection in the absence of reinfection. For some studies, this evaluation involved modifications to the original approach. Whereas some studies implemented their analyses by sampling progression parameters from a distribution, we used the point estimate (commonly the distribution mean) reported in the original paper. Even if the point estimate is equal to the mean of the parameter distribution, small differences in simulation results can be produced because of the non-linear relationship between parameters and modelled outcomes. Some studies reported adjusting parameter values as part of model calibration, but did not report these adjusted values, and in these cases we used the original (unadjusted) values reported in the paper. In some models, individuals progress through multiple epidemiological or demographic processes simultaneously. If these processes influence tuberculosis progression or survival risks (eg, ageing and HIV progression), then accurately reproducing long-term cumulative incidence estimates is impossible without reconstructing all of these different model components. Because we only reconstructed the tuberculosis-specific parts of these models, we do not report long-term cumulative incidence estimates in the presence of time-varying risk factors. We did not allow for background mortality. Although cumulative incidence estimates would be lower if background mortality were considered, this effect will be minor unless mortality rates are very high.

We stratified incidence predictions according to model structure, publication year, individual risk factors, study setting, and source of parameter assumptions. High-burden settings included countries on the WHO list of 30 countries with a high tuberculosis burden³² or, if a country was not specified, settings with an incidence of 100 per 100 000 individuals or higher. Low-burden settings included countries not on the WHO list or with an incidence below 100 per 100 000 individuals. Studies with multiple HIV strata used various approaches for describing HIV progression. Late HIV was used for strata described as AIDS, WHO stage 4 disease, advanced HIV, or with a CD4 cell count of less than 200 cells per μL. Early HIV was used for HIV strata not classified as late HIV, in models with multiple HIV strata. We also distinguished model strata for HIV-positive individuals receiving antiretroviral therapy (HIV, on antiretroviral therapy). For age, we classified strata as infant, if the midpoint of the age group fell in the range 0–2 years, and classified strata as children (excluding infants) if the midpoint of the age band fell in the range 2–10 years. We divided studies into those published in 2010 or before (the median publication year) and those published after 2010, and according to whether the study cited any previous publications to justify parameter values for progression of latent tuberculosis infection.

We plotted annual and cumulative incidence predictions to understand the behaviour of each model and summarised results as cumulative incidence at 2 and 20 years. The 2-year timepoint was chosen to represent rapid progression to active disease (primary progressive tuberculosis), and the 20-year timepoint to represent aggregate long-term risk. For studies of multiple population groups with different tuberculosis risk factors, we calculated risk ratios for tuberculosis incidence over the first 2 years, and for the 20th year, to provide within-study comparisons of how risk factors were treated.

Comparison with empirical evidence

We reviewed the tuberculosis literature to identify studies reporting direct empirical evidence on progression risks following initial infection. To identify these studies, we reviewed citations known to the authors, studies cited in related reviews, and evidence cited in the studies included in the systematic review. Because preventive treatment for latent tuberculosis infection reduces progression risks, the best evidence on natural history comes from historical studies done before preventive therapy became the standard of care for recently exposed individuals.³³ Narrative reviews of these early studies have been compiled by Ferebee,¹ Sutherland,² and Styblo.³⁴ From these reviews, we extracted information on studies reporting quantitative estimates of annual risks of developing active tuberculosis after initial infection. Many of these studies had major limitations for estimating general population progression risks in the absence of reinfection, including small sample sizes, non-representative populations, settings that were likely to feature ongoing transmission, and non-specific tuberculosis diagnostics. For other studies, the relevant features of study design, population, and setting were not sufficiently described or the original publication was not available. Two studies provided precise estimates of tuberculosis progression risks in the years following initial infection. In both cases, these estimates were from the control arm of an intervention trial: the British Medical Research Council’s BCG trials,^26,27 which included 12 867 individuals in the unvaccinated study arm, and the US Public Health Service’s trials of isoniazid prophylaxis for tuberculosis household contacts,²⁸ which included 12 594 individuals in the control arm. Using summary data from these two studies, we generated estimates of annual tuberculosis incidence for 10 years following tuberculin skin test conversion. We limited these comparisons to the first 10 years following infection to reduce the influence of attrition on the validity of empirical estimates. We compared these empirical estimates to model predictions for population groups with no individual risk factors affecting tuberculosis progression risk. All analyses were done in R version 3.3.2.³⁵ Replication data and analysis scripts are available at Harvard Dataverse.

The capacity of a model to fit the empirical estimates is determined by the model structure and the parameter values used. To separate these two factors, we assessed whether each model structure was capable of reproducing the empirical results by adjusting the parameter values. To do so, we created a simple loss function using the results from the British Medical Research Council’s BCG trials.²⁶ This loss function represented the root mean squared error between model results and the empirical estimate for cumulative tuberculosis incidence over the first 10 years after infection. We used optimisation algorithms (the Nelder-Mead and Broyden-Fletcher-Goldfarb-Shanno algorithms operationalised by the optim function in R) to identify parameter values that minimise the loss function. We compared the predictions from these fitted models to the empirical estimates to understand the extent to which each model structure was capable of reproducing this evidence.

Results

Descriptive statistics on eligible studies

We identified 5532 unique articles in the first stage of the review, and excluded 5006 of these papers through title and abstract review, and a further 214 through full-text review. 312 studies met inclusion criteria and were included in the analysis (figure 2; appendix pp 3–21).

Figure 2. Flow diagram of studies assessed for the review.

*Other sources included a database of modelling publications compiled by the TB Modelling and Analysis Consortium, the reference lists of eligible publications, a group of non-indexed journals, and the personal databases of the authors to identify publications not included in the electronic search.

The earliest study included in the Review was published in 1962, and 7% of studies were published before 2000. Of the 312 studies in the review (table), many included multiple strata to allow for differences in progression risk. A total of 680 observations were included in the analysis, where an observation represented an individual stratum within an included study. Most studies (62%) considered high-burden settings, and 39% included model strata considering individual-level factors that modify tuberculosis progression. The most common risk factor considered by these studies was HIV (25%), followed by age (9%). 12 different model structures were used by these studies (figure 1; appendix pp 22–23).

Table.

Descriptive statistics of included studies

	Number of publications (% of total)
Publication year
1960–69	4 (1·3%)
1970–79	1 (0·3%)
1980–89	1 (0·3%)
1990–99	15 (4·8%)
2000–09	95 (30·4%)
2010–17	196 (62·8%)
Model structure*
A	60 (19·2%)
B	27 (8·7%)
C	33 (10·6%)
D	3 (1·0%)
E	153 (49·0%)
F	35 (11·2%)
G	1 (0·3%)
H	2 (0·6%)
I	2 (0·6%)
J	1 (0·3%)
K	1 (0·3%)
L	1 (0·3%)
Setting*
High burden	193 (61·9%)
Low burden	72 (23·1%)
Not specified	72 (23·1%)
Risk strata*
Age	29 (10·0%)
Drug resistance	10 (3·2%)
Foreign born	5 (1·6%)
Genetic susceptibility	4 (1·4%)
Poverty	1 (0·3%)
Rural vs urban	1 (0·3%)
Sex	2 (0·7%)
Smoking	4 (1·4%)
Incarceration	2 (0·7%)
Diabetes	2 (0·7%)
Famine vs nutrition	2 (0·7%)
Hepatitis B virus	1 (0·3%)
HIV	79 (27·1%)
Malaria	1 (0·3%)
Silicosis	2 (0·7%)
Any risk stratification	122 (39·1%)

See figure 1 for the model structures.

^*Categories sum to more than 100% because some papers are included in multiple categories (ie, use multiple different structures, present results for multiple settings, or stratify progression risk along multiple dimensions).

We identified the sources for tuberculosis progression parameters most commonly cited by the studies in the review. The three most commonly cited sources were Vynnycky and Fine³⁶ (cited by 21% of all studies), Blower and colleagues³⁷ (12%), and Dye and colleagues³⁸ (10%), all of which are modelling papers included in our Review. The top 15 most cited sources included a mix of modelling studies, empirical studies, and review articles (appendix p 24). However, for 76 studies (24%), no citation was given for tuberculosis progression parameters.

Comparison of model predictions for population groups with no individual risk factors

We stratified model results by the population groups represented, study setting, model structure, and other study characteristics. Figure 3 presents model predictions of annual and cumulative tuberculosis incidence for model strata with no individual risk factors affecting tuberculosis progression, including model strata for healthy adults or for the overall population in those cases in which models did not stratify by age or other risk factor.

Figure 3.

Model predictions for annual (A) and cumulative (B) incidence of active tuberculosis by years since infection, for population groups with no individual risk factors

We calculated the median prediction for annual and cumulative incidence for each year. Median annual incidence dropped from 77 cases per 1000 in the first year following infection to 1·7 per 1000 by year 20. Median cumulative incidence was 7·7% after the first year and 14·2% by the end of year 20. Substantial variation was found between the predictions of individual models, with incidence rate predictions varying by several orders of magnitude. For the first year after infection, the 90th percentile of incidence rate estimates was 52 times the 10th percentile (270 vs 5·2 per 1000). For the 20th year, the same ratio was 786 (102 vs 0·13 per 1000). This variation is also evident in the cumulative incidence projections, with a ratio of 26 after 20 years (90% vs 3·5%).

Comparison of model predictions for different strata

Figure 4 presents the distribution of cumulative incidence predictions for various subsets of the model predictions after 2 years (commonly used to distinguish rapid progression from late reactivation) and 20 years. Cumulative incidence predictions were higher for strata including any individual risk factor, particularly HIV, than for those with no risk factors. Cumulative incidence predictions were higher for infants than for non-infant children. Distributions were approximately similar for studies done in high-burden and low-burden settings. Results for studies reporting no citations for tuberculosis progression parameters showed greater variation than did those with at least one citation, particularly for 20-year results. Studies published after 2010 had greater variation in 20-year cumulative incidence than did those published before that point. Results for the different model structures were somewhat similar except for structure A, which exhibited greater variation in cumulative incidence at both 2 and 20 years, and substantially higher median incidence at 20 years, than did other model structures. Median annual and cumulative incidence projections were stratified by model structure (appendix p 25). Whereas the trajectories of annual incidence differed by model structure, predictions produced using structure A were noticeably different from those produced by the majority of other structures, with no reduction in annual incidence over time, and steadily increasing cumulative incidence (this trend is also observed for predictions produced using structure J, although this approach was only used by one study).

Figure 4. Distribution of model predictions for cumulative incidence of active tuberculosis at 2 (A) and 20 (B) years since Mycobacterium tuberculosis infection; stratified by model structure, individual risk factors*, and other study characteristics.

ART=antiretroviral therapy. *Individual results not shown for structures D, G, H, I, J, and K, as less than five studies used these structures to model individuals with no other risk factors. †Only includes results for population groups with no individual factors modifying tuberculosis progression risks. ‡20-year cumulative incidence projections are not shown for these groups because of potential for unmodelled changes in risk factors.

We calculated incidence risk ratios associated with individual risk factors compared with model strata from the same study without the risk factor (ie, within-study comparisons; appendix p 26) and these results corroborate those shown in figure 4, with greater tuberculosis progression risk modelled for all forms of HIV (particularly advanced HIV), and reduced risk associated with provision of antiretroviral therapy for HIV treatment and late childhood. No clear trend was observed for the infant category: some models suggested increased risk and some suggested reduced risk compared with adulthood, with the median risk ratio close to 1·0. Much variation was seen between models across all of these comparisons, with the range of risk ratios for each comparison spanning several orders of magnitude.

Comparison of model predictions to empirical data

Figure 5 shows a comparison of the distribution of incidence predictions for population groups with no individual risk factors (5th, 25th, 50th, 75th, and 95th percentiles) with empirical estimates for these same quantities. Although the model results reproduce the general trend of the empirical estimates, with annual incidence rates declining over time, much greater variation exists in the modelling results than in the empirical results, and median cumulative incidence after 10 years is 50–100% greater than both empirical estimates. For 10-year cumulative incidence, only 60% of modelling results were within a factor of two of either empirical point estimate, and only 77% were within a factor of five. 10-year cumulative incidence was greater than 50% for 15% of all modelling results, and less than 1% for 4·6% of results.

Figure 5. Comparison between model predictions and empirical evidence for annual (A) and cumulative (B) incidence of active tuberculosis by years since Mycobacterium tuberculosis infection, for groups with no individual risk factors.

Empirical estimates based on the British Medical Research Council BCG trials (Sutherland)²⁶ and the US Public Health Service’s isoniazid trials (Ferebee).²⁸

As a sensitivity analysis, we assessed the extent to which each model structure could reproduce the empirical results. When we fitted each model structure to the empirical estimates from the British Medical Research Council’s BCG trials,²⁶ most structures were able to closely approximate the cumulative incidence estimates; the exceptions were structures A, D, and J, and to a lesser extent structure E (appendix pp 27–28). When we reproduced the empirical comparison shown in figure 5 excluding structures A, D, and J, the variation was reduced but only modestly, with 71% of modelling results for 10-year cumulative incidence within a factor of two of the empirical point estimates, and 88% within a factor of five. For results derived from structures A, D, and J, 21% of modelling results for 10-year cumulative incidence were within a factor of two of the empirical point estimates, and 40% were within a factor of five.

Discussion

We did a systematic review of studies using dynamic tuberculosis transmission models to understand how studies modelled progression to active disease after initial infection, and assessed the validity of modelling assumptions by comparing model results with empirical incidence estimates. We identified 312 studies that met our inclusion criteria, most of which were published after 2000.

We used the model structures and parameter values described by each study to reproduce the model predictions for tuberculosis incidence in the years following initial infection. These results demonstrated substantial disagreement between studies on a key feature of tuberculosis epidemiology: the rate at which individuals progress to active disease after initial infection. This variation was still apparent when we examined the subset of results that modelled the general population or population groups with no individual risk factors. When we compared the model results for groups with no individual risk factors with empirical evidence, a substantial proportion of the modelled results were found to be inconsistent with these data. For 10-year cumulative incidence, 40% of all modelled results were either more than double or less than half the empirical point estimates.

One potential explanation for these findings is that the model structures adopted by some studies were inadequate, and when we tried to fit each model structure to the empirical data we found that three structures (A, D, and J) provided poor fit to the empirical evidence. Structure A assumes that infection with M tuberculosis confers a constant rate of progression to active tuberculosis. This feature prevents these models from reproducing the declining time trend in tuberculosis progression risk shown in empirical data. By construction, these models will underestimate short-term progression risks, overestimate long-term progression risks, or both. Structure D assumes immediate progression to active disease for all newly infected individuals. Although this assumption is inconsistent with the natural history of tuberculosis in immunocompetent individuals, this structure was only used for individuals with advanced HIV who experience rapid disease progression, so this use might not be problematic. Structure J produces progression risks that increase as a function of time since infection, which is inconsistent with the available empirical evidence.

Although structure E allowed for an immediate decline in progression risk following infection, the fit to empirical data was still crude. A recent study³⁹ examining different model structures found that structure E performed either worst or second worst of the six structures examined (depending on the fitting method). In our analysis, structure E performed better than structures A, D, and J, but the root mean squared error was still ten times worse than that of the other structures. This finding is notable, given that almost 50% of published models adopted this structure. Whether this structure will produce valid results will depend on the analysis, but it is unlikely to be appropriate for analyses that need to distinguish the elevated progression risks several years after infection from the much lower risks many years later. Apart from structures A, D, J, and potentially E, the other structures reported in the modelling literature appeared to be reasonable based on their ability to reproduce empirical data when appropriate parameter values were used.

However, inadequate model structure provides only a partial explanation for the observed discrepancies. Even when we excluded structures A, D, and J, almost 30% of all modelled results were either more than double or less than half the empirical point estimates for 10-year cumulative incidence. There are reasons to believe that the epidemiology of tuberculosis progression will differ between populations: as some of the model strata we investigated pertained to the general population, each population will represent a different mix of factors (such as nutrition, smoking, and diabetes) that affects progression risks. As the distribution of these factors changes between populations, so will tuberculosis progression rates. Studies in other low-burden settings have found similar results to those in the empirical studies we used. In an observational study⁴⁰ of close contacts of tuberculosis cases in Australia, the authors estimated a cumulative incidence of 5·4% over 4·5 years of follow-up for adults converting to tuberculin skin test or interferon-γ releasing assay positivity. In a similar study in the Netherlands,⁴¹ the 5-year cumulative incidence of active tuberculosis in adults was 6·7%. For high-burden settings, it is possible that part of this burden is explained through elevated progression rates. Estimation of progression rates is difficult in settings with a high force of infection, given the need to distinguish reactivation from reinfection as a cause of incident disease, although some analyses have resolved this issue by studying individuals migrating from high-burden to low-burden settings.^42–44 However, differences in the distribution of factors determining progression risk are unlikely to explain the magnitude of variation that we observed in the modelling results. An alternative explanation is that a substantial proportion of these studies adopted assumptions that were incorrect, providing a poor representation of tuberculosis disease dynamics in their chosen population.

For population groups with individual factors modifying tuberculosis progression risks, model results were generally consistent with empirical evidence: HIV positivity was associated with higher tuberculosis incidence than was HIV negativity, advanced HIV was associated with higher incidence than was early HIV,^7,8 and antiretroviral therapy was protective against tuberculosis in HIV-infected individuals.⁴⁵ Although early infancy is empirically associated with rapid tuberculosis progression,⁶ this association was not evident in the modelling results, potentially because of variation in the age ranges adopted by the models, and the fact that tuberculosis progression changes rapidly during this period (high in early infancy and lower in later childhood).⁶ For later childhood, model results were consistent with the literature suggesting that incidence is lower than in adulthood,⁶ although some recent studies have suggested faster progression during these ages.^40,41 The trends in the risk group results were generally consistent with empirical evidence, but substantial variation was still seen between models.

We found a range of evidence sources cited in support of the parameter values used in the studies we reviewed. These evidence sources included modelling studies, empirical studies, and review articles. Some of the evidence sources classified as modelling studies were rigorously calibrated to empirical evidence (most notably the Vynnycky and Fine³⁶ analysis cited by 21% of all reviewed studies), and so it should not be inferred that papers citing earlier modelling papers are necessarily less valid. However, it is possible that using earlier modelled studies as a source of parameter values played a part in the heterogeneity of results we observed, since errors can be introduced in the process of extracting and repurposing these parameters. Even if the original model produced valid results, the same parameter values will have different implications when used in a model with a different structure, or if the values of related parameters are different. Consequently, even when appropriate evidence is cited, this does not necessarily imply that the predictions produced by the model will be accurate. For the 24% of studies that gave no citation for their parameter values, it is possible that these values were informed by empirical data collected as part of the study. However, this explanation is unlikely to apply to more than a very small number of studies, if any. For the rest, the source of evidence is simply unknown.

Our analysis has several limitations. First, because we reproduced model predictions on the basis of the content of published articles, it is possible that some of the extreme results represented typographical errors in how studies reported their approach or that parameter values used in the analysis were modified from those reported in the paper. Although we did double extraction, we did not contact original authors to confirm study assumptions. Second, the way we programmed the models might have differed from the approach used in the original analysis. These differences could produce discrepancies between our results and those of the original analysis, although these discrepancies are likely to be minor. Third, it is possible that some analyses were not attempting to reproduce tuberculosis epidemiology exactly, and that the disease was only used as a motivating example for investigating the properties of transmission models. Although this might be true for some studies, we were not able to distinguish these studies in any way. For example, no clear difference was seen between the predictions derived from analyses published in applied journals and those published in mathematical biology journals. Moreover, even if a particular study did not intend to fully capture tuberculosis epidemiology, it is still part of the tuberculosis modelling literature, and, as we did, readers might assume that the findings of these analyses pertain to real tuberculosis epidemiology even if this was not the intention. Finally, the empirical studies that we used as a point of comparison are not perfect. Not only do they represent particular populations, but the tests used to diagnose tuberculosis infection and active disease have imperfect sensitivity and specificity. Consequently, modelled results might not be expected to reproduce these results exactly.

Analyses that mischaracterise tuberculosis disease dynamics might produce biased estimates of descriptive epidemiology or the impact of policy change. For example, if model assumptions produce erroneously high incidence of active tuberculosis disease after initial infection, population-level incidence and prevalence could be overestimated, and therefore the beneficial impact of interventions to reduce tuberculosis transmission could also be overestimated. Similarly, if analyses do not allow for declines in incidence with time since infection, then estimates of the impact of latent tuberculosis infection prophylaxis for individuals with distant infection will be biased upwards. Incorrect assumptions about how risk factors modify tuberculosis incidence could harm the assessment of interventions targeted at these risk factors. Moreover, because many modelling studies calibrate their transmission model to reproduce commonly reported tuberculosis outcomes, an incorrect assumption in one part of the analysis can lead to incorrect assumptions in other parts of the analysis. For example, for analyses calibrated to tuberculosis case notifications, if model assumptions produce erroneously high incidence following initial infection, this could lead to, among other things, a downward bias in estimated tuberculosis transmission, a downward bias in latent tuberculosis infection prevalence, or a downward bias in the proportion of tuberculosis cases detected. Each of these changes could introduce biases into the primary outcomes of an analysis. For example, underestimation of latent tuberculosis infection prevalence could lead to underestimation of the costs of a programme to screen for and treat latent infection to avert active disease.

We evaluated a single characteristic of tuberculosis transmission models: the assumptions made about progression after initial infection. Since we did not reproduce all features of all modelled analyses, we cannot draw conclusions about whether the discrepancies that we described led to biased results in any given study. However, these discrepancies are likely to have led to biased results in some cases. Although re-evaluation of published results might be impractical, our findings have clear implications for future work. This research is accelerating; there were 33 tuberculosis modelling publications in the first 8 months of 2017, greater than the total for 2016, and greater than the sum of all papers published before 2000. For future studies that use mathematical models to investigate tuberculosis epidemiology or compare policies, our results provide strong motivation to ensure structural assumptions are appropriate, and to check that analyses reproduce known features of tuberculosis epidemiology. For consumers of modelling studies, our results suggest that the findings of these studies should not be accepted uncritically. Although major gaps exist in the evidence base for constructing and evaluating the validity of these models,¹⁵ it is still important (perhaps more important) to make the best use of the evidence that is available. Greater confidence might be placed in analyses in which modelling approaches are clearly explained and justified with reference to the available evidence and that can reproduce data relevant to the setting and population being modelled.