A Hierarchy of Time Scales for Discriminating and Classifying the Temporal Shape of Sound in Three Auditory Cortical Fields

Abstract

Auditory cortex is essential for mammals, including rodents, to detect temporal “shape” cues in the sound envelope but it remains unclear how different cortical fields may contribute to this ability (Lomber and Malhotra, 2008; Threlkeld et al., 2008). Previously, we found that precise spiking patterns provide a potential neural code for temporal shape cues in the sound envelope in the primary auditory (A1), and ventral auditory field (VAF) and caudal suprarhinal auditory field (cSRAF) of the rat (Lee et al., 2016). Here, we extend these findings and characterize the time course of the temporally precise output of auditory cortical neurons in male rats. A pairwise sound discrimination index and a Naive Bayesian classifier are used to determine how these spiking patterns could provide brain signals for behavioral discrimination and classification of sounds. We find response durations and optimal time constants for discriminating sound envelope shape increase in rank order with: A1 < VAF < cSRAF. Accordingly, sustained spiking is more prominent and results in more robust sound discrimination in non-primary cortex versus A1. Spike-timing patterns classify 10 different sound envelope shape sequences and there is a twofold increase in maximal performance when pooling output across the neuron population indicating a robust distributed neural code in all three cortical fields. Together, these results support the idea that temporally precise spiking patterns from primary and non-primary auditory cortical fields provide the necessary signals for animals to discriminate and classify a large range of temporal shapes in the sound envelope.

SIGNIFICANCE STATEMENT Functional hierarchies in the visual cortices support the concept that classification of visual objects requires successive cortical stages of processing including a progressive increase in classical receptive field size. The present study is significant as it supports the idea that a similar progression exists in auditory cortices in the time domain. We demonstrate for the first time that three cortices provide temporal spiking patterns for robust temporal envelope shape discrimination but only the ventral non-primary cortices do so on long time scales. This study raises the possibility that primary and non-primary cortices provide unique temporal spiking patterns and time scales for perception of sound envelope shape.

Introduction

Sound temporal cues including periodicity and envelope shape are essential for perception and classification of sound sequences including speech and other vocalizations (Drullman et al., 1994; Shannon et al., 1995; Irino and Patterson, 1996; Seffer et al., 2014). Periodicity cues are created by the repetition of sound onsets at regular time intervals and can induce rhythm, roughness and pitch perceptions for periodicities of up to ∼20, 200, and 800 Hz, respectively (Joris et al., 2004). In contrast, shape temporal cues include the rising and falling slopes and the duration of change in the sound envelope amplitude and are perceived as envelope timbre and loudness of sound (Long and Clark, 1984; Irino and Patterson, 1996; Turgeon and Bregman, 2001; Friedrich and Heil, 2016).

Temporally precise neuronal responses vary with sound envelope shape and periodicity but how this encoding changes along the ascending auditory pathway remains unknown. The latency of response provides a potential neural code of the rising slope of the sound envelope and becomes increasingly more sluggish as one ascends the auditory pathway (Heil, 2003). This ability breaks down as sound periodicity is increased with upper limits of 300, 100, and 20 Hz for auditory nerve, midbrain and cortex, respectively (Joris et al., 2004). For example, selectivity for sound envelope shape is limited to sound sequences with periodicities up to ∼100 Hz in midbrain (Krebs et al., 2008; Zheng and Escabí, 2008) and ∼20 Hz in cortex (Lu et al., 2001; Engineer et al., 2014; Lee et al., 2016). Moreover, single neurons respond independently to sound envelope shape and periodicity in midbrain and primary auditory (A1) cortex (Zheng and Escabí, 2013; Lee et al., 2016) but have joint sensitivities to these same temporal cues at higher non-primary cortical levels suggesting a functional hierarchy (Lee et al., 2016).

The rat is an excellent model to examine mechanisms underlying perception of temporal sound cues. Rats, like humans, have A1 and multiple non-primary cortices with neurons that are topographically organized to sense sound frequency (Formisano et al., 2003; Talavage et al., 2004; Kalatsky et al., 2005; Higgins et al., 2010). Rats discriminate sounds based on temporal cues (Schulze and Scheich, 1999; Gaese et al., 2006; Kelly et al., 2006) and silencing of A1 and non-primary auditory cortices abolishes this ability (Threlkeld et al., 2008). In rat A1 and two non-primary cortices, ventral auditory field (VAF) and caudal suprarhinal (cSRAF) auditory field, the variance (jitter) in timing of spikes synchronized to sound (aka, sound encoding time) changes with sound envelope shape, providing a potential temporal code for shape (Lee et al., 2016). Here, we examine the possibility that A1, VAF, and cSRAF could provide unique temporal codes for discriminating and classifying sound based on the temporal shape of the sound envelope.

Materials and Methods

Surgical procedure and electrophysiology.

Data were collected from 16 male Brown Norway rats (age 48–100 d). All animals were housed and handled according to a protocol approved by the Institutional Animal Care and Use Committee of the University of Connecticut. Craniotomies were performed over the temporal cortex. All recordings were obtained from the right cerebral hemisphere. Anesthesia was induced and maintained with a mixture of ketamine and xylazine throughout the surgery and during optical imaging and electrophysiological recording procedures. A closed-loop heating pad was used to maintain body temperature at 37.0 + 2.0°C. Dexamethasone and atropine sulfate were administered every 12 h to reduce cerebral edema, and secretions in the airway, respectively. A tracheotomy was performed to avoid airway obstruction and minimize respiration-related sound.

Wide-field intrinsic optical imaging.

The goal of this study was to determine whether and how single-unit spiking responses in A1, VAF, and cSRAF could be used to discriminate and classify sounds. Wide-field intrinsic optical imaging was used to map tone responses and to determine cortical areas corresponding to A1, VAF, and cSRAF based on direction of tone frequency gradient, as detailed previously (Lee et al., 2016). Briefly, intrinsic signal responses were imaged with a Dalsa 1M30 CCD camera with a 512 × 512 pixel array covering a 4.6 × 4.6 mm² area. Surface vascular patterns were visualized using a green (546 nm) interference filter at 0 μm plane of focus. Intrinsic activity was recorded at a plane of focus of 600 μm below the surface blood vessels using a red (610 nm) interference filter. Cortical field areas were determined with post hoc analysis of the wide-field intrinsic image and aligned with stereotaxic positions for subsequent electrode recordings in each field.

Sound design and delivery.

Three primary types of sound were used in this study including: (1) periodic tone sequences for wide-field mapping of cortical fields, (2) transient tones to assess single-unit sound frequency response sensitivities, and (3) periodic shaped noise sequences to assess sound envelope shape sensitivities. Sounds were generated by Beyer DT 770 dynamic speaker drivers housed in a custom designed sealed enclosure and delivered via tubes positioned ∼1 mm inside the ear canal. Sound delivery was calibrated between 750 and 48,000 kHz (±5 dB) in the closed system with a 400 tap finite impulse response inverse filter implemented on a Tucker Davis Technologies (TDT) RX6 multifunction processor. Sounds were delivered through an RME audio card or with a TDT RX6 multifunction processor at a sample rate of 96 kHz. The sound card and sampling frequency used produce tones and noise with minimal distortions for sound frequencies up to 45 kHz (SNR > 100 dB, THD < −100 dB). All sounds were presented with matched sound level to both ears with an interaural level difference (ILD) equal to zero to approximate a midline sound position (Higgins et al., 2010).

Periodic tone sequences used for wide-field optical response mapping.

Wide-field intrinsic optical imaging was performed to locate A1, VAF, and cSRAF. Wide-field optical images were obtained in response to continuous tone sequences consisting of 16 tone pips (50 ms duration, 5 ms rise and decay time) delivered with a presentation interval of 300 ms and presented with matched sound level to both ears. Tone frequencies were varied from 2 to 32 kHz (one-quarter-octave steps) in ascending and subsequently descending order, and the entire sequence was repeated every 4 s. Hemodynamic delay was corrected by subtracting ascending and descending frequency phase maps to generate a difference phase map (Kalatsky et al., 2005).

Pseudorandom tone sequences used for spike-rate response recordings.

Multiunit spike-rate response sensitivities to frequency and sound level were probed with transient pure tones (50-ms duration, 5 ms rise time) that varied over a frequency range of 1.4–44.2 kHz (in one-eighth-octave steps) and sound pressure levels (SPL) from 5 to 85 dB SPL in 10-dB steps. FRA-probing tones were presented in pseudorandom sequence with an intertone interval of 300 ms. As shown previously for this same dataset, spectral and temporal response characteristics obtained from frequency response areas confirm that the populations of cells we designated as belonging to A1, VAF, and cSRAF are consistent with those described previously (Lee et al., 2016).

Periodic noise-burst sequences probe spike-timing responses.

The periodic noise burst sounds used have been described in detail previously (Lee et al., 2016) and only a brief account is provided. Periodic noise burst sequences consisted of four shaped noise bursts delivered at a rate of twice per second (2 Hz) for a total duration of 2 s. Each sequence variation was separated by a 1 s silent gap. All sequences were delivered at 65 dB SPL peak amplitude and 100% modulation depth. The noise carriers were varied (unfrozen) across trials and for individual sound bursts to remove spectral biases and to prevent repetition of fine-structure temporal patterns. This guarantees that, on average, the only physical cues available to each neuron arise from the temporal envelope.

The envelopes of the periodic noise burst sequences were generated by convolving an eighth order B-spline filter function with a 2 Hz periodic impulse train (Lee et al., 2016). The B-spline filter has a single parameter, f_c, that is used to vary the envelope shape (i.e., duration and slope), as described in detail previously (Lee et al., 2016). This sound design is advantageous as it allows us to independently vary sound envelope shape and the modulation frequency (repetition rate) of the sound burst. In the current study, there were 10 different variations of the sound envelope shape with f_c ranging from 2 Hz to 64 Hz. Sound burst duration for each f_c was measured using 1 SD at 50% amplitude width (1 tail). For these sounds, the duration of the sound burst decreased as the f_c was increased from 2 to 64 Hz (Table 1). Conversely, the rate of rise and decay (i.e., slope) of the sound envelope increases as f_c increased from 2 to 64 Hz (Table 1). These sounds were presented in a pseudorandom shuffled order of f_c until 10 trials were presented under each condition. Sound bursts in each sequence were delivered at 2 Hz, as this periodicity generates highly reliable trial-to-trial responses (Lee et al., 2016).

Table 1.

Onset response time windows vary with sound shape and across cortical fields

fc	2	4	6	8	11	16	23	32	45	64	Mean (SEM)
Half-duration	80	40	28	20	14	10	7	5	3	2
Slope	0.32	0.66	0.91	1.33	1.90	2.62	3.70	5.14	7.52	10.07
A1	29.6	24.1	23.5	20.1	20.5	18.9	18.6	18.0	16.5	15.4	21 (1)
VAF	52.4	31.6	33.7	38.5	23.9	27.3	20.9	19.4	18.8	18.0	29 (3)
cSRAF	180.7	211.2	194.9	33.0	33.2	23.7	19.3	18.7	17.6	15.8	75 (27)

Onset response time windows, determined as described in Materials and Methods, vary with sound burst half-duration and slope as determined by the sound shaping filter (f_c ). Onset response times are given for each sound burst variation and cortical field.

Single-unit recording and sorting.

Data from 223 single neurons were examined in the present study. Extracellular electrophysiological responses were recorded with 16 channel tetrode arrays (4 × 4 recording sites across 2 shanks, with each shank separated by 150 μm along the caudal-rostral axis, 1.5–3.5 MΩ at 1 kHz, NeuroNexus Technologies). Data from penetration depths of 400–650 μm relative to the pial surface were included in the present study, as this corresponds to layer 4 where ventral division auditory thalamic neurons project (Storace et al., 2010, 2011, 2012). Recorded neurons were assigned to a cortical field according to wide-field image and stereotaxic positions, as described in detail previously (Lee et al., 2016).

Candidate action potential waveforms were first identified using custom software in MATLAB (MathWorks). Continuous voltage traces were digitally bandpass filtered (300–5000 Hz) and the cross-channel covariance was computed across tetrode channels. The instantaneous channel voltages across the tetrode array that exceed a hyper-ellipsoidal threshold of f = 5 (Rebrik et al., 1999) were considered as candidate action potentials. This method takes into account cross-channel correlations between the voltage waveforms of each channel and spikes are detected only if the instantaneous voltage power across the composite tetrode array exceed the average voltage power by a factor of f²= 25. Spike waveforms were aligned and sorted using peak voltage values and first principle components with automated clustering software (KlustaKwik software; Harris et al., 2000). Sorted neurons were classified as single neurons if the waveform signal-to-noise ratio exceeded 3 (9.5 dB) as detailed previously (Lee et al., 2016). For all data analyses, the first 500 ms was removed from each spike train to restrict analysis to the adapted steady-state segments of the neural responses.

Response timing and magnitude measures.

To quantify spike-timing patterns of neurons over the course of their response in relation to the time course of each sound burst in a sequence we computed population modulation period histogram (i.e., “response histogram” or “period histogram” for short) for the population of neurons from each cortical field (Figs. 1, Fig. 2). A similar approach has been used previously to quantify temporal response patterns in inferior colliculus (Zheng and Escabí, 2008) and cortex (Malone et al., 2007, 2015). The period histogram is constructed by aligning the spike-time histogram relative to the sound onset. Because in this study, sounds were delivered at a repetition rate of 2 Hz all period histograms lasted 500 ms. This repetition frequency was chosen because it yields highly reliable trial-by-trial responses in the three cortices examined here (Lee et al., 2016) and in A1 of awake monkeys (Malone et al., 2015). Population period histograms were computed by summing responses across all cycles for all neurons for a given cortical field, binned in 2 ms windows (Fig. 1).

Figure 1.

Population average period histogram of responses from (B) A1 (64 neurons), (C) VAF (104 neurons), and (D) SRAF (65 neurons) for all 10 variations of sound shape stimulus (A). Asterisks mark the peak of the period histogram. The blue bars indicate the difference between the peak PSTH and peak of sound. Red curves outline the envelope of the sound. Period histogram duration varies markedly with sound shape in SRAF and VAF and less so in A1. A1 responses remain precise across all shapes.

Figure 2.

Effects of changing sound shape on population histogram response parameters including: response delay, response duration, and peak spike rate. All metrics are derived from population period histograms shown in Figure 1. A, Response peak delay increases significantly (p < 0.001) with sound shape f_c in all three cortical fields. The corresponding log-linear regression slopes for A1, VAF, and SRAF are as follows: −122, −113, and −80, respectively; r² = 0.82, 0.83 and 0.89, respectively. B, Cumulative probability for response delay. C, Population response delays (averaged across all sound shapes) follow a rank order increase with: A1 < VAF < SRAF (See Results for statistics). D, Response duration decreases proportionally and logarithmically with sound shape f_c and sound burst duration (Table 1) in all three cortical fields. The corresponding regression fits are significant (p < 0.001) and slopes for A1, VAF, and SRAF are as follows: −5, −20, and −85, respectively (r² = 0.81, 0.90 and 0.61, respectively). E, Cumulative probability distributions for response duration indicate that A1 is more likely to have shorter (<50 ms) response durations than VAF and cSRAF. F, Across all sound conditions the average response duration decreases significantly (F_(2,2997) = 13.58, p < 0.001) in rank order with A1, VAF, and cSRAF mean (SEM) response durations of: 19.6 (±0.1), 28.9 (±0.4), 53.6 (±1.9), respectively. G, Population period histogram peak spike rate changes significantly (p < 0.001) as a function of sound temporal shape f_c in all fields (A1, VAF, cSRAF: slope = 11.13, 8.61, and 5.77 respectively; r² = 0.632, 0.740 and 0.886 respectively). H, Cumulative probability relative to the peak spike rate of period histogram indicates lower peak spike rates in SRAF than other fields. I, Mean period histogram peak spike rate different across cortical fields (F_(2,2997) = 1554, p < 0.001) follow a rank order of A1 > VAF > cSRAF with corresponding mean (SEM): 44.8 (± 0.28), 47.88 (± 0.2), and 33.6 (± 0.1) Hz, respectively. **p < 0.01, ***p < 0.001.

To determine regional differences in temporal response attributes, we quantified peak latency, duration, and amplitude for each population histogram, by determining the spike-rate responses that were significantly greater than the baseline level for each cortical field. For all analyses and simulations in this study the first 500 ms of the response to a given sound burst sequence was removed, as in a prior study (Lee et al., 2016). Next, baseline spike rate was estimated from a 50 ms window of the histogram corresponding to the end of the period between sounds. The population histogram was bootstrapped 100 times to estimate significant response level, variance of the response duration, and peak amplitudes. The peak spike rate was determined as the maximum rate in the period histogram (Fig. 1, asterisks). The response delay was measured as the time difference between the response peak and the stimulus peak (Fig. 1, length of blue bars indicates durations). Response duration was estimated by determining the period during which the spike rate increased significantly (p < 0.05, Student's t test) from baseline spike rate.

Neural sensitivity index metric.

To determine how single neuron spiking patterns might be integrated or decoded by subsequent stages of the auditory pathway to accurately discriminate pairs of sounds, we developed a normalized spike distance metric (Victor and Purpura, 1997; van Rossum, 2001). We examined the degree of sound discrimination (Fig. 3A–F) as well as the time constants needed to obtain optimal sound discrimination (Fig. 4). Our metric is motivated by the spike-distance metric of Van Rossum (2001), which uses an exponential smoothing kernel to change the temporal resolution for integrating spikes in spike trains. Our distance metric also uses multiple-trial responses. The distance metric was normalized by trial variances to compute a sensitivity index or discrimination index as commonly used to measure behavioral discriminability (Swets et al., 1978). Pairwise sound discrimination indices (D′) for single neurons' spike trains were determined and optimized as detailed below (Eqs. 1–8). Here, a D′ = 1 corresponds ∼70% accuracy, which is typically considered a critical limit for discriminating a signal behaviorally (von Trapp et al., 2016).

Figure 3.

Example of computing optimal discrimination indices for two sound shapes and two different time constants. A, B, Responses from a single neuron in cSRAF to sounds shaped with f_c of 8 Hz (A) and 64 Hz (B), respectively. Over 10 trial repeats, the sound envelope of the sound pressure waveform was the same but the underlying noise carrier was varied unfrozen noise (see Materials and Methods). A sequence of long duration sound bursts (A, top green envelope; f_c = 8 Hz) elicited sustained spiking followed by reduced spontaneous activity evident in the dot raster plot (A, bottom). A sequence of short duration sound bursts (B, top red envelope; f_c = 64 Hz) elicited transient phase-locking of spikes to sound onsets in the dot raster (B, bottom). C, D, Top, Color rendering of raster plots in A and B, respectively, convolved with an exponential decay function with time constant (τ or Tau) of 64 ms. C, D, Bottom, Sum of trials in color plot above. E, F, Top, Color rendering of raster plots in A and B, respectively, convolved with an exponential decay function with time constant (τ) of 256 ms. E, F, Bottom, Sum of trials in color plots above. The pairwise discrimination of sound bursts in A and B, changes from optimal to suboptimal with discrimination indices of 1.52 and 1.27, respectively, when the smoothing time constant is changed from 64 to 256 ms in this example. A time constant of 256 ms smooths spikes over more than half of the cycle period (500 ms) for a 2 Hz sound sequence and the resulting signal approaches a spike-rate signal. Thus, a more resolved time scale improves sound discrimination in this example.

Figure 4.

Determining time constants yielding optimal discrimination index. Discrimination indices for example neurons from A1, VAF, and cSRAF (A–C, respectively). The reference sound for pairwise comparisons has a shape f_c of 64 Hz. Pairwise comparisons are made between nine different sound combinations with varied shape f_c (2–45 Hz). Discrimination indices are computed for 16 different time constants (2–256 ms). Asterisks indicate optimal discrimination for one set of sound shape comparisons (f_c of 2 vs 64 Hz, red curves).

To calculate spike distance (D), we consider two smoothed response dot rasters, f_k(t) and g_k(t) to be compared, where k is the response trial number (N = 10 trials total), f represents the response to stimulus 1, and g is the response to stimulus 2. Both f_k(t) and g_k(t) are obtained by convolving the individual spike train from a given trial with an exponential kernel h_τ(t) with a smoothing time constant τ. The spike distance (D) between the kth and lth trial of f and g is as follows:

where ‖·‖ is the Euclidian norm and the average spike train distance across all trials is as follows:

where N is the number of trials. In the above, note that Equation 1 requires 2N convolutions along with N² norm calculation for computing the spike train distance between trials (Eq. 2). The average distance can be efficiently estimated by and is equivalent to computing the distance between the poststimulus time histograms (PSTHs) of f and g. That is,

and we use this alternative formulation to minimize computational cost (2N convolutions and 1 norm calculation).

Because our goal is to normalize the spike distance according to a sensitivity index measure, we next estimated the trial variance of f and g. To do so, we note that the individual trial responses:

where n_k(t) and m_k(t) represent the variable noise component for each of the smoothed response trial of f and g respectively. The response variance of f(t) at a specific temporal resolution is estimated as follows:

and similarly for g(t)

Finally, the spike distance is normalized by the trial variances of f and g yielding the sensitivity index (D′) or “discrimination index” (Fig. 3).

which is time-scale dependent. The exponential time constant, τ, determines the temporal resolution or integration time of the distance metric. For large values of τ, the signals being compared contain mostly slow fluctuations in the spike rate (Fig. 3E,F). For small τ, the spike distance metric is sensitive to the precise timing of spikes. We varied τ in 16 logarithmic intervals from 1 to 256 ms, and computed discrimination index (D′) for each τ and each reference sound (Fig. 4; reference sound f_c = 64 Hz) and then determined the time constant (τ or tau) that yields the optimal (aka, maximal) sound discrimination (Fig. 4, asterisks). The same approach was used for all possible sound pairings and sound references and discrimination indices are plotted in a matrix (Fig. 5). A discrimination index of zero was obtained when the two response conditions were identical (aka, sound vs itself) and plotted on the diagonal of the corresponding discrimination index matrix (Fig. 5, diagonal cells). Using a τ of 256 ms, the time constant is longer than half of the cycle period (500 ms), and the spike distance is closely related to the difference in the total spike rates. The range of time-constants tested enabled us to test the role precise spike timing at one extreme and the role of slow fluctuations in spike rate at the other extreme might play for neural discrimination of temporal envelope cues.

Figure 5.

Optimal discrimination indices and time constants used for a population of neurons in A1, VAF, and SRAF. A–C, Pairwise matrices of optimal discrimination indices. A1 and VAF have slightly (p < 0.05) higher mean discrimination than cSRAF on average for all 45 pairwise discriminations (F_(2,1323) = 13.58, two-way ANOVA) with mean (SEM) discrimination indices in A1, VAF, and cSRAF of: 0.97 (± 0.01), 0.98 (±0.01), and 0.92 (±0.01), respectively. For sound pairs with f_c <11 Hz, discrimination indices are rank ordered with cSRAF > VAF > A1 and corresponding mean (SEM) discriminations of: 0. 99 (±0.07), VAF: 0.97 (±0.06), and 0.94 (±0.04), respectively. D, Population mean and SEM of optimized discrimination indices for pairwise comparisons where the reference sound f_c is 64 (data correspond to matrix area indicated with overlaid black rectangles in A–C). Blue, green, and red lines correspond to A1, VAF, and cSRAF, respectively. E–G, Pairwise matrices of optimal time constants for sound discrimination. VAF and cSRAF have higher Tau (see Results). H, Population mean and SE of time constants for region outlined in black in E–G in A1 (blue), VAF (green), and cSRAF (red). A–C, E–G, Dark Blue voxels correspond to conditions were discrimination indices (D′) are equal to zero and the asterisk indicates the highest value in the matrix. E–G, Pairwise time constants used to achieve optimal discrimination indices in corresponding cortical fields. ***p < 0.001. For this range of f_c conditions, Time constants are rank ordered and increasing with A1 < VAF < cSRAF (Wilcoxon rank-sum, p < 0.01).

As τ approaches the total length of the spike train (2 s), the spike distance is biased and yields large values. When comparing two spike trains, slight difference in the spike rate will contribute to a large spike-distance metric because there is not enough time for the exponential function to decay. To minimize this confound, we extended the length of spike train by synthesizing a periodic spike train with matched temporal statistics to the measured data (Zheng and Escabí, 2008). For each cycle of the synthetic periodic spike train, both the spike rate and spike times were randomly sampled from the original spike train. This process was repeated to generate periodic spike trains with durations of 100 s.

Role of onset versus secondary spikes.

To compare the contribution of onset and sustained spikes to the discriminability of the periodic burst responses, we decomposed the spike trains into a sequence of onset and sustained spikes (Fig. 6) and determined how well sounds were discriminated by each response component (Fig. 7). Spikes were considered onset spikes only if their timing fell within a window starting at 50% of the peak evoked spike rate preceding the peak, and ending at the minimum in the histogram within 50 ms following the peak. A single onset response time window was measured for each f_c condition and each region from the corresponding population period histogram (Table 1). Spikes falling within this time window were initially classified as possible onset spikes and the onset response time window varied with the sound burst f_c and duration (Table 1). Furthermore, the onset response time window varied between cortical fields for many sound burst conditions (Table 1).

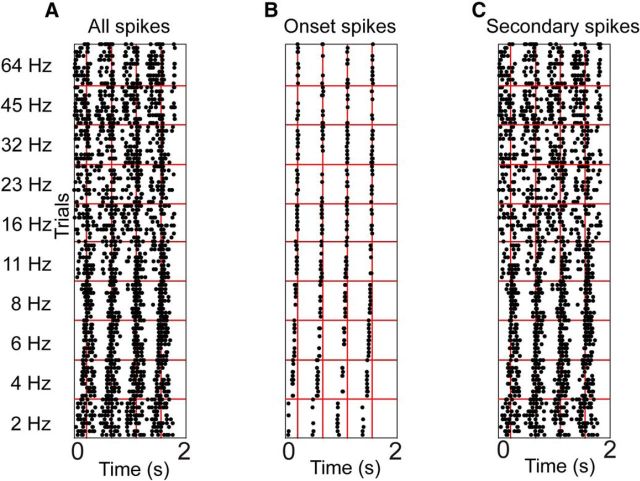
Figure 6.

Spike-timing dot rasters of an example cSRAF unit showing the separation of onset and sustained (secondary) spike time responses to 10 trial repeats for 10 different sound envelopes (f_c ranging from 2 to 64 Hz). A, Dot raster showing all spikes, (B) onset spikes, and (C) secondary spikes.

Figure 7.

Optimal discrimination indices using onset and sustained spikes for a population of neurons in A1, VAF, and cSRAF. A–C, Onset spike population mean optimal discrimination index in A1, VAF, and cSRAF respectively. D, For the matrix regions outlined in black in A–C, population mean and SE of optimal onset discrimination indices are plotted for A1 (blue), VAF (green), and cSRAF (red). E–G, Sustained spikes population mean optimal discrimination indices in A1, VAF, and SRAF. H, For the matrix regions outlined in black in E–G, population mean and SE are plotted for each cortical field using the same color convention. The secondary response discrimination performance changes marginally with f_c (F_(8,1323) = 41.96, p < 0.05, two-way ANOVA) and between cortical fields (F_(2,1323) = 44.76, p < 0.05, two-way ANOVA; H). A–C, E–G, Dark blue voxels correspond to conditions were discrimination indices (D′) are equal to zero and the asterisk indicates the highest value in the matrix. *p < 0.05, **p < 0.01, ***p < 0.001.

Onset spikes are composed of a mixture of both stimulus-evoked and spontaneous activity. To estimate the contribution of both sources of spiking, we measured the baseline spiking rate from a 50 ms window centered a half cycle before the stimulus peak, and assumed the baseline spike rate during the onset window varied about the mean spontaneous rate according to a Poisson distribution. Onset spike rates exceeding the 0.001% criterion level of this distribution were therefore assumed to include an additional contribution of evoked activity above the spontaneous rate. Accordingly, we categorized a subset of the onset spikes as spontaneous, by randomly sampling from the onset spikes with a spike rate up to the 0.001% criterion level. All remaining spikes were considered evoked onset spikes. Finally, the spontaneous onset spikes were added to the secondary spike train. In the remainder of this manuscript, we use the term “onset” spikes to denote the evoked onset spikes only.

Sound classification based on spike timing and spike-rate codes

To further explore the role of precise spike timing and spike-rate codes in neural classification of temporal envelope cues, we used a naive Bayes classifier to read the neural spike trains and classify sounds in a 10-sound category identification task (Fig. 8). Sound categories consisted of the 10 temporal envelope shape (aka, f_c) conditions tested and the classifier was required to identify the correct sound that was delivered using single response trials.

Figure 8.

Average single neurons and population (N = 50) temporal and rate code classifier in A1, VAF, and cSRAF. A–C, Single-neuron classification matrices based on temporal code classifier performance (% classified) for 10 different sounds and three cortical fields A1, VAF, and cSRAF, respectively. The x-axis corresponds to the sounds delivered to the classifier as input and the y-axis corresponds to sounds classified based on spike response (classifier output). D, Diagonal matrix values (for A–C) plotted with SE. In all scatter plots, blue, green, and red lines and symbols indicate A1, VAF, and cSRAF, respectively. E–G, Single-neuron classification matrices indicating rate code classifier performance (% classified) for 10 different sounds following the same convention as above. H, Diagonal matrix values (for E–G) plotted with SE for the three cortical fields. For f_c of 2 Hz (half-duration 80 ms) spike-rate classification performance is significantly greater for VAF and cSRAF than for A1. Hence, spike-rate classification performance is significantly changing with sound shape (H; F_(9,1323) = 14.12, p = 0, two-way ANOVA) and with cortical field (F_(2,1323) = 3.67, p = 0.026, two-way ANOVA). I–K, Population classification matrix based on a temporal code classifier when responses are pooled across neuron populations for a given cortical field. L, Diagonal matrix values (for I–K) and SE for temporal (solid lines) and rate code (dotted lines) for A1, VAF, and cSRAF. M–O, Population classification matrix based on a rate code classifier in A1, VAF, and SRAF respectively. P, Population classification performance based on temporal (solid line) and rate (dotted line) codes increases with the number of neurons in three cortical fields. Temporal code contributes significantly more than rate code classifier in all three regions for both single-unit average and population average. *p < 0.05, **p < 0.01, ***p < 0.001.

Prior studies have examined how single auditory neuron spike output could be used to classify sounds (Larson et al., 2009; Bizley et al., 2010; Schneider and Woolley, 2010; Carruthers et al., 2015). In this study, we examined potential classification of temporal envelope cues based on single trial responses at ∼5 ms temporal resolution. Furthermore, the multi-neuron classifier described below used the nonredundant response information between neurons to provide a statistically robust approach for testing spike-timing-based classification.

In the first implementation, we used the spike timing activity of single neurons with preserved temporal precision (i.e., temporal code) to identify each of the 10-alternative temporal sound shapes (aks, 10 f_c conditions) and assessed the average performance (Fig. 8A–H). A Bernoulli Naive Bayes classifier (McCallum and Nigam, 1998) is used to read out the spike trains from individual neurons to categorize the sound shape. The classified shape condition (s) is the one that maximizes posterior probability for a particular response according to:

where s includes the 10 shape conditions to be identified, r_i is the neuron's response in the ith time bin and p_s,i is the probability that a particular shape, s, generates a spike (1) or no spike (0) in a 5 ms temporal bin (ith time bin). It is important to note that this approach is advantageous because it allows us to determine the probability that each spike in a precise spike train encodes a particular sound shape. In practice, p_s,i corresponds to the period histogram for the ith shape condition where the total probability mass at each time bin has been normalized for unit probability. The normalized period histogram was interpolated using piecewise cubic spline to increases the temporal bin size resolution to 1 ms. The interpolated data were regularized by smoothing the raw period histograms with a 2 ms exponential function, which helps reduce estimation noise due to limited training data and avoid having zero values that will cause errors during the log likelihood calculation. Furthermore, the smoothing function limits the precision of the spiking activity to ∼5 ms temporal resolution is similar to that used previously to successfully demonstrate classification of vocalizations in rat A1 (Engineer et al., 2008). The classifier performance was tested using a cross validation approach in which a single randomly selected trial from each shape condition was used for validation and the remaining response trials (9 total) were used to generate p_s,i and subsequently classify each of the validation responses. The procedure was bootstrapped 500 times, which allowed us to estimate the average and SE on the classifier performance.

In the second implementation, we tested the classifier performance that could be achieved for a rate code. For this scenario, the classified shape is the one that maximizes the posterior probability

where p_s is the spike count probability distribution function measured over a 500 ms response cycle and r_i is the neuron's response (i.e., the spike count for the ith 500 ms stimulus cycle). In the above, the posterior probabilities are measured and accumulated over each of the four response cycles in the sound. Because the sounds are delivered at 2 Hz (500 ms period) there is no information available from the temporal response pattern that could contribute to the classifier results and thus the classifier contains only rate information. The spike count distribution p_s(k) was approximated as a Poisson model because it provided a good fit to spike-rate data (N = 223, χ²(d_f =50) < 11.26, p < 0.05, χ² test). Validation and classification was performed as for the spike-timing classifier by reserving a single trial from all shape conditions for validation and the remaining trials for training. The procedure was then bootstrapped 500 times to determine the average and SE on the classifier performance.

Multi-neuron classifier

We next extended the single-neuron classifiers to the multi-neuron case to determine how neural population activity contributes to classification of 10 temporal sound shapes (aks, 10 f_c conditions) and assessed the average performance (Fig. 8I–P). For the multi-neuron classifier, the spatiotemporal activity pattern from multiple neurons within a single cortical field was pooled for classification. This procedure treats neurons separately and preserves any stimulus information available from individual neuron responses. By design, the naive Bayes classifier treats responses bins from different neurons as if they are independent. This property allows the classifier to take advantage of any independent and nonredundant responses within the population to build more robust classification. For the spike-timing population classifier, the classified shape is the one that maximizes the posterior probability according to:

where n corresponds to the neuron number, N is the total number of neurons considered, p_s,n,i is the probability that neuron n generates a spike (1) in the ith time bin for stimulus s. Finally, r_n,i is the response (0 or 1) generated by neuron n in the ith time bin. The procedures for regularizing p_s,n,i, selecting validation and training data, and bootstrapping was identical to the single neuron case as described above. The number of neurons was varied by randomly selecting between 1 and 50 neurons during the bootstrapping procedure to quantify how the classifier performance improves with the population size in each of the three cortical fields.

For the multi-neuron rate classifier, the classified shape is obtained as follows:

where r_n,i is the response of the nth neuron (i.e., the spike count over the 500 ms observation window) during the ith 500 ms stimulus cycle and p_s,n(k) is the probability that neuron n generates k action potentials to shape s. As for the single-neuron classifier, the average performance and error bounds were obtained by selecting single trials for validation, the remaining nine trials for model generation, and bootstrapping the procedure 500 times. As for the spike-timing population classifier, the number of neurons was varied by randomly sampling between 1 and 50 neurons to determine how classifier performance depends on the population size.

Rendering and interpreting the confusion matrix

Single neuron and neural population response-based sound classification was rendered as a sound classification matrix (aka, confusion matrix) where the abscissa corresponds to the sounds that were delivered to the classifier as input and the ordinate corresponds to the sound that was classified (classifier output). Color in the matrix corresponds to the probability that a particular input was classified as a specific output. The cells of the matrix falling along the diagonal indicate the percentage correct classification of the original sound f_c and the cells that fall off the diagonal indicate to the percentage classification as other sounds (aka, miss-classification). Each cell indicates the percentage classification of the 10 trials or sound presentations. For perfect classifying performance, each cell on the diagonal of the matrix will equal 100% correct classification. Any classification off the diagonal indicates less than perfect classification and all rows off the diagonal in a corresponding column of the matrix sum up to 100% correct classification. Given that we have 10 sounds to compare, 10% classification is considered chance and 100% classification is perfect performance accuracy.

Experimental design and statistical analysis

Data were collected from 223 single neurons from 16 male Brown Norway rats. Number of single-neuron responses analyzed in A1, VAF, and cSRAF were 54, 104, and 65, respectively. We have analyzed how responses change with cortical field and sound shape. Specifically, we analyzed response histogram time course, sensitivities to pairwise sound shapes, and classification of 10 different sound shapes. For the classifier analysis, 50 neurons were selected at random from each cortical region, then single unit and population classifier analysis were conducted. The random selection of the neurons was bootstrapped 500 times to estimate the distribution. Statistical analyses were conducted using MATLAB (MathWorks).

Two-way ANOVAs were conducted to compare the effects of sound shape in A1, VAF, and SRAF with: optimized discrimination index performance (Fig. 5D), its associated time constant (Fig. 5H), onset discrimination index (Fig. 7D), sustained discrimination index (Fig. 7H), temporal classifier performance (Fig. 7D), and rate classifier performance (Fig. 7H) for average single neurons and temporal classifier performance (Fig. 7L, solid lines), and rate classifier performance (Fig. 7L, dotted lines) for population.

Student's t test was performed to determine the period during which the spike rate increased significantly from baseline spike rate and was also used to compare the effects each cortical region with response delay (Fig. 2C), response duration (Fig. 2F) and peak spike rate (Fig. 2I). Poisson distribution assumption with spike counts was tested using χ² test. Post hoc Student's t tests with Bonferroni correction were performed to compare effects of sound shape in A1 and cSRAF with: discrimination index (Fig. 5D, blue and red curves), its associated time constant (Fig. 5H, blue and red curves), onset discrimination index (Fig. 7D, blue and red curves), sustained discrimination index (Fig. 7H, blue and red curves), temporal classifier performance (Fig. 7D, blue and red curves), and rate classifier performance (Fig. 7H, blue and red curves) for average single neurons and temporal classifier performance (Fig. 7L, blue and red solid curves) and rate classifier performance (Fig. 7L, blue and red dotted curves) for population.

Results

Prior studies indicate that the synchronized response duration or sound encoding time increases with increasing sound burst duration in A1 (Malone et al., 2015) and non-primary cortex (Lee et al., 2016) providing a potential neural code for temporal shape in the sound envelope. The “encoding time” corresponds to the time window over which a neuron conveys information about an ongoing sound and it can be quantified as a spike-timing variance (Theunissen and Miller, 1995; Chen et al., 2012) or alternatively as the duration of the response measured in the period histogram; that is, the histogram that is synchronized to the sound (Malone et al., 2015). Here we use the latter approach to examine how spiking patterns change throughout the duration of a sound burst by plotting the population response histogram and examine whether similar principles hold for non-primary cortices (see Materials and Methods; Fig. 1). As illustrated, the response histogram has a complex shape including a “peak” (asterisk) and secondary sustained components that change with temporal shape of the sound envelope (Fig. 1). As shown all of our sounds peak at 250 ms in the sound burst cycle (Fig. 1) and as f_c increases, the sound burst slopes and durations increase and decrease, respectively (Fig. 1, see overlaid sound pressure waveform; Table 1, top rows). In all cortical fields, as f_c increases the response peak (asterisk) occurs at increasingly later time points in the sound cycle approaching and eventually surpassing the time at which the sound burst peaks (Fig. 1). Accordingly, peak response delay is positively correlated (p < 0.001) with our sound shape parameter (f_c) in all three cortical fields (Fig. 2A). Because the sound envelope slope increases and duration decreases with f_c, this result is consistent with the envelope slope and level sensitivities previously reported for A1 (Heil, 2001). A similar relationship holds for the two non-primary cortices examined here (Fig. 2A, green and red lines). Note that for all but one sound shape, response delays are completely overlapping for the three cortical fields: A1, VAF, and cSRAF (Fig. 2A, blue, green, red symbols, and lines). Accordingly, the cumulative probability distributions for the three cortices are highly overlapped (Fig. 2B). Together these results extend prior studies indicating that the peak response delays vary with temporal shape of the sound envelope in non-primary cortex as they do in A1.

In A1, response durations can vary with the slope and duration of change in the sound envelope providing potential neural codes for these temporal cues (Lu et al., 2001; Malone et al., 2015; Lee et al., 2016). Here, we quantify response duration for the segment of the population histogram that is significantly above baseline response level (see Materials and Methods). In A1, response duration decreases minimally with increasing sound shaping parameter, f_c (Fig. 2D, blue line). Because duration of the sound burst decreases with increasing f_c in our sounds (see Materials and Methods), this result is consistent with prior observations in A1 (Malone et al., 2015). Here, we find a logarithmic and proportional change in response duration with sound shaping parameter f_c in all three cortical fields (Fig. 2D). Regression fits of the data are significant (p < 0.0001) with corresponding slopes in VAF and cSRAF that are greater than that of A1 by fourfold and 17-fold, respectively (Fig. 2D, green and red lines, respectively). Moreover, the cumulative probability distributions are shifted with A1 showing significantly higher probabilities for shorter duration responses than VAF and cSRAF (Fig. 2E). Across all sound conditions the average response duration increases significantly (p < 0.001) and in rank order with: A1 < VAF < cSRAF (Fig. 2F). These results indicate that response duration varies in a distinct manner from response peak delay. Moreover, response duration could encode the slope and/or duration of the sound burst envelope in all three cortical fields and the time scale for such encoding increases logarithmically and in a hierarchical fashion as one moves ventral from A1 to non-primary cortex.

In A1, the peak spike rate can increase as the rising slope of the sound burst stimulus becomes sharper and its duration shorter with sinusoid amplitude modulated sounds for example (Malone et al., 2007, 2015). Likewise, here we find A1 and VAF have large response peaks that occur early after sound onset (Fig. 1B,C). In contrast, cSRAF has relatively small peaks associated with sound onset (Fig. 1D). In all three cortices, the peak spike rate is positively correlated (p < 0.0001) with sound shape f_c (Fig. 2G) and the slope of this relationship is larger in A1 and VAF than cSRAF (Fig. 2G and legend). This is consistent with the notion that onset responses in A1 and VAF are more sensitive to changes in sound shape f_c than those in cSRAF. Cumulative probability distributions indicate that A1 and VAF tend to have the highest peak spike rates compared with cSRAF (Fig. 2H). Accordingly, across all sound conditions, the average peak spike rates are larger (p < 0.001) in A1 and VAF than cSRAF (Fig. 2I). These results indicate that peak spike rate could provide a signal for discriminating differences in sound envelope temporal cues particularly in A1 and VAF.

The systematic changes in response timing described above could provide a neural signal for decoding and discriminating sounds that differ in the temporal shape of the sound envelope. To examine this possibility, we simulate how the spike timing of single auditory cortical neurons might be integrated or decoded at a subsequent stage of auditory pathway to optimally discriminate sound using a spike distance metric (see Materials and Methods). We first identify the integration time scale, that is, the exponential time constant (Tau or τ) of a hypothetical recipient neuron needed for optimal sound shape (f_c) discrimination. To do so, we assign individual spikes a magnitude of “1” and keep track of the spike times as shown with dot raster plots of spike train responses to 10 presentations of the same sound envelope (Fig. 3A,B). Each spike is convolved with an exponential function that has a defined time constant (Tau or τ; Eq. 1; see Materials and Methods). The approach is illustrated for responses from a single cSRAF neuron to a sound sequence with four shaped noise bursts that are each 20 ms in half-duration (Fig. 3A, top, with f_c of 8 Hz). The spike times plotted immediately below the sound pressure waveform continue throughout each sound burst and there is a silent period between sound bursts (Fig. 3A, bottom dot raster plot). The smoothed spike train responses for 10 individual sound presentation trials are illustrated in a color plot (Fig. 3C, top). The corresponding smoothed spike train response average of 10 sound trials illustrates the integrated response time course when the time constant is 64 ms (Fig. 3C, bottom plot, black line). When the half-duration of the sound burst is 20 ms (f_c of 8 Hz), a smoothing time constant of either 64 or 256 ms generates four large amplitude response peaks (Fig. 3C and Fig. 3E, bottom plots, black lines). When the sound burst half-duration is shorter (2 ms, f_c of 64 Hz) and corresponding slopes are faster, responses synchronize to sound onset and there is a less pronounced silent period between sound bursts (Fig. 3B, see dot raster). Here, it is easier to resolve discrete neural responses to the 4 sound bursts when the time constant is smaller (Fig. 3D, bottom, Tau equal to 64 ms) versus when it is larger (Fig. 3F, bottom, Tau equal to 256 ms). Accordingly, our estimated neural discrimination of 2 versus 20 ms half-duration sounds is better (index 1.52 vs 1.27) with shorter time constants (64 ms vs 256 ms, respectively). This example cSRAF neuron response illustrates visually how the time scale for integrating temporal responses can determine the optimal sound shape discrimination.

Because primary and non-primary cortices have different response durations for many sound shapes (Fig. 2D; f_c < 8 Hz), we question whether the different cortical fields have different optimal time scales for discriminating sounds. To examine this, the time constants are varied from 2 to 256 ms to determine the time constant that elicits the optimal discrimination index (aka, maximal discrimination index). The approach for determining the optimal discrimination index and time constant is illustrated for example neurons from each cortical field (Fig. 4A–C). Here, the different color symbols indicate 9 different sound shapes being compared with a short duration reference sound (2 ms, f_c = 64 Hz, Fig. 4A–C). Neural discrimination functions for a single comparison of the short duration reference sound versus a long (80 ms, f_c = 2 Hz) duration sound are shown for each example neuron (Fig. 4A–C, red symbols and curves). In all three neurons, the time constant generating the maximum or optimal discrimination is >16 ms (Fig. 4A–C, asterisks and light gray bar).

Though temporally precise spiking patterns provide a signal for discriminating the temporal shape of the sound envelope in A1(Malone et al., 2015), it is not clear if this is true for all non-primary cortices (Niwa et al., 2013). Here, we vary the sound envelope temporal cues independent of underlying fine spectral structure to examine neural discrimination for 45 pairs of sound envelope shape (see Materials and Methods; Fig. 5A–C). As expected, when the sound shapes being compared are identical (i.e., the sound vs itself), sound discrimination is zero (Fig. 5A–C, matrix diagonal, dark blue voxels). Though the differences are small, A1 and VAF have significantly higher mean discrimination than cSRAF averaged across all 45 pairwise discriminations (Fig. 5A–C). Conversely, cSRAF neurons are marginally better at discriminating across 30 pairwise sound comparisons when sound burst f_c is <11 Hz (Fig. 5A–C; f_c < 11 Hz) and corresponding sound burst half-duration is >14 ms. Discrimination performance drops (p < 0.05, f_c (F_(8,1323) = 44.8, two-way ANOVA) for sounds with half-durations shorter than 28 ms (shape f_c ≥ 8 Hz) when the reference sound half-duration is 2 ms (f_c of 64 Hz) suggesting a half-resolution limit on the order of 20 ms (Fig. 5D). These findings confirm the general principle that the temporal spiking pattern can be used to discriminate sound shape in primary as well as non-primary auditory cortices.

Next, the optimal time constant is computed for each variation and pairwise comparison of sound envelope shape to determine whether the time scale for optimal discrimination changes with sound shape and cortical field. As illustrated for all possible pairwise sound comparisons, the time constant for optimal discrimination varies systematically with sound shape f_c (Fig. 5E–H). Indeed, for f_c >6 Hz, optimal time constants decrease with increasing sound f_c following a power law relationship in all three cortical fields (Fig. 5H; e.g., reference sound f_c is 64 Hz). Accordingly, optimal time constants change significantly with sound shape in all three cortical fields (see Materials and Methods; F_(8,1323) = 11.57, p < 0.001, two-way ANOVA). A key difference across cortical fields is the time scale for optimal discrimination of sound shape. Across many pairwise conditions A1 requires short duration time constants for optimal discrimination (Fig. 5 E, see light blue and cyan voxels corresponding to 20–25 ms). In contrast, VAF and cSRAF neurons require long duration (≥40 ms) time constants for many pairwise sound discriminations (Fig. 5F,G, orange, yellow voxels). This difference is readily apparent in plots of optimal time constants versus sound f_c with a reference sound f_c of 64 Hz (Fig. 5H, blue vs red or green symbols). A1 has optimal time constants <25 ms on average for sound shape f_c between 6 and 16 Hz; whereas, cSRAF has optimal time constants >35 ms for these same sounds (Fig. 5H, asterisks; for A1 vs cSRAF: Student's t test, p < 0.001; Wilcoxon rank-sum, p < 0.01). The longer time scales needed for optimal discrimination in VAF and cSRAF suggest the longer response durations (Fig. 2D) contribute to sound discrimination. For the range of sound shapes where discrimination is near maximum, time constants are rank ordered and increasing with: A1 < VAF < cSRAF (i.e., for f_c between 6 and 16 Hz, Wilcoxon rank-sum, p < 0.01). These results indicate that the time scale for integrating and optimally discriminating changes with the sound shape and increases hierarchically as one moves from primary to ventral non-primary cortices.

Spikes that occur immediately after a sensory stimulus onset (onset spikes) as well as those that occur subsequently are thought to arise from distinct circuit mechanisms and to encode unique sound properties (Chase and Young, 2008; Zheng and Escabí, 2008). Here, we examine the potential contribution of onset versus sustained spiking to sound discrimination. First, we define a criterion level for sound-evoked versus spontaneous spikes and determine the onset response time window (see Materials and Methods; Table 1). Next, we remove the onset spikes and determine the optimal sound discrimination for residual spikes, which we refer to as “sustained spikes” (see Materials and Methods; Fig. 6). Discrimination matrices illustrate that all three cortical fields discriminate sound shape well with onset spikes alone for many pairwise sound comparisons (Fig. 7A–C, yellow, orange, red voxels). Using onset spikes alone, sound discrimination performance decreases significantly with increasing sound f_c (F_(8,1323) = 141.32, p < 0.001, two-way ANOVA) in all three cortical fields (Fig. 7D). In all three cortical fields, discrimination performance is generally lower when only the secondary spikes are used to estimate sound shape discrimination (Fig. 7E–G vs A–C). However, VAF and cSRAF outperform A1 when only these secondary spikes are used (Fig. 7H, asterisks). These results support the idea that onset responses strongly contribute to neural discrimination of sound shape in all cortical fields; whereas, sustained responses provide more effective discrimination in non-primary cortices, VAF and cSRAF.

In real acoustic scenes, animals must identify or classify many sounds that can have substantially different temporal shapes in the sound envelope. Here, we simulate how spike timing could be used to classify 10 different temporal sound shapes with a probabilistic naive Bayesian model. As a first step, we isolate and assign each spike in a spike train a value of “1” and each time bin where there is no spike a value of “0”. An average response histogram associated with each sound is used to generate a time-varying response probability distribution identifying that sound (i.e., the prior; see Materials and Methods). Next, the likelihood that measured spike train belongs to a particular sound shape is computed for all shapes. This allows us to determine which sound shape best accounts for a given spike train (aka, the observed evidence). The percentage correct classification is then computed for each individual spike train across all shape f_c conditions with appropriate cross-validation and rendered in a corresponding confusion matrix (see Materials and Methods). As shown, precise spike-timing of single neurons can be used to classify 10 different sounds at above chance levels in all three cortical fields with accuracies between ∼25 and 40% correct (Fig. 8A–C, red and orange voxels along diagonal). All cortical fields classify poorly (near chance levels) when the sound envelopes have steep slopes and shorter durations (aka, f_c ≥ 32 Hz; Fig. 8D). When all spikes are considered, A1 (blue line) outperforms cSRAF (red line) for classifying many sounds (Fig. 8D, blue vs red lines, asterisks) and VAF performs at intermediate levels (Fig. 8D, green line). Temporal classification performance is significantly changing with sound shape (F_(9,1323) = 29.6, p = 0, two-way ANOVA) and with cortical field (F_(2,1323) = 59.68, p = 0, two-way ANOVA). These results indicate that individual neurons on average can classify sound shape based on in the spike-timing temporal patterns.

Since peak spike rate changes with sound shape (Fig. 2G), it is possible spike rate could be used to classify 10 sound shapes in single neurons. To determine this, spike-rate data are fit with a Poisson distribution for each sound shape condition and a Naive Bayes classifier is used to classify the sound shape given observed single-trial spike count responses within a 2 s period to generate a rate metric (see Materials and Methods). All three cortical fields classify sounds with a low performance accuracy based on spike rate alone (Fig. 8E–G). Accordingly, on average A1 neurons have near chance levels of performance (i.e., <15%) across all sound shapes (Fig. 8H, blue line). In VAF and cSRAF, spike rate-based classification accuracy is only significantly higher for the sound burst with the longest half-duration (80 ms, f_c of 2 Hz; Fig. 8H, asterisk; p < 0.05). These results suggest that spike count or equivalent spike rate per 2 s is not an optimal neural signal for coding sound shape in primary and non-primary auditory cortices.

Above we determine how the average single-neuron responses can be used to classify sounds. However, real brains have the capacity to access and simultaneously pool responses across many neurons in a given population (Schneider and Woolley, 2010; Malone et al., 2015). Here we examine the possible advantage of pooling from up to 50 neurons within each cortical field for classifying sound envelope shape (see Materials and Methods). In all three cortices, population pooling increases the performance level compared with the single-neuron temporal response classifier (Fig. 8I–K vs A–C). Accordingly, maximal performance levels are between 80 and 100% accuracy with pooled neuron output (Fig. 8L, solid lines) achieving >2-fold more accuracy than obtained for the average single neuron in all three cortical fields (Fig. 8D). In all three cortical fields, pooled performance decreases as f_c increases indicating poor classification of sound bursts that have a rapid rate of change in amplitude and short duration (Fig. 8L). A1 outperforms cSRAF across all sound shapes when responses are drawn from the population (Fig. 8L, asterisks; p < 0.05, Student's t test). In contrast, the pooled output performance is close to chance levels when we use a spike-rate-based sound classifier in all cortical fields (Fig. 8L, dotted lines, M–O). Nevertheless, classification performance significantly varies with the method of classification (spike timing vs rate, A1: F_(9,980) = 144.2, p = 0; VAF: F_(9,980) = 144.37, p = 0; SRAF: F_(9,980) = 301.03, p = 0, two-way ANOVA) and across cortical fields (A1: F_(1,980) = 9362.78, p = 0; VAF: F_(1,980) = 7758.69, p = 0; SRAF: F_(1,980) = 4934.89, p = 0, two-way ANOVA). These results indicate that spike timing provides a robust signal for sound shape classification and performance improves when output from more neurons can be pooled to classify sounds.

Given that A1 and non-primary cortices have distinct time scales for responding to sequences of sound bursts, we question whether the advantage of pooling neural responses is similar for all sounds and cortical fields examined. To examine this, we create a ratio index between the classification performance obtained with the average single neuron versus the pooled temporal classifier for each sound and for each cortical field (Table 2). According to this index, ∼ 1- to 3-fold enhancement is evident for each sound condition in all three cortical fields (Table 2; p < 0.01, t test). The effect of pooling on classification performance was greater on average in A1 than in cSRAF (Table 2, far right column); however, the benefit of pooling was greater in cSRAF for two of the longest duration sound bursts (Table 2; f_c of 2 and 8 Hz). These results indicate that the advantages of pooling vary with the time scale of the sound and the response as well as across cortical fields.

Table 2.

Pooling enhances temporal classification performance

fc	2	4	6	8	11	16	23	32	45	64	Mean (SEM)
Half-duration	80	40	28	20	14	10	7	5	3	2
Slope	0.32	0.66	0.91	1.33	1.90	2.62	3.70	5.14	7.52	10.07
A1	2.3	2.2	2.4	2.6	2.7	2.9	2.7	1.57	2.2	2.9	2.4 (0.13)
VAF	2.5	2.6	2.6	2.8	3.0	2.1	2.3	2.95	2.1	2.2	2.2 (0.11)
cSRAF	3.1	2.1	2.2	2.8	2.3	2.2	1.3	1.30	1.4	1.7	2.1 (0.20)

A ratio index is computed for classification performance obtained using the pooled temporal classifier versus the average single neuron classifier for each sound condition and each cortical field. For every sound condition and cortical field there is a significant (p < 0.01, t test) improvement in performance with pooling.

Above we consider pooling output across 50 neurons in each cortical field; however, the rate at which a population converges toward a maximum performance provides a powerful benchmark for comparing performance across cortical fields (Carruthers et al., 2015). Here, we find performance increases as the number of neurons in the pool is increased in all three cortical fields (Fig. 8P, solid lines). Half maximal performance is achieved when pooling output from small (<10) populations of neurons for spike-timing-based classification in all cortices. Importantly, A1 and VAF require fewer neurons (3 and 5 respectfully) than cSRAF (16 neurons) and cSRAF converges less rapidly to achieve half maximal sound classification than A1 and VAF (Fig. 8P, blue and green vs red solid line). In contrast, spike-rate-based classification was near chance levels (Fig. 8P, dotted lines) and did not improve significantly with addition of more neurons (Fig. 8P, inset). Together these results indicate that spike-timing patterns provide a better signal than spike-rate patterns for classifying sound shape in primary and non-primary cortices. Furthermore, A1 and VAF outperform cSRAF in 10 alternative forced choice classification scenarios.

Discussion

This study finds cortical neuron population response delays and durations change with the temporal shape of the sound envelope, providing a potential neural code and extending prior studies in midbrain and A1 (Phillips et al., 2002; Heil, 2003; Zheng and Escabí, 2013) and non-primary auditory cortex (Lee et al., 2016). Here, we find peak response delays change similarly with sound shape f_c across A1 and non-primary cortices (Fig. 2A) but this is not the case for response duration (Fig. 2D). Though there is a logarithmic and proportional change in response duration with sound shape f_c in all cortices, the slope of this relationship is steeper in non-primary cortex (Fig. 2D, green and red lines). An example cSRAF neuron demonstrates this with a marked decrease in the duration of synchronized spiking following a decrease in sound burst duration (Fig. 3A). In contrast, changing sound shape f_c has modest effects on response duration in A1 (Fig. 2D, blue line). Here we cannot disambiguate potential neural codes for sound burst slope versus duration as these cues covary in our sounds (see Materials and Methods). However, these results raise the intriguing possibility that there are unique neural codes for the slope versus duration of a sound burst and that non-primary cortices are more sensitive to the latter. A related and compelling new contribution from this study is the finding that time scales for optimal and temporally precise sound discrimination are longer in non-primary than primary cortex (Fig. 5H, asterisks). This indicates that sustained spiking patterns in non-primary cortex contribute to their ability to discriminate the temporal shape of sound. These results support the concept that auditory cortical fields collectively provide temporally synchronized output on different time scales that could be used for behavioral discrimination and classification of sound envelope shape.

Though there is a long history supporting the concept that temporal sensory features are represented in spike-timing patterns, more recent studies indicate this occurs on multiple time scales (Lundstrom and Fairhall, 2006; Butts et al., 2007; Panzeri et al., 2010) and within spatially segregated cortical areas (Hamilton et al., 2018). Even in within A1 responses are heterogeneous and include onset, offset and sustained spiking that contributes to robust sound duration discrimination (Malone et al., 2015). The present study extends this concept providing evidence that sounds can be temporally encoded on unique time scales in primary and non-primary sensory cortices. In all three cortical fields examined, peak responses are synchronized to sound onset (Fig. 1) and can be used to discriminate sound shape (Fig. 7A–C). Prior studies find a similar relationship between the rate of rise of the sound envelope and onset response delay in auditory nerve, midbrain and A1 (Phillips et al., 2002; Heil, 2003). When we remove the onset spiking response, discrimination performance is markedly reduced for A1 neurons (Fig. 7H, blue line), as expected given most of the A1 response occurs immediately following sound onset. In contrast, following removal of onset spikes, non-primary cortices outperform A1 for sound discrimination. This indicates that longer duration responses of VAF and cSRAF contribute additional signal for sound discrimination. Cortices may in general specialize to classify sounds on different time scales, as this is also observed in human cortices for responses to extended sound sequences including speech (Hamilton et al., 2018). Here, these results indicate that output from non-primary cortex must be integrated on longer time scales to provide the optimal signal for discriminating pairs of sounds that differ in temporal envelope shape.

In more complex acoustic scenes animals are often faced with more than two sounds to discriminate. Here, we use a Naive Bayesian classifier to simulate how the output from cortex could be used for perceptual identification of 10 sound shapes much like individuals would have to do in a 10-alternative forced choice task. This classifier successfully classifies sound shapes across 10 alternative forced choices provided we use the precise spike-timing output from cortical neurons (Fig. 8A–D). If we remove the precise spike-timing patterns and use spike rate instead, the sound shape classifier performance drops dramatically. This result is true whether it is a single neuron contributing to the classifier or multiple neurons. This suggests that temporal integration mechanisms are likely necessary to readout and classify large sets of sound shapes in primary as well as non-primary cortices.

This study finds pooling activity from more neurons improves sound classification performance in A1 and non-primary cortices (Table 2) even though there is a rank order increase in temporal imprecision (jitter) of single-neuron responses to sound shape with: A1 < VAF < cSRAF (Lee et al., 2016). This supports the concept that pairwise discriminations are robust to differences in response duration or jitter, as reported previously (Larson et al., 2009). Here, we provide additional evidence that the ability to classify 10 sound shapes with spike-timing pattern is inversely related to the temporal imprecision of cortical responses with: A1 > VAF > cSRAF. Thus, cSRAF typically has weak onset and longer duration responses with correspondingly less accurate sound classification performance with the temporal-code-based classifier (Fig. 8P, solid lines). Conversely, cSRAF has a slightly more robust performance with the rate-code-based classifier (Fig. 8P, inset, dotted red line). The differences in accuracy for classification in non-primary cortices are not likely due to differences in spike rate or reliability, which are similar across cortical fields for sound burst sequences with repetition rates of 2 Hz (Lee et al., 2016). In all three cortices, our classifier has a 2 to threefold increase in performance when pooling output from the population of neurons compared with the average single neuron (Table 2). The pooling advantage in general is consistent with the proposition that pooling activity of groups of neurons can compensate for spike train imprecision in individual neurons (Zohary et al., 1994; Geffen et al., 2009; Bizley et al., 2010; Schneider and Woolley, 2010; Carruthers et al., 2015). The new twist in the present study is that pooling is also important for robust temporal-code-based sound classification in non-primary cortices like cSRAF, a region with temporally sluggish and imprecise responses that are longer in response duration (Fig. 2D) and encoding times (Lee et al., 2016).

A hierarchy in time scales between A1 and non-primary cortices may reflect functional hierarchies for pooling, decoding and classifying sounds. The degree of sound classification performance improvement with neuron response pooling is robust in A1 and cSRAF for short (Table 2; f_c > 8 Hz) and longer (Table 2; f_c < 8 Hz, half-durations ≥20 ms) duration sound bursts, respectively. Thus, cortices may have distinct optimal time scales for pooling and decoding cortical responses in much the same way that they have distinct optimal time scales for pairwise sound burst discriminations. Accordingly, brain structures that receive and pool output from cSRAF could require longer temporal integration times than structures that pool output from A1. In such a scenario, non-primary cortex could certainly pool responses from A1 to classify sounds but the reverse is less likely.

All hearing mammals have multiple auditory cortical fields (Hackett, 2011), and in the rat it has been demonstrated that each field is specialized to respond to distinct acoustic features (Higgins et al., 2010; Storace et al., 2011, 2012; Carruthers et al., 2015; Nieto-Diego and Malmierca, 2016). A1 resolves time better than non-primary cortices, VAF, and cSRAF (Lee et al., 2016). Conversely, non-primary cortices (VAF and cSRAF) resolve spectral frequency and spatial location cues in sound better than A1 (Polley et al., 2007; Higgins et al., 2010; Storace et al., 2011; Lee et al., 2016). Each cortical field receives distinct thalamocortical pathway inputs that could underlie these functional specializations (Storace et al., 2011, 2012). It is possible these specializations reflect time-frequency tradeoffs in sound processing where A1, and its corresponding thalamocortical pathway, have superior temporal resolution at the expense of spectral resolution. Conversely, non-primary fields, and corresponding thalamocortical pathways, could be better at resolving frequency cues at the expense of resolving timing cues. In addition, such differences may also reflect trade-offs in the ability to resolve spatial location of sound (Higgins et al., 2010). In the present study, we hold spectral and spatial cues constant to examine neural coding of temporal cues in the sound envelope independently. Future exploration will be needed to determine whether neuronal classification of sound's temporal shape is even more robust in non-primary auditory cortices when spectral, temporal and spatial features are combined (Carruthers et al., 2015; Engineer et al., 2015; Town et al., 2017) and when animals are attending during a behavioral tasks (von Trapp et al., 2016), as happens in natural settings.