Toward Fast and Efficient Visible‐Light‐Driven Molecular Motors: A Minimal Design

Abstract

A key goal in the development of light‐driven rotary molecular motors is to facilitate their usage in biology and medicine by shifting the required irradiation wavelengths from the UV regime to the nondestructive visible regime. Although some progress has been made toward this goal, most available visible‐light‐driven motors either have relatively low quantum yields or require that thermal steps follow the photoisomerizations that underlie the rotary motion. Here, a minimal design for visible‐light‐driven motors without these drawbacks is presented and evaluated on the basis of state‐of‐the‐art quantum chemical calculations and molecular dynamics simulations. The design, featuring dihydropyridinium and cyclohexenylidene motifs and comprising only five conjugated double bonds, is found to produce a full 360° rotation through fast photoisomerizations (excited‐state lifetimes of ≈170–250 fs) powered by photons with energies well below 3 eV.

1. Introduction

Molecular motors are molecules with the ability to produce directed mechanical motion by using energy from an external source.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 Among the various types of synthetic molecular motors available today, those that achieve 360° unidirectional rotary motion through the absorption of UV or visible light are commonly known as light‐driven rotary molecular motors.17, 18, 19, 20, 21, 22, 23, 24, 25 Typically, the clockwise (CW) or counterclockwise (CCW)—as determined by the molecular chirality—rotary motion results from consecutive E→Z and Z→E photoisomerizations around a carbon– or carbon–nitrogen double bond that connects two distinct molecular halves. Furthermore, for most motors of this type (but not all21) the reaction cycles also include slower thermal conformational relaxation steps.

The first synthetic light‐driven rotary molecular motors, based on sterically overcrowded alkenes, were developed in the late 1990s17 and have subsequently attracted considerable interest, both in terms of improving the performance of these motors26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 and in exploiting the mechanical motion that they produce for useful applications.39, 40, 41, 42, 43, 44, 45 Under ambient conditions, the intrinsic rotational frequencies attainable by freely floating (in solution) overcrowded‐alkene motors are limited in two different ways. First, the thermal steps of the reaction cycles are not as fast as the photoisomerizations around the central carbon– double bond that power the motors.28, 34 Second, the photoisomerization quantum yields (QYs) do not exceed 20–30 % because of the coupling of the desired torsional motion to an undesirable pyramidalization of one of the central carbon atoms.34, 35, 46, 47 From the point of view of applications, adding to these challenges is the fact that most overcrowded‐alkene motors are driven by energetic UV light, which is more damaging to the motors and their environment than visible light. Thus, a key goal in the development of light‐driven molecular motors is to make them responsive to visible light,22, 25, 48, 49, 50, 51, 52 so as to facilitate their usage in biological systems and other soft materials.53

Against this background, considerable efforts have been devoted both to finding ways to accelerate the thermal steps of overcrowded‐alkene motors26, 27, 28, 29, 30, 33, 36, 37, 38, 54, 55, 56, 57 and to put forth alternative light‐driven motor designs that require no thermal steps to complete a full 360° rotation.21, 58, 59, 60 Furthermore, progress has also been made in the design of new motors with photoisomerization QYs that are less hampered by pyramidalization at the isomerizing bond than overcrowded‐alkene motors.47, 61, 62, 63 For example, it has been found that it is possible to hinder the pyramidalization in motors that incorporate a protonated or alkylated nitrogen Schiff base,47 thanks to the electron‐withdrawing capability of the cationic nitrogen center, whereby both high QYs and short excited‐state lifetimes become attainable.61, 62 Moreover, a strategy to reach this goal even in the absence of a cationic moiety has been proposed, where the pyramidalization is rather curbed by enabling part of the motor to become aromatic in the photoactive excited state.63 The challenge to develop visible‐light‐driven motors, on the other hand, has started to be met only recently (see Scheme 1).

Scheme 1.

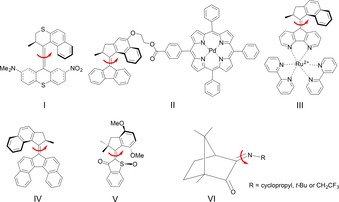
Rotary molecular motors driven by visible light.

For example, following an early (in 2003) design that utilized push–pull substituents to make an overcrowded‐alkene motor (compound I in Scheme 1) operable by λ=430 nm light,64 it has been shown that the use of a palladium–tetraphenylporphyrin (compound II in Scheme 1) or a ruthenium(II)–bipyridine (compound III in Scheme 1) complex as a photosensitizer allows overcrowded‐alkene motors to be driven by λ=530–550 and 450 nm light, respectively.50, 51 In a different approach, the extension of the aromatic core of one such motor yielded a motor (compound IV in Scheme 1) that similarly can be operated by light up to λ=490 nm.52 As for other motor designs, Dube and co‐workers22, 25 devised a hemithioindigo‐based motor (compound V in Scheme 1) functioning with light up to λ=500 nm, whereas Lehn and co‐workers21 introduced camphorquinone‐derived imine motors (compound VI in Scheme 1) involving only photochemical steps fueled by UV or visible light.

In this work, we propose a minimal design of molecular motors that not only are powered by visible light, but whose E→Z and Z→E photoisomerizations are also fast, efficient, and yielding 360° unidirectional rotary motion without intermediary thermal steps. In particular, by performing quantum chemical calculations and nonadiabatic molecular dynamics (NAMD) simulations65, 66, 67, 68, 69, 70, 71, 72 in the framework of complete active space self‐consistent field (CASSCF) theory,73, 74 we predict that visible‐light‐driven motors can be devised in a straightforward way by extending the π conjugation of UV‐powered Schiff‐base motors from three to five double bonds. Furthermore, importantly, we show that this can be done without compromising the speed and efficiency with which the photoisomerizations of the Schiff‐base motors occur.61, 62 For the purpose of the study, the UV‐powered Schiff‐base motor pictured in Scheme 2 and designed in our recent computational work62 is used as one (out of four, see below) reference system. This system, which features a pyrrolinium motif connected by an olefinic bond to a cyclohexenylidene motif, is hereafter referred to as motor 1 a.

Scheme 2.

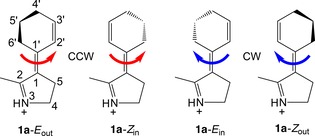
The E _out, Z _in, E _in, and Z _out isomers of Schiff‐base motor 1 a.

2. Results and Discussion

2.1. Motors Considered in this Work

Whereas 1 a, through minimum energy path (MEP) calculations and NAMD simulations, has been found to produce 360° unidirectional rotary motion in a purely photochemical fashion,62 it is worth pointing out that this is achieved despite the absence of a stereocenter in this motor. Instead, the CW or CCW direction of the E→Z and Z→E photoisomerizations around the central olefinic bond is, as shown by the MEP and NAMD data,62 controlled by the asymmetry introduced by the ring‐puckered cyclohexenylidene unit. Specifically, the E and Z isomers of 1 a have two possible orientations of the 5′‐carbon atom relative to the approximate plane formed by the other carbon atoms of the cyclohexenylidene moiety: outward (out) and inward (in). Accordingly, there are four different isomers of 1 a that can be labeled 1 a‐E _out, 1 a‐E _in, 1 a‐Z _out, and 1 a‐Z _in (see Scheme 2). Because of this out/in orientation of the 5′‐carbon atom, the 1 a‐E _out and 1 a‐Z _in pair of isomers complete a full 360° CCW rotation through consecutive E→Z and Z→E photoisomerizations, whereas the 1 a‐E _in and 1 a‐Z _out pair conversely complete a full 360° CW rotation.62

As the four isomers of 1 a form two pairs of axially chiral enantiomers, 1 a‐E _out/1 a‐E _in and 1 a‐Z _out/1 a‐Z _in, the thermal free‐energy barriers separating the E _out and E _in and the Z _out and Z _in enantiomers need to be sufficiently large for this motor design to be successful. Indeed, if this is not the case, it will be difficult to isolate an enantiopure out/in isomer by using established asymmetric synthesis techniques such as dynamic kinetic resolution75, 76 and, hence, to control the direction of photoinduced rotation. Thus, it is of interest to explore ways to increase the enantiomerization barriers as much as possible. In this work, we investigate the possibility that these barriers can be increased by introducing substituents bulkier than a hydrogen atom at the 4′,5′‐positions of the cyclohexenylidene, based on the idea that such substituents may exert steric hindrance for the enantiomerizations (an alternative strategy would have been to bridge the cyclohexenylidene, as in α‐pinene77). To this end, motors with the 4′ and 5′ hydrogen atoms (R=H) replaced by methyl groups, chlorine atoms, or bromine atoms were also considered, as shown in Scheme 3. The resulting motors, which together with 1 a constitute the reference systems for our study, are denoted 1 b (R=Me), 1 c (R=Cl), and 1 d (R=Br).

Scheme 3.

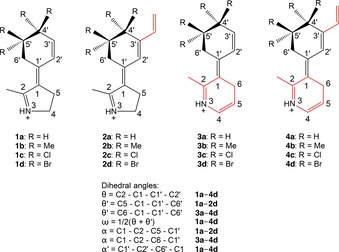
Schiff‐base motors considered in this work shown in their E _out isomeric forms and definitions of the dihedral angles for these motors. Motors 1 a–d are reference systems from which motor candidates 2 a–d, 3 a–d, and 4 a–d are obtained by extending the π conjugation, as indicated in red font.

To redshift the excitation wavelengths of 1 a–d toward the visible regime, three different approaches to extend the π conjugation were considered, as illustrated in Scheme 3. In the first approach, a vinyl group is added to the 3′‐position of 1 a–d to yield motor candidates 2 a–d, respectively. In the second approach, the pyrrolinium motif of 1 a–d is replaced by a dihydropyridinium motif, resulting in motor candidates 3 a–d. In the third approach, finally, the structural alterations in 2 a–d and 3 a–d are combined to give motor candidates 4 a–d, with a total of five conjugated double bonds (compared to three and four such bonds in 1 a–d and 2 a–d/3 a–d, respectively).

2.2. Light‐Absorption Features

First, the light absorption of all motors was investigated by calculating their lowest two excited singlet states (S₁ and S₂) by using both complete active space second‐order perturbation theory (CASPT2)78 and the approximate coupled‐cluster singles and doubles (CC2) method.79 As further described in the Supporting Information, the calculations were done with the cc‐pVTZ basis set,80 based on ground‐state (S₀) geometries optimized with the CASSCF method or with Møller–Plesset second‐order perturbation theory (MP2). The CASPT2 calculations were performed with active spaces comprising the full π systems of the motors, that is, by utilizing CAS(6,6), CAS(8,8), and CAS(10,10) for 1 a–d, 2 a–d/3 a–d, and 4 a–d, respectively.

The full results of the calculations are summarized in Tables S2 (CC2 data) and S3 (CASPT2 data) of the Supporting Information, which show that S₁ is consistently the bright and photoactive ππ* state characteristic of protonated Schiff bases81 and that this state is well separated from S₂, in most cases by more than 1 eV. Trends in the vertical S₀→S₁ excitation energies of the E _out and E _in isomers of the motors are highlighted in Figure 1 (being enantiomers, the E _out and E _in data sets are identical), whereas the corresponding trends for the Z _out and Z _in isomers are shown in Figure S2. As the latter trends are analogous to the former trends, the discussion below is focused on the E _out and E _in isomers.

Figure 1.

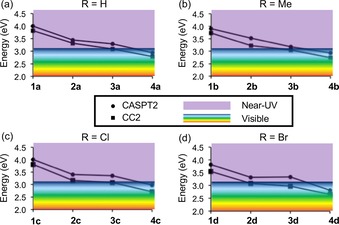
Vertical S₀→S₁ excitation energies of the E _out and E _in isomers of motors a) 1 a–4 a, b) 1 b–4 b, c) 1 c–4 c, and d) 1 d–4 d in the near‐UV (λ<400 nm, >3.1 eV) or visible (λ>400 nm, <3.1 eV) regime calculated with CASPT2 and CC2.

From the parallel curves in Figure 1, it can first be concluded that the CASPT2 and CC2 predictions as to how the energy of the photoactive S₁ state varies between the motors are very similar. Thus, for the present purposes, it suffices to discuss the CASPT2 results. Furthermore, focusing on these energies is sensible in that they throughout lie above the CC2 energies. Therefore, any CASPT2‐based conclusion regarding the possibility to bring the light absorption into the visible regime below 3.1 eV is also supported by the CC2 data.

Starting with reference motors 1 a–d, the S₁ energies in Figure 1 are solidly in the near‐UV region, falling between 3.8 and 4.0 eV. However, by adding a vinyl group to the 3′‐position to obtain 2 a–d, the S₁ energies are redshifted by an appreciable 0.5 eV, attaining values between 3.3 and 3.5 eV irrespective of whether the 4′,5′‐positions hold H atoms (as in 2 a), Me groups (as in 2 b), Cl atoms (as in 2 c), or Br atoms (as in 2 d). Alternatively, even larger redshifts are predicted to arise by replacing the pyrrolinium motif of 1 a–d by a dihydropyridinium motif in 3 a–d, which lowers the S₁ energies to between 3.2 and 3.4 eV. Furthermore, although neither the addition of a vinyl group nor the incorporation of a dihydropyridinium motif is by itself sufficient to reach the visible regime, the two strategies applied together are successful in this regard, as shown by the results for 4 a–d. In fact, the combined net effect appears essentially additive, helping redshift the S₁ energies by 1.0 eV down to between 2.8 and 3.0 eV for these motors. Accordingly, there appears to be a straightforward route to the design of visible‐light‐driven motors starting from UV‐powered Schiff‐base motors. Next, we turn to investigating whether this route may produce motors that are also fast and efficient, starting with an assessment of their enantiomerization barriers.

2.3. Enantiomerization Barriers

As discussed above, the potential of the motor design put forth in this work cannot be fully realized unless the thermal free‐energy barriers separating the E _out and E _in and the Z _out and Z _in enantiomers of the motors are fairly large. Therefore, it is of interest to calculate these barriers, which was done as described in the Supporting Information for all motors in the gas phase and in nonpolar (cyclohexane) and polar (water) solvents by using both MP2 and density functional theory (DFT) methods in combination with the cc‐pVTZ basis set. For the DFT calculations, three different functionals were used: B3LYP, M06‐2X,82 and ωB97X‐D.83 From the full results of the calculations summarized in Table S4, it can be seen that the variation between the methods in their estimates of the E _out↔E _in and Z _out↔Z _in barriers for any given motor is generally small, in most cases around 5 kJ mol⁻¹. Furthermore, the variation in how the barriers are predicted to change from one motor to another, which is our main focus, is naturally even smaller. Thus, for the sake of brevity, Figure 2 highlights the B3LYP/water results for how the E _out↔E _in barriers vary between the motors (the trends for the corresponding Z _out↔Z _in barriers are very similar).

Figure 2.

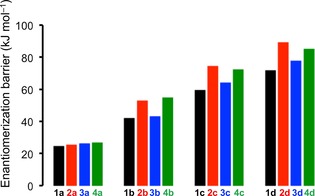
E _out↔E _in enantiomerization free‐energy barriers for motors 1 a–4 d calculated with B3LYP in a water solvent.

From Figure 2, it is clear that there is a steady increase in the enantiomerization barriers when the H atoms at the 4′,5′‐positions of 1 a/2 a/3 a/4 a (barriers of ≈25 kJ mol⁻¹) are replaced by bulkier Me groups in 1 b/2 b/3 b/4 b (≈40–50 kJ mol⁻¹), Cl atoms in 1 c/2 c/3 c/4 c (≈60–70 kJ mol⁻¹), and Br atoms in 1 d/2 d/3 d/4 d (≈70–90 kJ mol⁻¹). Hence, invoking the definition that the E _out/E _in and Z _out/Z _in enantiomers are separable if their half‐lives are at least 1000 s,84 especially the Br‐substituted systems have enantiomerization barriers of sufficient magnitude for the isolation of enantiopure out/in isomers to be feasible even at room temperature.

2.4. Photochemical Steps

Among the Br‐substituted systems 1 d/2 d/3 d/4 d, the motor with the longest‐wavelength absorption is 4 d, whose CASPT2 S₁ energies of 2.8 eV fall well within the visible regime (see Figures 1 and S2). Thus, it is of particular interest to assess the speed and efficiency of this motor. To this end, and as further described in the Supporting Information, the E→Z and Z→E photoisomerizations of 4 d were modeled by performing MEP calculations and NAMD simulations by using state‐averaged CASSCF (SA‐CASSCF) in combination with the cc‐pVDZ80 and SVP85 basis sets, respectively. For each geometry along the MEPs, dynamic electron correlation effects were accounted for through CASPT2 single‐point calculations. Starting from the vertically excited Franck–Condon (FC) points in the photoactive S₁ state, the MEPs of the E _out, Z _in, E _in, and Z _out isomers of 4 d are presented in Figure 3. For comparison, the corresponding MEPs were also computed for motors 1 d/2 d/3 d. These MEPs, which are very similar to the ones of 4 d, are shown in Figures S3–S5.

Figure 3.

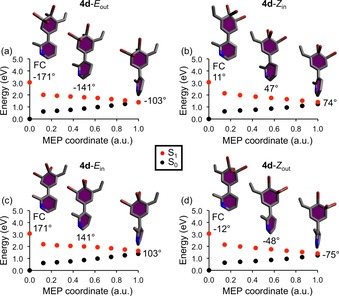
CASPT2//SA‐CASSCF photoisomerization MEPs from the S₁ FC points of the a) E _out, b) Z _in, c) E _in, and d) Z _out isomers of motor 4 d. Also shown are the molecular geometries along the respective paths and the corresponding ω dihedral angles.

From Figure 3, it is notable that the excited‐state evolution from the FC point is for each isomer of 4 d dominated by torsional motion around the central olefinic bond, which is in line with the ability of 4 d to function as a rotary motor. Furthermore, the torsional motion is favorably barrierless and brings the systems toward assumed S₁/S₀ conical intersection regions, where they can be funneled to the S₀ state. For the E _out and Z _in isomers, the direction of motion is such that the values of the ω dihedral angle (see Scheme 3) are continuously increasing, which is here defined as CCW motion. The E _in and Z _out isomers, conversely, produce CW motion occurring toward decreasing ω values. These E _out/Z _in and E _in/Z _out pairings of the isomers are further accentuated by the fact that CASSCF S₀ geometry optimizations started from the end points of the MEPs yield, by completing net 180° rotations around the central olefinic bond, Z _in as the photoproduct of the E _out path and E _out as the photoproduct of the Z _in path, and similarly Z _out as the photoproduct of the E _in path and E _in as the photoproduct of the Z _out path. Accordingly, 4 d appears capable of producing 360° unidirectional rotary motion from consecutive E→Z and Z→E photoisomerizations alone, without intermediary thermal steps, and is able to use the out/in orientation of the 5′‐carbon atom to control the direction of rotation—CCW for the E _out/Z _in pair and CW for the E _in/Z _out pair.

Another piece of valuable information from the MEPs is that the E→Z and Z→E photoisomerizations of 4 d proceed almost without any pyramidalization of the central olefinic carbon atoms. Specifically, as revealed by Table S5, the α and α′ dihedral angles (see Scheme 3) are consistently of small magnitudes (at most 4°) for all geometries along the MEPs. Given that a much more pronounced pyramidalization is thought to be a key factor in limiting the QYs of overcrowded‐alkene motors to 20–30 %,34, 35, 46, 47 one may then expect 4 d to show favorable photoisomerization dynamics.

Turning, thus, to the NAMD simulations, these were run for maximally 700 fs and with ten different initial nuclear configurations and velocities for each of the E _out, Z _in, E _in, and Z _out isomers of 4 d. Started in the S₁ state, the trajectories were allowed to hop to the S₀ state on the basis of criteria for the magnitudes of the energy gap and nonadiabatic coupling between the states that are specified in the Supporting Information. Following a previous assessment of the importance of multiple hopping events for the photoisomerization dynamics of Schiff‐base motors,62 only one single hop between the S₁ and S₀ states was allowed for each trajectory. Two key quantities estimated by the simulations are defined in the following way. First, the photoisomerization time (PIT) is defined as the time needed to form the Z _in isomer from the E _out isomer and vice versa (or to form the Z _out isomer from the E _in isomer and vice versa) by completing a net 180° CCW rotation (or a net 180° CW rotation) around the central olefinic bond relative to the initial nuclear configuration. Second, the excited‐state lifetime (τ) is defined as the time it takes before a CCW E _out/Z _in or a CW E _in/Z _out trajectory decays to the S₀ state. These results from the simulations are listed in Table 1.

Table 1.

τ and PIT values for the ten NAMD trajectories calculated for each of the E _out, Z _in, E _in, and Z _out isomers of motor 4 d.

Trajectory	τ [fs]	PIT [fs]	τ [fs]	PIT [fs]	τ [fs]	PIT [fs]	τ [fs]	PIT [fs]
	4 d‐E out		4 d‐Zin		4 d‐E in		4 d‐Z out
1	258	556	182	570	119	618	203	–[a]
2	316	538	189	569	268	526	220	–[a]
3	304	535	156	454	227	–[a]	182	452
4	308	–[a]	178	–[a]	262	–[a]	209	–[a]
5	151	584	158	–[a]	228	524	187	497
6	259	687	156	380	209	555	192	620
7	224	–[a]	176	–[a]	293	–[a]	179	–[a]
8	203	–[a]	170	625	293	530	162	–[a]
9	209	575	184	–[a]	253	544	167	–[a]
10	312	508	159	625	245	477	167	596
average[b]	254	569	171	537	240	539	187	541

[a] Trajectory does not complete the photoisomerization within 700 fs. [b] Average value over all trajectories.

From Table 1, it is first encouraging to note that the average τ and PIT values are small for all isomers of 4 d, amounting to only 170–250 (τ) and 540–570 fs (PIT) for the E _out/Z _in pair and 190–240 (τ) and 540 fs (PIT) for the E _in/Z _out pair. In this respect, 4 d compares very favorably to overcrowded‐alkene motors, which typically have excited‐state lifetimes of 1 ps or more.35, 46 Furthermore, it is actually the case that the values in Table 1 are not far off those previously attributed to UV‐powered Schiff‐base motors,61, 62 such as the τ values of 170–190 fs predicted for reference motor 1 a through the same type of modeling.62 Hence, besides establishing a simple route to transform UV‐powered Schiff‐base motors into visible‐light‐driven Schiff‐base motors, this work also predicts that this can be done without slowing down the photochemical steps, although obtaining quantitatively accurate τ and PIT values would clearly require that many more than ten NAMD trajectories be run for each of the four isomers.

As for obtaining well‐converged and quantitatively accurate estimates of the photoisomerization QYs of 4 d, this too would demand calculating a more numerous set of trajectories than deemed affordable herein. Furthermore, a more elaborate treatment of trajectory surface hopping would be needed, such as Tully's fewest‐switches algorithm.86 Although these are not feasible options, especially at the CAS(10,10) level, Table 1 shows that seven (E _out), six (Z _in), seven (E _in), and four (Z _out) trajectories among the ten calculated for each isomer do complete the corresponding photoisomerization within 700 fs. These results suggest that 4 d could well attain high photoisomerization QYs. Moreover, similar to the situation for 1 a,62 each isomer of 4 d exhibits perfect (100 %) directionality in that all reactive photoisomerization trajectories for the isomer in question proceed in one and the same direction.

To illustrate the full 360° rotations achieved by the E _out/Z _in and E _in/Z _out pairs of isomers of 4 d, Figure 4 highlights the changes in the ω dihedral angle along typical photoisomerization trajectories of the different isomers. In addition, two multimedia files in the Supporting Information contain molecular animations of these processes. As can be seen, Figure 4 corroborates the MEP results by showing that the E→Z and Z→E photoisomerizations produce 360° unidirectional rotary motion around the central olefinic bond with continuously increasing or decreasing ω values. Furthermore, the direction of rotation—CCW for the E _out/Z _in pair and CW for the E _in/Z _out pair—is controlled by the out/in orientation of the 5′‐carbon atom.

Figure 4.

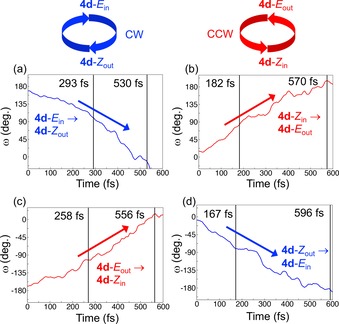
Changes in the ω dihedral angle along typical photoisomerization trajectories of the a) E _in, b) Z _in, c) E _out, and d) Z _out isomers of motor 4 d. τ and PIT values are indicated with vertical lines.

3. Conclusions

We have presented a minimal design of molecular motors that can be driven by visible light and are able to produce fast and efficient rotary motion without intermediary thermal steps. Specifically, with it proven difficult to realize all of these desirable features simultaneously in one and the same motor design, we have demonstrated computationally that a small Schiff‐base motor (4 d) comprising only five conjugated double bonds is successful in this regard. In particular, using state‐of‐the‐art techniques based on multi‐configurational quantum chemistry, it is found that this motor achieves a full 360° rotation from consecutive, visible‐light‐triggered (≈2.8 eV at the CASPT2 level) E/Z photoisomerizations alone, and that these processes are both fast (τ≈170–250 fs) and efficient. We hope that these results will stimulate further investigation of ways to exploit usefully the favorable features of synthetically realizable87 Schiff‐base systems in the future development and application of molecular motors. In this regard, a brief retrosynthetic analysis for the actual preparation of 4 d is presented in the Supporting Information (see Scheme S1).

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

Supplementary

J. Wang, B. Durbeej, ChemistryOpen 2018, 7, 583.