Abstract
Single Molecule Switching Nanoscopy (SMSN) beyond the coverslip surface poses significant challenges. The sample-induced aberrations distort and blur single-molecule emission patterns. Combining active point-spread function shaping and efficient adaptive optics enables robust 3D-SMSN imaging at large depths. This development allowed us to image through 30-μm thick brain sections, visualize the morphology and the nanoscale details of amyloid-β filaments in a mouse model of Alzheimer’s disease and reconstruct their volumetric arrangements.
Three Dimensional (3D) Single Molecule Switching Nanoscopy (SMSN) imaging beyond the coverslip surface poses significant challenges1. One major obstacle is that sample-induced aberrations distort and blur single molecule emission patterns, known as Point Spread Functions (PSFs), making 3D inference of molecular positions unreliable1. Adaptive Optics (AO) assisted SMSN developments helped push the volumetric 3D-SMSN imaging depth to whole cells. However, to date, robust 3D-SMSN reconstruction of more than a couple layers of cells or tissues remains a practical challenge1,2 due to the permanent information loss caused by aberrations induced by fixed or living specimens. Here, we introduce a method combining adaptive PSF shaping and an efficient AO routine to simultaneously correct sample-induced aberrations and enforce a consistent PSF response through large depths, therefore permitting robust 3D super-resolution volumetric imaging of fluorescence stained tissues. We demonstrate imaging through 30 μm brain sections from mouse frontal cortices by reconstructing fine details of fibrillar amyloid-β plaques found in Alzheimer’s disease.
3D-SMSN requires pinpointing thousands to millions of single molecules with high precision and accuracy3 in lateral and axial dimensions. This task becomes challenging when the specimen is thicker than a few microns1. Both light-sheet illumination4 and activation5 of fluorescent probes have been applied to significantly reduce background fluorescence, allowing detection of single molecules through large depths (Supplementary Table 1). At the same time, advanced sample preparation techniques provide significant background and scattering reduction in fluorescence microscopy of tissues and increase probe penetration depth during immunolabeling6,7 (Supplementary Note 1). Despite the success of these new techniques, the emitted photons from single molecules, the sole source of molecular information in SMSN, experiences inhomogeneous refractive indices while passing through the specimen and therefore their PSFs are distorted and, more importantly, blurred. Distortion of the PSF biases position estimation of single molecule centers8 but can be corrected through recently developed localization analysis9,10 or post-processing techniques8,11. The increased blurring due to aberrations leads to a permanent loss in the inherent information of the molecular position (Figure 1, Supplementary Figure 1), limiting the practical imaging depth of 3D-SMSN2. Wave-front correction methods compensate for aberrations by using a deformable mirror (DM) to restore the constant phase delay of an aberrated wave-front2,12–14. However, limited by the achievable wave-front correction complexity of the available methods and hardware, the practical imaging depth and robustness of 3D-SMSN is generally limited to within several microns from the coverslip surface2,13.
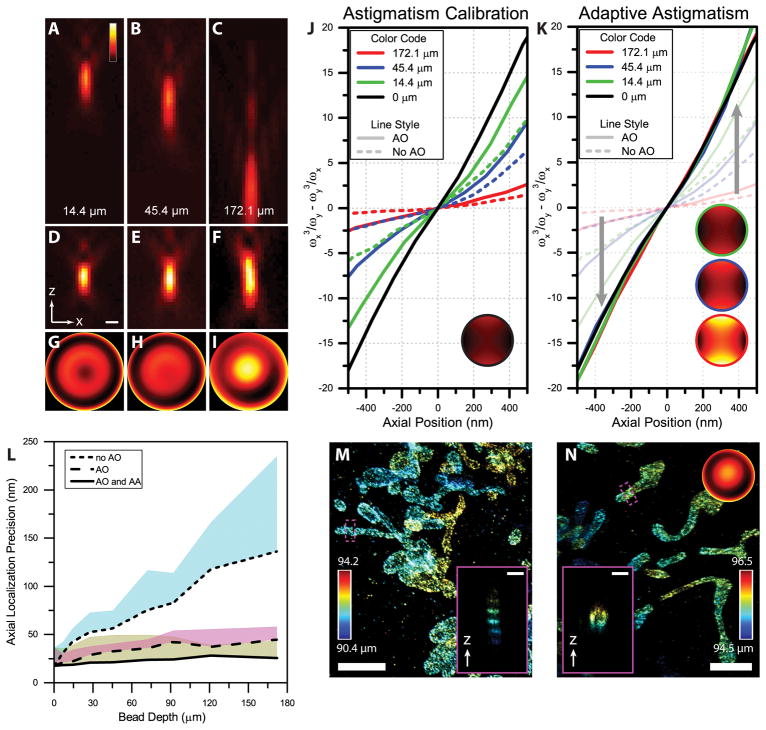
Figure 1.
Characterization and demonstration of AO and AA in beads and cultured cells. (A–C) x-z views of PSFs (100 nm beads) at depths of 14.4 μm, 45.4 μm and 172.1 μm, respectively, without AO correction. (D–F) AO corrected PSFs at depths corresponding to the PSFs in A–C. (G–I) Magnitude of Zernike Modes used to remove depth and sample aberrations in A–C. (J) Astigmatic shape modulation around the focal plane at different depths with AO correction (solid lines) and without AO correction (dashed lines). A constant astigmatism was used at all depths (see inset). (K) Astigmatic shape modulation with AA which adaptively changes the amplitude of astigmatism at each depth (see insets, color outlines correspond to depth) to create a consistent shape modulation through a large axial range. A total of nine beads at different depths were recorded (Supplementary Figure 2, 4) (L) Theoretical axial precision limit calculated using the Cramér-Rao Lower Bound for the beads in A–K. The line represents the optimal precision achievable within ±500 nm from the original focal spot. The shaded regions are an average of the axial localization precisions from ±500 nm from the optimal axial localization precision calculated for each depth. (M) Super resolution image of mitochondria in a COS-7 cell labeled with TOM20-Alexa647 without AO correction, imaged through a depth of ~90 μm. The inset shows the cross-section of the mitochondria. (N) Super resolution image of mitochondria in a COS-7 cell and imaged through a depth of ~95 um with AO correction and AA (Supplemental Note 1). The inset shows the axial profile of the region in the magenta box. M, N serve as demonstration of large aberrations and are representative images from three data sets. Scale bars for A–F and the insets in M and N are 500 nm. Scale bars in the main part of M and N are 2.5 μm.
Here, we developed a novel approach combining adaptive PSF shaping with an efficient sensor-less AO method to allow robust volumetric 3D-SMSN imaging through thick specimens. First, to enable efficient aberration correction through several tens of microns, we employed Nelder-Mead simplex optimization for AO correction. In our approach, the shape of the DM is optimized based on the Nelder-Mead simplex algorithm where the amplitudes of the microscope-calibrated aberration modes (Online Methods) are optimized by the directional search method based on the quality of single molecule blinking events (Online Methods). This approach avoids potential biases associated with presumptions from the coordinate search method2 and converges rapidly to the local minimum compared to stochastic approaches12. Furthermore, we found our system corrects high order aberration modes such as 1st and 2nd order spherical aberrations, the principal aberration modes when imaging through thick specimens (Supplementary Figure 2). This allowed us to remove aberrations and restore the PSF sharpness effectively, and was tested through a large sample depth, up to 170 μm (Figure 1A–L). Deterioration of the resolution along lateral (Supplementary Figure 1) and most significantly, the axial dimensions (Figure 1A–C, L), occurs due to sample-induced aberrations introduced primarily from refractive index mismatch between immersion media and the sample. This effect in the axial dimension has made robust reconstruction and quantification of super-resolution volumes at these depths difficult (Figure 1L, M). Using the developed methods, we found the corrected PSF closely approaches the PSF on the coverslip surface (Figure 1D–F). Removal of large aberrations (Figure 1G–I) allows us to restore a sharp focus for single molecule emissions through the thick cavity (Figure 1L, Supplementary Figure 3).
While maintaining a sharp focus through thick specimens provides the foundation for effective detection of single molecules, the axial positions of these detected single molecules are encoded by their astigmatic shape1. The precision in the axial dimension relies on the rate at which the PSF shape modulates along the axial dimension. While our approach largely restores the peak intensity and sharpness of single emitters at the focal plane throughout sample depths (Figure 1D–F, Supplementary Figures 4–5), the axial modulation of the PSF, however, still weakens with increasing imaging depth (Figure 1J, Supplementary Figure 5). This weakened modulation leads to significant losses of axial information in the detected PSFs, reducing resolution in the axial dimension, and thus introducing image artifacts. These aberration-induced reconstruction artifacts were visualized through cross-sections in the axial plane of a reconstructed super-resolution volume (Figure 1M, insert). To solve this challenge, we developed a method that adaptively changes the magnitude of astigmatism introduced by a single DM with respect to imaging depth, termed Adaptive Astigmatism (AA). With this approach, we achieved almost identical shape modulation of PSFs at various depths into the specimen (Figure 1K, Supplementary Figure 5). To quantify the information gain provided by combining the developed methods, we calculated the theoretical axial information limit for single molecule localizations at various depths (Figure 1L). We found that our approach significantly improves the axial localization precision limit while maintaining nearly the same precision from the coverslip surface up to a depth of ~170 μm (Figure 1L, Supplementary Figures 1, 3, 5, Online Methods).
As a demonstration, we imaged TOM20 in COS-7 cells labeled with Alexa Fluor 647 (Online Methods). We created a sample cavity with 90 μm diameter beads acting as spacers separating two coverslips (Online Methods) with the labeled cells on the upper coverslip. Without AO correction, imaging directly with astigmatism based conventional 3D-SMSN, we found the sample introduced large amounts of aberrations including 1st and 2nd order spherical aberration, astigmatism and coma (Supplementary Figure 2B). Left uncorrected, aberrations lead to artificial band structures in the axial direction caused by the significantly weakened shape modulation and therefore the loss of information in the PSF (Figure 1J, M). In contrast, with the developed method, we can achieve high resolution in each optical section and align them with high fidelity (Supplementary Figure 6). In the reconstructed 3D volume, our method enables restoration of the shape of the mitochondria as shown in the axial cross-section despite imaging through the ~95 μm cavity (Figure 1N, Supplementary Note 2), providing a proof-of-concept demonstration of the ability to recover the single molecule emission information.
Due to the large amount of aberrations introduced by the heterogeneous refractive index within the densely packed tissue, 3D-SMSN imaging of brain slices has been generally restricted to within a couple microns of the coverslip surface15,16. One approach to circumvent this problem is to image ultra-thin brain slices, each with a thickness of tens of nanometers. Two-dimensional-SMSN on these slices can be subsequently combined into 3D volumes through postprocessing17. This method allows high-quality reconstruction of brain sections as challenges of potential distortions and artifacts caused by the thick specimen are replaced by 2D-SMSN imaging of hundreds to thousands of ultra-thin slices. However, the requirement of highly specialized expertise and the sheer amount of effort could make this approach challenging and time consuming in studies where multiple reconstruction of brain slices are required for statistical quantification.
Here, based on our developed approach, we demonstrate 3D-SMSN imaging at various depths in 30 μm thick mouse frontal cortices of fibrillar amyloid-β (Aβ) plaques, a hallmark of Alzheimer’s disease (AD)18 (Figure 2A, Supplementary Figures 7–10, Supplementary Table 2); providing a significant improvement from previous demonstrations of 3D-SMSN of the brain. This capability is unlocked by two keys: an efficient AO approach which corrects aberrations at different depths and the Adaptive Astigmatism which restores the z-dependent PSF shape modulation (Supplementary Figure 11, Supplementary Data 1).
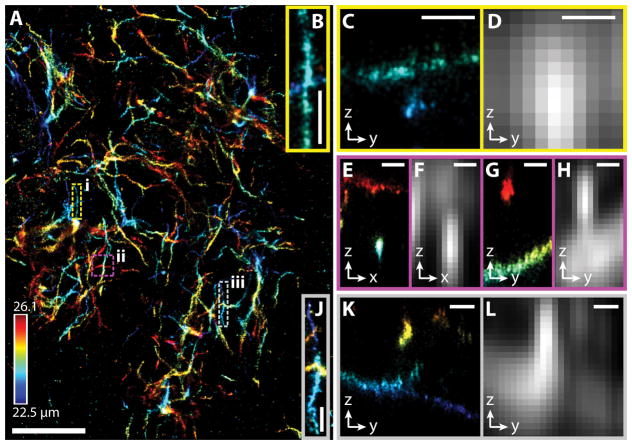
Figure 2.
3D-SMSN image of an amyloid plaque in a 30 μm mouse cortex section. (A) 3D-SMSN image of Aβ plaque located at a depth ~24 μm with a thickness of ~3.6 μm. (B) Zoom-in sub-region from A enclosed in the dashed yellow box (i). (C) y-z cross section from panel B. The two crossing filaments are ~650 nm apart. (D) Equivalent confocal images (Online Methods) created by convolving the localized molecules in (C) with the expected PSF from a confocal microscope imaging at a depth of ~24 μm. (E, G) x-z and y-z cross sections, respectively, from the magenta box (ii) in A. The two filaments are separated by ~1.7 μm. (F, H) Equivalent confocal microscope images from the regions E and G. (J) Region enclosed in the gray box (iii) in A. (K) y-z cross section from J. The filaments are separated by ~1.1 μm. (L) Equivalent confocal microscope image from K. Scale bars: 5 μm in A and 500 nm in B–L. Color bar in A corresponds to the depth from the coverslip surface. The presented image is representative of 37 different imaged plaques.
Aβ-plaque deposition is the earliest detectable pathological change in the brain and increases through the course of AD and in advance of impaired cognition. Aβ plaques are often measured by their number and area using confocal microscopy, however due to the diffraction limit, filaments blur together and small changes are susceptible to noise, resulting in opposing findings19. 2D-SMSN has shown morphological changes in Aβ fibrils, despite no change in overall plaque area or number using conventional imaging20. 3D-SMSN allows quantification of subtle changes in plaque morphology and 3D arrangements of the fibrils that are not observed with conventional imaging or 2D projections. We reconstructed super-resolution volumes of Aβ plaques and found their sizes vary from 5 μm with a low density of filaments to larger than 15 μm with a high density of filaments (Supplementary Figures 7, 12, Supplementary Note 3). In comparison with confocal equivalents20, we measured that larger plaques consist of filaments from 90–100 nm widths to as much as 200–300 nm (Figure 2, Supplementary Figures 7, 9, 10). We were able to distinctly observe morphology of individual filaments (Supplementary Figure 10) and reconstruct their 3D arrangement within the plaque center while imaging through the thick tissue (Figure 2B–L, Supplementary Figure 9).
We show the developed method enabled recovery of the information encoded within the PSF of individual probes through a highly aberrated specimen. Our method restores and enforces an effective and consistent PSF at the detector through a large sample depth and therefore enables the imaging and robust reconstruction of single molecule emission events in 3D through a thick specimen. This allows us to reconstruct the entire Aβ plaque volume in 3D permitting structural and potentially functional studies in densely packed brain tissues of a variety of Aβ fibril clusters which are known to be structurally heterogeneous, based on their differential reactivity with various antibodies and chemical probes. The future combination of advanced clearing techniques, sophisticated single molecule illumination and detection methods and new probes with the demonstrated method could permit nanoscale reconstructions revealing the interactions between plaques and the glial cells (which mediates plaque remodeling) during disease progression. Further, we hope our development will allow, in general, the study of the nanoscale details of cellular and tissue structures as well as the interaction with adjacent cell types.
Online Methods
Super-resolution Instrument Setup with Deformable Mirror
The system was built around an Olympus IX-73 microscope (IX-73, Olympus America Inc., Waltham, MA) with a 100x/1.35 NA silicone oil-immersion objective lens (FV-U2B714, Olympus America Inc.) and a PIFOC objective positioner (ND72Z2LAQ, Physik Instrumente, Karlsruhe, Germany). Samples were excited with a 642 nm laser (2RU-VFL-P-2000-642-B1R, MPB Communications Inc., Pointe Claire, Quebec, Canada) and activated with a 405 nm laser (DL-405-100, Crystalaser, Reno, NV). The lasers were focused to the back aperture of the objective and offset from the optical axis (for HILO21). A square aperture (SP60, OWIS, Breisgau, Germany) limited the excitation area to ~32 × ~32 μm2 and a HILO sheet-thickness of ~11 μm21. The filter turret held a quadband dichroic mirror and quad-bandpass filter (Di03-R405/488/561/635-t1 and FF01-446/523/600/677, Semrock Inc.). The fluorescence was magnified by relay lenses arranged in a 4f alignment to a magnification of 0.78 to achieve a pupil diameter of 3.8 mm at the surface of the deformable mirror (DM) (Multi-3.5, Boston Micromachines, Cambridge, MA) (Supplementary Note 4). Following the DM, relay lenses resulted in a final magnification of 52.7 for a 120 nm effective pixel size at the sCMOS camera (Orca-Flash4.0v3, Hamamastu, Tokyo, Japan)22. The fluorescence signal passed through an additional bandpass filter (FF01-731/137-25, Semrock Inc.) placed before the camera. The optical hardware was optimized to limit the inherent system aberrations (Supplementary Figure 13).
Generation of Microscope Specific Zernike Modes
The DM was calibrated following the protocol described in detail previously13. Briefly, theoretical mirror deformation modes (‘mirror modes’) were derived from the theoretical response of the membrane surface of the DM23,24. These mirror modes resemble Zernike polynomials commonly used to describe aberrations in microscope systems24. Subsequently, we retrieved pupil functions for 5 different amplitudes for each mirror mode using a phase retrieval algorithm by imaging an isolated bead on the coverslip surface13,25. Each pupil function (28 modes and 5 amplitudes per mode) was decomposed into 55 Zernike polynomials. For each mode, the amplitude coefficient associated with each theoretical Zernike polynomial was extracted for different amplitudes. The slope of these coefficients against input mirror mode amplitudes was linearly fit, resulting in an underdetermined system of 28 linear equations13. Solving these equations with least squares, each Zernike polynomial can be expressed as a linear combination of the theoretical mirror modes13. Although the system allows generation of a large number of higher order Zernike modes, we restricted our sample correction to six Zernike modes observed to have major contributions from sample induced aberrations26. Other aberration modes can be included in the simplex routine as desired.
Simplex Adaptive Optics Implementation
The Nelder-Mead Simplex algorithm (referred to as Simplex algorithm27) was implemented to optimize the DM shape to achieve an aberration-free, flat wave-front.
PSFs obtained from imaging 100 nm beads at the coverslip were optimized by the following method. An initial guess vector with N amplitudes that corresponds to N different Zernike modes is considered a single vertex. To generate a simplex, we generate multiple vertices by combining N initial guess vectors where each vector contains a single non-zero element for a specific Zernike mode with another guess vector which has non-zero elements for all Zernike modes. For example, to correct aberrations using two Zernike modes, the initial inputs, v, takes the following form.
a1 and a2 represent initial guesses for the two Zernike modes under optimization.
Here, correction of N Zernike modes requires a N+1 x N matrix, where N is the number of Zernike modes being corrected and N+1 is the number initial vertices in the simplex. For each vertex (vertexi, that is the ith row in matrix v), the DM is adjusted according to the amplitude of the vertex and a single camera frame was recorded. Subsequently, an image metric f(vertexi), was determined using image metrics (see below). After evaluating f(vertex1) through f(vertexN+1), the initial simplex is formed. Subsequently, the algorithm evaluates the image metric at new vertices generated through four defined processes, ‘Reflection’, ‘Expansion’, ‘Contraction’ and ‘Shrink’ to generate a new simplex. This process continues until the simplex converges (i.e. all rows were identical to within a user-set threshold) or until the maximum number of iterations have been exceeded. Typically, the algorithm converged within 10–20 iterations. This process was repeated over a range of depths (Figure 1, Supplementary Figure 2A, 4).
The AO corrections for beads at different depths serve as a guide for AO corrections in biological samples. The depth of the biological ROI was estimated by measuring the distance from the coverslip to the ROI using the PIFOC objective positioner. For large depths (>15 μm), the apparent focal shift due to the spherical aberration becomes significant enough to shift the axial position of the ROI away from the original focal position (Supplemental Figure 14B). To account for this, the 1st and 2nd order spherical aberrations were set to correspond with the approximate depth settings (Supplemental Figure 2A) and the position of the PIFOC was readjusted to ensure that the ROI was in focus before the simplex algorithm was initiated. The simplex process starts at the beginning of each data acquisition for a specific ROI when the molecular density is highest and readjusts for every ~1.6–2 μm of depth.
Image Metrics for Spherical Aberration and Other Zernike Modes
We used two different metrics to determine the PSF quality, the first of which was a modified version based on the sharpness metric reported previously2. For optical aberrations such as astigmatism and coma, we modified the sharpness metric2 to have additional weights. The metric has the profile:
| (1) |
Where, n and m are incremented by 1 and n, m ∈ [−L/2, L/2 − 1] (L is the number of pixels along a single dimension), În,m is the discrete Fourier transform magnitude of the image, OTFn,m is the discrete Fourier Transform of an ideal PSF for our system, α is an empirically determined value (α = 1.3 here), μn,m is a circular mask:
| (2) |
and , Δx and Δy represents the pixel size of the image in two dimensions (generally, Δx = Δy), where λ is the emission wavelength and NA is the numerical aperture of the objective lens. The highest weighted region of this metric is located where the deviation between the Fourier transform, În,m, and the ideal OTFn,m is most pronounced. We note that this metric works optimally when the Zernike modes under optimization do not influence the apparent focus of the image, such as astigmatism and coma.
For optimization of Zernike modes that induce apparent changes to the focal position, such as 1st and 2nd order spherical aberrations, we found the above metric could lead to an incorrect solution strongly dependent on the initial depth of the PSF. For optimization of spherical aberrations, we used the following metric in which higher frequencies were masked so that only lower frequencies are considered. Mathematically this metric is proportional to the intensity of the image in real space convolved with a blurring kernel similar to the intensity metric that was used in conventional microscopy methods28 and previous AO assisted interferometric nanoscopy approaches13.
| (3) |
and
| (4) |
The use of two different masks necessitated splitting the Simplex optimization into two steps. The Simplex algorithm corrected 1st and 2nd order spherical aberrations using the above metric (Eqs. 3–4) first, followed by Simplex correction on both astigmatisms and both comas using the first metric (Eqs. 1–2).
Data Acquisition Sequence
First, the ROI was found and the desired axial (thickness) region was determined. Next, the simplex algorithm optimized the DM for the best correction values (described above) for the initial image plane and again for every ~1.6 μm of depth. This distance was empirically chosen, as little change occurs to the PSF over an axial range of ~2 μm and the correction was performed with astigmatism for 3D imaging turned off. The correction values were recorded. It should be noted that determining the optimal DM shape prior to imaging only works for static samples. Once the DM correction values were found, typical imaging parameters were set (Supplementary Table 2) and the DM shape was adjusted based on the optimized DM parameters and the adaptive astigmatism values (Supplementary Figures 5, 14).
Typically, in 3D-SMSN, when imaging ROIs thicker than the optical section the raw data will be collected from multiple optical sections encompassing the ROI. These optical sections (or z-steps) are typically separated by 300–600 nm. Often, several thousand frames of raw data are taken at each z-step, with the stepping pattern repeated for many cycles. This cyclic approach enables uniform detection of molecules over the depth range and counters the effects of out of focus photobleaching. For thick ROIs, typically >3 μm, we employed an alternative stepping methodology to enhance correlation of a specific optical section between multiple cycles where large drift can cause loss of such correlation which is critical for high accuracy in drift correction and optical section alignment. SMSN imaging on the first five steps occurs as usual. When the next cycle begins, the first step is offset by one. Each subsequent cycle begins at one z-step deeper than the previous cycle. Recording data in such a way results in entire axial subsections of the ROI being recorded over shorter time periods, increasing the ability to properly align all optical sections and mitigating the effects of axial drift. Also importantly, implementation of HILO reduces the amount of photobleaching in the out-of-focus sections of the ROI and the lightsheet thickness can be further reduced with more sophisticated light-sheet illumination modalities4,29.
Bead Sample Preparation and Imaging
Cleaned coverslips were treated with Poly-L-lysine for 10–20 min and washed three times with PBS. 100 nm diameter beads (ThermoFisher Scientific, Waltham, MA) were diluted from the stock to a concentration of ~10−5. Approximately 100 μL of diluted beads were placed on the coverslip for ~20 min and washed three times with PBS. The coverslip was placed in a custom sample holder (Tristar, Methuen, MA). Agar (A9045-5G, Sigma-Aldrich, St. Louis, MO) was mixed with the diluted bead stock to a concentration of ~5% and warmed to ~70°C. Approximately 200 μL of the agar/bead solution was placed onto the bead coverslip. A second cleaned coverslip was placed on top of the agar/bead solution and the two coverslips were sealed together using two-component silicon dental glue (picodent twinsil speed 22, Dental-Produktions und Vertriebs GmbH, Wipperfürth, Germany). The entire sample was placed in 4°C to decrease the agar gelation time.
Immuno-staining of TOM20 in COS-7 Cells
COS-7 cells were washed three times with 37°C 1X PBS. Cells were fixed with 37°C pre-warmed 3% paraformaldehyde (PFA) (15710, Electron Microscopy Sciences, Hatfield, PA) and 0.1% glutaraldehyde (16019, Electron Microscopy Sciences) in PBS for 15 minutes at room temperature (RT) and washed twice with PBS. The cells were treated with 0.1% NaBH4 (452882, Sigma Aldrich) for 7 minutes at RT. Cells were washed three times with PBS and treated with 10 mM Tris, pH 7.3 for 10 minutes. After washing three times with PBS, cells were permeabilized and blocked with 3% IgG-free BSA (001-000-162, Jackson Immunoresearch, West Grove, PA) and 0.2% Triton-X-100 (X100, Sigma Aldrich) in PBS for 0.5 hour at RT gently rocking on a rocking platform. The blocking buffer was aspirated and rabbit anti-TOM20 (sc-11415, Santa Cruz Biotechnology, Santa Cruz, CA, USA) diluted 1:1000 in 1% BSA and 0.2% Triton-X-100 was incubated for 1 hour at RT while gently rocking. Cells were washed three times for 5 minutes at RT with 0.05% Triton-X-100 in PBS. The anti-rabbit Alexa Fluor 647 secondary antibody (A21245, Life Technologies, Carlsbad, CA) was diluted in 1% BSA and 0.2% Triton-X-100 with a 1:1000 dilution for 0.5 hour at RT gently rocking and covered with aluminum foil. Cells were washed three times for 5 minutes at RT with 0.05% Triton-X-100 in PBS. Cells were post-fixed with 4% PFA for 10 minutes at RT and rinsed three times with PBS and stored at 4°C.
Preparation of 90 μm Coverslip Cavity
A cleaned coverslip was placed in a custom-made sample holder (Tristar, Methuen, MA). ~20 μL of 90 μm diameter latex beads (AA42751AA, Alfa Aesar, Tewksbury, MA), diluted in PBS by ~10x, were placed in the center of a cleaned coverslip to act as a spacer. ~150 μL of imaging buffer was placed on the diluted beads. A second coverslip containing COS-7 cells fluorescently labeled with TOM20-Alexa 647 was gently placed on top of the imaging buffer (with the cells facing down). The two coverslips were sealed together using two-component silicon glue.
Sample Preparation from Trem2 deficient Alzheimer’s Disease Mice
Mice were housed in the Association for Assessment and Accreditation of Laboratory Animal Care International accredited facility in the Cleveland Clinic Biological Resources Unit and all experiment procedures were approved by the Cleveland Clinic Foundation Institutional Animal Care and Use Committee. The use of animal and/or animal derived materials in this study were performed in accordance with relevant guidelines and regulations.
Trem2 deficient mice (Trem2tm1(KOMP)Vlcg) with replacement of exons 2, 3, and part of 4 were crossed into the APPPS1-21 Alzheimer’s disease mouse model which expresses the Swedish APP mutation (KM670/671NL) and the L166P mutation in PSEN1 under the Thy-1 promoter30 to obtain 4-month-old Trem2−/−; APPPS1-21 mice and were previously characterized19. Briefly, following deep anesthetization with ketamine/xylazine, mice were perfused with ice-cold PBS, brains were rapidly removed, fixed for 24 hours in 4% PFA in PBS and cryoprotected in 30% sucrose in PBS at 4°C. Following embedding in Tissue-Tek OCT Compound (VWR, Radnor, PA), 30 μm sections were obtained on a Leica CM 1950 cryostat and stored in cryoprotectant solution containing 30% sucrose, 1% PVP-40, and 30% ethylene glycol in 0.1M phosphate buffer at −20°C. For detection of amyloid fibrils, sections were permeabilized with 0.1% Triton X-100 in PBS for 10 minutes at RT, subject to antigen retrieval in 10 mM sodium citrate, pH 6.0, with 0.5% Tween-20 for 10 minutes at 95°C, blocked in 5% normal goat serum (005-000-121, Jackson Immunoresearch, West Grove, PA), 0.3% Triton X-100 in PBS for 1 hour at RT and incubated in anti-β amyloid antibody (2454, Cell Signaling Technology, Danvers, MA) at 1:500 overnight at 4°C with agitation. Sections were washed with 0.1% Triton X-100 in PBS and incubated in anti-rabbit Alexa Fluor 647 conjugated secondary antibody (A-21244, Invitrogen, Eugene, OR) at 1:1000 for 1 hour at RT. After washing, sections were mounted onto cleaned coverslips and dried for 30 minutes at RT.
Three-Dimensional Single Molecule Localization
The sCMOS camera was calibrated for its pixel-dependent offset, gain and variance following the protocol described previously22. These calibrated maps were used for localization of single molecules imaged on our sCMOS sensor.
Single molecule localization was performed similarly as described previously22. Briefly, a series of uniform and maximum filters segmented each individual frame into sub-regions containing potential single molecules. These sub-regions were processed through localization algorithms based on a maximum-likelihood estimator (MLE) with an sCMOS noise model22. Molecule centers in the lateral dimension were obtained from the MLE while width measurements in both lateral dimensions of the astigmatic PSF were obtained (σx and σy). Estimations on detected photon numbers, background photon counts and log-likelihood ratio values31 were obtained for each sub-region. Axial position estimates were performed based on σx and σy by minimizing the error between the measured value and the calibrated curve as described previously32.
3D-SMSN Volume Drift Correction and Optical Stack Alignment
The work flow of drift correction and optical section alignment are illustrated in Supplementary Figure 6. Before alignment, drift within each optical section was corrected by 3D volume correlation with the redundancy method described previously13.
Subsequently, optical sections at different axial positions were aligned as described below. Volumetric super-resolution imaging requires precise alignment of adjacent optical sections. Due to the anisotropic resolution in 3D super-resolution imaging, 3D correlation based methods previously described13 for isotropic super-resolution volumes misalign the optical sections due to the significant lower resolution along the axial dimension. However, the consistent PSF performance throughout the depth (Figure 1L) enables alignment of optical sections based on the following method. 3D histograms were reconstructed for each optical section where the count for each voxel equals to the number of localizations within the voxel (40 nm voxel sizes were used). 3D correlation was performed for pairs of adjacent optical sections. The resulting correlation volume was smoothed to reduce noise. A 2D slice from the 3D correlation volume was selected based on the expected shift between the two optical sections. Within the slice, Fourier interpolation33 identifies the peak with an effective pixel size of 1.3 nm in the final interpolated image. The peak pixel position provides an estimate of lateral shift of the two adjacent optical sections given an estimated axial shift. One can often evaluate the reconstruction by visualizing through cross-sectional images in the axial direction as shown in Figures 1N and 2. Inaccurate volumetric reconstructions are much less apparent when visualized in the lateral projections as demonstrated in Figure 1M.
Calculation of Theoretical Localization Precision
The Cramér-Rao lower bound (CRLB)34 estimates the lowest localization error given a likelihood function of the emitter model. The emitter is modeled as a 2D Gaussian, with widths of σx and σy in each lateral dimension34 and the intensity as the number of photons emitted. The detected photons with and without AO at various depths were quantified as a ratio between the peak pixel intensity from the corrected and uncorrected PSFs. The variables σx and σy are functions of emitter’s axial position and calculated from two sets of calibration parameters obtained from the method described above. The likelihood function is calculated from a Poisson noise model9,34, and for simplicity, the readout noise of the sCMOS camera is ignored. Therefore, the CRLB can be calculated from
| (5) |
where F is the Fisher information matrix, and elements in F is given by
| (6) |
in which μ is the emitter model and θ are the estimation parameters, including emitter’s position in x, y and z, and the total photon count and the background photon count and k is the pixel index in the fitting region. The reported lateral CRLB estimated precision values are (Supplementary Figure 15). Here, in (6) the first derivative of μ respect to θ is calculated numerically from
| (7) |
Supplementary Material
Acknowledgments
We thank G. Sirinakis and E. Allgeyer for programming assistance with the deformable mirror. M.J.M, S.L. and F.H. were supported by grants from DARPA (D16AP00093 to F.H.) and NIH (R35 GM119785 to F.H.). P.J.C., S.M.B., B.T.L, and G.E.L. were supported by grants from the Indiana Clinical and Translational Sciences Institute, funded in part by grant # UL1TR001108 from the National Institutes of Health, National Center for Advancing Translational Sciences, Alzheimer’s Association, Jane & Lee Seidman Fund, generous donations from Chet & Jane Scholtz and Dave & Susan Roberts, NIA R01 AG050597, NIH R01 AG023012, and NIH RF1 AG051495 (to B.T.L. and G.E.L.), CWRU NDD T32 NS077888, CWRU MSTP T32 GM725039, and NIA NRSA F30 AG055261 (to P.J.C.).
Footnotes
Author Contributions
M.J.M and F.H. conceived the project. M.J.M. developed the microscope setup and instrumentation control. M.J.M, S.L., and F.H. performed data analysis and simulation. M.J.M., B.T.L., G.E.L., and F.H. designed the experiments. M.J.M., P.J.C-H., S.M.B., T.J.M., D.A.M. carried out the biological experiments. All authors wrote the manuscript.
Competing Financial Interests Statement
The authors declare no competing financial interests.
Data Availability Statement:
Two example datasets of raw camera frames showing single molecule blinking events without and with correction using the developed methods are included in Supplementary Data 1. Additional datasets are available from the corresponding author upon reasonable request.
Code Availability Statement:
The DM control and optimization modules (LabView, instrument control) are included in the Supplementary Software and further updates will be made available at https://github.com/HuanglabPurdue/AO_SMSN.
References
- 1.von Diezmann A, Shechtman Y, Moerner WE. Three-Dimensional Localization of Single Molecules for Super-Resolution Imaging and Single-Particle Tracking. Chem Rev. 2017 doi: 10.1021/acs.chemrev.6b00629. acs.chemrev.6b00629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Burke D, Patton B, Huang F, Bewersdorf J, Booth MJ. Adaptive optics correction of specimen-induced aberrations in single-molecule switching microscopy. Optica. 2015;2:177. [Google Scholar]
- 3.Baddeley D, Bewersdorf J. Biological Insight from Super-Resolution Microscopy: What We Can Learn from Localization-Based Images. Annu Rev Biochem. 2018;87 doi: 10.1146/annurev-biochem-060815-014801. annurev-biochem-060815-014801. [DOI] [PubMed] [Google Scholar]
- 4.Legant WR, et al. High-density three-dimensional localization microscopy across large volumes. Nat Methods. 2016;13:359–365. doi: 10.1038/nmeth.3797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cella Zanacchi F, Lavagnino Z, Faretta M, Furia L, Diaspro A. Light-Sheet Confined Super-Resolution Using Two-Photon Photoactivation. PLoS One. 2013;8 doi: 10.1371/journal.pone.0067667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ku T, et al. Multiplexed and scalable super-resolution imaging of three-dimensional protein localization in size-adjustable tissues. Nat Biotechnol. 2016;34:973–981. doi: 10.1038/nbt.3641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhao Y, et al. Nanoscale imaging of clinical specimens using pathology-optimized expansion microscopy. Nat Biotechnol. 2017;35:757–764. doi: 10.1038/nbt.3892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Diezmann A, von Lee MY, Lew MD, Moerner WE. Correcting field-dependent aberrations with nanoscale accuracy in three-dimensional single-molecule localization microscopy. Optica. 2015;2:985. doi: 10.1364/OPTICA.2.000985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu S, Kromann EB, Krueger WD, Bewersdorf J, Lidke KA. Three dimensional single molecule localization using a phase retrieved pupil function. Opt Express. 2013;21:29462–87. doi: 10.1364/OE.21.029462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Babcock HP, Zhuang X. Analyzing Single Molecule Localization Microscopy Data Using Cubic Splines. Sci Rep. 2017;7:552. doi: 10.1038/s41598-017-00622-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McGorty R, Schnitzbauer J, Zhang W, Huang B. Correction of depth-dependent aberrations in 3D single-molecule localization and super-resolution microscopy. Opt Lett. 2014;39:275–8. doi: 10.1364/OL.39.000275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tehrani KF, Xu J, Zhang Y, Shen P, Kner P. Adaptive optics stochastic optical reconstruction microscopy (AO-STORM) using a genetic algorithm. Opt Express. 2015;23:13677. doi: 10.1364/OE.23.013677. [DOI] [PubMed] [Google Scholar]
- 13.Huang F, et al. Ultra-High Resolution 3D Imaging of Whole Cells. Cell. 2016;166:1028–1040. doi: 10.1016/j.cell.2016.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ji N. Adaptive optical fluorescence microscopy. Nat Methods. 2017;14:374–380. doi: 10.1038/nmeth.4218. [DOI] [PubMed] [Google Scholar]
- 15.Dudok B, et al. Cell-specific STORM super-resolution imaging reveals nanoscale organization of cannabinoid signaling. Nat Neurosci. 2014;18:75–86. doi: 10.1038/nn.3892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tang AH, et al. A trans-synaptic nanocolumn aligns neurotransmitter release to receptors. Nature. 2016;536:210–214. doi: 10.1038/nature19058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sigal YM, Speer CM, Babcock HP, Zhuang X. Mapping Synaptic Input Fields of Neurons with Super-Resolution Imaging. Cell. 2015;163:493–505. doi: 10.1016/j.cell.2015.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cameron B, Landreth GE. Inflammation, microglia, and alzheimer’s disease. Neurobiology of Disease. 2010;37:503–509. doi: 10.1016/j.nbd.2009.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jay TR, et al. Disease Progression-Dependent Effects of TREM2 Deficiency in a Mouse Model of Alzheimer’s Disease. J Neurosci. 2017;37:637–647. doi: 10.1523/JNEUROSCI.2110-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yuan P, et al. TREM2 Haplodeficiency in Mice and Humans Impairs the Microglia Barrier Function Leading to Decreased Amyloid Compaction and Severe Axonal Dystrophy. Neuron. 2016;90:724–739. doi: 10.1016/j.neuron.2016.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tokunaga M, Imamoto N, Sakata-Sogawa K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat Methods. 2008;5:159–161. doi: 10.1038/nmeth1171. [DOI] [PubMed] [Google Scholar]
- 22.Huang F, et al. Video-rate nanoscopy using sCMOS camera-specific single-molecule localization algorithms. Nat Methods. 2013;10:653–8. doi: 10.1038/nmeth.2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Booth M. Wave front sensor-less adaptive optics: a model-based approach using sphere packings. Opt Express. 2006;14:1339–1352. doi: 10.1364/oe.14.001339. [DOI] [PubMed] [Google Scholar]
- 24.Wang B, Booth MJ. Optimum deformable mirror modes for sensorless adaptive optics. Opt Commun. 2009;282:4467–4474. [Google Scholar]
- 25.Hanser BM, Gustafsson MGL, Agard DA, Sedat JW. Phase-retrieved pupil functions in wide-field fluorescence microscopy. J Microsc. 2004;216:32–48. doi: 10.1111/j.0022-2720.2004.01393.x. [DOI] [PubMed] [Google Scholar]
- 26.Gould TJ, Burke D, Bewersdorf J, Booth MJ. Adaptive optics enables 3D STED microscopy in aberrating specimens. Opt Express. 2012;20:20998. doi: 10.1364/OE.20.020998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–313. [Google Scholar]
- 28.Débarre D, et al. Image-based adaptive optics for two-photon microscopy. Opt Lett. 2009;34:2495. doi: 10.1364/ol.34.002495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cella Zanacchi F, et al. Live-cell 3D super-resolution imaging in thick biological samples. Nat Methods. 2011;8:1047–1050. doi: 10.1038/nmeth.1744. [DOI] [PubMed] [Google Scholar]
- 30.Radde R, et al. Aβ42-driven cerebral amyloidosis in transgenic mice reveals early and robust pathology. EMBO Rep. 2006;7:940–946. doi: 10.1038/sj.embor.7400784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huang F, Schwartz SL, Byars JM, Lidke KA. Simultaneous multiple-emitter fitting for single molecule super-resolution imaging. Biomed Opt Express. 2011;2:1377–1393. doi: 10.1364/BOE.2.001377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang B, Jones Sa, Brandenburg B, Zhuang X. Whole-cell 3D STORM reveals interactions between cellular structures with nanometer-scale resolution. Nat Methods. 2008;5:1047–1052. doi: 10.1038/nmeth.1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li X, et al. Electron counting and beam-induced motion correction enable near-atomic-resolution single-particle cryo-EM. Nat Methods. 2013;10:584–90. doi: 10.1038/nmeth.2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Smith CS, Joseph N, Rieger B, Lidke KA. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat Methods. 2010;7:373–375. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.