Abstract
The data that have been used in almost all calculations of MIRD S value absorbed dose and effective dose are based on stylized anatomic computational phantoms and tissue-weighting factors adopted by the International Commission on Radiological Protection (ICRP) in its publication 60. The more anatomically realistic phantoms that have recently become available are likely to provide more accurate effective doses for diagnostic agents. 68Ga-DOTATATE is a radiolabeled somatostatin analog that binds with high affinity to somatostatin receptors, which are overexpressed in neuroendocrine tumors and can be used for diagnostic PET/CT-based imaging. Several studies have reported effective doses for 68Ga-DOTATATE using the stylized Cristy–Eckerman (CE) phantoms from 1987; here, we present effective dose calculations using both the ICRP 60 and more updated formalisms. Methods: Whole-body PET/CT scans were acquired for 16 patients after 68Ga-DOTATATE administration. Contours were drawn on the CT images for spleen, liver, kidneys, adrenal glands, brain, heart, lungs, thyroid gland, salivary glands, testes, red marrow (L1–L5), muscle (right thigh), and whole body. Dosimetric calculations were based on the CE phantoms and the more recent ICRP 110 reference-voxel phantoms. Tissue-weighting factors from ICRP 60 and ICRP 103 were used in effective dose calculations for the CE phantoms and ICRP 110 phantoms, respectively. Results: The highest absorbed dose coefficients (absorbed dose per unit activity) were, in descending order, in the spleen, pituitary gland, kidneys, adrenal glands, and liver. For ICRP 110 phantoms with tissue-weighting factors from ICRP 103, the effective dose coefficient was 0.023 ± 0.003 mSv/MBq, which was significantly lower than the 0.027 ± 0.005 mSv/MBq calculated for CE phantoms with tissue-weighting factors from ICRP 60. One of the largest differences in estimated absorbed dose coefficients was for the urinary bladder wall, at 0.040 ± 0.011 mGy/MBq for ICRP 110 phantoms compared with 0.090 ± 0.032 mGy/MBq for CE phantoms. Conclusion: This study showed that the effective dose coefficient was slightly overestimated for CE phantoms, compared with ICRP 110 phantoms using the latest tissue-weighting factors from ICRP 103. The more detailed handling of electron transport in the latest phantom calculations gives significant differences in estimates of the absorbed dose to stem cells in the walled organs of the alimentary tract.
Keywords: 68Ga-DOTATATE, PET/CT imaging, normal tissue, dosimetry, effective dose
Dosimetry for nuclear medicine imaging agents is performed to ensure that the long-term radiation risks of the imaging procedure are minimal compared with the benefits of obtaining a correct image-based diagnosis. In the late 1960s and early 1970s, the MIRD Committee of the Society of Nuclear Medicine and Molecular Imaging published a formalism that standardized the process for computing tissue-absorbed doses through the introduction of 2 essential terms, cumulated activity (Ã) and radionuclide S value (S) (1). Cumulated activity, currently known by the term time-integrated activity (abbreviated TIA but still represented by Ã) (2), depends on the pharmacokinetic properties of the diagnostic agent. These are typically characterized by longitudinal quantitative imaging in an appropriate patient population. S value is defined as the absorbed dose to a target region per unit TIA in the source region, such that the product of TIA and S value gives the absorbed dose contribution from a source region to a target region. S values depend on the emission characteristics of the radionuclide used in the diagnostic agent and on the reference anatomic model used in the Monte Carlo radiation transport simulations of the emitted radiation particles and photons. The S values that have been used in effective dose calculations over the past several decades have been derived primarily from the stylized Cristy–Eckerman (CE) phantom series developed in 1987 (3) and used extensively by the International Commission on Radiological Protection (ICRP). Reflecting the computational and imaging capabilities of the time, the CE phantoms comprised stylized organs composed of simple geometries defined by mathematic surface equations to describe the inner anatomy and outer body contour. In 2009, the ICRP and the International Commission on Radiation Units and Measurements released adult male and female CT-based voxelized reference phantoms (ICRP publication 110) (4), with organ and tissue masses matched to reference values (ICRP publication 89) (5). Specific absorbed fractions for the ICRP 110 voxelized reference phantoms have been published (ICRP publication 133) (6), as well as the latest reference tissue–weighting factors (ICRP publication 103) (7).
In the present study, we used 68Ga-DOTATATE PET/CT scans to compare dosimetry based on the most recent ICRP standards (ICRP 110 phantoms and ICRP 103 tissue-weighting factors) with dosimetry based on the prior standards (CE phantoms and ICRP 60 tissue-weighting factors (8)) and with previously reported dosimetry based on these prior standards (9,10). Such comparisons are important to understanding the impact of transitioning from the older phantoms and tissue-weighting factors to the most recently recommended ones.
MATERIALS AND METHODS
Patients
68Ga-DOTATATE PET/CT scans from 16 Brazilian patients with somatostatin-avid tumors were used in this study (11 female and 5 male; mean age, 53.8 ± 13.0 y; range, 36–79 y) (Table 1). PET was indicated for staging, follow-up, or planning of peptide receptor radionuclide therapy. Five of the patients had gastroenteropancreatic neuroendocrine tumors, 5 had medullary thyroid cancer with increasing calcitonin levels, 3 had neuroectodermic tumors (malignant pheochromocytoma or paraganglioma), 2 had associated adrenal and thyroid tumors, and 1 had ectopic Cushing syndrome requiring tumor localization. The institutional review board at São Paulo University School of Medicine approved this study, and all subjects signed an informed-consent form.
TABLE 1.
Patient and Imaging Data
| Patient | Age (y) | Weight (kg) | Height (cm) | Sex | Administered activity (MBq) | PET/CT scans (n) |
| 1F | 59 | 63 | 155 | F | 156.9 | 3 |
| 2F | 67 | 75 | 145 | F | 107.3 | 3 |
| 3F | 70 | 74 | 147 | F | 140.6 | 4 |
| 4F | 53 | 66 | 165 | F | 126.2 | 2 |
| 5F | 35 | 76 | 161 | F | 107.3 | 3 |
| 6F | 38 | 62 | 167 | F | 125.8 | 2 |
| 7F | 65 | 109 | 159 | F | 82.1 | 3 |
| 8M | 36 | 83 | 178 | M | 149.1 | 2 |
| 9F | 79 | 73 | 156 | F | 177.6 | 3 |
| 10M | 59 | 68 | 157 | M | 169.5 | 3 |
| 11M | 63 | 102 | 182 | M | 158.7 | 3 |
| 12M | 39 | 85 | 181 | M | 91.0 | 3 |
| 13F | 43 | 97 | 155 | F | 112.1 | 2 |
| 14M | 44 | 94 | 176 | M | 137.3 | 2 |
| 15F | 52 | 106 | 162 | F | 126.5 | 3 |
| 16F | 58 | 84 | 157 | F | 131.7 | 3 |
PET/CT Imaging
Two to four whole-body PET/CT scans were acquired at 2–240 min after injection of 68Ga-DOTATATE (mean, 131.2 ± 26.3 MBq) (Table 1). Imaging was performed in 3-dimensional time-of-flight mode on a Discovery PET/CT 690 system (GE Healthcare) at 2 min per bed position. The acquisition matrix was 192 × 192 pixels, the in-slice pixel size was 3.27 mm, and the transaxial slice thickness was 3.27 mm. Ordered-subsets expectation maximization was used for PET reconstruction, with CT-based attenuation correction using automatic exposure control for dose reduction.
Normal-Tissue Dosimetry
Overview
Patient-tissue activity concentrations rather than organ-specific activities were taken from the patient data and transposed into the 2 reference phantom models. Normal-tissue absorbed dose coefficients (absorbed dose per unit activity) were calculated using the MIRD S-value–based methodology (1,2). OLINDA/EXM software, version 1 (11), was used for the CE phantom dosimetry calculations, and a Microsoft Excel spreadsheet with S values obtained from the University of Florida was used for the ICRP 110 phantom dosimetry calculations. TIA (i.e., total number of nuclear transformations between 2 time points) was calculated from time–activity data within the source regions, defined by drawing organ contours on the CT portion of the first PET/CT image for each patient. These contours were transposed to later time points after deformable registration of the scans had been performed using Velocity software (version 3.1; Varian Medical Systems Inc.). Contours were drawn for the spleen, liver, kidneys, adrenal glands, brain, heart, lungs, thyroid gland, salivary glands, testes, red marrow (L1–L5), muscle (right thigh), and whole body. Dosimetry was performed for each patient and inserted into the respective phantom, after which the average for all patients was calculated.
TIA Calculations
The average activity concentration is , where A is activity, V is volume, rS is source region, and t is time after injection. Volume was derived from each patient’s PET/CT images. The specific organ/tissue activity (Bq) for a phantom κ was calculated for each patient’s organ/tissue activity as follows:
| Eq. 1 |
where M is mass and ρ is tissue density. Mass was taken from OLINDA/EXM (11,12) for the CE phantom calculations and from ICRP 133 for the ICRP 110 phantom calculations. Tissue density was according to ICRP 110. Source region rS in Equation 1 is an index over all tissues and the whole body for which TIA was assigned.
Excel was used to fit a monoexponential expression to each patient’s specific organ/tissue time–activity curve. The expressions were analytically integrated from 0 to infinity, resulting in the TIA corresponding to each phantom’s source region. Preserving activity concentration rather than total activity can lead to a discrepancy in the whole-body activity between the phantom and the patient at the time of administration. The TIA coefficient (TIAC) is defined as the TIA divided by the administered activity. In this scenario, the administered activity is the total virtually administered activity to the phantom rather than the administered activity to the patient. Scaling of each TIAC by the phantom-to-patient whole-body mass ratio accounts for this difference. The TIAs (Bq⋅s) used for the calculations were as follows:
| Eq. 2 |
The TIACs (s) where
| Eq. 3 |
where ã is TIAC, wb is whole body, and A0 is administered activity.
Remainder of Body
The remainder-of-body TIAC (s) was calculated as the difference between the TIAC of the whole body, the TIAC of the target region, and the TIAC of the source regions summed:
| Eq. 4 |
where rb is rest of body, wb is whole body, and rT is target region. The corresponding phantom masses (kg) were
| Eq. 5 |
Source region rS in Equations 4 and 5 is an index over all source regions for which a TIAC is assigned, except for the target region. The remainder-of-body mass excluded the contents of the walled organs.
Urinary Bladder
The TIAC for urinary bladder contents was calculated using the MIRD bladder-voiding model (13) as implemented in OLINDA/EXM. A 2-h voiding interval was used, with the whole-body biologic clearance half-life obtained from the PET/CT images and a fraction of 1. This TIAC was used both for the CE phantom calculations and for the ICRP 110 phantom calculations.
Pituitary Gland
To account for partial-volume effects arising from the small size of the pituitary gland, a hybrid dosimetric method developed by Plyku et al. (14) for small tumors was used. Briefly, the pituitary gland was modeled as a 0.6-g unit-density sphere. A 10% threshold of the maximum PET value was used for contouring. The volume of the pituitary gland contoured on the PET images was systematically larger than the ICRP volume and presumably larger than the real volume because of activity spill-out. However, this volume contains the activity in the pituitary gland plus some background activity (Bq) in the PET volume outside the real volume, which needs to be subtracted:
| Eq. 6 |
where pg is pituitary gland and bkg is background. The background activity concentration for the pituitary gland was determined by drawing a contour in the brain. A monoexponential expression was fitted to the time–activity data points and analytically integrated from zero to infinity, and the TIAC was calculated according to Equations 2 and 3 for the respective phantom.
Absorbed Dose Calculations
The MIRD Committee–derived equation was used for all calculations of absorbed dose coefficients (absorbed dose per unit activity (Gy/Bq)) (2):
| Eq. 7 |
where d is absorbed dose coefficient. The TIACs for the CE phantoms were used as input in OLINDA/EXM to obtain estimates of the CE phantom–derived absorbed dose coefficient. Because the CE phantoms do not have S values for the pituitary gland, the self-dose absorbed dose coefficient to the pituitary gland was calculated using the unit-density sphere model provided by OLINDA/EXM. An Excel spreadsheet was used for the ICRP dosimetric calculations.
Remainder-of-Body Contribution to Absorbed Dose
The CE phantom–based dosimetry specifies 25 target regions and 28 source regions. In contrast, the ICRP 110 phantom dosimetry allows TIAC apportionment in up to 76 source regions and provides the absorbed dose coefficients to 41 target regions. More significantly, the CE phantom–based formalism includes whole-body–to–individual-tissue S values, whereas no such S values are tabulated for the ICRP 110 phantoms. The remainder TIAC that has not been otherwise allocated is given the term remainder of body in CE phantom calculations. Target absorbed dose coefficients (Gy/Bq) for remainder of body are given by (15)
| Eq. 8 |
with the remainder-of-body to target S value (Gy/Bq⋅s) given by
| Eq. 9 |
Because almost all tissues in the body are accounted for by the ICRP 110 phantoms, whole-body–to–individual-tissue S values have not been calculated for the ICRP 110 phantoms. The contribution of the absorbed dose coefficient from remainder of body to each target tissue is obtained by apportioning the remainder-of-body TIAC (s) to each remaining source tissue not previously accounted for:
| Eq. 10 |
where is the index over source regions identified in the ICRP 110 phantoms that have not been specifically assigned a TIAC.
The absorbed dose coefficient (Gy/Bq) to each target region of the ICRP 110 phantoms is given by
| Eq. 11 |
Effective Dose Calculations
The effective dose coefficient (effective dose per unit activity (Sv/Bq)) for CE phantom calculations in an individual patient is given by
| Eq. 12 |
where e is effective dose coefficient, wT is ICRP 60 tissue-weighting factor, and h is equivalent dose coefficient (Sv/Bq).
The radiation-weighting factor for all 68Ga radiation emissions is equal to 1. Accordingly,
| Eq. 13 |
where α denotes the sex of each patient.
The effective dose coefficient per unit activity (Sv/Bq) is obtained by averaging the male- and female-averaged patient-specific effective dose coefficient:
| Eq. 14 |
where and are the number of males and females, respectively.
The effective dose coefficient (Sv/Bq) for ICRP is
| Eq. 15 |
where the tissue-weighting factor is from ICRP 103.
The percentage differences between the CE phantom values and the ICRP 110 phantom values were calculated as follows:
| Eq. 16 |
Statistical Analysis
Statistical analysis was performed using Prism software (version 7.03; GraphPad Software Inc.). All data are presented as the mean value ± SD. Groups were compared using a 2-tailed Student t test, and differences between groups were considered significant for P values of less than 0.05.
RESULTS
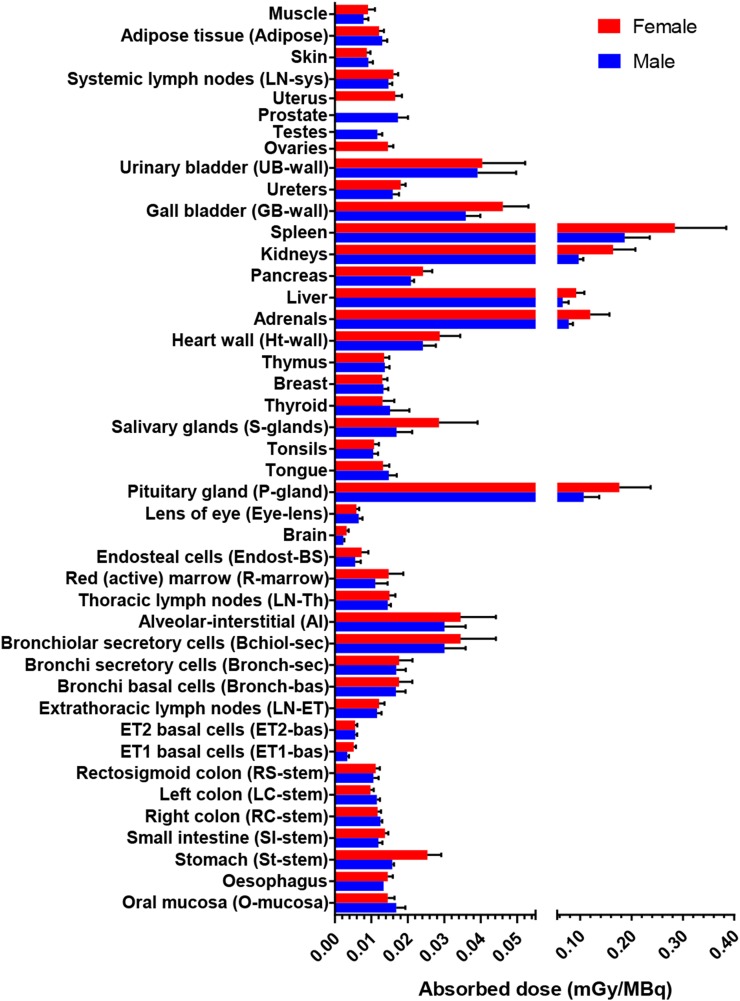
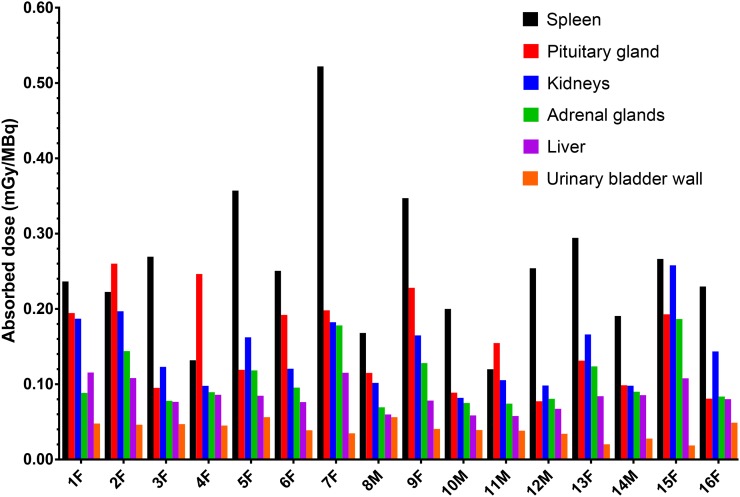
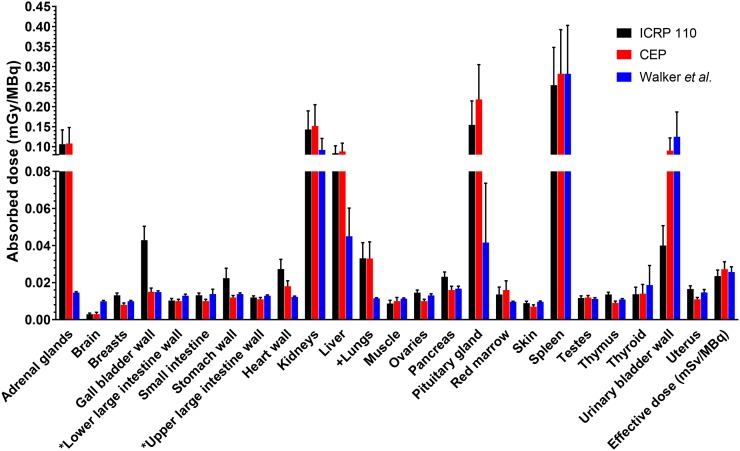
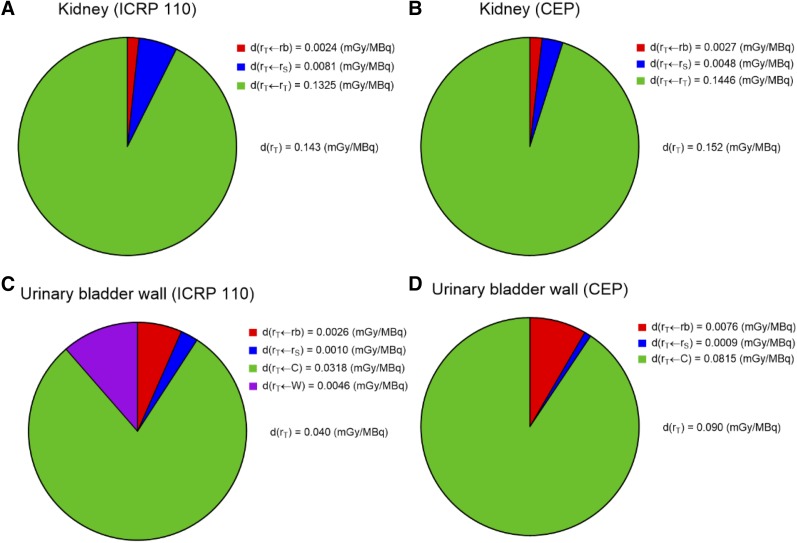
The absorbed dose coefficients calculated for the ICRP 110 phantoms are shown in Figure 1. The tissues with the highest 7 absorbed dose coefficients, as well as the effective dose coefficient, are listed and compared with previously published data (9,10) in Table 2. ICRP 110 phantom–based calculations for the 16 patients are shown in Figure 2. TIACs are listed in Table 3. The absorbed dose coefficients obtained in this study are compared with those in the literature (9) in Figure 3. The ICRP 110 phantom–derived effective dose coefficient (0.023 ± 0.003 mSv/MBq) obtained using tissue-weighting factors from ICRP 103 was significantly lower (P = 0.0114) than that (0.027 ± 0.005 mSv/MBq) derived from the CE phantoms using tissue-weighting factors from ICRP 60. Significant differences in calculated absorbed dose coefficients between the CE phantoms and the ICRP 110 phantoms were found for gallbladder wall, breast, thymus, pancreas, small intestine wall, stomach wall, uterus, ovaries, skin, heart wall, urinary bladder wall (P < 0.0001), and pituitary gland (P = 0.0252). The contributions from remainder of body, source tissues, and target tissue to the total absorbed dose coefficients for kidney and urinary bladder wall are shown in Figure 4.
FIGURE 1.
Mean absorbed dose coefficients for normal organs and tissues using ICRP 110 phantoms. Error bars = SD.
TABLE 2.
Absorbed Dose Coefficients for 68Ga-DOTATATE (mGy/MBq) in Normal Tissues and Organs
| Site | ICRP 110 | CE | Sandström et al. (10) | Walker et al. (9) |
| Spleen | 0.25 ± 0.097 | 0.28 ± 0.11 | 0.11 ± 0.058 | 0.28 ± 0.12 |
| Pituitary gland | 0.15 ± 0.062 | 0.22 ± 0.092 | — | 0.042 ± 0.032 |
| Kidneys | 0.14 ± 0.048 | 0.15 ± 0.055 | 0.093 ± 0.016 | 0.092 ± 0.028 |
| Adrenal glands | 0.11 ± 0.037 | 0.11 ± 0.041 | 0.086 ± 0.052 | 0.015 ± 0.001 |
| Liver | 0.084 ± 0.019 | 0.088 ± 0.022 | 0.050 ± 0.015 | 0.045 ± 0.015 |
| Gallbladder wall | 0.043 ± 0.008 | 0.015 ± 0.002 | 0.016 ± 0.002 | 0.015 ± 0.001 |
| Urinary bladder wall | 0.040 ± 0.011 | 0.090 ± 0.033 | 0.098 ± 0.048 | 0.13 ± 0.062 |
| Effective dose coefficient (mSv/MBq) | 0.023 ± 0.003 | 0.027 ± 0.005 | 0.021 ± 0.003 | 0.026 ± 0.003 |
FIGURE 2.
Absorbed dose coefficients for selected tissues from 16 patients using ICRP 110 phantoms.
TABLE 3.
Average TIACs (h) in Normal Tissues and Organs
| Male |
Female |
|||
| Site | ICRP 110 | CE | ICRP 110 | CE |
| Whole body | 1.48E+00 ± 5.67E−02 | 1.48E+00 ± 5.67E−02 | 1.48E+00 ± 9.77E−02 | 1.48E+00 ± 9.77E−02 |
| Remainder of body | 4.98E−01 ± 8.01E−02 | 6.49E−01 ± 6.28E−02 | 5.17E−01 ± 6.95E−02 | 6.01E−01 ± 7.63E−02 |
| Muscle | 3.17E−01 ± 8.14E−02 | 2.95E−01 ± 7.58E−02 | 2.11E−01 ± 7.34E−02 | 2.29E−01 ± 5.23E−02 |
| Liver | 2.90E−01 ± 4.89E−02 | 2.32E−01 ± 3.92E−02 | 3.18E−01 ± 5.48E−02 | 2.59E−01 ± 4.47E−02 |
| Kidneys | 8.56E−02 ± 7.97E−03 | 6.00E−02 ± 5.59E−03 | 1.25E−01 ± 3.35E−02 | 1.01E−01 ± 2.72E−02 |
| Spleen | 9.54E−02 ± 2.32E−02 | 7.59E−02 ± 1.84E−02 | 1.22E−01 ± 4.20E−02 | 1.03E−01 ± 3.55E−02 |
| Lungs | 6.78E−02 ± 1.39E−02 | 5.60E−02 ± 1.15E−02 | 5.98E−02 ± 1.97E−02 | 5.31E−02 ± 1.75E−02 |
| Urinary bladder contents | 6.07E−02 ± 1.92E−02 | 6.07E−02 ± 1.92E−02 | 5.76E−02 ± 2.16E−02 | 5.76E−02 ± 2.16E−02 |
| Red marrow | 4.47E−02 ± 2.41E−02 | 3.56E−02 ± 1.92E−02 | 4.59E−02 ± 2.36E−02 | 5.91E−02 ± 3.03E−02 |
| Heart wall | 8.59E−03 ± 1.54E−03 | 6.97E−03 ± 1.25E−03 | 7.48E−03 ± 1.83E−03 | 6.50E−03 ± 1.59E−03 |
| Salivary glands | 3.39E−03 ± 9.17E−04 | — | 4.87E−03 ± 1.91E−03 | — |
| Brain | 4.26E−03 ± 5.30E−04 | 3.95E−03 ± 4.91E−04 | 6.10E−03 ± 1.36E−03 | 5.72E−03 ± 1.27E−03 |
| Adrenal glands | 2.91E−03 ± 3.55E−04 | 2.72E−03 ± 3.32E−04 | 3.88E−03 ± 1.41E−03 | 3.69E−03 ± 1.34E−03 |
| Testes | 7.60E−04 ± 1.07E−04 | 7.91E−04 ± 1.11E−04 | — | — |
| Thyroid | 6.86E−04 ± 3.10E−04 | 6.01E−04 ± 2.72E−04 | 4.64E−04 ± 1.68E−04 | 4.26E−04 ± 1.54E−04 |
| Pituitary gland | 2.71E−04 ± 6.96E−05 | 2.68E−04 ± 6.90E−05 | 4.49E−04 ± 1.49E−04 | 4.73E−04 ± 1.58E−04 |
FIGURE 3.
Comparison of absorbed dose coefficients for ICRP 110 phantoms, CE phantoms (CEP), and previously published results by Walker et al. (9) using OLINDA/EXM, version 1. Error bars = SD. *Anatomic definition differs between ICRP 110 and CE phantoms. +ICRP 110 phantoms show alveolar–interstitial absorbed dose coefficient, compared with total lung for CE phantoms.
FIGURE 4.
Contribution from target region, source region, and remainder of body to total absorbed dose coefficient in target regions ICRP 110 kidney (A), CE kidney (B), ICRP 110 urinary bladder wall (with contribution from contents and wall) (C), and CE urinary bladder wall (with contribution from contents) (D). CEP = CE phantoms.
DISCUSSION
The main objective of radiopharmaceutical dosimetry for diagnostic agents is to ensure that the risks of the imaging procedure are minimal compared with the benefits. Accordingly, dosimetry for diagnostic agents is not performed for any individual patient. Rather, agent-specific pharmacokinetic data from an appropriate patient population are collected and used in conjunction with an internationally recognized standard reference geometry that provides the S values required to perform the calculation. Standardization of all elements required to arrive at an absorbed dose estimate is important in maintaining consistency across centers and ensuring that the values reported in publications reflect actual differences arising from the properties of the agent rather than from different data acquisition protocols and corresponding S values. The release of a new set of reference geometries and associated tissue-weighting factors requires that physicists and nuclear medicine practitioners transition from the older, CE phantom, set of standards to the newer, ICRP 110 phantom, set. Using data from 68Ga-DOTATATE, we have investigated the effect on absorbed dose calculations arising from the switch in phantoms and corresponding S values.
In the ICRP 110 phantom–based calculations, the remainder activity was uniformly distributed in the remaining tissues using the respective organ/tissue weights, including blood, according to ICRP 133. The remainder activity in walled organs was uniformly distributed in the wall according to Equation 10 and not in the contents (urinary bladder contents were the exception because urinary bladder was a source region). This explanation accounts to some extent for the higher absorbed dose coefficients in these walled organs for the ICRP 110 phantoms than for the CE phantoms using the contents as the source. There are also differences in tissues definitions between the ICRP 110 phantoms and the CE phantoms; for example, in the ICRP 110 phantoms, the right colon wall includes the ascending colon wall and the right half of the transverse colon wall, and the left colon wall includes the descending colon wall and the left half of the transverse colon wall. In the CE phantoms, the lower large intestine corresponds to the descending colon, sigmoid colon, and rectum, and the upper large intestine corresponds to the ascending colon and transverse colon (16). In addition, the lungs are divided into 4 target regions in the ICRP 110 phantoms, compared with 1 target region in the CE phantoms.
When the calculated self-dose S values were compared between the CE and ICRP 110 phantoms, the CE phantom values were higher for both females (range, −7.7% to +65.3%) and males (range, −961% to +59.6%), with the largest difference being for the urinary bladder contents to the urinary bladder wall (+65.3% in females and +59.6% in males) and an outlier for the self-dose breast S value (−961%) in males. The standard mass for the male breast was 351 g (11,12) and 26.2 g (6) for the CE and ICRP 110 phantoms, respectively, and is probably the main explanation for the large difference observed in the respective S values. A comparison of the CE and the ICRP 110 phantoms using the averaged male and female self-dose S values for all organs and tissues gave a difference of +26.3% and +27.1%, respectively, with a respective tissue mass difference of −2.2% and −6.7%. However, a comparison using the specific TIACs and organ/tissue masses from the ICRP 110 method in the CE method and comparing with the CE phantom results gave an averaged male and female absorbed dose difference of 2.1% for the urinary bladder wall and 1.8% for the kidneys; thus, the effect of mass differences on the results is small because of the scaling of input activity to the phantom organ mass.
In general, the results showed lower absorbed doses using ICRP 110 phantoms than using CE phantoms. This finding is likely explained by 2 fundamental differences between these phantoms. The first is a difference in organ topology, with the ICRP 110 phantoms having less interorgan tissue space and a better accounting and placement of distributed tissue (e.g., marrow, adipose tissue, and muscle). The second difference is that S values derived from the ICRP 110 phantoms have a better handling of the fraction of electron energy absorbed. This characteristic explains to some extent the larger differences seen in thin-walled organs (e.g., urinary bladder wall, which had a 125% higher absorbed dose coefficient in the CE phantom calculations than in the ICRP 110 phantom calculations). This advantage leads to a different and better approach to handling TIACs not specifically assigned to source organs. It is now possible to deposit TIACs uniformly throughout the remaining non-source tissue and then use specific source-to-target S values to account for the absorbed dose due to a TIAC that is not specifically allocated. Other differences in the calculations (e.g., updated radionuclide decay data (17) and tissue densities) had negligible effects on the differences, as previously shown by Hadid et al. (18).
Dosimetric calculations for 68Ga-DOTATATE have previously been published by Walker et al. (9) and Sandström et al. (10). The percentage difference between results obtained in this study using the CE phantoms and those of Walker et al. ranged from −229% to +86.5% (brain and adrenal glands, respectively). The absorbed dose coefficient to the adrenal glands reported by Sandström et al. was 21% lower than that obtained in this study. The large adrenal-gland difference for Walker et al. could be explained by their not using the adrenal glands as a source organ (no contour was drawn), whereas our study and that of Sandström et al. did use drawn contours. In addition, the absorbed dose coefficient to the salivary glands calculated by Walker et al. (0.012 ± 0.008 mGy/MBq) was 52% lower than that obtained using the ICRP 110 phantom calculation (0.025 ± 0.010 mGy/MBq). Similarly, the salivary glands were not included in the CE phantoms as a source or target region. In addition, Walker et al. used data exclusively from male patients, whereas our study used the average between male and female. For both the salivary and the pituitary glands, there were significant differences (P < 0.035) between the male and female absorbed dose coefficients (Fig. 1). In addition, because the ICRP 110 phantoms use the salivary glands both as a source and as a target region, the absorbed dose considers not only the self-dose but also contributions from adjacent and surrounding tissues (unlike version 1 of the OLINDA/EXM sphere model, for example). Furthermore, Walker et al. did not perform whole-body PET/CT and made estimates for the activity in the nonimaged extremities to get the whole-body activity. Sandström et al. also did not perform whole-body PET/CT but, rather, scanned from the base of the skull to the proximal femur. Because we performed whole-body (head to toes) scans in this work, we were able to account for all the activity in the body.
Figure 4 depicts the averaged male and female contribution from different source tissues to the kidneys and urinary bladder wall. These 2 tissues were chosen to illustrate the differences in relative contribution to the total absorbed dose between a solid organ and a walled tissue, respectively. As expected, self-dose is the dominant contributor to the total absorbed dose for the kidneys. In contrast, urinary bladder contents provide a greater contribution to the bladder wall dose than does the wall itself, as can be seen in the ICRP 110 bladder wall dose calculation. Urinary bladder wall self-dose S values are available for the ICRP 110 phantom calculations but not for the CE phantom calculations. The absorbed dose coefficient for the kidneys was 5.9% higher for the CE phantoms than for the ICRP 110 phantoms, as can be explained mainly by a 29.7% higher self-dose S value, a 30.7% lower average kidney TIAC, and the difference in contributions from source tissues and remainder of body. For the urinary bladder wall, the absorbed dose coefficient was 125% higher for the CE phantoms than for the ICRP 110 phantoms, as can be explained mainly by a 62.5% higher urinary bladder contents-to-wall S value, no difference in TIAC (the TIACs for urinary bladder contents were calculated using the MIRD bladder-voiding model as implemented in OLINDA/EXM, version 1, and is not phantom-dependent), and the difference in contributions from source tissues and remainder of body (including urinary bladder wall for the ICRP 110 phantoms). This difference stems from a difference in methods, with the CE phantoms using only contents as a source for walled organs (e.g., stomach, gallbladder, intestine, and urinary bladder) but the ICRP 110 phantoms using organ wall as a source as well.
As shown in Figures 2 and 3, the calculated absorbed dose coefficients for the different organs/tissues varied widely among patients, with the differences being in many cases larger than those between the ICRP 110 and CE phantom calculations. About half the compared organs/tissues (mainly those that are small or walled) differed significantly between the ICRP 110 and CE phantom calculations. The calculated absorbed doses for larger solid organs (e.g., liver) did not significantly differ between the ICRP 110 and CE phantoms. The significant differences in the smaller or walled organs represent relatively low absorbed doses compared with larger solid organs such as the spleen. Tissue-absorbed doses are already low for diagnostic agents. The modest reduction in tissue-absorbed doses and in effective dose will have a minimal impact on routine clinical practice. The main impact of these updated calculations will be in the development of new imaging agents. In this context, lower absorbed doses would allow slightly greater administered activities and therefore higher-quality images.
Another area that would be impacted, although negatively so, is the therapeutic use of radionuclides. Even though dosimetry for radiopharmaceutical therapy should account for individual patient anatomy and the spatial distribution of activity within organs, standard phantom-based dosimetry methods are still used for initial assessments of likely toxicity and for reporting to regulatory authorities.
The tissue-weighting factors used with the ICRP 110 phantoms were from ICRP 103, whereas those used with the CE phantoms were from ICRP 60. The main change from the earlier tissue-weighting factors is a decrease for gonads, an increase for breast, the use of separate weighting factors for salivary glands and brain, and an increase for the remainder category, both in value and in number of tissues included (7,8). The calculated effective dose coefficient was significantly lower for the ICRP 110 phantoms than for the CE phantoms. The recommended administered activity of 68Ga-DOTATATE (range, 100–200 MBq) (19)—and the average administered in this study—was 131.2 MBq. According to the ICRP 110 phantoms, this amount of activity results in an effective dose of 3.0 mSv (2.3–4.6 mSv for the recommended activity range), which is lower than the 3.6 mSv calculated using the CE phantoms. Accordingly, effective doses have been overestimated using the CE phantoms, as compared with the ICRP 110 phantoms in combination with specific absorbed fractions from ICRP 133 and tissue-weighting factors from ICRP 103.
CONCLUSION
CE phantom–based dosimetry has been shown to overestimate effective dose. The differences that were found between CE phantom–based dosimetry and ICRP 110–based dosimetry for 68Ga-DOTATATE may require a reevaluation of the dosimetry for other diagnostic agents as well. These new standards should be adopted rapidly so as to minimize confusion in the dosimetry literature.
DISCLOSURE
This work was supported by FAPESP 13/03876-4 (“Avaliação do uso do 68Ga-peptídeo análogo de somatostatina PET/CT como ferramenta diagnóstica em tumores neuroendócrinos e sua correlação com marcadores moleculares”) and by NIH R01 CA116477. No other potential conflict of interest relevant to this article was reported.
Acknowledgments
Drs. George Barberio Coura Filho and Ana Amélia Fialho de Oliveira Hoff, from Instituto do Cancer do Estado de São Paulo, are acknowledged for helping us acquire the PET/CT images. We also thank Dr. William Goodwin, from the Department of Biomedical Engineering at the University of Florida, for valuable information and insight on the ICRP 110 voxelized phantoms.
REFERENCES
- 1.Loevinger R, Budinger T, Watson E. MIRD Primer for Absorbed Dose Calculations. Reston, VA: The Society of Nuclear Medicine and Molecular Imaging; 1991:1–128. [Google Scholar]
- 2.Bolch WE, Eckerman KF, Sgouros G, Thomas SR. MIRD pamphlet no. 21: a generalized schema for radiopharmaceutical dosimetry–standardization of nomenclature. J Nucl Med. 2009;50:477–484. [DOI] [PubMed] [Google Scholar]
- 3. Cristy M, Eckerman KF. Specific Absorbed Fractions of Energy at Various Ages from Internal Photon Sources. III. Five-Year-Old. Oak Ridge, TN: Oak Ridge National Laboratory; 1987:1–42. ORNL/TM-8381/V3.
- 4.Menzel HG, Clement C, DeLuca P. ICRP publication 110: realistic reference phantoms—an ICRP/ICRU joint effort. A report of adult reference computational phantoms. Ann ICRP. 2009;39:1–164. [DOI] [PubMed] [Google Scholar]
- 5.Basic anatomical and physiological data for use in radiological protection: reference values—a report of age- and gender-related differences in the anatomical and physiological characteristics of reference individuals. ICRP publication 89. Ann ICRP. 2002;32:5–265. [PubMed] [Google Scholar]
- 6.Bolch WE, Jokisch D, Zankl M, et al. The ICRP computational framework for internal dose assessment for reference adults: specific absorbed fractions—ICRP publication 133. Ann ICRP. 2016;45:1–74. [DOI] [PubMed] [Google Scholar]
- 7.The 2007 recommendations of the International Commission on Radiological Protection: ICRP publication 103. Ann ICRP. 2007;37:1–332. [DOI] [PubMed] [Google Scholar]
- 8.1990 recommendations of the International Commission on Radiological Protection: ICRP publication 60. Ann ICRP. 1990;21:1–227. [PubMed] [Google Scholar]
- 9.Walker RC, Smith GT, Liu E, Moore B, Clanton J, Stabin M. Measured human dosimetry of 68Ga-DOTATATE. J Nucl Med. 2013;54:855–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sandström M, Velikyan I, Garske-Román U, et al. Comparative biodistribution and radiation dosimetry of 68Ga-DOTATOC and 68Ga-DOTATATE in patients with neuroendocrine tumors. J Nucl Med. 2013;54:1755–1759. [DOI] [PubMed] [Google Scholar]
- 11.Stabin MG, Sparks RB, Crowe E. OLINDA/EXM: the second-generation personal computer software for internal dose assessment in nuclear medicine. J Nucl Med. 2005;46:1023–1027. [PubMed] [Google Scholar]
- 12.Stabin MG, Tagesson M, Thomas SR, Ljungberg M, Strand SE. Radiation dosimetry in nuclear medicine. Appl Radiat Isot. 1999;50:73–87. [DOI] [PubMed] [Google Scholar]
- 13.Thomas SR, Stabin MG, Chin-Tu C, Samaratunga RC. MIRD pamphlet no. 14 revised: a dynamic urinary bladder model for radiation dose calculations. J Nucl Med. 1999;40(suppl):102S–123S. [PubMed] [Google Scholar]
- 14.Plyku D, Hobbs RF, Huang K, et al. Recombinant human thyroid-stimulating hormone versus thyroid hormone withdrawal in 124I-PET/CT based dosimetry for 131I therapy of metastatic differentiated thyroid cancer. J Nucl Med. 2017;58:1146–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Coffey JL, Watson EE. Calculating dose from remaining body activity: a comparison of two methods. Med Phys. 1979;6:307–308. [DOI] [PubMed] [Google Scholar]
- 16.Snyder WS, Cook MJ, Nasset ES, Karhausen LR, Howells GP, Tipton IH. Report of the Task Group on Reference Man: ICRP Publication 23. New York, NY: Pergamon Press; 1975:1–480. [Google Scholar]
- 17.Eckerman K, Endo A. ICRP publication 107: nuclear decay data for dosimetric calculations. Ann ICRP. 2008;38:1–96. [DOI] [PubMed] [Google Scholar]
- 18.Hadid L, Gardumi A, Desbree A. Evaluation of absorbed and effective doses to patients from radiopharmaceuticals using the ICRP 110 reference computational phantoms and ICRP 103 formulation. Radiat Prot Dosimetry. 2013;156:141–159. [DOI] [PubMed] [Google Scholar]
- 19.Virgolini I, Ambrosini V, Bomanji JB, et al. Procedure guidelines for PET/CT tumour imaging with 68Ga-DOTA-conjugated peptides: 68Ga-DOTA-TOC, 68Ga-DOTA-NOC, 68Ga-DOTA-TATE. Eur J Nucl Med Mol Imaging. 2010;37:2004–2010. [DOI] [PubMed] [Google Scholar]