 Field-based proteochemometric modelling predicts activities and visualizes features, which can support the design of more selective protease inhibitors.
Field-based proteochemometric modelling predicts activities and visualizes features, which can support the design of more selective protease inhibitors.
Abstract
The high similarity between certain sub-pockets of serine proteases may lead to low selectivity of protease inhibitors. Therefore the application of proteochemometrics (PCM), which quantifies the relationship between protein/ligand descriptors and affinity for multiple ligands and targets simultaneously, is useful to understand and improve the selectivity profiles of potential inhibitors. In this study, protein field-based PCM that uses knowledge-based and WaterMap derived fields to describe proteins in combination with 2D (RDKit and MOE fingerprints) and 3D (4 point pharmacophoric fingerprints and GRIND) ligand descriptors was used to model the bioactivities of 24 homologous serine proteases and 5863 inhibitors in an integrated fashion. Of the multiple field-based PCM models generated based on different ligand descriptors, RDKit fingerprints showed the best performance in terms of external prediction with Rtest2 of 0.72 and RMSEP of 0.81. Further, visual interpretation of the models highlights sub-pocket specific regions that influence affinity and selectivity of serine protease inhibitors.
Introduction
Serine proteases are enzymes known to modulate protein and peptide degradation by cleavage of peptide bonds and are involved in a wide range of biological functions such as cell cycle regulation, digestion, blood coagulation and immune response.1 The human genome encodes for more than 500 proteases2 and one-third of these constitute serine proteases.1 Serine proteases initiate the cleavage of peptide bonds through a serine, which forms a part of the catalytic triad together with histidine and aspartate. Their dysregulation is known to cause many diseases including cancer, inflammation, viral infections and cardiovascular diseases.1
Understanding the sub-pocket specificities of proteases is crucial to design inhibitors that act preferentially on a specific protease and thereby have limited off-target effects. Earlier studies on proteases have shown that selectivity of protease binding sites could be best understood by mapping their substrate sequences that support small molecule recognition and subsequent prediction of potential off-target effects.3 In yet another study, sub-pocket specific cleavage entropies were used to estimate protease selectivity quantitatively4 and in turn to correlate specificity with descriptors of protein structure and dynamics.5 Nevertheless, a quantitative approach such as proteochemometric modelling6–8 that accounts for polypharmacology and enables quantitative prediction of bioactivities of protease inhibitors could be useful for drug design purposes.
To date, proteochemometrics has been used to model the bioactivities of many target families including G protein-coupled receptors, kinases, lyases, antibodies, P450s, transport proteins, cyclooxygenases, carbonic anhydrases, PARP, aromatases as well as proteases.6–14 Previously conducted proteochemometric studies on serine proteases benchmarked the application of 21 different sequence-based descriptors in modelling the bioactivities of 67 serine proteases and 12 625 protease inhibitors.14 Even though most of these descriptors were efficient in generating models that can predict the bioactivities of external test sets with RMSEPs as low as 0.7, they had limited interpretability. An important aspect that the sequence-based descriptors fail to account for is the 3D orientation of amino acids in the binding pocket, which is crucial for ligand design. Therefore, generating proteochemometric models that rely on more informative field-based protein descriptors derived from 3D structural information would support visual interpretation. We have already shown that field-based proteochemometrics can be used to generate predictive and visually interpretable models for kinases.9,10
In this study, we aim to generate a unified proteochemometric model on a set of 24 human serine proteases and 5863 inhibitors, using field-based descriptors for proteins and different 2D and 3D ligand descriptors. We have conducted extensive validations such as leave one target out (LOTO) and leave one compound cluster out (LOCCO) validations to assess the credibility of the models and understand the diversity of target and ligand space. Our PCM models are not only effective in predicting bioactivities of serine protease inhibitors, but also highlight protein and ligand features that contribute to affinity and selectivity.
Materials and methods
Datasets
24 unique human serine proteases were downloaded from PDB based on their resolution (<3 Å) and completeness. Bioactivity values (pKi) for 5863 unique compounds were extracted from publicly available ChEMBL 2015 to generate a dataset with 7908 data points. Confidence score of 5 and above was used as the criterion to extract data from CHEMBL. The complete bioactivity matrix for a set of 24 serine proteases and 5863 compounds should include 140 712 (24 × 5863) data points. On compiling the bioactivity profiles of compounds against all targets, only 7908 data points were found, thereby leaving 94% of the bioactivity matrix incomplete.
The distribution of data points for the 24 serine proteases is compiled in Table S1‡ and the pKi distributions for each target are illustrated in Fig. S1 of the ESI.‡ The dataset is highly imbalanced with overrepresentation of some of the serine proteases like coagulation factor Xa (FXa) and thrombin (FIIa) that contribute to nearly 70% (5601/7908 data points) of the dataset. Even though other serine proteases have about 100 data points on average, hepsin (HPN) and the complement component 1S (C1s) are underrepresented with 1 data point each. Considering the bioactivity spectra of serine proteases, 26% of the total data points belong to the highly actives category (pKi: 7 to 11) with FXa, FIIa, plasma kallikrein (KLKB1) and granzyme B, being the most represented members. 63% represent the moderately actives (pKi: 5 to 7) and 10% of the data points fit the less potent category (pKi < 5). Kallikrein 7 (KLK7) and coagulation factor XII (FXII) have the highest percentage of compounds with low potencies.
Ligand descriptors
All the compounds were standardised using JChem Standardizer version 15.0.1 and applying filters such as neutralize, remove explicit hydrogens, clean 2D, clean 3D and tautomerize. The standardised compounds were employed to the calculation of 192 physiochemical descriptors using MOE version 2014 (ref. 16) and 256 circular hashed fingerprints (radius = 2, bits = 256) using RDkit fingerprint calculator.17 Further, to account for the spatial description of the ligands, the compounds were subjected to 4-point pharmacophoric fingerprint (4-PFP) calculations using Canvas.18 The fingerprint precision was set to 32-bit and 1000 informative bits were considered for each compound. Additionally, 1180 grid-independent descriptors (GRIND)19 were computed using pentacle to provide a 3D description of the ligands.
Prior to calculating 4-PFPs and GRIND descriptors, 3D structures of the ligands were generated by using the Ligprep module of Schrödinger,18 with the default settings. In order to explore the conformational space further, we generated multiple conformations using ConfGen18 in comprehensive mode by applying the OPLS-2005 force field for energy minimization. However, only the conformation with the lowest potential energy was considered for each ligand and subjected to descriptor calculations. It is possible that some chosen conformations do not correspond to the bioactive conformations of the ligands. Since e.g. docking to several protein targets is no sufficient method to choose a single bioactive conformation, we used the lowest energy conformation for further analysis.
Protein descriptors
Initially, structures were cleaned by deleting water molecules, additional protein chains and ligands. For structures with multiple chains, the more complete chain was used. All structures were then prepared by using a KNIME20 workflow which involved the following steps: addition of hydrogen atoms, modeling of residues with missing atoms, assignment of protonation states of charged amino acids and optimization of the geometry of hydrogen atoms. Following preparation, all the structures were superimposed on a common reference protein (Matriptase, PDB id: ; 1EAX).
Ligand binding pockets of proteases were described by knowledge-based16 and Watermap-derived fields.21 Knowledge-based contact potentials, which are derived from the structural information available in PDB, are expressed as a joint probability density of interatomic distance, lone-pair interaction angle and out-of-plane angle. Contact potentials for hydrophilic and hydrophobic probes were calculated by considering a grid that spans the binding site of aligned protease structures. The grid was defined by exploiting the crystallographic pose of the peptide like inhibitor bound to the activated protein C crystal structure (PDB id: ; 1AUT) that extends to all non-prime protease sub-pockets (S1–S4). The grid spacing was set to 0.5 Å and its boundary limited to 2 Å from the reference ligand. Following the grid definition, the knowledge-based contact potentials were calculated for each grid point. However, only those grid points, for which the polar and lipophilic contact probabilities exceed 0.9 were considered as significant and used as protein descriptors in proteochemometric models.
Additionally, the ligand binding sites were described by fields derived from Schrödinger's Watermap. The Watermaps were calculated with the default settings and projected on to the grid used for knowledge-based field calculations to enable easy comparison. Water densities were assigned to each grid point and those grid points whose density values exceed 0.06 were considered for further Gibb's free energy assignments. Grid points with Gibb's free energy, ΔG > 3 kcal mol–1 were classified as unstable water field points and those with ΔG < –1 kcal mol–1 were classified as stable water field points. Fields derived from Watermaps were used together with the knowledge-based fields to describe the binding pockets of proteases in proteochemometric models.
Besides, using the field-based descriptors for proteins, we also used sequence-based descriptors such as amino acid and dipeptide composition, autocorrelation descriptors, composition, transition and distribution descriptors, quasi-sequence-order descriptors and pseudo-amino acid composition. These descriptors were calculated for the amino acid sequences extracted from the superimposed protein 3D structures by using the PROFEAT server.22
Data pre-processing
All protein and ligand descriptors were mean centred and scaled to unit variance using preProcess() function from Caret package23 in R. The preProcess method scales the numeric data between the range [0, 1]. The factorial vectors were converted to numeric by using dummyvars() function. In order to remove the predictors with zero variance, nearZeroVar() method was applied using frequency cut-off of 30/1.
Further, the high dimensionality of protein descriptors entailed principal component analysis (PCA). PCA24 is a dimensionality reduction technique applied to extract relevant information from big datasets. PCA was applied using prcomp() method of stat package in R.25 24 principal components (PCs) were extracted from 47 354 hydrophilic, hydrophobic and unstable water field points to explain as much variation as possible. Only 18 PCs were generated for 47 354 stable water field points, as the remaining components contributed to less than 1% variance. Similar to the fields, 24 PCs were extracted for each of the sequence-based descriptor categories mentioned above. The extracted PCs were used as protein descriptors in proteochemometric modelling. In case of ligands, the number of descriptors being limited, PCA was not applied and the ligand descriptors were used as such in proteochemometric modelling.
Proteochemometric modelling
PCM modelling combines the ligand and protein descriptors and uses the combination for prediction of bioactivity of ligands against multiple protein targets. The complete dataset was divided into 70% training set and 30% test set using createDataPartition(). The 70% training set was further 5-fold divided to optimise the parameters for training the models.
Prior to model building, recursive feature elimination (RFE) was applied on both the target and compound space of the training set. This was done to reduce the dimensionality of the training space further and minimize over-fitting, resulting from the large number of descriptors. RFE was conducted by using the 5-fold cross validation parameter in rfeControl function, as implemented in Caret package. The number of features that remain after RFE to be used in PCM modelling is reported in Table S2 of the ESI.‡
PCM models were trained by employing random forests (RF) as a regression technique, using train() method in Caret package. The number of variables sampled at each split (mtry) was set to default value (p/3) where p is the total number of variables in training set. The total number of trees was set to the default value of 500. In addition to RF models, partial least squares (PLS) regression models were generated by using SIMCA.26 PLS, being a linear approach, cross-terms were included to study non-linear interactions existing between the proteins and ligands. Cross-terms27 were computed as the product of protein principal components and ligand descriptors using SIMCA's inbuilt function. Only the protein and ligand features that remained after applying RFE were used for cross-terms computation. The number of cross-terms used in each PLS model are listed in Table S2 of the ESI.‡ In PLS models, protein descriptors, ligand descriptors and cross-terms were considered as separate entities called blocks and the variables in each block were scaled by setting the block weights to 1.
Besides PCM modelling, we built global QSAR models, models with only protein field descriptors and models with CHEMBL IDs of proteins and ligands as descriptors. Performances of these controls were estimated and were later compared with PCM models.
Model validation
K-fold cross validation (K = 5) was employed as an internal validation on the 70% training set, where the training data was further split into K-folds. The model was trained on K-1 folds and tested on the remaining fold. 30% of the complete dataset was held out and was used as test set for external validation. Model performances were assessed by correlation coefficient of the fitted data (R2), predictabilities of the cross-validated data (Q2), correlation coefficient of the external test set data (Rtest2) and root mean square error of the fitted (RMSEE), cross-validated (RMSEPCV) and external test set data (RMSEPtest).
In addition to K-fold cross validation, the models were further validated by leave one target out (LOTO) and leave one compound cluster out (LOCCO) validation. LOCCO and LOTO validations were conducted by using the RDkit fingerprints and random forest approach, as this descriptor and machine learning combination gave the overall best performance in terms of model predictions. In LOTO, the observations corresponding to one target were excluded at a time. RF models on RDkit fingerprints were built by considering the observations of the remaining 23 proteases and the excluded target was used as a test set. This procedure was repeated until all the targets were predicted at least once. In order to perform LOCCO validation, the compounds were first divided into distinct clusters using the k-means approach. K-means clustering was performed in R by setting the nstart (number of random samples) parameter to 50. Clustering was repeated by considering a range of cluster numbers starting from 2 to 200. The optimal number of clusters ideal for grouping the compounds for LOCCO validation was decided by plotting the cluster numbers against the mean within group sum of squares (see Fig. S2 in ESI‡). Based on the elbow method, we chose 20 as the optimal number of clusters. While performing LOCCO, observations corresponding to one cluster were excluded at a time and used as the test set. RDkit based RF models built on the remaining 19 clusters were used to test the excluded sets.
Additionally, RF and PLS models were assessed by conducting permutation validations/Y-scrambling, which involved re-fitting of the models 20 times with randomly assigned bioactivity values. The performances of these models with permuted data were used to measure the degree of over-fitting based on the intercepts obtained by plotting the correlation coefficient of the original and random bioactivities against R2 and Q2 obtained from fitted and cross-validated data, respectively.
Model interpretation
Features related to affinity were assessed by analysing the PLS coefficients that have positive influence on affinity. Only those protein and ligand features, whose PLS coefficients were above 0.1 were considered for interpretation. Protein features, being the principal components, were interpreted by examining the top 10 loadings of these principal components. Since the interpretation of RDkit fingerprints is straightforward, the ligand features were interpreted by tracing back to the patterns encoded by these fingerprints. On the other hand, features that influence the selective binding of an inhibitor towards a specific protease were identified by considering the cross-terms. The component contribution values computed by SIMCA were used as the basis to rank the cross-terms. For practical reasons, the selectivity interpretation was restricted to the top 10 cross-terms that have a positive impact on the affinity of protease-ligand interaction pairs. Details regarding the distribution of PLS coefficients and cross-terms used for interpretation are shown in Fig. S3 and S4 of the ESI.‡
Applicability domain
Applicability domain28 (AD) analysis was conducted to examine the extent to which the models can be applied to a new chemical space. The extrapolation capabilities of the models to predict external test set compounds were assessed by using the K-nearest neighbour approach. Average Tanimoto similarities of the compounds in the test set were computed by considering their 5 closest neighbours in the training set. Tanimoto similarities were calculated based on the RDkit fingerprints in order to find the cut-off suitable for making reliable predictions.
Results and discussion
Field-based PCM modelling
We used partial least squares (PLS) regression and random forest (RF) approaches to build proteochemometric models that have the potential to predict pKi values of new protease ligands. Performances of PCM models derived from the PCA scores of protein fields and ligand descriptors are reported in Table 1. As shown in Table 1, all RF PCM models have nearly the same performance with R2 consistently above 0.9, irrespective of the ligand descriptors used. With respect to internal cross-validation, the predictabilities (Q2) vary from 0.4 for GRIND descriptors to 0.7 for RDkit fingerprints and MOE descriptors. However, PLS models show varying performances with both R2 and Q2 ranging from 0.2 to 0.6, depending on the ligand descriptors used. Considering external predictions, the RMSEPs of RF and PLS models are similar to those obtained from internal cross-validation. Models based on RDkit fingerprints have the highest predictive power with Rtest2 of 0.72 for RF models (RMSEPtest: 0.81) and 0.56 for PLS models (RMSEPtest: 1). Overall, RF models perform better than the PLS models, both in terms of internal cross-validation and external prediction. Nevertheless, the reasonable R2 (0.67) and Q2 (0.59) values of the training sets obtained for RDkit based PLS models makes them valid enough for further predictions and interpretation. All PLS models considered in this study, included cross-terms, whose importance can be ascertained by comparing the performances of models with and without cross-terms. Models without cross-terms had a significant drop in performance (R2 and Q2 for models without cross-terms: 0.349 and 0.300; models with cross-terms: 0.671 and 0.588). Further, the slight increase in RMSEPtest of models without cross-terms confirms that cross-terms also have an impact on external predictions. Additionally, the relevance of cross-terms in PLS models was assessed by generating models that excluded the protein and ligand descriptor blocks. The drop in correlation and predictabilities together with the increase in RMSEPtest (R2, Q2 and RMSEPtest for models without protein and ligand descriptors: 0.598, 0.471 and 1.107; models with protein descriptors, ligand descriptors and cross-terms: 0.671, 0.588 and 1.007) shows that cross-terms can significantly influence the internal and external predictions, provided they are used in combination with the original protein and ligand descriptor blocks.
Table 1. Results of PCM using different combinations of ligand descriptors and four protein field descriptors (polar, lipophilic, unstable and stable water fields).
| Ligand descriptors | Correlation (R2) | Predictability (Q2) | RMSEE a | RMSEPcv b | RMSEPtest c | R test 2 d |
| Random forest models | ||||||
| RDkit | 0.957 | 0.737 | 0.360 | 0.799 | 0.810 | 0.716 |
| MOE | 0.961 | 0.703 | 0.360 | 0.857 | 0.840 | 0.695 |
| 4-PFP | 0.928 | 0.566 | 0.480 | 1.025 | 0.990 | 0.569 |
| GRIND | 0.951 | 0.430 | 0.470 | 1.175 | 1.150 | 0.426 |
| RDkit e | 0.585 | 0.429 | 1.060 | 1.188 | 1.110 | 0.492 |
| Target only models f | 0.111 | 0.107 | 1.450 | 1.455 | 1.420 | 0.128 |
| ID based models g | 0.835 | 0.298 | 0.660 | 1.338 | 1.340 | 0.276 |
| Partial least squares regression models with cross-terms | ||||||
| RDkit | 0.671 | 0.588 | 0.884 | 1.024 | 1.007 | 0.557 |
| MOE | 0.504 | 0.433 | 1.085 | 1.194 | 1.129 | 0.439 |
| 4-PFP | 0.554 | 0.451 | 1.029 | 1.216 | 1.136 | 0.437 |
| GRIND | 0.311 | 0.264 | 1.278 | 1.348 | 1.285 | 0.273 |
| RDkit e | 0.349 | 0.300 | 1.243 | 1.295 | 1.226 | 0.338 |
| Target only models f | 0.103 | 0.100 | 1.458 | 1.461 | 1.428 | 0.113 |
| ID based models g | 0.000 | –0.001 | 45.282 | 45.307 | 43.439 | 0.000 |
| RDkit (no cross-terms) | 0.397 | 0.365 | 1.196 | 1.233 | 1.182 | 0.386 |
| RDKit (only cross-terms) h | 0.598 | 0.471 | 0.977 | 1.144 | 1.107 | 0.465 |
aRoot-mean-square error of estimation for observations in the training set.
bRoot-mean-square error of prediction resulting from 5-fold cross-validation.
cRoot-mean-square error of prediction calculated using the external test set.
dCorrelation between the observed and predicted values of the external test set.
eGlobal QSAR models.
fModels based on protein fields with exclusion of ligand descriptors.
gModels with CHEMBL ids of compounds and targets used as descriptors.
hModels based on cross-terms with exclusion of protein and ligand descriptors.
On comparing the RF model performances with respect to different ligand descriptors, models based on GRIND (Rtest2: 0.43; RMSEPtest: 1.15) have considerably lower performances as against the 4-PFPs (Rtest2: 0.57; RMSEPtest: 0.99) and 2D descriptors such as RDkit fingerprints (Rtest2: 0.72; RMSEPtest: 0.81) and MOE (Rtest2: 0.70; RMSEPtest: 0.84). Similar trends are observed with respect to the performances of PLS models. Decrease in Rtest2 of GRIND models can be attributed to the difficulties in generating relevant 3D conformations suitable for descriptor calculations. It is often challenging to find 3D conformations similar to the bioactive ones, owing to the flexibility of protease ligands. The calculations of GRIND descriptors are often influenced by the starting ligand conformations.29 Incorrect conformations can have a significant effect on the model performances, thereby resulting in poor predictions. Nevertheless, assessing the model performances based on different ligand conformations is not within the scope of our present study.
In order to assess the reliability of the models, we also built models as negative controls. The relevance of including protein information in PCM modelling was evaluated by training global QSAR models dependent exclusively on the ligand's RDkit fingerprints. Considering the prediction performances, the global QSAR models based on RDkit fingerprints performed worse than the PCM models with increase in RMSEPtest (RMSEPtest for RF models: 1.11; RMSEPtest for PLS models: 1.23). Furthermore, models built by considering only the protein fields with the exclusion of ligand descriptors performed worse than the global QSAR models (RMSEPtest for RF models: 1.420; RMSEPtest for PLS models: 1.428). The poor performances of models based on either ligand or protein descriptors imply that the combination of protein and ligand descriptors in PCM models is important for improving the model's overall performance and increasing the accuracies of the bioactivity predictions of external test sets. As an additional test case, the relevance of protein and ligand descriptors in PCM modelling was assessed by building models with CHEMBL IDs of ligands and proteins as descriptors. ID based models had a significant increase in RMSEPs of external test sets for both RF (RMSEPtest for ID based models: 1.340; RMSEPtest for field-based models: 0.810) and PLS models (RMSEPtest for ID based models: 43.349; RMSEPtest for field-based models: 1.007). The higher RMSEPtest of ID based models further confirms that the type of descriptors used in PCM has an impact on the model's predictive power.
To evaluate whether R2 and Q2 were obtained by pure chance, we analysed the model performances based on permutation validation experiments. Despite the use of a large number of ligand descriptors in RF and PLS models and thousands of cross-terms in PLS models, the models are not over-fitted, which is evident from the low R2 and negative Q2 intercepts (Table S3 in ESI‡). Results of permutation validation further confirm the validity of the models and their usefulness in making predictions and interpretations.
Sequence-based PCM modeling
In order to compare and assess the predictive powers of PCM models based on protein fields (3D) and sequences (1D), we built PCM models that depend on the amino acid sequence descriptors. Sequence-based PCM models were trained only by using ligand's RDkit fingerprints and the RF approach, as this descriptor and machine learning approach had the best performance in field-based models.
No significant differences in prediction performances are observed, regardless of the type of sequence descriptors used (Table 2). Rtest2 (0.714) and RMSEPtest (0.810) of the sequence-based models are in line with the field-based models Rtest2 (0.716) and RMSEPtest: (0.810), thereby showing that both field-based and sequence-based descriptors have the same impact in terms of prediction. However, the possibility of visual interpretation of protein and ligand features is a clear advantage of field-based models more compared to sequence-based models.
Table 2. Results of PCM using different protein sequence descriptors and ligand's RDkit fingerprints.
| Protein descriptors | Correlation (R2) | Predictability (Q2) | RMSEE | RMSEPcv | RMSEPtest | R test 2 |
| Random forest models | ||||||
| Amino acid + dipeptide composition | 0.956 | 0.740 | 0.360 | 0.795 | 0.810 | 0.713 |
| Autocorrelation descriptors | 0.956 | 0.739 | 0.360 | 0.796 | 0.810 | 0.714 |
| Composition, transition + distribution | 0.956 | 0.742 | 0.360 | 0.792 | 0.810 | 0.717 |
| Sequence order + pseudo amino acid composition | 0.955 | 0.739 | 0.360 | 0.795 | 0.810 | 0.710 |
Visual interpretation
Interpreting selectivity features based on random forest models is not straightforward. Therefore, we focus on the interpretation of the best performing PLS models based on RDkit fingerprints. Protein field points and ligand features related to affinity and selectivity was interpreted by considering their PCA scores and cross-terms respectively (for details see Materials and methods). The identified field points were then visualized in MOE using our in-house SVL scripts.
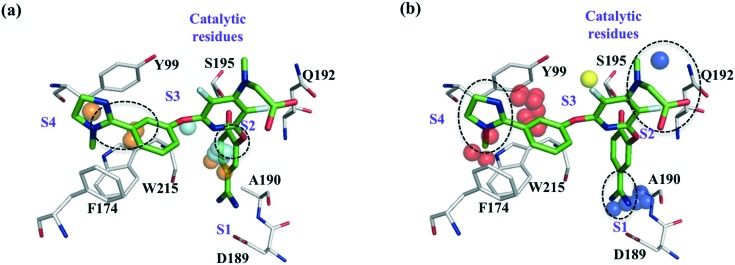
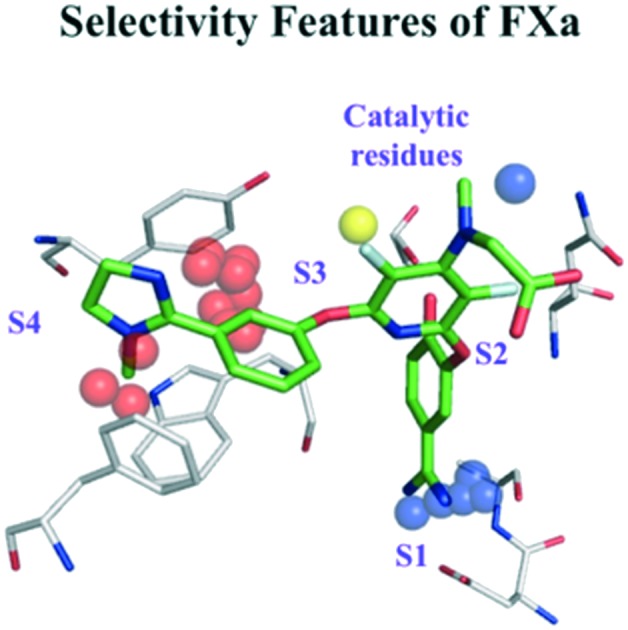
Fig. 1 shows the protein field points and ligand RDKIT fingerprints features to be important for the interactions of ZK-807834 with FXa. Polar field points near the catalytic serine contribute to commonly observed hydrogen bond interactions in many serine proteases. Additionally, the lipophilic field points near S1 and S4 sub-pockets might influence the affinity of all inhibitors that bind to FXa and show clear overlap with the chemical features of ligand ZK-807834 (Fig. 1a). The selective binding of ZK-807834 to FXa is influenced by polar field points in S1 sub-pocket that interact with the amidinium group of ZK-807834 (Fig. 1b). The importance of this region for selectivity is illustrated by the formation of a salt bridge with Asp189 in a FXa crystal structure (PDB id: ; 1FJS).30 This is also in agreement with the peptide substrate data for FXa, where a clear preference for positively charged amino acids (Arg, Lys) at position P1 has been described.31 Additionally, the presence of alanine at position 190 has been shown to influence the selectivity of tissue plasminogen activator (tPA) and FXa.32 The polar field points in close proximity to Ala190 confirm their relevance for the selectivity of FXa, although small molecule inhibitors binding to the S1 via hydrophobic halogen–pi interactions have been reported.33 We also speculate that the imidazole moiety of ZK-807834 enhances selectivity by displacing unstable water in the S4 sub-pocket (a region commonly exploited for protease selectivity known as “aromatic box”34 in FXa) (Fig. 1, right panel).
Fig. 1. Protein field points and ligand RDkit fingerprints relevant for the interactions of ZK-807834/CHEMBL73193 (green) and FXa (grey). Dotted circles mark ligand features related to affinity and selectivity. (a) Features relevant for affinity: cyan and orange coloured spheres correspond to the polar and lipophilic field points that influence affinity. (b) Features relevant for selectivity: dark blue, yellow and red coloured spheres correspond to the polar, lipophilic and unstable water field points that might contribute to the selective binding of ZK-807834 to FXa.
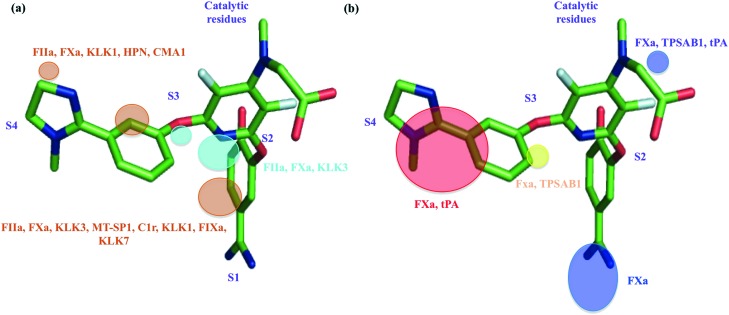
We have also conducted a systematic analysis to identify the proteases in which the field points discussed above are present (Fig. 2). The regions relevant for affinity are commonly found in many protease families, for instance FIIa, FXa, HPN, KLK7, coagulation factor IXa (FIXa), matriptase (MT-SP1), complement component 1R (C1r), chymase (CMA1), kallikrein 1 (KLK1) and kallikrein 3 (KLK3), thereby suggesting that these features are important for the binding of any ligand towards these proteases (Fig. 2a). Whereas, the regions important for selectivity (Fig. 2b) are restricted to certain proteases namely FXa, tryptase alpha/beta (TPSAB1) and tPA. The combination of these selectivity related field points could be considered as regions that have increased preference for FXa selectivity over other proteases.
Fig. 2. Protein regions which contribute to affinity and selectivity for protease ligands, mapped on bound ZK-807834. (a) Regions relevant for affinity: polar protein field (cyan), lipophilic protein field (orange). (b) Regions relevant for selectivity: polar field points (blue), lipophilic protein field (yellow), unstable water sites (red). Gene names of the proteases, in which these field points are present, are marked with the respective colors, as that of the fields.
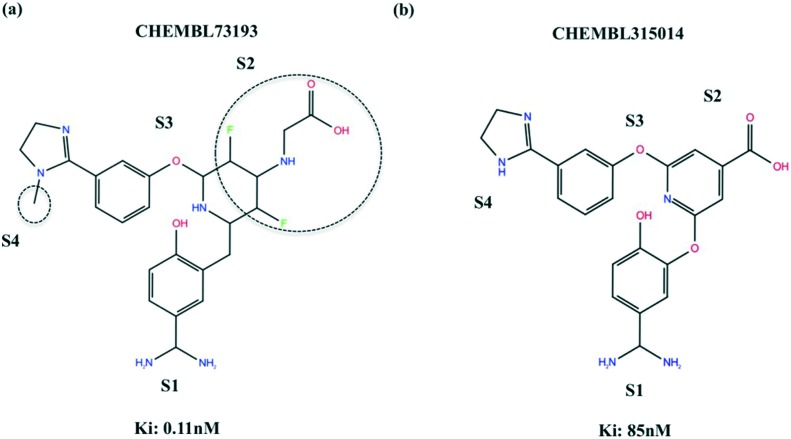
In order to verify the fingerprints identified as important for the selectivity of CHEMBL73193 towards FXa, we compared the features of CHEMBL73193 and CHEMBL315014 that act on FXa with different potencies. Structural replacements or absence of the fragments highlighted in Fig. 3a have led to a 800-fold decrease in potency of CHEMBL315014. The methyl group that is likely to bind by displacing unstable water molecules in S4 sub-pocket and the carboxyl group that participates in polar interactions contribute to the high potency of CHEMBL73193. Further, the observed decrease in binding affinities of CHEMBL315014 towards Thrombin and Trypsin, when compared to CHEMBL73193 confirms that these fragments affect the overall potency and selectivity of these ligands towards serine proteases (For Ki differences, see Table S4 in ESI‡).
Fig. 3. Fingerprints that contribute to the selectivity of ligands binding to FXa. Features contributing to the potency differences of the 2 ligands are highlighted with dotted circles. (a) CHEMBL73193 (b) CHEMBL315014.
Leave one target out (LOTO) validation
In order to assess the model's extrapolation power in terms of the target space, we performed LOTO validation (see Table S5 in ESI‡). The average correlation and predictabilities of the models trained by excluding one target at a time (R2: 0.957, Q2: 0.749) remains fairly close to the models, where all targets are included (R2: 0.957, Q2: 0.737). However, the average RMSEP resulting from LOTO (RMSEPtest: 1.302 ± 0.443) remains slightly higher than the model's overall RMSEP (RMSEPtest: 0.810). Increase in prediction errors of the LOTO models can be attributed to the diverse structural nature of the proteases present in the dataset. The field-based similarity of the proteases in our data set is less than 50% (see Fig. S5 in ESI‡), which in turn makes it difficult to predict the bioactivities of the excluded targets. In case of FXa and FIIa, the prediction errors are quite high (RMSEPtest for FXa: 2.13; FIIa: 1.61), despite the presence of some closer homologues. Since nearly 70% of the data points correspond to either FIIa (2822) or FXa (2779), excluding them completely makes it challenging for the models to predict those observations. Another reason for increase in RMSEPs could be the sparse distribution of the data points, in terms of targets. Only 30% of the data points (2307/7908) belong to proteases other than FXa and FIIa. The prediction errors for these proteases with few data points increase dramatically, after complete elimination. Overall, the model's extrapolative power is limited to the proteases with some closer homologues and a considerable number of data points.
Leave one compound cluster out (LOCCO) validation
To test the robustness of the models in terms of ligand space, we performed LOCCO validation on the entire dataset (7908 data points). R2, Q2 and RMSEPs of LOCCO validation based on RDkit fingerprints are summarized in Table S6 of the ESI.‡ In contrast to LOTO validation, excluding compound clusters results in a significant drop in model performances with R2 and Q2 as low as 0.50 and 0.25. The average RMSEPtest of the 20 compound clusters is 1.550 ± 0.269, which is comparatively higher than the models trained by random splitting (RMSEPtest: 0.810). On analysing the compound clusters, we found that there is a significant overlap in compound space between the different clusters, except C3, C4 and C17 (Fig. S6 in ESI‡). Cluster C9 that has high inter cluster similarity and includes compounds with polycyclic ring systems linked to chlorine or fluorine has the lowest RMSEPtest of 1.080. Cluster C17 that mostly includes compounds with pyrazopyrimidines, has the highest RMSEPtest value of more than two pChembl units, which is in agreement with the low inter cluster similarity shown in Fig. S3.‡ With respect to other compound clusters, no significant correlation was observed between the inter cluster similarity and RMSEPtest values. Altogether, the high RMSEPs of LOCCO validation reveal that it is challenging to extrapolate in terms of chemical space from the serine protease dataset.
Challenges in LOCCO and LOTO validation
Despite the presence of many similar compound clusters, it is difficult to predict the excluded compound clusters in LOCCO validations. The same is the case with LOTO validation, where the prediction errors are higher even for excluded targets with closer homologues. The low performances with respect to LOTO and LOCCO validations can be mainly attributed to the sparse activity space and imbalance in data point distribution, resulting from over or under representation of some of the targets/compounds. Yet, another reason could be conformational variation of protein structures affecting field calculations. With the majority of the serine protease inhibitors being large and flexible, their binding is likely to induce conformational changes in protease sub-pockets. For instance, in prostasin, binding of an inhibitor opens the S1 sub-pocket that was closed in the apo/ligand-free state.35 Similarly, binding of different inhibitors can lead to conformational changes, which will be reflected in the field calculations. These variations in fields could make it difficult to predict the bioactivities of ligands that bind and induce conformations differently and will have an impact on the LOTO and LOCCO validation performance. However, this issue could be resolved by calculating fields based on an ensemble of protein conformations that account for protein flexibility as demonstrated by Waldner et al.36
Applicability domain (AD)
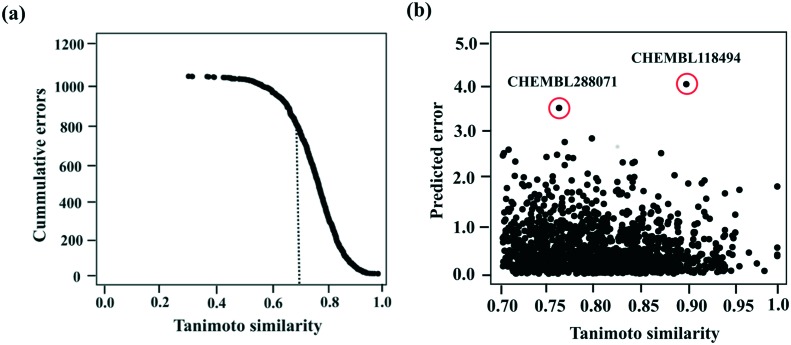
We conducted AD analysis to identify the similarity thresholds above which the compounds can be predicted with minimal errors. As shown in Fig. 4a, the cumulative errors decrease with increase in Tanimoto similarities; thereby justifying that test set compounds whose chemical space overlaps with the training space can be predicted with the lowest error rate. Of the 1709 compounds in the test set, 1339 have Tanimoto similarities over 0.7. Nearly 84% of these compounds have prediction errors of 1 or less. Despite having high Tanimoto similarities, the remaining 16% compounds have prediction errors of 1.5 on average. High error rate could be due to the sparse activity space used for modelling. Among these 16% of compounds, there are two outliers (CHEMBL 118494 and CHEMBL 288071 – structures shown in Fig. S7 of the ESI‡) whose prediction errors exceed 3.5 pChembl units (Fig. 4b). The large differences in predictions of one of the outliers is due to the lack of structurally similar compounds in the training set, while for the other compound structurally similar compounds exist, but they lie in a very different activity range.
Fig. 4. (a) Tanimoto similarity of the test set ligands based on RDkit fingerprints plotted against the cummulative errors. Dotted lines represent the cut-offs for predictions of external ligands. (b) Predicted error distributions of the compounds with Tanimoto similarities above 0.7. Outliers are highlighted in red.
Conclusions
We have shown that field-based proteochemometrics can be used to model the protease-ligand interaction space effectively, which is evident from the model's potential to predict new ligands with RMSEPs as low as 0.8. Field-based PCM models outperform global QSAR models, thereby proving the need to include explicit target information for predictive modelling. However, the models have limited extrapolative power in terms of target and chemical space, probably due to the sparse bioactivity matrix, diverse nature of ligands and proteases in the dataset and field calculation errors driven by conformational shifts in protease sub-pockets. Nevertheless, visually interpretable PCM models provide rapid access to key affinity and selectivity hot spots, which overlap well with published data on serine proteases. Additionally, proteochemometric models derived from fields for proteases have similar performances as previously published sequence-based models, but with the advantage of visual interpretation that is in line with the scientific literature.
Supplementary Material
Acknowledgments
V. S. acknowledges funding from the 3i project (TEKES). The Finnish National Doctoral Program in Integrative Life Sciences is thanked for organizing graduate studies and providing support to graduate education. Q. U. A. thanks the Cambridge Commonwealth Trust and the Islamic Development Bank (IDB) for funding.
Footnotes
†The authors declare no competing interests.
‡Electronic supplementary information (ESI) available. See DOI: 10.1039/c6md00701e
References
- Di Cera E. IUBMB Life. 2009;61:510–515. doi: 10.1002/iub.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puente X. S., Sanchez L. M., Overall C. M., Lopez-Otin C. Nat. Rev. Genet. 2003;4:544–558. doi: 10.1038/nrg1111. [DOI] [PubMed] [Google Scholar]
- Fuchs J. E., von Grafenstein S., Huber R. G., Kramer C., Liedl K. R. PLoS Comput. Biol. 2013;9:e1003353. doi: 10.1371/journal.pcbi.1003353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs J. E., von Grafenstein S., Huber R. G., Margreiter M. A., Spitzer G. M., Wallnoefer H. G., Liedl K. R. PLoS Comput. Biol. 2013;9:1–12. doi: 10.1371/journal.pcbi.1003007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs J. E., Huber R. G., Waldner B. J., Kahler U., Von Grafenstein S., Kramer C., Liedl K. R. PLoS One. 2015;10:1–14. doi: 10.1371/journal.pone.0140713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prusis P., Muceniece R., Andersson P., Post C., Lundstedt T., Wikberg J. E. S. Biochim. Biophys. Acta. 2001;1544:350–357. doi: 10.1016/s0167-4838(00)00249-1. [DOI] [PubMed] [Google Scholar]
- Van Westen G. J. P., Wegner J. K., IJzerman A. P., van Vlijmen H. W. T., Bender A. Med. Chem. Commun. 2011;2:16–30. [Google Scholar]
- Cortés-Ciriano I., Ain Q. U., Subramanian V., Lenselink E. B., Méndez-Lucio O., IJzerman A. P., Wohlfahrt G., Prusis P., Malliavin T. E., van Westen G. J. P., Bender A. Med. Chem. Commun. 2015;6:24–50. [Google Scholar]
- Subramanian V., Prusis P., Pietilä L. O., Xhaard H., Wohlfahrt G. J. Chem. Inf. Model. 2013;53:3021–3030. doi: 10.1021/ci400369z. [DOI] [PubMed] [Google Scholar]
- Subramanian V., Prusis P., Xhaard H., Wohlfahrt G. Med. Chem. Commun. 2016;7:1007–1015. [Google Scholar]
- Rasti B., Karimi-jafari M. H. Chem. Biol. Drug Des. 2016;88:341–353. doi: 10.1111/cbdd.12759. [DOI] [PubMed] [Google Scholar]
- Cortés-Ciriano I., Bender A., Malliavin T. Mol. Inf. 2015;34:357–366. doi: 10.1002/minf.201400165. [DOI] [PubMed] [Google Scholar]
- Simeon S., Spjuth O., Lapins M., Nabu S., Anuwongcharoen N., Prachayasittikul V., Wikberg J. E. S., Nantasenamat C. PeerJ. 2016;4:e1979. doi: 10.7717/peerj.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ain Q. U., Méndez-Lucio O., Ciriano I. C., Malliavin T., van Westen G. J. P., Bender A. Integr. Biol. 2014;6:1023–1033. doi: 10.1039/c4ib00175c. [DOI] [PubMed] [Google Scholar]
- Bento A. P., Gaulton A., Hersey A., Bellis L. J., Chambers J., Davies M., Kruger F. A., Light Y., Mak L., McGlinchey S., Nowotka M., Papadatos G., Santos R., Overington J. P. Nucleic Acids Res. 2014;42:D1083–D1090. doi: 10.1093/nar/gkt1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molecular Operating Environment (MOE), 2013.08, Chemical Computing Group Inc., 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7, 2015.
- RDKit: Open-source cheminformatics, http://www.rdkit.org.
- Maestro, 9.8, Schrödinger, LLC, New York, NY, 2014. LigPrep, version 3.0, Schrödinger, LLC, New York, NY, 2014. ConfGen, version 2.8, Schrödinger, LLC, New York, NY, 2014. Canvas, version 2.0, Schrödinger, LLC, New York, NY, 2014. Schrödinger Suite 2014 Protein Preparation Wizard; Epik version 2.2, Schrödinger, LLC, New York, NY, 2014. Impact version 5.7, Schrödinger, LLC, New York, NY, 2014. Prime version 3.0, Schrödinger, LLC, New York, NY, 2014.
- Pastor M., Cruciani G., McLay I., Pickett S., Clementi S. J. Med. Chem. 2000;43:3233–3243. doi: 10.1021/jm000941m. [DOI] [PubMed] [Google Scholar]
- Berthold M. R., Cebron N., Dill F., Fatta G. D., Gabriel T. R., Georg F., Meinl T., Ohl P., Sieb C. and Wiswedel B., Studies in Classification, Data Analysis, and Knowledge Organization, Springer, Germany, 2007, pp. 319–326. [Google Scholar]
- WaterMap, version 1.4, Schrödinger, LLC, New York, NY, 2012.
- Li Z. R., Lin H. H., Han L. Y., Jiang L., Chen X., Chen Y. Z. Nucleic Acids Res. 2006;34:W32–W37. doi: 10.1093/nar/gkl305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng R. D., Dominici F. J. Stat. Softw. 2009;29:1–26. [Google Scholar]
- Wold S., Esbensen K., Geladi P. Chemom. Intell. Lab. Syst. 1987;2:37–52. [Google Scholar]
- R Development Core Team. R, A language and environment for statistical computing, R Foundation for Statistical Computing, Austria, 2015, http://www.R-project.org.
- SIMCA-P version 12, Umetrix AB, Box 7960, SE-907, 19 Umea, Sweden, 2011.
- Wikberg J. E. S., Lapinsh M. and Prusis P., in Chemogenomics in Drug Discovery: A Medicinal Chemistry Perspective, ed. H. Kubinyi and G. Muller, Wiley-VCH, Weinheim, 2004, pp. 289–309. [Google Scholar]
- Jaworska J., Nikolova-Jeliazkova N., Aldenberg T. ATLA, Altern. Lab. Anim. 2005;33:445–459. doi: 10.1177/026119290503300508. [DOI] [PubMed] [Google Scholar]
- Caron G., Ermondi G. J. Med. Chem. 2007;3:5039–5042. doi: 10.1021/jm0704651. [DOI] [PubMed] [Google Scholar]
- Adler M., Davey D. D., Phillips G. B., Kim S. H., Jancarik J., Rumennik G., Light D. R., Whitlow M. Biochemistry. 2000;39:12534–12542. doi: 10.1021/bi001477q. [DOI] [PubMed] [Google Scholar]
- Schilling O., Auf Dem Keller U., Overall C. M. Biol. Chem. 2011;392:1031–1037. doi: 10.1515/BC.2011.158. [DOI] [PubMed] [Google Scholar]
- Katz B. A., Sprengeler P. A., Luong C., Verner E., Elrod K., Kirtley M., Janc J., Spencer J. R., Breitenbucher J. G., Hui H., McGee D., Allen D., Martelli A., Mackman R. L. Chem. Biol. 2001;8:1107–1121. doi: 10.1016/s1074-5521(01)00084-9. [DOI] [PubMed] [Google Scholar]
- Nazaré M., Will D. W., Matter H., Schreuder H., Ritter K., Urmann M., Essrich M., Bauer A., Wagner M., Czech J., Lorenz M., Laux V., Wehner V. J. Med. Chem. 2005;48:4511–4525. doi: 10.1021/jm0490540. [DOI] [PubMed] [Google Scholar]
- Nar H., Bauer M., Schmid A., Stassen J. M., Wienen W., Priepke H. W. M., Kauffmann I. K., Ries U. J., Hauel N. H. Structure. 2001;9:29–37. doi: 10.1016/s0969-2126(00)00551-7. [DOI] [PubMed] [Google Scholar]
- Spraggon G., Hornsby M., Shipway A., Tully D. C., Bursulaya B., Danahay H., Harris J. L., Lesley S. A. Protein Sci. 2009;18:1081–1094. doi: 10.1002/pro.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waldner B. J., Fuchs J. E., Huber R. G., Von Grafenstein S., Schauperl M., Kramer C., Liedl K. R. J. Phys. Chem. B. 2016;120:299–308. doi: 10.1021/acs.jpcb.5b10637. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.