Structure and properties of DOTA-chelated radiopharmaceuticals within the ²²⁵Ac decay pathway

The stability of DOTA-chelated complexes coordinated with H₂O has a strong correlation between the opening angle of DOTA and the atomic mass of the radioactive isotope.

Abstract

The successful delivery of toxic cargo directly to tumor cells is of primary importance in targeted (α) particle therapy. Complexes of radioactive atoms with the 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid (DOTA) chelating agent are considered as effective materials for such delivery processes. The DOTA chelator displays high affinity to radioactive metal isotopes and retains this capability after conjugation to tumor targeting moieties. Although the α-decay chains are well defined for many isotopes, the stability of chelations during the decay process and the impact of released energy on their structures remain unknown. The radioactive isotope ²²⁵Ac is an α-particle emitter that can be easily chelated by DOTA. However, ²²⁵Ac has a complex decay chain with four α-particle emissions during decay of each radionuclide. To advance our fundamental understanding of the consequences of α-decay on the stability of tumor-targeted ²²⁵Ac–DOTA conjugate radiopharmaceuticals, we performed first principles calculations of the structure, stability, and electronic properties of the DOTA chelator to the ²²⁵Ac radioactive isotope, and the initial daughters in the decay chain, ²²⁵Ac, ²²¹Fr, ²¹⁷At and ²¹³Bi. Our calculations show that the atomic positions, binding energies, and electron localization functions are affected by the interplay between spin–orbit coupling, weak dispersive interactions, and environmental factors. Future empirical measurements may be guided and interpreted in light of these results.

1. Introduction

The potential for the use of targeted α-particle emissions for the treatment of solid tumors and metastases was recently highlighted by the success of ²²³RaCl₂ (Xofigo®) in improving the outcomes of patients with prostate cancer bone metastases.1 When compared to ²²³Ra, the ²²⁵Ac radionuclide has a similar half-life and decay chain with multiple α-particle emissions, but ²²⁵Ac has the further advantage of being readily chelated into DOTA (1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid) with high stability, allowing attachment to a tumor targeting moiety.2 The long 10 day half-life of ²²⁵Ac,3 allows for centralized production and use as an in vivo α particle nanogenerator4 with a total of four α emissions during decay to stable ²⁰⁹Bi and high (28 MeV total) local energy deposition.5 The ²²⁵Ac–DOTA complex has been conjugated to cancer targeted monoclonal antibodies and peptides, and has been tested in a number of preclinical4,6–12 and clinical13,14 studies as targeted α-particle therapy (TAT).

The α-particle radionuclide ²²⁵Ac has a high linear energy transfer (LET) that allows for the direct breakage of covalent bonds in the DNA macromolecule, leading to double-strand breaks, irreparable damage and cell death. Nonnekens et al. have shown that a small molecule prostate-specific membrane antigen (PSMA) ligand conjugated to ²¹³Bi–DOTA induced DNA double-strand breaks in the LNCaP human prostate cancer cell line and tumors.15 Li et al. have shown that targeted α-particle emission therapy using ²¹³Bi-cDTPAa conjugated to the PSMA targeting J591 monoclonal antibody induces the apoptotic mechanism of cell death in LNCaP-LN3 cells and tumors.16 Notably, this mechanism does not rely on the generation of free-radicals for generation of double-strand breaks17 and thus bypasses a known mechanism of resistance to radiotherapy, i.e. upregulation of free-radical scavenging enzymes.18 Although the mean free-path of 40–60 μm for α-particles with weighted average energy of 5.78 MeV in tissue,19 is relatively short, they do travel through up to ten tumor cell diameter lengths23 allowing for extensive damage to surrounding tumor cells which may or may not express the target cell-surface marker. Hence, this property may address a known mechanism of resistance to targeted therapies, the clonal expansion of tumor cells that do not express the target marker and the eventual resistance to the targeted therapy.24 The short range of α-emissions has the added advantage of focusing the energy deposition primarily within the lesion, with minimal effect on the surrounding healthy tissues.

However, due to the complexity of the ²²⁵Ac decay chain (or that of other metallic α-emitting radionuclides), there are concerns regarding the stability of the chelation complex during the decay process, i.e. it is not known if daughter radionuclides will remain in the complex, or be free to distribute to other tissues of concern for toxicity.24–26 There is some evidence that ²²⁵Ac daughters are released from the DOTA chelator following decay. Schwartz et al. have reported that following intravenous administration of the ²²⁵Ac–DOTA-huM195 antibody conjugate, the free ²¹³Bi daughter product can be detected in the kidney.26 However, this observation was made in only a single, small study (n = 12 mice) and the reported results are not definitive. For example, observations were only presented for kidney tissue. Showing that other tissues do not have similarly elevated ²¹³Bi is a necessary control for the method, and this was not done. There are possible explanations for the reported observation of elevated ²¹³Bi prior to secular equilibrium other than release from the chelator, e.g. the results depend on the measured ratio of ²¹³Bi : ²²¹Fr and the data were acquired over a 30 min interval, which encompasses over 6 ²²¹Fr half-lives, but only 0.66 of a ²¹³Bi half-life. It does not appear that corrections were made to account for the differences in half-life.

There are concerns about free daughters leading to kidney toxicity, but also about decreased efficacy, i.e. diffusion of daughters away from tumors would account for less than four α emissions per ²²⁵Ac taken in to the tumor cell. However, the source of the free ²¹³Bi cannot be determined from the results presented in the in the Schwartz study, i.e. since it is well documented that antibody conjugates circulate in the blood for days following administration,27 it is possible and likely that all of the ²¹³Bi observed to be free in the kidney were released from ²²⁵Ac–DOTA-huM195 that was still in circulation and that decay products from intact ²²⁵Ac–DOTA-huM195 that was taken into the tumor cells were retained in the tumor for the duration of decay regardless of release from the chelator. Further, it is not possible to determine the ratio of free ²¹³Bi to chelated ²¹³Bi from the data presented in the Schwartz study, so it is not clear how significant the observation is in terms of the nanogenerator effect in tumors. The chelation energies of metal chelation complexes are in the range of tens of electron volts, which may not be sufficient to overcome damage arising from the recoil energy, which is in the order of hundreds of keV. However, α-decay is a quantum mechanics problem,28 not a classical mechanics problem and it is not a certainty that the recoil energy will result in dislocation of daughter isotopes from the chelator, or that the chelator will be damaged by recoil. To our knowledge, there are no other published studies, either empirical or computational, that evaluate the stability of ²²⁵Ac–DOTA chelation complex during decay. Therefore, it is also not clear to what extent α-emissions alone can deliver damage to the chelator. Hence, the processes following α-particle release and the structural rearrangements within radionuclide-chelation complexes remain undetermined as do the interactions between DOTA complexes and water molecules.

Although ²²⁵Ac has a complex decay chain with four α-emitting daughters in a branched decay chain, in this work we focus on the characterization of the DOTA chelation of ²²⁵Ac and the initial daughter radionuclides in the α-decay chain.24 We utilize ab initio simulations based on density functional theory (DFT) for an array of DOTA complexes to investigate their energetic stabilities and structure–property relationships from the quantum mechanical perspective. We have addressed the role of water in the aqueous environment and have determined preferred coordination states, structural rearrangements, and charge transfer, by simulations of the interactions between water molecules and DOTA complexes with chelated radionuclides. The effects of the relativistic spin–orbit coupling (SOC) and van der Waals (vdW) dispersive interactions are also taken into account. Since the Gd–DOTA chelation complex is well known due to its use as a magnetic resonance imaging (MRI) contrast agent, we have simulated its computational results with existing experimental structure data.29–33 The recoil energies of the daughter nuclei were estimated using non-relativistic kinematics and available data on the kinetic energy of emitted α-particles.

2. Computational approach

The simulations were performed using DFT as implemented in the Vienna ab-initio simulations package (VASP),34,35 in which the single-particle Kohn–Sham equations are solved via the projector augmented (PAW) method36,37 with a plane wave basis set. The exchange-correlation energy is calculated using the Perdew–Burke–Ernzerhof (PBE) functional. The calculations were initiated with ²¹³Bi–DOTA whose structure was adapted from.38 For the other complexes, the ²¹³Bi atom was substituted with ²²⁵Ac, ²²¹Fr, ²¹⁷At, or Gd atoms and the obtained structures were pre-optimized using the molecular builder and visualization software Avogadro.39 The ground state energies of the investigated molecules were calculated via the single k-point approach.40 For this purpose, each molecule is placed in the center of a cubic cell and allowed to relax with a plane wave cutoff of 520 eV and 10^–4 eV energy and 10^–5 eV A^–1 force relaxation criteria. Their dimensions for Gd–DOTA, ²¹³Bi–DOTA, ²¹⁷At–DOTA, ²²¹Fr–DOTA and ²²⁵Ac–DOTA are found as 11.65 Å, 12.25 Å, 12.12 Å, 13.45 Å and 14.50 Å, respectively.

Due to the presence of heavy metallic elements in the studied structures, the SOC effect was also investigated. This relativistic effect occurs as a result of the electronic angular momentum and spin coupling. In VASP, it is calculated via non-collinear magnetism as the valence electrons are taken into account through a variation method and scalar relativistic eigenfunctions. The long range dispersive vdW interactions are also important for the studied radionuclide chelation complexes as shown in our subsequent results. These are taken into account via the vdW-DF2 functional as implemented in VASP according to the Langreth–Lundqvist scheme.41,42

The vdW-DF2 nonlocal functional has been extensively used for electronic structure calculations for a variety of systems showing the importance of dispersive interactions not only at the nanoscale but also in 3D materials.43,44 The electron localization and charge transfer are calculated within VASP using (96 × 96 × 96) fast Fourier transform (FFT) mesh in the lattice vector space. The energy released by the α decay process (Q_α-value) and the recoil energy for daughter nuclei E_R were estimated from the experimental data available from the National Nuclear Data Center.45,46

3. Results and discussion

3.1. Structural stability of DOTA complexes

The DOTA complexes studied here constitute the initial daughter products of the ²²⁵Ac radioactive decay chain: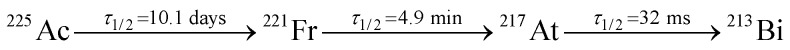where τ_1/2 corresponds to the half-life time.6,46 We have also included the Gd–DOTA complex in these studies for comparison, since it is well characterized due to extensive use as a magnetic resonance imaging (MRI) contrast agent.29–33

The energetic and structural stabilities for each molecule were investigated computationally using the outlined DFT approach. Specifically, the binding energy of the radioisotope to DOTA, E_B, was calculated as E_B = E_TOT – (E_DOTA + E_IS), where E_TOT is the total energy of DOTA containing the radioisotope (DOTA-complex), E_DOTA is the energy of DOTA chelator, and E_IS is the energy of radioisotope. The results for E_B as well as several characteristic distances with and without the SOC and vdW effects are summarized in Table 1. Based on the Table 1 E_B values, the most stable complexes were determined to be Gd–DOTA and ²²⁵Ac–DOTA, while ²²¹Fr–DOTA is the least stable if SOC or vdW effects are not included. Taking into account the SOC and vdW coupling does not change this order, however, their effects on E_B are different for different molecules. For example, the SOC hardly affects E_B of Gd–DOTA, while it makes ²²¹Fr–DOTA more stable by 0.90 eV. For the other molecules, the SOC reduces the magnitude of E_B. The effects of the dispersive interactions are also unusual. While vdW interactions have a stabilizing effect for Gd–DOTA and ²²¹Fr–DOTA (much weaker for the latter), the vdW interaction significantly reduces the magnitude of E_B for ²¹³Bi–DOTA, ²¹⁷At–DOTA, and ²²⁵Ac–DOTA as compared to E_B obtained with standard DFT methods.

Table 1. Calculated E_B and averaged bond distances between metal (X) and nearest neighbor O and N atoms for DOTA complexes. Results obtained with SOC and with the vdW potential are also shown. The average ionic radius R_IS between a pair of atoms as previously reported is also given20–22 .

E B = ETOT – (EDOTA + EIS), [eV per DOTA]
Complex	Gd–DOTA	213Bi–DOTA	217At–DOTA	221Fr–DOTA	225Ac–DOTA
No SOC, no vdW	–18.03	–12.41	–6.61	–5.00	–17.47
With SOC	–18.02	–10.05	–6.45	–5.90	–17.16
With vdW	–21.22	–10.91	–5.93	–5.16	–16.70

Averaged bond length, [Å]
Complex	Gd–DOTA		213Bi–DOTA		217At–DOTA		221Fr–DOTA		225Ac–DOTA
Bonds	Gd–O	Gd–N	Bi–O	Bi–N	At–O	At–N	Fr–O	Fr–N	Ac–O	Ac–N
No SOC, no vdW	2.28	2.84	2.36	2.79	2.32	3.22	3.14	3.75	2.48	2.99
With SOC	2.26	2.76	2.32	2.72	2.32	2.79	2.61	3.02	2.47	2.95
With vdW	2.31	2.86	2.38	2.72	2.44	2.84	3.22	3.93	2.52	2.98
R IS (exp)	2.40	2.51	2.52	2.63	1.97	2.08	3.15	3.26	2.47	2.58

The nearest neighbor characteristic bond lengths involving the radioactive metallic atom are given in Table 1. When compared with the results without SOC or vdW coupling, one finds that vdW interactions increase the lengths of many bonds with the exception of Bi–N, At–N, and Ac–N. The SOC, however, typically decreases the bond lengths, except for At–O where no change is found. The largest distance changes due to SOC or vdW are in the ²¹⁷At–DOTA and ²²¹Fr–DOTA chelates. The X–O and X–N nearest neighbor distances can be compared using R_IS, which characterizes the ionic radii sum of the two atoms.20–22 R_IS specifies a condition for the possibility of forming nearest neighbor chemical connections such that X–O, X–N ≤ R_IS. Our results show that based on those criterion, the weakest interactions are found in ²¹⁷At–DOTA (weak vdW interactions and shortest bond lengths) and ²²¹Fr–DOTA (weakest vdW interactions and longest bond lengths). The results presented in Table 1 indicate that due to the lowest magnitude of E_B, ²²¹Fr–DOTA has the least stable structure followed by ²¹⁷At–DOTA. We may further infer that the relatively elongated Fr–O and Fr–N bonds (>3 Å) would allow escape of the Fr atom and possibly further destabilize the complex, while the shorter bonds in ²¹⁷At–DOTA may make such destabilization more difficult. The remaining structures appear to be relatively stable.

3.2. Chemical bonding in DOTA chelation complexes

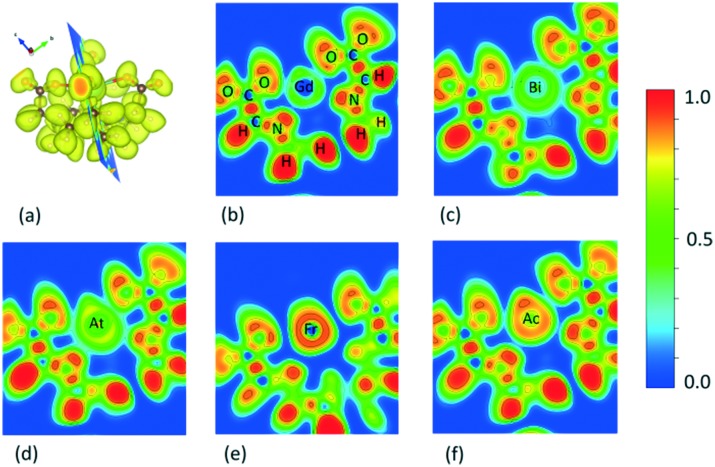
The DOTA materials are also examined in terms of their types of chemical interactions. The E_B and nearest neighbor distances suggest the following type of chemical bonds with the radionuclide: ionic for Gd–DOTA, ²¹³Bi–DOTA, ²²⁵Ac–DOTA; covalent-ionic for ²¹⁷At–DOTA; and weak intermolecular for ²²¹Fr–DOTA.47 For a more detailed analysis of the chemical bonding, the calculated electron localization function (ELF) and charge density contours were examined (Fig. 1).48–50 The ELF reflects the localization of electron density distributions with the following values: 0 ≤ ELF ≤ 1, such that 1 (red) corresponds to perfect localization, while ∼0.5 (green) corresponds to an electron gas and 0 (blue) corresponds to the absence of electron localization. Fig. 1 shows that all atoms belonging to the DOTA chelator are bound covalently as indicated by the red regions observed between the C, O, H and N atoms. However, the chemical bonding involving the radioisotopes is rather complex. The ELF for Gd (Fig. 1(b)), with an empty region in the center and three elongated green regions towards the O and N sites, suggests ionic bonding and this is also found in previous studies.31,32,51 Similar ionic bonding is found for the Bi atom (Fig. 1(c)). The yellow elongated region around At shifted towards O and N sites in Fig. 1(d) suggests higher electron density in the intersectional regions (turquoise color) indicating the possibility of electron sharing. The ELF around Ac (Fig. 1(f)) has an ionic character of bonding with electron density concentrated at the top of the radioisotope. The red well pronounced regions between Gd, Ac and N indicate a strong localization of electrons and provides evidence of electron donation from the radioisotopes to N. A quite different situation is observed for ²²¹Fr–DOTA. The absence of electrons in the regions between Fr and the surrounding atoms indicates that the radioisotope is loosely bound to the O and N sites (Fig. 1(e)), further implying low stability of the complex. Such low stability of ²²¹Fr–DOTA remains even if other DFT potentials with various valence/core electron shells are utilized.

Fig. 1. (a) The calculated ELF for DOTA. The 2D projection through the core and metallic ion of each complex follows: (b) Gd–DOTA, (c) ²¹³Bi–DOTA, (d) ²¹⁷At–DOTA, (e) ²²¹Fr–DOTA, (f) ²²⁵Ac–DOTA. The value of 1 (red) corresponds to the highest probability of electron distribution, the value of 0.5 (green) can be interpreted as an “electron gas” and the value of 0 (blue) indicates no electron distribution. The chelator H, C, N, O atoms are in the same positions for all DOTA complexes and they are shown for Gd–DOTA only. The ELF isosurface level is 0.741.

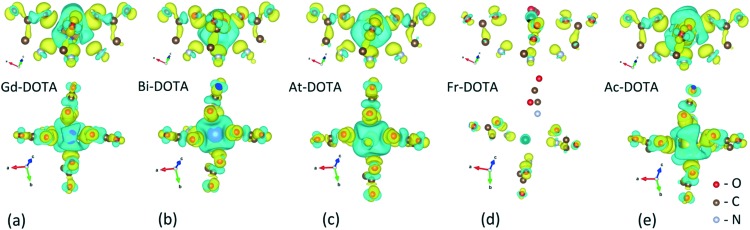
To obtain further insight into differences in the charge transfer predicted among the chelates with different radioisotopes, we present charge density differences (Fig. 2) calculated as ρ = ρ_X–DOTA – (ρ_X–DOTA + ρ_X), where ρ_X–DOTA is the charge density of the DOTA complex, ρ_DOTA is the charge density of the DOTA chelator and ρ_X is the charge density of the particular radioisotope X. Fig. 2 shows that charge transfer is observed in all DOTA complexes except in ²²¹Fr–DOTA. The localized blue regions indicate the electron depletions enveloping the metallic atoms. The yellow regions correspond to the transferred electrons found predominantly around the O and N atoms. These charge transfer profiles strongly suggest the ionic nature of bonding between the metals and the DOTA atoms. Interestingly, shared regions with accumulated electrons are found to be the greatest between the Gd or Ac metal atoms and O atoms (Fig. 2(a) and (e)) suggesting partially covalent interactions. The charge density difference for ²²¹Fr–DOTA (Fig. 2(d)), on the other hand, demonstrates the absence of chemical bonding in this complex.

Fig. 2. Side and top view representations of charge density differences among (a) Gd–DOTA, (b) ²¹³Bi–DOTA, (c) ²¹⁷At–DOTA, (d) ²¹⁷Fr–DOTA and (e) ²²⁵Ac–DOTA chelates. Yellow surfaces correspond to regions with electron accumulation, while blue surfaces correspond to regions with electron depletion. The charge density isosurface value is ρ = 3.49 × 10^–3 e Å^–3. Only ions with neighbour O, N and C atoms are shown since distant atoms are not participating in the charge transfer.

3.3. Interaction with H₂O

The interactions and exchange rates between water molecules and the DOTA complex are fundamental in order to understand the stability of ligands in serum and MRI techniques, which allow monitoring the effects of radioactivity during the diagnostic process. Specifically, the duration of longitudinal relaxation time of metallic ion has to be long enough in order to allow water proton relaxation and short enough to prevent relaxed water molecules from occupying a coordination site next to the metallic ion.29–33,52 A good understanding of the mechanisms underlying interactions between water molecules and DOTA complexes is necessary to provide the desired control of water exchange rates with MRI contrast agents for improved functionality.

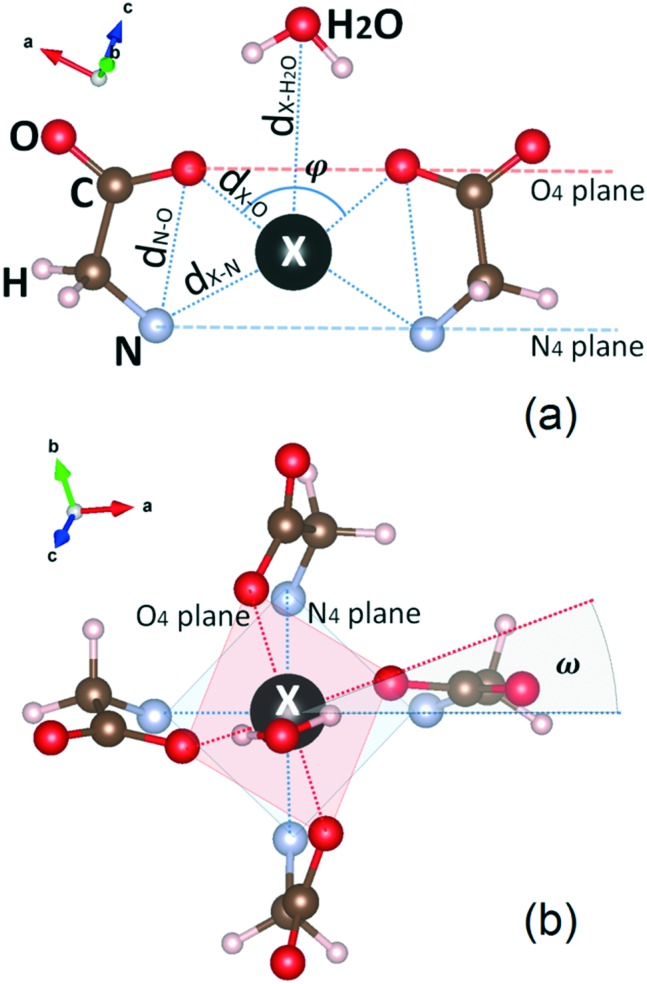
The interaction between a DOTA complex and bulk aqueous solvent is considered through the coordination environment of the central ion formed by the chelator atoms and one H₂O molecule from the inner-sphere of the bulk water.29–33 Therefore, we investigate the role of one H₂O molecule on each DOTA molecule by analyzing the computational results for various characteristic structural properties, binding energies and charge transfers. The structural properties used to describe H₂O–DOTA complexes are shown in Fig. 3. The X ion is surrounded by four oxygen atoms and four nitrogen atoms, forming two parallel O₄ and N₄ planes. The d_X–O and d_X–N distances describe the position of the X ion with respect to the O₄ and N₄ planes, d_N–O corresponds to the position of the O₄ and N₄ planes with respect to each other, and d_X–H2O corresponds to the position of H₂O with respect to X. The opening angle φ (in Fig. 3a) is defined between the X ion and the O₄ plane. The closest position of the X ion to the O₄ plane is characterized by the greatest value of φ, which also suggests a possible coordination with H₂O. The farthest location of the ion X with respect to the O₄ plane is characterized by the least value of φ. The relative twist between the O₄ and N₄ planes is described by the twist angle ω, shown in Fig. 3b.

Fig. 3. Structural characteristics of a DOTA complex coordinated with a H₂O molecule after relaxation. (a) Distances, opening angle φ and O₄ and N₄ planes are shown in this specific perspective; (b) top view showing the twist angle ω between the O₄ and N₄ planes. The radioisotope is denoted as X.

Previous studies for lanthanide containing DOTA chelators have shown that for φ > 135° the X ion becomes closer to the O₄ plane and the DOTA complex opens up for coordination with H₂O.31,53 Furthermore, these investigations showed that two types of characteristic structures exist: a square-antiprismatic isomer (SA) and a twisted square-antiprismatic isomer (TSA). These differ mainly by the twist angle, which has values of ω ∼ 40° and ω ∼ 22° for SA and TSA, respectively.32 We note that the TSA configuration is more desirable for MRI cell labeling and tracking because of its high exchange rate between the DOTA complex and water as compared to the same process involving SA configuration.29–33

For each chelate, the results from the process of applying DFT relaxation of the structural parameters to H₂O coordination are shown in Table 2. The SOC and vdW interactions have profound effects on all distances and angles. For example, the d_X–H2O is increased by 26% and ω is decreased by 32% due to the inclusion of SOC when simulating Gd–DOTA–H₂O. Other dramatic changes are found in ²²⁵Ac–DOTA–H₂O where d_X–N increases by 6% and ω decreases by 31% due to the SOC. It is notable that vdW interactions typically lead to an increase in d_X–N distances with the largest change of 6.2% for ²²⁵Ac–DOTA–H₂O, and the greatest effects are found for the angle ω showing a 20% increase for Gd–DOTA–H₂O, a 17% decrease for ²¹³Bi–DOTA–H₂O, a 26% decrease for ²¹⁷At–DOTA–H₂O, and a 39% decrease for ²²⁵Ac–DOTA–H₂O. The angle φ, on the other hand, is hardly affected. It also important to compare the calculated structural properties of ²¹³Bi–DOTA–H₂O and Gd–DOTA–H₂O DOTA with experimental data.29–31,38,54–56 For example, d_X–O = 2.537 Å, d_X–N = 2.526 Å, φ = 128°, and ω = 30° for ²¹³Bi–DOTA–H₂O according to Csajbók et al.38 The results from Table 1 shows that there is a good agreement between the distance parameters calculated with the vdW correction, however the obtained value for the twist angle is much smaller than the experimental one. For the case of Gd–DOTA–H₂O, reported experimental values range as d_X–O = 2.36–3.37 Å,30,54 d_X–N = 2.65–2.68 Å,30,54 d_N–O = 2.30–2.36 Å,31d_X–H2O = 2.38–2.56,29–31,55–57 φ = 135.9°,31 and ω = 38.5–38.7°.30,56 Since different bond lengths and angles are given in different reports the direct comparison with our calculations is difficult due to issues of consistency. Nevertheless, most bonds and the opening angles from Table 1 when the vdW correction is included show good agreement with the experimental values. The vdW dispersion is also necessary to describe accurately the H–O–H angle in bulk water. Specifically, our simulations show that the H–O–H angle is ∼104.5° upon the vdW correction as compared to standard simulations giving a value of ∼102.9° for this angle. We further note that the largest difference is the much smaller calculated twist angle ω when compared with the experiments. The fact that the main discrepancyis in ω for both DOTA complexes indicates that the particular environment has a greater effect on the twist angle rather than the other structural properties.

Table 2. Characteristic distances and angles for X–DOTA–H₂O.

X–DOTA–H2O
	Gd–DOTA–H2O			213Bi–DOTA–H2O			217At–DOTA–H2O			225Ac–DOTA–H2O
	Stand	SOC	vdW	Stand	SOC	vdW	Stand	SOC	vdW	Stand	SOC	vdW
d X–O, [Å]	2.31	2.28	2.34	2.34	2.33	2.40	2.41	2.41	2.46	2.50	2.50	2.54
d X–N, [Å]	3.01	2.80	3.02	2.66	2.67	2.68	2.73	2.74	2.77	2.92	3.09	3.10
d N–O, [Å]	2.78	2.76	2.80	2.85	2.85	2.87	2.82	2.84	2.86	2.82	2.81	2.86
d X–H2O, [Å]	2.51	3.15	2.54	3.84	4.04	3.79	3.75	3.80	3.76	2.71	2.71	2.74
φ, [°]	144.4	129.9	143.7	117.1	117.5	116.1	122.0	125.1	123.3	149.9	148.2	148.3
ω, [°]	17.8	12.1	21.5	19.0	17.8	17.7	18.1	16.7	15.4	23.8	16.6	16.8

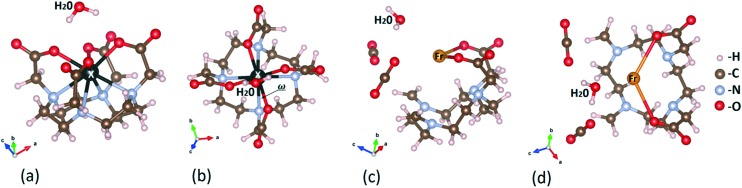
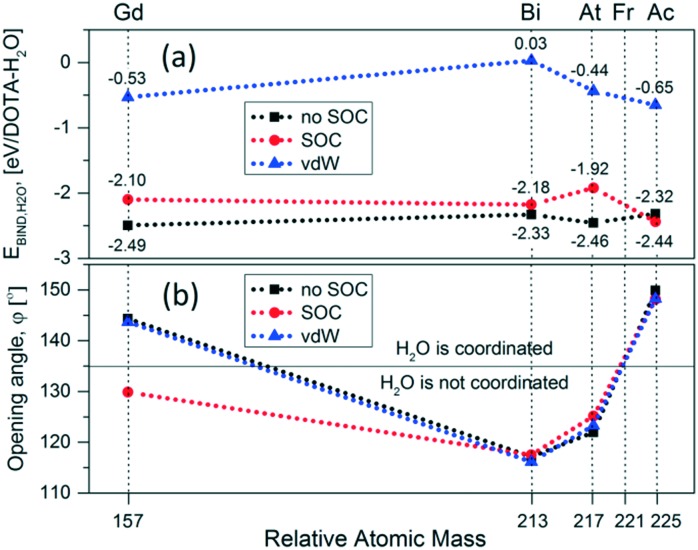
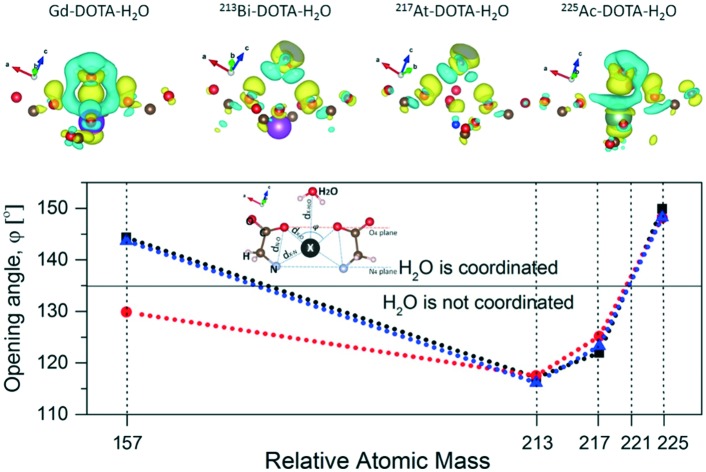
Fig. 4 provides a visual representation of the structural stability upon relaxation of the studied systems. One finds that the molecules stay intact, except ²²¹Fr–DOTA–H₂O, and they are in the TSA configuration with a twist angle ω smaller than the 22° value for the lanthanide containing DOTA chelators. A snapshot of the unstable ²²¹Fr–DOTA–H₂O system is also given in Fig. 4(c and d), showing breaking of the complex. Next, the binding energies between the DOTA complexes and H₂O were calculated as E_BIND,H2O = E_TOT+H2O – (E_X–DOTA + E_H2O), where E_TOT+H2O is the total energy of the DOTA complex and water (H₂O), where E_X–DOTA is the energy of the DOTA complex and E_H2O is the energy of the water molecule. The obtained values for E_BIND,H2O are summarized in Fig. 5(a), which suggest that the SOC and vdW interactions decrease the stability of each system except in the case of ²²⁵Ac–DOTA–H₂O, where the SOC reduces E_BIND,H2O by 0.12 eV as compared to the standard simulations.

Fig. 4. The relaxed structure of X–DOTA–H₂O for (a) side and (b) top views. Snapshots of the structural relaxation of ²²¹Fr–DOTA–H₂O shown for (c) side and (d) top views. ²²¹Fr–DOTA–H₂O is not stable.

Fig. 5. Calculated (a) E_BIND,H2O and (b) opening angle φ shown vs. the relative atomic mass of the radioactive isotope in each DOTA molecule. The horizontal line in panel (b) denotes the critical value above which water coordination in lanthanide containing DOTA chelators is possible.

Next, the binding energies between the DOTA complexes and H₂O were calculated as E_BIND,H2O = E_TOT+H2O – (E_X–DOTA + E_H2O), where E_TOT+H2O is the total energy of the DOTA complex and water (H₂O), where E_X–DOTA is the energy of the DOTA complex and E_H2O is the energy of the water molecule. The obtained values for E_BIND,H2O are summarized in Fig. 5(a), which suggest that the SOC and vdW interactions decrease the stability of each system except in the case of ²²⁵Ac–DOTA–H₂O, where the SOC reduces E_BIND,H2O by 0.12 eV as compared to the standard simulations. In particular, E_BIND,H2O = –0.53 eV (51.14 kJ mol^–1) for Gd–DOTA–H₂O was found to be in good agreement with the experimentally reported value of 49.8 ± 1.8 kJ mol^–1.30,55 One further notes that due to the smaller opening angle (φ = 120.1°) and the longer ²¹³Bi–H₂O distance (d_X–H2O = 3.79 Å), ²¹³Bi is located deeper in the DOTA environment and as a result does not interact with water (E_BIND,H2O = 0.03 eV). This observation coincides with earlier experimental measurements, where no water in the inner coordination sphere was found.38 Here it is important to note that all obtained results for binding energy of coordinated H₂O with DOTA complexes are found to be in the range of (–0.7, –0.4) eV. These values are typical for interaction energies between ions and solute atoms.47,58 Thus one may conclude that the over-stabilization of the bond energies that result from use of standard simulations, or simulations that include SOC, may not be realistic.

These findings can also be compared with the results for the opening angle φ shown in Fig. 5b. It is interesting to note that φ = 143.7° and φ = 148.3° with vdW interactions taken into account for Gd–DOTA–H₂O and ²²⁵Ac–DOTA–H₂O, respectively. The fact that the complex opening angles are greater than the threshold set by lanthanide containing DOTA chelators31,32 and the relatively larger E_BIND,H2O (with vdW interactions) indicate that H₂O coordination is possible in these cases. However, the deeper location of Bi in the DOTA cavity, characterized by φ = 116.1° < 135°, and the positive E_BIND,H2O together show that H₂O most likely interacts very weakly or not at all with ²¹³Bi–DOTA. In the case of ²¹⁷At–DOTA, E_BIND,H2O is relatively strong, however φ = 123°, which is below the threshold value of φ = 135°.

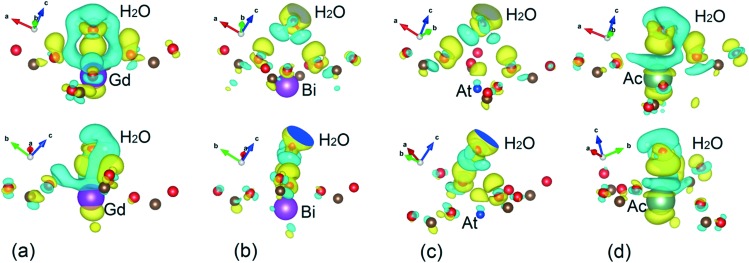
To understand the bonding characteristics between X–DOTA and H₂O, the charge density differences for each case are calculated as ρ_B,H2O = ρ_TOT,H2O – (ρ_X–DOTA + ρ_H2O) where ρ_TOT,H2O is the charge density of the DOTA complex coordinated with H₂O, ρ_X–DOTA is the charge density of the standalone DOTA complex and ρ_H2O is the charge density of H₂O. The obtained results are shown in Fig. 6 and they represent the charge transfer from the interstitial regions with depleted electrons (blue isosurfaces) to the regions with accumulated electrons (yellow isosurfaces). The charge transfer mechanisms in Gd–DOTA–H₂O and ²²⁵Ac–DOTA–H₂O are rather complex and consist of two types of interactions: dipole–dipole and ionic charge transfer. The ellipsoid-like blue isosurfaces localized at the tops of Gd, Ac and H₂O and yellow isosurfaces at the bottoms of Gd, Ac and H₂O represent the dipole–dipole charge density distribution (Fig. 6(a) and (d)). The interstitial regions (blue) between Gd, Ac and nearest O atoms (O₄ plane) and yellow isosurfaces around the same nearest O atoms indicate that ionic charge transfer is the primary interaction. Taking into account the E_BIND,H2O for these complexes one can suggest that there is a strong ion-dipole interaction between (Gd,²²⁵Ac)–DOTA and H₂O.

Fig. 6. Side views of charge density difference between H₂O and (a) Gd–DOTA, (b) ²¹³Bi–DOTA, (c) ²¹⁷At–DOTA and (d) ²²⁵Ac–DOTA. Yellow surfaces correspond to regions with accumulated electrons while blue surfaces correspond to regions with depleted electrons. Only atoms involved in the charge transfer process are shown in the depicted DOTA complexes. The isosurface value is ρ = 0.91 × 10^–3 e Å^–3.

The situation for ²¹⁷At–DOTA–H₂O and ²¹³Bi–DOTA–H₂O is quite different. Firstly, the water molecule is inverted and its H atoms are directed towards the O₄ plane forming a dipole–dipole like arrangement in both complexes (Fig. 6(b) and (c)). Secondly, in contrast with Ac and Gd, we observe that the isosurfaces with depleted charges around radioisotope is negligible for the At complex and factually absent for the Bi complex. Third, the presence of empty regions between H₂O and the O₄ plane indicate a weak interaction between H₂O and the complexes. In fact, this interaction for ²¹⁷At–DOTA–H₂O is carried out only by charge transfer between H₂O and the nearest O. Taking into account the E_BIND,H2O one can conclude there is a dipole–dipole interaction in ²¹⁷At–DOTA–H₂O. On the other hand, there is practically no chemical interaction ²¹³Bi–DOTA–H₂O. The latter results suggest the poor aqueous solubility of ²¹³Bi–DOTA. We conclude by noting that in recent studies57,59 authors have brought the importance of simulating more than one water molecule coordinating the chelators to compare with experimental data. Since these studies do not take into account relativistic effects from the SOC and dispersion from the vdW interaction, it is not clear if more than one coordinating water molecules are needed.

3.4. Recoil energy

In addition to the structural stability of the ²²⁵Ac radioisotope in the DOTA complex, we have examined the recoil energy due to the nuclear decay process. The recoil energy E_R for the daughter nuclei is estimated from the kinematic non-relativistic expression E_R = Q_αm_α/(m_D + m_α), where m_α is the mass of the α-particle, m_D is the mass of the daughter product and Q_α is available from National Nuclear Data Center.45,46 The E_R values for the ²²¹Fr, ²¹⁷At and ²¹³Bi daughter products are found to be 103.64 keV, 114.78 keV and 130.30 keV respectively. Considering classical mechanics, the magnitude of E_R in keV indicates that the chemical bonds in the DOTA chelator will likely be damaged due to the ballistic recoil process. However, from the quantum mechanical view,28 this interpretation must be reconsidered. From this perspective the recoil energy would be most probably transferred to excitation of the daughter nucleus as was shown by A. Migdal for beta decay.60 In terms of recoil energy, we hypothesize that it is possible that the daughter isotope will remain in the chelator and that the chelator will remain intact. Except that there is the possibility that α emissions could damage some percentage of the chelators and set the atoms free. Hence, this is a complex problem and further investigation is required.

4. Conclusions

In summary, of the DOTA chelation complexes containing the initial ²²⁵Ac radioactive decay daughter products, the ²²¹Fr–DOTA–H₂O complex is found to be least stable. The ²¹³Bi–DOTA molecule was shown to not be coordinated with H₂O, which is in agreement with earlier reported observations about its low solubility in water.61 Further, it was determined that the DOTA chelator has the strongest binding to the parent radionuclide, ²²⁵Ac, which is the most favorable complex for the TSA coordination with H₂O, and this observation is in agreement with previous studies.59,62 Recoil energies were calculated based on classical mechanics principles. However, since α decay recoil energy is a quantum mechanics problem, it is not a certainty that recoil energy will result in dislocation of daughter isotopes from the chelator or result in destruction of covalent bonds in the parent DOTA chelator. Our studies constitute an important step forward towards understanding processes governing the stability and interactions of relatively unexplored DOTA complexes, particularly for α-emitting radionuclides with complex decay chains that have potential applications for development of novel cancer treatments. The presented results will be invaluable for guiding and interpreting future empirical to investigate the structural integrity of these materials in various environments.

Conflicts of interest

The authors declare no competing interests.