Fluorescence anisotropy imaging in drug discovery

Abstract

Non-invasive measurement of drug-target engagement can provide critical insights in the molecular pharmacology of small molecule drugs. Fluorescence polarization/fluorescence anisotropy measurements are commonly employed in protein/cell screening assays. However, the expansion of such measurements to the in vivo setting have proven difficult until recently. With the advent of high-resolution fluorescence anisotropy microscopy it is now possible to perform kinetic measurements of intracellular drug distribution and target engagement in commonly used mouse models. In this review we discuss the background, current advances and future perspectives in intravital fluorescence anisotropy measurements to derive pharmacokinetic and pharmacodynamic measurements in single cells and whole organs.

Graphical abstract

1. Introduction

For a drug to become successful clinically it must produce a desired therapeutic effect at no, or only minimal and acceptable, toxicities. To better understand drug effects (or the lack thereof) in vivo it is highly desirable to directly measure drug-target engagement in single cells as well as in populations of cells making up tissues and organs [1]. Conventional pharmacology and most pharmacokinetics/pharmacodynamics (PK/PD) studies rely on bulk sampling of tissue or plasma where subtle nuances can be easily missed or “diluted out”. Conversely, in vitro assays against purified targets lack the barriers, pressures and effects that drugs face in vivo. Furthermore, even genetically identical cells are often heterogenous and these effects are difficult to model in vitro.

A number of recent technologies have been described to directly measure drug binding in cells. Among them are the drug affinity responsive target stability (DARTS) assay [2], competitive positron emission tomography (PET) [3, 4], or mass spectroscopy imaging (MSI) [5, 6]. All of these methods have inherent limitations with respect to cellular resolution (PET), subsequent analysis (MSI) or others.

The cellular thermal shift assay (CETSA) [7] has also been used to determine target engagement of unlabeled drugs in specimen as well as in vivo, and to measure off-target binding of thousands of proteins using mass spectrometry [8]. However CETSA yields average measurements of cell populations and temporal resolution is limited.

Fluorescence polarization (FP) and fluorescence anisotropy (FA) [9] are powerful fluorescence-based techniques originally employed as screening tools in the drug discovery field and in biomedical settings for measuring equilibrium binding, molecular interactions and enzymatic activity [10, 11]. The two techniques are interrelated and nearly equivalent, with FA preferably more used due to its intrinsic mathematical simplicity. The principle of FP/FA is based on the fact that the degree of anisotropy of a fluorophore, at constant temperature and solution viscosity, is inversely related to its molecular rotation and directly related to its apparent molecular weight which changes upon complex formation. Binding and dissociation constants between a target and a fluorescently labeled drug can then be measured by reading the value of fluorescence anisotropy of the small molecule.

FP/FA is an “intensive property”, i.e. independent on the amount of fluorophore [12]. Therefore FP/FA assays are inherently separation-free homogeneous assay, because they offer the ability to make quantitative measurements without a separation step i.e. without removing one of the components from the solution. Thanks to these features the current FP/FA methods have enjoyed wide distribution to study protein-ligand and protein-protein interactions [13, 14] and to determine the fraction of bound vs. free ligand for resolving their dissociation constants [12, 15, 16]. FP/FA have also been used in assays to enable high-throughput screening of small molecule libraries for drug discoveries [17].

Optical imaging technologies offer high spatial and temporal resolution, extended penetration depth, and the ability to distinguish multiple reporter. They are therefore the ideal detection technologies for in vitro and in vivo single-cell phenotypic screening [18]. Their availability concurrent with the emergence of a growing list of fluorescent drug derivatives that maintain comparable target specificity and affinity as the unlabeled drug [19], has enabled direct insight into drug delivery and drug action in vitro and in vivo, including target-selectivity, kinetics, drug exposure and resistance, and pharmacodynamics effects [20–24].

By extending FP/FA to optical microscopy imaging modalities, in combination with measurements of fluorescence intensity, and co-localization with fluorescent reporter proteins, we have demonstrated that one can obtain spatially and temporally resolved cellular mapping both in vivo and in vitro, enabling insights into the degree of drug accumulation within individual cells, the quantification of drug target expression, and the degree of specific drug-target binding and unspecific binding to off-target proteins [20, 22, 23, 25–34]. While live animal imaging at microscopic resolution is mostly performed by confocal or two-photon laser scanning microscopy, the latter is usually the preferred method of choice [35–39] and this is the modality we have been focusing in our studies.

The extended fluorescence anisotropy spatiotemporal resolution in combination with the fast acquisition speed, also allows for adaptation to high content screening in cell based assays [40]. Automated image-based analysis [41], can then be seamlessly conducted over large populations of single cells.

This review is intended to provide a general overview of fluorescence anisotropy and fluorescence anisotropy imaging, to describe the main sources of errors involved in the acquisition procedures and how these reflect on the measured fluorescence anisotropy, to illustrate the image processing methods and hardware designs, and to highlight the potential of two-photon fluorescence anisotropy imaging for drug-target engagement measurements.

2. Fluorescence anisotropy basic principles

2.1 History

Uneven fluorescence intensities along coordinate axes were first described by F. Weigert in 1920 [42]. This phenomenon has been called fluorescence polarization. Theories of fluorescence polarization were subsequently developed by Vavilov [43], Lewshin [44] (who also collected excessive experimental data), Jablonski [45, 46] and F. Perrin [47, 48] in 1920’ and 1930’.

The concept of fluorescence anisotropy was later introduced by A. Jablonski in 1957 [49] and the advantages of this notation were described by him in 1960’ [50, 51]. In the following years others started using the term fluorescence anisotropy. Although fluorescence polarization and fluorescence anisotropy can be used alternatively, the later seems to be more correct because describes the radiation field rather than just an incoming light. Also equations involved in the theory of fluorescence polarization become incomparably simpler when anisotropy notation is being used. Therefore, now most researchers use the fluorescence anisotropy notation. More detailed history of fluorescence polarization/anisotropy can be found in [52–58].

2.2 Definitions

With vertically polarized excitation (Fig. 1c) the fluorescence from a fluorescent sample (Fig. 2a,b) is observed through either vertically (parallel) or horizontally (perpendicular) oriented polarizer providing I_VV and I_VH fluorescence intensities, respectively. These usually uneven intensities can be described by the “fluorescence polarization” parameter p defined as:

$$p=\frac{(I_{VV}-I_{VH})}{(I_{VV}+I_{VH})}$$ (1)

Figure 1. Fuorescence anisotropy fundamentals.

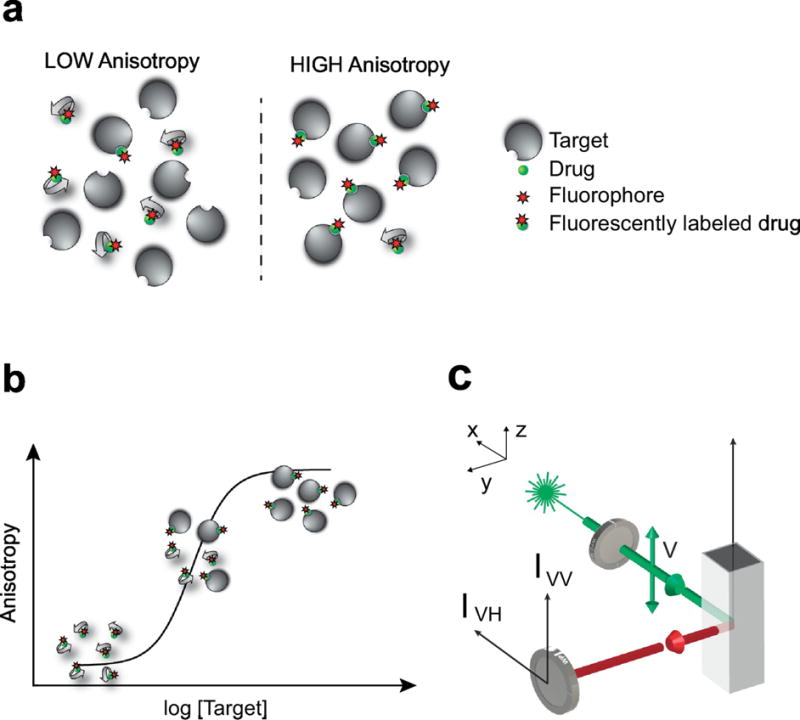
(a) Upon binding to its target, the fluorescently labeled small molecule drug presents an increase in anisotropy. (b) Titration and measurements of fluorescence anisotropy, enable accurate reconstruction of binding isotherms. (c) Standard optical arrangement for measurements of fluorescence anisotropy. The subscript letters V and H, stand for vertical and horizontal. The first subscript, indicates the direction of polarization of the excitation light. The second subscript, indicates the direction of polarization of the emission polarizer. Adapted with permission from [255], Nature Publishing Group.

Figure 2. One-photon and Two-photon fluorescence anisotropy.

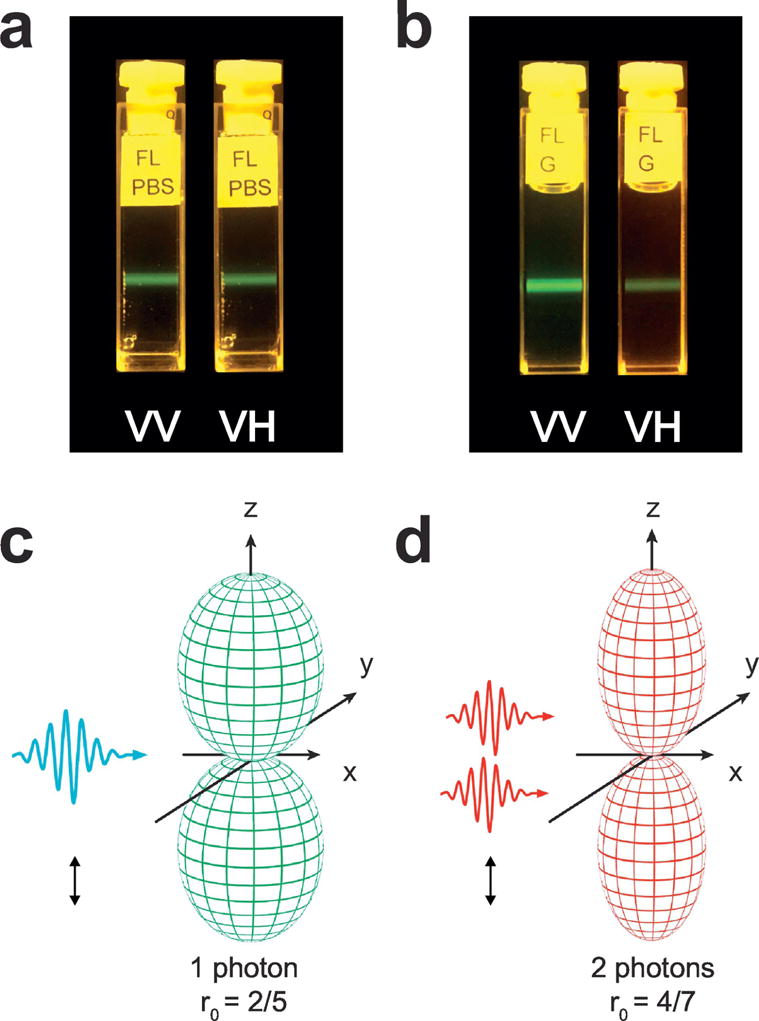
Images of fluorescence anisotropy for fluorescein. (a) In PBS, the rotational diffusion of the excited molecules is occurring on a time scale shorter than the fluorescence lifetime, and tends to scramble the orientation of the emission dipoles. No preferential emission direction is present. (b) In glycerol, the molecular rotation is occurring on a time scale slower than the fluorescence lifetime. A strong degree of fluorescence emission anisotropy is present. (c,d) Photoselection function for one- (a) and two-photon (b) excitation. The one-photon fundamental anisotropy is equal to 2/5. The two-photon fundamental anisotropy is higher and equal to 4/7, due to two-photon photoselection. Adapted with permission from [255], Nature Publishing Group

Considering that the fluorescence radiation has a cylindrical symmetry (with vertically polarized excitation) with two equal horizontal components, the total fluorescence intensity can be expressed by:

$$I_T=I_{VV}+2\cdot I_{VH}$$

and the fluorescence radiation can be characterized by a ratio called “fluorescence anisotropy” r defined as:

$$r=\frac{(I_{VV}-I_{VH})}{I_T}=\frac{(I_{VV}-I_{VH})}{(I_{VV}+2\cdot I_{VH})}$$ (2)

If we define a ratio Λ:

$$\mathrm{\Lambda }=\frac{I_{VV}}{I_{VH}}$$

the fluorescence anisotropy can be described with only one value of the ratio Λ:

$$\mathrm{r}=\frac{(\mathrm{\Lambda }-1)}{(\mathrm{\Lambda }+2)}$$

which sometimes can be convenient. For example Λ = 3 corresponds to r = 0.4, Λ = 2 corresponds to r = 0.25, and Λ = 1 gives r = 0. With a simultaneous measurement of both polarized components, the ratio “Λ” can be quickly calculated and used for calculation of anisotropy.

2.3 One-photon steady state and time-resolved anisotropy

2.3.1 Limiting and fundamental fluorescence anisotropies

In the following discussion we are assuming a random (isotropic) distribution of dye molecules in the ground state. With vertically polarized excitation, dye molecules with transition moments oriented along the vertical axis will be more likely excited. The effectiveness of the excitation depends on the angle θ between the dye transition moment and the light electric vector (in this case the vertical axis). The probability of the excitation is dependent on cos²θ, similar to the intensity of the light transmitted through the polarizer (Mallus law). Molecules with transition moments oriented (at the time of the excitation) along the horizontal axis will not be excited. The distribution of transition moments of the excited molecules is not isotropic, see Fig. 2c,d. The process of creation of an anisotropic distribution of transition moments by the excitation light is called photoselection. In the case of one photon excitation it is a cos²θ photoselection. In the absence of any depolarizing processes the value of fluorescence anisotropy with one photon excitation by linearly polarized light is called fundamental fluorescence anisotropy and is given by:

$$r_F=0.6\cdot (co{s}^2\beta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.)$$

where β is the angle between the absorption and the emission transition moments. Possible values of fundamental fluorescence anisotropies are within the range:

$$-0.2\le r_F\le 0.4$$

and its derivation (first done by F. Perrin for polarization notation [48]) can be found in most textbooks on this topic [57, 58]. In practice, one never observes one photon fluorescence anisotropies of 0.4. This is because even in rigid or frozen solutions torsional motions of molecules are possible [53, 55, 56, 59] and emission transition moments may slightly differ from absorption. Although this is a minor depolarizing factor comparing to Brownian rotation it lowers the fluorescence anisotropy from the maximum theoretical value. The highest measured value of fluorescence anisotropy, free of Brownian rotations is called the limiting fluorescence anisotropy r₀. The limiting anisotropy can be close, but never reaches 0.4. An example of steady-state anisotropy measurements (emission and excitation spectra) is presented in Figure 3. It is clear that fluorescence anisotropy strongly depends on the combination of excitation/emission wavelength. For example, the excitation of rhodamine 6G below 420 nm will result in a very low limiting anisotropy (see Figure 3A).

Figure 3. Fluorescence anisotropy spectra.

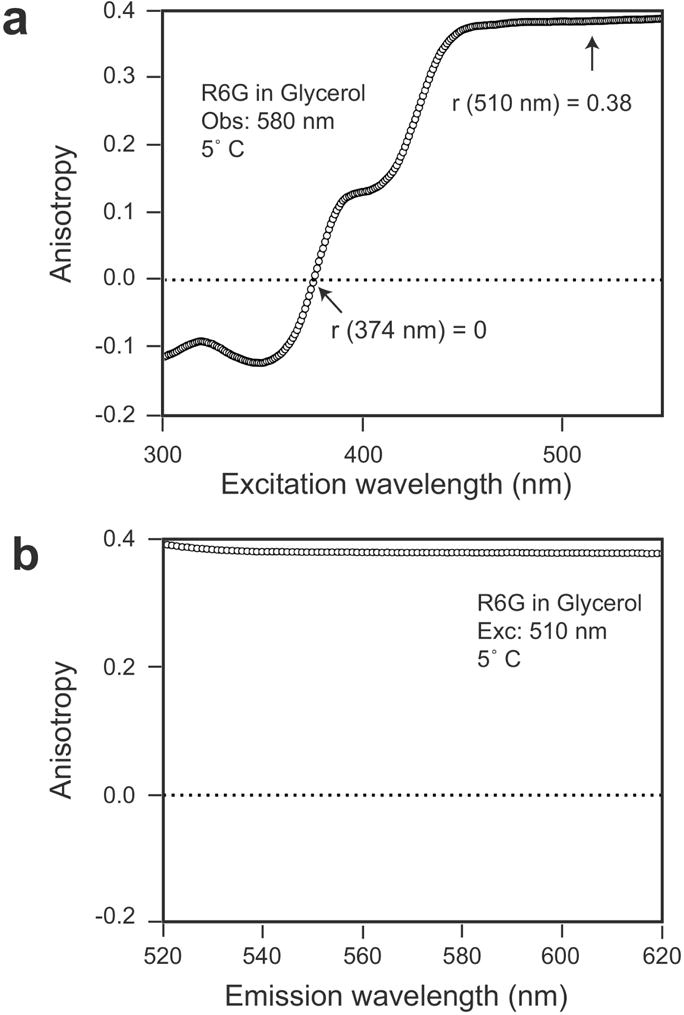
Fluorescence anisotropy spectra.of rhodamine 6G. (a) in excitation wavelengths, (b) in emission wavelengths. Note that at 350 nm (below 375 nm) the fluorescence anisotropy of rhodamine 6G is negative which indicates excitation to higher electronic state with perpendicular orientation of absorption transition moment.

2.3.2 Perrin equation

In homogenous solutions or intracellular environments, the rotational diffusion of the excited molecules tends to scramble the orientation of their transition moments during the lifetime emission of the fluorophores. As a result there is a loss in the preferential direction of the emitted fluorescence [58]. If tumbling of the molecule occurs on a time scale which is shorter than its fluorescence lifetime, the fluorescence emission will be isotropic with a value of anisotropy equal to zero. However, if molecules rotate on a time scale much slower than the fluorescence lifetime, fluorescence emission will present a strong preferential direction of emission, with a high value of anisotropy. Therefore, the observed steady-state fluorescence anisotropy r will depend, among other depolarization factors which are present during the timescale of the excited molecule lifetime, on the rotational diffusion of the excited dye.

This dependence, derived originally in polarization notation by F. Perrin [51, 52, 57, 58, 60], has a remarkably simple form in anisotropy notation, similar to the Stern-Volmer equation for fluorescence quenching [57, 58, 60].

$$\raisebox{1ex}{$r_0$}\!\left/ \!\raisebox{-1ex}{$r$}\right.=1+\raisebox{1ex}{$\tau $}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Theta }$}\right.$$ (3)

where r₀ is the limiting anisotropy, τ is the lifetime of the dye and Θ is the correlation time of the rotational diffusion. Θ here is given by:

$$\mathrm{\Theta }=\raisebox{1ex}{$\eta V$}\!\left/ \!\raisebox{-1ex}{$kT$}\right.$$ (4)

where η is the viscosity, k is the Boltzmann constant and V is the molecular volume (sphere approximation) of the rotating object (dye or dye conjugate).

The Perrin equation enables direct description of the viscosities of different media or the local viscosity of the cytoplasm [61, 62], and more importantly anisotropy–based assays.

It’s worth highlighting that in principle cellular environmental factors such as the cellular pH and the temperature may affect the values of τ and Θ respectively. However, in practice the anisotropy of a fluorescent molecule is largely defined by its fundamental anisotropy value, its molecular size and its fluorescence lifetime. Therefore for dyes with different values of lifetimes this characteristic allows for example to simultaneously resolve spectrally similar fluorophores [63, 64].

2.3.3 Additive property of fluorescence anisotropy

The benefits of the anisotropy notation is probably best illustrated when dealing with the fluorescence emission occurring from a mixture of multiple species of fluorophores. In this case the observed total anisotropy r_T is the sum of the anisotropies of the individual N fluorophores weighted by their fractions [50, 65–67]:

$$r_T={\displaystyle \sum _1^N{r}_i\cdot f_i}$$ (5)

where r_i is the anisotropy of the i-th individual specie and f_i is its fraction.

It should be noted that fluorescence polarization is not additive and derived equations have monstrous forms. The additive property of fluorescence anisotropy gives the possibility to resolve complex spectral properties and/or eliminate an undesired background. Additionally, its simple form allows to easily obtain an immediate resolution of freely rotated and bounded fluorophores.

2.3.4 Fluorescence anisotropy with excitation by unpolarized (natural) light

The excitation by unpolarized light might be considered as a composition of a simultaneous excitation by vertically and horizontally polarized lights with equal contributions. In such a case, the observed fluorescence anisotropy r_N will be given by:

$$r_N=0.4\cdot \left(\frac{1}{2}\right)+0\cdot \left(\frac{1}{2}\right)=0.2$$

This means that anisotropy measurements can also be carried with unpolarized light, however sacrificing the initial limiting anisotropy.

2.3.5 Anisotropy decays

For illustration, we consider an isotropic solution of a fluorophore excited by vertically polarized light pulses, much shorter in duration than the fluorophore’s lifetime. Immediately after a short excitation pulse the anisotropy is high (close to 0.4) but decreasing, as a function of time, to zero. The rate of this decrease is viscosity dependent and is governed by a Perrin equation. For anisotropy decay measurements, usually both polarized fluorescence intensity components (I_VV and I_VH) are measured and the anisotropy is calculated at any time of the decay. The analysis of the fluorescence anisotropy decay usually assumes an exponential decay:

$$r(t)=r_0\cdot \exp \left(-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Theta }$}\right.\right)$$

and rarely more exponentials are needed to fit the anisotropy decay of the individual fluorophore. In the case of macromolecules (labeled with dyes or with an intrinsic dye) the anisotropy decays need to be fitted to more complex models [57, 58]. An example of simple fluorescence anisotropy decay is shown in Fig. 4, where the polarized fluorescence intensity decay components of Rhodamine 110 in propylene glycol are shown with the corresponding anisotropy decay.

Figure 4. Fluorescence anisotropy decay.

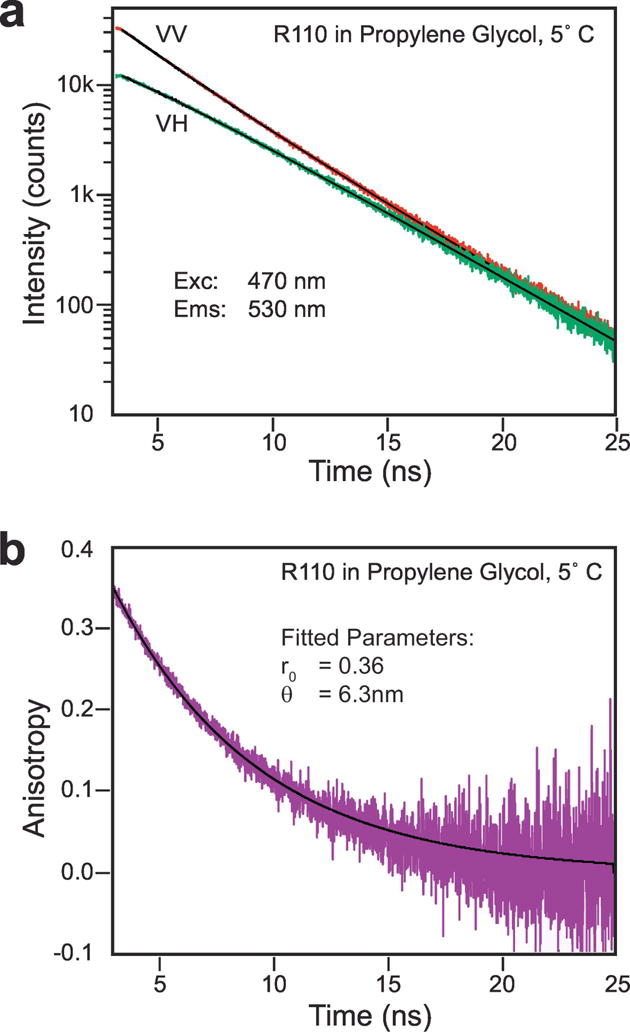
Time-domain measurements of a fluorescence anisotropy decay of rhodamine 110 in propylene glycol. (a) Fluorescence intensity decays of polarized components, (b) calculated anisotropy decay.

2.3.6 Associated anisotropy decays

The anisotropy decay measurements get more complicated when more than one fluorescent species is present in the solution. For example, during binding studies of fluorescent probes to macromolecules (protein, DNA, membrane), often unbounded fluorophores are also present. These free fluorophores rotate fast and usually have shorter lifetime than the fluorophores bounded to the macromolecules.

In this case two fluorescent species are effectively present in the studied sample: short lived and fast rotating (free) and longer lived slow rotating (bound). At the moment of the excitation by the short-light pulse the measured fluorescence anisotropy (combined from fractions of both species) will be high, close to 0.4. Shortly after the excitation the fraction of the shorter-lived specie significantly decreases lowering the measured anisotropy. Over time, the contributing fraction of the longer-lived specie will increase. In effect, the observed anisotropy initially will rapidly decreases than increases and finally decreases again with the rate corresponding to the slower rotating specie. Such anisotropy decay is called associated [58]. These unusual anisotropy decays were reported by many authors [68–70].

The associated anisotropy decays directly report on the amount of bound/unbound fluorophore fractions.

2.4 Two-photon fluorescence anisotropy

2.4.1 Simultaneous multi-photon excitation

Although theoretically predicted almost 90 years ago by M. Goppert-Mayer [71], two-photon excitation was experimentally observed after the first lasers were developed [72]. Theoretical studies of two-photon absorption and anisotropy, shortly followed [73–76].

The fundamental anisotropy with two-photon excitation is 4/7 (compared to 0.4 for one-photon excitation). This is a result of a higher photoselection for two-photon absorption process. The probability of the two-photon excitation is no longer proportional to cos² θ but instead is proportional to cos⁴ θ. The distribution of transition moments of the molecules excited by two-photon process is narrower than when excited with one-photon, see Fig. 2d. Experiments and theoretical descriptions of two-photon induced fluorescence anisotropy were reported more than two decades ago [77–80]. Shortly after, with the advance of the femtosecond lasers, three- and four-photon experiments have been also reported [81–86]. These follow cos⁶ θ and cos⁸ θ photoselection rules, and result in 2/3 and 8/11 fundamental anisotropies, respectively.

To note that the time-resolved (anisotropy decay) experiments with multi-photon excitation are similar to the one-photon ones, but offer higher resolution because they start with higher initial anisotropy values. Clearly these experiments can be done either in the time-domain or the frequency-domain formats [87, 88].

2.4.2 Two-color two-photon excitation

Two-photon excitation is also possible with synchronous illumination with two different colors of the light [89]. This excitation also follows cos⁴ θ photoselection with the fundamental anisotropy of 4/7. Unique features of two-color two-photon excitation are the possibility to adjust fundamental anisotropy [90] and reduce fluorescent backgrounds [91].

2.5 Depolarization factors

The experimentally measured values of anisotropy are usually lower than the fundamental values predicted by the theory, due to several “depolarization factors” d occurring during the lifetime of the excited molecule. According to the Soleillet’s rule [55, 92], the measured value of anisotropy r_d is equal to the product of the different depolarization factors occurring in a sample during a measurement, times the fundamental anisotropy value:

$$r_d=r_f{\displaystyle \prod _1^N{d}_i}$$ (6)

where d_i is the i-factor contributing to the depolarization.

Among the possible causes of depolarization the most important are the ones due to the instrumental effects, to the scattering, the orientation angle between absorption and emission dipoles, the molecular rotation occurring during excitation and emission, and Förster resonance energy transfer (FRET) induced effects. The first depolarization source is related to the imaging platform, the quality of the optical alignments between the different components and the optics utilized. The second depolarization source instead is related to the intrinsic properties of the fluorophore. The excitation at shorter wavelengths to the higher electronic state often occurs along an orthogonal absorption dipole moment which results in lower, sometimes negative anisotropy, see Section 2.3.1. The third source of depolarization, scattering, is related to the environment where the signal is generated and can detrimentally affect in vivo measurements in tissue. While important and not negligible, these three factors are not particularly revealing of any properties of the cellular environments. The dominant depolarization processes are usually the rotational diffusion of the fluorescent molecules which changes the direction of their transition moments, and FRET-induced effects [93, 94].

3. Fluorescence polarization/fluorescence anisotropy assay

In this Section we outline some considerations regarding the design of fluorescently labeled compounds. We consider how optimized compounds can be utilized in the context of high throughput and high content screenings.

3.1 Design of fluorescently labeled compounds

The development of a fluorescently-tagged small molecule reporter is critical for any FP/FA assay. Like a small molecule probe compound, the fluorescent tracer needs to be “fit-for-purpose”, i.e. it must satisfy several criteria, which depending on the specific application, can be more or less stringent [95, 96].

The canonical design scheme can be described as a pharmacophore-linker-fluorophore structure. Ideally the linker and fluorophore do not alter the selectivity, potency and physicochemical properties of the tracer molecule compared to the parent compound. This, of course, is almost impossible to accomplish and therefore care has to be taken when validating a tracer molecule for any given application.

In the following we will break down the important aspects that need to be considered, such as the choice of the bioactive small molecule, the linker attachment site, the type and length of the fluorophore, and the physical properties and target into several categories discussing them separately.

In general, the development takes a pragmatic approach that aims to synthesize a suitable fluorescent tracer in a few steps, often starting from the bioactive small molecule of interest. This ideally features functional groups which can be readily modified without loss of activity or change of selectivity.

The binding of a (fluorescently-tagged) small molecule ligand to its target(s) (Fig. 1a) follows a second order process, which qualitatively means that the higher the affinity of a ligand for a given protein and the more abundant the protein, the higher the ratio of bound vs free ligand will be, and consequently the better the signal to background. It follows that low affinity compounds are generally not suited for the development of fluorescent tracers for FP/FA assays. This is particularly true for fluorescence anisotropy imaging approaches where the abundance of the intracellular target is often much lower compared to biochemical assays. As a general rule of thumb, ligands with low nanomolar dissociation constants are well suited, and also higher affinity ligands allow for a wider range of resolvable inhibitor potency [97]. A second, and often overlooked, property of a small molecule ligand/target pair are the binding kinetics [98–100]. Many small molecules do not follow Michaelis-Menten kinetics, which assume that the equilibrium between free and bound form is reached quickly, but are characterized by slow binding and long target residence time. While this can be acceptable for biochemical assays such as illustrated for geldanamycin and HSP90, which take several hours to reach equilibrium, such ligands are not suitable to study the dynamic processes in live cells [101]. In particular, very high affinity ligands often have long target residence times once engaged with the target, which makes it difficult to use them in a competition assay with unlabeled drugs.

Concerning the fluorescent reporter, this is generally tethered to the bioactive small molecule via a short linker. Ideally the linker is just long and flexible enough to not interfere with the binding of the ligand but sufficiently short and rigid to limit the independent rotation of the attached fluorophore [102–104]. Longer linkers, such as oligo-PEG chains, which are often used to immobilize small molecule ligands on solid support for affinity pulldown experiments, do not restrict the rotational freedom of the fluorescent dye once the tracer is bound to the target. This phenomenon is often referred to as “propeller-effect” and results in dispersion of the fluorescence anisotropy similar to free tracers, making the bound and unbound compounds indistinguishable. Identifying a suitable attachment site that doesn’t perturb the biological activity of the ligand of interest is also critical. In some serendipitous examples, the ligand features a functional group, such as a primary or secondary amine, carboxylic acid, primary alcohol or thiol that allow for the specific conjugation of the linker using mild and selective coupling conditions. However, more often than not these functional groups are required for the biological activity or, in case of rationally developed drugs, have been introduced to optimize drug metabolism and pharmacokinetics (DMPK) properties [105]. Changing the nature of these functional groups by linker attachment can negatively impact the pharmacology, which is important for in vivo applications. Therefore, it is often required to modify the compound of interest semi-synthetically or to synthesize derivatives. In particular, the availability of co-crystal structures with the ligand bound to its target and/or published SAR studies facilitate the identification of promising attachment sites and synthetic strategies.

Previously, most approaches utilized conjugation methods that involved the reaction of an amine with an activated ester or isothiocyanate, sometimes requiring orthogonal protection of other functional groups [106]. However, in recent years the development of robust and selective bio-orthogonal conjugation chemistries, which are often referred to as click-chemistry, has expanded our toolbox with many alternatives that are highly selective, high yielding, clean, efficient and compatible with a wide range of functionalities [107]. In addition, the increased commercial availability of corresponding building blocks has significantly facilitated the adaptation of these methodologies.

The fluorophore choice is also critical for the successful development of a sensitive tracer molecule for fluorescence polarization measurements. Many fluorophore classes covering the entire visible and near IR spectrum have been developed [108–110]. However, not all fluorophores are suited for FP/FA applications. As discussed in Section 7.3.1 in greater detail, the fluorescence lifetime has to match the rotational correlation time of the target in order to achieve the best sensitivity [111]. Additional important characteristics are the brightness, which is defined as the product of absorbance coefficient at the excitation wavelength and the quantum yield (i.e. how much of the excitation light is emitted as fluorescence), of the respective fluorophore [112]. While the absorbance coefficient is generally less sensitive, the quantum yield can vary greatly depending on the polarity and nature of the environment (e.g. solvent or cellular localization) [112]. Often the quantum yield is determined in organic solvents like methanol and chloroform, largely due to the poor solubility of many fluorophores in water. However, the vast majority of biological studies are determined in an aqueous environment (and at a well-defined pH). Unfortunately, many fluorescent dyes exhibit significantly lower quantum yields in aqueous solution, therefore greatly diminishing the signal. To address this shortcoming, various dyes have been developed in recent years [110, 113–115].

As noted above, many fluorophore classes are poorly soluble in water, which can make the applicability for biological studies problematic. To overcome this limitation, highly soluble analogs have been also developed. This is often accomplished by attachment of PEG-chains or charged functional groups such as sulfonates. While such solubilizing groups greatly enhance the aqueous solubility, they can also greatly increase the molecular weight and therefore render the fluorophore less suitable for FP/FA experiments that depend on the differential mass change of bound vs unbound ligand. The addition of charged groups has a much smaller impact and accordingly modified fluorophores have been used successfully for FP/FA studies. However, charged molecules are usually not membrane permeable (except for active uptake), which substantially limits or entirely prevents cellular uptake. Therefore, such compounds are not suited for experimental approaches, such as fluorescence anisotropy microscopy, that study live cells and require the labeled ligand to efficiently cross unperturbed cellular membranes [109, 110, 113–115].

A wide variety of different competitive binding assays has been developed to measure analyte concentrations directly in solution and for understanding the mechanisms of drug action of various drug target classes [104, 111]. Extensive, non-exhaustive lists, can be found in Burke et al. [10] and Owicki [116].

3.2 High-throughput screening

Advances in fluorescence methods [117], detection schemes, and assay miniaturization [118] have increased throughput creating an increased reliance on high-throughput screening (HTS). Fluorescence polarization/fluorescence anisotropy assays in particular, have been extensively used for HTS in both pharmaceutical industry and academic settings [103, 104, 119]. Since the anisotropy signal is volume-independent, FP/FA assays are ideally suited for high-density, low-volume assays [120–122] such as ligand-receptor binding assays [123] and enzyme assays [124] (Fig. 1b). Therefore, FP/FA assays can be generally readily adapted to standard miniaturized HTS platforms, provided the ability of a suitable fluorescent ligand and functional protein. While fluorescent polarization assays can provide quantitative information on thermodynamic and kinetic parameters of ligand-target interaction, most high-throughput screening assays based on a fluorescence polarization readout are designed to determine steady-state binding in which a fluorescent ligand is displaced by a competitive binder. This assay approach is appealing as it does not depend on the turnover of a reported substrate but is equally applicable to targets that are devoid of enzymatic activity (such as receptors, adaptor proteins and nucleic acids) or can identify ligands for allosteric binding sites. Furthermore, the approach is relatively insensitive to timing and once equilibrium binding is reached, it is generally only limited by the stability of the protein (and small molecule ligands) in the assay media.

The ligand displacement approach has also been successfully implemented as enzyme coupled assay, in which the product of an enzymatic reaction displaces a fluorescent reporter. Attractive examples include the measurement of ADP, GDP, AMP, or UDP generated in enzymatic reactions [125]. Those small molecules have been notoriously difficult to accurately and sensitively quantify as surrogates for enzyme activity.

4. Imaging microscopy

Due to its intrinsic procedural simplicity, fluorescence polarization has been widely exploited across a large range of fields. The detection of polarized fluorescence emission is typically done following two common schemes [126–131]. In the L-format scheme, one photodetector is used to sequentially analyze the light or alternatively to measure the emitted fluorescence under the excitation of two orthogonal polarizations (Fig. 5a). In the T-format scheme instead two photodetectors are present in the experimental setup and both parallel and perpendicular components of the emission are measured simultaneously (Fig. 5b). While the first arrangement is quite common for fluorimeters, the second one is usually recommended to capture the signal in real time and to avoid errors due to biophysical or biochemical changes as well as biological related motion [132]. The possibility to integrate similar fluorescence polarization detection schemes in fluorescence light microscopy [133, 134] is quite attractive because it offers the capability to map the molecular behaviors of fluorescent molecules with high spatial and temporal resolution and to translate common in vitro fluorescence anisotropy assay measurements to cellular and in vivo imaging [135].

Figure 5. Detection schemes.

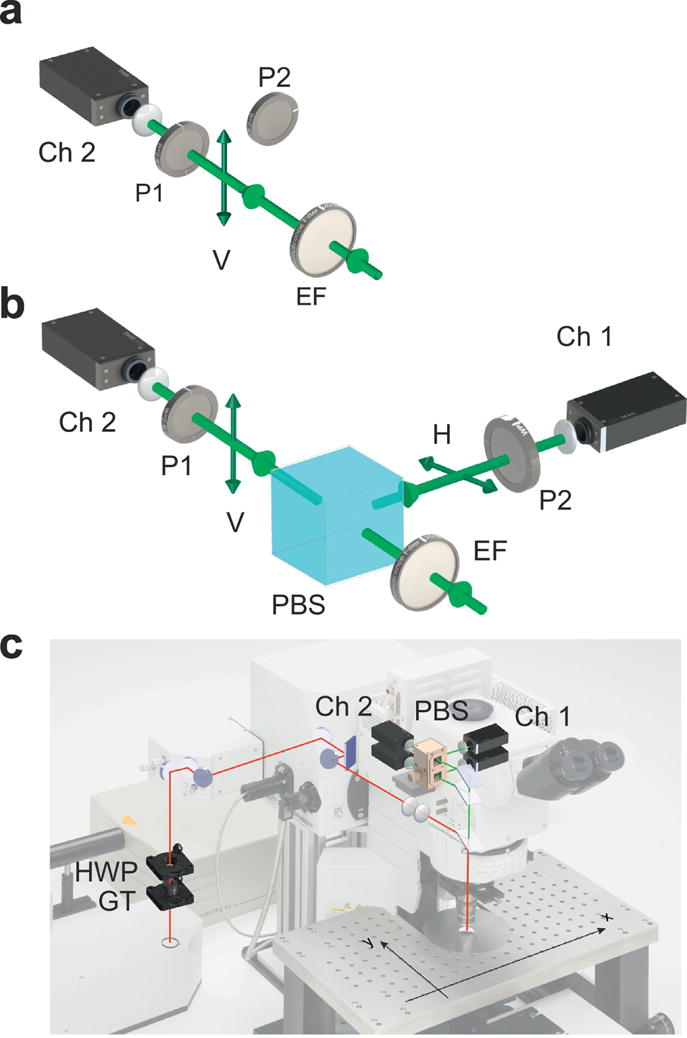
Detection schemes for fluorescence anisotropy measurements. In the L-format (a) all fluorescence intensities are measured using a single channel, sequentially, by replacing the analyzer P1, with the orthogonal one P2. In the T format (b) fluorescence intensities are measured simultaneously on two different channels (Ch1 and Ch2), by two different PMTs. The format is therefore more suited for rapid in vitro and in vivo imaging. (c) Scheme of principle of a two photon fluorescence anisotropy microscopy imaging system. GT, Glan-Thompson polarizer; HWP half-wave plate; PBS polarization beam splitter, EF emission filter. Adapted with permission from [255], Nature Publishing Group

So far most fluorescence anisotropy imaging applications have been confined to very specific areas, taking advantage of the intrinsic capability of fluorescence anisotropy to resolve for example subresolution order and disorder of different domains complex [136], or conformational changes in fluorescently labeled membrane proteins [137]. In [138] Shroder et al. present an ample range of fluorescence anisotropy single molecule imaging technologies capable to extract orientation and structural information from tagged probes.

In this Section we present a broad array of fluorescence optical imaging modalities capable to provide fluorescence anisotropy information through the implementation of polarization-resolved scheme detections [139–141]. Among them here we illustrate here wide field microscopy, confocal laser scanning microscopy, spinning disk microscopy, homo-Fret microscopy, time-resolved imaging microscopy, two-photon microscopy, and super-resolution microscopy. A brief summary of the pros and cons of the different imaging modalities is shown in Table 1.

Table 1.

4. Fluorescence anisotropy based imaging microscopy techniques.

Imaging Modality	+	−
Wide field microscopy	-Fast acquisition times -Inexpensive -High Throughput screening	-Background signal -Poor axial resolution -Mostly restricted to in vitro measurements -Limited volumetric information
Confocal microscopy	-Relatively inexpensive -Moderate acquisition times -High axial resolution	-Requires modifications of the imaging setup that are not always possible on commercial systems -Limited in vivo penetration depth
Spinning disk microscopy	-Relatively inexpensive -Large number of fluorophores available. -Very fast acquisition times	-Requires modification of the imaging setup that is not always possible in commercial systems -Best for in vitro or small organism imaging
Time-resolved fluorescence microscopy	-In addition to FA, it provides more information regarding the molecular environement	-Relatively expensive
Two photon microscopy	-The modifications of the setup in commercial systems is very simple. -High axial resolution -High in vivo penetration depth	-Relatively expensive -Restricted number of fluorophores available
Super-resolution microscopy	-High resolution (planar and axial) -Single molecule imaging -Relatively slow acquisition times	-Mostly in vitro based -Restricted choice of fluorophores

The Table provides the pros and cons of several fluorescence optical imaging modalities capable to provide fluorescence anisotropy information.

4.1 Wide field microscopy

In conventional wide field fluorescence microscopy, a sample is illuminated with excitation light from a lamp or a Light Emitting Diode (LED) and fluorescence is collected by an imaging objective and imaged on a Charged Coupled Device (CCD). The widespread use of this imaging modality for biological imaging is due to its simplicity in both use and assembly, while offering excellent planar resolution. Also recent advances in camera designs and technologies have led to the development of new CCDs with lower noise, higher sensitivity and increased temporal resolution, such as cooled CCD, Electron Multiplying Charge Coupled Device (EMCCD), and scientific-grade Complementary Metal Oxide Semiconductor (sCMOS) cameras [142]. Unfortunately, wide field microscopy presents two major limitations. First, light is collected not only from all points within the focal plane but also from regions of the sample in close proximity to it, causing a substantial blurring in the acquired images [143]. This problem can be in part solved using deconvolution algorithms [143–148] or structured illumination microscopy [149–151], but overall the technique is not optimal for signal quantification particularly when imaging in solution in the presence of background fluorescence. This is the case for example when imaging cells in the presence of fluorescently labeled drugs during the loading phase of drug accumulation. Here free unbound or unspecifically bound drug molecules are present at different axial positions, concomitantly with the intracellular signal, contaminating the measured anisotropy signal. Second, the penetration depth is severely constrained, restricting its suitability for the most part to in vitro imaging settings only. Despite these drawbacks most fluorescence anisotropy imaging methodologies are based on this imaging modality. Spectrally filtered fluorescence emission is typically split on a single CCD using a common aperture imaging system (e.g. DualView or Optosplit, BioVision Inc.) producing non-overlapping images with orthogonal polarizations [62, 132, 136, 152–154]. Other configurations use a combination of one CCD camera with a rotating analyzer [155]. Using a similar approach Gough et al. [156] mapped calmodulin binding during cellular contraction and locomotion. Another possible setup arrangement involves a polarization beam splitter followed by two separate cameras [157]. A polarization-sensitive multimodal imaging platform was also demonstrated by Rzeczycki et al [158] to detect formation or ordered molecular aggregates in drug sequestering macrophages. Applications range from both homo-FRET, steady state fluorescence anisotropy imaging microscopy, and super-resolution microscopy.

4.2 Confocal microscopy

In laser scanning confocal microscopy [159–162] the imaging sample is illuminated with a laser beam focused to a diffraction-limited point, and image acquisition is based on a sequential point-by-point excitation, with the laser point moving across a raster scan path over the field of view [163, 164]. A pinhole positioned in the emission light path, acts as a spatial filter and prevents out-of-focus light from reaching the detector, as opposed to wide field microscopy where light from out-of-focus regions is detected [165], reducing image blur and increasing both contrast, penetration depth and axial resolution [166, 167]. By optically sectioning [168, 169] through the sample, three-dimensional reconstructions can be computationally obtained in vitro and in vivo within thick layers of tissue [170–174]. Thanks also to recent advances in imaging hardware, as well as the development of new biological reporters [175], more efficient fluorophores, novel targeted and activatable contrast agents, and fluorescently labeled drugs, laser scanning confocal microscopy has become one of the most widely used optical imaging techniques greatly contributing to our understanding of biological processes in living systems [176, 177]. The application of confocal microscopy for the physicochemical characterization of pharmaceutical systems is also object of intensive research [178].

Common confocal laser scanning microscopy setups can be easily modified to incorporate polarization sensitive elements [179–183], in a similar fashion as described for two-photon imaging in Section 5.1. This modality has been used in its different implementations (e.g. linear dichroism) and in combination with other detection schemes (e.g. lifetime) by several groups [179–186]. Blackman et al. [187] for example derived a general model to describe the relative orientation of a membrane associated fluorophore to measure the orientation of eosin-5-maleimide on human erythrocyte band 3. In several seminal works Bigelow et al. [180, 181, 188] performed analysis of scattering induced depolarization effects on fluorescence anisotropy measurements through confocal microscopy [188] and beautifully demonstrated its application in tumor cell monolayers [180] and for imaging enzyme activity in vitro [181]. In a multimodal combination with FRAP (fluorescence recovery after photobleaching) Roberti et al. [189] assessed the intracellular association states of alpha-synuclein amyloid aggregates in living cells.

4.3 Spinning disk microscopy

Spinning disk confocal microscopy [190, 191] offers similar advantages as laser scanning confocal microscopy [192], however, instead of relying on two galvo mirrors, a pinhole and a PMT, it makes use of a microlens array disk (Yokogawa spinning disk) and a CCD camera. The net result is image acquisition with better signal-to-noise ratio (SNR), higher dynamic range and enhanced temporal resolution [193]. Because the optical setup is very similar as in wide field microscopy, this modality can be analogously extended for fluorescence anisotropy imaging [62] and commercial systems (e.g. Andor) are available. The extremely high frame rate acquisition can enable 3D volumetric acquisitions, and can allow to follow drug engagement at the cellular level in real time for detailed pharmacokinetic studies.

4.4 Homo-FRET imaging

Forster resonance energy transfer (FRET) [57, 194–196] is a phenomenon that occurs when energy absorbed by a fluorophore (i.e. donor) is transferred to another molecule (i.e. acceptor, which in most cases is a fluorophore) through a non-radiative pathway [197, 198]. The condition necessary for the energy transfer to occur require for the donor and the acceptor’s emission and excitation spectra to overlap, to have a favorable dipole-dipole orientation, and to be in close proximity (1-10nm) [199, 200]. This effect has been successfully adopted to study molecular self-assembly or clustering. If the donor and acceptor are identical [196], homo-FRET can be observed by exploiting the difference in polarization of the fluorophores. Here, contributions to the fluorescence emission are from both acceptors and donors as well, and it is therefore not completely polarized. Specifically, since FRET excitation is based on the proximity between donor and acceptor, FRET has the ability to excite molecules (acceptors) with an orientation that can effectively be outside the original photoselection plane [152]. This loss of polarization in the fluorescence emission provides therefore a sensitive assay for FRET occurring between the same fluorophores, which can be easily characterized by anisotropy measurements [201]. FRET and homo-FRET have been combined with different imaging modalities [62, 200, 202–206], and also in two-photon microscopy [207]. It has been extensively used for imaging molecular interactions in cells [208], monomer-dimer transitions of GFP-tagged proteins [209], nanoscale organization of cell surface molecules in living cells [210] and of GPI-anchored proteins [211–213], to determine protein cluster size by way of confocal steady-state [214] and time-gated fluorescence anisotropy imaging microscopy (FAIM) [185], and to quantitate the number of subunits in membrane protein oligomers [215].

4.5 Time resolved fluorescence imaging microscopy

In fluorescence lifetime imaging microscopy (FLIM) [216, 217], the imaging contrast is provided by the lifetime of the fluorophores present within each voxel, providing information of the molecular environment of the labeled macromolecules, and to follow over time biochemical reaction within the cellular environment [216, 218–221]. If fluorescence anisotropy analysis is incorporated into FLIM imaging systems, information about the fluorophores rotational diffusion can be determined [140], contributing in adding a new dimension to cellular imaging [132, 222, 223]. This has allowed among the others, to map viscosity in cells using fluorescent molecular rotors [224–226], to enhance imaging contrast between cancerous and normal tissue areas [227], to measure the hydrodynamic radii of anti-VEGF drugs [228], or in combination with homo-FRET to study the molecular self-assembly in live cells [229].

4.6 Two-photon microscopy

Two-photon microscopy is a raster scan based imaging modality for high resolution imaging in deep scattering tissue [230–235]. Localized nonlinear excitation based on two-photon absorption guarantees low phototoxicity, extended penetration depth [236, 237] and reduced scattering [238, 239]. The enhanced axial resolution and the fact that two-photon excitation in scattering solutions is due only to ballistic photons [240], enables for high resolution optical imaging with minimal out of focus fluorescence contribution. Localized excitation volumes (ca. 1 femtoL) guarantee the use of two-photon microscopy for high throughput screenings [241]. This is in stark contrast with confocal microscopy where optical sectioning, achieved controlling the pinhole diameter, goes at the expense of the signal level [242]. Also, because both hemoglobin, water and lipids have their lowest absorption coefficient in the near infrared (NIR) region of the spectrum [243], NIR light can penetrate deeper into tissue layers [35–39]. All these characteristics have contributed in making two-photon imaging microscopy the de facto imaging modality for intravital microscopy, particularly for mouse imaging, providing quantitative and dynamic insights into in vivo [244–247] cell biology, immunology and tumor biology [1, 176, 248, 249], and drug delivery [250, 251].

The implementation, within common two-photon hardware setups, of polarization sensitive components, has extended fluorescence anisotropy to this imaging modality (See Section 5.1), and it has been utilized for directly imaging protein-protein interactions or to study basic cellular processes among the possible different applications. For example the technique has been used by Vishwasrao et al. [252] to map actin-GFP fluorescence anisotropy and to obtain direct images of the actin polymerization state in live cells and tissue. Vishwasrao et al. [253] also managed to probe in neural tissue the metabolically free/enzyme-bound states of intracellular NADH. Orrego et al.[254] utilized two-photon microscopy fluorescence anisotropy imaging to determine the different degrees of stabilization of proteins immobilized at the interfaces with solid surfaces. Homo-FRET imaging by two-photon has been also reported in different contexts as reviewed by Tramier et al. [207]. Dubach et al. [64] demonstrated its use for resolving spectrally similar fluorophores and enable increased multilabel imaging. While some of these applications may be pharmaceutically relevant, our review is focused on the use of this approach for small molecules imaging. Recent works have indeed demonstrated that this imaging modality is extremely effective at measuring drug distribution and target engagement in vivo and in vitro using different cancer drugs [33, 34, 255].

4.7 Super-resolution microscopy

Conventional fluorescence microscopy imaging techniques are not able to resolve single molecules or proteins, particularly in the cellular environment. Recently, a new array of optical imaging techniques, known as super-resolution (SR) imaging microscopy [256], has allowed to break the diffraction limit barrier and to extend the resolving power of optical microscopy down to a few 10s of nanometers providing for the first time high resolution imaging of biological samples.

One primary class of techniques exploit the principle of single molecule localization-based super-resolution imaging. Here fluorophores are temporally separated, their profile center localized as a diffraction-limited spot on an imaging array [257–262], and super-resolution images are obtained from their coordinates [263]. Based on this approach, or variants of it, are imaging modalities such as stochastic optical reconstruction microscopy (STORM) [264], photoactivated localization microscopy (PALM) [265], fluorescence photoactivation localization microscopy (FPALM) [266], direct STORM (Dstorm) [267], and others.

Other classes of techniques are based on point spread function engineering and spatially patterned excitation such as stimulated emission depletion microscopy (STED) [268, 269], reversible saturable optical linear fluorescence transitions (RESOLFT) [256], and structured illumination microscopy (SIM) [270].

These novel techniques are becoming an essential tool for biological imaging offering a new imaging scale and contributing to a better understanding of cellular structures and functions at the single molecule level, both in vitro and in vivo [271]. Because the optical setups of these imaging modalities can be straightforwardly extended to enable fluorescence polarization analysis, novel single molecule optical technologies have been recently published, such as super-resolution dipole orientation mapping (SDOM) [272], demonstrating the use of polarization based super-resolution microscopy for effectively studying changes in the organization of the molecular components present within cells [138, 273–275]. Gould et al [276] also introduced polarization analysis in fluorescence activation localization microscopy (P-FPALM) for imaging fluorescence anisotropy of Dendra2-tagged hemagglutinin clusters in mouse fibroblasts.

5. Methods in fluorescence anisotropy microscopy

In this Section we present the specific methods-related problems present in fluorescence anisotropy microscopy, with particular emphasis on two-photon microscopy. Some of the following subchapters include a detailed technology discussion regarding noise and its effects on both fluorescence laser scanning microscopy and fluorescence anisotropy imaging. We consider these themes important but often poorly addressed. However, readers who are not involved or particularly interested in the optimization and design algorithm signal analysis may directly skip to Chapter 6. For the readers’ convenience we briefly illustrate in Table 2 the different steps usually required to adapt a custom-made or commercially available microscope, for two-photon fluorescence anisotropy imaging. In depth technical details of the single steps can be found in [255] where a protocol for the assembly, characterization and use of an Olympus FV1000MPE microscope system for FA imaging was illustrated. Because the hardware arrangements in different commercially available microscopes are fairly similar both in terms of design and components, these steps can be easily adapted to other systems.

Table 2.

Experimental design and setup.

Phases	Steps	Acting components
Excitation light	Polarization control	Waveplates Polarizers Glan-Thompson
	Components alignment	Adjustments
System Calibration	Detectors (PMTs)	Linearity PMTs Spectral range
	Beam splitter filter cube	Beam splitter, Filters Modifications of preexisting emission filter sliding cube holder, 3D printing
SNR	Image processing	Gaussian filter Median filter Combination of the two
	Hardware	Dwell-time Image averaging Laser power
Image acquisition	Software	Matlab, Labview
Analysis	Segmentation	Experiment specific algorightms Cellprofiler
	Visualization	Matlab software

The table illustrates the different steps usually required to adapt a custom-made or commercially available microscope, for two-photon fluorescence anisotropy imaging. Different phases of the setup are enumerated, with the corresponding steps and acting components

5.1 Experimental Setup

Several commercial systems for confocal and two-photon microscopy are available on the market, but at present there is no turn-key solution offering fluorescence anisotropy imaging. One possibility consists in building a custom-made microscope. This approach is cost-effective and with the advantage to be highly adaptable. Several papers are available [277–281] presenting different hardware platforms that could be readily modified for polarization sensitive detection. Two custom-made multimodal imaging setups implementing both fluorescence anisotropy and lifetime imaging and based on an IX71 (Olympus, Japan) and an IX80 (Olympus, Japan) are briefly illustrated by Orrego et al. [254] and Vishwasrao et al. [282] respectively. Ariola et al. [283] also implemented a similar setup for lifetime and fluorescence anisotropy imaging of lipid phase dynamics in giant unilamellar vesicles. The major drawback of a custom-based approach is that some experience in building optical imaging devices is required; as well as a considerable time investment. Alternatively, conventional two-channel commercial imaging systems can be modified very rapidly with minor modifications and efforts [255].

Wang et al. [284] and Li et al. [285] for example incorporated polarization control elements on a MRC-1024 (Bio-Rad) microscope demonstrating two-photon fluorescence anisotropy imaging in FITC-CD44Ab labeled PG cells. We have also in recent works [33, 34, 64, 255] illustrated a procedure for adapting a two-photon microscope FV1000 (Olympus, Japan) for both in vitro and in vivo measurements of drug target engagement.

Independently of the preferred solution, the setup principle is essentially the same for all different cases (Fig. 5c). While different strategies are feasible, control and analysis of the states of polarization is typically achieved using a combination of wave-plates, linear polarizers, and polarization beam splitters. Light from a laser, in a multiphoton microscope typically femtosecond laser pulses, is linearly polarized along a fixed predetermined axis and focused through an objective, onto the imaging sample. Fluorescence is then epi-collected, spectrally filtered, and separated in two orthogonal states of polarization, parallel and perpendicular with respect to the excitation light, using a polarization beam splitter. The parallel and perpendicular light components are simultaneously detected by two photomultiplier tubes (Fig. 5b) and images representing the fluorescence anisotropy distribution maps across the imaging field of view are calculated on a pixel-by-pixel basis according to Eq. 2. A detailed protocol providing guidelines for alignment and calibration can be found in [255].

For what concerns the interface software, several open source solutions are available for custom built systems such as ScanImage [286], HelioScan [287] or MPScope [288]. Software to sequentially process data-stream for calculation and visualization of fluorescence anisotropy images during time lapse acquisition, is instead given in [255]. Because data visualization is a crucial aspect of the acquisition process, this issue is discussed in detail in Section 7.1.

5.2 Fluorescence microscopy image acquisition

Fluorescence imaging microscopes digitally record images from an illuminated sample by converting fluorescence emitted photons to electric signals by means of special detectors. The most widely used detectors for wide field, confocal and multiphoton fluorescence imaging are photomultipliers tubes (PMTs), charge couple-coupled devices (CCDs), or complementary metal–oxide–semiconductor (CMOS) image sensors [289, 290]. These technologies are based on the exchange of energy between photons and the detection material. Photoconductivity, photovoltaic- and photoemissive effects are examples of the physical phenomena exploited to achieve photo-detection. The different classes of detectors present multiple characteristics which based on their design and construction features, can significantly differ in terms of response linearity, spectral range, speed and sensitivity, etc.

The best choice is never limited to the detectors’ characteristics themselves, but it is also related to the modality and the experiment to be performed which can involve among others, specimen and signal features, time constraints, etc.

Depending on the specific microscopy modality the imaging focal point is moved in space (flat plane shaper support) over time to cover the field of view to be imaged (i.e. pixels are acquired sequentially and rearranged to form an image) or a matrix of sensors can be exploited to simultaneously acquire a set of points to accelerate image acquisition. Neither technology is superior to the other, as a trade-off is always present. For instance in confocal imaging, high throughput can be achieved by combining a CCD matrix sensor and a Nipkow disk [291] at the expense of a reduced optical sectioning resolution. On the contrary PMTs based acquisitions (resonant scanning and linear scanning) which operate on a pixel by pixel base acquisition scheme, suffer from low acquisition speed, but provide high axial resolution and increased SNR due to the reduced background scattering signal.

As for all other imaging techniques, the sensing process that leads to image recording is affected by errors. Some errors can be ascribed to the deviation of the real system from an ideal one; others are related to the intrinsic characteristics of the physical phenomena at the basis of the recording, such as the discrete nature of light. Recent hardware technology advances had an important role for reducing the measurements errors. For the case of fluorescence imaging, this has been achieved through better detectors’ design, improved optical components, better electronics and optimized fluorophore probes. Other complementary strategies can additionally be used, by tackling the problem from a different point of view. In particular, the implementation of special acquisition and/or post processing techniques can be beneficial.

Post processing methods are generally applied to the final digitalized images. Once the analogical image is acquired by the microscope, it is then converted and recorded as an array of bytes. Numeric methods are coded into algorithms and are generally applied offline, i.e. once image acquisition is completed.

The use of processing techniques is not only utilized for overall image quality enhancing, but is also implemented to enhance quantitative information extraction and analysis of complex dynamic cellular events in different advanced microscopy techniques such as fluorescence recovery after photobleaching (FRAP), fluorescence correlation spectroscopy (FCM), and ratiometric imaging implementations such as fluorescence resonance energy transfer (FRET) and fluorescence anisotropy microscopy (FAM). Because in most cases the processing is relatively time consuming, it has been normally performed offline as the algorithm and its implementation into computational systems must comply with time constraints dictated by the instruments and the biology of interest. Only recently thanks to the availability and relative low costs of field programmable gate arrays (FPGA) or graphic processing units (GPUS), processing is performed in real time.

5.3 Noise in fluorescence microscopy

The signal-to-noise ratio (SNR) of a detector is a measure of its sensitivity performance and depends on the ratio between the detected signal and the sum of all noise components. Within the fluorescence signal acquisition process, it is possible to identify several sources of noise that limit the system performances and ultimately the SNR of the acquired images. Apart from the ones due to stray light detection, scattering, or filter bleed-through, we focus here on the two main noise components (intrinsic and fundamental) which are the mostly relevant and of greater importance for the topic discussed.

The fundamental limit on noise performance is set by the shot noise also know as photon- or Poisson noise. This component can be considered as an independent source of noise which cannot be reduced by any further improvement of the detecting system: in fact it is inherent to the statistical uncertainty in the arrival of the photons at the detector [292]. Its effects are more severe at low photon fluxes when errors in the signal detection play a greater role, as is the case for confocal or multiphoton imaging microscopy where a few (tens) photons per pixels are typically collected. A common statistical model to describe this noise component is the Poisson’s. For this distribution both expected value and variance of the number of photons at the detector are equal to the quantity λT, with λ the average number of recorded photons and T the considered time window. Thus the signal-to-noise ratio, computed as:

$$\frac{\lambda T}{\sqrt{\lambda T}}$$

is simply expressed by $\sqrt{\lambda T}$ [293, 294]. According to this formula, the SNR increases as the photon rate becomes higher.

An intrinsic component of the noise related to the detector is the dark noise. This component arises from thermal effects (major cause) on the sensor, which lead to spontaneous electrons formation even in the absence of incident light. It follows the dark noise is not correlated with the photon flux incident against the detector, but instead, it is strongly correlated with the temperature and the exposure time.

Another noise component, which is significantly present in CCD based imaging systems, is the readout noise. Here images are acquired by converting photons arriving on an array of pixels (typically 10⁶) into electric signals via an electronic system used for signal amplification and analog to digital conversion. The digital conversion requires the signal to be quantized, i.e. the signal intensity to be discretized so that. each pixel value can be represented as a multiple of a fixed quantum [295]. In digitalized images also space is discretized. Here pixels are arranged on a lattice with uniform spacing. The readout procedure introduces errors in the measured signal and this electronic source of noise can be statistically described by a zero mean Gaussian distribution for the amplification stage, when quantization error (uniformly distributed) is not included into the model.

The SNR computation, if all the previous noise components and the detector quantum efficieny Qe are considered (assuming negligible the quantization noise), leads to [293, 294]:

$$\frac{Q_e\lambda T}{\sqrt{Q_e\lambda T+n_d^2+{\sigma }^2}}$$

where n²_d and σ² s are the variances of the noise related to the dark and readout noise components respectively.

The readout noise contribution is therefore more important under low light emission.

Generally, PMTs and related recording circuitry can be considered as low noise-light detector devices with negligible readout noise and very low dark noise contribution, making them particularly suitable for confocal or two-photon imaging applications, specifically in our case for fluorescence anisotropy imaging.

5.4 Effects of noise in confocal microscopy

Noise contributions in confocal images are particularly relevant because the number of collected photons is usually low, so the consideration of all noise sources becomes relevant. The resulting effect is a final image presenting a low dynamic range, with reduced contrast and resolution [296].

The problem becomes more pronounced when imaging fluorescently labeled drugs within cells in vitro or in vivo, because in most cases only a few molecules are present within the excitation volume. Additionally, photobleaching effects are present, which require to work at low excitation intensities limiting therefore the amount of light that can be collected.

A trade-off also exists regarding the choice of the pinhole. Confocal fluorescence microscopy uses a variable diameter diaphragm as additional optical device to achieve better optical sectioning. The pinhole is located in the image plane of the microscope acting as a spatial filter and eliminating all fluorescence emission not originating from the focal plane. As the pinhole approaches the optimal Airy-disc diameter unit, photon collection is further reduced lowering the SNR. A viable approach for increasing the number of photons consists in opening the pinhole. However, the side effect is a limitation in the optical sectioning power of the instrument with associated reduced contrast. With increasing pinhole size, autofluorescence and out of focus specific fluorescence signal contribute to increase the image blur. In conjunction with other noise components this additional factor leads to poor quality fluorescence images, which is particularly detrimental for signal quantification or ratiometric measurements [297] such as fluorescence anisotropy images. This is true for both PMT- (laser scanning confocal microscopy) or CCD-based (confocal spinning disk microscopy) modalities.

When operating at very low photon fluxes such as during video-rate or high-frame rate acquisitions, the dark noise contribution in PMTs becomes predominant [298] strongly affecting signal detection. A possible way to obviate at this problem and achieve images with high SNR under shot noise limited conditions, is to switch the detection modality from analog (regular acquisition mode) to single photon counting detection (SPC) [295] Images obtained under this regime of acquisition, will indeed present high SNR but will present a reduced dynamic range with counts spreading from 10 to 100 Mega-counts per second [299] and a linear response limited to just 1 to 2 MHz [300]. For this reason this technology is restricted to very highly specialized applications.

5.5 Anisotropy imaging and noise filtering

Fluorescence anisotropy images are not the result of a direct measurement, but instead they are obtained post-acquisition after image digitalization. Briefly, anisotropy imaging is achieved by exciting a specimen with polarized light and measuring two orthogonally polarized components of the fluorescence emitted light. In a real-time fluorescence confocal/multiphoton imaging platform [33, 34, 255] images are collected using two different PMTs, and processed mathematically according to Eq. 2. However, the process is not straightforward. As we have previously described noise, and in particular shot noise, affects any fluorescence image acquisition with an impact more or less severe depending on several imaging and fundamental parameters. The noise component which is incorporated into the acquired fluorescence images will propagate by means of a nonlinear mapping with the resulting anisotropy images presenting a significant and more complex form of noise. Consequently, typical features within fluorescence anisotropy images can become poorly visible and the underlying signal low informative.

One possible way to improve the quality of the images in terms of SNR consists in increasing the total number of the collected photons. This can be achieved by increasing the total time during which fluorescence molecules are excited (dwell time) or alternatively by increasing the excitation light power. Both methods are not always suitable for live imaging experiments. In fact, they may cause phototoxicity and/or photobleaching, as well as lead to saturation, so that a further increase in the excitation light power does not yield an equal increase of emitted fluorescence signal. Neither dwell time increase and/or image averaging are beneficial whenever fast dynamic events are investigated as they both set limits on the minimum time window required to collect a single image.

When CCD acquisitions are considered as for spinning disk microscopy, the readout noise should be also included into the noise propagation model. But in this case the description of anisotropic image error is even more complex to be expressed mathematically.

Depending on the case of study a trade-off on parameters’ settings is always required. However other additional methods can be exploited to enhance the quality of anisotropic images. These methods exploit numerical manipulation of information after acquisition. Such an approach, even if potentially very effective, does not have to be considered as a substitute to proper microscope’s parameters setting, but complimentary. The concept is easier to understand by making a comparison with digital camera photography. Image processing algorithms applied to poor quality images (e.g. weak light illumination) lead to worse results compared to photos shot with proper optics, camera settings and environmental conditions. The same stands true for anisotropy imaging where also filtering approaches based on both linear and non-linear digital filters can be implemented [255, 301]. Filters can be applied either to anisotropic images or to raw images, i.e. before anisotropy is computed. While the first method is prone to bias [297], directly filtering the raw fluorescence images is mostly recommended as the model of noise statistics becomes otherwise more complicated, and leads to more complex denoising algorithms.

Gaussian and median filters [302] are basic examples of linear and nonlinear filtering techniques that can be used for denoising fluorescence anisotropy images.

Although numerical filters may lead to a loss of spatial resolution, their benefits typically overcome this limitation. Overall linear filtering such as Gaussian filtering is in general a better choice leading to less distortions and artifacts even if at the expense of a reduced image resolution. Non-linear filter processing as bi-dimensional median filters, instead, perform better against edge smoothing and outlier elimination. However, with large kernel sizes, they can give rise to severe artifacts. Another advantage in applying these filters is that they can be implemented in a numerically efficient way so that fast computation is achievable. This aspect is particularly useful whenever anisotropic images are needed to be visualized in real time while imaging to provide visual feedback.

6. Sources of errors in fluorescence anisotropy imaging

There are different sources of errors and uncertainties to take into account when determining fluorescence anisotropy, which must be always corrected for instrumentation artifacts. These sources depends on the specific design setup and the hardware components used within the imaging platform, both on the emission and the excitation side [303], as well as the imaging sample under consideration.

Concerning the emission side, these effects are typically compensated introducing the so-called G-factor:

$$G=\raisebox{1ex}{$I_{VV}$}\!\left/ \!\raisebox{-1ex}{$I_{VH}$}\right.$$ (7)

which represents the ratio of the sensitivity of the detection system for vertically and horizontally polarized light [130, 131]. This factor largely depends on the different polarization properties of the optical elements and the detectors. Jameson published several reports on these sources in particular focusing on how they affect the ultimate estimation of ligand-protein dissociation constants [12, 15, 56]. If possible it is usually preferable to break up the contributions of the different effects responsible for the depolarization of the signal (Eq. 6) or the recording of the wrong intensity estimates.

Among the different sources are the fluorescence background [56], the noise background [301], quenching effects [303, 304], photobleaching [305], different extinction ratios of the optically sensitive components [130, 131], etc. Because we focus our interest on a multiphoton imaging platform, in addition to detector noise, we consider here in more depth the scattering contributions and the effects introduced when using high numerical aperture (NA) objectives. Also we illustrate in this Section methods that can be adopted for proper two-photon fluorescence anisotropy instrumentation calibration, a crucial component for obtaining consisted data across multiple measurements.

6.1 Scattering

Deep imaging in biological specimens is severely hampered by light scattering phenomena, which not only are responsible for image degradation but also affect the polarization state purity [306].

While the fluorescence polarization of a solution of fluorophores is generally determined by depolarization effects occurring during the lifetime of the excited state [307], depolarization from events occurring within the sample before excitation or after emission, such as scattering in turbid media due to Rayleigh or Mie scattering, which tend to randomize the direction phase and polarization of the travelling photons [308], can also impact its value [307, 309, 310].

Scattering events decrease very rapidly the polarization of the incident light with an impact on the photoselection process [130], while also further depolarization occurs in the emission channel [307, 311].

Responsible for light scattering are variations of refractive index within a media. After travelling through it, elastically scattered photons consists of unscattered (ballistic) photons, snake photons and multiple scattered photons [312, 313]. While the ballistic photons maintain the characteristics of the incident light, the snake photons retain significant properties and only partially loose some degree of polarization. Multiple scattered photons instead loose most of the initial physical characteristics and suffer from increased depolarization, with their state of polarization partially or completely random [314]. The magnitude of the effect and the resulting polarization properties are determined by the characteristics of the scattering media as well as the photons’ wavelengths [314].

Elastic scattering of light by small particles can be mainly considered as part of two broad classes of scattering phenomena depending on the size of the scatterers.

Rayleigh scattering occurs when the size of the scatterer is much smaller than the wavelength of the incident light. The effect is isotropic i.e. independent of the scattered direction, and is proportional to the sixth power of the scatterer diameter and inversely proportional to the fourth power of the incident wavelength.

Sample turbidity will also impact the polarization of the fluorescence signal. For Rayleigh scattering the depolarization produced by a single scattering process at both excitation and fluorescence emission induces a decrease in fluorescence anisotropy up to 0.7 times its original value [307, 315]. The dependence of the reduction in fluorescence anisotropy, relative to the scatterer size, and its extension to multiple scattering events has been also extensively treated, and found that with increasing the scatterer radius the characteristic length of depolarization of linearly polarized light increases [315]. While this decrease in fluorescence anisotropy has been first noted by Teale when working on solutions containing glycogen and conjugates of bovine plasma albumin, it has been also evaluated and studied for a variety of turbid membrane suspensions confirming the applicability of Teale’s approach while proposing corrections schemes [316].

Since scattered light is usually completely polarized, a small percentage of the detected excitation scattered light affects the value of fluorescence anisotropy [317]. This property has been used to measure the instrument response function for calibration purposes of fluorescence anisotropy instruments [318]; e.g. to measure scattered light rejection by emission filters, dichroics, polarization beam splitters, pinhole apertures, monochromators [130]. For Rayleigh scattering the polarization should be complete, with fluorescence polarization values lower than 1 (under one-scattering event) indicating depolarization effects in the optics [319]. Diluted scattering solutions can be obtained from diluted Ficoll, colloidal silica or glycogen solutions [130], or nondairy coffee creamer such as Coffee-mate [318–321].

Scattering problems become even more important when considering imaging in tissue, where Mie scattering plays an important role [322].

Mie scattering [323, 324] is a bigger generalization of elastic scattering under the assumption that the scatterers are spherical in diameter; for large particles it is anisotropic and proportional to the square of the radius of the scatterer.

Biological tissue presents many refractive index discontinuities due to differences between specific cells components (cytoplasmic organelles, lipid droplets, nuclei, cell membranes, mitochondria, etc.) [325, 326], their organization [327], and the surrounding environment, giving rise to increased scattering properties. Also, the relative size of organelles and cells with respect to the incident wavelength varies across a broad range in size, from 100nm up to several microns [323, 328–331], determining the properties of the angular distribution of the scattered light [325, 332]. Due to their great structural complexities tissue are usually modeled as representative of a system made by discrete scattering particles where both Rayleigh and Mie scattering play a role.

To describe the polarization state transformation in tissue, the mean free path (MFP) and the transport mean free path (TMFP) are typically used [333]. Because in most tissue the absorption coefficient μ_a is less important than the scattering coefficient μ_s [334], the MFP is equal to the inverse of the scattering coefficient μ_s and corresponds to the average distance between scattering events (approximately 100 microns in biological tissue). This gives the characteristic penetration depth of the ballistic photons. For multiple scattered photons, as is the case in tissue, the distance between successive scattering events is of less importance than the scattering angle [335]. In this case the scattering process is better defined through the transport mean free path TMFP which is equal to the reduced scattering coefficient μ’_s, and indicates the mean propagation distance necessary for a photon to lose relation, on average, to its initial propagation direction [336]. The reduced scattering coefficient μ’_s is equal to:

$${\mathrm{\mu }}_s^{\prime }={\mathrm{\mu }}_s\cdot (1-g)$$

where g is the anisotropy function defining the degree of forward scattering [337]. Because in tissue the scattering is characterized by a strong forward-scattering component, with value of anisotropy factor in the range between 0.6 and 0.95 [35], the TMFP can be better utilized to describe the scattering. This takes into account the MFP and the average photon scattering angle [336], and determines the characteristic depolarization depth for the different tissue [329]. The relation between these two characteristics lengths is

$$\mathit{MFP}=\mathit{TMFP}\cdot (1-g)$$

High values of g will imply strong forward scattering and longer lengths before reaching diffusion, resulting in high penetration depth [336]. Typical values of reduced transport scattering coefficient vary considerable due to the different structural and functional properties of normal and malignant tissue [338–341] and typically range between 5 to 15 cm⁻¹ [35]. A review of the optical properties of biological tissues reporting a compilation of existing absorption, scattering, and anisotropy parameters is given in Cheong [330] and Sandell [341].

As a results of tissue scattering, multiple-scattered light will tend to randomize the photon propagation direction and reduce the polarization of fluorescence, resulting in a rapid decay of fluorescence anisotropy as a function of penetration depth within the tissue [342]. Average depolarizations produced by consecutive scattering processes has been object of extensive studies [307]. In confocal or multiphoton microscopy, penetration depths are usually smaller than the TMFP. To better understand the degree of depolarization and try to correct for its impact, different Monte Carlo approaches [343, 344] have been implemented. Bigelow et al [188] in particular focused on analyzing polarization preservation as a function of depth in turbid media, by imaging fluorophore-embedded polymer bar immersed in a suspension of polystyrene microspheres of different sizes. Results showed that anisotropy is slightly sensitive to pinhole size, and slightly sensitive on the objective numerical apertures (NA), with lower NA objective preserving anisotropy information more accurately at larger depths. Importantly, confocal microscopy yields anisotropy information accurate to within 10% of the zero depth values, up to approximately 4 times the MFP which is basically the imaging range in tissue.

While low numerical aperture objectives are recommended for confocal imaging, for two-photon microscopy high NAs are required to achieve high SNR, crucial for accurate fluorescence anisotropy images.

A decrease of the degree of polarization for two-photon excitation, with resulting lower values of anisotropy, was also evidenced by measurements on phantoms mimicking tissue optical properties [34, 345] and based on intralipid and India ink, mixed with fluorescein [346]. In vivo imaging of fluorescent microspheres injected into superficial tissue within a nude mouse dorsal window chamber showed that a slight depth-dependent depolarization is present with a 10% loss at a depth of 100 μm [34]. Characterization methodologies based on four wave mixing also show that depolarization mechanisms for nonlinearly generated photons are highly dependent on the scatterer size, the collection geometry used and the thickness of the sample. But at imaging depths commonly accessible by two-photon microscopy, the polarization state of the excitation photons is mostly preserved while image resolution is degraded [306].

6.2 Objective numerical aperture

Equation 2 is based under the assumption that the excitation polarization is perfectly polarized within the focal point. In practice this is certainly not the case, in particular when imaging with a high numerical aperture objective.

For single cell imaging at high resolution and magnification, objectives with high numerical aperture are recommended offering high sensitivity and localization [347] for both wide field and confocal microscopy [162, 166, 348]. High NA objectives also allow to generate high spatial energy densities which, due to the low efficiency of multiphoton absorption, are necessary in two-photon microscopy to generate a sufficient number of photons and to produce high signal-to-noise ratio images [349]. The numerical aperture, which describes the angular aperture of a lens over which the objective focuses or accepts light, is used to characterize different objectives.

When imaging, the polarization states of the excitation light and the detected fluorescence are distributed within wide cones centered at the objective focal point, where emission and excitation occur [350]. At high NA the excitation light near the focal point is far from a plane-wave [351] and to accurately describe the electromagnetic fields in this region it is necessary to account for the vector nature of the light [352, 353]. Essentially the objective can “look around” the focal spot [134] acting as an “integrating sphere” [354] and collecting fluorescence signal over a wide range of emission solid angle. As a result a mixing of polarization components, along different orthogonal axes, is present in the excitation field [61, 134, 355–359], with polarization distortion near the excitation focal point present toward the edge of the focusing beam. This is highly relevant in fluorescence microscopy because the light field orientation with respect to the molecule transition dipoles [347] directly affects the photoselection process within the focal volume. The resulting effect is to induce a depolarization factor dependent on the objective’s NA, leading to a decrease in the measured anisotropy [359], which is particularly troublesome for slowly rotating fluorophores with high anisotropy [61].

For example, measurements of fluorescence polarization for a TRITC solution in glycerol as a function of viscosity, show that at high numerical aperture the FP can be reduced, with a 32% drop in polarization when passing from 0.5 to 1.3 NA [360].

The problem regarding the distribution of the light focal fields under high NA focusing objective has been studied in detail by several groups [347, 361–363]. Among the first to give a theoretical treatment of the problem within the context of fluorescence imaging was Axelrod, who described how perturbation induced by high numerical aperture optics, gives rise to a decrease in fundamental anisotropy with increasing the NA of the objective [134, 305, 350, 351, 355, 356, 364].

In confocal and multiphoton laser scanning imaging microscopy the excitation laser beam is scanned across the back focal plane of the objective using two galvo mirrors [277, 278]. The mirrors’ movements translates into a raster scan over the imaged sample, and at large field of views the fiel curvature due to the off-axis position of the scanning beam becomes non negligible at the field-of-view (FOV) border areas. This will give rise to image border artifacts with decreased values of fluorescence anisotropy at the image edges.

Corrections on the measured FP values, based on different theoretical treatments, can be implemented [254, 351, 352, 360] as well as corrections based on empirical approaches [223]. In our experience the best imaging approach consists in acquiring images over a restricted field of view. For example in [34] it has been shown that utilizing a 25× water-immersion objective (25×, 1.05 NA, 2-mm working distance; Olympus, model no. XLPLN25XWMP2) it is possible to acquire images of FA over a field of view of 150 microns (for example by increasing the zooming factor) with minimal fluorescence anisotropy artifacts. If images with large field of views are required it is recommended to stitch multiple areas acquired separately with a restricted FOV. This is important when analyzing FA distributions over a large number of cells for statistical analysis in high-content screenings, as described in Section 7.3. Using this approach images over large areas can be obtained in mouse dorsal window chamber, as well as in other tissue or organisms.

6.3 Instrument calibration

The use of fluorescence standards is quite widespread across a range of different discipline for characterization and calibration of fluorescence instruments, and to enable quantitative fluorescence analysis [365–367]. For accurate fluorescence anisotropy systems calibration, the use of fluorophores as polarization standards is also recommended [297, 303], with values in fluorescence anisotropy covering a range as wide as possible within the theoretical limits. While their use can allow to measure the response function of the instrument and to determine the accurate G-factor (Eq. 7), they can be utilized also to verify the accuracy of G-factor measurements previously obtained with other methods.

Because spectral properties can influence the calibration (excitation, emission), it is important to consider fluorophores with spectral properties similar to those of the final intended sample. Since fluorescence lifetimes are very sensitive to their environment, standards need to be prepared in accordance to the conditions reported in the literature, such as concentration, solvent, pH and temperature [368]. If possible they should not pose health, safety or environmental problems and to be both chemically stable and photostable during typical measurements processes [369]. Finally, one important property is for the standard fluorophores to be compatible with aqueous buffers solution, as for cell measurements [303]. A series of optimal fluorophores as characterized independently from several groups, have been reported for FLIM measurements [130, 369].

One way to avoid all these problems, could be considering Rayleigh scatterers [320]. Providing a value of fluorescence polarization equal to one (100% polarized) under one-scatterer condition, they are very convenient as possible standards [130]. Typical procedures are given in [317], and have been used in FLIM to calculate the instrument response function [318, 368] or for obtaining detailed depolarization measurements by calibration via polystyrene beads [315].

Overall, to calibrate fluorescence anisotropy imaging instruments at zero anisotropy, it is recommended to use fluorescein over the use of a depolarizer [370], because polarized residual components can always be present in the collected light.

Fluorescein in aqueous buffer solution at 0.01M, pH 7.0 and 22C°, has been shown to produce a value of fluorescence polarization of 0.023, due to its moderate lifetime (ca. 4ns) and short correlation time (100ps) [370]. Particular attention needs to be taken to control the pH of the final solution, because slight variations can give rise to fluctuations in the final value of the calculated anisotropy. Moreover, a very well established number has not been yet determined. Because fluorescence emission is peaked at 525 nm, it is very convenient for proper calibration in the range of BODIPY-FL and fluorescent proteins such as eGFP, Venus, EYFP.

Since a spectral dependence of the G-factor is typically present in all imaging systems, especially for hyperspectral systems [223], it is recommended to test the calibration procedure for the appropriate emission filter.

An alternative fluorophore, with an increased lifetime due to a very long lived metal-to-ligand charge transfer excited state [303, 371] and less sensitive to the final pH solution, is ruthenium tris(bipyridyl) [Ru(bipy)₃], which presents a value of zero FP across most of its entire excitation band [303, 360]. Its emission is centered at 620 nm, making it particularly useful for calibration in the 600 nm emission range. Another dye with a low value of polarization is ethidium bromide in ethanol (23ns decay time) with a steady state fluorescence polarization value of 0.008 [360]. Also another standard fluorophore is Rhodamine B, which in ethanol at 546nm has a fluorescence polarization value of 0.0666 [370, 372].

The availability of standard fluorophores with low values of polarization is very useful because it allows for straghtforward calibrate readings at two different PMTs (separate detection of the two orthogonal components) or alternatively to verify that the G-factor is correct. But standards presenting high values of anisotropy are also valuable, because if depolarizing factors are present within the optical schemes, they will reduce the measured value [303]. Among them RoseBengal and Erythrosin B present in water a very short lifetime of around 70ps [373, 374] giving rise to high values of fluorescence polarization of around 0.335 and 0.325 respectively, in the range from 500 to 550nm. Rhodamine 101 with an emission peak at 615nm, presents also a high value of limiting anisotropy of 0.384 near the theoretical one-photon fundamental anisotropy value of 2/5 [375].

Measurements of fluorescence polarization of dyes oriented in stretched poly(vinyl alcohol) (PVA) films have been also used as high polarization standards for correcting instrumental factors in polarization measurements [376].

Another fluorescence standard we have used is pyridine 1 in propylene glycol. This is highly recommended for two-photon fluorescence anisotropy measurements, presenting a high degree of anisotropy along a wide range of two-photon excitation between 750 nm and 950 nm [255]. Also, measurements of solutions of fluorescein dissolved at different ratios of glycerol:water, can be used to monitor the accuracy of the alignment and to establish the sensitivity in detecting changes in anisotropy across a large range of values [255, 355].

Other dyes presenting high values of anisotropy in two-photon [77, 377, 378] are Cy5 labeled DNA with a value of fluorescence polarization close to the theoretical limits of 2/5 and 4/7 for one- and two-photon excitation [379], as well as DAPI- and Hoechst 33342-stained DNA which present a two or three-photon excitation also close to the theoretical limit [380].

6.4 Detectors acquisition schemes

Simultaneous dual detectors acquisition presents a series of advantages. First there is no reason to image the sample twice reducing therefore acquisition time and avoiding photobleaching. Second, all motion artifacts are avoided. This are very problematic when performing ratiometric measurements of data acquired at different time points, and are particularly troublesome for intravital imaging microscopy where motion can give rise to artifacts. As a drawback, the detectors present usually different gains and noise characteristics, therefore the recorded intensities need to be corrected for systematic errors and effects due to different sources [130], prior calculating fluorescence anisotropy. Several works present standard methodologies for correcting and minimizing these errors [381] [292, 382–384].

7. Measurements of drug-target engagement

7.1 Fluorescence anisotropy visualization

Confocal and two-photon fluorescence anisotropy microscopy enable to image live cells with accurate spatial and temporal maps of fluorophores distributions.

However, displaying fluorescence anisotropy images is not always a straightforward easy task. In fact, anisotropy images are very sensitive to the noise as the calculations used for obtaining the anisotropy give rise to images where the relevant information is buried within the noise of the FA image. This can be ascribed to the presence of noise in the original fluorescence images. As mentioned in Section 5, this negative outcome can be in part overcome by acting on the microscope settings, or by using denoising filters. However, all components of the fluorescence images, where the signal is low, will inherently possess a low SNR leading to uninformative results in the final FA images. Although anisotropy images are directly derived from florescence images, it is important to highlight that the information content they carry is substantially different. For instance, in experiments like drug delivery in living cells, fluorescence signal is more related to the cell morphology with detailed structural information. Fluorescence anisotropy images instead provide information at a more functional level, for example detailing the degree of anisotropy and how possible drug-target interaction occurs. As a result the two image representation may present a low degree of correlation, and different representation schemes are recommended.

Rather than considering fluorescence and anisotropy information content as separate information contribution, it is more appropriate to consider their contributions simultaneously, for example attributing statistical importance to image pixels that present higher SNR to overcome the lack of structural information present within the fluorescence anisotropy images. This can be achieved implementing an imaging fusion method, a methodology that has been largely adopted since a long time in multimodal imaging [385]. This merging strategy has also been exploited in other fields of fluorescence microscopy such as in fluorescence lifetime imaging microscopy (FLIM), where lifetime- and fluorescence-image features are merged into a single image representation in the Hue-Saturation-Value color space.

Recently we have developed a similar approach for information fusion in fluorescence anisotropy imaging by mapping fluorescence and anisotropy data into a color coded Red-Green-Blue (RGB) space [255]. The fusion algorithm divides the pixels anisotropy values into three distinct groups, with separation levels determined a priori. Blue, green and red are chosen such that the respective clusters correspond to increasing intervals values. Due to the presence of noise in the anisotropy images, this kind of pixel assignment leads to pixel groups which are not perfectly separated in space and is cause of visual artifacts. To attenuate visual defects in the fused images, sharp color transitions are avoided. Instead smoother color fading is applied around thresholds values. To include morphological information, colored anisotropy images are also multiplied (pixel-wise) to the fluorescence images, which act as statistical weights for intensity modulation. Regions with low accuracy in anisotropy estimates (low fluorescence level) are statistically less informative and are multiplied to low values, so they will appear dark. On the contrary, regions with high intensity levels appear bright in colors.

As a result, single images will contain both the functional and structural information.

7.2 Cell segmentation

After image acquisition, data are not directly available for analysis and only after proper image processing and computational steps, quantitative analysis can be performed, for instance for diagnostic purposes or for insights into functional mechanisms. Cell segmentation is the first crucial step necessary to identify cells and cell compartments, to choose the cells of interest, and conduct large-scale, image-based screens for high throughput microscopy [386].

The main cell feature we are typically interested, when analyzing data for fluorescence anisotropy imaging, are the temporal evolution of the cellular volume, shape, cell contour, and signal distribution (cytoplasmic and/or nuclear). These features can be obtained through cell segmentation. During this process image pixels are usually divided into two different classes, depending if they are related or not to the structures of interest. But segmentation processes can easily lead to the erroneous identification of cells, especially if two or more neighboring cells are in contact or overlap with each other or if a large dynamic range of fluorescence intensity is present [247]. Also, segmentation algorithms can perform poorly if directly applied to raw images [387, 388] and cell staining is preferable to label for example cytoplasmic membrane structures [389].

Segmentation can be achieved either manually or automatically. Both approaches have pros and cons. Manual segmentation is considered more accurate, as it relies on the high computational capabilities of the brain and is often used as a benchmark for performance comparison. Nevertheless, human segmentation can be non-accurate if performed on volumetric data such as in tumors (Section 7.3), as the human visual system is not designed to perform segmentation of three-dimensional data by means of two dimensional monitor interfaces. Moreover, manual segmentation is both operator dependent and time consuming such that it is unreasonable to be considered as a viable solution for high throughput data analysis. On the other side automatic segmentation can be more coherent and suitable for large scale screening.

To date many methods have been implemented to deal with segmentation based on different approaches [390]. These methods are in most cases implemented using well established mathematical tools. Thresholding is possibly the simplest one and it exploits the fact that cells/nuclei pixels’ intensities can generally be expressed as a mixture of two distinct distributions such that objects and background can be easily separated. Thresholding values can be selected manually or automatically, and could be categorized as global, i.e. the same value is assumed valid for processing the whole image, or local, i.e. the threshold value may change over the image location. Manual thresholds are selected based on what the operator expects and knows about the structures to extract. Automatic thresholding is usually obtained through computations applied to the images. The Otsu method [391] for instance, computes thresholds using statistical variance minimization of what is classified as an object and a non-object. Open source software for cell segmentation such as CellProfiler [392, 393] permit to choose over a number of thresholding methods mostly based on statistical means [394, 395] [396].

More sophisticated approaches are based on filtering algorithms based on mathematical morphology, which exploits geometrical and topological features of image structures to perform transformations suitable for segmentation. Examples of mathematical morphology filters are erosion, dilation, opening, closing [397]. Segmentation can also be the result of application of watershed procedure [398] a region-based segmentation method based on topographical concepts.

In nucleus and cells segmentation, a widely used class of algorithm under the name of deformable models has been also applied to microscopy [399]. Deformable models, or their special instances, snakes [400], are widely used methods in computer vision which aim at finding the best fitting between deformable lines and image features by solving a minimization problem. To this end a cost function is used and its minimum is generally computed through an iterative procedure.

Segmentation can be also performed by using methods based on clustering, e.g. k-means clustering, fuzzy c-means and expectation-maximization [390]. Also methods based on machine learning, such as support vector machine (SVM) [401] and artificial neural network [402] are of increasing interest.

These alternatives are quite useful for all those instances where phenotyping differences are present due to drug effects. In this case segmentation of the nuclei and cytoplasm can be quite challenging using conventional segmentation approaches, and quantification of drug-target engagement could fail.

Overall image segmentation is a well establish topic in image processing with wide application to medical imaging in general and in optical fluorescence in particular. All the listed methods presented above can be applied to high resolution fluorescence anisotropy imaging in-vivo as in Section 7. Moreover, in the next future if fluorescence anisotropy high-content screening, high throughput imaging and accurate automatic image segmentation will be combined, a very powerful platform will be likely allow for breakthroughs in drug discovery and disease treatment.

7.3 Measurement and quantification of single cell drug-target engagement

Recent work from our group has shown that fluorescence anisotropy can be extended to two-photon imaging for drug–target engagement imaging at high spatial and temporal resolution. This provides quantitative measurement and imaging at the cellular level, of the fraction of the amount of drug bound to its target, information that has been unavailable so far in traditional fluorescence anisotropy measurements or other modalities. The potential of this approach has been possible thanks to recent advances in chemical techniques that have allowed for the design of fluorescent drugs, prodrugs and activity-based probe to interrogate target engagement [25, 403, 404]. Particularly in vivo their use has been demonstrated for imaging drug distribution [24] or clinical tumor detection [405] highlighting several routes of drug failure and potential solutions, therefore making them as good candidates for pharmacodynamics studies.

In this Section, we present our recent results on multiphoton fluorescence anisotropy microscopy to image and quantitate intracellular drug–target binding distribution using different cancer drugs. We show also that our approach is applicable in live cultured cells and enables real-time imaging of drug–target engagement in vivo at subcellular resolution, in xenograft tumors following systemic drug delivery.

For what concerns all the problematics related to intravital microscopic imaging experiments in mouse models [176, 406–409], window chamber models [410], imaging platforms [176], and general acquisition procedures [163, 164, 244, 245, 411–414] we refer to other reviews.

7.3.1 Labeling fluorophore choice

There are several considerations to take into account concerning the choice of the possible labeling fluorescent dye (see Section 3.1). Crucial for building a good assay sensitivity, defined as the range of fluorescence anisotropy values between the free and the bound fluorophore [111] is the fluorophore’s fluorescence lifetime. An interesting discussion regarding this issue can be found in Zhang et al. [111]. In general, fluorescent dyes with short lifetime (e.g. Cy3, Alexa dyes) are highly inefficient for fluorescence anisotropy measurements, because their anisotropy in the unbound state is too near to the fundamental one, making difficult to discriminate between bound and unbound states. Fluorophores with very long lifetimes, are also not recommended because the small increase in rotation correlation time, upon binding, does not increase sufficiently the fluorescence anisotropy value. Finally, we would like also the dye to present a high two-photon cross section at near infrared wavelengths, due to the advantageous features for tissue imaging compared to one-photon probes [415]. We found that BODIPY-FL is an ideal candidate for polarization-based assays, due to its fluorescence lifetime of approximately 4 ns which is larger than the rotational correlation of the bound complexes considered herein. Also BODIPY dyes present other properties [416, 417] that make them particularly suitable for two-photon fluorescence anisotropy intracellular imaging. They are relatively non-polar, minimizing perturbation to the modified drug. They are generally highly cell permeable, present a high fluorescence quantum yield, and extinction coefficient, and have a large two-photon cross section.

7.3.2 Fluorescence anisotropy two photon imaging of fluorescently labeled drug

The main hypothesis behind the imaging strategy here presented is that fluorescence polarization imaging can be adapted and used with fluorescently labeled drugs to measure drug target engagement in vitro and in vivo. As a proof of principle for our imaging modality we chose a drug belonging to the class of the reversible inhibitors which bind non-covalently.

Poly(ADP-ribose)polymerase (PARP) comprises a family of enzymes playing a fundamental role for DNA repair [418–420] and is upregulated in a large number of types of cancer [421–425]. Therefore, PARP inhibitors (PARPis) present a potential chemotherapeutic target through inhibition and several PARPis have been developed and translated to the clinical arena. The small molecule olaparib (AZD2281), is a reversible PARP inhibitor [426] and has been recently approved for clinical use by the US Food and Drug Administration for prostate cancer [427]. Due to its characteristics we chose this molecule as candidate for a fluorescently labeled imaging drug, and used BODIPY-FL as labeling dye. We first reported on the small molecule PARPi-FL [428], and showed that it retains the same functional activity for PARP1 as the parent drug [24]. Also Kossatz et al.[429] demonstrated its use for oral cancer screening. A detailed protocol for its synthesis can be found in [255].

HT1080 cells, a well understood fibrosarcoma cell line expressing PARP, were chosen as experimental model. Due to the high molecular weight of PARP1 (ca. 120 kDa), there is a significant change in molecular mass between free and target-bound or intracellular PARPi-FL (Fig. 6a,b). This change of mass can be monitored through two-photon fluorescence anisotropy imaging, allowing to follow the intracellular binding of the fluorescent analog of the PARP inhibitor to its target (Eq. 3,4).

Figure 6. Two-photon fluorescence anisotropy imaging of drug-target engagement.

(a,b) Comparison between the rotation of the free fluorescently labeled drug (PARPi-FL) in solution and when bound to its target (PARP). Due to the large difference in molecular weight between the target (ca. 120 kDa) and the small molecule, the fluorescence anisotropy of the drug-target complex will increase following two-photon excitation (Θ >> τ). (c,h) Temporal evolution of the fluorescence anisotropy (c-e) and intensity (f-h), for HT1080 cells incubated with PARPi-FL, at three representative time points during loading and washing phases. Adapted with permission from [255], Nature Publishing Group

Following image processing for proper denoising (Section 5.5), fluorescence anisotropy images can be calculated on a pixel-by-pixel basis. After assigning an anisotropy threshold to distinguish among the different bound and unbound states, weighted fluorescence anisotropy images are then color-mapped using the weighted RGB color-mapping scheme discussed in Section 7.1. Real time time-lapse imaging of HT1080 cells during drug loading and washing phases (Fig. 6c-h), shows that PARPi-FL enters the cells through the plasma membranes, and accumulates rapidly in the cytoplasm more than in the nucleus (Fig. 6c,f). But high values of anisotropy are present only in the nuclei (Fig. 6d,g), suggesting direct PARP binding. After the washing phase, there is a decrease in drug concentration in the cytoplasmic region, while the bound fraction of the drug increases in the nuclei, where PARP is present (Fig. 6e,h) Using appropriate segmentation protocols (Section 7.2) it’s possible to quantify numerically the fluorescence intensity and the degree of engagement, calculating the fluorescence anisotropy within the nuclei and the cytoplasmic area, and obtain the spatial-temporal evolution of target engagement in vitro (Fig. 7a-d).

Figure 7. Quantification of drug-target engagement.

(a-d) Normalized intensity and anisotropy as a function of time for HT1080 cells incubated with PARPi-FL, during loading and washing phases in the absence (black circles) and presence (grey squares) of five-fold higher concentration of unlabelled drug (competition). After segmentation, values are calculated in both cytoplasms and nuclei. (e-h) In vivo measurements of target engagement, in a tumor implanted in a skinfold dorsal window chamber at different time points following drug administration. Adapted with permission from [34], Nature Publishing Group

Because the imaging technique is based on two-photon microscopy, it is particularly viable for acquisitions in tissue (Section 4.6, 6.1) and real time imaging of drug-binding was demonstrated in tumor implanted in mice skinfold dorsal window chambers, following intravenous infusion. Due to the reduced scattering and extended imaging penetration depth (Section 6.1), fluorescence anisotropy can be accurately determined deep within the tissue and tumors, allowing to follow binding interaction in physiologically relevant contexts (Fig. 7e-h).

7.4 Competitive binding of matched fluorescently labeled drugs

The capability to modify drugs to create fluorescently-tagged small molecule reporters can offer insights into tissue distribution and target engagement measurements. Unfortunately the addition of the labeling fluorophore may change the physiochemical properties of the original small molecule, and the results obtained may substantially differ from the ones valid for the parent drug. Using the technique and tools illustrated in the previous Section, we have therefore developed an approach to quantify target occupancy of unlabeled drugs using competitive binding with fluorescently labeled analogues also known as CIP (companion imaging probes) [33]. Both parent drug and CIP share the same molecular target.

The main idea behind this strategy is that by monitoring target engagement of CIP via two-photon fluorescence anisotropy microscopy, we can determine the binding properties of the unmodified drug which is competing with the matched fluorescent CIP. High values of anisotropy will indicate no or low presence of unlabeled drug. Low values of anisotropy will indicate presence of unlabeled drug target engagement.

As a proof of principle for two-photon FA imaging of competitive binding, two small molecule drugs belonging to two different classes of inhibitors have been chosen. PARPi-FL, described above in Section 7.3.2 and belonging to the class of the reversible inhibitors, and a drug belonging to the class of the irreversible inhibitors, which usually react with the target enzyme via covalent bond. As a representative example of the latest ibrutin (PCI-32765, brand name: Imbruvica) [430, 431], a Bruton’s tyrosine kinase (BTK) inhibitor, has been selected.

Bruton’s tyrosine kinase (BTK) is a cytoplasmic non-receptor tyrosine kinase largely expressed in B lymphocytes, macrophages/monocytes, and certain cancer cells [432–435]. BTK is crucial for B cell development and is involved in the regulation of cell survival, proliferation, and differentiation, making it an attractive therapeutic target for B-cell disorders [431]. Ibrutinib is a selective, irreversible BTK inhibitor, whose covalent binding results in long-lasting target occupancy. While several BTK inhibitors are available or under development, ibrutinib has been shown to potently bind to BTK, to inhibit BCR signaling, and to decrease tumor cell survival and proliferation in many B cells malignancy models [436]. Due to these properties we synthesized a fluorescent irreversible BTK binder based on ibrutinib (ibrutinib-BFL) and used BODIPY-FL as the labeling dye [437].

The experimental approach presented in the schematic of Fig. 8 illustrates the protocol used to measure the covalent binding activity of ibrutinib. While in [33] the focus was on this specific compound, the idea can be extended to other drugs belonging to the class of the irreversible inhibitors.

Figure 8. Protocol schematic for covalent inhibitor competitive binding.

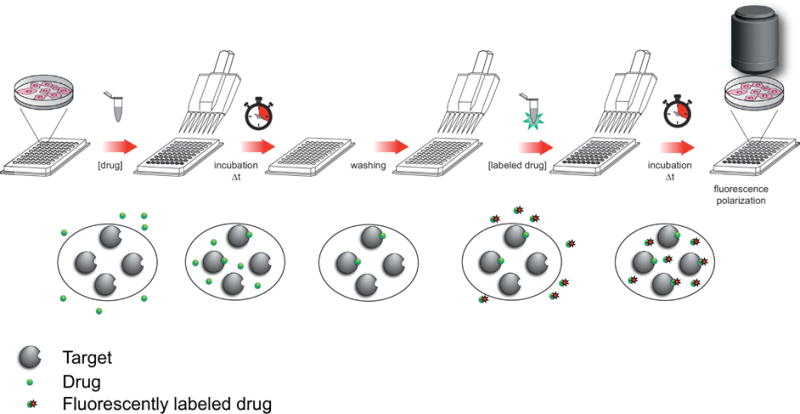
Cells are incubated at different concentrations ([]) and for different times (Δt), with the inhibitor. Excess is washed, and cells are incubated with the fluorescently labeled companion imaging probe, without washing. Adapted with permission from [33], Nature Publishing Group

Cells are first incubated at different drug concentrations for different times. Afterwards, excess drug is washed off. Cells are then incubated with the CIP ibrutinib-BFL for the desired time and fluorescence anisotropy images are taken without any washing. When ibrutinib-BFL is bound to its BTK target, values of fluorescence anisotropy will be high. But in the presence of the unlabeled parent drug, only a few ibrutinib-BFL molecules will find a free target available for binding, which will result in an overall decrease of fluorescence. Now, as discussed in greater detail in Section 2.3.3, values of measured anisotropy correspond to the fraction-weighted sum of all the possible states present within the two-photon probing volume. Therefore, when imaging the fluorescence anisotropy of CIP in cells, the measured values will be dependent on the total cellular CIP concentration (Eq. 5), and it would be wrong to directly infer target-engagement from absolute values of FA. To obviate this problem the value Δr*Int has been introduced [33]. This value is defined as the product of the difference in measured and unbound (nonspecific) fluorescence anisotropy multiplied by the total fluorescence intensity [33], representing the concentration of the CIP-bound target protein.

In [33] Toledo was chosen as a model of BTK-positive cells. Cells were incubated with different doses of ibrutinib before loading with ibrutinib-BFL. Because of the presence of the unlabeled drug, the measured fluorescence anisotropy of the CIP will be reduced in a concentration-dependent manner (Fig. 9a,b). After proper data processing and segmentation, measurements of cytoplasmic Δr*Int, as a function of ibrutinib concentration (Fig. 9c) indicated an intracellular ibrutinib inhibitor constant K_i of 2 nM and an intracellular second order binding constant k₂/K_i of 4.5 10⁵ s⁻¹M⁻¹. The imaging protocol was then extended to in vivo settings (Fig. 9d,e) using as a model HT1080 tumor cells transfected with BTK-mCherry, finding also dose dependent target engagement (Fig. 9f).

Figure 9. Competitive binding of matched fluorescently labeled drugs.

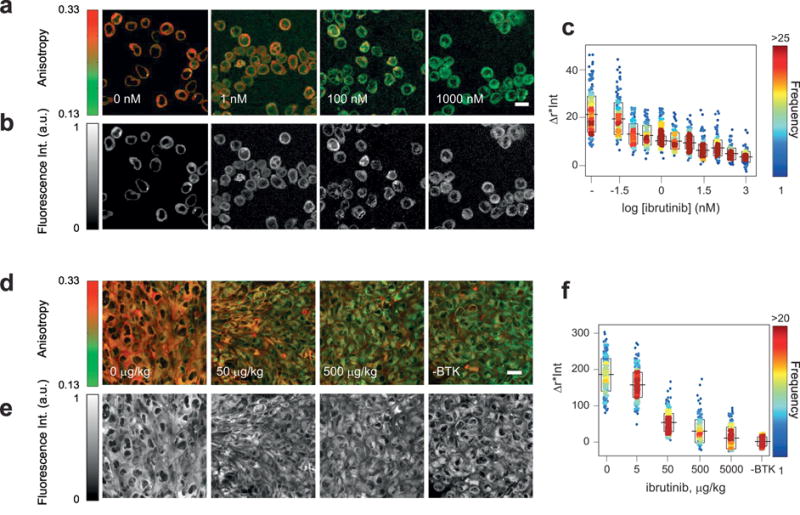
Fluorescence anisotropy (a) and intensity (b) images of Toledo cells in vitro, loaded at different concentration of ibrutinib, followed by ibrutinib-BFL. (c) Measurements on single cells cytoplasms after segmentation, of Δr*Int, at varying concentration of ibrunitb, followed by ibrutinib-BFL. Fluorescence anisotropy (d) and intensity (e) of HT1080 BTK-mCherry and BTK free HT1080 H2B apple dorsal window chamber tumors, following systemic ibrutinib delivery, and ex vivo ibrutinib-BFL loading. (f) Measurements on single cells cytoplasms after segmentation, of Δr*Int, at varying concentration of ibrunitb delivery, following ibrutinib-BFL loading. Adapted with permission from [33], Nature Publishing Group

Olaparib was also investigated, using the same competitive strategy and using the CIP described before i.e. PARPi-FL. For this case HT1080 cells were also chosen as experimental model. Incubating the cells with olaparib at different concentration, single-cell nuclei Δr*Int, were measured demonstrating target engagement dose dependence. Using Schild analysis apparent intracellular k_d values for olaparib in HT1080 were found to be equal to 2.0 nM. Similar analysis were then conducted on in vivo tumor models, following systemic olaparib delivery, revealing single cells with low target occupancy at high average target engagement.

8. Conclusions

Despite the progress in recently developed techniques aimed at measuring the cellular distribution and target-engagement of small molecule drugs in cell culture and in vivo, there is still a lack of methodologies capable to offer direct and quantitative measurement of drug-target engagement in live cells with both subcellular and temporal resolution.

Fluorescence polarization/fluorescence anisotropy has been widely used in biomedical research as a platform for high throughput screening campaigns, and to kinetically and thermodynamically profile protein-small molecule and protein-protein interactions. However, fluorescence anisotropy has been mostly limited to biochemical assays. In contrast, optical imaging technologies such as fluorescence microscopy, are ideal for both in vitro and in vivo single-cell phenotypic studies thanks to the high spatiotemporal resolution and extended depth imaging they offer.

The possibility to integrate fluorescence polarization/fluorescence anisotropy detection schemes in fluorescence light microscopy methodologies can provide direct insights into the molecular pharmacology of drugs in vitro and in vivo, thanks to the emergence of a growing list of fluorescent drug derivatives with comparable target specificity and affinity as the parent drug. In particular, the quantification of time-resolved specific drug-target engagement and the distinction from unspecific binding to off-target proteins, enables the direct correlation of treatment efficacy with cellular activity.

Finally, the possibility to apply this approach exploiting the competitive binding of unlabeled drugs with a fluorescent tracer also offer the opportunity to direct quantify target occupancy of unlabeled drugs in live intact cells both in vivo and in vitro.