Functional capacity of kangaroo rat hindlimbs: adaptations for locomotor performance

Abstract

Many cursorial and large hopping species are extremely efficient locomotors with various morphological adaptations believed to reduce mechanical demand and improve movement efficiency, including elongated distal limb segments. However, despite having elongated limbs, small hoppers such as desert kangaroo rats (Dipodomys deserti) are less efficient locomotors than their larger counterparts, which may be in part due to avoiding predators through explosive jumping movements. Despite potentially conflicting mechanical demands between the two movements, kangaroo rats are both excellent jumpers and attain high hopping speeds, likely due to a specialized hindlimb musculoskeletal morphology. This study combined experimental dissection data with a static analysis of muscle moment generating capacities using a newly developed musculoskeletal model to characterize kangaroo rat hindlimb musculoskeletal architecture and investigate how morphology has evolved to meet hopping and jumping mechanical demands. Hindlimb morphology appears biased towards generating constant moment arms over large joint ranges of motion in this species, which may balance competing requirements by reducing the need for posture and movement specific excitation patterns. The ankle extensors are a major exception to the strong positive relationship exhibited by most muscles between muscle architecture parameters (e.g. L_fibre) and joint moment arms. These muscles appear suited to meeting the high moments required for jumping: the biarticular nature of the ankle extensors is leveraged to reduce MTU strain and create a four-bar linkage that facilitates proximal force transfer. The kangaroo rat hindlimb provides an interesting case study for understanding how morphology balances the sometimes competing demands of hopping and jumping.

1. Introduction

One determinant of an animal's evolutionary success is its ability to move across terrain in its environment [1,2]. Thus, metabolic efficiency is believed to be an important factor during locomotion, with several documented behavioural and morphological adaptations consistent with this idea. For example, many animals (e.g. humans, horses, ostriches) actively switch between gait patterns in a manner that reduces metabolic cost [3–5]. Additionally, many cursorial species such as ostriches have a number of morphological adaptations that presumably enable efficient movement. Musculoskeletal adaptations include elongated distal limb segments, highly derived muscle–tendon unit (MTU) characteristics (e.g. short-fibred, pennate ankle extensors), and long, slender tendons. Combined, these characteristics may reduce mechanical demands during locomotion by allowing muscle mass to be located more proximal on the limb and/or providing a spring-like mechanism that can store and return energy [6–8].

Relatively few animals use hopping as a primary form of locomotion. Large hopping animals (e.g. kangaroos and wallabies) share many of the musculoskeletal adaptations associated with cursorial species. Indeed, large hopping animals are more efficient than similarly sized quadrupedal cursorial species, with tendon energy storage and return accounting for an energy saving of up to 25% during hopping in kangaroos [4,9–11]. However, small hopping mammals such as kangaroo rats (Dipodomys) or jerboas (Jaculus) are less efficient locomotors with efficiencies comparable to similar-sized quadrupedal species [12–14]. One possible reason for the decreased efficiency—relative to larger hoppers—is that small hoppers have thicker ankle extensor tendons that do not prioritize tendon energy storage and return [15–18]. Regardless, the elongated limbs and correspondingly long tendons in these rodents result in a highly derived and specialized muscle arrangement that appears adapted for desert movement [13].

For small prey animals, the ability to evade predators may be equally if not more important than locomotor efficiency. Hence, kangaroo rats have evolved an extraordinary ability to perform high powered jumping movements to evade predation. These movements present a second, distinct set of mechanical demands and constraints acting on the hindlimb musculoskeletal system. In some cases, a single musculoskeletal adaptation may improve both movements' performance. For example, jumping and hopping both benefit from elongated limbs. However, the underlying mechanical reasons why long limbs benefit each motion are different. During jumping, longer limbs can increase ground contact time during vertical body acceleration, allowing an animal to produce mechanical energy over longer time periods to improve maximum jump performance [19–21]. On the other hand, in hopping, longer limbs allow for musculotendon designs with longer tendons to increase tendon energy storage and return capacity and the utilization of longer stride lengths, resulting in more efficient hopping mechanics [9–11].

However, in other instances the mechanical demands of jumping compete directly with those associated with efficient hopping, which may be reflected in MTU design. Kangaroo rat survival rate has been shown to be inversely related to the time required to displace its body (i.e. a quicker movement response increases evasion success) [22,23]. Thus, minimizing reaction time (i.e. time from neural command to limb and body movement) is critical. One way to improve both reaction time and evasion speed is by modifying MTU design to increase power by improving force generating capacity and/or the rate of force production. In other species, flexible tendons increase power by allowing MTUs to release previously stored tendon energy (i.e. pre-loaded tendon) during a subsequent movement (i.e. ‘power amplification’) [24,25]. However, in kangaroo rats, the extremely fast reaction times likely preclude an MTU's ability to pre-load a tendon to increase power output. If not pre-loaded, MTU designs incorporating flexible tendons become detrimental to explosive movements as they must first be stretched by the muscle fibres to some threshold, resulting in mechanical delays between muscle force generation and segment/body movement. As a result, there is a likely trade-off in MTU design in these animals, with more flexible tendons improving hopping efficiency through tendon energy storage and return and stiffer tendons improving reaction times during jumping.

There are also potential trade-offs in muscle fibre architecture [26–28]. In steady hopping, joint ranges of motion (ROMs) are relatively small during stance and high priority is placed on muscle efficiency. At the most basic level, corresponding muscle designs that meet these requirements would have short muscle fibres arranged in a pennate fashion. On the other hand, one-time explosive movements like jumping prioritize maximum force capacity and rate of force production over efficiency. Joints also go through much larger ROMs, beginning in highly crouched postures and ending in very extended positions, usually requiring larger MTU length changes [16,29,30]. As a result, the ideal muscle design for quick, high force jumping would consist of long fibres in a parallel arrangement. However, when considered in the larger context of its ability to move (or restrain) a joint, alternative muscle designs may be possible by altering a muscle's moment arm throughout a joint's ROM (i.e. variable gearing) [31,32]. Thus, muscle design should be discussed relative to its moment arm when evaluating performance during functional movements [26–28].

Despite conflicting mechanical demands between hopping and jumping, kangaroo rats are both extremely good jumpers and hoppers, capable of quickly jumping over nine times hip height [16,18,30] and hopping at speeds up to 8.3 m s⁻¹ [33]. Their ability to perform both movements well is likely due to a specialized hindlimb musculoskeletal design that balances the competing mechanical demands associated with the two movements. Thus, this study aims to characterize kangaroo rat (Dipodomys deserti) hindlimb musculoskeletal architecture, with a specific focus on understanding how hindlimb morphology has evolved to achieve exceptional hopping and jumping capabilities. To address this aim, experimental dissection is combined with a static analysis of jumping and running movements using a newly developed musculoskeletal model of a kangaroo rat hindlimb to investigate relationships between muscle architecture, moment arms, and muscle moment generating capacity during jumping and hopping movements.

2. Methods

2.1. Animals

A total of 16 adult kangaroo rat (D. deserti) cadavers were used to obtain the necessary data for this study. All animals had been previously sacrificed for an unrelated study. Although genders were not identified, there is no significant sexual dimorphism in this species. Average animal mass was 105.9 g and ranged from 85.7 g to 132.7 g (table 1).

Table 1.

Average (standard deviation) for each measured segment property (mass, centre of mass, inertia, and length) with the corresponding musculoskeletal model value.

	experimental mean (s.d.)a	model value
mass (g)
whole animal	105.86 (12.09)	100.00
body/head	56.00 (9.90)	53.89
pelvis	18.00 (2.83)	17.37
femur	8.28	8.28
tibia	4.58	4.58
metatarsals	0.95	0.95
toes	0.56	0.56
COM (mm)
body/head: posterior to eye	30.24 (1.64)	29.72
body/head: ventral to eye	3.99 (3.46)	4.38
pelvis: anterior to hip	3.34 (2.31)	2.38
pelvis: dorsal to hip	1.33 (1.00)	1.32
femur: distal to hip	16.98	16.17
tibia: distal to knee	17.50	17.12
metatarsals: distal to ankle	16.40	13.86
toes: distal to MTP	7.53	7.54
inertias (kg mm2)
body/head	55.90 (14.70)	66.28
pelvis	15.74 (2.50)	17.51
thigh	0.084	0.084
shank	0.025	0.025
midfoot	0.008	0.008
toes	0.004	0.004
lengths (mm)
body/head	64.80 (4.94)	67.00
pelvis	19.90 (2.52)	20.10
femur	27.04 (1.19)	27.04
tibia	45.55 (2.63)	48.41
midfoot	24.07 (2.09)	24.34
toe	17.88 (1.70)	18.10

^aIf no standard deviation is provided, only a single measurement was available to report.

2.2. Anatomical dissection

A total of 16 animals were used to obtain the anatomical data necessary to complete the study. Specimens were fresh frozen immediately after sacrifice (for a non-related study) and preserved frozen until dissection. Eight specimens were used to characterize muscle properties and five were used to define MTU length and joint angle relationships. Prior to dissection, these specimens were thawed at 40°F (4.4°C). The last three specimens used to determine mass and centre of mass (COM) values were maintained frozen throughout the data collection process.

After thawing, the eight specimens used for anatomical muscle dissection had the hindlimbs oriented in approximately a midstance hopping posture with the femur perpendicular to the pelvis/body, the knee flexed to 45°, and the foot oriented perpendicular (i.e. 90°) to the shank segment. In each specimen, muscles were systematically removed working from superficial to deep structures. Muscle masses (m) were measured to the nearest milligram (H51; Sartorius Lab Instruments, Göttingen, Germany). Following this, each muscle was bisected with a sharp scalpel to measure pennation angle (θ) and fibre length (L_fibre, mm). The sections of the muscle belly were exposed by removing one half of bisected muscle and care was taken to minimize stretching or deforming the muscle belly, as this can affect the pennation angle. Because values are dependent on measurement location within a muscle (e.g. proximal versus distal), L_fibre and θ were obtained from at least three different locations throughout the muscle. These values were then averaged to provide a representative muscle value. Physiological cross-sectional area (PCSA, mm²) was then calculated from the average L_fibre and θ measurements according to the equation:

2.1

where ρ is the density of skeletal muscle (0.001056 g mm⁻³ [34]). Maximum isometric force (F_max, N) for each muscle was estimated from PCSA using a muscle specific-tension value of 300 kPa [35].

2.2

Overall sample mean and deviation values were then calculated from the individual animal measurements.

Five additional animals were used to determine joint ROMs and characterize the relationship between MTU length (L_MTU) and joint angle (i.e. muscle line of action). ROM values were obtained using intact hindlimbs by manually manipulating the joints to the flexion and extension limits. The L_MTU joint angle relationships were determined using the tendon travel method (figure 1a), which has been shown to reduce errors caused by potential inaccuracies in joint axis estimation [36]. A detailed account of the methodology can be found elsewhere [37], but its adaptation to this study will be briefly described here.

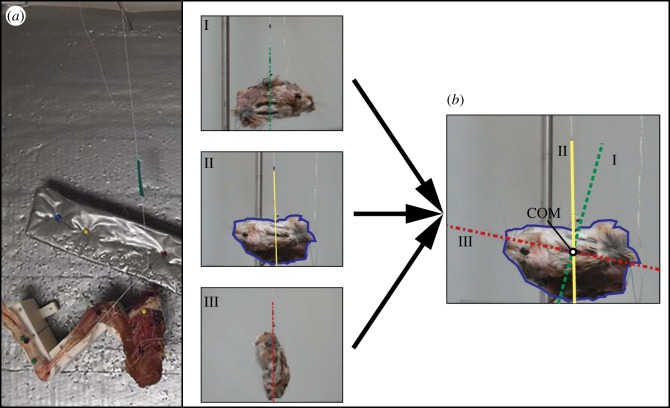
Figure 1.

(a) Experimental set-up used for determining the relationships between joint angle and musculotendon length (i.e. tendon travel). (b) Approach used to determine the location of the centre of mass (COM) of each body segment. Calibrated photos of a segment attached to a string at three different points (I, II, III) are taken, with the line represented by the string in each photo passing through the COM. The images are then overlaid and rotated: the intersection of the lines from each rotated image provides the COM location. (Online version in colour.)

In each trial, either the origin or insertion site of one muscle was carefully removed from its bony attachment. In uniarticular muscles, origin points were solely used as the point of removal. However, biarticular muscles required a minimum of two trials: one with the origin removed and a second with the insertion removed to represent muscle length changes as joint angle was varied. Following site removal, all but a small portion of the MTU was detached and replaced with suture (figure 1a). The joint about which the MTU crossed was then identified and the entire hindlimb was mounted to a custom-built device that allowed: (i) rigid mounting of all segments proximal to the joint of interest, (ii) placement of the estimated joint centre over a pin joint on the device, and (iii) additional mounting of segments distal to the joint of interest. This device allowed the user to freely rotate the joint of interest over the entire ROM while maintaining a rigid base for each hindlimb segment. After mounting the limb, the muscle of interest was replaced in its anatomical location such that the suture crossed the originally removed site (e.g. origin for uniarticular muscles). To ensure a consistent path but still allowing for translation along its length the suture was thread through a needle. A weight suspended on the end of the suture provided constant tension (figure 1a). Photographs were used to record the location of a marked point on the suture versus joint angle at approximately 5 degree intervals as the limb was moved twice through the full ROM. In the case of biarticular muscles, this process was repeated three times, with the posture of the fixed joint systematically varied to ensure that all possible length angle relationships could be quantified. Calibrated camera images were used to determine the relationship between joint angle (ϕ) and L_MTU.

Last, three specimens were used to calculate segment masses and inertia properties for use as input into the detailed musculoskeletal model. Hindlimb (i.e. femur, tibia, midfoot and toes) and body (i.e. pelvis and body/head) segments were isolated by cutting through joint centres of rotation (e.g. femur segment was cut at the hip joint and knee joint centres), with care taken to preserve all soft tissue material that corresponds to the segment (observed while determining joint ROM). Segment masses were recorded to the nearest milligram (L420P; Sartorius). COM values were determined by taking a series of photographs (minimum 3) of a segment within a calibrated plane. For each photograph, the segment was suspended using a single string attached to a unique segment location. A line defined by the string was extended across the entire segment in each photograph after which the photographs/lines were superimposed. The segment COM location corresponded to the intersection point of the individual lines (figure 1b).

Although not specifically required for this study, inertia values were calculated in order to fully define the segments in the musculoskeletal model. This was done using the pendulum method, which involves suspending each segment from a string and allowing it to oscillate [38]. A single high-speed video camera (XC-2; Xcitex Inc., Woburn, MA, USA) was used to record (250 Hz) the oscillations within a calibrated plane. Because jumping and hopping are primarily planar motions, only the sagittal plan inertia value (kg mm²) was calculated for each segment, according to the equation:

2.3

where τ is the period of oscillation (seconds), m is the mass (kg), g is acceleration due to gravity (ms⁻²) and L (m) is the distance from the pendulum attachment point to the segment's COM.

2.3. Musculoskeletal model

A detailed planar musculoskeletal model of a kangaroo rat right hindlimb was developed within SIMM (Musculographics Inc., Santa Rosa, CA, USA) based on the experimental data. The model consisted of five segments representing the pelvis, femur, tibia, midfoot (tarsals and metatarsals) and toes. Experimental segment masses, COM locations and sagittal plane inertia values were set by scaling the experimental segment data to a representative animal's whole-body mass (100 g) (table 1). Digital 3D skeletal geometry of the pelvis and hindlimb were obtained by cleaning the bones, painting them grey to improve contrast, and placing them within a 3D scanner (Model 2020i, NextEngine Inc., Santa Monica, CA, USA).

Model segment lengths and joint articulations were calculated from the 3D bone scans. To do this, the scans were imported into Maya 2015 (Autodesk Inc., San Rafael, CA, USA) and arranged in an anatomically neutral posture (i.e. straight limb). Volume primitives (i.e. spheres and cylinders) were then visually fit to joint surfaces using anatomical landmarks (e.g. ankle condyles, femoral head) using the approach described by Panagiotopoulou et al. [39]. Joint articulations were defined to be at the centre (sphere) or midpoint of the central axis (cylinder) of these objects. For this model, joints were defined to only allow flexion–extension and ROMs were set based on the experimental data. Joint articulations were verified by visually ensuring that bone geometry did not intersect across each joint ROM. Segment lengths were defined as the distances between adjacent joint centres. The final model had seven degrees of freedom. Four degrees of freedom were used to represent joint motion; flexion–extension of the metatarsal–phalangeal (MTP), ankle, knee and hip joints. The final three degrees of freedom represented the planar position (horizontal, vertical) and orientation of the pelvis segment with respect to the global (i.e. ground) coordinate system (for angle references see insets in figures 3–5). The skeletal geometry and joint definitions were then imported into SIMM to add muscle representations.

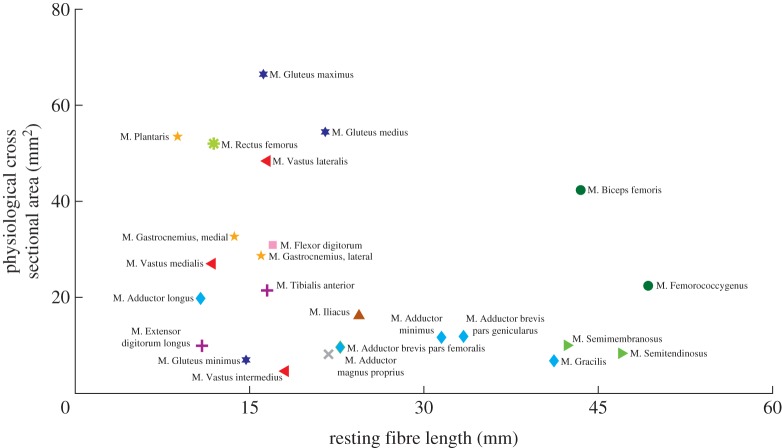
Figure 3.

Relationship between optimal fibre length (L_fibre) and physiological cross-sectional area (PCSA) derived from anatomical dissection for each muscle. The different shapes represent muscles of similar anatomical action (e.g. diamond: biarticular hip adductors). See table 2 ‘Model abbreviation’ for list of symbols. (Online version in colour.)

Figure 5.

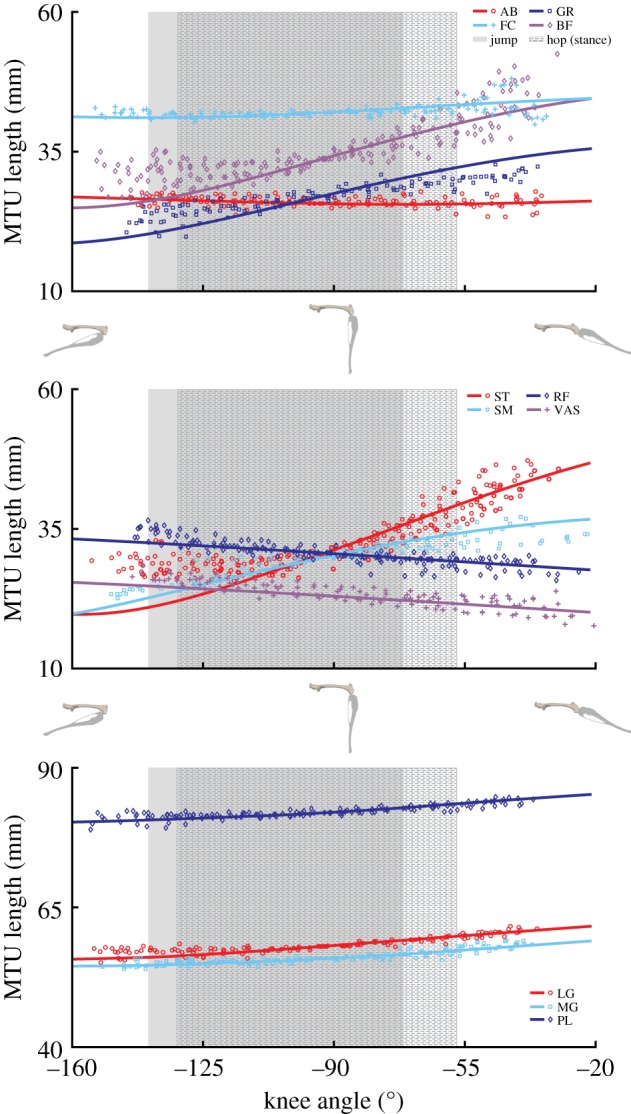
Experimental (symbols) and model-generated (lines) musculotendon lengths of muscles crossing the knee throughout the range of motion. Shaded areas represent the functional knee range of motion during representative jumping and hopping (stance phase) movements. For definitions of abbreviations, see table 2. Skeletal images provide a visual representation of the knee joint angles at the range of motion midpoint and extremes. (Online version in colour.)

The hindlimb muscles identified in the anatomical dissection were represented by defining 20 musculotendon actuators (some muscles combined in model, see Results). Origin and insertion points for each actuator were set using landmarks on the bone geometry previously identified during dissection. Muscle–tendon paths, origins and insertions were initially estimated based on dissection data and using bony landmarks then refined to match the empirical L_MTU joint angle relationships (see Anatomical dissection). To account for size differences between the model geometry and animal specimens, experimental MTU lengths were normalized to match the corresponding model musculotendon actuator length at the midpoint of each joint's ROM.

Musculotendon actuators were defined using a generic Hill-type muscle model [40]. The generic model was then made muscle-specific for each actuator by setting four parameters: maximum isometric force (F_max), optimal fibre length, pennation angle (θ) and tendon slack length (L_tsl). Maximum isometric forces and pennation angles were taken directly from the experimental data. Model optimal fibre lengths were initially set to be equal to the average value of the empirically measured fibre lengths (L_fibre) for each muscle. When a single musculotendon actuator represented multiple muscles (e.g. hip adductor group), F_max was set to be the sum of individual muscles in the group (table 2), while model fibre length and θ were set to the group average values. Tendon slack lengths were estimated using the approach described by Manal & Buchanan [42]. First, the desired muscle fibre operating range for each muscle was set a priori to [0.70, 1.25] of optimal fibre length. Minimum and maximum MTU lengths were then obtained for each muscle from the musculoskeletal model. These lengths, the desired operating range, and optimal fibre length were used within a Monte Carlo simulation to estimate L_tsl. In a few instances, the L_tsl estimate resulted in physiologically impossible (i.e. negative) values. For these musculotendon actuators, optimal fibre length was systematically decreased until the L_tsl estimate provided a non-negative number.

Table 2.

Major hindlimb muscles of D. deserti with their physiological parameters obtained via dissection and associated musculoskeletal model values. Tendon slack lengths are estimated using the approach proposed by Manal & Buchanan [41]. Anatomical functions listed in italics represent the primary action of each muscle/group.

muscle	muscle mass (g)	measured fibre length (Lfibre, mm)	pennation angle (degrees)	PCSA (mm2)	maximum isometric force (Fmax, N)a	model abbreviation	model optimal fibre length (mm)	model tendon slack length (Ltsl, mm)	model pennation angle (degrees)	origin	insertion	anatomical action
M. Adductor brevis pars genicularus	0.403 (0.153)	33.4 (7.8)	parallel	11.9 (5.3)	3.6 (1.6)	ABa	28.8	1.5	parallel	pelvis	tibia	hip adduction, hip extension, knee flexion
M. Adductor brevis pars femoralis	0.248 (0.161)	22.8 (8.1)	parallel	9.6 (3.9)	2.9 (1.2)
M. Adductor minimus	0.428 (0.212)	31.5 (6.7)	parallel	11.7 (7.4)	3.5 (2.2)
M. Adductor longus	0.232 (0.266)	10.8 (0.5)	parallel	19.8 (22.4)	6.0 (6.7)
M. Adductor magnus proprius	0.193 (0.080)	21.8 (4.0)	parallel	8.2 (2.1)	2.4 (0.6)	AMP	21.8	1.2	parallel	pelvis	femur	hip adduction, hip extension
M. Biceps femoris	2.167 (0.412)	43.5 (6.9)	parallel	42.3 (5.3)	12.7 (1.6)	BF	38.5	0.5	parallel	pelvis	tibia	hip abduction, hip extension, knee flexion
M. Femorococcygenus	1.095 (0.103)	49.3b	parallel	22.4b	6.7b	FC	45.3	0.5	parallel	pelvis	tibia	hip abduction, hip extension, knee flexion
M. Extensor digitorum longus	0.128 (0.035)	10.9 (1.9)	17.4 (2.5)	9.9 (4.3)	3.0 (1.3)	EDL	10.9	61.4	17.4			ankle flexion, digital extension
M. Flexor digitorum	0.222 (0.015)	16.2 (6.3)	24.3 (0.6)	30.9 (30.8)	9.3 (9.2)	FD	17.0	11.4	24.3	midfoot	toes	digital flexion
M. Gluteus maximus	1.137 (0.210)	16.2 (2.7)	15.0 (3.2)	66.5 (20.2)	20.0 (6.1)	GMAX	16.2	6.6	15.0	pelvis	femur	hip extension
M. Gluteus medius	1.104 (0.107)	21.5 (4.2)	12.3 (3.1)	54.5 (11.8)	16.4 (3.5)	GMED	20.7	5.0	12.6	pelvis	femur	hip extension
M. Gluteus minimus	0.104 (0.013)	14.7 (2.4)	15b	7.0 (3.6)	2.1 (1.1)
M. Gracilis	0.304 (0.162)	41.2 (8.3)	parallel	6.8 (2.8)	2.0 (0.8)	GR	31.2	0.5	parallel	pelvis	tibia	hip extension, hip adduction, knee flexion
M. Iliacus	0.410 (0.151)	24.4 (5.1)	parallel	16.2 (5.4)	4.9 (1.6)	IL	24.4	0.5	parallel	pelvis	femur	hip flexion
M. Gastrocnemius, lateral	0.489 (0.112)	16.0 (4.0)	18.8 (6.5)	28.7 (8.1)	8.6 (2.4)	LG	16.0	40.4	18.8	femur	midfoot	ankle extension, knee flexion
M. Gastrocnemius, medial	0.432 (0.111)	13.7 (6.5)	22.6 (3.7)	32.7 (15.4)	9.8 (4.6)	MG	13.7	40.4	22.6	femur	midfoot	ankle extension, knee flexion
M. Plantaris	0.394 (0.111)	8.8 (3.4)	22.8 (7.4)	53.5 (46.3)	16.0 (13.9)	PL	8.8	72.4	22.8	femur	midfoot	ankle extension, knee flexion
M. Rectus femoris	0.672 (0.128)	11.9 (3.0)	22.2 (6.1)	52.0 (11.7)	15.6 (3.5)	RF	11.9	17.8	22.2	pelvis	tibia	hip flexion, knee extension
M. Tibialis anterior	0.342 (0.103)	16.5 (5.9)	16.0 (4.0)	21.4 (13.9)	6.4 (4.2)	TA	16.5	26.0	26.0	tibia	midfoot	ankle flexion
M. Semitendinosus	0.406 (0.130)	47.0 (9.5)	parallel	8.4 (3.1)	2.5 (0.9)	ST	38.0	0.5	parallel	pelvis	tibia	hip extension, knee flexion
M. Semimembranosus	0.515 (0.262)	42.3 (7.5)	parallel	10.0 (3.4)	3.0 (1.0)	SM	34.8	0.5	parallel	pelvis	tibia	hip extension, knee flexion
M. Vastus lateralis	0.849 (0.130)	16.5 (3.1)	16.7 (6.4)	48.4 (12.1)	14.5 (3.6)	VL	16.5	12.8	16.7	femur	tibia	knee extension
M. Vastus intermedius	0.098 (0.045)	18.1 (4.4)	parallel	4.6 (1.7)	1.4 (0.5)	VI	18.1	5.1	parallel	femur	tibia	knee extension
M. Vastus medialis	0.300 (0.072)	11.8 (4.5)	19.5 (7.3)	27.0 (4.7)	8.1 (4.4)	VM	11.8	7.0	19.5	femur	tibia	knee extension

^aIn the model, AB and GMED represent multiple muscles. The maximum isometric force in the model represents the summed forces of these muscles (AB: 16.0N, GMED: 18.5N).

^bOnly one measurement was available for this parameter. Symbols correspond to those used in figure 3.

2.4. Estimating muscle moment capacity

Joint kinematics of representative jumping [30] and hopping [43] trials were taken from unrelated studies and used as inputs into the model for further analysis. Jumping data were collected using high-speed video (200 Hz). Hopping data were collected using a single fluoroscope connected to a video camera (500 Hz). For both movements, joint angles were calculated based on digitized landmarks [30]. A single representative trial was selected from each dataset and used to determine functional joint angles (see electronic supplementary material, table S1).

To estimate each muscle's potential to contribute to joint moments during hopping and jumping, a maximum theoretical moment for each joint (i.e. moment generating capacity, M) was calculated at two degree intervals over each joint's ROM. To perform this calculation, individual muscle moment capacities were first estimated using the musculoskeletal model. Because the measurement of optimal fibre length used in this study has a moderate degree of uncertainty, muscle force values were calculated using optimal lengths ±10% of the model defined rest length by updating each muscle's F_max based on the new rest length according to equations (2.1) and (2.2). Operating fibre lengths were then estimated for each angle (ϕ) assuming a stiff tendon, according the equation:

2.4

where L_fibre,ϕ is the operating fibre length at the angle of interest and L_MTU,ϕ is the total MTU at the same angle. The muscle's peak force generating capacity for the angle (F_scale,ϕ) was determined by scaling F_max by its intrinsic force–length relationship (i.e. assuming a maximally activated muscle) [40]. Moment generating capacity for each angle across the ROM of each joint was then obtained from the individual muscle force capacities (F_scale,ϕ) and the model predicted muscle moment arm (r) according to the equation:

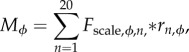2.5

where n = [1,20] represents each individual musculotendon actuator in the model. From these data, peak extension and flexion moments were obtained as well as maximum muscle moment capacity over the joint operating ranges during hopping and jumping.

3. Results

3.1. Hindlimb anatomy

As detailed anatomical sketches for similar species are available elsewhere [44], this study focused primarily on variables related to how muscle and hindlimb anatomy might influence hopping and jumping capability. Twenty-four muscles from the kangaroo rat (D. deserti) hindlimb were characterized, comprising all the major hindlimb muscles (table 2, figure 2a). Total single-limb hindlimb muscle mass averaged 12.67 g, accounting for approximately 12.9% of the total animal body mass. Over half of the muscles (15) were biarticular, with their MTU crossing the hip and knee. There was a large variation in muscle architecture, including muscles with large PCSA and short L_fibre (e.g. Gluteus maximus) and small PCSA and long L_fibre (e.g. M. Semitendinosus; figure 2). Consistent with the distribution of hindlimb muscle mass, individual limb segment mass and inertia values followed a decreasing proximal to distal gradient. Mass centres were located approximately at the midpoint in the pelvis, midfoot, and toe segments, two-thirds along the femur length (measured from hip joint), and one-third along the tibia length (measured from the knee joint; table 1; figure 2b).

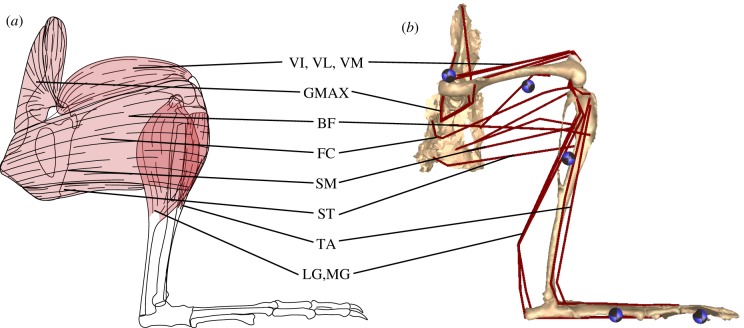
Figure 2.

(a) Schematic of the major lateral hindlimb muscles and (b) corresponding musculotendon actuators on the hindlimb musculoskeletal model. Segment names and centre of mass locations (circles) are also provided as a reference. See table 2 (‘Model abbreviation’) for muscle abbreviations. (Online version in colour.)

Fifteen distinct muscles were found to cross the hip joint, comprising the majority of the overall hindlimb muscle mass (66%). Of these muscles M. Adductor magnus proprius (AMP), M. Iliacus (IL), M. Gluteus maximus (GMAX), and Mm. Gluteus medius and minimus (GMED) were uniarticular. The gluteal muscle group, whose anatomy suggests they primarily act as hip extensors, was moderately pennate (15.9°) and short fibred. Together these muscles comprised 18.5% of the total hindlimb muscle mass. Similar to the gluteal group, the biarticular M. Rectus femoris (RF) had a high degree of pennation (23°), resulting in an arrangement of short fibres with a large PCSA (figure 2). This large bi-articular muscle, along with the uniarticular IL, are anatomically antagonistic to the gluteal group and act primarily as hip flexors. All other muscles crossing the hip were parallel fibred and tended towards longer optimal fibre lengths (figure 2). AMP was the sole uniarticular hip adductor. Based on anatomy, four additional muscles (Mm. Adductor brevis pars genicularus, Adductor brevis pars femoralis, Adductor minimus, and Adductor longus; AB) were identified to have hip adduction as a primary action. These muscles were bi-articular, originating from medial-ventral pelvis locations and inserting on proximal-medial tibia locations. As a result, these muscles had a secondary action as knee flexors. The lateral bi-articular muscles (M. Biceps femoris, BF; M. Femoroccygenus, FC) comprised the largest mass of all the hip muscles (26% of total hindlimb mass). Their muscle paths allowed them to act as hip abductors, hip extensors and/or knee flexors. These muscles represented one extreme in the hindlimb muscle architecture: the parallel fibred muscles had both long L_fibre and large PCSA values (figure 2). Mm. Semitendinosus (ST) and Semimembranosus (SM) originated most ventrally on the pelvis and inserted on the medial (SM) or lateral (ST) tibia near its midshaft. These muscles had some of the longest L_fibre and smallest PCSA values, with their anatomical location suggesting that they primarily act as hip extensors and knee flexors.

Besides the biarticular hip muscles, six additional muscles crossed the knee joint. Three of these muscles (M. Vastus lateralis, VL; M. Vastus intermedius, VI; M. Vastus medialis, VM) comprised the vasti muscle group, which was uniarticular and acted as knee extensors, originating from the proximal femur and inserting into the patella. Similar to the gluteal group, the vasti muscle group comprised a large percentage of the total hindlimb muscle mass (31.2%), were moderately pennate (approx. 18°), short fibred, and had high PCSAs. The other three muscles were the M. Plantaris (PL), and the medial and lateral heads of the M. Gastrocnemius (MG and LG, respectively). All three muscles originated on the distal and ventral side of the femur, potentially assisting in knee flexion.

A total of six muscles were identified that crossed the ankle. The anatomy of the aforementioned biarticular PL, MG, and LG suggest they function primarily as ankle extensors. All three muscles were pennate (18.8°–22.8°) with short fibre lengths and large PCSAs (table 2, figure 2). Despite their large force generating capacity (table 2) the muscles are relatively small, only comprising 10% of the total hindlimb muscle mass. In addition, most of this mass is located just distal to the knee joint, with long tendons allowing the muscles to act as ankle extensors. Two muscles, the uniarticular M. Tibialis anterior (TA) and biarticular M. Extensor digitorum longus (EDL), originated on the proximal anterior portion of the tibia. Both had insertion points on the foot with the EDL additionally spanning the metatarsophalangeal joint (MTP). As a result, the muscles' primary anatomical action was ankle flexion. The TA was moderately pennate (16°) while the EDL was parallel fibred. Both muscles had short optimal fibre lengths (table 2; figure 2) and, similar to the ankle extensors, used long tendons to locate the majority of their mass close to the knee joint. The final muscle identified was the M. Flexor digitorum (FDL), a uniarticular digital flexor that acted antagonistic to EDL at the MTP joint.

3.2. Musculoskeletal model

As previously discussed (see Musculoskeletal model above), individual segment and musculotendon actuator values were derived directly from the experimental data (tables 1 and 2). Due to their spatial proximity and similar anatomical actions, the biarticular adductors were modelled as a single musculotendon actuator, AB, in the model. Mm. Gluteus medius and Gluteus minimus were combined for similar reasons (GMED). Estimated tendon slack lengths (L_tsl) varied greatly, from 0.5 (BF, FC) to 72.4 mm (PL; table 2). The distal limb muscles (e.g. PL, LG, TA) had the largest L_tsl values while the smallest L_tsl values tended to be associated with the proximal biarticular muscles (e.g. AB, BF, FC; table 2). Differences between the model-defined optimal fibre lengths and the average measured fibre length (L_fibre) occurred in six muscles (BF, FC, FD, GR, ST and SM; table 2). However, only GR required an optimal fibre length outside one standard deviation of the experimental data.

Eighteen of the 20 musculotendon actuators were compared directly to the experimental tendon travel data to validate the modelled muscle paths (exceptions: FD, EDL). In most cases the defined muscle path resulted in an MTU length joint angle relationship similar to the experimental values, with the largest deviations occurring at the knee in BF, ST, and GR (figures 3–5). In the model, changes in BF and ST MTU length changes were overestimated (i.e. had shorter lengths) in flexed knee postures (knee angles less than −90°), while GR overestimated length changes at both highly flexed and extended postures (figure 4). In the other muscles, the largest differences between the model and experimental data points occurred at the extremes of each joint's ROM, which was outside the typical operating range of hopping and jumping. At the hip, IL and RF had a negative relationship. All other muscles crossing the joint had a positive relationship (figure 3). At the knee, all three vasti muscles have the same insertion so these muscles were combined into a single group (VAS) for comparison. Both VAS and RF had a negative MTU length angle relationship. The adductor group AB and FC showed no relationship (flat line). All other muscles crossing the knee exhibited positive relationships of varying strength, as indicated by the different slopes (figure 4). The ankle extensors (LG, MG, PL) showed positive relationships in both the ankle and the knee of similar strength (figures 3 and 4). The ankle flexors (TA, EDL) had a negative relationship between MTU length and ankle angle (figure 5).

Figure 4.

Experimental (symbols) and model-generated (lines) musculotendon lengths of muscles crossing the hip throughout the range of motion. Shaded areas represent the functional hip range of motion during representative jumping and hopping (stance phase) movements. For definitions of abbreviations, see table 2. Inset: skeletal images provide a visual representation of the hip joint angles at the range of motion midpoint and extremes. (Online version in colour.)

3.3. Estimated muscle moment capacities

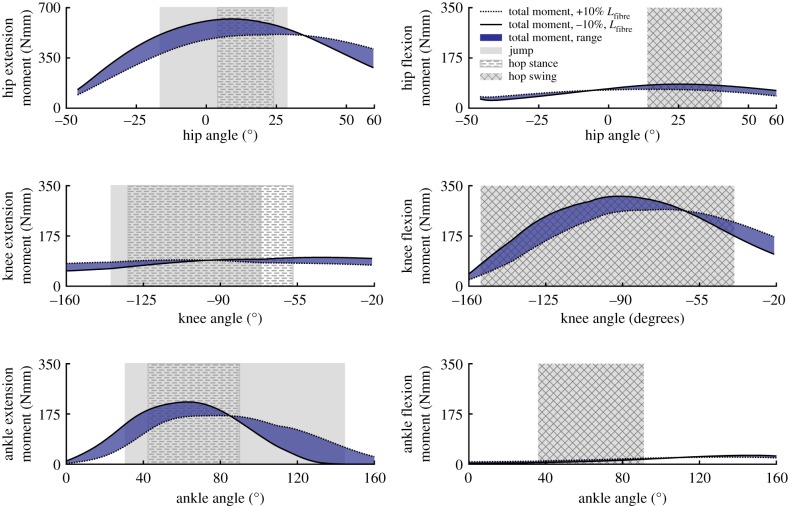
The hip muscles could generate the largest extension moment (514–638 Nmm), which occurred between 14° and 22° of flexion (figures 7 and 8). This moment was approximately twice the amount of the next largest peak moment (figure 7). Peak hip and ankle flexion had the smallest moments. Unlike the hip and ankle joints, the peak knee flexion moment was greater than the knee extensor moment. Knee extension had the smallest extensor moment at all joint angles, having a peak value range of 92–117 Nmm (figure 7).

Figure 7.

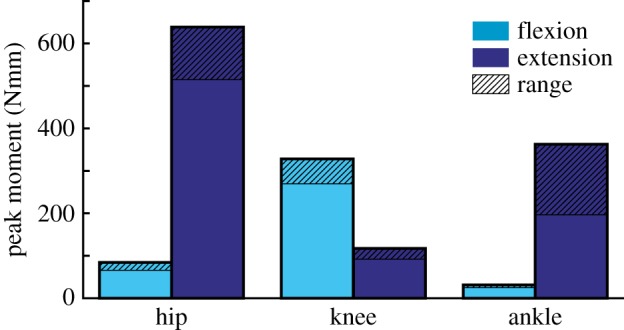
Model estimates of peak moments that all hindlimb muscles combined could generate at each joint. Moments were estimated from the peak isometric force (F_max) and corresponding joint moment arm of each muscle (see equations (2.4) and (2.5) for details). Range: indicates the possible range for peak capacity when accounting for ±10% errors in L_fibre. (Online version in colour.)

Figure 8.

Model estimates of maximum moment generating capacity of the combined hindlimb muscles over each joint range of motion. The shaded regions between the lines represent the range of possible capacities when accounting for ±10% errors in L_fibre. The joint angles used during jumping and hopping (stance & swing) are represented by the hatched, crossed, and grey rectangles. (Online version in colour.)

The net moment generating capacity of the muscles varied greatly at extreme joint angles in hip extension, ankle extension and knee flexion (figure 8, also see electronic supplementary material, figures S1–S3). Maximum hip extension moment was lowest when the hip was fully extended, with muscle capacity increasing gradually to a plateau that occurred when the hip was slightly flexed (0° to 25°), before falling slightly at extreme flexion angles. Maximum muscle generated moments were less variable in hip flexion than hip extension, but also had an identifiable plateau region that occurred during the same slightly flexed hip posture (10°–30° flexion). The lowest knee flexion moments occurred at highly flexed postures and increased dramatically until reaching approximately 100° of flexion, at which point capacity was fairly level until falling again at around 65° of flexion. In contrast, knee extension moments remained fairly constant over the entire ROM. The ankle extension moment was most sensitive to optimal fibre length definition. However, in both cases, peak values occurred around 65° of ankle extension, with dramatic reductions in capacity occurring at both extreme flexion and extension angles (figure 8). Maximum ankle flexion moment was the smallest of all moments, reaching a peak value (range 25–31 Nmm) near 140° of flexion (figure 8).

4. Discussion

4.1. Muscle moment capacity during hopping and jumping

An overarching question related to understanding musculoskeletal design can be posed as: ‘is animal musculoskeletal morphology adapted to provide maximum performance during key animal movements?’ In the case of desert kangaroo rats (D. deserti) there does appear to be some adaptation of overall morphology to two ecologically and evolutionary relevant movements: hopping and jumping. Ideally, the moment generating capacity of the hindlimb muscles would be compared directly to the joint moments required over the movement. For example, the limb postures at peak moment requirements could be used to estimate how much of the muscle moment capacity is required to accomplish the movement. However, even without moment data, comparisons of the model estimated muscle joint moment capacities to each movement's functional ROM still provides evidence for adaptation (figure 8). Consistent with findings in other cursorial species [36,45], model estimations of peak hindlimb joint moments in this study suggest a division of labour between functional muscle groups, likely related to the demands associated with hopping and jumping.

Peak muscle-generated hip extension and knee flexion moments were largest due to contributions from the high number of biarticular muscles crossing both joints (greater than 30% of total hindlimb mass). Yet, the lower peak knee flexion moment suggests these muscles are biased towards generating hip extension moments (figure 7). The hip extends from a similar, moderately flexed initial posture, in both hopping and jumping, but total hip extension during jumping is more than twice that used during hopping (figure 8). The peak hip extension moment falls within the range of both movements. However, this point occurs near the end of the stance phase of hop but at the midpoint of the jumping movement. The moment generating potential of the hip muscles have a moderate reduction in capacity at the highest hip extension angles during jumping, with a 19–27% drop relative to the peak value due to fibres dropping below the optimal fibre length. However, these estimates likely represent a maximum possible reduction in capacity, as the calculation does not account for the simultaneous knee extension that occurs during jumping (see biarticular muscle discussion, below). Because jump initiation and hopping start from similar hip angles, the musculoskeletal configuration of the hip extensors appears suited to satisfy the demands associated with both movements, instead of prioritizing one over the other. In both cases, the highest capacities occur within both movements, allowing these muscles to provide much of the required work. This result is consistent with previous findings in other animals that the proximal muscles act as motors to provide energy during jumping and other gaits [7,46]. However, the relatively flat capacity over the larger hip extension angles during jumping suggests that some adaptation has occurred to improve jumping capability.

The peak knee extension moment is much lower than the hip and ankle extension moments (figure 7). The lower moment follows trends observed in other cursorial and bipedal species [36,45], but kangaroo rat peak values were much lower than those reported for other bipeds (17.5–18.5% of peak extension versus 40–52%). Knee angles were similar in hopping and jumping, avoiding small flexion angles (i.e. straight-legged postures). Model estimated extension moments were flat over the entire anatomical range ROM, varying by only 10–15% from peak values (figure 8). The uniarticular knee extensors (VAS; figure 5) are the primary contributors to this moment. Morphological specializations may exist at the knee in order to maintain a flat moment arm (e.g. patellae [47,48]), but identifying these is beyond the scope of this study.

The ankle extensors (LG, MG, PL) can generate a relatively high peak ankle extension moment (figure 7). However, unlike the hip and knee extension moments, the peak ankle extension moment varied dramatically across the ankle angles observed during hopping and jumping. Even accounting for potential inaccuracies in determining optimal fibre length, moment generating capacity appears to be biased towards extended postures (e.g. 40°–80°, figure 8). These angles are associated with those used at mid-jump and closely match the typical range observed during hopping; suggesting that specializations in kangaroo rat distal limb morphology may be biased slightly towards improving hopping versus jumping performance. Although moment requirements for jumping are not currently available for kangaroo rats, peak ankle moment requirements for jumping in a similar species (jerboas) [16] occur during early to mid-jump, which would begin at flexion angles outside of the range of peak capacity. However, the additional reductions in capacity observed during the flexed postures associated with jump initiation (i.e. angles greater than 90°) were highly sensitive to fibre length inaccuracies with capacity either remaining fairly constant (figure 8: +10% L_fibre) or decreasing rapidly (figure 8: −10% L_fibre). The reduced capacity is also a result of highly stretched fibres that likely is negated in part through the stretching of passive fibre structures. Despite this, the notion that ankle morphology prioritizes hopping may be consistent with previous observations: although jumping requires higher ankle forces relative to hopping [18], jumping in small mammals is primarily driven by the ankle [2,16,30]. Indeed, because the tendons attached to the ankle extensor muscles in kangaroo rats are too rigid to substantially improve hopping efficiency there may an additional need to have the muscles operate over a more optimal range [17,18].

The large overlap in the functional joint ranges of jumping and hopping makes it difficult to definitively conclude whether hindlimb muscle arrangement is strongly adapted towards a specific function. However, this in itself may be an adaptation to allow similar capacities in both of these primary movements. How other movements are related to these morphological adaptations is unclear, and there may be a trade-off in performance between these two critical forms of movement and other movements (e.g. foot drumming).

4.2. Muscle architecture and function

Muscle architecture parameters such as PCSA and optimal fibre length (L_fibre) have been found to be good indicators of anatomically distinct muscle groups in humans and other animals [27]. In this study, kangaroo rat hindlimb muscle architecture varied greatly between individual muscles. However, there exist similarities between anatomically similar muscle groups, consistent with the idea that architecture is adapted to functional movement [27,45]. In particular, most hindlimb muscles' architecture appear to be tuned to its moment arm.

The two extremes found in kangaroo rat muscle design further support the general principle that larger moment arms are associated with architectures consisting of longer L_fibre and smaller PCSAs to compensate for the higher MTU strains. The hip muscles GR, ST, and SM have small PSCAs and long fibre lengths (figure 2). Because the origin and insertion sites of these muscles are far from joint centres, they undergo the largest MTU length changes across joint rotations; clearly indicated by their moderate to strong positive MTU length angle relationships (figures 3 and 4). Thus, these muscles need the capacity to operate over large strains and the long fibre lengths are presumably a direct compensation. Interestingly, the functional range of these muscles during hopping and jumping is much smaller, suggesting that the ability to reach extreme postures is necessary for other movements not investigated in this study (e.g. standing up). At the other extreme, GMAX has a short L_fibre and high PCSA. This muscle has the weakest relationship between MTU length and hip angle (figure 3), meaning the MTU undergoes little excursion during movement, allowing for short L_fibre and high PCSA. Due to their capacity to generate large forces during movement the proximal muscles may contribute substantial work during hopping and jumping, similar to other cursorial species [7,8,29,30]. The results of this study provide further evidence to support the idea that a fundamental relationship exists between fibre architecture and gearing, balancing the competing movement requirements of maximizing muscle moment generating capacity with the ability to do so over large ROMs [45,49].

Like muscle architecture, muscle moment arms can be tailored to functional movements. Thus, the relationship between muscle architecture, tendon properties and joint moments can evolve in various ways to help circumnavigate the trade-off between joint moment generation and MTU strain. For example, morphologies that allow moment arms to vary dynamically across a joint's ROM (i.e. variable gearing) have been shown to improve frog jumping performance (e.g. [41]), help attenuate peak muscle loads during landing [50], and improve dog running economy [32]. Unexpectedly, despite being excellent jumpers, kangaroo rat hindlimb muscle design does not use variable gearing to improve performance. Instead, as evidenced by the linear trends in the MTU length angle relationships, kangaroo rat hindlimb morphology exhibits a preference for constant moment arms over most joint angles, especially angles used during hopping and jumping (figures 3–5). A constant moment arm during movement may be beneficial in this species, in that it reduces the need to account for a posture dependent relationship between muscle capacity and joint capacity during movement. Escape jumps are not planned and kangaroo rats may be required to generate powerful jumps quickly from any posture. Similarly, these animals use erratic hopping (i.e. non-steady state) to escape predators, which likely has high variability in joint ROM. In both cases, a constant moment arm may assist in performing these behaviours by reducing the need to follow a stereotyped pattern to perform the movement. Constant moment arms also exist in the greyhound hindlimb (ankle and hip extension) and the ostrich pelvic limb (ankle extension) [36,45]. However, whether or not this is a general principle in musculoskeletal design for cursorial animals cannot be determined from the limited data here and should be tested over a wide range of functional movements and species.

4.3. Exceptions to the rule—tendons and biarticularity

In kangaroo rats, the ankle extensors (LG, MG, PL) have small L_fibre values and relatively large ankle moment arms, which is inconsistent with the aforementioned strong positive relationship between fibre length and moment arm. One possible explanation for this discrepancy is that the tendon attached to these muscles reduces fibre strain. In many animals, flexible tendons are used to decouple fibre strain from moment arm, allowing short fibred muscles to operate with larger moment arms. For example, frogs preload flexible tendons to store energy during jumping, resulting in fibre strains that are no longer strongly correlated to MTU length changes [51]. In addition to improving hopping economy, the flexible distal tendons of wallabies and kangaroos also reduce fibre strain relative to MTU length changes [8,10]. Similarly, the human Achilles tendon reduces ankle extensor fibre strain despite large changes in MTU length during various movements [52,53]. But the tendon attached to the ankle extensors in kangaroo rats is relatively thick, limiting its ability to decouple fibre strain from MTU length changes and cannot explain the relatively short L_fibre for the observed moment arm. An alternative explanation is that this species takes advantage of the biarticular nature of these muscles.

Like flexible tendons, biarticularity can be leveraged to circumnavigate the typical relationship between fibre length and MTU strain. The MTU strains presented in this study represent single joint strains (figures 4–6). However, during hopping and jumping, the hip, knee and ankle extend simultaneously throughout much of the movement. Depending on the rate at which each joint angle changes and the muscle's moment arms, a biarticular muscle may undergo isometric, concentric or eccentric length changes, effectively decoupling moment arms from MTU and fibre strain. For example, in kangaroo rat jumps, large ankle extensions are coupled with knee extension. Because LG, MG, and PL are biarticular and have positive knee and ankle MTU angle relationships (figures 4 and 5), knee extension partially negates any MTU length changes resulting from ankle extension during jumping and the muscles do not undergo large MTU strains despite the large ankle moment arm. Model predictions of in vivo MTU length changes confirm this notion: the ankle extensors maintain an almost constant length during hopping and over the first half of jumping. Thus, biarticularity effectively removes the constraint usually associated with a large moment arm (i.e. having to undergo large MTU strains) allowing relatively short fibres to operate on joints with large moment arms. Similar findings have been described in previous studies of human jumping, where simultaneous changes in adjacent joint angles reduced total MTU strain in biarticular muscles and allowed for consistent generation of large forces [54–61].

Figure 6.

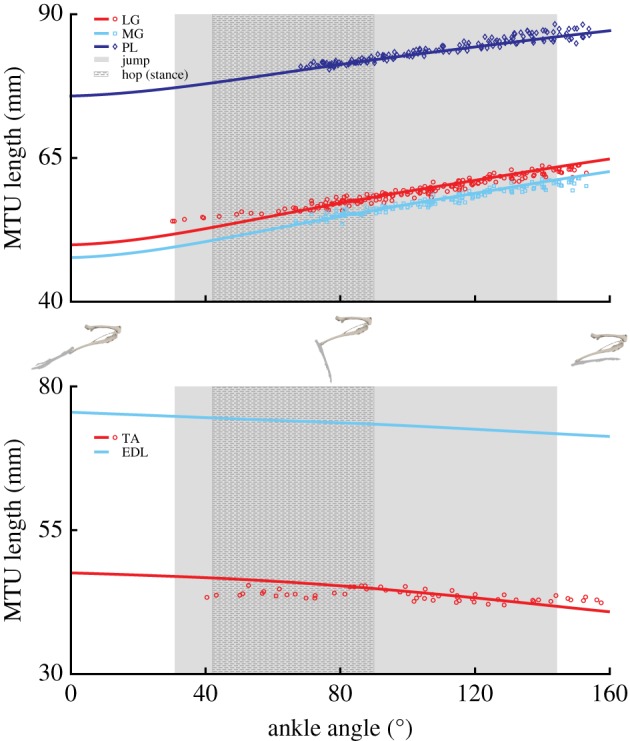
Experimental (symbols) and model-generated (lines) musculotendon lengths of muscles crossing the ankle throughout the range of motion. Shaded areas represent the functional ankle range of motion during representative jumping and hopping (stance phase) movements. For definitions of abbreviations, see table 2. No experimental data were collected for EDL, but the model representation is provided here for completeness. Skeletal images provide a visual representation of the ankle joint angles at the range of motion midpoint and extremes. (Online version in colour.)

The biarticular design of the kangaroo rat ankle extensors appears to have an additional functional role beyond decoupling the ankle moment arm from fibre architecture. Muscles can function in multiple ways during a movement including as a motor, as a brake, as a strut, or in some combination [62]. If the ankle extensors act as a strut, the almost 2 : 1 ratio between the ankle and knee moment arms (figures 5 and 6) has an interesting functional implication. As a strut, the muscles complete a four-bar linkage with the femur, tibia and hindfoot. In this configuration, any torque generated about the knee would be converted into a torque about the ankle of twice the magnitude (like a lever system). The ankle extensors would then act as a crucial link in transferring force generated by proximal muscles into an ankle extensor moment, ultimately contributing to the ground reaction force during jumping and hopping. This notion is consistent with those found in human jumping, where the gastrocnemius also acts as a link to transfer proximal forces to the ground [54–61]. If these muscles are being used as a strut to transfer high forces, the four-bar mechanism identified here may be a key adaptation for performing explosive jumps and help explain why kangaroo rat tendons are thick [17,18]. It is also interesting that, like large hoppers, there were no uniarticular ankle extensors (e.g. soleus) of notable size in any of the study specimens. Previous human studies have suggested different functional roles for the uniarticular and biarticular ankle extensors during steady-state movements: the soleus provides weight support and the biarticular gastrocnemius assists in forward progression [63]. Without uniarticular ankle extensors, the biarticular ankle extensors in kangaroo rats must provide both functions, but how they do so cannot be ascertained from this study and should be investigated further.

4.4. Limitations

In most cases, the musculoskeletal model represented the empirical hindlimb muscle data well when considering the functional ranges of each joint during hopping and jumping. However, there were some inconsistencies between the two datasets, which may influence the study findings. The most notable differences occurred in setting the L_fibre values for muscles with little to no observable free tendon (BF, FC, FD, GR, ST and SM; table 2) and in fitting the relationship between knee angle and MTU length for the biarticular hip extensors GR, ST and BF. Of the muscles with differences in L_fibre values, only one muscle (GR) had a model value outside of the experimental data range (±1 standard deviation). For GR, there was a 25% decrease in the model value (31.2 mm) relative to the experimental average (41.2 mm). In addition GR, along with ST and BF, had substantial differences in model predicted MTU lengths over knee angles used during hopping and jumping. These differences between the model and experimental data are likely a result of modelling the muscles as a single line, as all three have broad insertion areas on the tibia. The exaggerated trends (i.e. large slopes predicted by the model; figure 4) and reduced L_fibre in GR would act to overestimate the moment generating capacity for these muscles at the knee. However, because there are eight muscles that provide similar contributions to the total knee flexion moment capacity (electronic supplementary material, figure S2), these inaccuracies have little effect on the total moment generating capacity (figure 7), and will not change the study findings.

Another potential limitation of this study relates to how muscle fibre lengths (L_fibre) were determined during dissection. Fibre lengths were measured from animals placed in a mid-stance posture. This posture was assumed to correspond to the optimal length for all muscles (i.e. the length at which the sarcomeres are near optimal for force production). To test this assumption, sarcomere lengths were measured in two animals for which the muscles were fixed in place and partially digested in nitric acid [64,65]. Three intact muscle fibres were dissected free from each muscle and the average sarcomere length for each fibre was determined over 30 consecutive sarcomeres (i.e. measured length divided by 30). The values from each of the three fibres were then averaged together to get the average sarcomere length for the muscle. Across all muscles, the average sarcomere length was 2.25 ± 0.22 μm with a range of 1.88–2.70 μm. The optimal sarcomere lengths for kangaroo rat muscles are not known; however, these values fall within the range which has been reported for mammalian skeletal muscle [66,67]. If the optimal sarcomere length value for rats (2.4 μm) is assumed then the values for rest length measured here would underestimate the L_fibre by approximately 6%, which falls within the ±10% L_fibre range evaluated. Thus, the findings presented in this study are likely to hold true despite potential inaccuracies in determining L_fibre.

Although static analyses like the one performed using the model in this study are useful in providing novel insight into form–function relationships, there are some limitations when attempting to assess dynamic function. First, our static analysis of muscle capacity assumes that muscles act with a rigid tendon throughout the movement. As a result, any changes in MTU length occur solely in the muscle fibres. Due to their short fibres and long tendons, the ankle extensors would likely be most affected by this assumption. However, the tendons associated with these muscles are relatively stiff in kangaroo rats [16,17], suggesting that differences in fibre length due to tendon stretch will be small. Regardless, our stiff tendon assumption will likely overestimate fibre strain in all muscles, as tendons tend to reduce fibre strain relative to MTU strain [52,53]. Therefore, the changes in fibre lengths here are likely exaggerated relative to in vivo values and represent the largest possible effect that a muscle's intrinsic force–length relationship could have on muscle force generation and any drop-off in moment capacity at extreme postures presented here (figures 7 and 8) is likely overestimated. Second, the static analysis performed here is not able to account for the influence of each muscle's intrinsic force–velocity relationship during the movement, which may influence the muscle moment capacities. However, how each muscle's MTU length changes during jumping and hopping can provide some basic insight into which muscle may be most susceptible to changes in capacity due to velocity effects. A post hoc analysis shows that the largest changes in MTU length occur in LG, MG and PL (up to 76% of optimal fibre length) during jumping and ST and GR during hopping (up to 43%). In rapid movements like hopping and jumping, these muscles may have higher fibre velocities, resulting in force (and moment) reductions. However, no data currently exist with respect to fibre type or fibre properties, making it difficult to quantify the extent to which fibre velocity influences force generation. Future work should include a detailed analysis of fully dynamic simulations to determine tendon–fibre interactions and account for effects due to the intrinsic muscle force–velocity relationship, which is beyond the current study's scope.

5. Conclusion

The newly developed musculoskeletal model combined with the anatomical and tendon-travel data collected in this study provides a detailed representation of a kangaroo rat hindlimb that can be used to study form–function relationships. An analysis of MTU joint angle relationships in this species reveals that hindlimb morphology is likely biased towards providing constant moment arms over large joint ROM, which may assist in performing erratic hopping and rapid jumping movements by reducing the need to account for posture dependent relationships between muscle capacity and joint capacity during movement. Like that observed in other species, the majority of the muscles in the kangaroo rat hindlimb have a strong positive relationship between muscle architecture (e.g. L_fibre) and joint moment arms, presumably due to large moment arms requiring higher MTU strains. However, the ankle extensors (LG, MG, PL) are a major exception to this relationship with relatively small L_fibre relative to their ankle moment arms. As a result, these muscles are capable of generating very high ankle moments, but only over a limited ankle range during single joint movements. However, the biarticular nature of these muscles is leveraged to bypass this limitation in jumping (instead of a flexible tendon), where simultaneous knee extension reduces ankle extensor MTU strain resulting from the large ankle excursion observed in this movement. In addition, the ankle extensors appear to be specialized to engage a four-bar linkage mechanism that is highly suited to transfer forces generated in proximal segments through the ankle to the foot. Unlike the proximal muscles, in which no clear specializations were observed, both of these ankle muscle adaptations seem particularly suited to generating high powered jumps without requiring the additional time involved in using flexible tendons to store and return energy. Kangaroo rat (D. deserti) hindlimb musculature provides an interesting case study for understanding how morphology balances the sometimes competing demands of two key movements: hopping and jumping.

Data accessibility

The musculoskeletal model, dissection data and jumping and hopping kinematics used in this study are available via Dryad at http://dx.doi.org/10.5061/dryad.r18b12m. [68]

Authors' contributions

All authors contributed to the study conception and participated in anatomical dissections and associated analyses. J.W.R. and C.P.M. developed the musculoskeletal model. J.W.R. wrote the custom analysis scripts and drafted the manuscript. C.P.M. provided comments on manuscript drafts and assisted with data interpretation. All authors gave final approval for publication.

Competing interests

The authors have no competing interests.

Funding

This project was partially supported by grants from the National Science Foundation (CAREER #1553550 and BEACON #DBI-0939454 to C.P.M.), National Institutes of Health (IDeA #P2GM103408 to C.P.M. and K.M.D.) and Army Research Office (66554-EG to C.P.M.).