Bound electron nonlinearity beyond the ionization threshold

Abstract

We present absolute space- and time-resolved measurements of the ultrafast laser-driven nonlinear polarizability in argon, krypton, xenon, nitrogen, and oxygen up to ionization fractions of a few percent. These measurements enable determination of the strongly non-perturbative bound electron nonlinear polarizability well beyond the ionization threshold, where it is found to remain approximately quadratic in the laser field, a result normally expected at much lower intensities where perturbation theory applies.

The nonlinear dipole moment per unit volume (P_NL), driven by strong laser fields beyond the perturbative limit in atoms and molecules, can play a central role in the propagation of intense ultrashort optical pulses in material media. It is integral to the process of high harmonic generation and its phase matching [1, 2] It leads to extremely wide bandwidths in supercontinuum generation [3], which can be applied to single cycle pulse generation [4] and ultrafast spectral interferometry [5] The space- and time-dependence of P_NL also controls the collapse and collapse arrest of optical beams in femtosecond filamentation [6, 7] In this regime, the optical field is no longer a small perturbation on the atomic potential; it is of comparable strength.

While extensive absolute measurements of P_NL have been done in neutral atomic and molecular gases below the ionization threshold [8–10], the nonlinear response above the ionization threshold is composed of contributions from the free electrons and the residual neutrals, where the free electron response strongly masks that of the bound electrons. Separating out these contributions requires determination of the absolute transient ionization rate. It is such measurements that will complete the picture of the nonlinear polarization in intense non-perturbative fields.

In this Letter, we fully map the nonlinear polarization of several atomic and molecular gas species through the ionization transition with sufficient accuracy to reveal the bound contribution surviving above the ionization threshold. For the surviving atoms (molecules), the near-instantaneous bound nonlinear electronic response to a laser field E can be written ${\text{P}}_{NL}^b=\Delta {\chi }_b\text{E }=(\Delta n_b/2\pi )\text{E}$, where Δχ_b = Nα_NL is the bound electron nonlinear susceptibility, N is the gas density, α_NL is the nonlinear polarizability, and Δn_b = 2πNα_NL is the laser field-induced nonlinear refractive index shift. We find that in all gases studied, the relationship between the bound electronic response and laser field observed at lower intensities [8, 9], $\Delta n_b\propto {\left|\text{E}\right|}^2$, extends to intensities where up to ~ 10% of atoms or molecules are ionized, a region significantly beyond the limits of perturbation theory [11].

Prior measurements of the ionization of atoms and molecules by intense ultrashort optical pulses were performed in vacuum chambers at very low pressure. In those experiments, ionization byproducts (electrons and ions) are directly captured long after the ionizing pulse has passed through the interaction volume, approximately the beam waist region [12, 13], and ionization yields are scaled and compared to space and time integrations of ionization rate models. Those experiments were not intended to address the absolute nonlinear polarizability of atoms and molecules in intense fields.

There has recently been considerable discussion about the effect of strongly nonperturbative fields on the atomic/molecular dipole response underlying nonlinear propagation. In particular, debate has arisen (see, for example, [14] and references therein) regarding potentially exotic contributions [14, 15] to the dipole moment, wherein strongly driven bound electrons have been speculated to exhibit a negative polarizability, with this scenario advanced to explain collapse arrest in femtosecond filamentation [16–18] This debate has persisted due to both experimental and theoretical complications. Experimentally, at high fields, propagation effects of ionization have been very difficult to avoid. Theoretically, it has been challenging to cleanly separate the contributions of bound and free electrons [15, 19, 20] Here, we present new experimental results showing beyond any doubt that the nonlinear bound response continues to increase approximately quadratically with the laser field (or linearly with the intensity), even in the presence of substantial and increasing ionization.

A diagram of the experiment is shown in Fig. 1. The experiment employs single-shot supercontinuum spectral interferometry (SSSI) [5, 21] which measures, in a single shot, the transient refractive index shift Δn induced by an intense pump pulse in a medium. Broadband supercontinuum (SC) probe and reference pulses (Δλ > 100 nm) are co-propagated with the pump pulse into a very thin gas target, with the pump and probe temporally overlapped and the reference preceding them. The probe picks up a phase shift ΔΦ = kΔnL_eff from the pump-induced refractive index change Δn in the gas, where k is the vacuum wavenumber. The effective gas target thickness, $L_{eff}={\displaystyle \int (N(z)/N_0})dz\sim 450\mu m$ satisfies L_eff/z_p,pr « 1, where N(z) is the gas density profile along the pump/probe path, N₀ is the profile mean density, and z_p,pr is the pump (probe) Rayleigh length [8,22] The probe and reference pulses are imaged from the interaction region to the entrance slit of an imaging spectrometer, forming a spectral interferogram. Analysis of the interferogram yields the probe phase and amplitude shifts resolved in time and one transverse spatial dimension (along the slit, x), yielding Δn = Δ(x, t). The technique provides sub-10 fs time resolution set by the inverse probe bandwidth, and few micron scale spatial resolution [5, 21].

Figure 1.

Experimental apparatus for 2D+1 SSSI measurement of field-induced ionization. DM1, DM2, DM3: diclnoic mirrors. Not shown: 800 nm rejection mirror after Xe gas cell, auxiliary interferometer for gas target characterization, and pre-target pump spot imaging camera.

A new scheme, which we call 2D+1 SSSI, yields Δn(x, y, t). Here, the image of probe/reference beam in the thin gas target is scanned perpendicular to the spectrometer slit - along y - by a motorized scanning mirror downstream of the second imaging lens. Each shot captured yields a spectral interferogram at a particular value of y (= y_i, say). Multiple interferograms are averaged before extraction to significantly improve the signal-to-noise ratio [23, 24], yielding Δϕ (x, y_i,ω) and then ΔΦ(x, y_i, t) [21], A 2D+1 map ΔΦ(x, y, t) = kΔn(x, y, t)L_eff is built over ~10⁴ shots by scanning y. An important feature of 2D+1 SSSI is that a single 2D phase profile at a particular time slice encodes the response over a wide range of intensity, greatly improving the statistics of our measurements.

Figures 2a and 2c show 1D+1 SSSI traces for ionization of N₂ and Ar. The more complex N₂ trace shows the prompt electronic (Kerr) response, a delayed positive alignment rotational response (which is larger than the Kerr contribution [8]), followed by molecular anti-alignment/alignment and plasma contributions. The Ar trace shows the early Kerr response followed by the rapid tunnel ionization to long-lived plasma. Fig. 2b is a lineout of the Kerr response in Ar below the onset of ionization, which gives the pump intensity envelope. Temporal slices of 2D+1 ΔΦ(x, y, t) traces in Ar are shown in Fig. 2e-g for a 42 fs pump pulse of peak intensity 95 TW/cm² and show the whole beam spatial effect of the positive and negative transient index contributions. Unlike in our previous results [23–25], these new measurements are absolute and quantitative at intensities where ionization is observed. This required increasing the pump spot size to minimize refraction of the pump and probe by the plasma transverse gradient, increasing the time between pump pulses to 100 ms to avoid cumulative thermal effects in the gas [26], and improving the temporal resolution of SSSI by minimizing the probe chirp (consistent with the desired temporal window) and optimizing the spectrometer resolution [21], Results for the other gases studied, including movies of ΔΦ(x, y, t), are provided in [27].

Figure 2.

Results in Ar for peak pump intensity of 95 TW/cm² and in N₂ for peak pump intensity of 115 TW/cm². The pulsewidth is 42 fs. (a) 1D+1 phase shift ΔΦ(x, y₀=0,t) in N₂. The complex structure results from the bound electronic (be), rotational (r), and free electron (fe) contributions to the transient polarizability; (b) pump pulse envelope given by ΔΦ(x₀=0,y₀=0,t) in Ar at 47 TW/cm², with the Kerr phase shift proportional to the pump intensity envelope, (c) 1D+1 phase shift ΔΦ(x,y₀)=0,t) in Ar, showing bound electronic (be) and free electron (fe) contributions; (d) Image of the pump spot at the gas target for Ar data. 2D+1 SSSI-derived phase shift images in Ar: (e) ΔΦ(x,y,t = − 14 fs), dominated by the Kerr response, (f) ΔΦ(x,y,t =+25 fs, showing the Kerr response on the wings and the growing plasma contribution in the center of the beam, (g) ΔΦ(x,y,t = +100 fs), showing the dominant plasma contribution after the pump pulse. A movie of ΔΦ(x,y,t) is provided in [26]. The peak of the pump pulse defines zero for the x,y, and t coordinates.

We first examine the pure plasma component of the phase shift, which can be isolated by examining time delays long after contributions by the bound electron response, which includes the prompt Kerr response and, in the case of N₂ and O₂, the delayed rotational response [24, 25] For our case of a thin gas target in which the probe experiences negligible refraction, the refractive index profile Δn(x,y,t) = ΔΦ(x,y,t)/kL_eff gives N_e(x,y) = −2N_cr Δn(x, y, t₁) for the axially averaged electron density profile, where t₁ > 50 fs for the noble gases and t₁ > 250 fs for N₂ and O₂. Here we have used the refractive index shift induced by a low density collisionless plasma, Δn = −N_e/2N_cr, where N_cr = 3.1 × 10²¹ cm⁻³ is the critical electron density at the probe central wavelength, λ_pr ≈ 600 nm. For negligible probe refraction, each probe ray centered at (x_i, y_i) samples the dynamics induced by the intensity profile I(x_i, y_i,t). The ionization yield Y = N_e/N₀ as a function of intensity is shown in Fig. 3. For each data set (a complete 2D+1 scan of ~10⁴ consecutive shots at the same nominal peak laser power), Y (for times t > t₁) was sorted into 20 intensity bins. The points in Fig. 3 are average values for Y in each bin.

Figure 3.

Ionization yield (points) as a function of peak intensity I₀ for (a) Ar (red), Kr (green), Xe (blue) and (b) N₂ (black) and O₂ (magenta). PPT [28] rates are shown as solid lines. MESA calculations for Ar and Kr are shown as large open circles [29,30], Fits to Y = c₁I₀^m, described in [27], are shown as dashed lines, where c₁ and m are detennined from the fit. The accuracy of the ionization yield measurement is set by the vertical scatter of the points, while the intensity accuracy is ~13% as discussed in the main text.

As in most measurements of the nonlinear response, the error is dominated by the uncertainty in the peak intensity. Here, in a new procedure, we use our previous measurement of the nonlinear refractive index of Ar, n₂ = (9.7±1.2)× 10⁻²⁰ cm²/W, applicable for intensities to nearly the ionization threshold [9], to provide full 2D calibration of our intensity profiles through Δn(x, y) = 2n₂I(x,y) by directly comparing CCD camera images of the pump spot to 2D Kerr phase shift profiles measured with 2D+1 SSSI at sub-ionization intensities of <50 TW/cm² Intensities above this level, for which the focal spot and pulsewidth remain the same, are determined through scaling by the pulse energy. The uncertainty in the intensity is 13%, mostly arising from the uncertainty in n₂, with the residual uncertainty due to shot-to-shot fluctuations in the measured phase shift of ~3 mrad.

We compare our results to two ionization models. The single-active-electron Peremolov-Popov-Terent’ev (PPT) model [28] (solid lines) shows ionization yields in reasonable agreement with the curves of Fig. 3. We also performed a full simulation of the pump-probe experiment using the unidirectional pulse propagation equation [29, 30] to model pump and probe propagation, and the metastable electronic state approach (MESA) [31–33] to model the full nonlinear response. The results, shown as open circles, are in similarly reasonable agreement with the experimental curves for Ar and Kr [31] Detailed comparisons of the measured spatiotemporal nonlinear response and MESA simulations, which largely agree, are described in a separate publication [33].

The measured time-dependent index shift in argon, Δn(x = 0, y = 0, t) = Δn(t), from the onset of the Kerr response through ionization, is shown in Figs. 4a and 4b. Similar figures for the other gases are found in [27] At low intensity the response follows the pump pulse intensity envelope, which is well-fit by I (t) = I₀e^−t2/τ2 where τ = τ_FWHM/(2√ln2) corresponds to our pulse full width at half maximum τ_FWHM = 42 fs (Fig. 4a). Figure 4b shows the time-dependent refractive index shift in Ar for increasing intensity and ionization levels, along with fits to Δn(t) = Δn_ke^−t2/τ2 + Δn_p (1 + erf [m^1/2t/Δ])/2, where Δn_K is a fitting parameter and Δn_p is the peak plasma index shift. The first term, modeling the bound response Δn_b (t), is a Kerr-like (instantaneous) response for a Gaussian pulse of peak intensity I₀, where Δn_K = 2n₂I₀ is the peak index shift experienced by a probe pulse [8] The second term models the plasma contribution as $N_e\left(t\right)∕N_0=Y\left(t\right)\approx {\int }_{-\infty }^{t}w\left(t^{\prime }\right){\mathit{dt}}^{\prime }$ using an ionization rate w(t) = c₂(I₀e^−t2/Δ2)^m, for which the yield is $Y(t\to \infty )=c_1{I}_0^m$, and where c₁ and m are determined from fits to the ionization curves in Fig. 3 and $\Delta n_p=-N_0{c}_1{I}_0^m{\left(2N_{cr}\right)}^{-1}$ [27], The approximate reduction in Kerr response due to the reduction of the neutral atom density by ionization is accounted for by multiplying the Δn_K value found from the fit by 1 − Y/2. This adjustment, which assumes that the Kerr response from the ions is negligible, reduces Δn_K by at most 3% at the highest intensity. This simple model is seen to be an excellent fit to the measured transient index shift. The point of the expression used for Y is not to advance a multiphoton-ionization (MPI)-like model for ionization; it is to provide an analytic model fit to the ionization yield data to enable separation of the bound and free electron contributions. In fact, as seen in [27], the best fit values for m are notably smaller than their corresponding MPI values for each species, indicating the significant contribution of tunneling ionization.

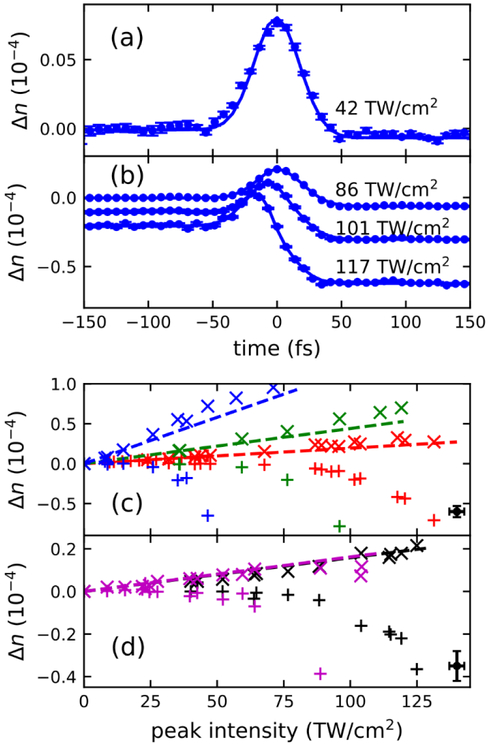
Figure 4.

Response during pump pulse, (a) Nonlinear index shift in Ar vs. time for peak intensity 42 TW/cm² (dots), below the threshold for ionization, fit to a Gaussian pulse with Δ_FWHM =42 fs (solid line), (b) Nonlinear index shift vs. time and tits to the standard model (Kerr effect plus ionization) for Ar(solid lines). The curves have been offset vertically for clarity, (c) Plot of Kerr index change Δn_K (×)and plasma index change Δn_p (+) from fits as a function of intensity in Ar (red), Kr (green), and Xe (blue), (d) Same as part (c) for N₂ (black) and O₂ (magenta). The black points on the lower right of panels (c,d) indicate typical uncertainty. Dashed lines show tire extrapolated Kerr response 2n₂I from previous low intensity measurements [8,9].

Figures 4c and 4d plot, as a function of peak intensity, the peak Kerr index shift Δn_K and the peak plasma shift Δn_p extracted from fits to transient index data, as in Fig. 4b, for each species, with Fig. 4c showing atomic results and Fig. 4d showing molecular results. Remarkably, it is seen for all species that Δn_K continues to rise with intensity even as Δn_p becomes increasingly negative up to the limit of our measurements. In Ar, Kr, and Xe, the Kerr index shift observed above the ionization threshold is somewhat higher than the curve extrapolated from below the threshold [9], shown as a dashed line in Fig. 4cd. Apparently, Δn_K rises slightly faster than ∝ |E|² in the noble gases, but confirmation awaits more accurate measurements. In the molecular gases, the result is somewhat different. In N₂, the Kerr index shift above the ionization threshold closely follows the ∝ |E|² curve extrapolated from the sub- threshold response [8], while in O₂ it is below the extrapolated curve. In these gases, the analysis is complicated by the need to separate the bound electronic and rotational responses [27].

That the simple field-quadratic response of bound electrons continues to apply well beyond the ionization threshold is consistent with our Kramers-Kronig (KK) simulations presented in [9] A physical interpretation of the KK results [9, 34] is that in atoms dressed by the intense field, the change to the single photon absorption coefficient (which contributes to the imaginary part of the effective susceptibility) is non-negligible and dominated by strong ac Stark shifts, which then causes the real nonlinear response (the real part of the effective susceptibility) to be quadratic in the field. This also applies to enhanced single-photon absorption from resonantly populated high lying states. For nonground state levels, the range of shifts can be as large as the ponderomotive energy, U_p ~ 8 eV at 120 TW/cm², and population can be easily resonantly transferred to states within one photon from the continuum [35].

In summary, absolute measurements of ionization in Ar, Kr, Xe, N₂, and O₂ have enabled absolute determination of the transient free and bound electron contributions to the nonperturbative nonlinear polarizability. For our conditions, the bound component of the nonlinear polarizability is, to within our measurement accuracy, quadratic in the laser field amplitude over the full range of the interaction up to >100 TW/cm², which is well past the ionization threshold of the gases measured here and manifestly in the non-perturbative regime.