If perception is probabilistic, why does it not seem probabilistic?

Abstract

The success of the Bayesian perspective in explaining perceptual phenomena has motivated the view that perceptual representation is probabilistic. But if perceptual representation is probabilistic, why does normal conscious perception not reflect the full probability functions that the probabilistic point of view endorses? For example, neurons in cortical area MT that respond to the direction of motion are broadly tuned: a patch of cortex that is tuned to vertical motion also responds to horizontal motion, but when we see vertical motion, foveally, in good conditions, it does not look at all horizontal. The standard solution in terms of sampling runs into the problem that sampling is an account of perceptual decision rather than perception. This paper argues that the best Bayesian approach to this problem does not require probabilistic representation.

This article is part of the theme issue ‘Perceptual consciousness and cognitive access'.

1. Introduction

One motivation for treating neural representations as probabilistic is that neurons are stochastic devices: identical inputs to identical neurons will inevitably yield variation in firing patterns. That applies to all neural representation, but there is a reason to expect perceptual representation, in particular, to be probabilistic because, given any activation of a perceptual system, there are many different environmental situations with different perceptible properties that could have produced it, some more probable than others. The visual system is said to cope with these facts by representing many of the possible environmental situations, each with a certain probability [1,2]. Perceptual representation of a range of environmental situations, each with a certain probability, is what is meant in this article by ‘probabilistic representation’.

For example, Vul et al. say that ‘… that internal representations are made up of multiple simultaneously held hypotheses, each with its own probability of being correct …’ [3]. Gross & Flombaum [4] describe ‘… a growing body of work that emphasizes the probabilistic nature of the computations and representations involved in a perceiver's attempts to “infer” the distal scene from noisy signals and then store the representations it constructs’. They advocate probabilistic representations in which perceptual properties are attributed to places or things with a certain probability.

It is often noted that perception does not normally seem probabilistic [3,5–7]. But how would perception seem if it did seem probabilistic? The phenomenology of perception would reflect the probability distributions of probabilistic perceptual representations.

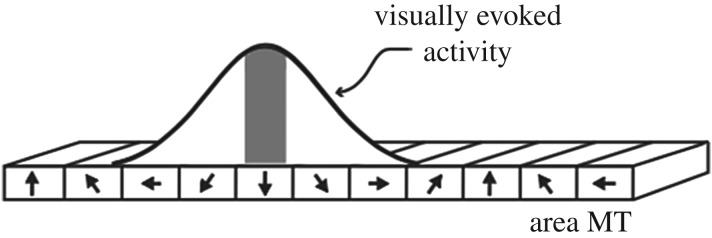
An example from motion-sensitive area MT that illustrates the problem is in figure 1. Tuning curves in individual neurons for direction of motion have broad sensitivities. (I will discuss populations of neurons later.) Tuning curves for neurons tuned to vertical downward motion respond also to a range of other motions, from horizontal motion to the left to horizontal motion to the right [8]. Still, when you look at a close medium-size object moving vertically in good conditions, you do not normally see any hint of horizontal motion.

Figure 1.

The response of a patch of cortex tuned to downward motion in area MT of monkey cortex. (The curve is representative but hypothetical.) The height of the curve represents level of neuronal discharge. The shaded area indicates the most active neurons. Reproduced with permission from [8] the Society for Neuroscience.

The same point applies to detectors for orientation in early cortical areas of the visual system. Seeing a vertical bar or grid activates neurons whose maximum response is to vertical grids. Simple cells tuned to vertical respond to a wide range of other orientations, but to a lesser degree, typically with substantial activations by grids tilted up to 30° in either direction, clockwise and anticlockwise [9,10]. But when one views a vertical grid foveally in normal conditions, there is no hint of the 30° tilts. You can verify this for yourself by looking at figure 2. (The fovea is the centre of the retina where cones are the densest. A thumb at arm's length is seen entirely foveally.)

Figure 2.

Oriented grids tilted from minus 30° to plus 30°. Ask yourself whether in viewing the central grid, you see any hint of the minus 30° or plus 30° grids.

The probabilistic point of view as applied to individual neurons dictates that these degrees of activation in neurons are representations of probabilities that the stimulus has one or another of these orientations, so the representation of the orientation of a grid is often thought of as a set of hypotheses attributing different probabilities to various different grids, or, alternatively, as a probability function over orientations.

The reader may wonder whether the cortical areas mentioned really do support conscious perception rather than unconscious perception. It is controversial whether visual area V1 supports conscious perception [11,12], but other orientation-specific areas (e.g. V2 and V3) do support conscious perception. The evidence is overwhelming that MT/MST supports conscious perception. Micro-stimulation to MT/MST affects direction perception in monkeys according to the dominant tuning of the cells stimulated [13]. Damage to this area causes deficits in motion perception, including the total inability to see motion [11]. Subjects' perception of motion are correlated with the dominant tuning of motion-selective cells including three-dimensional (3D) as well as 2D motion [14]. Even illusory motion correlates with activation in this area [15].

In brief, the problem to be discussed here is that conscious perception does not normally reflect the probabilistic hypotheses other than the dominant one. The response that I have often gotten from Bayesians is that it is a mistake to focus on the level of individual neurons. A Bayesian computation that combines information from many neurons in a population can be used to decide which hypothesis or narrow band of hypotheses best predicts the overall neural activations. (These are ‘likelihoods’ in a sense to be explained.) If the perceiver is in a scanner, combining responses of many neurons allows for decoding of the visual input orientation [16]. However, it is unclear how the procedures that allow the neuroscientist to decode from a population relate to the perceiver's decoding from a population. There is no inner eye that looks at populations. There has to be some mechanism of combination. Unless some such mechanism is found, we should not suppose there is any explicit representation [17] of these likelihoods. That is, we should treat the likelihoods or likelihood functions ‘instrumentally’, i.e. as ‘as if’ constructs.

The subject of this article is probabilistic representation in perception, not cognition (thinking, reasoning, deciding). And it is probabilistic representation, not representation of probabilities. Let me explain the difference. The probabilistic perceptual representations at issue here are of this sort: <red, there_i, 0.7>, to be read as a representation of redness at the location indicated by ‘there_i’, with a 0.7 probability. But what if what is represented in perception is not redness but itself a probability, say that the probability is 0.3 that something is red? This is a representation of a probability. Humans certainly have cognitive representations of probabilities. We know that if A causally influences B, then the presence of A makes B more probable. And, we use such representations in reasoning and problem solving [18,19]. There is some evidence of representations of probabilities in perception [20], though I am not persuaded that this study concerns perception as opposed to perceptual judgement. If there is perception of probability, the question arises as to whether there could be a probabilistic representation of probability; for example, a representation of the form: <probability of redness of 0.3, there_i, 0.7>. (If this seems unintelligible, note that I can have a 0.9 credence that the probability of decay of a certain subatomic particle is 0.1.) In any case, this article concerns probabilistic representation, not representation of probabilities; and in perception, not cognition.

I will mention two proposals that have been made concerning the role of probabilistic representation in the phenomenology of perception, confidence and precision, arguing that they do not deal with the problem at hand. Then I will return to a discussion of more promising approaches which focus on populations of neurons.

2. Confidence

Some say that a conscious reflection of probabilistic representation can be found in conscious confidence. One can have a conscious sense of a low degree of confidence that that is Isaac in the distance. As one gets closer, one's conscious confidence that it is Isaac might increase [21]. However, such confidences involve cognitive categorization of perception (where cognition is the domain of thought and reasoning). One can be very confident that one sees something, less confident that one sees a person, still less confident that one sees a guy in a ill-fitting suit and still less confident that one sees Isaac [6]. The fact that conscious confidence depends on the imposition of cognitive categories raises the question of the extent to which the phenomenology of confidence is perceptual phenomenology.

Morrison has countered by appealing to perceptual categorization, saying it is the perceptual categories that make the confidences perceptual [22]. However, it is not the case that perceptual categorization is involved in all perception. The operational index of perceptual categorization is faster and more accurate discrimination across perceptual categories than within perceptual categories. And that obtains in only some cases of perception, for example, colour perception and phoneme perception. Using the example of oriented grids, there may be categorical perception of cardinal orientations, but the same issue arises for ±15° from a 25° tilt where no cardinal orientations are involved.

In any case, perceptual categorization does nothing to solve the problem of the perception of direction or orientation that we started with. In normal foveal perception of a vertical grid, we are not aware of the 30° tilts at all, so we are certainly not aware of them with low confidences.

Another confidence-based approach would be metacognitive confidence, the confidence that a certain probability estimate is correct. Confidence in this sense is strongly conceptual; for example, it requires the concept of probability. So, metacognitive confidence is unlikely to be perceptual.

3. Precision

Another proposal about the manifestation of probabilistic representation in the phenomenology of perception is that what Vul et al. and Gross & Flombaum interpret probabilistically should instead be seen in terms of representational precision [6]. In the case of the orientation cells that are tuned to verticality but are also activated by a wide range of other orientations, the manifestation of this wide responsiveness might be blur. Of course, vertical things may look blurry in a fog, but the problem at hand is why they do not look blurry in foveal perception in standard conditions, despite the wide tuning of individual neurons.

It has been suggested that the low quality of colour information in the peripheral retina shows that perception really is highly indeterminate. Our impression of determinacy is supposed to be an illusion [23–27]. My first point against this claim is that it is a myth that there are insufficient colour receptors in the periphery of the retina to see vivid colours. Discrimination of one hue from another is as good at 50° as in the fovea if the colour stimuli are large enough [28]. And there is some colour sensitivity out to 80°–90°. I called this a myth ([29, p. 534]) and a recent article describes it as a ‘widespread misconception even among vision scientists' [30]. Second, it is well known that there is integration of colour information over time within visual cortex. Third, ‘memory colour’ effects are well known. Similar points are made in [29,31].

It might be said that, rather than blur, the perception represents a determinable rather than a determinate [32]. A determinate is a more specific way of having a determinable, as red is a more specific way of being coloured. The determinable/determinate relation is relative—red is determinate relative to coloured but determinable relative to scarlet. The suggestion that we are aware of determinables does have the advantage of predicting that we do not see low probability alternatives, but it throws out the baby with the bathwater by denying that we see the high probability alternatives as well. How would the determinable hypothesis apply to the vertical grid or vertical motion examples? Perhaps, the determinable would be motion that deviates from vertical at most by a small acute angle. If ‘small’ is supposed to cover the full range of putatively represented angles, the problem is just restated, and if ‘small’ covers a smaller range, the proposal does not face up to the problem how it is that perception does not reflect the probabilistic representations outside that range.

4. Populations

Thus far, it may seem that I am arguing that if perception is probabilistic, it would seem probabilistic; it does not seem so, so it is not probabilistic. That is not my argument. There are a number of ways in which probabilistic perception might not seem probabilistic. The most promising candidates involve populations of neurons. I mentioned earlier that the information required to determine the conscious perception is spread over populations. The question at hand is whether the mechanisms by which this information is integrated requires actual probabilistic representation. My overall point is that the best approach to population responses does not involve commitment to actual explicit probabilistic representations because they are to be understood in terms of Marr's ‘computational’ level, to be explained below.

The next two sections concern two population-based approaches: sampling and competition. I endorse the latter and go on to explain that it is compatible with Bayesian approaches.

5. Sampling

Sampling is a way of moving from probabilistic representations to narrower probability distributions or to non-probabilistic representations in populations of neurons. Any such process can be described as sampling but as we will see in the next section, there is another approach that is less naturally described as sampling. The big attraction of sampling from a Bayesian perspective is that optimal Bayesian inference is intractable but sampling is not. My objection to sampling is that standard sampling models model perceptual decision rather than perception itself.

The term ‘sampling’ covers any process in which items are chosen from a distribution, e.g. drawing balls from an urn. The ‘standard’ form of sequential sampling according to a recent review [33] is the diffusion decision model in which the subject is given a task, say of deciding whether a bar is tilted to the left or to the right. A threshold of evidence is set for each of the choices, and the system samples from the distribution of responses. Samples are the input and the output is a decision. (Some writers treat the decision itself as a sample [34].) In one version, each sample is treated as an item of evidence in a Bayesian calculation of posterior probability. If the accumulation of evidence reaches the threshold for clockwise before the threshold for anticlockwise, the perceptual decision is clockwise [33,35].

Applied to the problem at hand, the suggestion would be that probabilistic representations are unconscious, but conscious perception reflects the sampling, not the probabilistic representations themselves. The sampling answer to ‘If perception is probabilistic, why does it not seem probabilistic?’ then is that unconscious perception is probabilistic but conscious perception is not.

Vul et al. say ‘Internal representations are graded probability distributions, yet responses about, and conscious access to, these representations is limited to discrete samples. Our mind appears to perform Bayesian inference without our knowing it’. Gross & Flombaum (p. 361), referencing Vul et al., put it this way: ‘perceivers construct from noisy transduced signals probabilistic representations (assignments of credences over a space of possibilities concerning the distal scene) that take into account, as best they can, expected relationships among the scene's various features; performance, in response to a specific query, then involves “sampling” from the probabilistic representations stored in visual memory’ (italics added).

However, we do not need a query for the vertical grid or vertical motion to look vertical. Without any particular task or query or focused attention, vertical objects in the world seen foveally in normal conditions tend to look vertical. You may be reading this on a computer screen whose sides are vertical and look vertical despite the fact that there is no task concerning them and you are not attending directly to them. Further, Bayesian models of sampling standardly require cognitive categories imposed in advance as part of the subject's task. In the example above, the categories were tilted left and tilted right. But then the same problem arises as already mentioned in connection with confidence. When sampling depends on the imposition of cognitive categories, that raises the question of the extent to which the phenomenology of the conscious state is genuinely perceptual phenomenology.

The basic problem is that sampling models model perceptual decision rather than perception, i.e. the formation of a percept. Perception takes place routinely with no task, explicit or implicit, and without any need for perceptual decision as to which cognitive category to apply. I am appealing here and in what follows to the difference between perception and cognition—where cognition includes thought, reasoning and decision-making. Although I cannot argue for it here, I believe that perceptual representations are constitutively iconic, non-conceptual and non-propositional in content, whereas cognitive representations do not have these properties. There is an important divide between the types of representations involved in perception and cognition [36–38].

An advocate of sampling might suggest that there is always sampling in conscious perception, independently of any task. If there are many samples, the problem this article started with arises: The samples will be samples of different orientations, so why does not vision reflect all the samples? The supposition that there is a single random sample leading to a point estimate would predict widespread illusion.

The evidence for probabilistic representation in ordinary perception is problematic. To get evidence for sampling, Vul et al. had to produce a perceptual situation in which subjects were making weakly informed guesses, something that does not happen in prototypical foveal vision. They presented 26 letters in quick succession for 20 ms each with 47 ms in between letters. In the series, one letter was surrounded by a circle and the subjects' task was to say which letter was circled. The innovation of Vul et al. was to ask for multiple guesses about the same perception, the results of which they describe as sampling from a distribution of hypotheses in that very perception.

However, anyone who has been a subject in such a rapid series of percepts—15 letters in a single second—knows that the subjective impression is one of guessing. A similar problem arises for a second experiment in which letters were ‘crowded’ together in space. In crowded perception, most notably in the periphery of the visual field, there is more than one object in an ‘integration field’, making the perception bewildering. One subject in a (different) crowding experiment was quoted as saying ‘It looks like one big mess … I seem to take features of one letter and mix them up with those of another’. Another subject said: ‘I know that there are three letters. But for some reason, I can't identify the middle one, which looks like it's being stretched and distorted by the outer flankers' ([39, p. 1139]) . The evidence for probabilistic perception in a case in which subjects are subjectively guessing does not automatically apply to ordinary foveal perception in which a vertical line looks vertical, despite representations in the visual system of lower probability tilts. In the Vul et al. cases, competition has broken down and there are many simultaneously present percepts.

Further, what Vul et al. describe as sampling from a distribution was a matter of making a series of four decisions about what letter was cued. Subjects got monetary rewards, more money for getting the letter right on the first guess and less for the subsequent three guesses, so they had to evaluate which of these conceptual categorizations they were most sure of. Their responses required complex cognition involving the imposition of concepts on whatever perceptual information they had.

In sum, standard forms of sequential sampling require the imposition of cognitive categories, something that may never be involved in genuine perception. Sampling is more of a model of perceptual decision than of perception, i.e. the formation of percepts. And a highly cited item of evidence for sampling involves uncertain perception that is quite different from the kind of perception that gives rise to the original problem.

The problems with the sampling approach motivate looking at another approach to populations of neurons, competition.

6. Competition

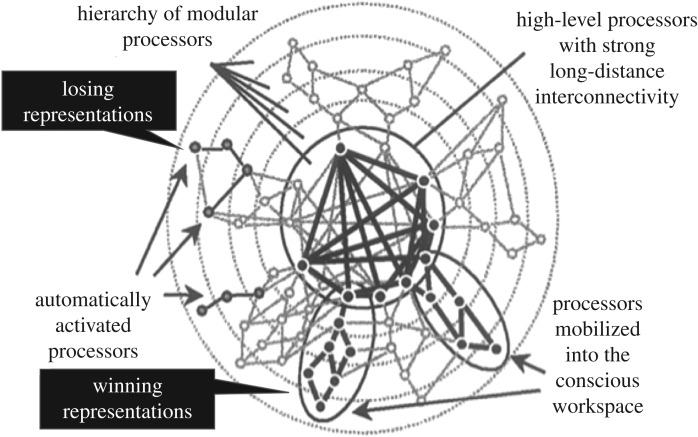
What seems to me the most promising approach is based on the notion of competition. I know that some will see competition as an implementation of sampling but the key difference, as I have been saying, is that competition routinely happens without any need for a perceptual decision. One kind—not the only kind—of competition is involved in the ‘global workspace’ model of consciousness [40] (figure 3). The outer ring indicates the sensory surfaces of the body. Circles are neural systems and lines are links between them. Filled circles are activated systems and thick lines are activated links. Activated neural coalitions compete with one another to trigger recurrent (reverberatory) activity, symbolized by the ovals circling strongly activated networks. Sufficiently activated networks trigger recurrent activity in cognitive areas in the centre of the diagram and they in turn feed back to the sensory activations, maintaining the sensory excitation until displaced by a new dominant coalition. Not everyone accepts the global workspace theory as a theory of consciousness (including me), but it does serve to illustrate one kind (again, not the only kind) of competition among sensory activations that in many circumstances is ‘winner-takes-all’, with the losers precluded from consciousness.

Figure 3.

Schematic diagram of the global workspace. I am grateful to Stan Dehaene for supplying this drawing. Dark pointers added.

(I have argued that recurrent activations confined to the back of the head can be conscious without triggering central activation. Because of local recurrence, these are ‘winners’ in a local competition without triggering global workspace activation [41]. Strong recurrent activations in the back of the head normally trigger ‘ignition’, in which a winning neural coalition in the back of the head spreads into recurrent activations in frontal areas that in turn feed back to sensory areas (figure 3). As Dehaene et al. [42] have shown, such locally recurrent activations can be produced reliably with a strong stimulus and strong distraction of attention. As I am concerned in this paper with normal perception, I will ignore my disagreement with the model here.)

Another case in which losing representations are precluded from consciousness is rivalry, both rivalry that can be experienced with one or both eyes (as with the Necker cube and standard figure/ground stimuli) and binocular rivalry. In rivalry, alternative representations compete for dominance because of mechanisms of reciprocal inhibition. The losing representations rise again when the dominant perceptions are weakened by adaptation. One evolutionary explanation for reciprocal inhibition is that vision has to cope with damage to the eye in which there is some distorted registration that must be inhibited in favour of a dominant percept [43]. In this winner-takes-all competition, the mechanism is competition and dominance.

Although the explanation of rivalry in terms of reciprocal inhibition and adaptation is very well confirmed [44], there are Bayesian accounts, including accounts based on sampling, that have some utility in predicting some specific details of the dominance of rivalrous stimuli. Some of these accounts take neural noise to be the factor that triggers switches [45], whereas others suggest the driving factor is predictions in the frontal cortex in triggering switches [43,46,47]. In addition, there are Bayesian approaches to adaptation itself [48]. The sampling accounts in this application avoid the problem for sampling mentioned earlier of explaining perceptual decision rather than perception, because the rivalrous states are first and foremost rivalrous perceptions rather than perceptual decisions, and also obtain when there is no task [49]. However, what is most obviously probabilistic about rivalry is the transitions between perceptions, because one cannot predict the time or length of one episode of dominance on the basis of those that preceded it [50]. Sampling accounts can model probabilistic transitions among non-probabilistic representations rather than probabilistic representations [51]. One could say that Bayesian theories of perceptual transitions involve ‘implicit’ probabilistic representation [51], but it is explicit perceptual representation that leads to the question of the title of this article. Further, Bayesian models do not supplant models that appeal to adaptation and competition (reciprocal inhibition), but rather provide a framework for integrating rivalry with other perceptual phenomena [52].

Interestingly, in some perceptual situations, not only is the losing representation suppressed—its putatively probabilistic aspect is repressed too. Hakwan Lau and Megan Peters and their colleagues recorded from intracranial electrodes in epilepsy patients as they were viewing noisy stimuli that could either be faces or houses. They found that face/house decisions were based on the strength of both face and house representations but that confidence judgements did not take into account the strength of the decision-incongruent representation [53]. The face representation can beat out the house representation by a slight margin but only the strength of the face representation is involved in determining confidence. This result is compatible with probabilistic representation but suggests limitations on it.¹ Like Trump, consciousness likes winners, not losers, even if the losers are almost on a par with the winners, probabilistically speaking.

In a binocular rivalry set-up if the two pictures are locally compatible, the perception will reflect merger of the pictures. For example, a male and a female face that are locally compatible will be seen as a combined androgynous face [55]. (Local compatibility has to do with whether small patches are lighter or darker than the background. If they are locally of opposite polarity (one patch lighter, one darker), then they are incompatible.) So, in a binocular set-up, competing images can lead to rivalry or to merging, depending on local compatibility. Merging can sometimes involve patches of both stimuli. These two modes are often contrasted, with only rivalry being classified as ‘winner-takes-all’. But merging can also be considered as a kind of winner-takes-all process that is different from rivalry in which the male and female faces are losers and the androgynous face is the winner.

A similar process occurs in perception of motion direction. When neurons representing opposite directions are stimulated, the result is that one direction wins. When neurons represent different but not opposite directions, there is a kind of vector averaging process [8]. In both cases, varying representations give way to a single winner. Using electrodes that stimulate areas of MT in monkey cortex, Nichols and Newsome were able to show that when there are activations representing directions that differ by more than 140°, one direction is completely suppressed (as in rivalry), whereas when they differ by less than 140°, the result is a perception that averages the vectors.

The proposal then is that we should think about population codes in terms of competition for dominance. What is conscious is the result of competition, the competing representations prior to that resolution being unconscious. Competing representations resolve either with the weak dying out so that the strong can live or with merging or averaging. The big advantage of the framework of competition over sampling is that competition does not require a perceptual decision.

Why are the losing representations not represented in consciousness? It may be that consciousness requires a minimal level of strength of activation or local recurrent circuits, both of which have independent support [56,57]. The global workspace and higher order accounts are alternatives. My hope is that getting clear about the role of competition in perception will help to guide research on this question.

Advocates of sampling may say that competition is just an implementation of sampling and that losing representations are just representations that represent low probabilities. Further, the strongest activations do not always win, and that could be used to suggest probabilistic representation. Although the strongest, most skilled and heaviest wrestler probably will win, that does not show that the wrestlers represent probabilities or that representations of probabilities are involved in wrestling matches. One event can be more probable than another without any representation of probabilities. To reiterate: the competition framework does not require the imposition of cognitive categories and so is distinct from the sampling framework.

I do not deny that competition can be understood in probabilistic terms. Winning a competition could be described as a probabilistic decision. Any detailed model of competition could be described in probabilistic terms. My conclusion is not that the probabilistic view is false but that it should be understood instrumentally rather than as describing actual probabilistic representations. As I will argue in the next section, the best attitude towards the Bayesian formalism is an ‘as if’ or instrumentalist attitude, and that attitude is very common in Bayesian writing.

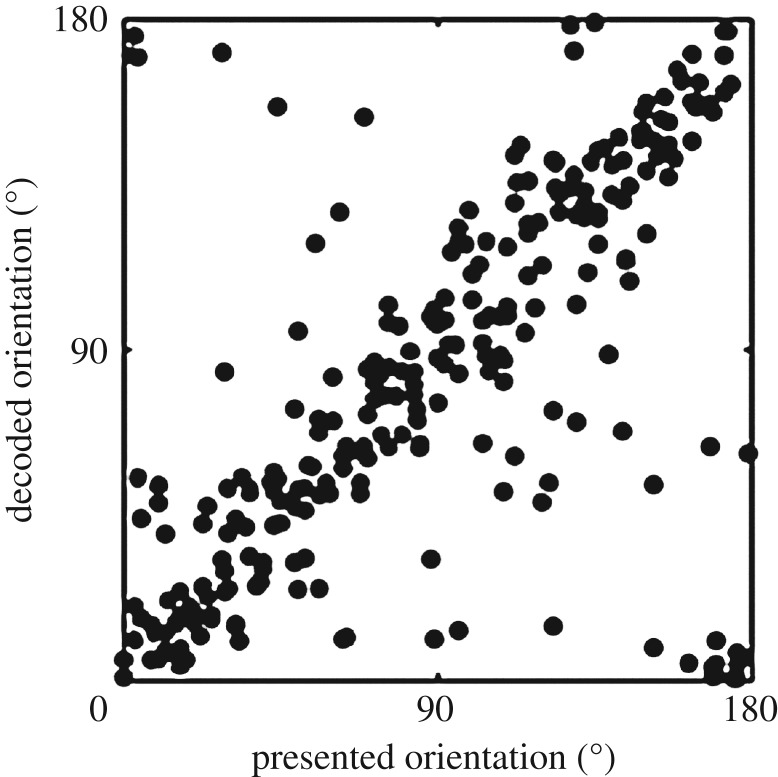
There are a number of experimental studies that purport to show probabilistic representations in human visual cortex. van Bergen et al. [34] start by conceding, of the probabilistic hypothesis that ‘direct neural evidence supporting this hypothesis is currently lacking’. They purport to remedy this situation. They showed subjects randomly oriented grids while doing brain scans (fMRI), focusing on early visual cortical areas (V1,V2, V3). Subjects were required to rotate a bar to match the orientations they saw, giving the experimenters a behavioural measure of precision of response. Using fMRI, they were able to decode the orientations subjects were seeing. They measured the ‘cortical uncertainty’ of orientations in an individual perception. The measure they adopted is not easy to describe in a non-technical way but what is easy to describe is the way they chose among various candidates: by looking for the measure of uncertainty in an individual perception that correlated best with variation from perception to perception. This variation is depicted in figure 4. The width of the distribution in the graph of actual orientation versus decoded orientation is a measure of ‘cortical uncertainty’ over time.

Figure 4.

A graph of decoded orientation versus actual orientation of the stimulus. Thanks to Weiji Ma for this figure. See [34], Supplementary Material 1.

There are three results, all involving the notion of ‘cortical uncertainty’. My response to those results is that what they call ‘cortical uncertainty’ is equally well described as ‘degree of cortical competition’. One reason that the dots in figure 4 are scattered instead of clustered tightly is that neurons respond to many different orientations, creating many competing representations for each stimulus. Of course, degree of cortical competition can be regarded as an implicit representation of uncertainty. But, merely implicit probabilistic representation does not give rise to the puzzle of the title of this article.

The first of van Bergen et al.'s three results has to do with something called the ‘oblique effect’, a phenomenon not mentioned here so far (and one that has nothing to do with the discussion of orientations earlier). The phrase ‘oblique effect’ refers to the phenomenon that subjects are more accurate in reporting cardinal (horizontal and vertical) orientations than for oblique orientations. The van Bergen result is that their measure of cortical uncertainty was higher for oblique than for cardinal grids. They say cortical uncertainty explains behavioural uncertainty. However, degree of cortical competition gives essentially the same explanation, but without commitment to probabilistic representation.

van Bergen et al. also showed (this is the second result) that when they presented the same orientation repeatedly, subjects' behavioural precision was predicted by the cortical uncertainty. Again, this fact can be seen as behavioural precision predicted by degree of cortical competition.

The third result is the most impressive. They argue that the visual system tracks its own uncertainty. It is well known that subjects’ orientation judgements are biased towards oblique and against cardinal orientations (a different sort of oblique effect). They found that when cortical uncertainty was high, the bias towards oblique orientations was stronger than when cortical uncertainty was low, suggesting that the visual system monitors its own uncertainty on a trial-by-trial basis, relying more on bias when cortical uncertainty is high. But ‘monitoring competition’ and ‘monitoring uncertainty’ can be descriptions of the same facts.

Similar points apply to the observation that the weight given to different senses when they are integrated in perception depends on the relative reliability of those senses and how quickly it can be computed [58,59]. ‘Monitoring reliability’ and ‘monitoring competition’ can refer to the same process.

van Bergen et al. conclude that this is ‘strong empirical support for probabilistic models of perception’ (p. 1729), but their results do not distinguish between instrumentalist and realist construals of this claim.

There are independent grounds for caution in concluding that perceptual representations are probabilistic or that uncertainty is represented in perception. A useful corrective comes from a recent study of pea plants that shows that growth of roots of pea plants involves sensitivity to variation in nutrients [60].

Individual pea plants had their roots separated into different pots as indicated in figure 5. The conditions could be rich (lots of nutrients) or poor, and variable (i.e. fluctuating) or constant. In rich conditions, the plants grew a larger mass of roots in the constant pot; in poor conditions, the plants grew a larger mass of roots in the variable plot. As the authors note, the plants were risk prone in poor and risk averse in rich conditions, fitting the predictions of risk sensitivity theory. Were the plants monitoring the uncertainty in nutrients reaching their roots? The plants have no nervous system and no one has found anything that could be called a representation of uncertainty. Any talk of plants ‘monitoring’ uncertainty would have to be regarded as ‘as if’ talk unless there is evidence to the contrary. I suggest we should take a similar attitude towards the sensitivity to uncertainty shown in the van Bergen study: it should be understood in an ‘as if’ framework unless we have evidence for a more realistic interpretation.

Figure 5.

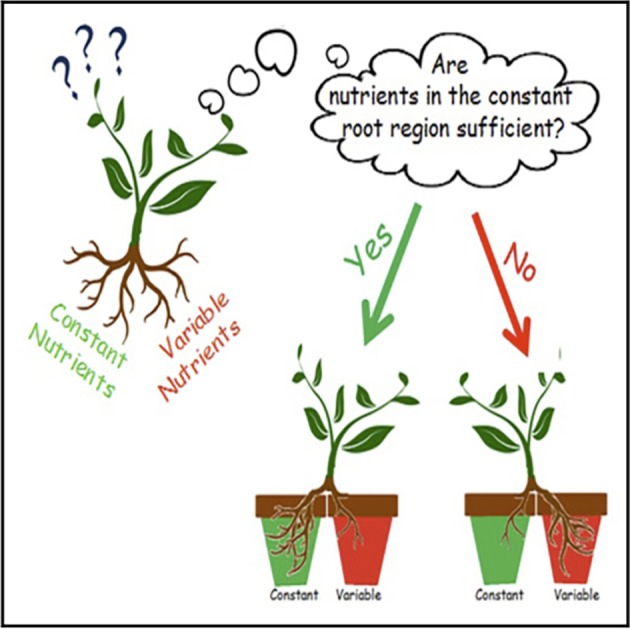
This is the ‘graphical abstract’ for [60]. Reproduced with permission from Elsevier. (Online version in colour.)

The conclusion of Dener et al. (p. 1766) fits with my methodological suggestion:

Plants’ risk sensitivity reinforces the oft-repeated assertion that complex adaptive strategies do not require complex cognition (adaptive strategies may be complex for us to understand, without necessarily being complex for organisms to implement). Bacteria … fungi … , and plants generate flexible and impressively complex responses through ‘decision’ processes embedded in their physiological architecture, implementing adaptive responses that work well under a limited set of ecological circumstances (i.e. that are ecologically rational)

In sum, sensitivity to uncertainty does not require representation of anything, including uncertainty.

7. Why Bayesian approaches do not require probabilistic representation

One argument for probabilistic representation in perception is that Bayesian models of perception have been highly successful and that they (putatively) presuppose probabilistic representation. I will argue that on the most plausible construal of Bayesian models, they do not presuppose probabilistic representation. Bayesian accounts of visual perception compute the probability density functions of various configurations of stimuli in the environment on the basis of prior probabilities of those environmental configurations and likelihoods of visual ‘data’ if those environmental configurations obtain. (Visual data are often taken to be activations in early vision.)

Bayes’ theorem states that the probability of a hypothesis about the environment (e.g. that there is a certain distribution of colours on a surface) given visual data is proportional to the prior probability of that hypothesis multiplied by the probability of the visual data given the hypothesis. If h is the environmental hypothesis, e is the evidence from visual data and p(h|e) is the probability of h given e, then p(h|e) is proportional to p(e|h) × p(h). p(e|h) is the ‘likelihood’ (of the visual data given the environmental hypothesis) and p(h) is the prior probability of the environmental hypothesis. (An equivalence rather than a statement of proportionality requires a normalizing factor, so that probabilities sum to 1.)

In Bayesian updating, the system uses the previous probability of the environmental hypothesis as the prior in changing the hypothesis about the environment in response to new visual data. So, Bayesian updating requires multiplying one's current prior probability estimate times one's current estimate of likelihood to get the probability of the environmental hypothesis, given current stimulation. Then the posterior probability of the environmental hypothesis becomes the new prior. The most plausible version of these theories are hierarchical in that the visual system is divided into stages with distinct priors and likelihoods at each stage. In the ‘predictive coding’ version of the account, predictions in the form of priors are sent down the visual hierarchy (i.e. towards the sense organs) while error signals (the prediction minus the data) are sent upwards [52,61].

What would show that something that deserves to be called Bayesian inference actually occurs in perception? In the most straightforward implementation, there would have to be perceptual representations of prior probabilities for alternative hypotheses, perceptual representations of likelihoods and some process that involves something that could be described as multiplication of these values. (Additional arithmetic complexity would be added by utility functions that compare the utility of the various environmental hypotheses.)

It is common for those who emphasize Bayesian processes in perception to appeal to global optimality. Many perceptual processes are Bayes optimal but many are not. As Rahnev & Denison [62] note in a review of suboptimal processes in perception, there is an extensive literature documenting suboptimal performance. In any case, Bayes optimality is neutral between instrumentalist and realist construals.

Often, Bayesian theories of perception are held as computations in an ideal observer, an observer who uses Bayesian principles to optimally compute what is in the environment on the basis of visual data. Ideal observer theories are instrumentalist in that they are not committed to the representation in real visual systems of priors or likelihoods or their multiplication within the system. Bayesian models, construed from the ideal observer point of view, do not licence attributions of probabilistic representation [63,64]. For example, Maloney & Mamassian [65] show how non-Bayesian reinforcement learning can result in behaviour that comports well with an ideal Bayesian observer.

Sanborn & Chater [66] argue that an approximation process that samples from representations but does not compute over probabilities would mimic standard probabilistic fallacies in reasoning. They suggest implementation of the sampling process in a connectionist network of a sort that would not plausibly support probabilistic representation.

However, some Bayesian accounts are more ‘realist’ about priors and likelihoods (and utilities) that are represented explicitly in perceptual systems. A major problem with realist theories in which Bayesian inference literally takes place in the brain is that the kind of Bayesian computations that would have to be done are known to be computationally intractable [66]. So, any realist version of Bayesianism will have to tell us what exactly is supposed to be involved in the computations.

Michael Rescorla argues for a realist version of Bayesianism in which priors are explicitly represented [64,67]. He does not say explicitly that likelihoods are explicitly represented and that the multiplication of one by the other is real. Rescorla's argument is based on the fact that we have good Bayesian models of how priors evolve in response to changing environmental conditions. For example, such models predict that if one exposes a subject to stimulation in which luminance and stiffness are correlated, the priors will change so that stiff objects are seen as more luminant. And, this prediction is born out. Further, the ‘light comes from overhead’ prior can be changed by experience. Overall, he says, a realist interpretation yields explanatory generalizations that would be missed on an instrumentalist interpretation. The principle is that the best explanation of successful prediction is that the entities referred to in the theories that generate the prediction really exist and to a first approximation really have the properties ascribed to them in the theory [68]. The specific application here is that our ability to predict how priors will change supports the hypothesis that priors are really represented in perception.

I find this argument unconvincing because whatever it is about the computations of a system that simulates the effect of represented priors (for example, the proposal by Sanborn & Chater) might also be able to simulate the effect of change of priors. Without a comparison of different mechanisms that can accomplish the same goal, the argument for realism is weak.

Further, perception is an inherently noisy process in part because the neural processing is characterized by random fluctuations. The representations must be regarded as approximate. But what is the difference between approximate implementation of Bayesian inference and behaving roughly as if Bayesian inference is being implemented [7,64]? Until this question is answered, the jury is out on the dispute between realist and anti-realist views.

Recent debates about Bayesianism in perception have appealed to David Marr's famous three levels of description of perception. The top level, the computational level, specifies the problem computationally, whereas the next level down, the algorithmic level, specifies how the input and output are represented and what processes are supposed to move from the input and output. To use one of Marr's examples, in the characterization of a cash register, the computational level would be arithmetic. One variant of the algorithmic level would specify a base 10 numerical system using Arabic numerals plus the techniques that elementary school students learn concerning adding the least significant digits first. An alternative to this type of algorithm and representation might use binary representation and an algorithm level involving AND and X-OR gates [69]. The lowest level, the implementation level, asks how the algorithms are implemented in hardware. In an old-fashioned cash register, implementation would involve gears and in older computer implementations of binary arithmetic, magnetic cores that can be in either one of two states [70].

Many prominent Bayesians say that most Bayesians are working at the computational level. For example, Griffiths et al. [2]: ‘Most Bayesian models of cognition are defined at Marr's [71] “computational level,” characterizing the problem people are solving and its ideal solution. Such models make no direct claims about cognitive processes—what Marr termed the “algorithmic level”’.

In sum, the Bayesian perspective is powerful, but it does not require a realist or algorithmic interpretation. Instrumentalist versions of Bayesianism as giving explanations at Marr's computational level are well supported and are not committed to probabilistic representations.

8. Conclusion

My proposal is that competition among unconscious representations yields conscious representations through winner-takes-all processes of elimination or merging. The competition framework does not require any particular task or cognitive categorization and in that respect is better than the sampling framework. The process can be considered Bayesian but only on an instrumentalist interpretation pitched at Marr's computational level rather than the algorithmic level.

Perhaps, the strongest challenge to my account is Bayesian sampling accounts of competition, especially the use of sampling models to predict some of the details of binocular rivalry [45,46]. However, (i) the conflict between different Bayesian models (noise versus predictions as the driving factor), (ii) the fact that probabilistic transitions in rivalry do not require probabilistic representations, (iii) the point made in connection with pea plants, and (iv) the strong considerations in favour of the computational rather than algorithmic level in Bayesian explanations counter the challenge.

To head off one misinterpretation, I am not suggesting that there is a single stage of processing (a ‘Cartesian theatre’ [72]) where competition is resolved. The competition at any stage of the visual hierarchy may perhaps be resolved at the same stage or at a higher stage, but that does not entail that there is a single stage at which everything is resolved.

In sum, my answer to the question ‘If perception is probabilistic, why doesn't it seem probabilistic?’ is that we would do well to think of probabilities in perception instrumentally, avoiding the realist interpretations that motivate the question of the title.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

I received no funding for this study.