SUMMARY
Our increased understanding of the mechanistic heterogeneity of diseases has pushed the development of targeted therapeutics. We do not expect all patients with a given disease to benefit from a targeted drug; only those in the target population. That is, those with sufficient dysregulation in the biomolecular pathway targeted by treatment. However, due to complexity of the pathway, and/or technical issues with our characterizing assay, it is often hard to characterize the target population until well into large-scale clinical trials. This has stimulated the development of adaptive enrichment trials; clinical trials in which the target population is adaptively learned; and enrollment criteria are adaptively updated to reflect this growing understanding. This paper proposes a framework for group-sequential adaptive enrichment trials. Building on the work of Simon & Simon (2013). Adaptive enrichment designs for clinical trials. Biostatistics 14(4), 613–625), it includes a frequentist hypothesis test at the end of the trial. However, it uses Bayesian methods to optimize the decisions required during the trial (regarding how to restrict enrollment) and Bayesian methods to estimate effect size, and characterize the target population at the end of the trial. This joint frequentist/Bayesian design combines the power of Bayesian methods for decision making with the use of a formal hypothesis test at the end of the trial to preserve the studywise probability of a type I error.
Keywords: Adaptive enrichment, Bayesian statistics, Clinical trials
1. Introduction
Many difficult-to-treat diseases are actually a heterogeneous collection of similar syndromes with potentially different causal mechanisms. A new molecule which inhibits a defined pathway can only be expected to effectively treat a subset of patients whose disease is driven by that pathway. With these new targeted therapeutics, there is significant interest in using clinical and genomic features to find this subset of patients which will benefit for each given treatment.
Often there is insufficient data to clearly specify this subset at the beginning of a large-scale clinical trial. Common practice has been to broadly enroll patients, and upon conclusion of the trial, attempt to characterize those who benefit from treatment (Assmann and others, 2000). This has a number of difficulties. Enrolling patients who will not benefit decreases the power of the trial, exposes those patients to unnecessary toxicity and restricts them from receiving more personally effective therapies. In addition, we may end up with little information for patients on the boundary (those for whom the trial shows no clear data indicating benefit or no benefit).
Instead, the idea of adaptively enriching our population has received increasing attention. We might begin by broadly enrolling patients, but as the trial progresses, from the outcomes of previous patients we may be able to characterize those patients who benefit. At that stage, we would restrict entry to only that subgroup (or perhaps more conservatively, exclude those patients we deem very unlikely to benefit). This was initially proposed by Follmann (1997) for the setting of discrete patient strata and subsequently investigated by Wang and others (2007), Rosenblum and Van Der Laan (2011), and Rosenblum and others (2014) for the case of a single binary biomarker. Others have also considered this problem in simple stratified settings or with a small number of pre-specified subsets (Magnusson and Turnbull, 2013; Wang and others, 2009; Friede and others, 2012; Lai and others, 2013). Simon and Simon (2013) proposed a general class of adaptive enrichment designs, including single and multiple biomarkers of any type, which allow investigators to alter the enrollment criteria of a trial in progress, and yet still control the probability of a type one error, even in the presence of unknown time trends. These designs are flexible and allow nearly any (potentially data dependent) change in enrollment criteria.
Simon and Simon (2013) leaves many questions open: How might we learn , the subset which benefits, during a trial? Based on a noisy estimate
, the subset which benefits, during a trial? Based on a noisy estimate 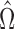 of
of  , how should we choose whether or not to enroll a potential patient? (There is a tradeoff between learning new information, power, and patient benefit.) At the end of the trial what should we use as our treatment indication? and what is a reasonable estimate of effect size in the indicated population?
, how should we choose whether or not to enroll a potential patient? (There is a tradeoff between learning new information, power, and patient benefit.) At the end of the trial what should we use as our treatment indication? and what is a reasonable estimate of effect size in the indicated population?
In this paper we attempt to answer these questions. We use a Bayesian framework, as we believe the answers are most tractable there and that the Bayesian framework is most appropriate for decision problems. One should note, however, that while use the Bayesian formalism for enrollment decisions, and indication/effect size estimation, because we work in the framework of Simon and Simon (2013), these designs will still control the probability of a type one error. Other work has looked at making decisions in biomarker-guided trials using Bayesian methods (Kim and others, 2011; Barker and others, 2009; Zhou and others, 2008). These have all been in a different context, however: they are phase 2 trials for deciding between multiple treatment arms with no formal type one error control. Joint frequentist/Bayesian designs have been proposed in the context of a two stage trial with a single pre-specified subset (Brannath and others, 2009; Song, 2014; Graf and others, 2015). These designs use a multiple testing framework that is feasible with a single pre-specified subset. Graf and others (2015) discusses utility functions but does not attempt to maximize posterior expected benefit for patients treated based on the results of the clinical trial as described here.
2. A refresher on adaptive enrichment designs
We will illustrate the adaptive enrichment design approach using binary outcome, though these ideas are equally applicable to continuous, or time-to-event data. Assume we have a single new treatment we are comparing to control. We randomize each patient that we accrue with equal probability to one of the two arms. Let  (
( ) denote a vector of covariates measured on patient
) denote a vector of covariates measured on patient 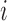 . Let
. Let 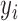 be the outcome for patient
be the outcome for patient 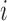 , where
, where  for response and
for response and  for non-response, and let
for non-response, and let  be the treatment assignment (
be the treatment assignment (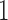 for treatment,
for treatment,  for control).
for control).
We will focus on the block adaptive enrichment design from Simon and Simon (2013). We describe it here in a slightly more specific form. Suppose we accrue patients sequentially in  blocks. In the
blocks. In the  th block we accrue
th block we accrue  patients with
patients with  randomized to treatment and
randomized to treatment and 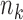 to control. Assume that we observe the responses (
to control. Assume that we observe the responses ( ) for patients on the
) for patients on the  th block before accruing patients for block
th block before accruing patients for block 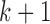 .
.
Further, assume we have some rule, which for each block ( ) takes in all the data from previous blocks (covariates, assignments, and outcomes) and creates a decision function
) takes in all the data from previous blocks (covariates, assignments, and outcomes) and creates a decision function  , with
, with 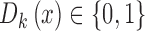 for all covariate vectors
for all covariate vectors 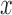 . For each block we admit only patients with
. For each block we admit only patients with 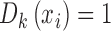 .
.
More formally, let  be the
be the  ,
,  , and
, and  values for block
values for block  , let
, let  . We define our “rule”
. We define our “rule” 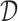 as a function which takes in
as a function which takes in  and returns an enrollment criteria
and returns an enrollment criteria  .
.
We use the following procedure to test  :
:
(1) Pre-specify
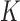 and
and 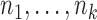 .
.(2) For the first block use
 for all
for all 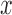 . Enroll (without restriction) and randomize
. Enroll (without restriction) and randomize  patients for this block.
patients for this block.-
(3) For blocks
 repeat:
repeat:(a) Calculate
 based on previous patients outcomes.
based on previous patients outcomes.(b) Enroll
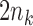 new patients with
new patients with  , and randomize treatment assignment.
, and randomize treatment assignment.
- (4) At the final analysis a single significance test is performed using as test statistic
where  and
and 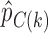 are the response proportions for the treatment and control arms in block
are the response proportions for the treatment and control arms in block 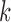 ,
, 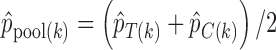 , and
, and  . This is the usual inverse normal combination test statistic that has been widely used in adaptive trial designs (Bauer and others, 2016). Comparing this statistic to the tails of a standard Gaussian distribution provides a test which asymptotically controls type
. This is the usual inverse normal combination test statistic that has been widely used in adaptive trial designs (Bauer and others, 2016). Comparing this statistic to the tails of a standard Gaussian distribution provides a test which asymptotically controls type  error essentially regardless of how we construct the
error essentially regardless of how we construct the 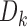 . The power of this test and its ability to identify
. The power of this test and its ability to identify  , however, strongly depend on that construction. This tests the strong null hypothesis
, however, strongly depend on that construction. This tests the strong null hypothesis 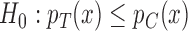 for all covariates
for all covariates 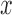 , where
, where  and
and 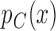 are the true response probabilities on the test treatment and control for a patient with covariate vector
are the true response probabilities on the test treatment and control for a patient with covariate vector  . This test preserves the type I error regardless of the method used for making enrichment decisions and regardless of (possibly data dependent) time trends in the characteristics (measured or not) of the patients. One might consider using a rerandomization test; however, as discussed in Simon and Simon (2013), simple rerandomization tests which are nominally level
. This test preserves the type I error regardless of the method used for making enrichment decisions and regardless of (possibly data dependent) time trends in the characteristics (measured or not) of the patients. One might consider using a rerandomization test; however, as discussed in Simon and Simon (2013), simple rerandomization tests which are nominally level 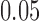 can have type I error in excess of
can have type I error in excess of 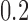 . Other authors have considered an alternative to testing the strong null, the seamless phase II/III trial: They use a closed testing procedure in a two block design to test the specific hypothesis selected in the second stage (Bretz and others, 2006; Jennison and Turnbull, 2007). While rejection in that framework allows stronger statements to be made, it greatly limits the flexibility of the design. We discuss the tradeoffs of testing a strong null versus seamless phase II/III trials further in Section 7.
. Other authors have considered an alternative to testing the strong null, the seamless phase II/III trial: They use a closed testing procedure in a two block design to test the specific hypothesis selected in the second stage (Bretz and others, 2006; Jennison and Turnbull, 2007). While rejection in that framework allows stronger statements to be made, it greatly limits the flexibility of the design. We discuss the tradeoffs of testing a strong null versus seamless phase II/III trials further in Section 7.
3. An overview of the procedure
A brief outline of our procedure is:
(1) Choose a prior for
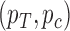 , and a measure of “utility” for the trial.
, and a measure of “utility” for the trial.(2) Enroll the first block of patients without restriction.
(3) Update our prior based on the observed treatments, outcomes, and covariates of enrolled patients to get a posterior.
(4) Using the posterior, simulate the rest of the trial (many times) to find an “optimal” enrollment decision rule (with respect to our utility) for enrolling patients in the next block.
(5) Enroll a new block of patients using our “optimal” rule.
(6) Repeat steps 2–4 for each additional block. Several decisions must be made: we need a prior distribution for
 , as well as a utility function. To make things computationally tractable, a few simplifications will be employed in developing an “optimal” enrollment decision rule. These will be discussed further, below.
, as well as a utility function. To make things computationally tractable, a few simplifications will be employed in developing an “optimal” enrollment decision rule. These will be discussed further, below.
4. The Bayesian framework
We begin by assuming that  and
and 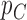 are functions that map from covariates to probabilities. Denote the prior for
are functions that map from covariates to probabilities. Denote the prior for  by
by 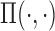 . As a simple illustrative example, one might consider
. As a simple illustrative example, one might consider
with some (prior) density 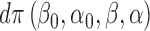 on the coefficients. Note. This logistic model assumes monotonicity of the effects (in
on the coefficients. Note. This logistic model assumes monotonicity of the effects (in 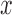 )—for some scenarios this may not be inappropriate.
)—for some scenarios this may not be inappropriate.
We will also assume that the  values of patients who attempt to enroll in the trial are drawn independently from some probability distribution
values of patients who attempt to enroll in the trial are drawn independently from some probability distribution 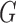 on
on 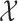 .
.
4.1 Determining enrollment criteria
Our enrollment criteria must depend on the goal of the clinical trial—there are a number of potentially conflicting goals: maximizing power, accurately estimating  , and minimizing accrual time among others. Our approach in this paper is to codify these goals into a utility function
, and minimizing accrual time among others. Our approach in this paper is to codify these goals into a utility function 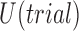 , and come up with an enrollment strategy to approximately maximize this utility.
, and come up with an enrollment strategy to approximately maximize this utility.
4.1.1. Utility
There are many possibilities for codifying utility. We believe one strong option is what we term expected future patient outcome (EFPO) penalized by accrual time:
where EFPO is
and 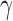 is some pre-specified parameter that trades off between future patient benefit and accrual time. Note that because we only allow the treatment to be used for future patients if we successfully reject
is some pre-specified parameter that trades off between future patient benefit and accrual time. Note that because we only allow the treatment to be used for future patients if we successfully reject 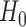 , this criterion takes power into account.
, this criterion takes power into account.
4.1.2. Utility-based enrollment criteria
In what follows one may use the utility of the previous section, or some other personal preference. How can we use this utility to decide on 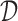 ? The standard choice would be to select
? The standard choice would be to select 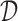 to maximize expected utility. For an enrollment rule
to maximize expected utility. For an enrollment rule  , our expected utility is
, our expected utility is
| (4.1) |
Unfortunately, this involves a functional maximization over an infinite dimensional space, and to our knowledge the solution in general is computationally intractable.
We first simplify the problem by restricting the class of decision functions 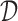 can produce. Rather than having
can produce. Rather than having  as a general function of the covariates, we will instead use
as a general function of the covariates, we will instead use
| (4.2) |
where  is some pre-specified, minimum relevant treatment efficacy, and
is some pre-specified, minimum relevant treatment efficacy, and  is a single parameter per block over which we optimize. We believe this functional of the data effectively combines information about the expectation and variability of
is a single parameter per block over which we optimize. We believe this functional of the data effectively combines information about the expectation and variability of 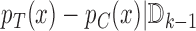 , though other functionals may also work well. We write
, though other functionals may also work well. We write  as
as 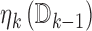 to make clear that it is a function of the previous data—this allows us to be more conservative or liberal in our enrollment, based on the quality of information we have attained so far in the trial.
to make clear that it is a function of the previous data—this allows us to be more conservative or liberal in our enrollment, based on the quality of information we have attained so far in the trial.
We will optimize the 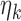 values over a grid
values over a grid  . Even maximizing utility over this class is non-trivial because the solution involves a stochastic recursion whose computational complexity increases exponentially with the number of blocks. For two block trials, the computation is quite tractable, and we can maximize utility over this restricted class. We believe that the two block scenario is of interest—it is logistically intractable to change enrollment criteria too often in large, multi-center trials—however, in the supplemental material available at Biostatistics online we give a heuristic approach for the multi-block setting which balances performance with computational tractability.
. Even maximizing utility over this class is non-trivial because the solution involves a stochastic recursion whose computational complexity increases exponentially with the number of blocks. For two block trials, the computation is quite tractable, and we can maximize utility over this restricted class. We believe that the two block scenario is of interest—it is logistically intractable to change enrollment criteria too often in large, multi-center trials—however, in the supplemental material available at Biostatistics online we give a heuristic approach for the multi-block setting which balances performance with computational tractability.
Note that we are not just enrolling patients in each block who are in our current best estimate of 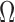 : At intermediate stages of the trial we need to take into account both (i) if we expect a given patient to benefit and (ii) how likely that expectation is to change given additional data. Thus our enrollment criteria is a bit broader than what our estimated indication would be if the trial terminated at that stage: In addition to enrolling patients whom we expect to benefit, we also enroll patients for whom there is large uncertainty. A criterion based on (4.2) contains a happy medium of information from (i) and (ii).
: At intermediate stages of the trial we need to take into account both (i) if we expect a given patient to benefit and (ii) how likely that expectation is to change given additional data. Thus our enrollment criteria is a bit broader than what our estimated indication would be if the trial terminated at that stage: In addition to enrolling patients whom we expect to benefit, we also enroll patients for whom there is large uncertainty. A criterion based on (4.2) contains a happy medium of information from (i) and (ii).
4.2. Indication and effect size
After the trial terminates, if the trial is a success and we reject the null hypothesis, we are left with several labeling questions. Who should the treatment be indicated for and what should we report as the effect size of the treatment? Our framework allows us to address these questions.
4.2.1. Indication
For any individual with covariate vector  , the expected benefit is
, the expected benefit is 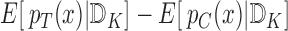 where the expected values are taken with regard to the posterior distributions at the end of the trial. These expected benefit values may depend only on some of the covariates. This information can sometimes be conveniently presented in nomogram form to be used by physicians and their future patients in deciding whether or not to use the test treatment.
where the expected values are taken with regard to the posterior distributions at the end of the trial. These expected benefit values may depend only on some of the covariates. This information can sometimes be conveniently presented in nomogram form to be used by physicians and their future patients in deciding whether or not to use the test treatment.
For regulatory labeling, the test treatment may be indicated for patients with the disease and covariates  in
in  , with
, with
where 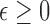 is specified based on the risk and toxicity of the new drug versus standard of care. If the drug is no more toxic or risky, then one would likely use
is specified based on the risk and toxicity of the new drug versus standard of care. If the drug is no more toxic or risky, then one would likely use 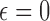 . For individual decision making, the appropriate
. For individual decision making, the appropriate  may vary by patient.
may vary by patient.
One might note that it is possible (though unlikely) that an adaptive enrichment trial is run as per our prescription above, that successfully rejects the strong null; but for which 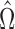 is empty. This was extremely rare in our simulation experiments. In this case the trial is likely quite marginal, and one might choose not to approve the drug. One might further disincentivize this through a modification to the utility (Section 4.1.1). Even with current non-adaptive designs, there are examples where a pivotal clinical trial produces a statistically significant result but with such limited size of benefit for the eligible population that the drug is not approved, particularly if it is associated with significant adverse events.
is empty. This was extremely rare in our simulation experiments. In this case the trial is likely quite marginal, and one might choose not to approve the drug. One might further disincentivize this through a modification to the utility (Section 4.1.1). Even with current non-adaptive designs, there are examples where a pivotal clinical trial produces a statistically significant result but with such limited size of benefit for the eligible population that the drug is not approved, particularly if it is associated with significant adverse events.
4.2.2. Effect size
The expected effect size for any particular patient with covariate-vector 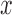 can be calculated as
can be calculated as  . If we are interested in average effect size for the indicated population, we can integrate this with respect to
. If we are interested in average effect size for the indicated population, we can integrate this with respect to  , over
, over 
The first factor of the integrand is a posterior expected value for a given 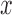 . The posterior distributions are obtained by Bayes’ theorem and are not effected by the fact that eligible x vectors for a block are selected based on results for previous blocks.
. The posterior distributions are obtained by Bayes’ theorem and are not effected by the fact that eligible x vectors for a block are selected based on results for previous blocks.
4.3. Choice of prior
Biomarker driven clinical trials are initiated with a range of prior information about the candidate biomarkers (Karuri and Simon, 2012). In cases with little prior information, we may choose non-informative working priors on the parameters of the response distributions of the two treatment groups for purposes of adaptation. Alternatively, we may choose a prior where the components of  are independently normal with mean zero and variance calibrated to reflect the prior assumption that treatment by biomarker interactions are unlikely. It is important to note that the frequentist statistical significance test conducted at the conclusion of the clinical trial will be valid regardless of what prior or decision functions are used. We could even use non-informative priors for developing the decision functions during the trial and switch to a more conservative prior which indicates that treatment biomarker interactions are unlikely after the trial for identifying an intended use population and estimating the treatment effect for that population.
are independently normal with mean zero and variance calibrated to reflect the prior assumption that treatment by biomarker interactions are unlikely. It is important to note that the frequentist statistical significance test conducted at the conclusion of the clinical trial will be valid regardless of what prior or decision functions are used. We could even use non-informative priors for developing the decision functions during the trial and switch to a more conservative prior which indicates that treatment biomarker interactions are unlikely after the trial for identifying an intended use population and estimating the treatment effect for that population.
5. imulated trials
We evaluate the performance of our designs in several simulated scenarios. We compare a design that optimizes over cutpoints to a simpler approach with fixed cutpoints, and a fixed design.
5.1. Data generation
We consider six different basic scenarios, three with logistic generative models, and three with cutpoint models. In each scenario we assume that we have measured two features, 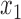 and
and 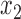 upon which we may wish to restrict enrollment. We simulated these features as independent
upon which we may wish to restrict enrollment. We simulated these features as independent  .
.
For the first three scenarios we simulated from a logistic model for response:
| (5.1) |
Model 1:  ,
,  (Subgroup, but no global effect),
(Subgroup, but no global effect),
Model 2:  ,
,  (Global treatment effect, but no biomarker),
(Global treatment effect, but no biomarker),
Model 3:  ,
,  (Global effect with additional predictive biomarker).
(Global effect with additional predictive biomarker).
For the next three scenarios we simulated from a cutpoint model, but analyzed using the logistic models. We set cutpoints 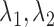 , and
, and 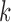 (
( ). If
). If  then our patient is “biomarker positive,” and otherwise, “biomarker negative.” We then had four different response probabilities
then our patient is “biomarker positive,” and otherwise, “biomarker negative.” We then had four different response probabilities 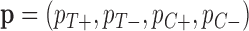 for biomarker positive and negative patients under treatment and control.
for biomarker positive and negative patients under treatment and control.
Model 4:  ,
,  ,
, 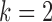 (Predictive biomarker),
(Predictive biomarker),
Model 5: 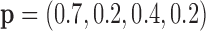 ,
, 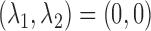 ,
, 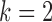 (Predictive + Prognostic biomarker),
(Predictive + Prognostic biomarker),
Model 6}: 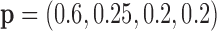 ,
,  ,
,  (Global effect + Predictive marker).
(Global effect + Predictive marker).
For each of these six scenarios we accrue 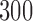 patients, but consider two different accrual strategies. In the first we accrue patients in two blocks of
patients, but consider two different accrual strategies. In the first we accrue patients in two blocks of 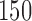 patients. In the second we instead use three blocks of
patients. In the second we instead use three blocks of  patients. Results are based on
patients. Results are based on  simulated replications.
simulated replications.
5.2. Enrichment strategy
For our enrichment we use the logistic models (5.1) with independent non-informative priors on the coefficients 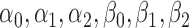 . We base our enrollment decisions on
. We base our enrollment decisions on 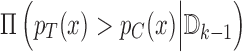 as discussed in Section 4.1. We use
as discussed in Section 4.1. We use  as candidate cutpoints for this criterion. For both enrollment decisions, and indication we use
as candidate cutpoints for this criterion. For both enrollment decisions, and indication we use 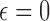 . That is, if the posterior probability that
. That is, if the posterior probability that  for a patient with covariate vector
for a patient with covariate vector 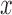 is greater than the candidate cutpoint, e.g. 0.3, then such a patient is eligible for the next period.
is greater than the candidate cutpoint, e.g. 0.3, then such a patient is eligible for the next period.
We consider two different types of enrichment strategies: fixed cutpoint and hybrid adaptive cutpoint strategies. For the fixed cutpoint we choose our cutpoints to be used in the decision function at each stage before the start of the trial. For the hybrid adaptive cutpoint strategy we choose our cutpoints adaptively at each block by greedily attempting to optimize for our EFPO (the utility described in Section 4.1.1 with  ) based on previous block outcomes. This stochastic adaptive strategy is further described in supplemental material available at Biostatistics online. For two blocks, the hybrid adaptive strategy is equivalent to the full adaptive cutpoint strategy discussed in the supplemental material available at Biostatistics online.
) based on previous block outcomes. This stochastic adaptive strategy is further described in supplemental material available at Biostatistics online. For two blocks, the hybrid adaptive strategy is equivalent to the full adaptive cutpoint strategy discussed in the supplemental material available at Biostatistics online.
We also allowed early stopping for futility in our adaptive trials: If at a given block, the posterior indicates that either there is less than an 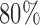 probability that at least someone will benefit, or there is no one who meets the enrollment criterion, then we terminate the trial.
probability that at least someone will benefit, or there is no one who meets the enrollment criterion, then we terminate the trial.
5.3. Results
The results are displayed in Tables 1 and 2. In terms of power, the enrichment designs outperformed the unenriched strategy in all settings (save for  where there was no subgroup to find). The enrichment designs were most effective in the scenarios with true logistic generative models (
where there was no subgroup to find). The enrichment designs were most effective in the scenarios with true logistic generative models ( ), however, they still performed well for the cutpoint models (
), however, they still performed well for the cutpoint models ( ). While we see an increase in accrual-time for the adaptive designs, we note that, for all scenarios (save
). While we see an increase in accrual-time for the adaptive designs, we note that, for all scenarios (save  ), increasing power of the non-adaptive design to that of the adaptive designs would require an accrual time larger than that of the adaptive design. We also note that in comparing Tables 1 and 2, we see that enrolling three blocks of
), increasing power of the non-adaptive design to that of the adaptive designs would require an accrual time larger than that of the adaptive design. We also note that in comparing Tables 1 and 2, we see that enrolling three blocks of  patients generally has higher power and favorable specificity/sensitivity to designs enrolling two blocks of
patients generally has higher power and favorable specificity/sensitivity to designs enrolling two blocks of 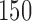 .
.
Table 1.
Operating characteristics for the six scenarios, averaged over  simulated trials, for two blocks with
simulated trials, for two blocks with 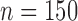 patients per block. Each column is a different trial design: AC, FC (0.3), FC (0.5), FC (0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses an adaptive cutpoint in the second block with candidate values
patients per block. Each column is a different trial design: AC, FC (0.3), FC (0.5), FC (0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses an adaptive cutpoint in the second block with candidate values 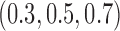 , ‘F-C(
, ‘F-C( )’ uses a fixed cutpoint with value
)’ uses a fixed cutpoint with value 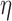 . ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
. ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
| AC | Non-A | FC (0.3) | FC (0.5) | FC (0.7) | ||
|---|---|---|---|---|---|---|
| 1 | Power | 0.52 | 0.04 | 0.35 | 0.51 | 0.6 |
| Sensitivity | 0.95 | 1 | 0.96 | 0.95 | 0.94 | |
| Specificity | 0.9 | 0 | 0.89 | 0.9 | 0.91 | |
| Accrual time | 486 | 300 | 428 | 471 | 515 | |
| Effect size | 0.21 | 0 | 0.21 | 0.21 | 0.21 | |
| Bias | 0.04 | 0.14 | 0.06 | 0.05 | 0.04 | |
| Root-MSE | 0.06 | 0.14 | 0.08 | 0.06 | 0.06 | |
| 2 | Power | 0.36 | 0.35 | 0.34 | 0.35 | 0.36 |
| Sensitivity | 0.9 | 1 | 0.91 | 0.9 | 0.88 | |
| Specificity | X | X | X | X | X | |
| Accrual time | 372 | 300 | 328 | 366 | 403 | |
| Effect size | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | |
| Bias | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | |
| Root-MSE | 0.06 | 0.07 | 0.06 | 0.06 | 0.06 | |
| 3 | Power | 0.84 | 0.59 | 0.75 | 0.82 | 0.86 |
| Sensitivity | 0.9 | 1 | 0.92 | 0.9 | 0.89 | |
| Specificity | 0.78 | 0 | 0.76 | 0.78 | 0.79 | |
| Accrual time | 380 | 300 | 341 | 371 | 411 | |
| Effect size | 0.19 | 0.12 | 0.19 | 0.19 | 0.19 | |
| Bias | 0.03 | 0.04 | 0.04 | 0.03 | 0.02 | |
| Root-MSE | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 | |
| 4 | Power | 0.22 | 0.19 | 0.2 | 0.23 | 0.25 |
| Sensitivity | 0.99 | 1 | 0.99 | 1 | 1 | |
| Specificity | 0.24 | 0 | 0.18 | 0.23 | 0.28 | |
| Accrual time | 416 | 300 | 362 | 403 | 432 | |
| Effect size | 0.06 | 0.05 | 0.06 | 0.06 | 0.07 | |
| Bias | 0.08 | 0.07 | 0.08 | 0.08 | 0.07 | |
| Root-MSE | 0.08 | 0.07 | 0.09 | 0.08 | 0.07 | |
| 5 | Power | 0.41 | 0.29 | 0.37 | 0.42 | 0.46 |
| Sensitivity | 0.99 | 1 | 1 | 0.99 | 0.99 | |
| Specificity | 0.3 | 0 | 0.24 | 0.31 | 0.34 | |
| Accrual time | 413 | 300 | 352 | 398 | 445 | |
| Effect size | 0.1 | 0.07 | 0.09 | 0.1 | 0.11 | |
| Bias | 0.06 | 0.06 | 0.07 | 0.06 | 0.05 | |
| Root-MSE | 0.07 | 0.07 | 0.08 | 0.07 | 0.06 | |
| 6 | Power | 0.51 | 0.5 | 0.5 | 0.48 | 0.51 |
| Sensitivity | 0.85 | 1 | 0.89 | 0.87 | 0.83 | |
| Specificity | X | X | X | X | X | |
| Accrual time | 374 | 300 | 331 | 362 | 402 | |
| Effect size | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| Bias | 0.05 | 0.04 | 0.05 | 0.05 | 0.05 | |
| Root-MSE | 0.06 | 0.05 | 0.06 | 0.06 | 0.06 |
Table 2.
Operating characteristics for the six scenarios, averaged over  simulated trials, for three blocks with
simulated trials, for three blocks with 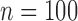 patients per block. Each column is a different trial design: AC, FC (0.3,0.3),..., FC (0.5,0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses adaptive cutpoints in the second and third blocks with candidate values
patients per block. Each column is a different trial design: AC, FC (0.3,0.3),..., FC (0.5,0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses adaptive cutpoints in the second and third blocks with candidate values 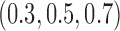 . ‘F-C(
. ‘F-C(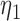 ,
,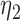 )’ uses fixed cutpoints with value
)’ uses fixed cutpoints with value 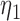 in block
in block 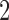 and
and  in block
in block 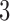 . ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
. ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
| AC | Non-A | FC(0.3,0.3) | FC(0.5,0.5) | FC(0.7,0.7) | FC(0.5,0.7) | ||
|---|---|---|---|---|---|---|---|
| 1 | Power | 0.82 | 0.03 | 0.64 | 0.78 | 0.88 | 0.82 |
| Sensitivity | 0.92 | 1 | 0.93 | 0.92 | 0.9 | 0.91 | |
| Specificity | 0.92 | 0 | 0.91 | 0.92 | 0.93 | 0.92 | |
| Accrual time | 542 | 300 | 468 | 526 | 604 | 558 | |
| Effect size | 0.22 | 0 | 0.22 | 0.22 | 0.23 | 0.22 | |
| Bias | 0.03 | 0.14 | 0.04 | 0.02 | 0.01 | 0.02 | |
| Root-MSE | 0.06 | 0.14 | 0.06 | 0.06 | 0.05 | 0.05 | |
| 2 | Power | 0.38 | 0.38 | 0.39 | 0.39 | 0.38 | 0.37 |
| Sensitivity | 0.87 | 1 | 0.91 | 0.89 | 0.85 | 0.86 | |
| Specificity | X | X | X | X | X | X | |
| Accrual time | 426 | 300 | 345 | 404 | 483 | 441 | |
| Effect size | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | |
| Bias | 0.05 | 0.06 | 0.05 | 0.05 | 0.04 | 0.05 | |
| Root-MSE | 0.06 | 0.07 | 0.06 | 0.06 | 0.05 | 0.06 | |
| 3 | Power | 0.87 | 0.6 | 0.82 | 0.88 | 0.91 | 0.88 |
| Sensitivity | 0.88 | 1 | 0.9 | 0.88 | 0.87 | 0.88 | |
| Specificity | 0.76 | 0 | 0.75 | 0.77 | 0.78 | 0.78 | |
| Accrual time | 414 | 300 | 358 | 402 | 468 | 430 | |
| Effect size | 0.19 | 0.12 | 0.19 | 0.19 | 0.19 | 0.19 | |
| Bias | 0.02 | 0.04 | 0.03 | 0.02 | 0.02 | 0.02 | |
| Root-MSE | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | |
| 4 | Power | 0.29 | 0.18 | 0.2 | 0.29 | 0.32 | 0.34 |
| Sensitivity | 1 | 1 | 0.99 | 0.99 | 0.99 | 0.99 | |
| Specificity | 0.31 | 0 | 0.2 | 0.31 | 0.34 | 0.34 | |
| Accrual time | 512 | 300 | 393 | 485 | 521 | 527 | |
| Effect size | 0.07 | 0.05 | 0.06 | 0.07 | 0.07 | 0.07 | |
| Bias | 0.07 | 0.07 | 0.08 | 0.07 | 0.06 | 0.06 | |
| Root-MSE | 0.08 | 0.07 | 0.09 | 0.08 | 0.07 | 0.07 | |
| 5 | Power | 0.48 | 0.32 | 0.38 | 0.46 | 0.53 | 0.51 |
| Sensitivity | 0.99 | 1 | 0.99 | 0.99 | 0.98 | 0.99 | |
| Specificity | 0.37 | 0 | 0.29 | 0.37 | 0.38 | 0.39 | |
| Accrual time | 468 | 300 | 378 | 450 | 510 | 491 | |
| Effect size | 0.11 | 0.07 | 0.1 | 0.11 | 0.11 | 0.11 | |
| Bias | 0.05 | 0.06 | 0.06 | 0.05 | 0.04 | 0.05 | |
| Root-MSE | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.06 | |
| 6 | Power | 0.53 | 0.5 | 0.51 | 0.52 | 0.55 | 0.53 |
| Sensitivity | 0.81 | 1 | 0.87 | 0.83 | 0.76 | 0.81 | |
| Specificity | X | X | X | X | X | X | |
| Accrual time | 423 | 300 | 347 | 408 | 501 | 448 | |
| Effect size | 0.1 | 0.1 | 0.1 | 0.1 | 0.11 | 0.1 | |
| Bias | 0.05 | 0.04 | 0.06 | 0.05 | 0.04 | 0.05 | |
| Root-MSE | 0.06 | 0.05 | 0.06 | 0.06 | 0.05 | 0.06 |
Because we use an uninformative (and sometimes more mis-specified) prior, we see that our effect size estimates are biased. In scenarios with more signal this bias is slight. However, in a setup like scenario  this bias can become significant. It is interesting to note, however, that the fixed design (with no enrichment) actually has bias at least as severe as our adaptive enrichment designs. This bias is due to averaging over only successful trials.
this bias can become significant. It is interesting to note, however, that the fixed design (with no enrichment) actually has bias at least as severe as our adaptive enrichment designs. This bias is due to averaging over only successful trials.
Comparing adaptive versus fixed cut-points, we see that in many of these scenarios it does not make a large difference (with the exception of FC(0.3,0.3) and FC(0.3) which perform poorly). We still advocate using an adaptive cutpoint: it allows us to tie our cutpoint decision to an objective criterion (utility), and in principle trades a bit of computing power for improved patient outcomes.
This is not an exhaustive set of simulations. In practice when choosing a strategy one should explore the operating characteristics of each method in the specific scenario of interest. That said, these simulations show the effectiveness of this Bayesian approach to adaptive enrichment.
6. Redesign of cetuximab trial
In addition to the previous simulations, we illustrate the approach to adaptive enrichment design described here using the clinical trial described by Bokemeyer and others (2009). The trial compared the standard of care chemotherapy regimen FOLFOX-4 to the same regimen with the addition of the anti-EGFR antibody cetuximab as first-line treatment for newly diagnosed patients with metastatic colorectal cancer. A total of 337 patients were randomized equally to the two treatments in a clinical trial involving 79 centers. The sample size was established to have 90% power at a 0.05 significance level for detecting an odds ratio of 2.33 for response rate comparing the two treatment groups overall. At the start of the trial there was uncertainty about the influence of EGFR expression or KRAS mutation on the probability of response to cetuximab.
The primary analysis of Bokemeyer and others (2009) gave a response rate for the cetuximab containing arm of 46% compared to 36% for the chemotherapy only control. The 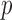 -value reported was
-value reported was 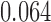 , interpreted as not significant at the
, interpreted as not significant at the 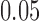 level.
level.
We developed an adaptive enrichment design for this clinical trial that included EGFR expression level and KRAS mutation status as candidate predictive biomarkers. Response is modeled separately for the cetuximab and control groups using logistic regression. For details on how the parameters of the models were estimated from the published data see the supplemental material available at Biostatistics online.
We simulated two period designs with 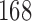 patients accrued per period. If the null hypothesis is rejected, then we determine the intended use population based on the posterior estimates of the logistic regression models, where the posterior distributions of the regression coefficients are based on the full dataset of the clinical trial. In tabulating the average sensitivity in Table 3 we have not included the replications in which the null hypothesis is not rejected.
patients accrued per period. If the null hypothesis is rejected, then we determine the intended use population based on the posterior estimates of the logistic regression models, where the posterior distributions of the regression coefficients are based on the full dataset of the clinical trial. In tabulating the average sensitivity in Table 3 we have not included the replications in which the null hypothesis is not rejected.
Table 3.
Operating characteristics for the three redesign scenarios of Bokemeyer and others (2009), averaged over  simulated trials, for two blocks with
simulated trials, for two blocks with 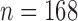 patients per block. Each column is a different trial design: AC, FC (0.3), FC (0.5), FC (0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses an adaptive cutpoint in the second block with candidate values
patients per block. Each column is a different trial design: AC, FC (0.3), FC (0.5), FC (0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses an adaptive cutpoint in the second block with candidate values 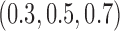 , ‘F-C(
, ‘F-C( )’ uses a fixed cutpoint with value
)’ uses a fixed cutpoint with value 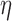 . ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
. ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
| AC | Non-A | FC (0.3) | FC (0.5) | FC (0.7) | ||
|---|---|---|---|---|---|---|
| 1 | Power | 0.68 | 0.23 | 0.62 | 0.69 | 0.73 |
| Sensitivity | 0.99 | 1 | 0.99 | 0.99 | 0.99 | |
| Specificity | 0.92 | 0 | 0.92 | 0.93 | 0.89 | |
| Accrual time | 454 | 336 | 423 | 452 | 478 | |
| Effect size | 0.21 | 0.06 | 0.21 | 0.21 | 0.2 | |
| Bias | 0.04 | 0.07 | 0.05 | 0.04 | 0.04 | |
| Root-MSE | 0.06 | 0.08 | 0.07 | 0.06 | 0.06 | |
| 2 | Power | 0.81 | 0.68 | 0.79 | 0.84 | 0.86 |
| Sensitivity | 0.98 | 1 | 0.98 | 0.98 | 0.98 | |
| Specificity | 0.56 | 0 | 0.51 | 0.58 | 0.58 | |
| Accrual time | 412 | 336 | 376 | 406 | 442 | |
| Effect size | 0.18 | 0.13 | 0.18 | 0.18 | 0.18 | |
| Bias | 0.04 | 0.03 | 0.05 | 0.04 | 0.03 | |
| Root-MSE | 0.06 | 0.05 | 0.06 | 0.06 | 0.06 | |
| 3 | Power | 0.38 | 0.03 | 0.22 | 0.37 | 0.45 |
| Sensitivity | 1 | 1 | 1 | 1 | 1 | |
| Specificity | 0.76 | 0 | 0.83 | 0.8 | 0.74 | |
| Accrual time | 488 | 336 | 452 | 488 | 488 | |
| Effect size | 0.15 | 0.01 | 0.17 | 0.16 | 0.14 | |
| Bias | 0.08 | 0.12 | 0.09 | 0.07 | 0.08 | |
| Root-MSE | 0.09 | 0.12 | 0.1 | 0.09 | 0.09 |
As shown in the first block of rows in Table 3, the adaptive enrichment designs provide much greater power than does the analysis used by Bokemeyer and others (2009). The power increases from about 30% to about 70%. The average sensitivity and specificity for the adaptive trials are also excellent indicating that in almost all cases the correct classifier was found; i.e. the correct classifier indicates that the intended use population consists of all patients with wild-type KRAS regardless of the level of EGFR expression. It can be seen that the adaptive enrichment designs with fixed cutpoints of 0.5 or 0.7 do as well as the design in which the cutpoint used is adaptively chosen based on the data in the first block.
Part of the reason for the outstanding performance of the adaptive enrichment designs in the first block of rows in Table 3 is that the treatment effect is reversed for the KRAS mutant population compared to the KRAS wild-type subset. Consequently we repeated the simulations in which the data was generated assuming that for the KRAS mutant patients the response probability was the same for both treatments, 41%, the average of the response probabilities used previously. The results of these simulations are shown in the second block of rows in Table 3. With the data generated in this way, the power of the non-adaptive design used by Bokemeyer and others (2009) improves considerably, but is still not as good as for the adaptive enrichment designs and the specificity of the non-adaptive design is also inadequate. The adaptive enrichment designs here retain excellent sensitivity but reduced specificity compared to the simulation based on the actual data of the trial.
We also conducted simulations in which patients benefited from cetuximab only if KRAS was wild-type and EGFR expression was moderate or high. The results are shown in the final block of rows in Table 3. The power of the non-adaptive trial is almost nil because the subset of patients who benefit from cetuximab is smaller with this scenario. The power of the adaptive design has also decreased substantially although it is still much greater than for the non-adaptive design. The sensitivity of the adaptive enrichment designs remains excellent and the specificity has increased compared to the previous scenario indicating that when the strong null is rejected, the correct indication for patients with wild-type KRAS and medium or high EGFR expression is selected about 80% of the time.
Table 4 shows results using three period adaptive enrichment designs. Using three periods results in substantial power gains for the adaptive designs for scenarios 1 and 3.
Table 4.
Operating characteristics for the three redesign scenarios of Bokemeyer and others (2009), averaged over 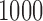 simulated trials, for three blocks with
simulated trials, for three blocks with  patients per block. Each column is a different trial design: AC, FC (0.3,0.3),..., FC (0.5,0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses adaptive cutpoints in the second and third blocks with candidate values
patients per block. Each column is a different trial design: AC, FC (0.3,0.3),..., FC (0.5,0.7) are all enrichment trials. These designs do not restrict entry in the first block. ‘A-C’ uses adaptive cutpoints in the second and third blocks with candidate values 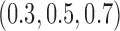 . ‘F-C(
. ‘F-C( ,
, )’ uses fixed cutpoints with value
)’ uses fixed cutpoints with value  in block
in block  and
and  in block
in block  . ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
. ‘Non-A’ is a standard unenriched design. ‘Sensitivity’ and ‘Specificity’ are given for detecting the population which benefits. ‘Effect size’ is the true effect size for the designated population. ‘Bias’ is the amount by which each procedure over-estimates that effect size. ‘root-MSE’ is the root-mean-square error of the effect size estimate for the designated population. All operating characteristics, other than power and accrual time, are averaged only over successful trials
| AC | Non-A | FC(0.3,0.3) | FC(0.5,0.5) | FC(0.7,0.7) | FC(0.5,0.7) | ||
|---|---|---|---|---|---|---|---|
| 1 | Power | 0.78 | 0.21 | 0.74 | 0.82 | 0.82 | 0.83 |
| Sensitivity | 0.98 | 1 | 0.99 | 0.98 | 0.97 | 0.98 | |
| Specificity | 0.92 | 0 | 0.93 | 0.95 | 0.89 | 0.92 | |
| Accrual time | 511 | 336 | 461 | 503 | 552 | 525 | |
| Effect size | 0.21 | 0.06 | 0.21 | 0.22 | 0.2 | 0.21 | |
| Bias | 0.03 | 0.07 | 0.03 | 0.02 | 0.02 | 0.02 | |
| Root-MSE | 0.06 | 0.08 | 0.06 | 0.06 | 0.06 | 0.06 | |
| 2 | Power | 0.86 | 0.65 | 0.8 | 0.86 | 0.87 | 0.88 |
| Sensitivity | 0.97 | 1 | 0.98 | 0.98 | 0.96 | 0.97 | |
| Specificity | 0.62 | 0 | 0.58 | 0.67 | 0.64 | 0.67 | |
| Accrual time | 459 | 336 | 400 | 451 | 512 | 480 | |
| Effect size | 0.19 | 0.13 | 0.18 | 0.19 | 0.19 | 0.19 | |
| Bias | 0.03 | 0.03 | 0.04 | 0.03 | 0.02 | 0.03 | |
| Root-MSE | 0.06 | 0.05 | 0.06 | 0.06 | 0.06 | 0.05 | |
| 3 | Power | 0.49 | 0.03 | 0.35 | 0.5 | 0.58 | 0.57 |
| Sensitivity | 1 | 1 | 1 | 1 | 0.99 | 1 | |
| Specificity | 0.8 | 0 | 0.84 | 0.83 | 0.74 | 0.79 | |
| Accrual time | 544 | 336 | 502 | 556 | 564 | 569 | |
| Effect size | 0.16 | 0.01 | 0.17 | 0.17 | 0.14 | 0.15 | |
| Bias | 0.06 | 0.13 | 0.07 | 0.06 | 0.07 | 0.06 | |
| Root-MSE | 0.08 | 0.13 | 0.08 | 0.07 | 0.08 | 0.08 |
None of the other published adaptive enrichment approaches known to us are applicable to this clinical trial. Most are based on multiple testing with either a single binary covariate (Wang and others, 2007; Rosenblum and Van Der Laan, 2011), disjoint strata of patients (Follmann, 1997; Magnusson and Turnbull, 2013), or selection of one out of a small number of pre-specified strata (Mehta and Gao, 2011; Jennison and Turnbull, 2007). Although our case could be converted to six strata, the ordering of EGFR expression would be lost. Additionally, the number of strata would grow exponentially in the number of covariates.
7. The strong null hypothesis
In this paper, we have discussed trial designs that test the strong null hypothesis:  for all
for all  , where
, where 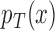 and
and 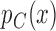 are the response probabilities for a patient with covariate vector
are the response probabilities for a patient with covariate vector  under treatment and control, respectively. One limitation is that we do not formally test for efficacy in the subpopulation indicated at the end of the trial (the weak null). We do not believe this discrepancy (wherein the strong null is correctly rejected, but the weak null is true) is a common occurrence—one should only have additional power (over
under treatment and control, respectively. One limitation is that we do not formally test for efficacy in the subpopulation indicated at the end of the trial (the weak null). We do not believe this discrepancy (wherein the strong null is correctly rejected, but the weak null is true) is a common occurrence—one should only have additional power (over 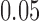 ) to reject
) to reject  when our enrollment algorithm is actually enrolling patients for whom treatment is effective. Our empirical results in Section 5 verify that in the settings we tested this was not an issue. Nevertheless, currently for regulatory clinical trials, a subsequent extension phase or separate study restricted to the intended use population may be required.
when our enrollment algorithm is actually enrolling patients for whom treatment is effective. Our empirical results in Section 5 verify that in the settings we tested this was not an issue. Nevertheless, currently for regulatory clinical trials, a subsequent extension phase or separate study restricted to the intended use population may be required.
There is a literature on seamless phase II/III trials (Bretz and others, 2006; Jennison and Turnbull, 2007) that takes another approach to this problem: They use a closed testing procedure in a two block design to reject the specific hypothesis selected in the second stage. We do not take this approach as (i) it requires pre-specified strata; our framework is developed for a potentially continuous covariate space without the need to stratify; (ii) if there are many strata, then the closed testing procedure will require testing many intersection hypotheses. However, for problems with a small number of discrete covariates (with few levels) this approach could be a fruitful alternative.
Determining which patients benefit from a new treatment once the study-wise null is rejected is a problem for all clinical trials, including standard broad eligibility trials. Serious adverse drug reactions (ADRs) from FDA approved drugs administered according to the labeling indication is a major medical problem. One study claimed that such ADRs represented the fourth to sixth leading cause of death in the United States (Lazarou and others, 1998). Using the eligible population in pivotal studies as the intended use population simplifies statistical significance testing but can result in many patients being exposed to the risk of ADR without likelihood of benefit. This is evident in the small effect sizes seen in many “positive” pivotal trials with broad eligibility. An approach to labeling based on a quantitative risk-benefit assessment that takes account of covariates effecting risk and benefit, rather than statistical significance for a population, might provide physicians more effective guidance. Although specifying an intended use population may be necessary for determining how the drug may be advertised, a more individualized based approach such as described in this paper for benefit may provide a framework for a more satisfactory way of communicating the uncertainties in benefits and risks.
7.1. Estimation versus testing
In this framework we have used the Bayesian paradigm for all aspects of the trial except testing. It is natural to consider testing in the Bayesian paradigm as well. We believe, however, that the frequentist paradigm is more robust here for ensuring that the trial-wise type I error is controlled at a specified level. For a Bayesian test to be valid we need valid models for 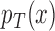 and
and 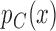 , and we would need to demonstrate that the repeated sampling properties of the design are robust for a range of priors different than the ones used in the trial. Our frequentist test requires no modeling or parametric assumptions, and relies only very lightly on asymptotics. For pivotal regulatory clinical trials strong emphasis is placed on stringent control of the study-wise type I error in a manner not heavily dependent on model assumptions. However, in phase II trials, a Bayesian test could be appropriate.
, and we would need to demonstrate that the repeated sampling properties of the design are robust for a range of priors different than the ones used in the trial. Our frequentist test requires no modeling or parametric assumptions, and relies only very lightly on asymptotics. For pivotal regulatory clinical trials strong emphasis is placed on stringent control of the study-wise type I error in a manner not heavily dependent on model assumptions. However, in phase II trials, a Bayesian test could be appropriate.
8. Discussion
In this paper, we have proposed a class of strategies for the choices one needs to make in an adaptive trial and carry through Bayesian machinery to make decisions. The paper also gives suggestions for these choices, and explores how those suggestions pan out on simulated data. By combining these strategies with the proposal of Simon and Simon (2013), we have a recipe for carrying out adaptive clinical trials. This recipe uses a frequentist test to control the study-wise type  error and this type
error and this type  error control is valid regardless of unknown time-trends in the data (Simon and Simon, 2013). When the global null hypothesis is rejected, Bayesian methods are used to effectively find a subset of patients who will benefit from treatment and to estimate the average treatment effect in that subset. This may serve to reduce the over-treatment of the patient population that takes place in many clinical trials that use the initial eligibility criteria as the basis for defining the intended use population. This approach can be used with a wide variety of utility functions. For our examples we have used a utility function that reflects expected benefit for future patients. This incorporates power as well as the value of information in a natural way, and with modification could include the “cost” of serious side effects of treatment.
error control is valid regardless of unknown time-trends in the data (Simon and Simon, 2013). When the global null hypothesis is rejected, Bayesian methods are used to effectively find a subset of patients who will benefit from treatment and to estimate the average treatment effect in that subset. This may serve to reduce the over-treatment of the patient population that takes place in many clinical trials that use the initial eligibility criteria as the basis for defining the intended use population. This approach can be used with a wide variety of utility functions. For our examples we have used a utility function that reflects expected benefit for future patients. This incorporates power as well as the value of information in a natural way, and with modification could include the “cost” of serious side effects of treatment.
Biomarker-based trials raise an additional interesting question: As we get better at predicting who will respond, do we lose the rationale for randomization (Simon and others, 2015)? This is mostly relevant in the context of non-adaptive enrichment designs but additional work is needed on trials which combine adaptive enrichment and early rejection for efficacy in a subset (while continuing the trial in a larger subset to potentially broaden the indication).
Although there remain additional aspects of adaptive enrichment designs to be studied, the developments here provide important details about utilizing this design in practice.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
Office of the Director of the National Institutes of Health (grant number DP5OD019820) to N.S.
References
- Assmann S. F., Pocock S. J., Enos L. E. and Kasten L. E. (2000). Subgroup analysis and other (mis) uses of baseline data in clinical trials. The Lancet 355(9209), 1064–1069. [DOI] [PubMed] [Google Scholar]
- Barker A. D., Sigman C. C., Kelloff G. J., Hylton N. M., Berry D. A. and Esserman L. J. (2009). I-spy 2: an adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy. Clinical Pharmacology & Therapeutics 86(1), 97–100. [DOI] [PubMed] [Google Scholar]
- Bauer P., Bretz F., Dragalin V., König F. and Wassmer G. (2016). Twenty-five years of confirmatory adaptive designs: opportunities and pitfalls. Statistics in Medicine 35(3), 325–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokemeyer C., Bondarenko I., Makhson A., Hartmann J. T., Aparicio J., De Braud F., Donea S., Ludwig H., Schuch G., Stroh C.. and others (2009). Fluorouracil, leucovorin, and oxaliplatin with and without cetuximab in the first-line treatment of metastatic colorectal cancer. Journal of Clinical Oncology 27(5), 663–671. [DOI] [PubMed] [Google Scholar]
- Brannath W., Zuber E., Branson M., Bretz F., Gallo P., Posch M. and Racine-Poon A. (2009). Confirmatory adaptive designs with Bayesian decision tools for a targeted therapy in oncology. Statistics in Medicine 28(10), 1445–1463. [DOI] [PubMed] [Google Scholar]
- Bretz F., Schmidli H., König F., Racine A. and Maurer W. (2006). Confirmatory seamless phase ii/iii clinical trials with hypotheses selection at interim: general concepts. Biometrical Journal 48(4), 623–634. [DOI] [PubMed] [Google Scholar]
- Follmann D. (1997). Adaptively changing subgroup proportions in clinical trials. Statistic Sinica 7, 1085–1102. [Google Scholar]
- Friede T., Parsons N. and Stallard N. (2012). A conditional error function approach for subgroup selection in adaptive clinical trials. Statistics in Medicine 31(30), 4309–4320. [DOI] [PubMed] [Google Scholar]
- Graf A. C., Posch M., and Koenig F. (2015). Adaptive designs for subpopulation analysis optimizing utility functions. Biometrical Journal 57(1), 76–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennison C. and Turnbull B. W. (2007). Adaptive seamless designs: selection and prospective testing of hypotheses. Journal of Biopharmaceutical Statistics 17(6), 1135–1161. [DOI] [PubMed] [Google Scholar]
- Karuri S. W. and Simon R. (2012). A two-stage Bayesian design for development of new drugs and companion diagnostics. Statistics in Medicine 31, 901–914. [DOI] [PubMed] [Google Scholar]
- Kim E. S., Herbst R. S., Wistuba I. I., Lee J. J., Blumenschein G. R., Tsao A., Stewart D. J., Hicks M. E., Erasmus J., Gupta S.. and others (2011). The battle trial: personalizing therapy for lung cancer. Cancer Discovery 1(1), 44–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai T. L., Liao O. Y. and Kim D. W. (2013). Group sequential designs for developing and testing biomarker-guided personalized therapies in comparative effectiveness research. Contemporary Clinical Trials 36(2), 651–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarou J., Pomeranz B. H. and Corey P. N. (1998). Incidence of adverse drug reactions in hospitalized patients: a meta-analysis of prospective studies. Journal of the American Medical Association 279(15), 1200–1205. [DOI] [PubMed] [Google Scholar]
- Magnusson B. P. and Turnbull B. W. (2013). Group sequential enrichment design incorporating subgroup selection. Statistics in Medicine 32(16), 2695–2714. [DOI] [PubMed] [Google Scholar]
- Mehta C. R. and Gao P. (2011). Population enrichment designs: case study of a large multinational trial. Journal of Biopharmaceutical Statistics 21(4), 831–845. [DOI] [PubMed] [Google Scholar]
- Rosenblum M. and Van Der Laan M. J. (2011). Optimizing randomized trial designs to distinguish which patients benefit from treatment. Biometrika 98(4), 845–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblum M., Liu H. and Yen E.-H. (2014). Optimal tests of treatment effects for the overall population and two subpopulations in randomized trials, using sparse linear programming. Journal of the American Statistical Association 109(507), 1216–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon N. and Simon R. (2013). Adaptive enrichment designs for clinical trials. Biostatistics 14(4), 613–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon R., Blumenthal G. M., Rothenberg M. L., Sommer J., Roberts S. A., Armstrong D. K., LaVange L. M. and Pazdur R. (2015). The role of nonrandomized trials in the evaluation of oncology drugs. Clinical Pharmacology & Therapeutics 97(5), 502–507. [DOI] [PubMed] [Google Scholar]
- Song J. X. (2014). A two-stage patient enrichment adaptive design in phase ii oncology trials. Contemporary Clinical Trials 37(1), 148–154. [DOI] [PubMed] [Google Scholar]
- Wang S. J., O’Neill R. T. and Hung H. M. (2007). Approaches to evaluating treatment effect in randomized clinical trials with genomic subset. Biopharmaceutical Statistics 6, 227–244. [DOI] [PubMed] [Google Scholar]
- Wang S. J., Hung H. M. and O’Neill R. T. (2009). Adaptive patient enrichment designs in clinical trials. Biometrical Journal 51(2), 358–374. [DOI] [PubMed] [Google Scholar]
- Zhou X., Liu S., Kim E. S., Herbst R. S. and Lee J. J. (2008). Bayesian adaptive design for targeted therapy development in lung cancera step toward personalized medicine. Clinical Trials 5(3), 181–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


