SUMMARY
In many randomized controlled trials, the primary analysis focuses on the average treatment effect and does not address whether treatment benefits are widespread or limited to a select few. This problem affects many disease areas, since it stems from how randomized trials, often the gold standard for evaluating treatments, are designed and analyzed. Our goal is to learn about the fraction who benefit from a new treatment using randomized trial data. We consider the case where the outcome is ordinal, with binary outcomes as a special case. In general, the fraction who benefit is non-identifiable, and the best that can be obtained are sharp lower and upper bounds. Our contributions include (i) proving the plug-in estimator of the bounds can be inconsistent if support restrictions are made on the joint distribution of the potential outcomes; (ii) developing the first consistent estimator for this case; and (iii) applying this estimator to a randomized trial of a medical treatment to determine whether the estimates can be informative. Our estimator is computed using linear programming, allowing fast implementation. R code is provided.
Keywords: Non-identifiable parameter, Randomized trial, Treatment effect heterogeneity
1. INTRODUCTION
We aim to estimate bounds on the fraction of the population who benefit from a treatment. This fraction is defined in the potential outcomes framework. Each participant has two potential outcomes, one representing the participant’s outcome if assigned to treatment and the other if assigned to control. The fraction who benefit is defined as the fraction of the population whose potential outcome under treatment is better than that under control. In other words, it is the fraction who would be better off under treatment. Since only one potential outcome can be observed for any given individual (Holland, 1986), the fraction who benefit is generally a non-identifiable parameter. Because of this, we focus on estimating sharp bounds on the fraction (Williamson and Downs, 1990; Manski, 1997; Fan and Park, 2009, 2010; Kim, 2014).
We derive bounds using the marginal distributions of the potential outcomes, and show they can be narrowed using a prognostic baseline variable and/or user-defined assumptions that restrict the support of the joint distribution. Our main contributions include (i) proving the plug-in estimator of the bounds can be inconsistent if support restrictions are made; (ii) developing the first consistent estimator for this case; and (iii) applying this estimator to a randomized trial data set of a medical treatment to determine whether the estimates can be informative. We assume a simple randomized trial design, i.e., each participant’s treatment assignment is an independent draw from a Bernoulli distribution. Our estimator can be computed using linear programming, i.e., the optimization of a linear objective function subject to linear equality and inequality constraints (Vanderbei, 2014). The bound estimates are typically computed in under a second.
We apply our estimator to the MISTIE II (Minimally Invasive Surgery for Intracerebral Hemorrhage Evacuation Phase II) randomized trial (Morgan and others, 2008; Hanley and others, 2016), which compared a new surgical intervention for stroke to standard medical management. As an example of our results in one case, the lower and upper bound estimates on the fraction who benefit are 0.10 and 0.73 when the outcome is a rating of functional disability 180 days post-stroke, and 0.82 and 0.96 when the outcome is reduction in clot volume.
Related work includes Manski (1997); Gadbury and others (2004); Fan and Park (2009, 2010); Zhang and others (2013); Kim (2014); Borusyak (2015). Fan and Park (2009, 2010) prove sharp bounds on the fraction who benefit, given the marginal distributions of the potential outcomes. Kim (2014) tightens those bounds using support restrictions on the joint distribution. Both propose estimators for their respective bounds. A key difference of our work, compared to Fan and Park (2009, 2010) and Kim (2014), is that we handle an ordinal outcome, while they handle a continuous outcome. Applying their formulae to an ordinal outcome can yield erroneous results (Section 3.1). Unlike Fan and Park (2009, 2010), we allow the incorporation of support restrictions, which leads to a more challenging estimation problem. We propose a new estimator that can be computed efficiently using linear programming. In contrast, the estimator of Kim (2014) generally requires solving a non-convex optimization problem to incorporate support restrictions. Non-convex problems are much more computationally difficult than linear programs.
Gadbury and others (2004) derive bounds on the fraction who are harmed, given the marginal distributions of the potential outcomes, when the outcome is binary and no baseline variable/support restrictions are used (see Section 3.1); in contrast, we consider ordinal outcomes, baseline variables, and support restrictions. For an ordinal outcome, Borusyak (2015) shows that sharp bounds on the fraction who benefit can be computed with linear programming. Borusyak does not address estimation for these bounds, which is the focus of this article.
Manski (1997) derives sharp bounds on the fraction who benefit given the no harm assumption, without using the marginal distributions of the potential outcomes. We use the marginal distributions since they are identifiable in the randomized trial context. Manski allows for endogenous treatment selection, under which they may not be identifiable. We can impose but do not require the no harm assumption. Zhang and others (2013) estimate the fraction who benefit, rather than bounds on it, by assuming the potential outcomes are independent given a set of measured baseline covariates.
The structure of this article is as follows. The MISTIE II trial is introduced in Section 2. The bound parameters are defined in Section 3. In Section 4, we prove that the plug-in estimator can be inconsistent, propose a new estimator, and discuss inference based on this estimator (which is challenging due to potential non-regularity). We apply our estimator to MISTIE II in Section 5, and present simulation results in Section 6. Future directions are discussed in Section 7.
2. MISTIE II TRIAL
MISTIE II is a recently completed Phase II randomized trial for intracerebral hemorrhage (ICH), a type of stroke that can impair cognitive/motor functions and cause death (Morgan and others, 2008). The MISTIE II trial assessed the effectiveness of image-guided minimally invasive surgery (i.e., treatment), relative to standard medical care (i.e., control). There were 96 participants, with 54 assigned to treatment and 42 to control. The randomization ratio gave a higher likelihood of being assigned to treatment, yielding the higher proportion of treatment participants.
The primary outcome was functional disability at 180 days post-stroke, measured by the modified Rankin Scale (mRS) (Quinn and others, 2009). The mRS score is ordinal, defined as an integer between 0 (no symptoms) and 6 (death), with lower values corresponding to improved functioning (Cheng and others, 2014). In the primary analysis comparing treatment to control, the average treatment effect (ATE) was inferred, i.e., the difference in population proportions with 180-day mRS  . The estimate of ATE was 0.11 (95% CI: [
. The estimate of ATE was 0.11 (95% CI: [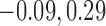 ]), using the 52 treatment and 38 control participants with recorded 180-day mRS scores. Patients and doctors may also be interested in the fraction who benefit, i.e., the fraction of patients who would have a better 180-day mRS under treatment than under control. Since it divides mRS into two categories (
]), using the 52 treatment and 38 control participants with recorded 180-day mRS scores. Patients and doctors may also be interested in the fraction who benefit, i.e., the fraction of patients who would have a better 180-day mRS under treatment than under control. Since it divides mRS into two categories (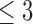 or
or 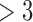 ), the ATE misses In general, the population ATE is not designed to be informative about the fraction. If the outcome is ordinal, the ATE (e.g., the mean difference in the outcome between treatment and control) can be large, while the fraction is small; this could occur if the majority get zero benefit while a minority have a large benefit.
), the ATE misses In general, the population ATE is not designed to be informative about the fraction. If the outcome is ordinal, the ATE (e.g., the mean difference in the outcome between treatment and control) can be large, while the fraction is small; this could occur if the majority get zero benefit while a minority have a large benefit.
3. BOUND PARAMETERS
Denote 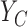 and
and 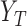 as the potential outcomes under control and treatment, respectively. Suppose the outcome is ordinal with
as the potential outcomes under control and treatment, respectively. Suppose the outcome is ordinal with 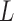 levels, i.e.,
levels, i.e., 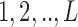 , ordered from least to most favorable. For MISTIE, we recode mRS score in this way with
, ordered from least to most favorable. For MISTIE, we recode mRS score in this way with 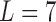 , setting 1 to represent death, and 7 to represent no symptoms. This definition of mRS score will be used in the rest of the article. Let
, setting 1 to represent death, and 7 to represent no symptoms. This definition of mRS score will be used in the rest of the article. Let 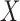 be a prognostic baseline variable collected in the randomized trial. For each participant, define the vector including the baseline variable and both potential outcomes as
be a prognostic baseline variable collected in the randomized trial. For each participant, define the vector including the baseline variable and both potential outcomes as 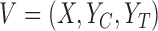 . We let
. We let 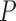 denote a generic joint distribution on
denote a generic joint distribution on 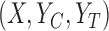 and
and 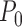 denote the true (unknown) distribution on
denote the true (unknown) distribution on 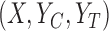 . We assume that each participant’s vector
. We assume that each participant’s vector  is an independent, identically distributed draw from
is an independent, identically distributed draw from 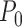 . For each participant, the observed data is
. For each participant, the observed data is 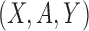 , where
, where 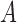 is the random treatment assignment (1 if treatment, 0 if control) which is independent of
is the random treatment assignment (1 if treatment, 0 if control) which is independent of 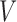 , and
, and 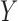 is the observed outcome corresponding to the treatment assigned, i.e.,
is the observed outcome corresponding to the treatment assigned, i.e., 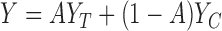 .
.
Our goal is to learn about the fraction who benefit, i.e., the parameter 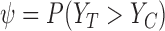 . Although
. Although 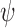 is generally non-identifiable, certain possibilities can be ruled out using the marginal distributions of
is generally non-identifiable, certain possibilities can be ruled out using the marginal distributions of 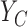 and
and  , which are identifiable. Let
, which are identifiable. Let 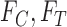 denote the marginal distribution functions of
denote the marginal distribution functions of 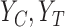 under
under 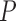 ; let
; let 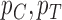 denote the corresponding probability mass functions. Section 3.1 gives bounds on
denote the corresponding probability mass functions. Section 3.1 gives bounds on 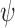 based on
based on 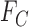 and
and 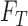 . The bounds can be improved by incorporating
. The bounds can be improved by incorporating  or assumptions about the joint distribution on
or assumptions about the joint distribution on 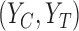 , as discussed in Section 3.2.
, as discussed in Section 3.2.
3.1. Sharp bounds on the fraction who benefit based on 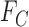 and
and 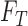
Let 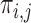 be the fraction of the population with
be the fraction of the population with 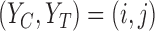 , i.e.,
, i.e., 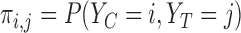 . Let
. Let 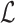 be the set of integers from 1 to
be the set of integers from 1 to 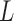 . The
. The 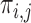 ’s
’s 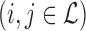 form an
form an 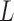 x
x  matrix giving the joint distribution of the potential outcomes (JDPO), depicted in Figure 1a for MISTIE.
matrix giving the joint distribution of the potential outcomes (JDPO), depicted in Figure 1a for MISTIE.
Fig. 1.
Joint distribution of the potential outcomes. As shown, the row sums correspond to the marginal distribution under control, 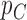 , where
, where 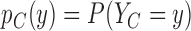 for each
for each 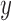 . The column sums correspond to the marginal distribution under treatment,
. The column sums correspond to the marginal distribution under treatment, 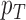 , where
, where  for each
for each 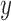 . The functions
. The functions 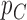 and
and 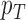 are equivalent to
are equivalent to 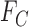 and
and  , respectively.
, respectively.
The population can be partitioned into three categories based on potential outcomes  : those for whom assignment to treatment (compared to control) would have no effect (
: those for whom assignment to treatment (compared to control) would have no effect ( ), harm (
), harm (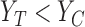 ), or benefit (
), or benefit (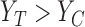 ). These categories correspond to the yellow, red, and green regions in Figure 1a, respectively. The parameter
). These categories correspond to the yellow, red, and green regions in Figure 1a, respectively. The parameter 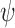 is the fraction of the population in the green region, i.e., the sum of
is the fraction of the population in the green region, i.e., the sum of 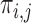 over indices
over indices  with
with 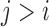 . The value of
. The value of  , in general, is non-identifiable since for each participant we only observe one component of
, in general, is non-identifiable since for each participant we only observe one component of 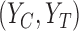 , and therefore do not know which of the three regions she/he belongs to.
, and therefore do not know which of the three regions she/he belongs to.
Let  and
and 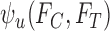 denote the sharp lower and upper bounds on
denote the sharp lower and upper bounds on 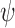 , given
, given 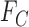 and
and  , i.e., the best possible bounds for
, i.e., the best possible bounds for 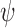 that could be obtained if
that could be obtained if 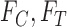 were known.We say a joint distribution
were known.We say a joint distribution 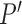 on
on  is consistent with
is consistent with 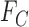 ,
, 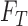 if, under
if, under 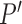 , the marginal distribution of
, the marginal distribution of  equals
equals 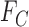 and the marginal distribution of
and the marginal distribution of  equals
equals 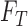 . The lower bound
. The lower bound  is:
is:
| (3.1) |
| (3.2) |
The upper bound 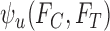 is (3.1) with
is (3.1) with 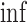 replaced by
replaced by 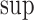 , and (3.2) with
, and (3.2) with 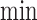 replaced by
replaced by 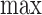 . We drop the dependence on
. We drop the dependence on 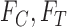 for conciseness. If one were to compute
for conciseness. If one were to compute 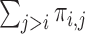 for every possible matrix of
for every possible matrix of 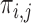 ’s with row and column sums consistent with
’s with row and column sums consistent with 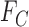 and
and 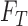 ,
, 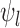 and
and  would be the minimum and maximum. Given the form of (3.2),
would be the minimum and maximum. Given the form of (3.2), 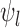 and
and  are solutions to linear programs (Borusyak, 2015). In the binary case (
are solutions to linear programs (Borusyak, 2015). In the binary case (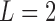 ), they simplify to
), they simplify to 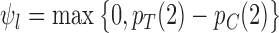 and
and 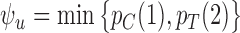 (Gadbury and others, 2004). For a continuous outcome, the sharp lower and upper bounds, given only
(Gadbury and others, 2004). For a continuous outcome, the sharp lower and upper bounds, given only 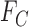 and
and  , have formulae
, have formulae
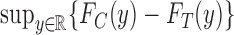 and
and  , respectively (Williamson and Downs, 1990; Fan and Park, 2010). For ordinal outcomes, the lower bound
, respectively (Williamson and Downs, 1990; Fan and Park, 2010). For ordinal outcomes, the lower bound 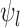 equals the former formula, while the upper bound
equals the former formula, while the upper bound  can be less than the latter formula, as proved in Appendix A of the supplementary materials available at Biostatistics online.
can be less than the latter formula, as proved in Appendix A of the supplementary materials available at Biostatistics online.
3.2. General formulation of sharp bounds on the fraction who benefit
We generalize the bound formulation to incorporate a baseline variable and support restrictions. Since they offer new information, these features can narrow the bounds (Fan and Park, 2010; Kim, 2014). We consider a baseline, i.e., pre-randomization, variable that is categorical and conjectured to be prognostic for (i.e., correlated with) the outcome. Suppose the baseline variable  has
has 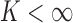 possible values:
possible values: 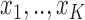 . Let
. Let  be its probability mass function, with
be its probability mass function, with 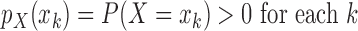 . The population can be stratified into
. The population can be stratified into 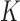 subpopulations, based on
subpopulations, based on 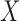 . For each
. For each  , let
, let  and
and 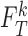 be the distribution functions of
be the distribution functions of  and
and 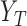 conditional on
conditional on 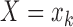 .
.
Support restrictions are assumptions that 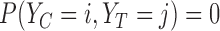 for specific
for specific 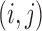 pairs. They are encoded by a function
pairs. They are encoded by a function 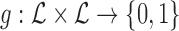 that maps a potential outcome pair
that maps a potential outcome pair 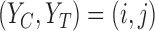 to 0 if the pair is assumed not possible, and 1 otherwise. Equivalently,
to 0 if the pair is assumed not possible, and 1 otherwise. Equivalently,  encodes the assumption that
encodes the assumption that 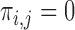 . The support restrictions in our application (Section 5) are restrictions on harm/benefit. The restriction Harm
. The support restrictions in our application (Section 5) are restrictions on harm/benefit. The restriction Harm 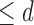 levels is:
levels is: 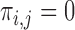 if
if 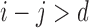 . The no harm assumption is a special case. The restriction Benefit
. The no harm assumption is a special case. The restriction Benefit 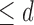 levels is:
levels is:  if
if 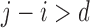 . Figure 1b illustrates Benefit
. Figure 1b illustrates Benefit 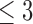 levels for MISTIE. We refer to support restrictions simply as restrictions. We assume the restrictions, i.e., the function
levels for MISTIE. We refer to support restrictions simply as restrictions. We assume the restrictions, i.e., the function 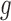 , are prespecified and known. Let
, are prespecified and known. Let 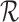 be the subclass of joint distributions
be the subclass of joint distributions 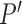 on
on  that satisfy the restrictions, i.e.,
that satisfy the restrictions, i.e., 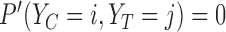 if
if  .
.
Assumption 1
The true joint distribution
is consistent with
, i.e., the distribution
, which is formed by marginalizing
over
, is in
.
Let 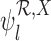 and
and  denote the sharp lower and upper bounds on
denote the sharp lower and upper bounds on 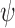 , respectively, given the baseline variable
, respectively, given the baseline variable  and restrictions
and restrictions 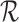 . These bounds are functions of
. These bounds are functions of 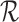 and the identifiable components of
and the identifiable components of 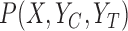 in a randomized trial where study arm is assigned independent of
in a randomized trial where study arm is assigned independent of 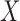 , i.e., the components
, i.e., the components 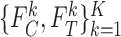 and
and 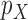 . Formally, we have
. Formally, we have
| (3.3) |
| (3.4) |
The upper bound 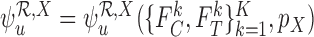 is (3.4), with
is (3.4), with 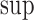 in place of
in place of 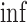 .
.
Let 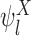 denote the lower bound with the baseline variable but no restrictions
denote the lower bound with the baseline variable but no restrictions 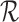 , i.e., (3.3) and (3.4) with
, i.e., (3.3) and (3.4) with 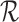 omitted. Analogous definitions apply for the upper bounds. The bounds
omitted. Analogous definitions apply for the upper bounds. The bounds 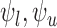 from Section 3.1 are equivalent to (3.3) and (3.4) with
from Section 3.1 are equivalent to (3.3) and (3.4) with 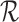 omitted and
omitted and 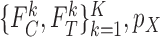 replaced by
replaced by 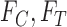 . Each of the bounds
. Each of the bounds 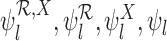 is a function of the joint distribution
is a function of the joint distribution  through the corresponding identifiable components. We suppress the dependence of these parameters on
through the corresponding identifiable components. We suppress the dependence of these parameters on 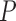 for conciseness.
for conciseness.
Incorporating a baseline variable or restriction leads to a larger or equal lower bound, and smaller or equal upper bound.
Theorem 3.1.
Consider any restrictions
, baseline variable
, and joint distribution
on
consistent with
. Then (i)
and
(ii)
and
, where each bound parameter is evaluated at
.
This is proved in Appendix B of the supplementary materials available at Biostatistics online. Just as Fan and Park (2010), the baseline variable 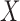 will not affect the bounds if it is independent of
will not affect the bounds if it is independent of 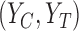 (Appendix C of the supplementary materials available at Biostatistics online).
(Appendix C of the supplementary materials available at Biostatistics online).
Restrictions 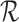 may be inconsistent with a set of marginal distributions
may be inconsistent with a set of marginal distributions 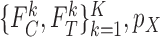 , i.e., there may not exist a joint distribution
, i.e., there may not exist a joint distribution 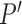 on
on 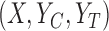 that is consistent with
that is consistent with 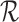 and
and 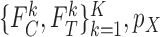 . In this case, the bound parameter (3.4) is undefined, since the set of distributions on the right hand side is empty. This cannot occur if the distribution
. In this case, the bound parameter (3.4) is undefined, since the set of distributions on the right hand side is empty. This cannot occur if the distribution 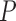 is consistent with
is consistent with 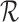 . However, the user may impose restrictions
. However, the user may impose restrictions 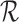 that are in violation of Assumption 1. This can lead to the bound parameters evaluated at
that are in violation of Assumption 1. This can lead to the bound parameters evaluated at 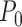 , such as
, such as 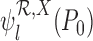 , being undefined.
, being undefined.
Bounds on the fraction who benefit can be derived for a subpopulation. For any given 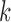 , let
, let  and
and 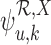 denote the sharp lower and upper bounds for subpopulation
denote the sharp lower and upper bounds for subpopulation 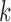 , given
, given 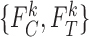 and the restrictions
and the restrictions  . The lower bound
. The lower bound 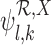 is:
is:
| (3.5) |
| (3.6) |
In (3.6), we let 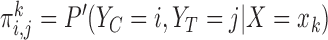 for each
for each 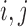 . The equality of (3.5) and (3.6) is proved in the lemma in Appendix C of the supplementary materials available at Biostatistics online. The upper bound
. The equality of (3.5) and (3.6) is proved in the lemma in Appendix C of the supplementary materials available at Biostatistics online. The upper bound  is (3.5) with
is (3.5) with 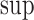 in place of
in place of 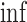 , and (3.6) with
, and (3.6) with 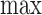 in place of
in place of  . As proved in Appendix D of the supplementary materials available at Biostatistics online, the population bounds are weighted sums of the subpopulation bounds:
. As proved in Appendix D of the supplementary materials available at Biostatistics online, the population bounds are weighted sums of the subpopulation bounds: 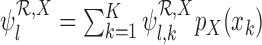 and
and  . This also holds with the restrictions
. This also holds with the restrictions 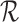 omitted.
omitted.
4. BOUND ESTIMATORS
We discuss estimators for the bound parameters defined in Section 3, using data from a randomized trial with 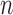 participants. We make the assumption below:
participants. We make the assumption below:
Assumption 2
(i) For each participant
, her/his vector
is an independent, identically distributed draw from
. (ii) The treatment assignments,
,
, are independent, identically distributed Bernoulli
, and are independent of
. (iii) The observed data vector for participant
is
where
.
Above, (ii) is justified by randomization and we assume the randomization probability 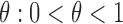 . The equality in (iii) is called the consistency assumption, which connects potential outcomes
. The equality in (iii) is called the consistency assumption, which connects potential outcomes 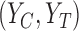 and treatment assignment
and treatment assignment 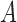 to the observed outcome
to the observed outcome 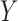 .
.
4.1. Plug-in estimator
One might consider a plug-in (also called substitution) estimator, where in place of 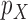 ,
, 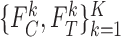 , (or of
, (or of 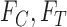 ), the following sample proportions are used:
), the following sample proportions are used: 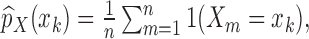
for any  and
and 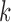 . Define
. Define 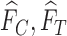 as in the above display, with
as in the above display, with  omitted. Above,
omitted. Above, 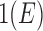 has value 1 if
has value 1 if 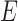 occurs and 0 otherwise. We use the hat symbol to denote plug-in estimators, e.g.,
occurs and 0 otherwise. We use the hat symbol to denote plug-in estimators, e.g., 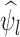 .
.
The plug-in estimator can be inconsistent when support restrictions are made, even if they are correct. Consider the case where the outcome is binary, the baseline variable is ignored, and the true, unknown joint distribution 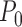 on
on  satisfies
satisfies 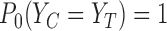 . Then the true marginals satisfy
. Then the true marginals satisfy 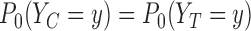 for each
for each 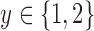 . Let the restrictions
. Let the restrictions 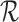 represent no harm, i.e., the event
represent no harm, i.e., the event 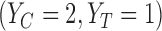 is assumed to have probability
is assumed to have probability 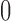 . The restrictions are consistent with
. The restrictions are consistent with 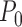 . The bound parameters at
. The bound parameters at 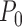 satisfy
satisfy 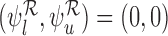 . Let the randomization probability
. Let the randomization probability 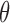 be
be  . If
. If 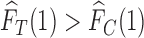 , no joint distribution on
, no joint distribution on 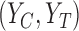 is consistent with both
is consistent with both 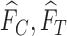 and
and 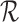 ; in this case,
; in this case, 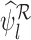 and
and  are undefined. The probability
are undefined. The probability 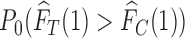 converges to
converges to 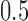 as
as 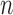 goes to infinity, as proved in Appendix E of the supplementary materials available at Biostatistics online. Therefore,
goes to infinity, as proved in Appendix E of the supplementary materials available at Biostatistics online. Therefore,  and
and 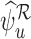 are undefined with approximately 0.5 probability for arbitrarily large
are undefined with approximately 0.5 probability for arbitrarily large 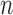 .
.
In general,  and
and 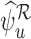 are inconsistent if the linear programs for
are inconsistent if the linear programs for 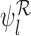 and
and 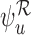 are feasible but an arbitrarily small perturbation to
are feasible but an arbitrarily small perturbation to 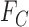 and
and  could make them infeasible. (The linear programs for
could make them infeasible. (The linear programs for  and
and  are like (3.2), except with the constraint “
are like (3.2), except with the constraint “ if
if 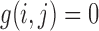 ” included.) Analogously,
” included.) Analogously, 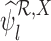 and
and 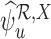 are inconsistent if, for some
are inconsistent if, for some 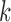 , the linear programs for
, the linear programs for  and
and 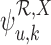 given by (3.6) are feasible but an arbitrarily small change to
given by (3.6) are feasible but an arbitrarily small change to  and
and 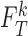 can make them infeasible. We refer to these cases as boundary cases. Boundary cases can only occur if restrictions are made. As shown in Appendix F of the supplementary materials available at Biostatistics online, they can occur when the true fraction who benefit and the bound parameters are nonzero.
can make them infeasible. We refer to these cases as boundary cases. Boundary cases can only occur if restrictions are made. As shown in Appendix F of the supplementary materials available at Biostatistics online, they can occur when the true fraction who benefit and the bound parameters are nonzero.
4.2. Proposed estimator
Our estimators of the parameters 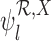 and
and 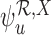 , respectively, are defined as
, respectively, are defined as
| (4.1) |
where for each 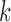 , the term
, the term 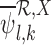 is computed by the following sequence of two linear programs:
is computed by the following sequence of two linear programs:
| (4.2) |
| (4.3) |
The term 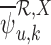 is (4.3), with
is (4.3), with 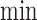 replaced by
replaced by 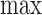 . (4.2) and (4.3) are linear programs because each absolute value statement can be converted to a pair of linear inequalities.
. (4.2) and (4.3) are linear programs because each absolute value statement can be converted to a pair of linear inequalities.
The key idea in (4.3) is that we relaxed the constraint that the marginal distribution functions corresponding to 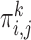 equal the empirical marginal distribution functions in stratum
equal the empirical marginal distribution functions in stratum 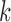 ; we instead allow these to differ by at most
; we instead allow these to differ by at most 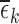 . As defined in (4.2), the value of
. As defined in (4.2), the value of 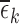 is the minimum value that allows the linear programs for
is the minimum value that allows the linear programs for 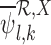 and
and 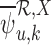 to be feasible. If the plug-in estimators
to be feasible. If the plug-in estimators 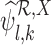 and
and 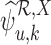 are well-defined, we have
are well-defined, we have  and thus
and thus 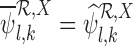 and
and 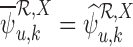 . If
. If 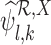 and
and 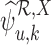 are undefined, we have
are undefined, we have 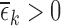 allowing
allowing 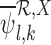 and
and 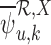 to be well-defined.
to be well-defined.
Our estimators that ignore baseline variables and/or have no restrictions, e.g., 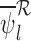 , are defined analogously. See Appendix G of the supplementary materials available at Biostatistics online for their definition. With no restrictions, our estimator is equivalent to the corresponding plug-in estimator. As proved in Appendix H of the supplementary materials available at Biostatistics online,
, are defined analogously. See Appendix G of the supplementary materials available at Biostatistics online for their definition. With no restrictions, our estimator is equivalent to the corresponding plug-in estimator. As proved in Appendix H of the supplementary materials available at Biostatistics online, 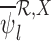 and
and 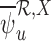 are consistent, i.e., they converge to the corresponding bound parameters as
are consistent, i.e., they converge to the corresponding bound parameters as 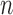 goes to infinity. By a similar proof, the estimators that ignore baseline variables and/or have no restrictions are consistent.
goes to infinity. By a similar proof, the estimators that ignore baseline variables and/or have no restrictions are consistent.
Theorem 4.1
For any
and
, if
is consistent with
, then
and
are consistent estimators of
and
, respectively.
Theorems 3.1 and 4.1 imply that, if 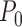 is consistent with
is consistent with 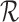 , then the probability limits of the estimators
, then the probability limits of the estimators  satisfy the inequalities in Theorem 3.1. This means that including a baseline variable or restriction can only improve (or leave unchanged) the limiting value of the bound estimators. However, at a given sample size, neither the plug-in estimators from Section 4.1 nor the above estimators are guaranteed to satisfy the corresponding inequalities in Theorem 3.1.
satisfy the inequalities in Theorem 3.1. This means that including a baseline variable or restriction can only improve (or leave unchanged) the limiting value of the bound estimators. However, at a given sample size, neither the plug-in estimators from Section 4.1 nor the above estimators are guaranteed to satisfy the corresponding inequalities in Theorem 3.1.
4.3. Inference based on the proposed estimator
Our estimator can be non-regular when the parameter (representing the lower or upper bound) is 0 or 1, which also occurs for Gadbury and others (2004); Fan and Park (2009, 2010). Furthermore, our estimator can be non-regular at boundary cases as defined in the last paragraph of Section 4.1. Intuitively, non-regularity means that the asymptotic distribution of the estimator can change dramatically under small perturbations of the data generating distribution. Formally, an estimator 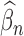 of
of  is non-regular if, for some sequence of distributions
is non-regular if, for some sequence of distributions 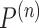 satisfying
satisfying  , the distribution of
, the distribution of  under
under  converges to a different limit than
converges to a different limit than 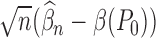 under
under 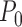 , where
, where  is total variation distance (Durrett, 2010).
is total variation distance (Durrett, 2010).
To show an example of non-regularity for our problem, consider a binary outcome. Let 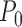 be the unique joint distribution on
be the unique joint distribution on 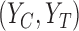 satisfying:
satisfying: 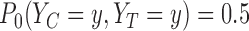 for each
for each 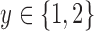 , and
, and 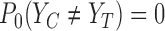 . The lower bound
. The lower bound 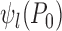 is 0. Let the randomization probability
is 0. Let the randomization probability 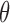 be 0.5. The results below are proved in Appendices I and J of the supplementary materials available at Biostatistics online. Under
be 0.5. The results below are proved in Appendices I and J of the supplementary materials available at Biostatistics online. Under 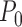 , the distribution of
, the distribution of 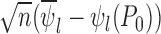 converges to
converges to 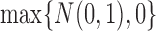 . Let
. Let 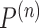 be the joint distribution with:
be the joint distribution with: 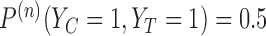 ,
,  ,
, 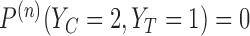 ,
, 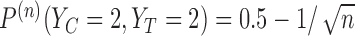 . It follows that
. It follows that 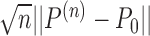 is
is  . Under
. Under 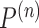 , the distribution of
, the distribution of 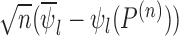 converges to
converges to 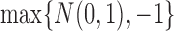 , not
, not 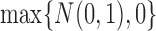 . Intuitively, the sequence
. Intuitively, the sequence 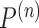 is like
is like 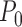 except it makes the small perturbation
except it makes the small perturbation 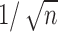 to the marginal distribution under control, which results in a strikingly different limit distribution than under
to the marginal distribution under control, which results in a strikingly different limit distribution than under 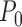 . Figure 1 of the supplementary materials available at Biostatistics online illustrates the above behavior using simulations, which agree with the theoretical results. In this example, the above limit distributions are the same if we modify the parameter and estimator to incorporate the no harm assumption.
. Figure 1 of the supplementary materials available at Biostatistics online illustrates the above behavior using simulations, which agree with the theoretical results. In this example, the above limit distributions are the same if we modify the parameter and estimator to incorporate the no harm assumption.
The impact of non-regularity is that confidence intervals based on the standard nonparametric bootstrap (called the 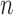 -bootstrap) are typically inconsistent, as shown by Bickel and others (1997) (whose Example 6 is similar to ours in the previous paragraph). They recommend to remedy this by using the
-bootstrap) are typically inconsistent, as shown by Bickel and others (1997) (whose Example 6 is similar to ours in the previous paragraph). They recommend to remedy this by using the 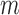 -out-of-
-out-of-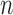 bootstrap, where each bootstrap replicate data set is generated by resampling
bootstrap, where each bootstrap replicate data set is generated by resampling 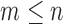 participants with replacement. Fan and Park (2010) use
participants with replacement. Fan and Park (2010) use 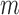 -out-of-
-out-of-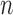 bootstrap to construct confidence intervals, and report that coverage probability is relatively close to the desired 95% level in their simulations. We also use the
bootstrap to construct confidence intervals, and report that coverage probability is relatively close to the desired 95% level in their simulations. We also use the 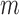 -out-of-
-out-of-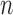 bootstrap in our simulations in Section 6. Just as Fan and Park (2010), we select
bootstrap in our simulations in Section 6. Just as Fan and Park (2010), we select 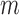 based on Bickel and Sakov (2008), whose algorithm aims to achieve correct asymptotic coverage without sacrificing efficiency as described in Appendix K of the Supplementary Materials available at Biostatistics online. For a given data generating distribution, the
based on Bickel and Sakov (2008), whose algorithm aims to achieve correct asymptotic coverage without sacrificing efficiency as described in Appendix K of the Supplementary Materials available at Biostatistics online. For a given data generating distribution, the 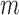 -out-of-
-out-of-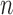 bootstrap has asymptotically correct coverage probability (called pointwise consistency) for our problem if both
bootstrap has asymptotically correct coverage probability (called pointwise consistency) for our problem if both  and
and 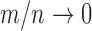 as
as 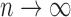 ; this result follows from Theorem 1 of Bickel and others (1997). However, depending on the growth rate of
; this result follows from Theorem 1 of Bickel and others (1997). However, depending on the growth rate of 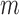 as a function of
as a function of 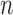 , the coverage probability can fail to be uniformly consistent (i.e., coverage probability converging to the correct value uniformly over all possible data generating distributions), as shown by Andrews and Guggenberger (2010). In their example in Section 1, which is similar to ours in the previous paragraph, such failure occurs if
, the coverage probability can fail to be uniformly consistent (i.e., coverage probability converging to the correct value uniformly over all possible data generating distributions), as shown by Andrews and Guggenberger (2010). In their example in Section 1, which is similar to ours in the previous paragraph, such failure occurs if 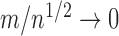 . The convergence rate of
. The convergence rate of 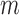 is difficult to determine, due to the complexity of the Bickel and Sakov (2008) algorithm. It is difficult even to establish pointwise consistency; the proof of this property in Bickel and Sakov (2008) requires six assumptions that would be very hard to verify from data. Therefore, just as for Fan and Park (2010), the resulting confidence intervals may fail to be uniformly or even pointwise consistent. Fan and Park (2009, Section 5.2) give an alternative approach requiring substantially weaker (but still hard to verify) assumptions. An important open problem is to construct confidence intervals that overcome the above issues. Despite the lack of asymptotic guarantees, the
is difficult to determine, due to the complexity of the Bickel and Sakov (2008) algorithm. It is difficult even to establish pointwise consistency; the proof of this property in Bickel and Sakov (2008) requires six assumptions that would be very hard to verify from data. Therefore, just as for Fan and Park (2010), the resulting confidence intervals may fail to be uniformly or even pointwise consistent. Fan and Park (2009, Section 5.2) give an alternative approach requiring substantially weaker (but still hard to verify) assumptions. An important open problem is to construct confidence intervals that overcome the above issues. Despite the lack of asymptotic guarantees, the 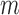 -out-of-
-out-of-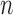 bootstrap has relatively good performance in our simulation studies at sample size
bootstrap has relatively good performance in our simulation studies at sample size 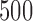 or greater.
or greater.
Our estimator can have substantial bias (in terms of its contribution to the mean squared error) in finite samples (Section 6), just as the estimators of Fan and Park (2009, 2010). They derive a first-order bias correction for their estimator. In our case, deriving a general bias correction would be quite challenging since our estimator does not have a simple analytic form (and instead is represented as a solution to linear programs).
Define the asymptotic distribution of our estimator 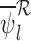 as the limit of
as the limit of 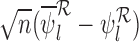 as
as  under
under 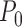 . If this is not a boundary case (as defined at the end of Section 4.1), then the asymptotic distribution is the maximum of the components of a mean zero (possibly degenerate) multivariate normal distribution with covariance matrix depending on
. If this is not a boundary case (as defined at the end of Section 4.1), then the asymptotic distribution is the maximum of the components of a mean zero (possibly degenerate) multivariate normal distribution with covariance matrix depending on 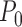 and
and 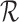 . For a boundary case, the asymptotic distribution can be more complex since then
. For a boundary case, the asymptotic distribution can be more complex since then 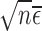 has a non-degenerate limit distribution and affects the asymptotic distribution of our estimator. It is an open problem to precisely characterize the limit distribution in boundary cases; however, even if this were solved, it would not immediately lead to a confidence interval procedure since the limit distribution would generally depend on the unknown
has a non-degenerate limit distribution and affects the asymptotic distribution of our estimator. It is an open problem to precisely characterize the limit distribution in boundary cases; however, even if this were solved, it would not immediately lead to a confidence interval procedure since the limit distribution would generally depend on the unknown  .
.
5. MISTIE APPLICATION USING BOUND ESTIMATORS FROM SECTION 4.2
Using MISTIE II, we estimate bounds on the fraction of ICH patients who benefit from treatment relative to control. We apply the estimators from Section 4.2.
5.1. 30- and 180-day mRS scores
For both 30- and 180-day mRS, four types of sharp lower/upper bounds are estimated: (i) 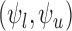 , (ii)
, (ii)  , (iii)
, (iii) 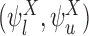 , (iv)
, (iv) 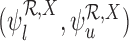 . The restrictions
. The restrictions 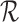 considered are Benefit
considered are Benefit 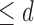 levels and Harm
levels and Harm 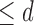 levels. The value
levels. The value 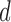 is varied from 1 to 5 for the former, and 0 to 5 for the latter. The baseline variable
is varied from 1 to 5 for the former, and 0 to 5 for the latter. The baseline variable 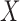 is stroke severity as measured by the National Institutes of Health Stroke Scale (NIHSS), where a stroke is classified as non-severe if the score
is stroke severity as measured by the National Institutes of Health Stroke Scale (NIHSS), where a stroke is classified as non-severe if the score 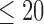 and severe otherwise (Kreutzer and others, 2011). When estimating bounds for a given outcome (e.g., 180-day mRS), we exclude participants who are missing that outcome; for both mRS outcomes, we exclude the single patient with missing baseline NIHSS score. The resulting sample sizes are 53 treatment and 39 control participants for 30-day mRS, and 52 treatment and 37 control participants for 180-day mRS. Figure 2 shows the empirical distributions of mRS under treatment and control, used to estimate (i) and (ii). It also shows the distributions after stratifying by the baseline variable, used to estimate (iii) and (iv). The proportion in each subpopulation is estimated by the corresponding sample proportion of MISTIE II participants after excluding participants as described above.
and severe otherwise (Kreutzer and others, 2011). When estimating bounds for a given outcome (e.g., 180-day mRS), we exclude participants who are missing that outcome; for both mRS outcomes, we exclude the single patient with missing baseline NIHSS score. The resulting sample sizes are 53 treatment and 39 control participants for 30-day mRS, and 52 treatment and 37 control participants for 180-day mRS. Figure 2 shows the empirical distributions of mRS under treatment and control, used to estimate (i) and (ii). It also shows the distributions after stratifying by the baseline variable, used to estimate (iii) and (iv). The proportion in each subpopulation is estimated by the corresponding sample proportion of MISTIE II participants after excluding participants as described above.
Fig. 2.
Empirical probability mass functions of (a) 30-day mRS score and (b) 180-day mRS score, under treatment and control. For each mRS score, the top panel shows the empirical distributions for the total population and the bottom two panels show the empirical distributions for the subpopulations.
The bound estimates are plotted in Figure 3. The values are recorded in Tables 1 and 2 of the supplementary materials available at Biostatistics online. The pair of estimated bounds 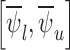 is [0.07,0.61] for 30-day mRS, and [0.10,0.73] for 180-day mRS. The widths of these estimated bounds, i.e., the difference between the upper and lower bound estimates, are 0.54 and 0.63, respectively. Restrictions and the baseline variable can narrow the width of the estimated bounds. For 180-day mRS, the width narrows by 0.17 under Benefit
is [0.07,0.61] for 30-day mRS, and [0.10,0.73] for 180-day mRS. The widths of these estimated bounds, i.e., the difference between the upper and lower bound estimates, are 0.54 and 0.63, respectively. Restrictions and the baseline variable can narrow the width of the estimated bounds. For 180-day mRS, the width narrows by 0.17 under Benefit 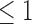 , 0.31 under Harm
, 0.31 under Harm 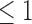 , and 0.55 under no harm, relative to no restrictions. These reductions are absolute differences in widths, as is the case throughout the article. Without restrictions, the baseline variable narrows the width by 0.19 for 30-day mRS, and 0.12 for 180-day mRS. With the restriction
, and 0.55 under no harm, relative to no restrictions. These reductions are absolute differences in widths, as is the case throughout the article. Without restrictions, the baseline variable narrows the width by 0.19 for 30-day mRS, and 0.12 for 180-day mRS. With the restriction 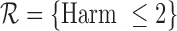 , the upper bound estimate with the baseline variable (
, the upper bound estimate with the baseline variable (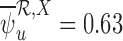 ) is slightly above that without the baseline variable (
) is slightly above that without the baseline variable (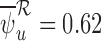 ). This can occur since, as mentioned in Section 4.2, the bound estimators need not obey the corresponding inequalities in Theorem 3.1.
). This can occur since, as mentioned in Section 4.2, the bound estimators need not obey the corresponding inequalities in Theorem 3.1.
Fig. 3.
Estimated lower and upper bounds (using method from Section 4.2) on the fraction who benefit, with respect to (a) 30-day mRS score and (b) 180-day mRS score. Each bar ranges from the lower to the upper bound estimate. A bar is gray if the baseline variable is not used, and black otherwise. The restriction imposed, if any, is indicated on the 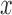 -axis. For conciseness, restrictions whose grey and black bars are identical to those under no restrictions are excluded from these figures. For gray bars, the value of
-axis. For conciseness, restrictions whose grey and black bars are identical to those under no restrictions are excluded from these figures. For gray bars, the value of 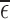 (defined in Appendix G of the supplementary materials available at Biostatistics online) is listed above the bar, if it is nonzero. For black bars,
(defined in Appendix G of the supplementary materials available at Biostatistics online) is listed above the bar, if it is nonzero. For black bars, 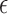 =* indicates that one or more of the
=* indicates that one or more of the 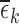 ’s (defined in Section 4.2) is nonzero.
’s (defined in Section 4.2) is nonzero.
Table 1.
Properties of Estimators and 95% Confidence Intervals. In (a), columns labeled “lower" give results for the lower bound estimator. Columns labeled “upper” give results for the upper bound estimator. In (b), columns labeled “lower” give results for CI’s for the lower bound, and columns labeled “upper” give results for CI’s for the upper bound.
| (a) Estimator properties. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | Standard error | ||||||||
| Case | 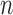 |
lower | upper | lower | upper | ||||
| RICV5 | 100 | 0.002 | 0.000 | 0.055 | 0.027 | ||||
| 500 |
 0.000 0.000 |
 0.000 0.000 |
0.025 | 0.012 | |||||
| 1000 |
 0.000 0.000 |
 0.000 0.000 |
0.018 | 0.008 | |||||
| Binary | 100 | 0.040 |
 0.040 0.040 |
0.059 | 0.059 | ||||
| (no restrictions) | 500 | 0.018 |
 0.018 0.018 |
0.026 | 0.026 | ||||
| 1000 | 0.012 |
 0.013 0.013 |
0.018 | 0.018 | |||||
| Binary | 100 | 0.040 | 0.040 | 0.058 | 0.058 | ||||
| (no harm) | 500 | 0.018 | 0.018 | 0.026 | 0.026 | ||||
| 1000 | 0.013 | 0.013 | 0.018 | 0.018 | |||||
| (b) Confidence interval properties. | |||||||||
| Coverage | Average width | ||||||||
 - - |
 -out-of- -out-of-
|
 - - |
 -out-of- -out-of-
|
||||||
| bootstrap | bootstrap | bootstrap | bootstrap | ||||||
| Case | 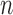 |
lower | upper | lower | upper | lower | upper | lower | upper |
| RICV5 | 100 | 0.937 | 0.839 | 0.943 | 0.848 | 0.205 | 0.088 | 0.218 | 0.093 |
| 500 | 0.943 | 0.941 | 0.971 | 0.947 | 0.098 | 0.046 | 0.116 | 0.049 | |
| 1000 | 0.950 | 0.948 | 0.973 | 0.960 | 0.070 | 0.033 | 0.084 | 0.037 | |
| Binary | 100 | 0.973 | 0.898 | 0.987 | 0.930 | 0.196 | 0.243 | 0.231 | 0.278 |
| (no restrictions) | 500 | 0.975 | 0.893 | 0.987 | 0.934 | 0.088 | 0.109 | 0.106 | 0.129 |
| 1000 | 0.978 | 0.886 | 0.989 | 0.927 | 0.062 | 0.077 | 0.075 | 0.092 | |
| Binary | 100 | 0.974 | 0.974 | 0.985 | 0.985 | 0.196 | 0.196 | 0.231 | 0.231 |
| (no harm) | 500 | 0.975 | 0.975 | 0.987 | 0.987 | 0.088 | 0.088 | 0.107 | 0.107 |
| 1000 | 0.974 | 0.974 | 0.988 | 0.988 | 0.062 | 0.062 | 0.076 | 0.076 | |
In Figure 3, there are five cases in which 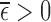 or some
or some 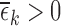 . (The value
. (The value 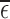 is the analog of
is the analog of 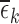 when no baseline variable is used. It is defined in Appendix G of the supplementary materials available at Biostatistics online.) We point out two features. First, these bound estimates may not be contained within the interval formed by estimates under a less stringent restriction. For 30-day mRS, the lower bound estimate under
when no baseline variable is used. It is defined in Appendix G of the supplementary materials available at Biostatistics online.) We point out two features. First, these bound estimates may not be contained within the interval formed by estimates under a less stringent restriction. For 30-day mRS, the lower bound estimate under 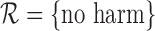 is
is  , which is below the lower bound estimate
, which is below the lower bound estimate 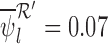 under the weaker restriction
under the weaker restriction 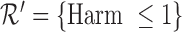 . This behavior is either due to a boundary case (see Section 4), small sample performance of the estimator, or the data generating distribution not satisfying the no harm assumption. In the third case, the bound estimators may be inconsistent. Second, for a given restriction, an upper bound estimate can be much larger, or a lower bound estimate much smaller, with the baseline variable than without it. For 180-day mRS, under the restriction
. This behavior is either due to a boundary case (see Section 4), small sample performance of the estimator, or the data generating distribution not satisfying the no harm assumption. In the third case, the bound estimators may be inconsistent. Second, for a given restriction, an upper bound estimate can be much larger, or a lower bound estimate much smaller, with the baseline variable than without it. For 180-day mRS, under the restriction 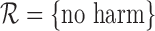 , the upper bound estimate is
, the upper bound estimate is 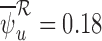 without the baseline variable, and
without the baseline variable, and 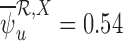 with it. One possible cause for this behavior is that the no harm assumption is false. In this case, the parameter
with it. One possible cause for this behavior is that the no harm assumption is false. In this case, the parameter 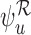 could be well-defined while
could be well-defined while 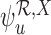 is undefined, as discussed in Section 3.2. Then
is undefined, as discussed in Section 3.2. Then  could be much smaller than
could be much smaller than 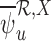 , even at large sample sizes.
, even at large sample sizes.
5.2. Reduction in clot volume
Reduction in clot volume (RICV) is the difference between clot volume at baseline and end of treatment, as defined by Mould and others (2013). In MISTIE II, the observed RICV range was [ 2.57, 75.45] mL under treatment, and [
2.57, 75.45] mL under treatment, and [ 14.86, 12.01] mL under control.
14.86, 12.01] mL under control.
We discretize RICV to an ordinal outcome. The appropriate bin length depends on the change in RICV that would be a clinically meaningful difference. Based on personal communications with neurologist Daniel Hanley (author), there currently is not enough biologic evidence to define a clinically meaningful change. Therefore, we consider various bin lengths, including 2, 5, 10, and 20 mL. We call the corresponding ordinal outcomes RICV2, RICV5, RICV10, and RICV20. They are defined in Appendix L of the supplementary materials available at Biostatistics online. We focus on the RICV5 analysis below, but the procedure is analogous for the other discretizations.
For an RICV of 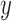 mL, RICV5 is 1 if
mL, RICV5 is 1 if 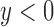 , 2 if
, 2 if 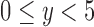 , 3 if
, 3 if  , 4 if
, 4 if 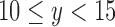 , 5 if
, 5 if 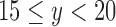 , and 6 if
, and 6 if  . The fraction who benefit, with respect to RICV5, is the fraction who would have a higher RICV5 under treatment than under control. We estimate sharp bounds (i)–(iv) as in Section 5.1. The restrictions
. The fraction who benefit, with respect to RICV5, is the fraction who would have a higher RICV5 under treatment than under control. We estimate sharp bounds (i)–(iv) as in Section 5.1. The restrictions 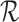 considered are Benefit
considered are Benefit 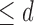 levels and Harm
levels and Harm  levels, where
levels, where 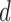 is varied from 1 to 4 for the former, and 0 to 4 for the latter. The baseline variable
is varied from 1 to 4 for the former, and 0 to 4 for the latter. The baseline variable 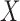 is an indicator of the baseline clot volume being above or below the median baseline clot volume of the MISTIE II participants (
is an indicator of the baseline clot volume being above or below the median baseline clot volume of the MISTIE II participants (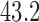 mL). There are no missing data, and all MISTIE II participants are included in the analysis. The empirical distributions of RICV5 under treatment and control, with and without stratifying by baseline clot volume, are shown in Figure 2 of the supplementary materials available at Biostatistics online. While all control participants had RICV5 of 4 or less, 74% of treatment participants had RICV5 higher than 4. This suggests that treatment has a major effect on RICV5.
mL). There are no missing data, and all MISTIE II participants are included in the analysis. The empirical distributions of RICV5 under treatment and control, with and without stratifying by baseline clot volume, are shown in Figure 2 of the supplementary materials available at Biostatistics online. While all control participants had RICV5 of 4 or less, 74% of treatment participants had RICV5 higher than 4. This suggests that treatment has a major effect on RICV5.
The estimated bounds on the fraction who benefit are plotted in Figure 4. The values are recorded in Table 3 of the supplementary materials available at Biostatistics online. The estimated bounds are [0.82, 0.96] with neither the baseline variable nor restrictions, and [0.83, 0.96] with only the baseline variable. Assuming Benefit 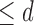 levels (
levels ( 1,2, or 3), the bound estimates are much wider than without restrictions. The values
1,2, or 3), the bound estimates are much wider than without restrictions. The values 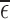 and
and 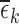 range from 0.12 to 0.43. Large values of
range from 0.12 to 0.43. Large values of 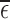 or
or 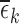 raise doubts about the validity of the restrictions; it is an area of future work to construct formal hypothesis tests, to determine with high confidence whether a large observed value of
raise doubts about the validity of the restrictions; it is an area of future work to construct formal hypothesis tests, to determine with high confidence whether a large observed value of  or
or 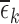 can be explained by chance variation or is due to violations of the restrictions. The restrictions on harm are not shown because the results are the same as under no restrictions.
can be explained by chance variation or is due to violations of the restrictions. The restrictions on harm are not shown because the results are the same as under no restrictions.
Fig. 4.
Estimated bounds on the fraction who benefit, with respect to RICV5. Each bar ranges from the lower to the upper bound estimate. A bar is gray if the baseline variable is not used, and black otherwise. The restriction imposed, if any, is indicated on the  -axis. For conciseness, restrictions whose grey and black bars are identical to those under no restrictions are excluded from these figures. For gray bars, the value of
-axis. For conciseness, restrictions whose grey and black bars are identical to those under no restrictions are excluded from these figures. For gray bars, the value of  is listed above the bar, if it is nonzero. For black bars,
is listed above the bar, if it is nonzero. For black bars, 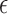 =* indicates that one or more of the
=* indicates that one or more of the 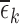 ’s is nonzero.
’s is nonzero.
The results for RICV2, RICV10, and RICV20 are shown in Tables 4–6 and Figures 3–5 of the supplementary materials available at Biostatistics online. The bound estimates are almost identical among RICV2, RICV5, and RICV10. The estimates for RICV20 are smaller because many improvements that would be benefits at the smaller bin lengths no longer qualify when the bin length is 20 mL.
Using 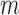 -out-of-
-out-of-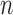 bootstrap, we compute two-sided 95% CI’s for the lower bound
bootstrap, we compute two-sided 95% CI’s for the lower bound  and the upper bound
and the upper bound 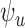 for all outcomes. See Appendix K of the supplementary materials available at Biostatistics online for the detailed procedure. The CI’s for
for all outcomes. See Appendix K of the supplementary materials available at Biostatistics online for the detailed procedure. The CI’s for  and
and 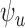 are
are 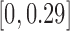 and
and 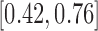 for 30-day mRS;
for 30-day mRS;  and
and 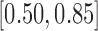 for 180-day mRS;
for 180-day mRS; 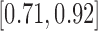 and
and 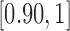 for RICV5. These CI’s should be interpreted with caution. The
for RICV5. These CI’s should be interpreted with caution. The  -out-of-
-out-of- bootstrap can have lower than nominal coverage at
bootstrap can have lower than nominal coverage at 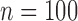 (Section 6), and the sample size of MISTIE II is
(Section 6), and the sample size of MISTIE II is 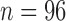 .
.
6. SIMULATION STUDIES
Two outcomes are separately considered: RICV5 and a binary outcome. No baseline variable is used. For RICV5, the data generating distributions under treatment and control are the empirical distributions in MISTIE. No restrictions are made. The bounds are 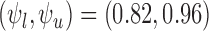 .
.
For the binary outcome, the data generating distribution is 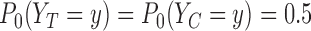 for
for 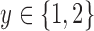 . We consider the cases of no restrictions and the no harm assumption; the bounds are
. We consider the cases of no restrictions and the no harm assumption; the bounds are 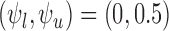 and
and  , respectively, where
, respectively, where 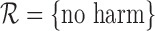 . We call these two cases binary (no restrictions) and binary (no harm).
. We call these two cases binary (no restrictions) and binary (no harm).
For each case, we simulate 10000 randomized trials each with 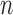 participants (
participants (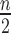 in treatment,
in treatment, 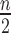 in control). We consider
in control). We consider  , respectively. Using each simulated trial, the estimators from Section 4.2 are computed. Also, we compute a two-sided 95% CI for the lower bound and a separate two-sided 95% CI for the upper bound, using
, respectively. Using each simulated trial, the estimators from Section 4.2 are computed. Also, we compute a two-sided 95% CI for the lower bound and a separate two-sided 95% CI for the upper bound, using 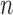 -bootstrap and
-bootstrap and 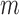 -out-of-
-out-of- bootstrap. For
bootstrap. For  -bootstrap, we generate 10000 replicated data sets by resampling
-bootstrap, we generate 10000 replicated data sets by resampling  participants, with replacement, from the simulated trial. The percentile method is used to get the 95% CI. For
participants, with replacement, from the simulated trial. The percentile method is used to get the 95% CI. For  -out-of-
-out-of-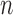 bootstrap, we generate the 10000 replicated data sets each by sampling
bootstrap, we generate the 10000 replicated data sets each by sampling  participants with replacement. The choice of
participants with replacement. The choice of 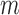 is discussed in Appendix K of the supplementary materials available at Biostatistics online.
is discussed in Appendix K of the supplementary materials available at Biostatistics online.
Table 1a shows the empirical bias and standard error of the bound estimators for each case. Bias is negligible for RICV5. For the binary outcome, bias is substantial; the bias contribution to the mean squared error, as a percentage, ranges from 31% to 34%. The results for the lower bound in the no restrictions case and for both bounds in the no harm case are almost identical. This is because 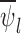 ,
, 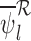 , and
, and 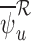 are identical if the outcome is binary and
are identical if the outcome is binary and 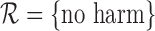 (Appendix M in the supplementary materials available at Biostatistics online). Any small differences are due to sampling variability.
(Appendix M in the supplementary materials available at Biostatistics online). Any small differences are due to sampling variability.
We compare the plug-in estimator to our estimator in the binary (no harm) case, in which they can differ due to the restriction. The plug-in estimator is undefined in 46% of simulations for  , 48% for
, 48% for 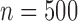 , and 49% for
, and 49% for 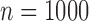 . Conditional on being well-defined, it has bias 0.074 (
. Conditional on being well-defined, it has bias 0.074 (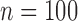 ), 0.034 (
), 0.034 (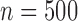 ), 0.024 (
), 0.024 (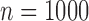 ). Our estimator is less biased (Table 1a) since it is equivalent to the plug-in estimator if the latter is well-defined, and is
). Our estimator is less biased (Table 1a) since it is equivalent to the plug-in estimator if the latter is well-defined, and is  (i.e., equal to the true lower and upper bounds) otherwise, as proved in Appendix M of the supplementary materials available at Biostatistics online. Conditional on being well-defined, the plug-in estimator has standard error 0.061 (
(i.e., equal to the true lower and upper bounds) otherwise, as proved in Appendix M of the supplementary materials available at Biostatistics online. Conditional on being well-defined, the plug-in estimator has standard error 0.061 ( ), 0.027 (
), 0.027 (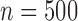 ), 0.019 (
), 0.019 (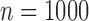 ). Our estimator has similar standard errors (Table 1a).
). Our estimator has similar standard errors (Table 1a).
Table 1b shows the empirical coverage probability of the nominal 95% CI’s constructed using 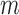 -out-of-
-out-of-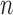 and
and 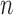 -bootstrap. For the binary outcome, the empirical coverage is above 95% except for the upper bound in the no restrictions case, where coverage is as low as 92.7% for
-bootstrap. For the binary outcome, the empirical coverage is above 95% except for the upper bound in the no restrictions case, where coverage is as low as 92.7% for 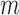 -out-of-
-out-of-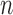 bootstrap and 88.6% for
bootstrap and 88.6% for 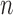 -bootstrap. For RICV5, empirical coverage is close to the nominal coverage, except the coverage rates for the upper bound are
-bootstrap. For RICV5, empirical coverage is close to the nominal coverage, except the coverage rates for the upper bound are  % when
% when  . In our simulations,
. In our simulations,  -out-of-
-out-of-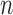 bootstrap has higher coverage probability and average CI width than
bootstrap has higher coverage probability and average CI width than 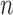 -bootstrap. Fan and Park (2010) report the coverage probabilities of
-bootstrap. Fan and Park (2010) report the coverage probabilities of 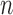 - and
- and 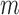 -out-of-
-out-of-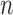 bootstrap both have approximately the nominal coverage in simulations for their problem.
bootstrap both have approximately the nominal coverage in simulations for their problem.
We ran another set of simulations with a baseline variable to evaluate how subdividing into more, equally-sized strata affects the properties of our bound estimator. These simulations are discussed in Appendix N of the supplementary materials available at Biostatistics online. Bound estimates can be undefined if the treatment or control arm is empty for one of the strata. At 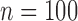 , the bound estimates are well-defined in all 10000 simulations, when two or four strata are used; when eight strata are used, 2% of 10000 simulations have undefined estimates. Interestingly, the bias and standard error of our estimator (conditional on it being well-defined) are not adversely affected (and sometimes can be even better), when the baseline variable is discretized finely compared to coarsely. Bias, standard error, and the probability of undefined estimates may be highly dependent on the data generating distribution. An open problem is to incorporate information from a continuous baseline variable without discretizing it. In a related problem, Cai and others (2011) use kernel smoothing to estimate
, the bound estimates are well-defined in all 10000 simulations, when two or four strata are used; when eight strata are used, 2% of 10000 simulations have undefined estimates. Interestingly, the bias and standard error of our estimator (conditional on it being well-defined) are not adversely affected (and sometimes can be even better), when the baseline variable is discretized finely compared to coarsely. Bias, standard error, and the probability of undefined estimates may be highly dependent on the data generating distribution. An open problem is to incorporate information from a continuous baseline variable without discretizing it. In a related problem, Cai and others (2011) use kernel smoothing to estimate 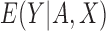 for
for 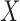 a continuous risk score; it is more challenging to apply kernel smoothing to estimate the proportion who benefit, due to this parameter being a complicated function of the entire distribution of
a continuous risk score; it is more challenging to apply kernel smoothing to estimate the proportion who benefit, due to this parameter being a complicated function of the entire distribution of 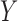 given
given 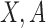 , rather than only depending on the conditional mean.
, rather than only depending on the conditional mean.
7. DISCUSSION
In the MISTIE application, the interval corresponding to the lower and upper bound estimates is wide for the mRS outcome, and narrow for RICV. Depending on the outcome, the proposed estimator of the bounds can be informative.
For 180-day mRS, we have 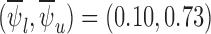 and
and  when
when 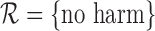 . The latter bound estimates, though much closer together than in the former case, are only valid if the no harm assumption is true. It is possible to generate evidence against the restriction being true by considering the value of
. The latter bound estimates, though much closer together than in the former case, are only valid if the no harm assumption is true. It is possible to generate evidence against the restriction being true by considering the value of 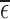 . Though certain deviations from the restrictions may be detectable through
. Though certain deviations from the restrictions may be detectable through 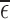 , other deviations may not be.
, other deviations may not be.
Our method can be applied to a continuous outcome that has been discretized. Discretization should be done such that a change from one level to the next is clinically meaningful. We focus on the case where there are relatively few levels compared to the sample size; it is an open problem to handle the case where the number of levels is not small relative to the sample size.
It is possible to extend our approach to handle missing outcomes, such as by using double robust estimators of the marginal distributions instead of the empirical marginal distributions ignoring missing outcomes. Under the missing at random assumption, one could use estimators of the marginal distribution functions that adjust for baseline confounders, e.g., using methods of Diaz and others (2016).
SOFTWARE
Our code is available online at https://github.com/emhuang1/fraction-who-benefit. Currently, our latest commit is 91ae5f4. In the “demo” folder, we show how our code could be used to analyze a simulated data set. We give the results in Appendix O of the supplementary materials available at Biostatistics online.
Supplementary Material
ACKNOWLEDGMENTS
We thank the anonymous referees for their helpful comments. Conflict of Interest: None declared.
FUNDING
The MISTIE II trial was funded by R01NS046309 (PI: D.H.) U.S. National Institute of Neurological Disorders and Stroke. The MISTIE III trial was funded by U01NS080824 (PI: D.H.) U.S. National Institute of Neurological Disorders and Stroke. E.J.H. was supported by the U.S. Food and Drug Administration (U01 FD004977-01) and the National Institute on Aging, USA (T32AG000247). M.R. was supported by the Patient-Centered Outcomes Research Institute (ME-1306-03198) and the U.S. Food and Drug Administration (HHSF223201400113C). This paper’s contents are solely the responsibility of the authors and do not represent the views of these organizations.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
REFERENCES
-
Andrews D. W. K. and Guggenberger P..
(2010).
Asymptotic size and a problem with subsampling and with the
 out of
out of  bootstrap. Econometric Theory 26(02), 426–468. [Google Scholar]
bootstrap. Econometric Theory 26(02), 426–468. [Google Scholar] -
Bickel P. J. Götze F. and van Zwet W. R..
(1997).
Resampling fewer than
 observations: Gains, losses, and remedies for losses. Statistica Sinica 7, 1–31. [Google Scholar]
observations: Gains, losses, and remedies for losses. Statistica Sinica 7, 1–31. [Google Scholar] -
Bickel P. J. and Sakov A..
(2008).
On the choice of
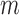 in the
in the 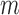 out of
out of 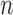 bootstrap and confidence bounds for extrema. Statistica Sinica 18(3), 967–985. [Google Scholar]
bootstrap and confidence bounds for extrema. Statistica Sinica 18(3), 967–985. [Google Scholar] - Borusyak K. (2015). Bounding the population shares affected by treatments. Technical Report: SSRN: http://ssrn.com/abstract=2473827. [Google Scholar]
- Cai L. T. and Tian, Wong P. H. and Wei L. J.. (2011). Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics 12(2), 270–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng B., Forkert N. D., Zavaglia M., Hilgetag C. C., Golsari A., Siemonsen S., Fiehler J., Pedraza S., Puig J., Cho T. H. and others (2014). Influence of stroke infarct location on functional outcome measured by the modified Rankin Scale. Stroke 45(6), 1695–1702. [DOI] [PubMed] [Google Scholar]
- Diaz I. Colantuoni E. and Rosenblum M.. (2016). Enhanced precision in the analysis of randomized trials with ordinal outcomes. Biometrics. 72(2), 422-422. [DOI] [PubMed] [Google Scholar]
- Durrett R. (2010). Probability: Theory and Examples. New York: Cambridge University Press. [Google Scholar]
- Fan Y. and Park S. S.. (2009). Partial identification of the distribution of treatment effects and its confidence sets. Advances in Econometrics 25, 3–70. [Google Scholar]
- Fan Y. and Park S. S.. (2010). Sharp bounds on the distribution of treatment effects and their statistical inference. Econometric Theory 26(03), 931–951. [Google Scholar]
- Gadbury G. L. Iyer H. K. and Albert J. M.. (2004). Individual treatment effects in randomized trials with binary outcomes. Journal of Statistical Planning and Inference 121(2), 163–174. [Google Scholar]
- Holland P. W. (1986). Statistics and causal inference. Journal of the American Statistical Association 81(396), 945–960. [Google Scholar]
- Hanley D. F., Thompson R. E., Muschelli J., Rosenblum M., Mcbee N., Lane K., Bistran-Hall A. J., Mayo S. W., Keyl P., Gandhi D. and others (2016). Safety and efficacy of minimally invasive surgery plus alteplase in intracerebral haemorrhage evacuation (MISTIE): a randomised, controlled, open-label, phase 2 trial. Lancet Neurol 15(12), 1228–1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J. H. (2014). Identifying the distribution of treatment effects under support restrictions. Technical Report: arXiv:1410.5885 [stat.ME]. [Google Scholar]
- Kreutzer J. S. Caplan B. and DeLuca J.. (2011). Encyclopedia of Clinical Neuropsychology. New York: Springer. [Google Scholar]
- Manski C. F. (1997). Monotone treatment response. Econometrica 65(6), 1311–1334. [Google Scholar]
- Morgan T. Zuccarello M. Narayan R. Keyl P. Lane K. and Hanley D.. (2008). Preliminary findings of the minimally-invasive surgery plus rtPA for intracerebral hemorrhage evacuation (MISTIE) clinical trial. Acta Neurochirurgica Supplement 105, 147–51. [DOI] [PubMed] [Google Scholar]
- Mould W. A. Carhuapoma J. R. Muschelli J. Lane K. Morgan T. C. McBee N. A. Bistran-Hall A. J. Ullman N. L. Vespa P. Martin N. A.. and others (2013). Minimally invasive surgery plus recombinant tissue-type plasminogen activator for intracerebral hemorrhage evacuation decreases perihematomal edema. Stroke 44(3), 627–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinn T. J. Dawson J. Walters M. R. and Lees K. R.. (2009). Reliability of the modified rankin scale: a systematic review. Stroke 40(10), 3393–3395. [DOI] [PubMed] [Google Scholar]
- Vanderbei R. J. (2014). Linear Programming: Foundations and Extensions. New York: Springer. [Google Scholar]
- Williamson R. C. and Downs T.. (1990). Probabilistic arithmetic. I. Numerical methods for calculating convolutions and dependency bounds. International Journal of Approximate Reasoning 4(2), 89–158. [Google Scholar]
- Zhang Z. Wang C. Nie L. and Soon G.. (2013). Assessing the heterogeneity of treatment effects via potential outcomes of individual patients. Journal of the Royal Statistical Society Series C, Applied Statistics 62(5), 687–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






