Feature Selection Methods for Optimal Design of Studies for Developmental Inquiry

Abstract

Objectives

As diary, panel, and experience sampling methods become easier to implement, studies of development and aging are adopting more and more intensive study designs. However, if too many measures are included in such designs, interruptions for measurement may constitute a significant burden for participants. We propose the use of feature selection—a data-driven machine learning process—in study design and selection of measures that show the most predictive power in pilot data.

Method

We introduce an analytical paradigm based on the feature importance estimation and recursive feature elimination with decision tree ensembles and illustrate its utility using empirical data from the German Socio-Economic Panel (SOEP).

Results

We identified a subset of 20 measures from the SOEP data set that maintain much of the ability of the original data set to predict life satisfaction and health across younger, middle, and older age groups.

Discussion

Feature selection techniques permit researchers to choose measures that are maximally predictive of relevant outcomes, even when there are interactions or nonlinearities. These techniques facilitate decisions about which measures may be dropped from a study while maintaining efficiency of prediction across groups and reducing costs to the researcher and burden on the participants.

Feature Selection Methods for Optimal Design of Studies for Developmental Inquiry

Developmental researchers have often prioritized the use of longitudinal designs. In recent years, advances in technology and computation have made it possible to obtain more and more frequent assessments from more and more persons. Creative merging of large-scale annual or biennial panel studies (e.g., Headey, Muffels, & Wagner, 2010) with more intensive collection methods, including day reconstruction method (Kahneman, Krueger, Schkade, Schwarz, & Stone, 2004), daily and momentary experience sampling (Mehl & Conner, 2012), and automated computer vision (e.g., Brick, Hunter, & Cohn, 2009) or wearable sensor systems (e.g., Intille, 2012) opens the possibility for new, population-scale study paradigms (Gerstorf, Hoppmann, & Ram, 2014). These new technologies provide opportunities to obtain larger and more diverse samples and to more precisely track and study change. Looking forward, however, we see that as reach expands, participants may feel increasingly burdened, drop out of studies, never participate, or quit halfway through a questionnaire. Efficiency of assessment will be key. Cost per participant must also be kept in check as the number of participants or number of assessments increases. For example, taking an annual survey to the monthly time scale likely requires at least 1/12 reduction in length, if not more. In this article, we illustrate how data-mining methods, specifically feature selection methods, may be used to optimize item selection—to maximize prediction with a shortened assessment protocol.

With limited resources and limits on participant tolerance, there is great incentive for researchers to precisely determine which of many possible measures warrant inclusion in data collection and analysis. Such a vital question in methodological design must consider the study’s theoretical frameworks and past literature in the context of feasibility metrics such as the costs and benefits of each measurement instrument and the burden in terms of time, effort, and difficulty for the participants. As options for viable measures proliferate, it becomes increasingly time consuming for researchers to select an optimal combination of measures by hand. For example, the German Socio-Economic Panel (SOEP) data set (SOEP, 2015) contains thousands of measures across tens of thousands of individuals. An exhaustive search of all possible combinations of 10 measures from the set would take a very long time. One solution is to turn to automated model selection approaches.

Feature Selection and Feature Importance

The aim of feature selection is to inform decisions about which measures (“features” in machine learning parlance) in the data set should be included in data collection or analysis to optimally predict the outcomes with a minimum number of predictors. When designing a new study, the determination of a statistically optimal model is only the first part of a larger process. A wide range of other concerns, such as the value of a feature from a theoretical perspective, the effort and cost required to measure it, the generalizability of the measure across different participant groups (e.g., across younger, middle, and older adults), the burden it places on those participants, and the rate at which change is likely to be detectable, must all be examined in the context of the feature’s predictive power when making selections. For example, the variables derived from a blood draw may provide high predictive power for a variety of outcomes but may be quite expensive both in terms of study funding and participant time (particularly when dealing with a fear of needles). A set of 10 self-report measures, with collectively lower burden than the blood draw, may have more total value, even if the individual measures themselves have significantly lower predictive value. The goal of feature selection is to find the design that provides maximum predictive power while accounting for these pragmatic concerns.

For illustration, consider a simplified case where we begin by fitting a simple regression model wherein one single outcome is regressed on 1,000 predictors. The study might be simplified by identifying the 50 predictors with the highest regression coefficients and only using these 50 variables in a follow-up study. This is the basic idea of feature selection. A slightly more intricate form of feature selection uses a backward selection process (e.g., Hocking, 1976). We begin with a complete model and proceed stepwise by identifying the predictor with the lowest t value, running a significance test to check if removing that variable significantly reduces predictive power. If predictive power is reduced, the predictor would be retained, if not, the variable would be removed. After many steps, an optimal set of predictor variables set is obtained. A variety of approaches targeted at the selection of an optimum model from a set of predictors have been in the literature for decades (Cattell, 1966). In recent years, more advanced and computationally heavy approaches have become available, including SEM trees (Brandmaier, von Oertzen, McArdle, & Lindenberger, 2013), Group Iterative Multiple Model Estimation (GIMME; Gates & Molenaar, 2012), various approaches based on Bayesian modeling (e.g., Bayesian SEM; Muthén & Asparouhov, 2012) and power equivalence metrics (e.g., von Oertzen, 2010; von Oertzen & Brandmaier, 2013). Feature selection for study design tackles a similar problem using approaches from the data mining and machine-learning literatures but is specifically targeted at the selection of measures that maximize predictive power while managing pragmatic problems such as cost and participant burden.

Feature Selection for Study Design

We propose the use of feature selection techniques in the design of new studies or addition of intensive assessment modules to existing studies. Feature selection is a data-driven technique, wherein important features are identified using some already available (e.g., pilot) data. As such these techniques will be particularly useful in situations where existing large-scale studies are being extended, expanded, or continued. For example, feature selection will be especially useful when determining which measures to prioritize in follow-up waves of intervention studies, extensions (e.g., refunding) of panel studies, spinoff studies that closely examine one aspect of the larger data set, and when determining which predictor variables should be included in theoretical explorations (e.g., inductive theory building).

Our proposed method of feature selection for study design uses two analytical tools: feature importance and recursive feature elimination (RFE). Feature importance is a value assigned to a given measure that quantifies the contribution of that measure to the prediction of the outcome. Recursive feature elimination is a process that reduces a potentially very large number of measures to a more manageable subset that retains predictive value in a given predictive model. We will use decision tree ensembles (DTEs) as the predictive model for this task because of their computational efficiency and ability to capture nonlinear interactions among the predictors (e.g., Johnson & Zhang, 2014).

Analytic Tools

Feature importance is a quantification of the contribution of a given feature to the effectiveness of a model. Just as there are a number of ways to quantify the overall effectiveness of a model, there are many ways to quantify feature importance. For example, feature importance in a regression model might be quantified in terms of the t value used to compute the predictor’s level of statistical significance (see, e.g., Bursac, Gauss, Williams, & Hosmer, 2008; Guyon & Elisseeff, 2003). Features with higher t values would have higher importance. Generalizing across many types of prediction tools, feature importance can be quantified by selecting a goodness-of-fit (e.g., R²) measure and quantifying the contribution to that measure via permutation testing. We shall use this general approach here.

In permutation testing, the model (e.g., DTE) is first fitted with the entire set of measures and a fit statistic (e.g., residual squared error, R²) is computed. Then, the rows of a single measure are scrambled repeatedly (e.g., 1,000 times) to create pseudo-data sets in which the correspondence between that measure and the outcome is broken but the distribution of the measure remains intact. The same predictive model is fitted to each of these pseudo-data sets to provide a distribution of the fit statistic. The importance of the chosen measure is the difference between the fit statistic computed with the actual data and the mean fit across these pseudo-data sets. Feature importance therefore assigns to each measure the unique contribution that the measure provides to prediction in the context of the other measures (see, e.g., Edgington, 1995 for more information).

RFE is a model selection approach with many similarities to the traditional backward-elimination approach to model selection (see, e.g., Kubus, 2014). In the stepwise regression case, we would begin with a single regression model containing all the predictors of a given outcome and at each step remove the one with the lowest t score until some fit criterion, such as Akaike Information Criterion (AIC), was minimized. RFE similarly begins with a model containing all possible predictors. At each step, a measure of feature importance is computed for each predictor. A subset of features with the lowest importance is removed and the process is repeated on the smaller model until some minimum number of features or minimum level of fit is reached. The result is a model with a minimal number of features but which retains as much predictive power as possible. RFE ensures generalizability and protects itself against problems commonly associated with stepwise regression (e.g., overfitting) using cross-validation techniques such as k-fold cross-validation (e.g., Stone, 1977).

DTE, such as random forests (Breiman, 2001) or boosted regression trees (Friedman, Hastie, & Tibshirani, 2000) provide a robust and flexible prediction framework that can be used for feature selection. A DTE is a collection of decision tree prediction models, such as Classification and Regression Trees (CARTs; Breiman, 1984), C4.5 trees (Quinlan, 1996), or Conditional Inference trees (e.g., Hothorn, Hornik, & Zeileis, 2006), each of which indicates the hierarchy of predictors and thresholds that provide for optimal prediction of a given outcome. By combining the predictions of a set of decision trees into an ensemble (e.g., a forest), DTEs become more robust and more generalizable than individual decision trees (Breiman, 1996, 2001). DTEs are well suited for feature selection because they are capable of capturing nonlinear effects (such as quadratic or logistic effects), interactions among measures, are computationally efficient, can be quickly applied to large data sets, and are readily available through free and open-source software. Particularly useful for feature selection, DTEs can provide tree-unique feature importance metrics like Gini impurity in addition to traditional fit statistics like R² and residual sum of squares (e.g., Grömping, 2009; Strobl, Boulesteix, & Augustin, 2007).

The Present Study

In this article, we illustrate how feature selection may be useful for designing studies in developmental and aging research. As an example, we use the method to design a monthly study of self-reported health and life satisfaction by choosing a set of measures from the existing SOEP data. Our goal is to select a small subset of measures that minimize participant burden, maximize predictive power across the adult life span (explicitly acknowledging that the predictors may differ for younger, middle, and older adults) and whose relations with health and life satisfaction are of scientific interest.

All the tools we use are freely available online. Specifically, we use the statistical software language R (R Core Team, 2016) and the caret (Kuhn et al., 2016) and randomForest (Liaw & Wiener, 2002) packages. Example scripts and a walkthrough of the analyses performed in this article can be found on the Penn State Quantitative Developmental Systems website (http://quantdev.ssri.psu.edu).

Method

Measures for our hypothetical monthly study are selected from the battery used in the SOEP Study (Headey et al., 2010). Here, we illustrate how the data may specifically inform design of a more intensive study. Comprehensive information about the design, participants, variables, and assessment procedures in the larger SOEP is reported in Wagner, Frick, & Schupp, 2007. A brief overview of details relevant to the present analysis is given below.

Data Source

The SOEP began in 1984 and now encompasses an annual assessment of more than 20,000 participants and more than 10,000 households that are nationally representative (inclusive of immigrants and resident foreigners) of former West and East Germany. Potential households of participants were randomly sampled from randomly selected geographic locations in Germany. Within each household, all family members older than 16 years of age were eligible for participation and recontacted each year for completion of the annual survey. Initial response rates were between 60% and 70%, with relatively low longitudinal attrition (about 15% for the second wave and less than 5% yearly attrition across various subsamples). Data were primarily collected via face-to-face interviews, with a small portion of repeatedly sampled participants completing self-administered questionnaires. Particularly relevant for our purposes here, the annual survey captures a broad range of measures, including objective economic measures (e.g., employment status, income, and wealth), nontraditional objective concept measures (e.g., doctor visits, physical health measures such as height and weight), performance-based measures (e.g., cognitive functioning), and subjective measures (e.g., tastes and traits, expectations, and well-being; Wagner et al., 2007). In total, the core data set contains 506,401 records, with 65,595 persons, 30 survey years, and 2,454 variables.

Measures and Participants

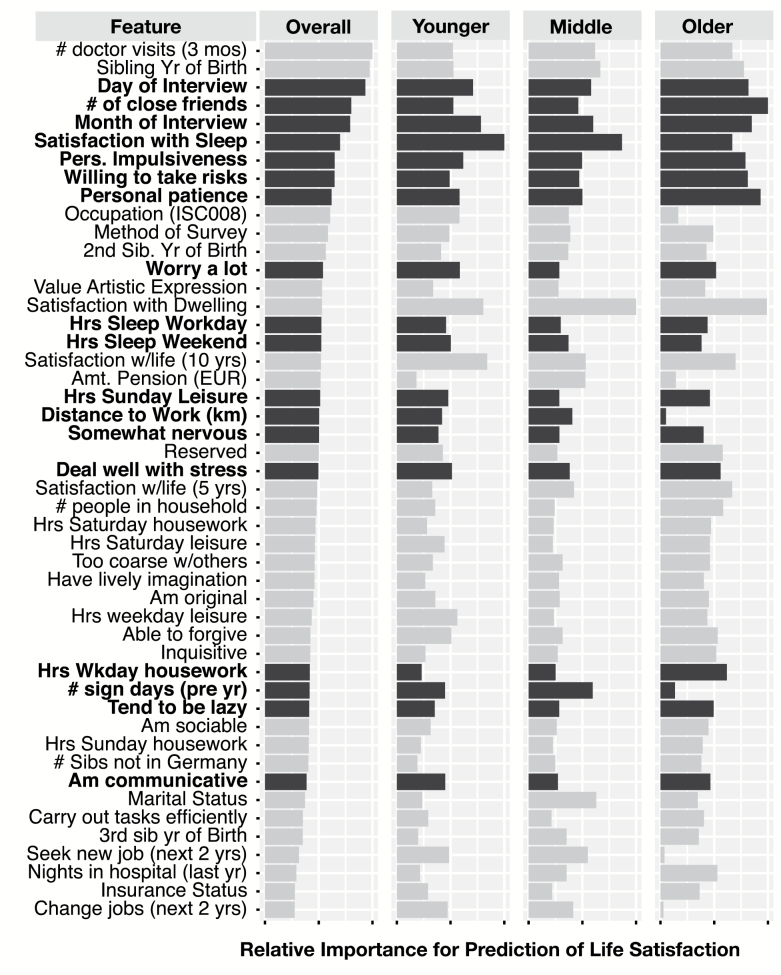
The purpose of feature selection is to narrow the measures of interest relevant for a particular inquiry. For this illustration, we engage with a subset of the data that is both sufficiently large for meaningful analysis and sufficiently small for didactic interpretation. Specifically, as detailed below, we apply feature importance, RFE, and DTE to a subset of 598 variables/features obtained from 11,461 participants in the 2013 data collection. As seen in the partial lists in Figures 1 and 2, the 598 variable set that we use spans the full range of topics addressed in the SOEP. Allowing for age-related differences in feature importance, we divide the sample into the following three age groups: younger = age 18–34 years (n = 2,746), middle-aged = 35–65 years (n = 6,060), and older = 65–103 years (n = 2,655).

Figure 1.

Relative feature importance of top 50 measures for the prediction of life satisfaction in overall sample and three subpopulations (younger, middle-aged, and older). Importance (length of bar) is shown as a proportion of the highest importance in the subgroup. Bolded entries (darker bars) indicate selected subset of measures.

Figure 2.

Relative feature importance of top 50 measures for the prediction of subjective health status in overall sample and three subpopulations (younger, middle-aged, and older). Importance (length of bar) is shown as a proportion of the highest importance measure in the subgroup. Bolded entries (darker bars) indicate selected subset of measures.

Data Analysis

Feature selection for study design is a model search procedure that combines automated selection tools (e.g., backward selection via recursive feature elimination) with human expertise. The search returns an optimized model, for example, a model that provides best prediction of subjective health and life satisfaction with minimal experimenter cost and participant burden. In this section, we outline the following five-step process for implementing feature selection: (a) selecting an outcome variable or variables, (b) choosing a predictive model, (c) preprocessing the data set to handle missingness and highly correlated variables, (d) reducing the data set using a model selection technique and ordering the remaining data columns by feature importance, and finally, (e) choosing the best features based on the quantified feature importance and practical concerns such as collection cost, theoretical focus, and participant burden. At each step, we provide instructions on the choices to be made and recommendations on how to make those choices.

Step 1: Identify Outcome(s) and Subgroups

Feature selection methods optimize with respect to prediction of a researcher-specified target outcome(s). Thus, an outcome variable must be selected. For example, and portending the empirical illustration below, researchers might prioritize prediction of individuals’ subjective health status or self-reported life satisfaction. The feature selection process is then applied with the goal of identifying the set of features that together provide the best prediction of the chosen outcome. If more than one outcome is to be considered in the study, it is best to jointly consider feature importance for all outcomes when making the final measure selections (Step 5).

From a developmental perspective, it is important to consider heterogeneity across subgroups with regards to what constitutes the best predictive model. If there are different predictors that hold bearing on each subpopulation, it may be helpful to examine the importance of predictors independently within each subgroup and tailor the final selection so that the measures deemed important span across subgroups. For example, if the predictive models for life satisfaction are expected to be different for older adults and younger adults (or clinical and preclinical populations), these subgroups should be identified before model fitting.

Step 2: Select a Predictive Model and Choose a Specific Predictor

Our recommended procedure for feature selection for study design relies on the selection of a predictive model. In principle, any statistical tool capable of finding associations among multiple variables (even simple regression; see Grömping, 2007) may be used but the choice impacts what types of associations are included in the resulting measures of feature importance. Feature selection using regression, for example, might remove a predictor that has limited linear predictive power and miss a quadratic or interaction effect.

For more comprehensive coverage of associations, we strongly recommend the use of a nonlinear prediction model in the feature selection process. In this article, we take advantage of decision tree ensembles. DTEs, rule-based predictors, and other nonlinear classifiers are each well suited for feature selection because they are capable of finding nonlinear and interactive associations and they can quickly and efficiently deal with data sets that contain large numbers of both features and rows (see Auret & Aldrich, 2011). Alternatives, such as radial-basis support vector machines or neural network predictors, may be particularly useful in some cases where highly nonlinear interactions are present.

If computation time is not a concern, it may be helpful to employ more than one predictive model and compare the results. For cases where computation time is limited, we provide this general guideline: DTEs offer an excellent tool for the general case. However, when working with high-dimensional nonlinear data in continuous spaces, it may be more appropriate to use a support vector machine (see, e.g., Kotsiantis, Zaharakis, & Pintelas, 2006 for more). Note that although DTEs are still capable of discovering nonlinear associations, they may undercredit complex nonlinear associations (e.g., quadratic structures or high-level interactions).

Step 3: Preprocess Data

As with other modeling frameworks, feature selection may be biased by inclusion of highly related or nearly collinear measures, large proportions of missingness, and measures with large numbers of rare categories. As detailed below, we recommend reducing or removing highly correlated measures, removing or imputing missing values, and removing or collapsing rare categories before performing feature selection. If there are variables in the data that have no relevance to the question of study, they may also be removed at this point. Unrelated variables will not bias the feature selection process (although they may increase computation time) and they can be removed equally well as part of the manual selection of features in Step 5.

Transform highly correlated measures

Model selection procedures like RFE may be biased in their selection of highly correlated measures (Guyon & Elisseeff, 2003). Standard practice suggests there is reason for concern if measures correlate higher than .8 or .9 (e.g., Kuhn, 2008). The importance scores reported by decision trees and DTEs may overestimate the importance of these highly correlated features (see Grömping, 2009; Strobl, Boulesteix, Kneib, Augustin, & Zeileis, 2008), resulting in biased reporting of feature importance scores. A researcher selecting those highly correlated variables because of their estimated feature importance scores might end up with a selected set of features that had less predictive power than anticipated because of this overestimation. We recommend that researchers therefore transform or remove such measures feature selection approaches.

In behavioral data, high correlations may indicate that the variables were designed to be indicators of a common factor. In such cases, reduction to a single-scale score is appropriate, for example, by replacing the individual measurements with a single computed factor score. In cases where two measures represent highly correlated constructs but not aspects of a common scale, it is still possible to reduce them to fewer scores using, for example, principal components analysis. An alternative solution is to simply remove the less-desirable measures (i.e., less reliable, more difficult/costly to measure). If the measures contribute nearly identical information to the prediction of the outcome, the removal of one or the other is unlikely to negatively affect the overall prediction of the model.

Reduce nominal variables with large numbers of rare categories

Many data sets include nominal variables that have large numbers of rare responses. For example, the SOEP includes a question related to the heritage of the participant. Responses include over a hundred different country names, many of them reported by only one or two participants. Although these variables will neither bias nor degrade the results of feature selection, they may increase computation time dramatically. For example, in a traditional regression analysis, a nominal variable is frequently transformed into a series of dummy-coded (0,1) condition variables. In a model with 200 binary features, the addition of a single nominal variable with 200 categories would effectively double the number of features that must be searched. In the use of a DTE, a similar problem occurs.

If data are plentiful, computation time is limited, and the measure has no particular import, it may simply be removed. Removal does eliminate the possibility of detecting an interaction between the removed feature and other predictors, although the more rare each case is, the lower the power to detect such an interaction. As a result, it may be more beneficial to reduce the number of nominal categories by collapsing, rather than removing the feature from consideration entirely. For example, countries might be collapsed into continents or an “other” category might be used to hold all categories with very few responses.

When there are no theoretical concerns against it and data are sufficient, we recommend collapsing categories in any variable that contains more than about 10 responses, or any response category that appears in fewer than 15 rows in a moderate-sized data set or with less than about 2% of the sample in a larger data set. If no single response category appears in the data more than 15 times, there is no meaningful way to collapse them, and computation time is a concern, we recommend removal of the feature.

Handle missingness

There are several ways to deal with missing data. The choice depends in part on the predictive model chosen in Step 2. For example, it is possible to implement a version of a DTE that is capable of handling missingness via methods such as surrogate splits (Hapfelmeier & Ulm, 2013; Hapfelmaier, Hothorn, Ulm, & Strobl, 2014). Although choosing or implementing a predictive model that is capable of handling missingness natively is the best approach, many predictive models do not have this capability and at time of writing, many common suites of DTE software (e.g., the R randomForest package; Liaw & Wiener, 2002) have not implemented these techniques. Other standard methods for handling missingness, for example, through multiple imputation or, in the case of large data sets, listwise or blockwise deletion are therefore also viable options. Readers are cautioned that deletion carries with it all the usual possibilities for bias if missingness is not completely at random (Little & Rubin, 2002) and that multiple imputation approaches may dramatically lengthen computation time.

Step 4: Compute Feature Importance Measures

Once the data set is ready, feature importance can be computed for each subgroup and each outcome. In cases with large numbers of predictors, such as our example below, we first use an automatic model selection process to reduce the number of variables before computing feature importance. Specifically, we recommend running RFE to select a model for each outcome with a number of measures that is two to three times the final number of measures desired. This permits human expertise enough freedom to choose the best set from among the likely candidates. As described earlier, RFE can use any measure of goodness of fit as a selection metric. For continuous outcomes with DTEs or support vector machines, we recommend RMSEA, R², or AIC; for categorical outcomes, prediction accuracy may be more appropriate (see Forman, 2003; Menze et al., 2009; Olden, Joy, & Death, 2004; Saeys, Inza, & Larrañaga, 2007 for evaluations of different metrics on data from several fields).

Once the set of measures is reduced, feature importance can be computed for each remaining measure using permutation testing. For each outcome, we recommend computing the importance of each feature first for the overall data set and then for each selected subgroup individually to provide easy comparisons during Step 5.

Step 5: Select Features

The most difficult decisions must be made in the final step. Although feature importance provides a quantification of the value that each variable adds to the predictive power of the model, it should not be used as the only input in the process of feature selection for study design unless the sole concern of the study is prediction. More commonly, a variety of other factors nincluding the technology needed to collect the data, the likelihood of true responses, the cognitive, effort, or time burden on the participant, the theoretical value of the constructs, and the ease and cost of assessment delivery should all be weighed along with the importance measures. Candidate subsets chosen with these concerns in mind can be evaluated using the same fitness measure used by RFE to ensure that the final subset maintains reasonable predictive accuracy after manual selection. Keep in mind that manual selection will almost always result in a lower predictive accuracy than automatic selection, so some loss of fit is expected (and indeed, required).

It is possible at this point to encounter problems overfitting to the data, especially if several different subsets of features are examined. Overfitting can be overcome through the use of a holdout set, that is, the researcher may split the data into two subsets before feature selection and use only one subset throughout the feature selection process. When an optimal set of features is chosen, it can be tested against the withheld subset of data to validate the predictive power of the feature set or additional cross-validation techniques can be used (Blum, Kalai, & Langford, 1999; Kim, 2009).

Visualization of feature importance with plots is extremely useful for the manual selection process. Feature importance plots like Figures 1 and 2 make it easy to identify the most important measures and directly compare the relative importance of each measure across subgroups. We recommend that researchers work from the top of the list, choosing measures that show at least moderate importance for different groups, high importance for at least one group and that require minimal burden on participants, experimenters, and the study budget. Further, priority should be given to measures that are predictive of more than one outcome in at least one subgroup. It is worthwhile to remember that feature importance is a measure of the predictive accuracy of the feature, not a measure of the theoretical importance of the underlying construct. For example, a self-report question about social likeability may show high importance in predicting life satisfaction even if it does not actually correlate with social fluency, simply because people with positive self-conceptions may rate themselves high on likeability.

Results

In our illustrative example, the goal is to select a minimal number of measures from the SOEP data for a more intensive study of life satisfaction and subjective health across the life span. We are interested in maintaining as much of the predictive value of the full SOEP battery as possible while acknowledging potential for age-group differences and keeping participant burden minimal.

Step 1: Identify Outcome(s) and Subgroups

Using previous SOEP publications as our guide, we identified two popular measures as our primary outcomes: a direct rating of satisfaction with life (PLH0182) and current subjective health status (PLE008). Because we are specifically interested in being able to examine age-related differences, we identified and separated three subgroups in the data, namely young adults (aged <35 years), middle-aged adults (aged 35–65 years), and older adults (aged >65 years). This allows identification of a set of measures that are important for prediction in all three groups.

Step 2: Select a Predictive Model and Choose a Specific Predictor

We first selected the predictive model on which we will base our feature selection process. In this case, we expect few nonlinear effects; so, we selected a DTE, implemented using the randomForest package in R (Liaw & Wiener, 2002). Alternative, more simple, choices might include a forward or backward selection multiple regression model. An initial test using stepwise regression forward selection approach to predict life satisfaction provides an R² of .67, whereas the DTE (as shown in Table 1) showed an R² of .78. Although not enormously different, the DTE results illustrate the value of using a model that allows for nonlinear effects.

Table 1.

Predictive Power of Optimal Subsets With Different Numbers of Predictors

Number of predictors	DTE-estimated R2		DTE-estimated SE of R2
	Life satisfaction	Health	Life satisfaction	Health
20	.77	.66	.013	.025
50	.77	.67	.014	.024
598	.78	.67	.013	.025
Selected 20	.34	.66	.011	.008

Note: DTE = decision tree ensemble. Bottom row indicates the feature set selected in this article.

Step 3: Preprocess Data

For didactic simplicity, we began by limiting the analysis to only those data collected in the most recent complete wave in 2013, which we cast into a “wide” format, with one row per participant. We removed one measure (PLH0166: Expected satisfaction with life a year from now) as being too highly correlated (r = .84) and conceptually overlapping one of the outcomes of interest (life satisfaction). We then identified all measures with more than 50 different response categories (threshold based on potential implementation cost, e.g., difficulty of presenting large number of response options in smartphone-based surveys). These variables were all country- or occupation-related variables that were unlikely to change month-to-month. Thus, we removed them from consideration for our assessment.

Missingness was handled using blockwise deletion. We marked participants who responded to more than 500 measures as “high responders” and removed any measure missing for more than one-quarter of the members of this group. This new set had very little missingness and so, we used listwise deletion to remove any row that still contained a missing value. The size of the SOEP is such that this leaves us with a data set of 598 measures from each of 11,461 people, which we deem sufficient for our task.

Step 4: Compute Feature Importance

With our data ready, we used RFE with a DTE separately for each outcome (life satisfaction, subjective health status) to automatically select an optimal set of 50 features based on the overall improvement in the DTE-estimated R² measure. To accommodate the possibility that the most important features may differ with age, we repeated this process for each of our predefined age groups (younger, middle-aged, and older). A partial list of the optimized measures is shown in Figures 1 and 2. Table 1 shows R² measures for predicting life satisfaction using optimal sets of 20 and 50 measures as compared with the original 598-feature subset, as estimated by RFE. As is visible in the table, a large number of the features contribute very little to the overall fit of the model (e.g., via R²) and it is possible to identify a small subset of measures that retains much of the predictive power (R² = .78 vs R² = .77 for 598 vs 20 predictors, respectively, for life satisfaction). Our goal in this case, however, is not to retain an optimal set of measures but to choose a set of measures that has good predictive power and is appropriate for a monthly survey design.

We quantified the feature importance for each measure and each age group using permutation testing. Figure 1 (life satisfaction) and Figure 2 (subjective health status) show the feature importance of the 50 most predictive measures on the entire data set and relative importance within each age group. Feature importance, indicated by the length of the bars, is shown relative to the most important measure shown in that group. It can be seen that, for example, the number of close friends is an important feature (relatively long bar) for prediction of life satisfaction in the overall sample and that the importance differs across the three age groups.

Step 5: Select Features

As a final step, we examined Figures 1 and 2 and selected our optimal set of measures. Bringing in empirical and theoretical knowledge, we see that several of these measures are not suited to being asked in a monthly survey because of their slow rate of change. For example, sibling year of birth should remain stable from month-to-month. Other measures, however, such as the number of hours spent working each day, are still likely to be useful in the context of a monthly survey. As stated previously, the removal of features that do not meet the theoretical needs of the study can be performed in Step 3 to reduce computation time.

Of particular note in Figures 1 and 2 are the differences between younger, middle-aged, and older adults in the importance various measures have for prediction. For example, satisfaction with sleep and distance driven to work are important for younger and middle-aged adults’ life satisfaction but less important for older adults, whereas number of close friends is important among older adults but not younger and middle-aged. Similarly, number of days off work sick is primarily important only to middle-aged adults’ life satisfaction.

Variability between groups in the importance of a predictor is indicative of an interaction between the feature and the grouping variable. For example, limitations in life due to health problems show high importance within each group for overall health but lower importance in the overall sample. This can happen when the grouping variable is an important predictor of the outcome, that is, there is larger between-group variance than within-group variance. The limitations feature is better at distinguishing subjective health within a given group than between groups and its contribution is small in the overall sample when compared with other measures, which may distinguish both within- and between-group variation. These differences highlight the utility of considering subgroups in the feature selection process.

Because the SOEP is delivered by interview and written questionnaire, most of the questions available here are based on self-report, which means that there are minimal differences between measures in terms of participant burden or cost of assessment. However, some small differences can still be considered. For example, day of interview and month of interview are selected for inclusion in the monthly survey because they have low burden relative to predictive value.

The 20 predictors we selected for our final set are bolded in the two figures. These are chosen through consideration of feature importance (e.g., high importance for at least one group on at least one outcome), ease of response, and likelihood of changing from month-to-month. For example, satisfaction with sleep is chosen because of its high overall importance and hours of weekday housework because of its importance to older adults. Limitations in daily life is selected because, although health problems and worries about health problems do not appear in the 50 most predictive measures of life satisfaction, these measures are very important for health status within each age group. Because we will be running only one study, we must include features important to both outcome and weight the relative benefits of each measure to predicting each outcome against the costs of additional features.

This reduced set of measures has lower prediction of between-person differences in life satisfaction (R² = .34, SE = 0.011) than does an optimal set of 20 measures (R² = .77, SE = 0.008), as shown on Table 1 and maintains roughly this level across all age groups, as shown on Table 2. We expect that this significant drop is due to our decision to avoid purely between-person difference measures, such as sibling year of birth, from our set of questions. Naturally, this reduces our ability to predict between-person differences in life satisfaction. Were these our only outcome, our selection should likely be revisited and expanded. However, the same set of measures maintains almost all of the predictive power of the 598-measure set for prediction subjective health status (R² = .66 for selected; SE = 0.008, R² = .67, SE = 0.024 for complete model) and so, we retain it at this point.

Table 2.

Predictive Power of the Final Selected Set Using DTEs Across Different Age Groups

	Young		Middle-aged		Older		Overall
	LS	Health	LS	Health	LS	Health	LS	Health
DTE-estimated R2	.28	.47	.38	.61	.35	.62	.34	.57

Note: DTE = decision tree ensemble; LS = life satisfaction.

Ultimately, our selected set of measures keeps a reasonable amount of predictive power for both outcomes, is small enough that it can be answered every month, and consists only of measures likely to vary month-to-month and whose month-to-month variation likely reflects month-to-month variation in life satisfaction and subjective health. This minimal set will have a significantly reduced participant burden without losing the important associations that will potentially drive month-to-month predictive power.

Discussion

Selecting Features for Study of Satisfaction With Life

With the goal of designing a short monthly survey, we selected a small subset of features from the larger SOEP battery that we expect will allow prediction of life satisfaction and subjective health status. In doing so, we identified features with high predictive ability and examined how predictive power differed across younger, middle-aged, and older age groups.

The Feature Selection Approach

The process of feature selection provides a method for quantifying the importance of a feature in terms of its pure predictive power. By combining automated selection and quantification approaches with human scientific and study design expertise, the feature selection process provides new possibilities for data-informed design of studies that fulfill a wide array of requirements (e.g., low burden) without significant sacrifice in predictive accuracy. As intensive data collection approaches spread into new domains, we expect that feature selection approaches can significantly shorten the time needed for the development of intensive longitudinal assessments, screeners for psychiatric disorders, risk assessments for medical or behavioral problems (e.g., falls, automotive accidents, or dementia), and the design of other instruments where the tradeoff between predictive accuracy and instrument efficiency is important.

Cautions and Limitations

It is important to note that this article only touches the surface of how feature selection procedures might be used. Our example, based on the analysis of cross-sectional panel data, provided a good testbed for and illustration of the method, in part because the data were easily considered to be independent and identically distributed scores obtained from a nationally representative sample. When data include time sequences (e.g., happiness measured daily for 2 weeks) or multilevel data, these approaches should be modified both to avoid bias and to capitalize on the predictive information embedded in the repeated measures (e.g., intraindividual variability). As with any data-driven approach, there is always a risk of overfitting and finding spurious results. We recommend using cross-validation techniques alongside human expertise to minimize the risk that spurious correlations cause inflated feature importance. For example, in the current illustration, it would be possible to set aside a random subsample of the data before beginning the feature selection process and to test the predictive power of the selected set of measures on that smaller data set to evaluate generalizability.

Our provided feature selection approach focuses on the case where there are only a few outcomes of particularly interest. The literature of feature selection, however, includes some approaches known as multitarget feature selection (see, e.g., Dhillon et al., 2009; Zhang, Yeung, & Xu, 2010) in which a large number of outcomes can be predicted simultaneously. The combination of these highly data-driven approaches with human theoretical knowledge, however, has yet to be explored. Future work may also be needed to see if recent advances in theory-guided exploratory approaches such as SEM forests (Brandmaier et al., in press; Brandmaier et al., 2014) can be adapted into solutions for multioutcome feature selection.

Conclusions

Feature selection approaches make it possible to combine data-driven insights with substantive and practical expertise to choose an optimal set of predictors for a study or analysis. We expect that feature selection will also be useful in areas where predictive ability is particularly important, for example, in the development of risk assessments and screening tools. Feature selection approaches can also provide important insights into the designers of intensive longitudinal studies where minimizing participant burden and drop out is tantamount. This article provides one example of feature selection, which is a broad subfield of machine learning in its own right. As developmentalists make use of more and more intensive data collection approaches, these data-driven techniques for handling large-scale data and selecting important features of note will become increasingly valuable.

Funding

This work was supported by the National Science Foundation (IGERT 1144860), National Institute on Health (R01 HD076994, R24 HD041025, UL TR000127, T32 AG049676), the Penn State Social Science Research Institute, the German Research Foundation (Grants GE 1896/3-1 and GE 1896/6-1), and German Federal Ministry of Education and Research (InterEmotio/EMOTISK).