Development and Validation of a 10-Year Mortality Prediction Model: Meta-Analysis of Individual Participant Data From Five Cohorts of Older Adults in Developed and Developing Countries

Abstract

Background:

Existing mortality prediction models for older adults have been each developed using a single study from the United States or Western Europe. We aimed to develop and validate a 10-year mortality prediction model for older adults using data from developed and developing countries.

Methods:

We used data from five cohorts, including data from 16 developed and developing countries: ELSA (English Longitudinal Study of Aging), HRS (Health and Retirement Study), MHAS (Mexican Health and Aging Study), SABE-Sao Paulo (The Health, Well-being and Aging), and SHARE (Survey on Health, Ageing and Retirement in Europe). 35,367 older adults were split into training (two thirds) and test (one third) data sets. Baseline predictors included age, sex, comorbidities, and functional and cognitive measures. We performed an individual participant data meta-analysis using a sex-stratified Cox proportional hazards model, with time to death as the time scale. We validated the model using Harrell’s C statistic (discrimination) and the estimated slope between observed and predicted 10-year mortality risk across deciles of risk (calibration).

Results:

During a median of 8.6 years, 8,325 participants died. The final model included age, sex, diabetes, heart disease, lung disease, cancer, smoking, alcohol use, body mass index, physical activity, self-reported health, difficulty with bathing, walking several blocks, and reporting date correctly. The model showed good discrimination (Harrell’s C = 0.76) and calibration (slope = 1.005). Models for developed versus developing country cohorts performed equally well when applied to data from developing countries.

Conclusion:

A parsimonious mortality prediction model using data from multiple cohorts in developed and developing countries can be used to predict mortality in older adults in both settings.

The number of people aged 65 or older is expected to triple in the next four decades with most of the increase occurring in developing countries (1). This rapid demographic change will impose increasing costs on already strained health systems (2). To limit costs and improve efficiency, preventive and therapeutic services should focus on patients who would benefit the most. For example, cancer screening or strict glycemic control is not recommended for older adults with limited life expectancy (3–5). Although a comprehensive geriatric assessment, which includes medical, psychological, social, environmental, and functional assessments, can be used to qualitatively judge how long the patient is expected to survive (6), it may be difficult for health professionals with limited time and training to perform this comprehensive assessment. Therefore, using mortality prediction models can be more practical in providing clinical guidance.

However, all available mortality prediction models have been developed using data from a single study, but all from the United States and Western Europe (7–17), which greatly limits their validity for use even in other high-income countries, let alone in the developing countries. For instance, a model developed using data from the Health and Retirement Study (HRS) in the United States showed poor performance when it was applied to older adults in England (18). In addition, a recent meta-analysis concluded that none of the prediction models are ready for use in clinical practice, because their validity has not been tested in other populations (15). Another limitation of the existing prediction models is the need for laboratory tests, which increases the costs and reduces the feasibility of using them in developing countries (10,12,19,20). In addition, most models predict mortality for 5 years and may not be adequate for making decisions about chronic disease care such as cancer screening and treatment that may only affect long-term risk (eg, bisphosphonates) (10,12). To overcome these limitations, we developed and validated a 10-year prediction model for mortality in adults aged 60 years and older, using data from 16 countries from five cohorts (ELSA [English Longitudinal Study of Aging], HRS [Health and Retirement Study], MHAS [Mexican Health and Aging Study], SABE-Sao Paulo [The Health, Well-being and Aging], and SHARE [Survey on Health, Ageing and Retirement in Europe]) and limiting the predictors to risk factors that can easily be assessed in the office.

Methods

Data Sources and Study Population

We included individual-level data from publicly available population-based prospective studies of older adults. The five cohorts that were included in this study are (i) ELSA (21), (ii) HRS (22), (iii) MHAS (23), (iv) Sao Paulo-SABE (24), and (v) SHARE (25). These cohorts collectively cover populations in 16 countries in North America, Latin America, and Europe. Details of study design and sample size are presented in Supplementary Table 1. In each cohort, we included participants who were 60 years or older at baseline. We excluded participants who had incomplete data for time of death or for the 13 selected predictors of mortality yielding a final analytic sample of 35,367 respondents (Figure 1).

Figure 1.

Flowchart of participant selection for the pooled data sets.

The outcome was time to death in years. Participants were contacted by study interviewers in every wave and those who were not located or whose relatives informed they had died, had their mortality information confirmed by the national vital statistics records or by a next-of-kin (in SHARE and MHAS). In all cohorts, information on age, gender, comorbidities, lifestyle factors, and functional status were collected through structured interviews. All studies were approved by the corresponding institutional review boards, and this analysis was approved by the Harvard T.H. Chan School of Public Health Office of Human Research Administration.

Choice of Predictors

We considered 29 predictors of mortality that were measured using similar tools and procedures in the five cohorts. These included age, sex, comorbidities, lifestyle factors, and functional status. Comorbidities and lifestyle factors included disease history (heart disease, lung disease, stroke, cancer, diabetes, and hypertension), depression, body mass index (BMI), alcohol use, smoking, and physical activity. Disease status was self-reported by participant according to previous diagnosis by a physician. Depression was defined by the Center for Epidemiologic Studies Depression Scale score ≥3 in ELSA, HRS, and MHAS (26); by 15-item Geriatric Depression Scale score ≥5 in SABE (27); and by EURO-D score ≥4 in SHARE (28). Height and body weight were self-reported in all cohorts, except SABE in which both were measured during a visit. We calculated BMI and categorized it in four groups: underweight (<18.5kg/m²), normal weight (18.5 to <25kg/m²), overweight (25 to <30kg/m²), and obese (≥30kg/m²). Participants were considered physically active if they had engaged in vigorous physical activity (sports, heavy housework, or a job that involves physical labor) at least three times a week in HRS, MHAS, and SABE; and at least once a week in ELSA and SHARE. Although vigorous physical activity was defined consistently across cohorts, the study questionnaires differed in how they categorized the frequency of physical exercise per week. We examined 17 measures of functional status: ability to correctly report the date of the interview as a measure of cognition, difficulty in independently performing basic activities of daily living (bathing, dressing, feeding, transferring, and toileting) (29), difficulty in mobility, strength, and motor skills (getting up from a chair; walking several blocks; pushing or pulling heavy objects; climbing a flight of stairs; stooping, kneeling, or crouching; picking up a dime; reaching above one’s shoulders; lifting objects that weigh over 5kg) (30,31), history of falls (participant referred to be bothered by the presence of fall in the last 6 months in SHARE; and 2 or more falls in the last 2 years in the other cohorts), and self-reported health (which we categorized as excellent/very good/good versus regular/bad).

Statistical Analysis

We randomly divided the pooled observations into training (two thirds of observations) and testing (one third) and used an individual participant data (IPD) meta-analysis approach to estimate the parameters of the prediction model (32), using a sex-stratified Cox proportional hazards model, with time to death as the time scale. To select predictors in the training data set, we first determined the relationships between time to death and each of the 29 potential risk factors in univariate Cox models using the IPD meta-analysis approach. We excluded variables that were not associated with mortality at the less than .0001 level because we had a large sample size and we aimed to have a parsimonious model. To avoid using two highly correlated variables, we screened all pairs of variables within each cohort, and if correlation ratio was ≥0.5 in most cohorts, we excluded the variable with the smaller hazard ratio. We then included the remaining risk factors in a multivariable Cox model using the IPD meta-analysis approach and kept the risk factors that had an independent association with mortality with a p value of less than .0001. The final coefficients were generated using a multivariable Cox model that contained only these risk factors. The proportional hazard assumption was checked by graphical inspection of both the Kaplan–Meier survival curves and the log-log survival curves of each risk factor. We used the ipdmetan command in Stata to implement the IPD meta-analysis (33). Models with random effects were used because we found significant heterogeneity among studies.

Model Validation

We first recalibrated the model using standard methods to incorporate differences in prevalence of predictors and average death rates between the entire training sample and each specific cohort-sex subgroup (34,35). We then validated the model by calculating discrimination and calibration in the test data set. Discrimination was evaluated using Harrell’s C statistic, which measures the ability of the prediction model to assign a higher risk to individuals with short time to event (36). Calibration was evaluated by comparing the predicted and observed risk of death by deciles of predicted risk. We used a standard exponential model to estimate 10-year risk of mortality in MHAS and SHARE that had 9 and 8 years of follow-up, respectively. Because MHAS participants were followed for a maximum of 9 years, we estimated the cumulative risk of death at 9 years using Kaplan–Meier survival curves. We then extrapolated the 9-year risk to 10 years using the exponential formula S₁₀ = 1 – (1 − S₉)^9/10 and used the extrapolated S₁₀ as the average death rate in MHAS by sex (37). Similarly, SHARE participants were followed for a maximum of 8 years, and we followed the same steps to extrapolate the survival rate to 10 years in SHARE separately by sex. The mortality prediction model had the form:

P (10-year absolute risk of death) = 1 − S_0cs(t)^exp(f[x,M]), where f(x,M) = β₁(x₁ − M₁)+ … +β_p(x_p − M_p) and β₁, …, β_p were the sex-specific Cox regression coefficients associated with each predictor in the model derived from the training data set; x₁, …, x_p were the individual’s risk factor in the training data set; and M₁, …, M_p were the means of the predictors within each cohort and sex. S_0cs(t) is the average survival probability at follow-up time t (in years), which varied by cohort (c) and sex (s). To recalibrate the model, we replaced the mean values of the predictors and the average survival probability with those observed in each cohort and sex.

As a measure of calibration, we calculated the absolute differences between observed and predicted 10-year mortality risks within each decile of predicted risk and considered differences in risk of less than 10% points as an indication of acceptable calibration (15). We also fitted a linear regression model to compare the predicted and observed 10-year risks of death. If the model is “correct,” the slope should be 1.0. An Excel spreadsheet that reports the estimated 10-year risk of mortality was developed and can be found in Supplementary Material. To recalibrate this model and make it applicable to an “average” older adult, we used pooled survival probability and pooled mean values of the predictors across all cohorts, for men and women separately. Ideally, such recalibration should be done with nationally representative data for the older adults in the target population. However, this information is often not available or unreliable.

We tested if the association between each risk factor and mortality was different in cohorts from developed (ie, United States, UK, and Europe) versus developing countries (ie, Mexico and Brazil) by pooling coefficients separately in these two groups of cohort studies. We then evaluated the advantage of having two separate models for developed and developing countries by comparing the observed mortality risk in the two cohorts from Mexico (MHAS) and Brazil (SABE) with two separate predictions, one using the “developing country model” and one using the “developed country model.” In addition, because model performance may vary among the youngest and the oldest participants, we divided the sample at age 70 (median age). We then investigated calibration and discrimination in these two age groups. Statistical analyses were performed with SAS version 9.3 (Cary, NC) and Stata 12.0 (College Station, TX). We used the Stata somersd package to calculate Harrell’s C (38).

Results

We included 35,367 eligible participants with a mean age of 70.0 (SD of 7.5) years at baseline (Table 1 and Figure 1). Slightly less than half (46%) were men and 13% reported having difficulty with at least one item on the activities of daily living. During a median follow-up of 8.6 years, 6,407 participants were lost to follow-up and 8,325 died. About half of the participants were from Europe, 20% from Latin America (5% from Brazil and 15% from Mexico), and 28% from the United States. The 10-year mortality risk varied substantially across cohorts: for example, for 60-year-old men, it ranged from 12% in ELSA in England to 20% in SABE in Brazil and for 60-year-old women from 6% in SABE to 15% in MHAS in Mexico (Table 1). Some predictors such as “difficulty with eating,” lung disease, and stroke had fairly similar frequencies across studies, whereas others including self-reported health, depression, and alcohol use varied substantially (Table 2).

Table 1.

Time of Follow-Up, Vital Status, and 10-Year Mortality Risk of the Pooled Data and by Cohort

	Pooled Data	ELSA	HRS	MHAS	SABE	SHARE
	n = 35,367	n = 4,170	n = 10,044	n = 5,453	n = 1,776	n = 13,924
Time of follow-up, median (IQR)	8.6 (5.7–10.0)	9.8 (5.9–10.2)	10.0 (7.8–10.0)	9.2 (7.9–9.3)	9.5 (4.9–10.6)	7.1 (4.5–8.6)
Vital status at the end of follow-up
Alive	58.3	58.1	69.2	63.5	46.6	47.4
Dead	23.6	21.1	28.9	26.7	31.9	17.0
Lost to follow-up	18.1	20.8	1.9	9.8	21.5	35.6
10-year mortality risk for 60-year-old participants (%)
Total	11.8	8.7	12.5	16.8	11.7	9.5
Men	14.9	11.6	16.2	18.6	19.8	12.7
Women	9.1	6.4	9.6	15.1	6.1	6.5

Note: ELSA = English Longitudinal Study of Aging; HRS = Health and Retirement Study; IQR = Interquartile range; MHAS = Mexican Health and Aging Study; SABE = Survey on Health, Well-being and Aging (Sao Paulo); SHARE = Survey on Health, Ageing, and Retirement in Europe.

Table 2.

Baseline Characteristics (%) of the Selected Study Population of the Pooled Data and by Cohort

Variables	Pooled Data	ELSA	HRS	MHAS	SABE	SHARE
	n = 35,367	n = 4,170	n = 10,044	n = 5,453	n = 1,776	n = 13,924
Age groups (years)
60 to <65	28.7	24.1	29.8	32.6	33.4	27.2
65 to <70	24.5	27.6	23.6	25.5	17.4	24.7
70 to <75	19.8	21.7	20.0	19.1	14.6	20.0
75 to <80	14.5	14.6	14.7	12.3	19.2	14.6
80 to <85	8.3	8.9	7.8	6.4	10.9	8.9
≥85	4.2	3.1	4.1	4.1	4.5	4.6
Male	46.1	44.8	45.1	49.1	40.3	46.7
Hypertension	41.5	40.6	45.4	51.0	53.4	38.6
Diabetes	12.8	7.5	12.9	20.1	17.0	12.0
Heart diseasea	17.5	18.8	21.1	5.9	18.1	20.1
Lung disease	6.3	6.0	6.8	9.9	9.8	6.1
Stroke	4.7	4.4	6.2	3.4	4.9	5.1
Cancer	6.9	6.9	11.4	2.5	3.3	6.5
Smoking
Never	49.4	36.4	41.2	54.7	53.8	56.6
Former	37.1	50.4	45.8	30.9	32.0	29.9
Current	13.5	13.2	13.0	14.4	14.2	13.5
Current alcohol use	38.7	54.7	30.9	24.0	19.8	47.8
BMI (kg/m2)
Underweight (<18.5)	1.7	1.0	1.6	3.0	2.8	1.4
Normal weight (18.5 to <25)	35.7	27.2	37.0	35.8	35.5	37.3
Overweight (25 to <30)	42.2	43.9	41.0	39.6	38.7	44.1
Obese (≥30)	20.4	27.9	20.4	21.6	23.1	17.2
Physical activityb	35.6	36.0	46.1	33.0	24.3	30.5
Difficulty with bathing	6.1	11.8	4.9	4.0	3.0	6.6
Difficulty with dressing	8.7	13.0	7.7	7.7	12.7	8.1
Difficulty with using the toilet	3.1	2.7	4.3	4.0	2.2	2.2
Difficulty with eating	1.8	1.3	1.9	1.9	1.6	1.8
Difficulty with getting in and out of the bed	4.6	4.9	4.8	5.2	7.9	3.6
Difficulty with walking several blocks	19.0	10.0	24.6	30.4	27.3	12.2
Difficulty with getting up from a chair	27.3	27.7	35.7	26.3	31.0	21.1
Difficulty with climbing one flight of stairs	16.5	14.0	14.4	26.3	25.4	13.9
Difficulty with stooping, kneeling, or crouching	37.7	39.1	40.2	38.2	47.5	34.1
Difficulty with reaching or extending your arms above shoulder level	11.0	10.0	14.2	11.1	12.3	8.8
Difficulty with pulling or pushing large objects	19.7	17.3	22.3	24.2	26.3	15.8
Difficulty with lifting objects that weigh over 5 kg	23.0	25.7	21.3	23.4	31.7	22.1
Difficulty picking up a coin from the table	5.1	5.4	6.1	7.1	4.3	3.7
Difficulty reporting the date of the interview	27.5	22.4	22.9	38.4	21.6	16.3
Self-reported health
Excellent, very good, good	62.3	75.5	72.5	30.0	46.2	65.6
Fair, poor	37.7	24.5	27.5	70.0	53.8	34.4
Depressionc	28.1	21.8	22.2	51.0	17.8	26.5
History of having fallsd	10.2	13.7	8.0	24.0	12.5	5.1

Notes: BMI = body mass index; ELSA = English Longitudinal Study of Aging; HRS = Health and Retirement Study; MHAS = Mexican Health and Aging Study; SABE = Survey on Health, Well-being and Aging (Sao Paulo); SHARE = Survey on Health, Ageing, and Retirement in Europe.

^aDefined by “ever been told by a doctor to have heart disease,” except in MHAS that was defined by “ever been told by doctor to have heart attack.”

^bDefined by “participating in sports, heavy housework, or a job that involves physical labor” ≥3 times/week in HRS, MHAS, and SABE; and ≥1 times/week in ELSA and SHARE.

^cDefined by CESD-D (Center for Epidemiologic Studies Depression Scale) ≥3 in ELSA, HRS, and MHAS, by 15-item GDS (Geriatric Depression Scale) ≥5 in SABE, and by EURO-D ≥4 in SHARE.

^dParticipant bothered by the presence of fall in the last 6 months in SHARE, two or more falls in the last 2 years in the other cohorts.

All 29 potential predictors were significantly associated with mortality in univariate analyses at less than .0001 level. We excluded two functional measures, “difficulty climbing several flights of stairs” and “difficulty with lifting objects that weigh over 5kg,” because they were strongly correlated with other functional measures that had larger associations with mortality (“difficulty walking several blocks” and “pushing or pulling large objects,” respectively). The remaining predictors were included in the IPD meta-analysis using a multivariable Cox model (Supplementary Table 2). Thirteen variables were still associated with mortality at the .0001 level, and the final coefficients for each predictor were generated using a Cox model with these predictors (Table 3). These were age, diabetes, heart disease, lung disease, cancer, smoking, current alcohol use, BMI, physical activity, difficulty with bathing, walking several blocks, reporting the date of the interview, and self-reported health (Supplementary Box 1). The estimated coefficients differed significantly across cohorts, both between and within the two sets of developing and developed country cohorts. Some coefficients were larger in the Brazilian and Mexican cohorts (eg, diabetes) and others were smaller (eg, current smoking; Supplementary Figure 1). The “developed country model” underestimated the mortality risk in the Mexican cohort (MHAS) by 8.5% in women and 11.6% in men and in the Brazilian cohort (SABE) by 10.0% in women and 9% in men (Supplementary Figure 2).

Table 3.

Selected Risk Factors for the Final Model and their Hazard Ratio for 10-Year Mortality in the Training Data Set (N = 23,615)

Risk Factorsa	HR (95% CI)b
Age groups (years)
60 to <65	1.0 (reference)
65 to <70	1.53 (1.23–1.91)
70 to <75	2.45 (2.09–2.86)
75 to <80	3.94 (3.53–4.39)
80 to <85	5.89 (4.89–7.09)
≥85	9.32 (7.14–12.18)
Diabetes	1.53 (1.25–1.88)
Heart disease	1.26 (1.10–1.45)
Lung disease	1.41 (1.29–1.54)
Cancer	1.79 (1.25–2.58)
Smoking
Never	1.0 (reference)
Former	1.17 (1.10–1.25)
Current	1.70 (1.35–2.13)
Current alcohol use	0.83 (0.78–0.89)
BMI (kg/m2)
Underweight (<18.5)	1.60 (1.38–1.85)
Normal weight (18.5 to <25)	1.0 (reference)
Overweight (25 to <30)	0.81 (0.77–0.87)
Obese (≥30)	0.81 (0.71–0.92)
Physical activity	0.80 (0.75–0.85)
Difficulty with bathing	1.40 (1.10–1.77)
Difficulty with walking several blocks	1.49 (1.32–1.69)
Difficulty reporting the date of the interview	1.18 (1.11–1.25)
Self-reported health
Excellent, very good, good	1.0 (reference)
Fair, poor	1.25 (1.10–1.42)

Notes: CI = confidence interval; HR = hazard ratio.

^aAs defined in Table 1.

^bIndividual patient data meta-analysis stratified by sex.

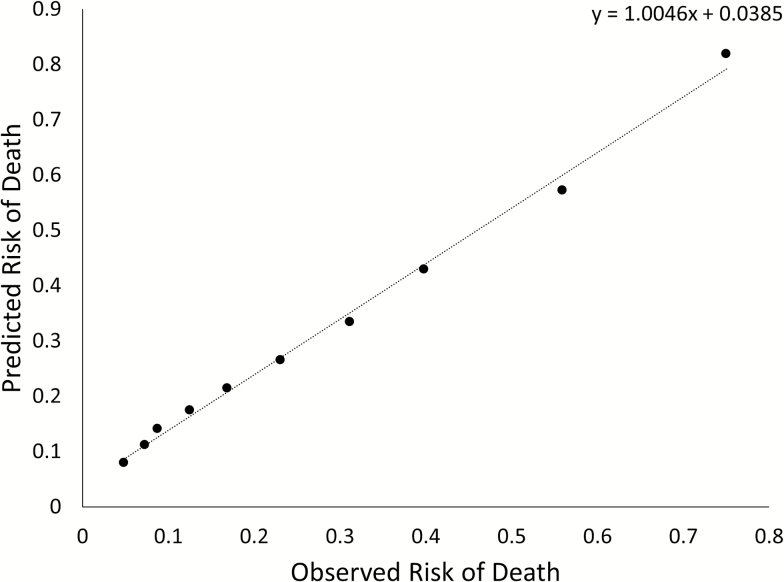
The pooled model showed good discrimination in the testing data set with a Harrell’s C statistic of 0.756 (95% confidence interval = 0.748–0.765) and calibration (slope of 1.005 and intercept of 0.039; Figure 2). The difference between observed and predicted 10-year mortality risk was less than 10% points in all deciles of predicted risk in the test data set. We observed good discrimination and calibration in both younger and older participants. Harrell’s C was 0.716 (0.706–0.727) for participants younger than 70 years and 0.708 (0.702–0.715) for those aged 70 or older; the slope of the regression line for observed versus predicted mortality risk by decile was 0.89 for participants younger than 70 years and 0.97 for those aged 70 or older (Supplementary Figure 3).

Figure 2.

Scatter plot and linear regression line of observed and predicted 10-year risk of death in the testing data set (n = 11,752).

Discussion

We developed and validated a 10-year mortality prediction model for adults aged 60 years and older using data from five cohorts in 14 developed and 2 developing countries. The model included a parsimonious set of 13 variables that can be measured during a clinical interview and showed good discrimination and calibration. Previous mortality prediction models were all developed using data from a single study and mostly from the United States and Europe (7–9,13,39–42) and therefore have limited generalizability in other populations (18). We found that the best set of predictors were age, comorbidities, lifestyle factors, and functional status, similar to previous models developed for community-dwelling older adults (7–9,13,40). In addition, although we included data from 16 countries with widely different mortality rates, our model showed similar discrimination to previous single-study models that had C statistics from 0.69 to 0.83 and less than 10% points difference between observed and predicted risk of mortality across deciles of risk (15). Moreover, our model had good performance both among the youngest and oldest participants.

Apart from good predictive ability and generalizability, our model has several other advantages. It is easy to apply in both clinical and community settings as it does not require laboratory tests, allowing mortality predictions with only simple answers to a questionnaire that can be entered into a spreadsheet. Moreover, to ensure that the difference in prevalence of predictors and mortality levels between cohorts would not affect prediction, we recalibrated the model to the entire study population using standard methods (34,35). The association between several risk factors and mortality differed between and within developing and developed country cohorts potentially indicating the influence of study design and measurement quality rather than true biological differences across countries. We evaluated if using two separate models for developing versus developed countries would improve mortality prediction but did not find any evidence that model performance would substantially improve.

A previous IPD meta-analysis of eight American and one Italian cohort studies had been conducted to investigate the association between gait speed and mortality among older adults (17). However, the model developed here is the first to use IPD meta-analysis of data from countries other than the United States and Western Europe, which makes it more applicable to developing countries.

Our model also has several limitations. Although the cohorts used similar questionnaires, a few potential predictors were assessed differently. For example, in SABE weight and height were measured, whereas in all other cohorts they were self-reported. In addition, participants in all cohorts were asked whether they had “heart disease,” whereas in MHAS they were asked about “heart attack,” and the frequency of vigorous physical activity were different between HRS, MHAS, and SABE (≥3 times/week), and ELSA and SHARE (≥1 time/week). We also did not have consistent measures of other potential predictors of mortality, such as number of recent hospitalizations (8) and size of the participant’s social network (42) across the five cohorts. Moreover, cohorts lost up to 36% of their participants during follow-up, and this may have biased our results if loss to follow-up is associated both with the included predictors and with mortality (43). Additionally, we used sex- and cohort-specific survival probabilities and mean values of predictors to validate our models. However, users of the mortality prediction model will probably not have access to their country-specific estimates. Finally, we did not have access to prospective data on older adults in Eastern Europe, Asia, Africa, and the Middle East. Several cohort studies are currently recruiting older participants in these regions, and including their information in a future pooling study should be a priority once the follow-up data become available.

The proposed model can be easily applied in clinical practice to guide decisions regarding cancer screening and chronic disease prevention. For example, clinical guidelines support cancer screening for older adults with a life expectancy ≥10 years (3,44). Based on our model, a 77-year-old woman who has diabetes, a BMI of 28kg/m², engages in physical activity twice a week, does not have heart disease, lung disease, or cancer, has never smoked or used alcohol, does not have difficulty to shower or walk several blocks, reports today’s date correctly, and considers her health as “good,” has a predicted 10-year mortality risk of 33%, which would indicate a reasonable potential for benefit from cancer screening. However, a 77-year-old woman with diabetes, heart disease, and a BMI of 18kg/m² who is physically inactive and has difficulty walking several blocks will have a predicted 10-year mortality of 77% which may be used by herself and her physician to discuss whether cancer screening procedures (eg, sigmoidoscopy) should be recommended.

Our model has important implications for improving quality and reducing cost of care for adults aged 60 years and older worldwide. Many developing countries, especially the so-called “economies in transition,” are facing a rapidly ageing population and this rapid aging imposes a significant challenge for resource allocation in healthcare. Therefore, to better allocate the scarce economic and human resources, healthcare professionals need to be empowered with objective prognosis information to best target certain clinical services to older adults who would benefit the most.

Supplementary Material

Supplementary material can be found at: http://biomedgerontology.oxfordjournals.org/

Funding

G.D. was supported by the National Institute of Health through NIDDK (1R01-DK090435).

ELSA: The data were made available through the UK Data Archive. ELSA was developed by a team of researchers based at the NatCen Social Research, University College London, and the Institute for Fiscal Studies. The data were collected by NatCen Social Research. The funding is provided by the National Institute of Aging in the United States and a consortium of UK government departments co-ordinated by the Office for National Statistics. The developers and funders of ELSA and the Archive do not bear any responsibility for the analyses or interpretations presented here.

HRS: Health and Retirement Study, RAND public use data set, was produced and distributed by the University of Michigan with funding from the National Institute on Aging (U01AG009740), Ann Arbor, MI.

MHAS: The study receives support from the National Institute on Aging (NIA R01 AG018016) and the Mexican Government. The first phase was a collaborative effort among researchers from the Universities of Pennsylvania, Maryland, and Wisconsin in the United States, and the Instituto Nacional de Estadística, Geografía e Informática (INEGI) in Mexico. The second phase was a collaborative effort among researchers from the University of Texas Medical Branch (UTMB), the University of Wisconsin, the Instituto Nacional de Estadística y Geografía (INEGI, México), the Instituto Nacional de Geriatría (INGER, Mexico), and the Instituto Nacional de Salud Pública (INSP, México).

SABE: This study was supported by Sao Paulo Research Foundation (FAPESP) (1999/051257, 2005/549472, and 2009/537783).

SHARE: This paper uses data from SHARE Wave 5 release 1.0.0 of March 31, 2015 (doi:10.163/SHARE.w5.100); SHARE Wave 1 release 2.6.0, as of November 29, 2013 (doi:10.6103/SHARE.w1.260). The SHARE data collection has been primarily funded by the European Commission through the 5th Framework Program (project QLK6-CT-2001-00360 in the thematic program Quality of Life), through the 6th Framework Program (projects SHARE-I3, RII-CT-2006-062193, COMPARE, CIT5-CT-2005-028857, and SHARELIFE, CIT4-CT-2006-028812) and through the 7th Framework Program (SHARE-PREP, N° 211909, SHARE-LEAP, N° 227822 and SHARE M4, N° 261982). Additional funding from the U.S. National Institute on Aging (U01 AG09740-13S2, P01 AG005842, P01 AG08291, P30 AG12815, R21 AG025169, Y1-AG-4553-01, IAG BSR06-11, and OGHA 04-064) and the German Ministry of Education and Research as well as from various national sources is gratefully acknowledged (see www.share-project.org for a full list of funding institutions). This analysis uses data or information from the Harmonized SHARE data set and Codebook, Version B as of February 2014 and the Harmonized ELSA data set and Codebook, Version C as of October 2014 developed by the Gateway to Global Aging Data. The development of the Harmonized SHARE was funded by the National Institute on Ageing (R01 AG030153, RC2 AG036619, and 1R03AG043052). For more information, please refer to www.g2aging.org.