SUMMARY
Many populations of early-stage cancer patients have non-negligible latent cure fractions that can be modeled using transformation cure models. However, there is a lack of statistical metrics to evaluate prognostic utility of biomarkers in this context due to the challenges associated with unknown cure status and heavy censorship. In this article, we develop general concordance measures as evaluation metrics for the discriminatory accuracy of transformation cure models including the so-called promotion time cure models and mixture cure models. We introduce explicit formulas for the consistent estimates of the concordance measures, and show that their asymptotically normal distributions do not depend on the unknown censoring distribution. The estimates work for both parametric and semiparametric transformation models as well as transformation cure models. Numerical feasibility of the estimates and their robustness to the censoring distributions are illustrated via simulation studies and demonstrated using a melanoma data set.
Keywords: c-index, Concordance probability, Cure fraction, Predictive accuracy, Prognostics for censored survival, Mixture cure model
1. Introduction
Recent advancements in cancer screening have led to the identification of a large number of early-stage cancers including many curable ones. For example, a high percentage of resected early-stage melanoma patients are cured by surgery although no available method can reliably distinguish them from the uncured patients. Currently, the only way to accurately identify the uncured melanoma patients after surgery is to await cancer recurrence, by then, the best chance to treat cancer may have been lost. Thus, effective adjuvant therapies are needed to prevent or delay cancer progression and recurrence of uncured patients. Accordingly, there is an urgent and unmet need to develop statistical metrics to evaluate the efficacy of candidate adjuvant therapies (e.g. immunotherapies) and prognostic utility of biomarkers for survival of uncured patients without knowing who are surely cured.
The transformation mixture cure models jointly model the latent cure status using logistic regression and model the survival of uncured patients using transformation models (Lu and Ying, 2004). Important special cases include the proportional hazard mixture cure models (Farewell, 1982; Kuk and Chen, 1992; Sy and Taylor, 2000) and the proportional odds (PO) mixture cure models. Another type of transformation cure models that can account for the cure fraction are often referred as promotion time cure models (Zeng and others, 2006), originally proposed by Yakovlev and Tsodikov (1996) and Chen and others (1999) based on some biological mechanistic considerations.
These two-type of transformation cure models are better suited for prognostic analysis of many early-stage cancers with cure fractions than the conventional survival models [e.g. Cox proportional hazards model (PHM)] that ignore the cured subjects (Othus and others, 2012; Asano and others, 2014). In particular, these models can potentially allow the possibility of making unbiased assessments of prognostic utilities of biomarkers (e.g. primary tumor thickness and ulceration status of melanoma) for predicting survival of uncured patients without knowing exactly who are cured. Due to the challenges associated with unknown cure status, there has been a lack of statistical metrics for evaluating the prognostic accuracy of transformation cure models (Asano and others, 2014). In particular, measuring the prognostic utility of biomarkers for the survival of the uncured subjects has been an important open problem, even for parametric cure models (Farewell, 1982).
Concordance probability has been used for measuring prognostic accuracy in survival setting. However, the conventional concordance probability estimator as proposed in Harrell and others (1982, 1984) and Gönen and Heller (2005) are not directly applicable for measuring prognostic accuracy in the context of unknown cure status of patients. Specifically, let 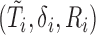 ,
,  denote the observed time, censoring indicator, and risk score. Herrell’s c-index can be written as
denote the observed time, censoring indicator, and risk score. Herrell’s c-index can be written as
| (1.1) |
As pointed out by Pencina and D’Agostino (2004) and Uno and others (2011), Harrell’s c-index depends on censoring distribution and is not consistent to the concordance probability 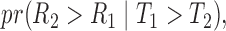 where
where 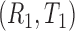 and
and 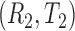 are two randomly selected pair of bivariate observations of risk score and failure time. Under the Cox proportional hazard (PH) models, Gönen and Heller (2005) propose to estimate the concordance probability
are two randomly selected pair of bivariate observations of risk score and failure time. Under the Cox proportional hazard (PH) models, Gönen and Heller (2005) propose to estimate the concordance probability  by
by
| (1.2) |
where the risk scores  is the linear combination of covariates for the
is the linear combination of covariates for the  th subject in Cox PHM. Gonen and Heller’s estimator has several desirable properties compared with Harrell’s c-index: (i) Gonen and Heller’s estimator does not depend on the censoring distribution. (ii) Gonen and Heller’s estimator is consistent and asymptotic normal. However, Gonen and Heller’s estimator cannot be applied to proportional odds model (POM), Accelerated Failure Time (AFT) model and other non-Cox PH transformation models. Furthermore, when the population is a mixture of cured and uncured patients, both Harrell’s c-index and Gonen and Heller’s estimator cannot be directly used. To fill in these knowledge gaps, we extend the concordance probability measures of Gönen and Heller (2005) for Cox PHM to general transformation models. Moreover, the general concordance index is also applicable for measuring accuracy in predicting the survival of the uncured subjects in transformation cure models that include both the promotion time cure models (Zeng and others, 2006) and transformation mixture cure models (Lu and Ying, 2004).
th subject in Cox PHM. Gonen and Heller’s estimator has several desirable properties compared with Harrell’s c-index: (i) Gonen and Heller’s estimator does not depend on the censoring distribution. (ii) Gonen and Heller’s estimator is consistent and asymptotic normal. However, Gonen and Heller’s estimator cannot be applied to proportional odds model (POM), Accelerated Failure Time (AFT) model and other non-Cox PH transformation models. Furthermore, when the population is a mixture of cured and uncured patients, both Harrell’s c-index and Gonen and Heller’s estimator cannot be directly used. To fill in these knowledge gaps, we extend the concordance probability measures of Gönen and Heller (2005) for Cox PHM to general transformation models. Moreover, the general concordance index is also applicable for measuring accuracy in predicting the survival of the uncured subjects in transformation cure models that include both the promotion time cure models (Zeng and others, 2006) and transformation mixture cure models (Lu and Ying, 2004).
The rest of the article is organized as follows. In section 2, We propose the general concordance-based prognostic measures, the k-index, for standard transformation models as well as for the two types of transformation cure models. We also provide explicit formulas for the estimators of the newly defined measures and establish their consistency and asymptotic normality. Section 3 reports simulation studies that illustrate the numerical feasibility of the estimates and their robustness to the unknown censoring distributions, and also provides real data illustrations of the proposed method. Section 4 contains discussion and final remarks. Technical proofs are contained in the Appendices. In the supplementary material available at Biostatistics online, the proofs of the proposed theorems are provided.
2. Methods
2.1. The transformation models and cure fraction
Let  denote the response with
denote the response with 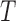 being the failure time and
being the failure time and  the censoring time. The event indicator is
the censoring time. The event indicator is  . Let
. Let  and
and 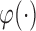 denote two monotone increasing functions. The generalized transformation model can be written as
denote two monotone increasing functions. The generalized transformation model can be written as
| (2.1) |
where  is a regression parameter vector associated with covariate vector
is a regression parameter vector associated with covariate vector 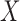 , and
, and 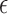 is random error such that for some function
is random error such that for some function 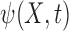 and some survival function
and some survival function  we have
we have
| (2.2) |
A special case of the generalized transformation models defined via (2.1) and (2.4) assumes that  is independent of
is independent of 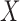 with
with 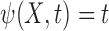 in (2.4), and
in (2.4), and  in (2.3). That is
in (2.3). That is
| (2.3) |
where 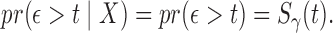 Indeed, model (2.3) is the conventional transformation model that contains many widely used survival models (Kalbfleisch and Prentice, 2011). For example, if
Indeed, model (2.3) is the conventional transformation model that contains many widely used survival models (Kalbfleisch and Prentice, 2011). For example, if 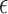 has the extreme value distribution with
has the extreme value distribution with  , then the model (2.3) is the Cox PHM. Similarly, when
, then the model (2.3) is the Cox PHM. Similarly, when 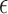 has the logistic distribution with
has the logistic distribution with 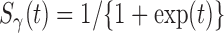 , then the model (2.3) is the POM. In particular, consistent and asymptotically normal estimates for the conventional transformation model (2.3) can be obtained based on martingale estimating equations (Chen and others, 2002) or maximum likelihood estimates (Zeng and Lin, 2007).
, then the model (2.3) is the POM. In particular, consistent and asymptotically normal estimates for the conventional transformation model (2.3) can be obtained based on martingale estimating equations (Chen and others, 2002) or maximum likelihood estimates (Zeng and Lin, 2007).
The general promotion time cure model as considered in Zeng and others (2006) is also a special case of the generalized transformation model, when  for some unknown CDF
for some unknown CDF 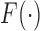 in (2.1), and
in (2.1), and  in (2.4). Then the conditional survival function of
in (2.4). Then the conditional survival function of 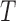 is given as
is given as
| (2.4) |
Note that 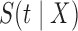 is an improper survival function since
is an improper survival function since  . In particular,
. In particular,  is the proportion of latent cured individuals given covariate
is the proportion of latent cured individuals given covariate 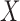 . Zeng and others (2006) assumed both
. Zeng and others (2006) assumed both 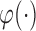 and
and 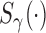 are known functions to ensure identifiability of the promotion time cure model defined in (2.4), and established asymptotic efficiency of semiparametric maximum likelihood estimates. So, we also assume
are known functions to ensure identifiability of the promotion time cure model defined in (2.4), and established asymptotic efficiency of semiparametric maximum likelihood estimates. So, we also assume 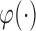 and
and 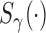 are both known functions.
are both known functions.
In addition to the promotion time cure model defined in (2.4), another type of transformation cure models is the transformation mixture cure models (Lu and Ying, 2004). The transformation mixture cure models assume the failure time 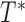 of the uncured subjects following the conventional transformation models in (2.3) and model the binary uncured status
of the uncured subjects following the conventional transformation models in (2.3) and model the binary uncured status  using a generalized linear model. Specifically, given covariate
using a generalized linear model. Specifically, given covariate 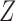 for the binary uncured status
for the binary uncured status  (
(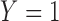 denotes a patient being uncured), then
denotes a patient being uncured), then
| (2.5) |
where the common choice of the link function 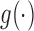 include logit, log–log and probit link functions. The covariate
include logit, log–log and probit link functions. The covariate 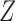 contains intercept and may share common components with covariates
contains intercept and may share common components with covariates  . General consistent and asymptotically normal estimates of
. General consistent and asymptotically normal estimates of  and
and 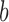 in (2.5) have been obtained by Lu and Ying (2004).
in (2.5) have been obtained by Lu and Ying (2004).
2.2. The concordance measures
2.2.1 The concordance index for transformation models without cured subjects
We first consider concordance measures for the conventional transformation model in (2.3) in the absence of cured subjects and extend it later to models in the presence of cured subjects. For a randomly selected pair of subjects 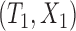 and
and 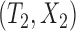 , a Kendall’s type concordance index
, a Kendall’s type concordance index 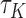 for model (2.3) is as follows:
for model (2.3) is as follows:
| (2.6) |
When  , larger
, larger 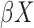 can almost surely predict a shorter survival
can almost surely predict a shorter survival  . Therefore,
. Therefore, 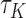 is a natural measure of discriminatory accuracy for shorter versus longer survival based on
is a natural measure of discriminatory accuracy for shorter versus longer survival based on  in generalized transformation models. Under commonly existing symmetry between the two subjects in the pair, i.e.
in generalized transformation models. Under commonly existing symmetry between the two subjects in the pair, i.e.  and
and 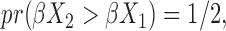 we have
we have
In fact, the well-known Harrell’s c-index is often referred as an estimator of 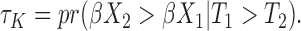 Unfortunately, Harrell’s c-statistics in (1.1) is not a generally consistent estimate of
Unfortunately, Harrell’s c-statistics in (1.1) is not a generally consistent estimate of  and the magnitude of the asymptotic bias depends on the unknown censoring distribution (Uno and others, 2011). Fortunately, we can derive asymptotically unbiased estimate for
and the magnitude of the asymptotic bias depends on the unknown censoring distribution (Uno and others, 2011). Fortunately, we can derive asymptotically unbiased estimate for 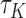 under the generalized transformation models in (2.1). When
under the generalized transformation models in (2.1). When 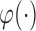 is strictly increasing, we have
is strictly increasing, we have
Let 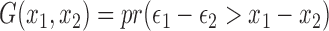 , the above
, the above  is equivalent to
is equivalent to
| (2.7) |
Given a random sample of 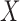 of size
of size  , by the properties of U-statistics, we have
, by the properties of U-statistics, we have 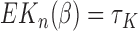 , where
, where
Let 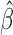 be a consistent estimator of
be a consistent estimator of 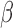 , which generally exists under random right censoring and some regularity conditions, e.g. Zeng and Lin (2007). Then, in contrast to the inconsistency of Harrell’s C-statistics, we have a generally consistent estimate
, which generally exists under random right censoring and some regularity conditions, e.g. Zeng and Lin (2007). Then, in contrast to the inconsistency of Harrell’s C-statistics, we have a generally consistent estimate 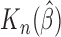 of
of 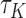 . From Corollary 1.1 in supplementary material available at Biostatistics online,
. From Corollary 1.1 in supplementary material available at Biostatistics online,  has an asymptotically normal distribution that does not depend on the unknown censoring distribution. In short, the Kendall’s type concordance index
has an asymptotically normal distribution that does not depend on the unknown censoring distribution. In short, the Kendall’s type concordance index 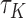 for the transformation model in (2.3) can generally be consistently estimated using the following U-statistic
for the transformation model in (2.3) can generally be consistently estimated using the following U-statistic
| (2.8) |
where 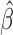 is a consistent estimator of
is a consistent estimator of  . As a special case, under the Cox PHM,
. As a special case, under the Cox PHM, 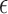 has the extreme value distribution. Then the kernel function
has the extreme value distribution. Then the kernel function 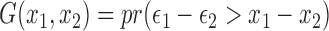 relates to the survival function of the standard logistic distribution:
relates to the survival function of the standard logistic distribution:
| (2.9) |
It is easy to see that plugging the  in (2.9) into (2.8) would yield exactly the same estimate in (1.2) for the concordance measure proposed by Gönen and Heller (2005) for the Cox PHM. Thus the general estimate in (2.8) naturally extends the concordance index proposed by Gönen and Heller (2005) for the Cox PHM to generalized transformation models in (2.1). As another example, when
in (2.9) into (2.8) would yield exactly the same estimate in (1.2) for the concordance measure proposed by Gönen and Heller (2005) for the Cox PHM. Thus the general estimate in (2.8) naturally extends the concordance index proposed by Gönen and Heller (2005) for the Cox PHM to generalized transformation models in (2.1). As another example, when  follows the POM,
follows the POM,  provides a consistent estimate for the concordance probability
provides a consistent estimate for the concordance probability  with the following kernel function
with the following kernel function 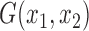 :
:
| (2.10) |
provided 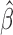 is a consistent estimate of
is a consistent estimate of 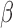 . Note that Gönen and Heller (2005) established asymptotic normality of
. Note that Gönen and Heller (2005) established asymptotic normality of 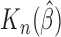 in (1.2) for the Cox PHM. In general, when
in (1.2) for the Cox PHM. In general, when 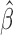 is asymptotically normal, for the conventional transformation models in (2.3), the general consistency and asymptotic normality of the concordance estimate in (2.8) follows directly as an easy corollary of Theorem 2 for transformation mixture cure models proved in Appendix A of supplementary material available at Biostatistics online.
is asymptotically normal, for the conventional transformation models in (2.3), the general consistency and asymptotic normality of the concordance estimate in (2.8) follows directly as an easy corollary of Theorem 2 for transformation mixture cure models proved in Appendix A of supplementary material available at Biostatistics online.
When we have two competing cure models, it is of interest to compare the prognostic accuracy of these models based on their k-indices 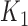 and
and 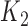 . Let
. Let  . Then a consistent estimator for
. Then a consistent estimator for 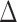 is
is  where
where 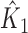 and
and 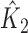 are the corresponding k-indices in (2.8). Note that the difference of two Harrell’s c-statistics generally depends on the unknown censoring distribution while the difference of two k-indices,
are the corresponding k-indices in (2.8). Note that the difference of two Harrell’s c-statistics generally depends on the unknown censoring distribution while the difference of two k-indices, 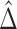 , does not depend on the unknown censoring distribution and is consistent to
, does not depend on the unknown censoring distribution and is consistent to 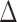 . We can use similar arguments as in the proof of Theorem 2 to show that
. We can use similar arguments as in the proof of Theorem 2 to show that 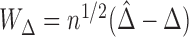 can be approximated by a mean zero normal distribution. The estimated variance
can be approximated by a mean zero normal distribution. The estimated variance  of
of  can be obtained via bootstrap. Similar to the procedure proposed in Uno and others (2011), we suggest to report a two-sided 95% confidence interval (CI) of
can be obtained via bootstrap. Similar to the procedure proposed in Uno and others (2011), we suggest to report a two-sided 95% confidence interval (CI) of 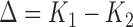 that is
that is 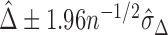 .
.
2.2.2 The k-index for promotion time cure model
Many populations of early stage cancers have non-ignorable latent fractions of cured patients that can be modeled using transformation cure models. Let  indicate the binary uncured status such that
indicate the binary uncured status such that  (or
(or 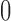 ) when the subject is uncured (or cured), respectively. In the special case, when all subjects are uncured, one can simply use (2.8) for an unbiased assessment of the discriminatory accuracy for predicting survival of the uncured subjects. In populations with cured patients, we define the k-index for uncured patients as follows:
) when the subject is uncured (or cured), respectively. In the special case, when all subjects are uncured, one can simply use (2.8) for an unbiased assessment of the discriminatory accuracy for predicting survival of the uncured subjects. In populations with cured patients, we define the k-index for uncured patients as follows:
| (2.11) |
where 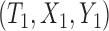 and
and 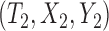 are a randomly selected pair of subjects. For the promotion time cure model, we have
are a randomly selected pair of subjects. For the promotion time cure model, we have 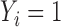 iff
iff  Then it is straightforward to show that
Then it is straightforward to show that
where  . Then, we can estimate the k-index in (2.11) by a ratio of U-statistics
. Then, we can estimate the k-index in (2.11) by a ratio of U-statistics
| (2.12) |
When all patients are uncured, the concordance probability in (2.12) is clearly equivalent to the estimate in (2.8). As shown below, 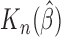 is consistent to
is consistent to  when
when 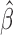 is a consistent estimate of
is a consistent estimate of 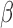 . Moreover,
. Moreover, 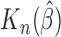 is asymptotically normal under the following assumptions (A1)–(A3).
is asymptotically normal under the following assumptions (A1)–(A3).
(A1)
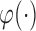 is differentiable.
is differentiable. 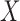 has a continuous component and
has a continuous component and 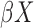 is bounded in probability.
is bounded in probability.- (A2) Let
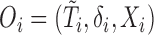 denote the observed data that are independent copies of
denote the observed data that are independent copies of 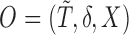 . There exists a square-integrable random vector
. There exists a square-integrable random vector 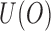 such that
such that  and
and  is nonsingular, and
is nonsingular, and
(2.13) - (A3) Asymptotic linearity of
 : In a neighborhood of the true parameter
: In a neighborhood of the true parameter  , we have
, we have
where(2.14) 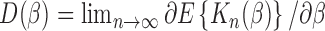 .
.
Theorem 1
Denote
. Under the above assumptions (A1)–(A3) we have, in distribution,
Condition (A1) is assumed in Zeng and others (2006) in order to derive the consistency and asymptotic normality of 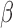 . Condition (A2) assumes that
. Condition (A2) assumes that 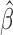 is a regular asymptotically linear (RAL) estimator of
is a regular asymptotically linear (RAL) estimator of 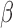 (Tsiatis, 2007) that is commonly hold for asymptotically normal estimator (Lu and Ying, 2004; Lu, 2008). Condition (A3) is a technical condition that assume the local linear expansion holds for
(Tsiatis, 2007) that is commonly hold for asymptotically normal estimator (Lu and Ying, 2004; Lu, 2008). Condition (A3) is a technical condition that assume the local linear expansion holds for  . A similar condition is used in Gönen and Heller (2005). The proof of Theorem 1 and the plug-in estimator of
. A similar condition is used in Gönen and Heller (2005). The proof of Theorem 1 and the plug-in estimator of  are provided in supplementary material available at Biostatistics online. To compare the prognostic accuracy for two sets of covariates based on the difference of their k-indices
are provided in supplementary material available at Biostatistics online. To compare the prognostic accuracy for two sets of covariates based on the difference of their k-indices  , we can construct a 95% CI for the difference of two k-indices as discussed in the last section.
, we can construct a 95% CI for the difference of two k-indices as discussed in the last section.
2.2.3 The k-index for transformation mixture cure models
In transformation mixture cure models defined in (2.5), the k-index in (2.11) can be written as
| (2.15) |
where 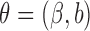 and
and  ,
,  . Similarly
. Similarly  can be estimated by
can be estimated by
| (2.16) |
where 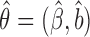 . The estimator
. The estimator 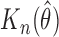 is also consistent and asymptotically normal under three regularity conditions as described below.
is also consistent and asymptotically normal under three regularity conditions as described below.
- (B1) Let
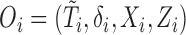 denote the observed data that are independent copies of
denote the observed data that are independent copies of 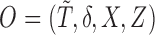 . There exists a square-integrable random vector
. There exists a square-integrable random vector  such that
such that  and
and 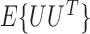 is nonsingular, and
is nonsingular, and
(2.17) (B2) A positive proportion of the sample is uncured, i.e.
 as
as 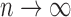 , where
, where  is a constant.
is a constant.- (B3) Asymptotic linearity of
 : In a neighborhood of true parameter
: In a neighborhood of true parameter 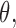 we have
we have
where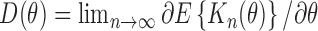 .
.
Theorem 2
Denote
. Under conditions (B1)–(B3), in distribution,
Condition (B2) is just to ensure the existence of events when sample size is large. That is clearly a minimal assumption. These conditions (B1) and (B3) are similar to those in Theorem 1. In particular, for parametric models, these regularity conditions can be verified straightforwardly. Thus, our proposed estimates work for many parametric as well as semiparametric models. The proof of Theorem 2 and the evaluation of plug-in estimator of  are provided in supplementary material available at Biostatistics online. To compare the prognostic accuracy for two sets of covariates based on the difference of their k-indices
are provided in supplementary material available at Biostatistics online. To compare the prognostic accuracy for two sets of covariates based on the difference of their k-indices  , we can construct a 95% CI for the difference of two k-indices as in the Section 2.2.1.
, we can construct a 95% CI for the difference of two k-indices as in the Section 2.2.1.
3. Numerical studies
We conducted extensive simulations to evaluate the performance of the newly proposed k-index in both the promotion time cure models and the mixture cure models.
3.1. A simulation study for promotion time cure model
We consider promotion time cure model defined in formula (2.4) with conditional survival function 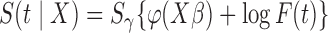 . Following Zeng and others (2006), let
. Following Zeng and others (2006), let 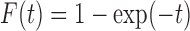 ,
,  and
and 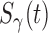 follow the Box-Cox type transformations:
follow the Box-Cox type transformations:
In this family, we considered the situation  for PHM and
for PHM and  for POM. We assumed that the covariate
for POM. We assumed that the covariate 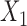 from a uniformly distributed random variable in
from a uniformly distributed random variable in  and the covariate
and the covariate 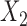 from a Bernoulli distribution with “success” probability
from a Bernoulli distribution with “success” probability 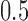 . Let
. Let 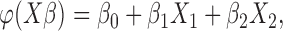 where
where 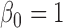 ,
, 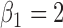 and
and  . The censoring time was generated from an exponential distribution with selected rates such that the censoring proportions are between
. The censoring time was generated from an exponential distribution with selected rates such that the censoring proportions are between  and
and  . We tried other censoring distributions but the results are similar, thus not presented. We also tried different sample sizes for our simulations, since the results and patterns are similar, we only present the case with the sample size
. We tried other censoring distributions but the results are similar, thus not presented. We also tried different sample sizes for our simulations, since the results and patterns are similar, we only present the case with the sample size  . For each simulated dataset, we estimated the parameter
. For each simulated dataset, we estimated the parameter 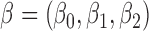 by fitting a parametric promotion time cure model. Then we calculated the k-index in the formula (2.12). We used
by fitting a parametric promotion time cure model. Then we calculated the k-index in the formula (2.12). We used  independent replications of the same procedure and compared the estimated
independent replications of the same procedure and compared the estimated 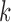 -index with the true value
-index with the true value  that was calculated based on
that was calculated based on  replicates. Table 1 summarizes the simulation results.
replicates. Table 1 summarizes the simulation results.
Table 1.
Simulation results for parametric promotion time cure models with 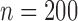
| Model | Censored Proportion (%) | Cured Proportion (%) |
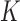
|
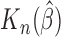
|
SE of 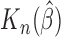
|
Simulation SE of 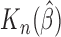
|
|---|---|---|---|---|---|---|
| PHM | 50 | 30 | 0.645 | 0.641 | 0.014 | 0.014 |
| PHM | 60 | 30 | 0.645 | 0.639 | 0.015 | 0.015 |
| PHM | 70 | 30 | 0.645 | 0.640 | 0.016 | 0.016 |
| POM | 40 | 20 | 0.699 | 0.696 | 0.012 | 0.012 |
| POM | 50 | 20 | 0.699 | 0.695 | 0.012 | 0.012 |
| POM | 60 | 20 | 0.699 | 0.695 | 0.013 | 0.013 |
As can be seen from Table 1, the estimator  is close to the true value and the bootstrap standard deviation of
is close to the true value and the bootstrap standard deviation of 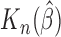 is close to the empirical standard deviation in all scenarios.
is close to the empirical standard deviation in all scenarios.
3.2. A simulation study for transformation mixture cure models
For uncured subjects, we generated survival time data from the following transformation model,
where  was sampled from a normal distribution with standard deviation
was sampled from a normal distribution with standard deviation 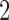 , and
, and 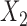 was a Bernoulli random variable with “success” probability
was a Bernoulli random variable with “success” probability 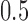 . We considered two scenarios for the distribution of
. We considered two scenarios for the distribution of 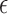 that included extreme value distribution for PHM, and standard logistic distribution for POM. Censoring times were generated from a uniform distribution,
that included extreme value distribution for PHM, and standard logistic distribution for POM. Censoring times were generated from a uniform distribution, 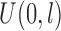 , where
, where  is selected to control the percentage of censored observations in uncured subjects. We also tried exponential distribution and other censoring distributions but the results are similar, thus not presented. For the cure status, we chose the following logistic model with the same covariates
is selected to control the percentage of censored observations in uncured subjects. We also tried exponential distribution and other censoring distributions but the results are similar, thus not presented. For the cure status, we chose the following logistic model with the same covariates  and
and 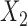 :
:
| (3.1) |
We selected 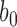 to control the percentage of cured observations in each replication. Uncured status
to control the percentage of cured observations in each replication. Uncured status  were then generated from a Bernoulli distribution with “success” probability
were then generated from a Bernoulli distribution with “success” probability  in (3.1). We selected
in (3.1). We selected  and
and 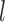 such that the cured and overall censored proportion were [(0.5,0.6),(0.3,0.6),(0.5,0.8)]. We tried different sample sizes for our simulations, since the results and patterns are similar, we only present the case with the sample size
such that the cured and overall censored proportion were [(0.5,0.6),(0.3,0.6),(0.5,0.8)]. We tried different sample sizes for our simulations, since the results and patterns are similar, we only present the case with the sample size  . For each simulated dataset, we estimated parameters by fitting a parametric mixture cure model. Then we calculated the k-index in the formula (2.16). We repeated the procedure
. For each simulated dataset, we estimated parameters by fitting a parametric mixture cure model. Then we calculated the k-index in the formula (2.16). We repeated the procedure 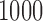 times and compared the estimated
times and compared the estimated  -index with the true value
-index with the true value 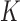 that was calculated based on
that was calculated based on 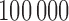 replicates. Table 2 summarized the simulation results.
replicates. Table 2 summarized the simulation results.
Table 2.
Simulation results for parametric transformation mixture cure models with 
| Model | Censored Proportion (%) | Cured Proportion (%) |
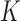
|
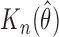
|
SE of 
|
Simulation SE of 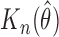
|
|---|---|---|---|---|---|---|
| PHM | 60 | 50 | 0.798 | 0.798 | 0.017 | 0.017 |
| PHM | 60 | 30 | 0.798 | 0.807 | 0.015 | 0.017 |
| PHM | 80 | 50 | 0.798 | 0.800 | 0.022 | 0.022 |
| POM | 60 | 50 | 0.739 | 0.739 | 0.021 | 0.022 |
| POM | 60 | 30 | 0.739 | 0.750 | 0.021 | 0.022 |
| POM | 80 | 50 | 0.739 | 0.741 | 0.029 | 0.027 |
As shown in Table 2, 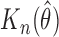 is stable and close to the nominal truth. The standard error of
is stable and close to the nominal truth. The standard error of  is similar to the empirical variability of
is similar to the empirical variability of 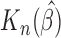 obtained by simulation. We also fitted semiparametric Cox PH cure model (Peng and Dear, 2000; Sy and Taylor, 2000). Results were similar to the parametric Cox PHM. The simulation results demonstrate that
obtained by simulation. We also fitted semiparametric Cox PH cure model (Peng and Dear, 2000; Sy and Taylor, 2000). Results were similar to the parametric Cox PHM. The simulation results demonstrate that  is not sensitive to the censoring distribution. This is similar to those findings reported in Gönen and Heller (2005) where k-index is insensitive to censoring distribution while the c-index of Harrell is sensitive. We show different types of censoring distributions for transformation mixture cure models and promotion time cure models to illustrate that our proposed method does not depend on the type of censoring distributions.
is not sensitive to the censoring distribution. This is similar to those findings reported in Gönen and Heller (2005) where k-index is insensitive to censoring distribution while the c-index of Harrell is sensitive. We show different types of censoring distributions for transformation mixture cure models and promotion time cure models to illustrate that our proposed method does not depend on the type of censoring distributions.
3.3. An example: a well-known Denmark melanoma dataset
In this section, we analyzed the dataset on malignant melanoma collected by K. T. Drzewiecki. In this study, investigator collected 205 stage I melanoma patients at the Department of Plastic Surgery, University Hospital of Odense, Denmark from 1962 to 1977. The data were summarized in Appendix 1 of Andersen and others (1993) and public available in the  package
package  (Dalgaard, 2008). The median follow-up time is 5.5 years, and the overall censoring proportion is 72%. Gender, tumor thickness and ulceration status are provided for all patients. We took log transformation for tumor thickness. The Kaplan–Meier survival curves in Figure 1 shows a plateau near the end of the study that suggests the possibility of a cured sub-population. To model the cure fraction, we fit Cox PH mixture cure model and report the parameter estimates in Table 3. The Cox PH mixture cure model indicates that patients with ulceration have lower chance to be cured after surgery (P-value = 0.040); patients with thicker tumor tend to have a shorter lifetime among uncured patients (P-value = 0.008).
(Dalgaard, 2008). The median follow-up time is 5.5 years, and the overall censoring proportion is 72%. Gender, tumor thickness and ulceration status are provided for all patients. We took log transformation for tumor thickness. The Kaplan–Meier survival curves in Figure 1 shows a plateau near the end of the study that suggests the possibility of a cured sub-population. To model the cure fraction, we fit Cox PH mixture cure model and report the parameter estimates in Table 3. The Cox PH mixture cure model indicates that patients with ulceration have lower chance to be cured after surgery (P-value = 0.040); patients with thicker tumor tend to have a shorter lifetime among uncured patients (P-value = 0.008).
Fig. 1.
Kaplan–Meier curves for the melanoma data stratified by above or below the median of tumor thickness (left) and Yes or No for ulceration status (right).
Table 3.
Parameter Estimates (standard errors) and P-values fitted by semiparametric Cox PH cure model for the melanoma data
| Cox PH model | Logit cure model | |||
|---|---|---|---|---|
| Log HR | P-value | Log OR | P-value | |
| Intercept | N/A |
 3.00(1.46) 3.00(1.46) |
0.039 | |
| Gender | 0.69(0.46) | 0.132 | 0.22(0.45) | 0.632 |
| log(tumor thick) | 0.79(0.30) | 0.008 | 0.35(0.28) | 0.209 |
| Ulceration | 0.27(0.49) | 0.581 | 1.07(0.52) | 0.040 |
The k-index based on Cox PH mixture cure model with covariates gender, log of tumor thickness, and ulceration is 0.72, and the 95% CI is (0.63, 0.81). From the k-index and 95% CI, we can see that the linear combination of gender, the logarithm of tumor thickness and ulceration have statistically significant predictive utility for the survival of uncured patients. However, the predictive accuracy of such prognostic models might be further improved by inlcuding other clinico-pathologic characteristics (Cymerman and others, 2016), treatment profiles(Sun and others, 2016), and biomarkers such as levels of circulating microRNA (Friedman and others, 2012) and ctDNA (Chang and others, 2016). Nevertheless, this example illustrates that we can assess the prognostic utility of log-thickness and ulceration without the need to know who is surely cured.
4. Discussion
Even though mixture cure models and other cure models have been introduced for decades in statistics literature, they have not been widely used in clinical practice (Othus and others, 2012). In particular, there has been a lack of statistical metrics to evaluate treatment effects of adjuvant therapies and prognostic utility of biomarkers in this context due to the challenges associated with unknown cured status. Although more than 90% of stage I melanoma patients are cured by surgery, there is no timely and reliable way to tell who is surely cured. It seems unrealistic to think there is ever a magic method capable of predicting with certainty that a patient has been cured soon after surgery. When the cure fraction is high, statistical metrics and analysis based on overall survival of the patient population and ignoring existence of cured patients are inadequate to characterize cancer prognosis.
There is a recent surge in developing immunotherapies or cancer vaccines that can strengthen patients’ immune system to prevent or delay cancer progression and recurrence (Hodi and others, 2010; Couzin-Frankel, 2013; Wolchok and others, 2013; Robert and others, 2015). Many of the candidate agents for cancer vaccine are known to be non-toxic or minimal toxic thus without the need of the typical stage I trials for assessment of their toxicity profile (Simon and others, 2001; Mukhi and Shao, 2009; Schlom, 2012). Also, there have been sustained interest in the medical community to use some of these non-toxic cancer vaccine agents to develop effective adjuvant therapies for early stage cancers with high percentage of curable subjects. Thus, one potential application of the newly proposed evaluation metric is to directly evaluate long-term treatment effects of adjuvant therapies (e.g. immunotherapies) for uncured patients with or without the presence of cured ones. Further applications of the proposed evaluation metrics for discriminative accuracy can be found in various applications of the mixture cure model as discussed in Maller and Zhou (1996) and Liu and others (2006).
In this article, we develop general concordance measures as evaluation metrics for the discriminatory accuracy of the conventional transformation models as well as transformation cure models extending the pioneering work of Gönen and Heller (2005) originally designed for the Cox PH models. We introduce explicit formulas for the consistent estimates of the concordance measures, and show that their asymptotic distributions do not depend on the unknown censoring distribution. The proposed concordance measures and estimates work for both parametric and semiparametric transformation models as well as transformation cure models. Numerical feasibility of the estimates and their robustness to the censoring distributions are illustrated via simulation studies. However, the proposed measures and estimates work well only when the assumed statistical models are correctly specified. Thus, goodness of fit or model diagnostic procedures should be identified and applied properly to ensure the transformation models and mixture cure models are suitable for the data (Wileyto and others, 2013; Peng and Taylor, 2016). Additionally, it is of interest to compare predictive accuracy of two competing predictive models by a formal hypothesis testing procedure. However, there is a well-known difficulty associated with testing correlated predictive models even for binary outcomes (Vickers and others, 2011; Demler and others, 2012; Pepe and others, 2013, 2014). Thus the testing problem is worth further systematic investigation in the future. Finally, we have written an R package to calculate k-index, with bootstrap CIs. The GitHub repo of the R package is available at https://github.com/elong0527/evacure with commit number 629d91087b950cc788326d8d1eb159a55d8fc4e0; last accessed date 21 April 2017.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
National Institutes of Health grant P30 CA16087-23 and P30 AG0851.
References
- Andersen P. K., Borgan r., Gill R. D. & Keiding N. (1993). Statistical Models Based on Counting Processes. New York, NY: Springer. [Google Scholar]
- Asano J., Hirakawa A. and Hamada C. (2014). Assessing the prediction accuracy of cure in the cox proportional hazards cure model: an application to breast cancer data. Pharmaceutical Statistics 13, 357–363. [DOI] [PubMed] [Google Scholar]
- Chang G., Tadepalli J., Shao Y., Zhang Y., Weiss S., Robinson E., Spittle C., Furtado M., Shelton DN., Karlin-Neumann G. & Pavlick A. (2016). Sensitivity of plasma braf mutant and nras mutant cell-free dna assays to detect metastatic melanoma in patients with low recist scores and non-recist disease progression. Molecular Oncology 10, 157–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M.-H., Ibrahim J. G. & Sinha D. (1999). A new Bayesian model for survival data with a surviving fraction. Journal of the American Statistical Association 94, 909–919. [Google Scholar]
- Chen K., Jin Z. & Ying Z. (2002). Semiparametric analysis of transformation models with censored data. Biometrika 89, 659–668. [Google Scholar]
- Couzin-Frankel J. (2013). Cancer immunotherapy. Science 342, 1432–1433. [DOI] [PubMed] [Google Scholar]
- Cymerman R., Shao Y., Wang K., Zhang Y., Murzaku E., Penn L., Osman I. & Polsky D. (2016). De novo vs nevus-associated melanomas: Differences in associations with prognostic indicators and survival. Journal of the National Cancer Institute 108, pii: djw121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalgaard P. (2008). Introductory Statistics with R. New York, NY: Springer-Verlag. [Google Scholar]
- Demler O. V., Pencina M. J. & D’Agostino R. B. (2012). Misuse of delong test to compare aucs for nested models. Statistics in Medicine 31, 2577–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farewell V. T. (1982). The use of mixture models for the analysis of survival data with long-term survivors. Biometrics 38, 1041–1046. [PubMed] [Google Scholar]
- Friedman E., Shang S., de Miera E., Fog J., Teilum M., Ma M., Berman R., Pavlick A., Hernando E., Baker A., Shao Y. And others (2012). Serum microRNAs as biomarkers for recurrence in melanoma. Journal of Translational Medicine 10, 155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gönen M. & Heller G. (2005). Concordance probability and discriminatory power in proportional hazards regression. Biometrika 92, 965–970. [Google Scholar]
- Harrell F. E., Califf R. M., Pryor D. B., Lee K. L. & Rosati R. A. (1982). Evaluating the yield of medical tests. Journal of the American Medical Association 247, 2543–2546. [PubMed] [Google Scholar]
- Harrell F. E., Lee K. L., Califf R. M., Pryor D. B. & Rosati R. A. (1984). Regression modelling strategies for improved prognostic prediction. Statistics in Medicine 3, 143–152. [DOI] [PubMed] [Google Scholar]
- Hodi F. S., O’Day S. J., McDermott D. F., Weber R. W., Sosman J. A., Haanen J. B., Gonzalez R., Robert C., Schadendorf D., Hassel J. C. et al. (2010). Improved survival with ipilimumab in patients with metastatic melanoma. New England Journal of Medicine 363, 711–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalbfleisch J. D. & Prentice R. L. (2011). The Statistical Analysis of Failure Time Data, Volume 360 New York, NY: John Wiley & Sons. [Google Scholar]
- Kuk A. Y. & Chen C.-H. (1992). A mixture model combining logistic regression with proportional hazards regression. Biometrika 79, 531–541. [Google Scholar]
- Liu M., Lu W. & Shao Y. (2006). Interval mapping of quantitative trait loci for time to event data with the proportional hazards mixture cure. Biometrics 62, 1053–1061. [DOI] [PubMed] [Google Scholar]
- Lu W. (2008). Maximum likelihood estimation in the proportional hazards cure model. Annals of the Institute of Statistical Mathematics 60, 545–574. [Google Scholar]
- Lu W. & Ying Z. (2004). On semiparametric transformation cure models. Biometrika 91, 331–343. [Google Scholar]
- Maller R. A. & Zhou X. (1996). Survival Analysis with Long-Term Survivors. New York: Wiley. [Google Scholar]
- Mukhi V. & Shao Y. (2009). Optimal two-stage designs to evaluate a series of new agents or treatments. Statistics in Biopharmaceutical Research 1, 377–387. [Google Scholar]
- Othus M., Barlogie B., LeBlanc M. L. & Crowley J. J. (2012). Cure models as a useful statistical tool for analyzing survival. Clinical Cancer Research 18, 3731–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pencina M. J. & D’Agostino R. B. (2004). Overall c as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Statistics in Medicine 23, 2109–2123. [DOI] [PubMed] [Google Scholar]
- Peng Y. & Dear K. B. (2000). A nonparametric mixture model for cure rate estimation. Biometrics 56, 237–243. [DOI] [PubMed] [Google Scholar]
- Peng Y. & Taylor J. M. (2016). Residual-based model diagnosis methods for mixture cure models. Biometrics. [DOI] [PubMed] [Google Scholar]
- Pepe M. S., Janes H. & Li C. I. (2014). Net risk reclassification p values: valid or misleading? Journal of the National Cancer Institute 106, dju041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M. S., Kerr K. F., Longton G. & Wang Z. (2013). Testing for improvement in prediction model performance. Statistics in Medicine 32, 1467–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert C., Long G. V., Brady B., Dutriaux C., Maio M., Mortier L., Hassel J. C., Rutkowski P., McNeil C., Kalinka-Warzocha E. et al. (2015). Nivolumab in previously untreated melanoma without braf mutation. New England Journal of Medicine 372, 320–330. [DOI] [PubMed] [Google Scholar]
- Schlom J. (2012). Therapeutic cancer vaccines: current status and moving forward. Journal of the National Cancer Institute 104, 599–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon R. M., Steinberg S. M., Hamilton M., Hildesheim A., Khleif S., Kwak L. W., Mackall C. L., Schlom J., Topalian S. L. & Berzofsky J. A. (2001). Clinical trial designs for the early clinical development of therapeutic cancer vaccines. Journal of Clinical Oncology 19, 1848–1854. [DOI] [PubMed] [Google Scholar]
- Sun X., Bao J. & Shao Y. (2016). Mathematical modeling of therapy-induced cancer drug resistance: Connecting cancer mechanisms to population survival rates. Scientific Reports 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sy J. P. & Taylor J. M. (2000). Estimation in a cox proportional hazards cure model. Biometrics 56, 227–236. [DOI] [PubMed] [Google Scholar]
- Tsiatis A. (2007). Semiparametric Theory and Missing Data. New York, NY: Springer Science & Business Media. [Google Scholar]
- Uno H., Cai T., Pencina M. J., D’Agostino R. B. & Wei L. (2011). On the c-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine 30, 1105–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vickers A. J., Cronin A. M. & Begg C. B. (2011). One statistical test is sufficient for assessing new predictive markers. BMC Medical Research Methodology 11, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wileyto E. P., Li Y., Chen J. & Heitjan D. F. (2013). Assessing the fit of parametric cure models. Biostatistics 14(2), 340–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolchok J. D., Kluger H., Callahan M. K., Postow M. A., Rizvi N. A., Lesokhin A. M., Segal N. H., Ariyan C. E., Gordon R.-A., Reed K. et al. (2013). Nivolumab plus ipilimumab in advanced melanoma. New England Journal of Medicine 369, 122–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yakovlev A. Y. & Tsodikov A. D. (1996). Stochastic Models of Tumor Latency and Their Biostatistical Applications, Volume 1 OECD Publishing. [Google Scholar]
- Zeng D. & Lin D. (2007). Maximum likelihood estimation in semiparametric regression models with censored data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 69, 507–564. [Google Scholar]
- Zeng D., Yin G. & Ibrahim J. G. (2006). Semiparametric transformation models for survival data with a cure fraction. Journal of the American Statistical Association 101, 670–684. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



