Abstract
Drinking water treatment plants rely on purification of contaminated source waters to provide communities with potable water. One group of possible contaminants are enteric viruses. Measurement of viral quantities in environmental water systems are often performed using polymerase chain reaction(PCR) or quantitative PCR (qPCR). However, these results can often be underestimated due to challenges involved in a multi-step viral concentration process and PCR inhibition. In this study, water samples were concentrated from 25 drinking water treatment plants (DWTPs) across the US to study the occurrence of enteric viruses in source water and removal after treatment. The five different types of viruses studied were adenovirus, norovirus GI, norovirus GII, enterovirus, and polyomavirus. Quantitative PCR was performed on all samples to determine presence or absence of these viruses in each sample. Ten DWTPs showed presence of one or more viruses in source water, with four DWTPs having treated drinking water testing positive. Furthermore, PCR inhibition was assessed for each sample using an exogenous amplification control, which indicated that all of the DWTP samples, including source and treated water samples, had some level of inhibition, confirming that inhibition plays an important role in PCR based assessments of environmental samples. PCR inhibition measurements, viral recovery, and other assessments were incorporated into a Bayesian model to more accurately determine viral load in both source and treated water. Results of the Bayesian model documented that viruses are present in source water and treated water. By using a Bayesian framework that incorporates inhibition, as well as many other parameters that affect viral detection, this study offers an approach for more accurately estimating the occurrence of viral pathogens in environmental waters.
Keywords: Bayesian statistics, enteric viruses, drinking water treatment, norovirus, enterovirus, adenovirus
1 INTRODUCTION
Waterborne viruses are a leading cause of illness and responsible for many nationwide gastro-intestinal illnesses (Bradbury et al., 2013; Brunkard et al., 2011; CDC, 2017; Okoh et al., 2010). To address waterborne contaminants, the U.S. Environmental Protection Agency publishes the Contaminant Candidate List (CCL), which includes chemical and microbial contaminants known to occur in public water systems and which could potentially result in adverse effects on human health (USEPA, 2015). The listed contaminants are considered as priorities for targeted research related to occurrence, dose-response, and health risk from exposure to drinking water. Of the 12 microbial contaminants listed on the current CCL (CCL4), 4 include specific virus groups, namely, adenoviruses, caliciviruses (i.e., norovirus), Hepatitis A viruses, and enteroviruses. These viruses can replicate in the human gastrointestinal tract, and are thus referred to as enteric viruses, and can be transmitted via the fecal-oral route (Okoh et al., 2010; Parshionikar et al., 2003).
Enteric viruses are released from infected persons into sewage in high concentrations, up to 1011 particles/g of stool (Okoh et al., 2010). Although sewage treatment generally reduces virus concentrations, many are discharged in the effluent and can enter receiving waters (Kitajima et al., 2014). Moreover, run-off from urban and agricultural areas, leakage from sewers and septic systems, storm water, and sewer overflows can contribute to the increased pathogenic viral load in rivers, lakes, groundwater, and reservoirs (Abbaszadegan, 2003; Borchardt et al., 2012). The contamination of receiving waters by pathogenic viral contaminants becomes a public health hazard as illness may result from ingestion of this water.
For a drinking water treatment plant (DWTP), the removal efficiency of pathogens is often based on the presence of fecal indicator bacteria, which does not serve as an accurate indicator for virus presence in many cases (Liang et al., 2015). The presence of fecal indicator bacteria is interpreted as an indication of surface water infiltration with potential occurrence of fecal pathogens. Given the different survival rates and transport mechanisms of bacteria and viruses, it is not accurate to assume that fecal indicator bacteria are indicative of viral presence (Ferguson et al., 2012). Moreover, it is unclear how different virus groups are removed via different treatments due to limited data regarding newer and combined treatment technologies.
Accurate determination of virus levels in environmental waters remains a challenge for several reasons. For example, viral concentrations have been observed to vary in space and time, owing to their tendency to form aggregates and bind to suspended solids, leading to non-uniform distributions in a water body (da Silva et al., 2011; da Silva et al., 2008; Gassilloud and Gantzer, 2005). A common strategy to increase the probability of detecting enteric viruses has been to sample large volumes (100s-1000s of liters) of water. Towards this end, a variety of methods have been used which typically involved filtration of the water through charged filter cartridges or through ultrafilters (Cashdollar and Wymer, 2013; Fout et al., 2010; Gerba et al., 1978; Karim et al., 2009; Lambertini et al., 2008; Sobsey and Jones, 1979). Ultrafilters concentrate virus by removing water through pores too small for a virus cell to pass (Rhodes et al., 2011), while charged filters retain virus by charge interactions. Following primary concentration from water, virus particles are eluted from filters with an elution efficiency that also is dependent upon viral capsid composition and co-concentrated water components. The diversity of procedures results in varied recovery efficiencies for different enteric viruses in different water matrices (Cashdollar et al., 2013; Karim et al., 2009).
One of the most important factors that complicate viral detection is the co-concentration of substances which inhibit PCR-based assays during the various processing steps (Gibson et al., 2012; Hata et al., 2015). In environmental samples, inhibition and low numbers of pathogenic virus can make it difficult to extrapolate concentrations using a standard curve method. Moreover, the standard curve quantitative analysis assumes that all viruses are distributed normally in all ranges. For these reasons, robust data analysis techniques, such as Poisson statistics, are needed to better measure and assess PCR inhibition and viral load. These data can then be combined into an approach that describes the impact of such confounding parameters on the prediction of viral quantities.
One approach that shows particular promise is the use of model using Bayes’ theorem, which provides a framework for determining the probability of human virus in water samples by incorporating measurements of PCR inhibition (i.e., false negatives), PCR contamination (i.e., false positives), or loss during large–volume concentration (analytical bias). Bayes’ theorem has been used to model waterborne virus concentrations and associated uncertainties (Choi et al., 2009; Follestad et al., 2010; Gronewold et al., 2008; Sivaganesan et al., 2008; Wu et al., 2014; Wu et al., 2013). This theorem can be expressed as the posterior probability that is proportional to a prior probability distribution and a likelihood function. The prior probability distribution confers background information (e.g., previous relevant studies, Monte Carlo simulations) that is combined with current evidence to fully describe the uncertainty of the relevant Bayesian parameters. Coupled with Poisson statistics for estimating virus in samples, the Bayesian framework provides a powerful tool to mitigate the intrinsic problems with measuring virus in aquatic matrices.
This study was a part of a broader study in which paired water samples were collected from 25 DWTPs across the United States to study the occurrence of an array of pharmaceuticals, chemicals, and microbes in various types of untreated waters and corresponding treated drinking waters (Batt et al., 2017; Benson et al., 2017; Conley et al., 2017; Furlong et al., 2017; Glassmeyer et al., 2017; King et al., 2016; Kolpin et al., 2017; Kostich et al., 2017). This portion of the study investigated the occurrence of multiple human-pathogenic viruses in source and treated water from various DWTPs across the nation. Specifically, the presence of 5 enteric viruses was examined: adenovirus (AdV), enterovirus (EV), norovirus GI (NoV GI), norovirus GII (NoV GII), and polyomavirus (PyV). PCR count data for each virus was integrated with other parameters such as recovery efficiency and PCR inhibition into a Bayesian model to estimate viral loads (viral genome molecules/L) in the sampled source and treated waters. Employing multiple parameters to address measurement uncertainties not only allowed us to achieve a more accurate understanding of viral quantities from the sampled water systems, but increased our knowledge of tracking and removal of pathogenic human viruses.
2 Materials and methods
2. 1 Sample Collection
Source and treated waters from DWTPs across the nation were concentrated and processed for the purpose of isolating and quantifying human enteric viruses: adenovirus (AdV), norovirus GI (NoV GI), norovirus GII (NoV GII), enterovirus (EV), and polyomavirus (PyV). To assess potential contamination of drinking water sources and subsequent contaminant removal during drinking water treatment, 12 pairs of DWTP source and treated water plus 13 additional DWTP source water samples were collected from the network of 25 DWTPs (Table 1). Treated water samples from 13 DWTPs were not collected since these DWTPs implement a pre-chlorination step, and for virus detection, water samples prior to chemical disinfection were desired, as residue disinfection chemicals on the filter can affect the results. Each DWTP had different types and combinations of treatment technologies (Glassmeyer et al., 2017), and each treated sample was acquired prior to any chemical disinfection. Source water samples were derived from rivers, lakes, reservoirs, or groundwater. All water samples were collected by filtering water on-site at the respective DWTP with a NanoCeram cartridge filter (Argonide) at a flow rate of approximately 10 L per min (Cashdollar et al., 2013; Karim et al., 2009). For river, reservoir, and lake water, the desired volume for filtration was 200 L, and for treated water and untreated groundwater, 2000 L. These volumes were based on reference volumes from EPA Method 1615 (Fout et al., 2010). For water with high turbidity, clogging of the NanoCeram filter prevented reaching the desired sampling volume. For these samples, the volume was recorded and accounted for in the final calculations. The paired source and treated samples were collected with a delay to account for the time required for the water to pass through the DWTP (i.e. residence time).
Table 1. Description of water samples analyzed.
Paired samples of source and treated water were analyzed for 12 DWTPs, while only source water samples were analyzed for 12 DWTPs. Source water type and sampling month are also detailed.
| DWTP | Paired Source & Treated | Only Source | Source Type* | Sampling Month |
|---|---|---|---|---|
| 1 | + | R | December | |
| 2 | + | R | September | |
| 3 | + | R | October | |
| 4 | + | R | October | |
| 5 | + | G | March | |
| 10 | + | R | January | |
| 11 | + | R | March | |
| 12 | + | G | February | |
| 13 | + | Res | May | |
| 14 | + | L | April | |
| 15 | + | R | April | |
| 16 | + | R | April | |
| 17 | + | R | May | |
| 18 | + | R | June | |
| 19 | + | R | June | |
| 20 | + | R | January | |
| 21 | + | R | July | |
| 22 | + | R | November | |
| 23 | + | Res | August | |
| 24 | + | G | December | |
| 25 | + | L | October | |
| 26 | + | R | January | |
| 27 | + | R | February | |
| 28 | + | Res | November | |
| 29 | + | Res | March |
R = River; G = Groundwater; Res = Reservoir; L = Lake
2.2 Filter elution and secondary concentration by organic flocculation
The filters from the DWTPs were shipped overnight on ice to the laboratory in coolers at 4°C, and eluted and processed within 48 hours of sampling. Viruses were recovered from the filters as previously described (Cashdollar et al., 2013; Fout et al., 2010). Elution of the virus from the positively-charged filter was performed by adding a high pH beef extract. Briefly, 500 ml of 1.5% desiccated beef extract (BD Bacto, Franklin Lakes, NJ) containing 0.05 M glycine (pH 9.0) was added to the housing with the filter, and allowed to soak 1 min. Using positive pressure, the beef extract then was forced through the filter, and the eluate was collected into a beaker. The filter was submerged again in an additional 500 ml of 1.5% beef extract–0.05 M glycine (pH 9.0) and allowed to soak a second time for 15 min. After the 15 min soak, the remaining beef extract eluate was forced through the filter and added to the first eluate. The pH of the combined eluate then was adjusted to 3.5, and mixed slowly for 30 min to allow beef extract proteins to form a floc to which viral particles adsorbed. The sample was then centrifuged for 15 min at 2,500 × g at 4°C to collect the floc. Following centrifugation, the supernatant was discarded and the resulting pellet containing viral particles was dissolved in 30 ml of 0.15 M sodium phosphate (pH 9.0). The resuspended pellet was centrifuged again at 4,000 × g for 10 min at 4°C to remove any non-dissolved materials from the sample. The supernatant was retained, the pH was adjusted to 7 to 7.5, and sterilized by using a 0.22-μm syringe filter to remove any possible bacterial contamination. The final 30 ml sample was stored at − 80°C, until ready for extraction.
2.3 Extraction of nucleic acid
Extraction of nucleic acid was performed on 10 ml of the 30 ml of water sample concentrate. Two different extractions methods, a two-step and a one-step, were compared and the one-step method was found to improve recovery (Supplemental Fig. A1). Briefly, the one-step method involved extraction of 10 ml of the concentrate from organic flocculation, using the QIAamp DNA Blood Maxi Extraction Kit (Qiagen), as per manufacturer's instructions, with slight modifications. The lysis buffer provided in the kit was replaced with Buffer AVL (Qiagen). Additionally, carrier RNA (Qiagen) was supplemented at 275 μg per extraction event to buffer against loss of targeted nucleic acids and the protease digestion step was omitted. Finally, during elution of nucleic acids from the maxi column, 1 ml Buffer AE was supplemented with 400 units of Recombinant RNasin Ribonuclease Inhibitor (Promega) and the volume of the eluate was reloaded onto the column for a second elution, for a total extract volume of 1 ml. For each batch of samples, an extraction negative control was done using 10 ml of 1×PBS. Extracts were stored at −80°C, until processed by qPCR. The products of one-step extraction samples were analyzed by reverse transcriptase (RT)-qPCR as shown below.
2.4 RT-qPCR/qPCR for enteric viruses
Using the primers and probes used for the detection of EV, NoV GI, NoV GII, AdV, and PyV (Supplemental Table A1), RT-qPCR and qPCR was performed as detailed previously (Brinkman et al., 2013). For each virus type, 2-10 replicates of at least two different dilutions were performed. All samples were initially tested with two replicates at two different dilutions, and if a positive PCR detection was determined, then more replicates at various dilutions was performed. For EV, NoV GI, and NoV GII assays, RT was performed in 15 μl reactions containing 5 μl of the 1 ml of nucleic acid extracted sample, 1.5 mM MgCl2, 1X PCR Buffer II (Life Technologies), 0.67 mM dNTPs (Promega), 0.5 μM reverse primer, 15 U Recombinant RNasin Ribonuclease Inhibitor, and 25 U MuLV RT (Life Technologies). RT reactions were incubated at 43°C for 1 h, followed by RT inactivation at 94°C for 5 min. The entire RT reaction was used in 25 μl qPCR reactions, in which the final reaction volume contained 5 mM MgCl2, 1X PCR Buffer II (Life Technologies), 0.5 μl ROX dye (Invitrogen), 0.5 μM forward primer, 0.1 μM probe, and 1.25 U AmpliTaq Gold (Life Technologies). The qPCR reactions were run using an ABI 7900HT (Life Technologies, Inc.) with the conditions of 95°C for 10 min, followed by 40 cycles of 95°C for 15 s, and 60°C for 1 min. The AdV and PyV qPCR assays were carried out in 25 μL reactions with either 0.5 μM of AdV primers, and 0.1 μM of AdV probe, or 0.5 μM of PyV primers, and 0.15 μM of PyV probe. Each qPCR assay contained 5 μl of sample, 1X PCR Buffer II (Life Technologies), 5 mM MgCl2, 0.4 mM dNTPs, and 1.25 U AmpliTaq Gold. PCR ensued on the ABI 7900HT as specified above. The number of positive detections among replicate reactions for each dilution were tallied for incorporation into the Bayesian model to determine virus concentrations.
(RT)-qPCR negative controls were tested using PCR grade water in place of template. Positive controls were prepared in several ways, as follows. For EV, NoV GI, and NoV GII, Armored RNA Quant Enterovirus (Asuragen) was extracted and used at various dilutions. For AdV positive controls, genomic DNA extractions were prepared from a commercially available, high titer wild-type AdV, serotype 5 preparation (Ad5WT; OD260) was used. Finally, for PyV, various dilutions of a plasmid extract were used as a positive control.
2.5 Assessment of Method Recovery
To assess the recovery efficiency of enteric viruses using the complete, modified method, a separate group of eight 200L of source water samples were collected and filtered on-site at one of the DWTP sites, as described above, and shipped to the lab overnight on ice at 4°C. Once at the lab, four of the filters were spiked by filtering an additional 9 L of sterile distilled water spiked with 1 L of archived primary effluent, a source of enteric viruses. Primary effluent is wastewater that has been settled to remove the majority of suspended and floating solids. The other four filters were not spiked to assess indigenous virus. All 8 filters were eluted and concentrated by organic flocculation. One-third of the eluate was further concentrated by nucleic acid extraction, as described above. Quantities of AdV in spiked and non-spiked samples were determined using droplet digital PCR (ddPCR). The ddPCR technology is a digital PCR method utilizing a water-oil emulsion droplet system, which form the partitions that separate the template DNA molecules. The droplets serve the same function as individual test tubes or wells in a plate in which the PCR reaction takes place, but in a nanoscale format. PCR reactions were prepared using 5 μl of the 1 ml nucleic acid extract, 12.5 μl of 2X ddPCR Supermix (BioRad Laboratories, Inc), 0.7 μM primers, and 0.25 μM probe (Supplemental Table A1) in 25 μl. PCR plates were sealed using the PX1 PCR Plate Sealer (Bio-Rad) and droplets were made as instructed by the manufacturer using the QX200 Droplet Generator (BioRad Laboratories, Inc.). PCR was performed in a C1000 Touch Thermal Cycler (BioRad Laboratories, Inc.) by heating to 95°C for 5 min, followed by 40 cycles of 94°C for 30 s and 55°C for 1 min and a final enzyme inactivation for 98°C for 10 min. The QX200 Droplet Reader (BioRad Laboratories, Inc.) and QuantaSoft Software (BioRad Laboratories, Inc.) was used to measure fluorescence in each droplet and assess positive and negative amplification. The data were used to inform the method loss parameter of the Bayesian model described below.
2.6 Inhibition Test (IT)
To assess inhibition of PCR in concentrated water samples, a commercially available Armored RNA Hepatitis G Virus (HepG) (Asuragen, Austin, TX) was used as an exogenous amplification control (EAC), similar to previously described studies (Borchardt et al., 2012; Fout et al., 2010). Extractions of the HepG armored RNA were prepared using the QIAamp DNA Blood Mini Kit as described above and three different concentrations (9, 1.8, 0.9 molecules per well of PCR assay) of EAC were added to nuclease-free water (pristine control) and in DWTP sample extracts. These concentrations were chosen to allow a mix of positive and negative detects in each dilution, which is needed for Poisson statistics. The targeted concentrations of EAC ensured that the highest dilution (1:10) had both positive and negative (presence and absence of EAC, respectively) values in pristine samples, as required for analysis. The assay was designed in this manner to accommodate MPN or count analysis. Two-step RT-qPCR was carried out as described above with the EAC primers and probe (Supplemental Table A1), except 4.5 μl of EAC extract was used in each reaction. The resulting replicate reactions were counted as positive or negative and these data were used to inform the inhibition parameter of the Bayesian model described below.
2.7 Estimating virus concentrations
The mathematical symbols for the equations described below are in Supplemental Table A2. The Bayesian model assumes that the dispersion of viruses in the ith DWTP water sample follows a lognormal (LN) distribution as described by Williams (Williams and Ebel, 2012). The non-informative prior is written as:
| (1) |
The units for λ are virus genome molecules per ml. The stochastic distribution of purified virus nucleic acid (NA) dispersed in each PCR was described by the Poisson distribution, which describes the probability of k number of events occurring in an interval given an average rate (λ), written as:
| (2) |
Two assumptions were stipulated: 1) virus target molecules are homogenous, distributed randomly, and likely are to be detected in any sample used for PCR, 2) Each virus target molecule will be detected by PCR if the sample contains one or more target molecules. The probability no virus target molecules are present in a PCR is given by the zero-term of the Poisson distribution:
| (3) |
Where dj represents the relative dilution level per PCR (e.g., relative dilution levels 1, 0.2, 0.1 represent an undiluted sample, followed by 1 to 5 and 1 to 10 dilutions, respectively) and the constant v represents the mL (0.005 mL) of sample added to each PCR. The complement of Eq. (3) is the probability of a positive PCR:
| (4) |
Estimating λi entails Poisson and binomial probability distributions (Cochran, 1950; McCrady, 1915). The binomial distribution requires two parameters, ni, and Equation 4, written as:
| (5) |
Where xij and nij are the virus PCR count data and number of binomial trials of the ith DWTP sample. PCR tubes were considered positive and counted if the reaction exceeds a fixed fluorescence threshold (i.e., the cycle threshold or Ct). Failure was defined as a reaction that did not produce a fluorescent signal within a total of 40 PCR cycles. These probability distributions were used to estimate virus concentrations using Markov Chain Monte Carlo (MCMC) in OpenBUGS software version 3.2.3 rev 1012 (available at http://openbugs.net/). Convergence of Markov chain simulations was confirmed by determining the Brooks-Gelman-Rubin (BGR) statistic for 3 different chains using 150,000 iterations. The first 75,000 of 150,000 Markov iterations were removed during the burn-in phase. Also, Deviance Information Criterion (DIC; i.e., the sum of Dbar and pD) was used for comparing Bayesian models. The EAC control (EACc) and spike (EACs) concentrations were estimated by MCMC using these two equations:
| (6) |
| (7) |
Where EAC(c or s)ij is the EAC PCR count data of the count and spike for the ith DWTP sample. The constant v represents the mL (0.0045 mL) of EAC added to each PCR. The error due to PCR inhibition was then calculated using relative error here defined as the absolute error divided by the control:
| (8) |
where subscripts refer to the ith EAC spike (λs) and pristine control (λc) concentrations estimated by MCMC.
The concentration of virus genomes (vg) in a liter of the ith DWTP original water sample was estimated using equations 6 and 7. In addition, this estimate was adjusted by considering the influence of error (i.e., Eq. 8) as well as sample recovery described by a beta prior (Wu et al., 2014), written as:
| (9) |
The shape parameters (α and β) for the beta distribution were estimated from the sample-loss mean (c) and variance (σ2) calculated using Eq. 10 and their individual values were then estimated using equations 11 and 12 as follows:
| (10) |
| (11) |
| (12) |
Thus, virus concentration was given as Model 1 (see Supplemental File 1 for BUGS code) written as:
| (13) |
where f is the total volume (3 ml) of the nucleic acid extract that could be derived from 30 ml of organic flocculate and Li is liters of ith source or treated water filtered with the NanoCeram® filter.
PCR inhibition was generalized with a beta prior distribution, written as:
| (14) |
The shape parameters were estimated from the EAC relative-error mean (μ1) and variance (σ21) that was calculated using Eqs. 10, 11, and 12. Virus concentration was calculated using Model 2 (see Supplemental File 2), written as:
| (15) |
Bayesian estimation supersedes the t Test (BEST) which is used to determine if the difference between concentration means are significant (Kruschke, 2013).
3 RESULTS AND DISCUSSION
3. 1 Overall Strategy
The goal of this study was to study the occurrence of 5 different types of viruses in 25 different drinking water treatment plants (DWTPs). The flow diagram in Fig. 1 depicts the overall strategy in achieving this goal. The first part of the flow diagram shows the virus filtration, concentration, and extraction procedures used prior to running the qPCR, Inhibition Test, and the Bayesian model. The first step of concentration (primary concentration) involved the filtration of large volumes of source and treated waters collected from the DWTPs using a NanoCeram® filter, followed by a secondary concentration using organic flocculation, which concentrated the sample to 30 ml. Further nucleic acid extraction concentrated 10 ml of the organic flocculation concentrate further to 1 ml. The nucleic acid extraction step used in this study was an improved method from nucleic acid extraction used in EPA Method 1615. By using a one-step nucleic acid extraction method, virus recovery efficiency was improved by mean of 2.1-fold (Supplemental Fig. A1). The (RT)-qPCR data was converted to count data and inputted into a Markov Chain Monte-Carlo (MCMC) Bayesian Analysis. Relative sample inhibition calculated via the Inhibition Test (IT), recovery, as well as other parameters were incorporated into the Bayesian analysis to improve the overall accuracy in assessing final viral quantities (virus genome molecules/L) for DWTP samples.
Figure 1. Flow diagram of Bayesian analysis.
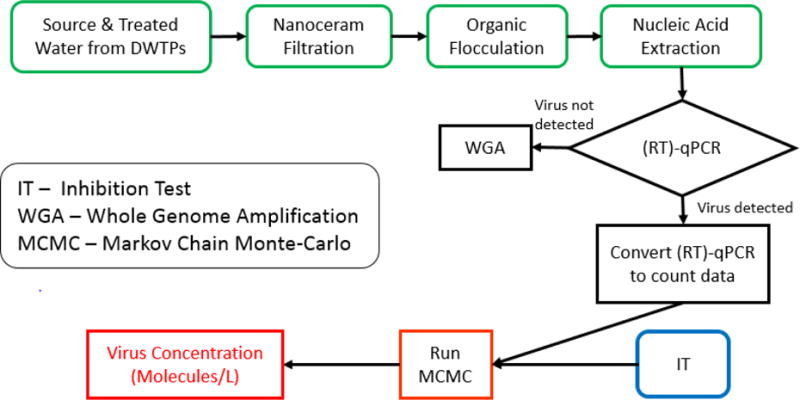
Flow diagram describing process to assess total virus loads using concentration steps (green), RT-qPCR, qPCR, and WGA (black), inhibition tests (blue), and Bayesian analysis (red).
3.2 The occurrence of human enteric viruses in DWTP samples
By using qPCR count data alone, one or more virus groups were detected by PCR in 10 DWTP source samples (3S, 4S, 10S, 11S, 22S, 23S, 24S, 25S, 26S and 27S), compared to four DWTP treated samples (3T, 20T, 23T, and 25T) (Table 2). Twenty-three DWTP samples were PCR-negative, which means that either the 5 virus types were not present or that the nucleic acid of the 5 virus types were below detection due to various confounding factors discussed earlier. Of the PCR-negative samples, 15 were source samples (1S, 2S, 5S, 12S, 13S, 14S, 15S, 16S, 17S, 18S, 19S, 20S, 21S, 28S, and 29S) and 8 were treated samples (1T, 2T, 10T, 11T, 12T, 15T, 16T, and 18T). The detection rates for adenovirus (AdV), norovirus GI (NoV GI), norovirus GII (NoV GII), enterovirus (EV), and polyomavirus (PyV) in the source water samples were 28%, 16%, 16%, 28%, and 16%, respectively. The rates, respectively, for treated water samples were 16.7%, 16.7%, 16.7%, 8.3%, and 0%. There was a 1.8-fold greater detection rate in source compared to treated water samples. Often, detection of virus was observed in higher dilutions, suggesting PCR inhibition was likely impacting virus quantity assessment.
Table 2. Presence data for 5 human viruses present in DWTP.
Presence data for 5 human viruses present, grouped according to each DWTP for source and treated water. Data presented are count data via qPCR. Numbers represent number of positive wells over the number of replicates for each relative dilution.
| DWTP* | PCR Assay | Relative Dilution#
|
|||||
|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.1 | 0.04 | 0.03125 | 0.02 | ||
| 3S | AdV | 0/2 | 2/2 | 4/5 | |||
| 3S | EV | 0/2 | 6/7 | 3/5 | |||
| 3S | NoV GI | 2/2 | 7/7 | 7/10 | 1/5 | 1/5 | |
| 3S | NoV GII | 2/2 | 2/2 | 5/5 | 5/5 | 1/5 | 0/5 |
| 3S | PyV | 0/2 | 3/7 | 0/5 | |||
| 3T | EV | 0/7 | 3/7 | 0/5 | |||
| 4S | AdV | 2/2 | 2/2 | 4/5 | |||
| 4S | EV | 0/2 | 5/7 | 4/5 | |||
| 4S | NoV GI | 2/2 | 2/2 | 4/5 | 3/5 | ||
| 4S | NoV GII | 0/2 | 7/7 | 5/5 | 4/5 | 3/5 | |
| 4S | PyV | 0/2 | 4/7 | ||||
| 10S | AdV | 2/12 | 1/12 | ||||
| 10S | PyV | 0/2 | 1/7 | ||||
| 11S | AdV | 0/2 | 2/7 | ||||
| 11S | NoV GI | 0/2 | 4/7 | ||||
| 11S | NoV GII | 0/7 | 2/2 | 2/5 | |||
| 20T | NoV GI | 1/7 | 0/2 | ||||
| 22S | NoV GII | 0/2 | 2/7 | ||||
| 23S | AdV | 1/2 | 4/7 | ||||
| 23T | AdV | 2/2 | 2/2 | 1/5 | |||
| 24S | AdV | 2/7 | 0/2 | ||||
| 24S | EV | 0/7 | 2/7 | ||||
| 24S | NoV GI | 2/7 | 0/2 | ||||
| 24S | NoV GII | 0/2 | 1/7 | ||||
| 25S | AdV | 0/2 | 0/2 | 1/5 | |||
| 25T | AdV | 5/7 | 1/7 | ||||
| 25T | EV | 2/7 | 0/7 | ||||
| 25T | NoV GI | 1/2 | 4/7 | 1/5 | |||
| 25T | NoV GII | 2/2 | 3/7 | 1/5 | |||
| 26S | EV | 0/2 | 7/7 | 9/10 | 4/5 | 3/5 | |
| 26S | NoV GII | 0/2 | 3/7 | ||||
| 26S | PyV | 0/2 | 1/7 | 0/5 | |||
| 27S | NoV GII | 0/2 | 5/5 | 3/5 | |||
These are river water samples except for DWTP 5 and 24 (ground water), DWTP 23 (reservoir) and DWTP 25 (lake). S= Source; T= Treated
The numerator contains the number of positive PCR reactions per number of PCR attempts (denominator)
3.3 Assessing PCR inhibition in water samples
To quantify the impact of PCR inhibition on count data for each DWTP sample, approximately 9, 1.8, and 0.9 molecules of the exogenous amplification control (EAC) were spiked into serial dilutions of concentrated DWTP samples. The number of positive PCR samples for each DWTP sample, spiked with EAC were scored and statistically compared to the positive control, which is the number of positive PCR samples of EAC pristine control (spiked in nuclease-free water). For each dilution, respectively, the pristine samples spiked with the EAC would be on average 5 positives out of 5 replicates, 8 positives out of 10 replicates, and 6 positives out of 10 replicates. If the sample is inhibited, the numbers were low for the first one or two dilutions, and as the sample is further diluted the counts started behaving similar to the pristine spiked controls. The number of positive PCR samples in the DWTP sample extracts (Table 3) did not behave similarly to the number of positive samples seen in the pristine spiked samples, clearly indicating that inhibition was a factor in all the samples. The effect was more evident in the first dilution of many of the DWTP samples.
Table 3. Determination of PCR Inhibition.
The number of PCR positives after spiking of DWTP samples with an external amplification control (EAC). Lower number of positives for the undiluted and the 1:5 dilution indicate the presence of inhibitors.
| DWTPa | Source Sample Positivesb | Treated Sample Positivesb | ||||
|---|---|---|---|---|---|---|
| Undiluted (n=5) |
1:5 (n= 10) |
1:10 (n=10) |
Undiluted (n=5) |
1:5 (n= 10) |
1:10 (n=10) |
|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 6 | 5 | 10 | 8 |
| 3 | 0 | 5 | 3 | 0 | 8 | 9 |
| 4 | 0 | 3 | 0 | – | – | – |
| 5 | 0 | 10 | 9 | – | – | – |
| 10 | 0 | 8 | 8 | 0 | 10 | 9 |
| 11 | 0 | 6 | 3 | 2 | 9 | 10 |
| 12 | 0 | 9 | 7 | 3 | 10 | 6 |
| 13 | 0 | 0 | 3 | – | – | – |
| 14 | 0 | 8 | 4 | – | – | – |
| 15 | 0 | 4 | 2 | 0 | 8 | 7 |
| 16 | 0 | 0 | 0 | 0 | 10 | 9 |
| 17 | 0 | 2 | 6 | – | – | – |
| 18 | 0 | 0 | 0 | 0 | 10 | 9 |
| 19 | 0 | 0 | 0 | – | – | – |
| 20 | 0 | 0 | 1 | 2 | 9 | 8 |
| 21 | 0 | 3 | 1 | – | – | – |
| 22 | 0 | 9 | 9 | – | – | – |
| 23 | 0 | 10 | 6 | 0 | 7 | 4 |
| 24 | 0 | 7 | 5 | – | – | – |
| 25 | 0 | 0 | 0 | 0 | 7 | 4 |
| 26 | 0 | 0 | 1 | – | – | – |
| 27 | 0 | 0 | 0 | – | – | – |
| 28 | 0 | 0 | 2 | – | – | – |
| 29 | 0 | 4 | 2 | – | – | – |
Identification number of each drinking water treatment plant in the study.
The three numbers of sample positives represent number of positive counts (out of 5,10, and 10 replicates for each dilution; with dilutions of water sample concentrates at undiluted, 1:5, and 1:10, respectively) via EAC qPCR. The pristine spiked samples produce an average of 5.00, 8.65, and 5.55 positive counts for undiluted, 1:5, and 1:10, respectively.
The 19 EAC pristine control PCR reactions were fully positive (average = 5.00) for undiluted, with an average of 8.65 positive reactions out of a possible 10 for the 1 to 5 dilution, and an average of 5.55 positive reactions (out of 10) for the 1 to 10 dilution. The EAC spike in DWTP source waters had an average of zero positives for the lowest dilution, 3.52 positive reactions for the 1 to 5 dilution, and 3.08 positive reactions for the 1 to 10 dilution. The EAC spike in treated DWTP samples had an average of one positive reaction for the lowest dilution, 8.91 positive reactions in the 1 to 5 dilution, and 6.92 positive reactions for the 1 to 10 dilution.
A non-parametric Kruskal-Wallis comparison of the EAC spiked in pristine control and EAC spiked in DWTP samples indicated a significant difference between their medians (Table 4). The EAC control was significantly different at all three dilutions from the source DWTP samples (Dunn’s p <0.05) and the lowest dilution of the treated DWTP samples (p <0.05). No significance, however, was observed between the 1 to 5 and 1 to 10 dilutions of the EAC-spiked control and treated DWTP samples. In addition, the inhibition in source and treated DWTP samples were different from each other for the 1 to 5 (p <0.05) and 1 to 10 dilutions (p <0.05). To confirm this, the MCMC and BEST statistics (see Materials and Methods) were used to estimate 95% Highest Density Interval (HDI) for the differences of the EIC spike concentration means for the following 12-paired source and treated DWTP samples: 2S/2T, 3S/3T, 10S/10T, 11S/11T, 12S/12T, 15S/15T, 16S/16T, 18S/18T, 20S/20T, 21S/21T, 23S/23T and 25S/25T. A Bayesian credible interval plot is shown in Supplemental Fig. A2. The 95% HDI for these comparisons was −935 to −48.9, indicating the differences were credible because the interval did not contain zero. A two-tailed t-test confirmed the BEST statistics indicating there was a difference in inhibition between source and treated samples (p-value of 0.041; mean group difference −657.8, t =−2.168).
Table 4. Statistical analysis of EAC spike in DWTP samples.
Statistical analysis of exogenic amplification control (EAC) spike in DWTP samples using Kruskal-Wallis and Dunn’s test. Significant differences indicate that DWTP samples did not perform similarly to pristine samples when both were spiked with EAC.
| Dilutiona | Average ± Std.Dev. (CV)b | Kruskal-Wallisc | Dunn’sc EAC Control vs. Source | Dunn’sc EAC Control vs. Treated | Dunn’sc Source vs. Treated | ||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Pristine Control | Source | Treated | |||||
| undiluted | 5.00±0.00 (0) |
0.00±0.00 (0) |
1.00±1.65 (165) |
<0.0001 | <0.05 | <0.05 | NS |
| 1 to 5 | 8.65±1.69 (19) |
3.52±3.79 (108) |
8.91±1.22 (14) |
<0.0001 | <0.05 | NSd | <0.05 |
| 1 to 10 | 5.55±2.59 (47) |
3.08±3.05 (99) |
6.92±2.94 (42) |
0.0014 | <0.05 | NSd | <0.05 |
The number of PCR reactions per dilution was 5, 10, and 10 for undiluted, 1 to 5 and 1 to 10
Averages represent average number of PCR-positives. CV is the percent coefficient of variation
p-values are shown below the Kruskal-Wallis and Dunn’s test columns
NS refers to non-significance
Taken together, these statistical analyses documented significant false negative rates for the DWTP samples, which was more pronounced in the source than the treated waters. Given that both RNA and DNA nucleases were either removed or inactivated in the DWTP concentrated samples, it is hypothesized that PCR inhibition was responsible for these false negatives. In samples where inhibition is thought to be occurring, the remedy often used is to dilute the sample until the effect of the inhibition is reduced. However, this approach may reduce the detection rate because dilutions used to mitigate inhibition result in the loss of the target signal. Alternatively, a spike-and-recovery approach has been used where a high concentration of a specific gene is spiked into the concentrated sample, followed by assessment of recovery by comparing cycle threshold (CT) values of the same spike in a pristine sample (Gibson et al., 2012; Green and Field, 2012; Rodriguez et al., 2012). This procedure assumes a constant PCR efficiency that is often challenging to reconcile with PCR inhibition in environmental samples. In this study, we elected to use Poisson statistics, which does not solely rely on PCR efficiency, but rather scores the presence or absence of target molecules in PCR reactions. Moreover, with this approach we can include environmental samples that are partially inhibited since they would still be considered positive by PCR.
Furthermore, to confirm that inhibition may be contributing to false negative results, whole genome amplification (WGA) was used on all samples negative in initial qPCR results. Whole genome amplification (WGA) has been used to increase target DNA/RNA concentrations prior to downstream molecular techniques (e.g., deep sequencing) and might be efficacious for the detection of virus in environmental samples. WGA has been used to increase target DNA/RNA concentrations prior to downstream molecular techniques (e.g., deep sequencing) and might be efficacious for the detection of virus in environmental samples. Of the samples we analyzed, 6 samples that were previously negative by qPCR were found to be positive by WGA (Supplemental Table A3).
3.4 Modeling the occurrence of human enteric viruses in DWTP samples
A Bayesian model using MCMC was developed to estimate virus concentrations (see Eq. 13) in PCR-positive samples (Model 1, Supplemental File 1). The recovery efficiency through the entire method was assumed to follow a beta distribution as described by Wu et al (2014) and was found to be 7.62 ± 1.31% for adenovirus. This recovery is similar or better to previous studies done in our lab (unpublished) and what has been seen in other studies using NanoCeram filtration (Francy et al., 2013).
Both the recovery efficiency and the individual sample inhibition tests were incorporated in the model to estimate error (ε) due to loss and PCR inhibition. Bayesian posterior means and 95% credible intervals were monitored for the model parameters as well for the final estimate of the mean virus concentration for each DWTP sample. Using a Bayesian credible interval (BCI) plot, virus concentrations are expressed as virus genome molecules/L for PCR-positive DWTP samples (Fig. 2). Convergence of Model 1 Markov chain simulations was confirmed by determining the Brooks-Gelman-Rubin (BGR) statistic for 3 different chains. This statistical technique identifies the model conditions where the variability of each chain simulation is approximately the same as the variability due to mixing chain simulations together. The Markov chain simulations were performed until the BGR ratio was less than 1.1 for the model parameters. An example of a BGR convergence profile for 5 human viruses is shown in Supplemental Figure A3. Sensitivity analysis of the μ parameter revealed that Model 1 was robust up to 3 orders of magnitude because the DICs were statistically similar to each other (Supplemental Table A4). The range of point-estimate concentrations was 3.52 (DWTP 20T, NoV GI) to 15,860 (DWTP 26S, EV) molecules per liter and the average concentrations of AdV, EV, NoV GI, NoV GII and PyV in PCR-positive source DWTP samples were 1,913 (n=7, CV=120%), 4,319 (n=4, CV=178%), 2,218 (n=4, CV=127%), 1,731 (n=7, CV=92%) and 539 (n=4, CV=81%) molecules per liter, respectively. The range of AdV and PyV concentrations observed here were similar to concentrations reported by Albinana-Gimenez et al (2006; 2009). In contrast, the treated DWTP samples contained very little virus: AdV (42.2, n=1), EV (10, n=2, CV=47%), NoV GI (40.7, n=2, CV=129%), NoV GII (102, n=1,), and PyV (n=0). Of the 5 virus types that were studied, source water samples had 26 PCR detections, while treated water only had 7 PCR detections. Of the 12 paired source and treated water samples, 3 paired samples had one more virus in the treated sample compared to the source sample. The detection of virus in some treated samples, but not in source samples may be related to the severe inhibition in those source samples, which shows the importance of measuring the inhibition. At a 95% confidence interval, the treated water was significantly different (95%CI =0.05274, 0.2448; p = 2.9 × 10−7) from the source water (null proportion = 0.4727).
Figure 2. Bayesian credible interval plots of virus concentration.
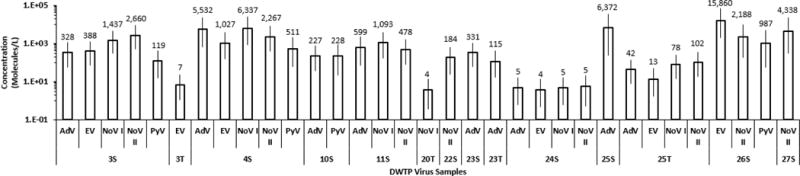
Bayesian credible interval plot of virus concentration estimates from PCR-positive DWTP water samples. AdV =adenovirus, EV=enterovirus, NoV I=Norovirus GI, NoV II=Norovirus GII, PyV =polyomavirus. Numbers represent DWTP identification. S and T suffixes represent source and treated water samples, respectively. Bars represent 95% credible intervals. The values above each bar is the concentration of virus genome molecules per liter.
The Bayesian model (“Model 1”) showed that there was more virus in the samples than was predicted by the PCR assay alone. This is because the Bayesian approach adjusts for recovery efficiency and PCR inhibition to improve the overall accuracy of the detection system. In Model 1, the approach included a parameter corresponding to individual inhibition test results for each DWTP sample, which is expensive and laborious. Therefore, a second approach (“Model 2”) was devised that includes a random variable to estimate PCR inhibition rather than relying on paired ITs for each sample. For this purpose, Eq. 8 was used to calculate ε from inhibition test experiments and equations 10 to 12 were used to estimate beta distribution shape parameters α1 and β1, which were 5.17 and 1.48 and 18.88 and 8.81 for source and treated DWTP samples, respectively. The accuracy of Model 2 was assessed for PCR-positive samples by comparison to Model 1 (Fig. 3). Agreement was observed around the axis of symmetry (the diagonal line in Fig. 3 has a slope of 1) for both source (R2 = 0.792) and treated (R2 = 0.955) DTWP samples. Furthermore, Bayesian model-to-data fit analysis of DWTP samples indicated that Model 2 (DIC 441.5) was indistinguishable from Model 1 (DIC 440.5).
Figure 3. Confirmation of Model 2 using a beta distribution.
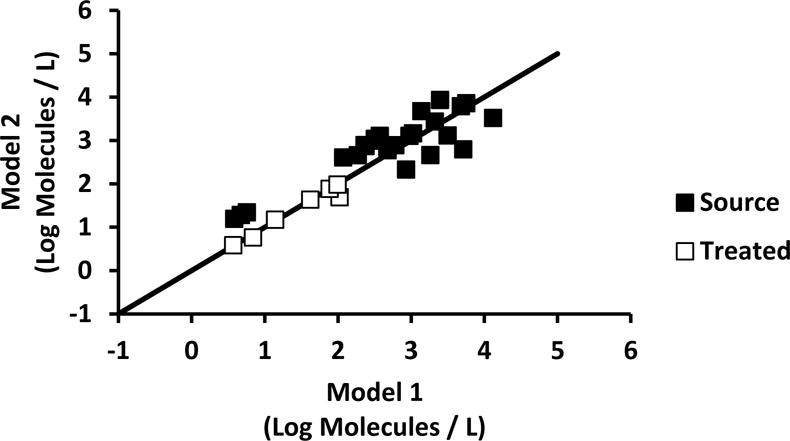
Confirmation of Model 2 using a beta distribution inferred from EAC PCR inhibition. Diagonal line represents axis of symmetry showing the agreement of Model 1 and Model 2 virus estimates. Model 1 used the EAC relative error paired to each DWTP sample. The log molecules represent virus genome molecules.
4 CONCLUSIONS
In this study, a combination of PCR and Bayesian statistics was successfully used to estimate the concentration of viruses in source and treated water samples obtained from a nationwide survey of 25 DWTPs. The models described in the study herein used performance analysis to quantify method recovery and a PCR control to quantify some uncertainties related to viral enumeration in water. Because many source water samples were found to be inhibitory to PCR, future studies should include mitigating the compounds that cause inhibition. However, when PCR inhibition is observed, a mechanism for quantifying the level of inhibition is important for better estimation of viral loads in water samples. Although all 25 source water concentrates from the sampled DWTPs were identified as inhibited samples, the Bayesian model improved estimates of virus levels by incorporating the uncertainties associated with inhibition and recovery. The combination of PCR and Bayesian modeling demonstrated that treated water contained significantly (p < 0.05) less virus than the source water. Treated water, even prior to chemical disinfection, showed a significant reduction of virus, which indicates that treatment methodologies used in the United States are generally helpful to reduce viral levels for the viruses we studied. The levels of targeted virus in source and the reduction of these levels in treated water may be useful for assessing reduction of potential public health risks via drinking water treatment. The observed variation and wide dissemination of multiple virus types in natural water environments underscores the need to characterize and model measurement uncertainties to estimate virus concentrations in source water environments.
Supplementary Material
Acknowledgments
The information in this document has been funded partially or wholly by the U.S. Environmental Protection Agency. The research described in this article has been funded in part by the U.S. Environmental Protection Agency through DW14922330 to the U.S. Geological Survey, and through programmatic support of the USGS Toxic Substances Hydrology Program and the USEPA’s Office of Research and Development, Office of Water, Office of Chemical Safety and Pollution Prevention, and Region 8. Information Collection Rule approval for the Phase II Questionnaire was granted under EPA ICR No. 2346.01, OMB Control No. 2080–0078. This document has been reviewed in accordance with USEPA policy and approved for publication. Approval does not signify that the contents reflect the views of the USEPA and mention of trade names or commercial products does not constitute endorsement or recommendation for use by USEPA. This document has also been reviewed in accordance with USGS policy and approved for publication. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. The authors would like to thank all participating drinking water treatment plants for their involvement in the project and for their assistance in collecting the samples.
Footnotes
DISCLAIMER
The authors declare no competing financial interest.
References
- Abbaszadegan M, Lechevallier M, Gerba C. Occurrence of viruses in US groundwaters. American Water Works Association Journal. 2003;95:107. [Google Scholar]
- Albinana-Gimenez N, Clemente-Casares P, Bofill-Mas S, Hundesa A, Ribas F, Girones R. Distribution of human polyomaviruses, adenoviruses, and hepatitis E virus in the environment and in a drinking-water treatment plant. Environ Sci Technol. 2006;40:7416–22. doi: 10.1021/es060343i. [DOI] [PubMed] [Google Scholar]
- Albinana-Gimenez N, Miagostovich MP, Calgua B, Huguet JM, Matia L, Girones R. Analysis of adenoviruses and polyomaviruses quantified by qPCR as indicators of water quality in source and drinking-water treatment plants. Water Res. 2009;43:2011–9. doi: 10.1016/j.watres.2009.01.025. [DOI] [PubMed] [Google Scholar]
- Batt AL, Furlong ET, Mash HE, Glassmeyer ST, Kolpin DW. The importance of quality control in validating concentrations of contaminants of emerging concern in source and treated drinking water samples. Sci Total Environ. 2017;579:1618–1628. doi: 10.1016/j.scitotenv.2016.02.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson R, Conerly OD, Sander W, Batt AL, Boone JS, Furlong ET, et al. Human health screening and public health significance of contaminants of emerging concern detected in public water supplies. Sci Total Environ. 2017;579:1643–1648. doi: 10.1016/j.scitotenv.2016.03.146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borchardt MA, Spencer SK, Kieke BA, Lambertini E, Loge FJ. Viruses in nondisinfected drinking water from municipal wells and community incidence of acute gastrointestinal illness. Environ Health Perspect. 2012;120:1272–9. doi: 10.1289/ehp.1104499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradbury KR, Borchardt MA, Gotkowitz M, Spencer SK, Zhu J, Hunt RJ. Source and transport of human enteric viruses in deep municipal water supply wells. Environ Sci Technol. 2013;47:4096–103. doi: 10.1021/es400509b. [DOI] [PubMed] [Google Scholar]
- Brinkman NE, Haffler TD, Cashdollar JL, Rhodes ER. Evaluation of methods using celite to concentrate norovirus, adenovirus and enterovirus from wastewater. J Virol Methods. 2013;193:140–6. doi: 10.1016/j.jviromet.2013.05.014. [DOI] [PubMed] [Google Scholar]
- Brunkard JM, Ailes E, Roberts VA, Hill V, Hilborn ED, Craun GF, et al. Surveillance for waterborne disease outbreaks associated with drinking water–United States, 2007–2008. MMWR Surveill Summ. 2011;60:38–68. [PubMed] [Google Scholar]
- Cashdollar JL, Brinkman NE, Griffin SM, McMinn BR, Rhodes ER, Varughese EA, et al. Development and evaluation of EPA method 1615 for detection of enterovirus and norovirus in water. Appl Environ Microbiol. 2013;79:215–23. doi: 10.1128/AEM.02270-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cashdollar JL, Wymer L. Methods for primary concentration of viruses from water samples: a review and meta-analysis of recent studies. J Appl Microbiol. 2013;115:1–11. doi: 10.1111/jam.12143. [DOI] [PubMed] [Google Scholar]
- CDC. Near Real-Time Surveillance of U.S. Norovirus Outbreaks by the Norovirus Sentinel Testing and Tracking Network — United States, August 2009–July 2015. Morbidity and Mortality Weekly Report (MMWR), 66. 2017 doi: 10.15585/mmwr.mm6607a1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi S, Jeliazkov I, Jiang SC. Lysogens and free viruses in fresh, brackish, and marine waters: a Bayesian analysis. FEMS Microbiol Ecol. 2009;69:243–54. doi: 10.1111/j.1574-6941.2009.00705.x. [DOI] [PubMed] [Google Scholar]
- Cochran WG. Estimation of bacterial densities by means of the “most probable number”. Biometrics. 1950;6:105–16. [PubMed] [Google Scholar]
- Conley JM, Evans N, Mash H, Rosenblum L, Schenck K, Glassmeyer S, et al. Comparison of in vitro estrogenic activity and estrogen concentrations in source and treated waters from 25 U.S. drinking water treatment plants. Sci Total Environ. 2017;579:1610–1617. doi: 10.1016/j.scitotenv.2016.02.093. [DOI] [PubMed] [Google Scholar]
- da Silva AK, Kavanagh OV, Estes MK, Elimelech M. Adsorption and aggregation properties of norovirus GI and GII virus-like particles demonstrate differing responses to solution chemistry. Environ Sci Technol. 2011;45:520–6. doi: 10.1021/es102368d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Silva AK, Le Guyader FS, Le Saux JC, Pommepuy M, Montgomery MA, Elimelech M. Norovirus removal and particle association in a waste stabilization pond. Environ Sci Technol. 2008;42:9151–7. doi: 10.1021/es802787v. [DOI] [PubMed] [Google Scholar]
- Ferguson AS, Layton AC, Mailloux BJ, Culligan PJ, Williams DE, Smartt AE, et al. Comparison of fecal indicators with pathogenic bacteria and rotavirus in groundwater. Sci Total Environ. 2012;431:314–22. doi: 10.1016/j.scitotenv.2012.05.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Follestad T, Jorstad TS, Erlandsen SE, Sandvik AK, Bones AM, Langaas MA. Bayesian hierarchical model for quantitative real-time PCR data. Stat Appl Genet Mol Biol. 2010;9 doi: 10.2202/1544-6115.1427. Article 3. [DOI] [PubMed] [Google Scholar]
- Fout GS, Brinkman NE, Cashdollar JL, Griffin SM, McMinn BR, Rhodes ER, et al. Method 1615: measurement of enterovirus and norovirus occurrence in water by culture and RT-qPCR. U.S. Environmental Protection Agency; Cincinnati, OH: 2010. [Google Scholar]
- Francy DS, Stelzer EA, Brady AM, Huitger C, Bushon RN, Ip HS, et al. Comparison of filters for concentrating microbial indicators and pathogens in lake water samples. Appl Environ Microbiol. 2013;79:1342–52. doi: 10.1128/AEM.03117-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furlong ET, Batt AL, Glassmeyer ST, Noriega MC, Kolpin DW, Mash H, et al. Nationwide reconnaissance of contaminants of emerging concern in source and treated drinking waters of the United States: Pharmaceuticals. Sci Total Environ. 2017;579:1629–1642. doi: 10.1016/j.scitotenv.2016.03.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gassilloud B, Gantzer C. Adhesion-aggregation and inactivation of poliovirus 1 in groundwater stored in a hydrophobic container. Appl Environ Microbiol. 2005;71:912–20. doi: 10.1128/AEM.71.2.912-920.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerba CP, Farrah SR, Goyal SM, Wallis C, Melnick JL. Concentration of enteroviruses from large volumes of tap water, treated sewage, and seawater. Appl Environ Microbiol. 1978;35:540–8. doi: 10.1128/aem.35.3.540-548.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson KE, Schwab KJ, Spencer SK, Borchardt MA. Measuring and mitigating inhibition during quantitative real time PCR analysis of viral nucleic acid extracts from large-volume environmental water samples. Water Res. 2012;46:4281–91. doi: 10.1016/j.watres.2012.04.030. [DOI] [PubMed] [Google Scholar]
- Glassmeyer ST, Furlong ET, Kolpin DW, Batt AL, Benson R, Boone JS, et al. Nationwide reconnaissance of contaminants of emerging concern in source and treated drinking waters of the United States. Sci Total Environ. 2017 doi: 10.1016/j.scitotenv.2016.03.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green HC, Field KG. Sensitive detection of sample interference in environmental qPCR. Water Res. 2012;46:3251–60. doi: 10.1016/j.watres.2012.03.041. [DOI] [PubMed] [Google Scholar]
- Gronewold AD, Borsuk ME, Wolpert RL, Reckhow KH. An assessment of fecal indicator bacteria-based water quality standards. Environ Sci Technol. 2008;42:4676–82. doi: 10.1021/es703144k. [DOI] [PubMed] [Google Scholar]
- Hata A, Katayama H, Furumai H. Organic substances interfere with reverse transcription-quantitative PCR-based virus detection in water samples. Appl Environ Microbiol. 2015;81:1585–93. doi: 10.1128/AEM.03082-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karim MR, Rhodes ER, Brinkman N, Wymer L, Fout GS. New electropositive filter for concentrating enteroviruses and noroviruses from large volumes of water. Appl Environ Microbiol. 2009;75:2393–9. doi: 10.1128/AEM.00922-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King DN, Donohue MJ, Vesper SJ, Villegas EN, Ware MW, Vogel ME, et al. Microbial pathogens in source and treated waters from drinking water treatment plants in the United States and implications for human health. Sci Total Environ. 2016;562:987–95. doi: 10.1016/j.scitotenv.2016.03.214. [DOI] [PubMed] [Google Scholar]
- Kitajima M, Iker BC, Pepper IL, Gerba CP. Relative abundance and treatment reduction of viruses during wastewater treatment processes–identification of potential viral indicators. Sci Total Environ. 2014;488–489:290–6. doi: 10.1016/j.scitotenv.2014.04.087. [DOI] [PubMed] [Google Scholar]
- Kolpin DW, Glassmeyer ST, Furlong ET. An introduction to joint research by the USEPA and USGS on contaminants of emerging concern in source and treated drinking waters of the United States. Sci Total Environ. 2017;579:1608–1609. doi: 10.1016/j.scitotenv.2016.03.052. [DOI] [PubMed] [Google Scholar]
- Kostich MS, Flick RW, Batt AL, Mash HE, Boone JS, Furlong ET, et al. Aquatic concentrations of chemical analytes compared to ecotoxicity estimates. Sci Total Environ. 2017;579:1649–1657. doi: 10.1016/j.scitotenv.2016.06.234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruschke JK. Bayesian estimation supersedes the t test. J Exp Psychol Gen. 2013;142:573–603. doi: 10.1037/a0029146. [DOI] [PubMed] [Google Scholar]
- Lambertini E, Spencer SK, Bertz PD, Loge FJ, Kieke BA, Borchardt MA. Concentration of enteroviruses, adenoviruses, and noroviruses from drinking water by use of glass wool filters. Appl Environ Microbiol. 2008;74:2990–6. doi: 10.1128/AEM.02246-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang L, Goh SG, Vergara GG, Fang HM, Rezaeinejad S, Chang SY, et al. Alternative fecal indicators and their empirical relationships with enteric viruses, Salmonella enterica, and Pseudomonas aeruginosa in surface waters of a tropical urban catchment. Appl Environ Microbiol. 2015;81:850–60. doi: 10.1128/AEM.02670-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrady MH. The Numerical Interpretation of Fermentation-Tube Results. J Infect Dis. 1915;17:183–212. [Google Scholar]
- Okoh AI, Sibanda T, Gusha SS. Inadequately treated wastewater as a source of human enteric viruses in the environment. Int J Environ Res Public Health. 2010;7:2620–37. doi: 10.3390/ijerph7062620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parshionikar SU, Willian-True S, Fout GS, Robbins DE, Seys SA, Cassady JD, et al. Waterborne outbreak of gastroenteritis associated with a norovirus. Appl Environ Microbiol. 2003;69:5263–8. doi: 10.1128/AEM.69.9.5263-5268.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhodes ER, Hamilton DW, See MJ, Wymer L. Evaluation of hollow-fiber ultrafiltration primary concentration of pathogens and secondary concentration of viruses from water. J Virol Methods. 2011;176:38–45. doi: 10.1016/j.jviromet.2011.05.031. [DOI] [PubMed] [Google Scholar]
- Rodriguez RA, Thie L, Gibbons CD, Sobsey MD. Reducing the effects of environmental inhibition in quantitative real-time PCR detection of adenovirus and norovirus in recreational seawaters. J Virol Methods. 2012;181:43–50. doi: 10.1016/j.jviromet.2012.01.009. [DOI] [PubMed] [Google Scholar]
- Sivaganesan M, Seifring S, Varma M, Haugland RA, Shanks OC. A Bayesian method for calculating real-time quantitative PCR calibration curves using absolute plasmid DNA standards. BMC Bioinformatics. 2008;9:120. doi: 10.1186/1471-2105-9-120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobsey MD, Jones BL. Concentration of poliovirus from tap water using positively charged microporous filters. Appl Environ Microbiol. 1979;37:588–95. doi: 10.1128/aem.37.3.588-595.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- USEPA. USEPA Drinking Water Contaminant Candidate List - Draft 80. 2015 FR6076. [Google Scholar]
- Williams MS, Ebel ED. Methods for fitting a parametric probability distribution to most probable number data. Int J Food Microbiol. 2012;157:251–8. doi: 10.1016/j.ijfoodmicro.2012.05.014. [DOI] [PubMed] [Google Scholar]
- Wu J, Gronewold AD, Rodriguez RA, Stewart JR, Sobsey MD. Integrating quantitative PCR and Bayesian statistics in quantifying human adenoviruses in small volumes of source water. Sci Total Environ. 2014;470–471:255–62. doi: 10.1016/j.scitotenv.2013.09.026. [DOI] [PubMed] [Google Scholar]
- Wu J, Simmons OD, 3rd, Sobsey MD. Uncertainty analysis of the recovery of hollow-fiber ultrafiltration for multiple microbe classes from water: a Bayesian approach. J Microbiol Methods. 2013;93:161–7. doi: 10.1016/j.mimet.2013.03.005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


