Photoacoustic Source Detection and Reflection Artifact Removal Enabled by Deep Learning

Abstract

Interventional applications of photoacoustic imaging typically require visualization of point-like targets, such as the small, circular, cross-sectional tips of needles, catheters, or brachytherapy seeds. When these point-like targets are imaged in the presence of highly echogenic structures, the resulting photoacoustic wave creates a reflection artifact that may appear as a true signal. We propose to use deep learning techniques to identify these types of noise artifacts for removal in experimental photoacoustic data. To achieve this goal, a convolutional neural network (CNN) was first trained to locate and classify sources and artifacts in pre-beamformed data simulated with k-Wave. Simulations initially contained one source and one artifact with various medium sound speeds and 2-D target locations. Based on 3,468 test images, we achieved a 100% success rate in classifying both sources and artifacts. After adding noise to assess potential performance in more realistic imaging environments, we achieved at least 98% success rates for channel signal-to-noise ratios (SNRs) of −9dB or greater, with a severe decrease in performance below −21dB channel SNR. We then explored training with multiple sources and two types of acoustic receivers and achieved similar success with detecting point sources. Networks trained with simulated data were then transferred to experimental waterbath and phantom data with 100% and 96.67% source classification accuracy, respectively (particularly when networks were tested at depths that were included during training). The corresponding mean ± one standard deviation of the point source location error was 0.40 ± 0.22 mm and 0.38 ± 0.25 mm for waterbath and phantom experimental data, respectively, which provides some indication of the resolution limits of our new CNN-based imaging system. We finally show that the CNN-based information can be displayed in a novel artifact-free image format, enabling us to effectively remove reflection artifacts from photoacoustic images, which is not possible with traditional geometry-based beamforming.

I. Introduction

Photoacoustic imaging has promising potential to detect anatomical features or metal implants in the human body [1]–[3]. It is implemented by transmitting pulsed laser light, which is preferentially absorbed by structures with higher optical absorption than their surroundings. This absorption causes thermal expansion, which then generates a sound wave that is detected with conventional ultrasound transducers. Potential uses of photoacoustic imaging and its microwave-induced counterpart (i.e., thermoacoustic imaging) include cancer detection and treatment [3]–[6], monitoring blood vessel flow [7] and drug delivery [8], detecting metal implants [4], [6], and guiding surgeries [6], [9]–[15].

The many potential clinical uses of photoacoustic imaging are hampered by strong acoustic reflections from hyperechoic structures. These reflections are not considered by traditional beamformers which use a time-of-flight measurement to create images. As a result, reflections appear as signals that are mapped to incorrect locations in the beamformed image. The surrounding acoustic environment additionally introduces inconsistencies, such as sound speed, density, or attenuation variations, that make acoustic wave propagation difficult to model. Although photoacoustic imaging has not yet reached widespread clinical utility (partly because of the presence of these confusing reflection artifacts), the outstanding challenges with reflection artifacts would be highly problematic for the clinicians reading the images when relying on existing beamforming methods. These clinicians would be required to make decisions based on potentially incorrect information, which is particularly true in brachytherapy for treatment of prostate cancers [4], [16] as well as in minimally invasive surgeries where critical structures may be hidden by bone [9], [17].

Several alternative signal processing methods have been implemented to reduce the effect of artifacts in photoacoustic images and enhance signal quality, such as techniques using singular value decomposition [18] and short-lag spatial coherence [6], [19], [20]. However, these methods exhibit limited potential to remove artifacts caused by bright acoustic reflections. A recent technique called photoacoustic-guided focused ultrasound (PAFUSion) [21] differs from conventional photoacoustic artifact reduction approaches because it uses ultrasound to mimic wavefields produced by photoacoustic sources in order to identify reflection artifacts for removal. A similar approach that uses plane waves rather than focused waves was similarly implemented [22]. These two methods assume identical acoustic reception pathways, which may not always be true. In addition, the requirement for matched ultrasound and photoacoustic images in a real-time environment severely reduces potential frame rates in the presence of tissue motion caused by the beating heart or vessel pulsation. This motion might also introduce error into the artifact correction algorithm. Methods to reduce reflection artifacts based on their unique frequency spectra have additionally been proposed [23], [24], but these methods similarly rely on beamforming models that ignore potential inter- and intra-patient variability when describing the acoustic propagation medium.

We are proposing to address these outstanding challenges by exploring deep learning with convolutional neural networks (CNNs) [25]–[29]. CNNs have experienced a significant rise in popularity because of their success with modeling problems that contain a high degree of complexity in areas such as speech [30], language [31], and image [25] processing. A similar level of complexity exists when describing the many patient-specific variables that impact the quality of photoacoustic signal beamforming. Despite the recent trend toward CNNs, neural networks have been around for much longer. For example, Nikoonahad and Liv [32] used a neural network to estimate beamforming delay functions in order to reduce artifacts in ultrasound images arising from speed of sound errors. Although this approach [32] is among the first to apply neural networks to beamforming, it does not effectively address the multipath reflection artifacts which arise in photoacoustic images.

Reiter and Bell [33] demonstrated that a deep neural network can be applied to learn spatial impulse responses and locate photoacoustic point sources with an average positional accuracy of 0.28 mm and 0.37 mm in the depth and lateral image dimensions, respectively. Expanding on this previous work, we propose the following key contributions which build on results presented in our associated conference papers [34], [35]. First, we develop a deep neural network capable of locating both sources and artifacts in the raw photoacoustic channel data with the goal of removing artifacts in the presence of multiple levels of channel noise and multiple photoacoustic sources. Second, we remove artifacts from the photoacoustic channel data based on the information provided by the CNN. Finally, we explore how well our network, which is trained with only simulated data, locates sources and artifacts in real experimental data with no additional training, particularly in the presence of one and multiple point sources.

II. Methods

A. Simulating Sources and Artifacts for Training

1) Initial Simulations

Simulations are a powerful tool in the context of deep learning, as they allow us to generate new application-specific data to train our algorithm without the need to expensively gather and hand-label experimental data. We simulated photoacoustic channel data with the k-Wave simulation software package [36]. In our initial simulations, each image contained one 0.1 mm-diameter point source and one artifact. Although reflection artifacts can be simulated in k-Wave, the amplitudes of the reflections are significantly lower than that of the source, which differs from our experimental observations. To overcome this discrepancy, a real source signal was shifted deeper into our simulated image to mimic a reflection artifact, which is viable because reflection artifacts tend to have wavefront shapes that are characteristic of signals at shallower depths. Thus, by moving a wavefront to a deeper location in the image, we can effectively simulate a reflection artifact. The range and increment size of our simulation variables for this initial data set are listed in Table I. Our initial dataset consisted of a total of 17,340 simulated images with 80% used for training and 20% used for testing. This dataset was created using a range of sound speeds, and this range was included to ensure that the trained networks would generalize to multiple possible sound speeds in experimental data.

TABLE I.

Range and Increment Size of Simulation Variables

Case	Parameter	Min	Max	Increment
Initial (no noise)	Depth Position (mm)	5	25	5
	Lateral Position (mm)	5	30	5
Initial (with noise)	Depth Position (mm)	5	25	5
	Lateral Position (mm)	5	30	5
	Channel SNR (dB)	−21	−3	6
Lateral Shift*	Depth Position (mm)	5	25	5
	Lateral Position (mm)	7.5	27.5	5
Depth Shift*	Depth Position (mm)	7.5	22.5	5
	Lateral Position (mm)	5	30	5
Depth & Lateral Shift*	Depth Position (mm)	7.5	22.5	5
	Lateral Position (mm)	7.5	27.5	5
Noiseless, Fine	Depth Position (mm)	5	25	0.25
	Lateral Position (mm)	5	30	0.25
Multiple Sources, Multiple Noise Levels	Number of Sources	1	10	1
	Depth Position (mm)	5	25	0.25
	Lateral Position (mm)	5	30	0.25
	Channel SNR (dB)	−5	2	random
	Object Intensity (multiplier)	0.75	1.1	random
All Cases	Speed of Sound (m/s)	1440	1640	6

^*indicates datasets that were used for testing only

2) Incorporating Noise

Most experimental channel data contain some level of background noise. Thus, to study CNN performance in the presence of noise, our initial dataset containing reflection artifacts was replicated four times to create four additional datasets with white-Gaussian, background noise (which is expected to simulate experimental channel noise). The added channel noise corresponded to channel signal-to-noise ratios (SNRs) of −3dB, −9dB, −15dB, and −21dB SNR, as listed in Table I and depicted (for the same source and artifact combination) in Fig. 1. Each of these new datasets were then used independently for training (80% of images) and testing (20% of images).

Fig. 1.

The channel data noise levels used in this work: (a) noiseless, (b) −3dB, (c) −9dB, (d) −15dB, and (e) −21dB SNR. Gaussian noise was added to simulate the noise floor for a typical imaging system. Note that as noise level increases beyond −9dB channel SNR, it becomes more difficult to see the wavefronts.

3) Testing With Previously Unseen Locations

Our initial networks were trained using source and artifact locations at 5 mm increments. Thus, in order to test how well the trained networks adapted to signal locations that were not encountered during training, three additional noiseless datasets were created by: (1) shifting the initial lateral positions by 2.5 mm to the right while keeping the initial depth spacing, (2) shifting the initial depth positions by 2.5 mm while keeping the initial lateral spacing, and (3) shifting the initial lateral and depth dimensions by 2.5 mm each. The placement of all shifted points relative to the initial point locations is depicted in Fig. 2. These shifted datasets were only used for testing with the previously trained noiseless network, as indicated in Table I.

Fig. 2.

Diagram showing the location of simulated source signals used to create training and testing datasets. A network was trained using the red points indicated as initial, while the blue, magenta, and green points were used to test against the initial trained network.

4) Source Location Spacing

Building on our initial simulations, which were tailored to clinical scenarios with a high probability of structures appearing at discrete 5 mm spacings (e.g., photoacoustic imaging of brachytherapy seeds [4]), a new set of simulated point sources was generated with more finely spaced points. The depth and lateral increment was reduced from 5 mm to 0.25 mm, as listed in Table I. While the initial dataset contained 1,080 sources, this new dataset contained 278,154 sources. Because of this larger number of sources, point target locations were randomly selected from all possible source locations, while artifact locations were randomly selected from all possible points located less than 10 mm from the source. A total of 19,992 noiseless channel data images were synthesized, and a new network was trained (80% of images) and tested (20% of images).

5) Shifting Artifacts

When generating reflection artifacts, two different methods were compared. In the first method, the artifact wavefront was shifted 5 mm deeper into this image. This 5 mm distance was chosen because it corresponds to the spacing of brachytherapy seeds [4], which motivated this work. In the second method, the shift was more precisely calculated to equal to the Euclidean distance, Δ, between the source and artifact, as described by the equation:

$$|\mathrm{\Delta }|=\sqrt{{(z_s-z_r)}^2+{(x_s-x_r)}^2}$$ (1)

where (x_s, z_s) are the 2D spatial coordinates of the source location and (x_r, z_r ) are the 2D spatial coordinates of the physical reflector location, as illustrated in Fig. 4. A similar shifting method was implemented to simulate artifacts in ultrasound channel data [37]. To compare our two shifting methods, two networks were trained with the noiseless photoacoustic data containing finely spaced sources noted in Table I. One of the two shifting methods were implemented for each network.

Fig. 4.

Schematic diagram showing a geometry that causes reflection artifacts. The arrows indicate the direction of wave propagation for the imaged reflection artifact.

6) Multiple Sources

To test the proposed method with more complex images containing more than one photoacoustic source, we created 10 additional datasets each with a fixed number of sources that ranged from 1 to 10, with example images shown in Fig. 3. A summary of the parameters used for this training and testing are listed in Table I. One major difference between this network and previous networks is that multiple noise levels and multiple source and artifact intensities were included in each training data set. There was no fixed increment size for these two parameters, and these parameters were instead randomly chosen from the range of possible values, as indicated in Table I. To compare performance, 10 separate networks were trained, one for each fixed number sources. The 10 trained networks were then tested with the test set reserved for each fixed number of sources (i.e., 20% of the data generated for each fixed number of sources).

Fig. 3.

The channel data for multiple sources: (a) 2, (b) 4, (c) 6, (d) 8, and (e) 10 sources and reflectors. Note that as number of sources increases, the images become increasingly complex.

7) Modeling a Linear Discrete Receiver

We additionally compared network performance with two different receiver models. First, the acoustic receiver was modeled as a continuous array of elements, which was the method used for all networks described in Sections II-A1 to II-A6. The default k-Wave setting for these networks varies the sampling frequency as a function of the speed of sound in the medium, which is not realistic when transferring these networks to experimental data [35]. Therefore, we also modeled a receiver with a nonzero kerf and a fixed sampling frequency. In both cases, the element height was limited to a single point. The network for each receiver model was trained with one source and one artifact over multiple noise levels and object intensities, as described for the multisource dataset summarized in Table I. The parameters for each acoustic receiver model are summarized in Table II.

TABLE II.

Simulated Acoustic Receiver Parameters

Parameter	Continuous	Discrete
Kerf (mm)	0	0.06
Element Width (mm)	0.1	0.24
Sampling Frequency (MHz)	48 – 54.6	40

B. Network Architecture and Evaluation Parameters

We preliminarily tested the discrete receiver dataset with a standard histogram of oriented gradients features and classified the results with an ensemble of weak learners [38]. Although we achieved 100% classification accuracy, we obtained 4.82 false positives per image (i.e., misclassification and missed detection rates of 229–253%), which further motivates our exploration of a deep learning approach rather then a more standard classifier machine learning approach. Based on this motivation, independent CNNs corresponding to the various cases listed in Tables I & II were trained with the Faster-RCNN algorithm, which is composed of two modules [28]. The first module was a deep fully convolutional network consisting of the VGG16 network architecture [29] and a Region Proposal Network [28]. The second module was a Fast R-CNN detector [27] that used the proposed regions. Both modules were implemented in the Caffe framework [39], and together they form a single unified network for detecting wavefronts in channel data and classifying them as sources or artifacts, as summarized in Fig. 5.

Fig. 5.

Summary of our network architecture.

The unified network illustrated in Fig. 5 was initialized with pre-trained ImageNet weights and trained for 100,000 iterations on the portion of the simulated data reserved for training. The PC used for this process was an Intel Core i5-6600k CPU with 32GB of RAM alongside an Nvidia GTX Titan X (Pascal) with 12GB of VRAM and a core clock speed of 1531MHz. With this machine, we trained the networks at a rate of 0.22 seconds per iteration and tested them at a rate of 0.068 seconds per image, which translates to 14.7 frames per second when the trained network is implemented in real time.

The Faster R-CNN outputs consisted of the classifier prediction, corresponding confidence score (a number between 0 and 1), and the bounding box image coordinates for each detection, as illustrated in Fig. 5. These detections were evaluated according to their classification results as well as their depth, lateral, and total (i.e. Euclidean) positional errors. To determine classification and bounding box accuracy, each simulated image was labeled with the classes of the objects in the image (i.e., source or artifact), as well as the bounding box corresponding to the known locations of these objects. The bounding box for each object measured approximately 8 mm in the lateral dimension by 2 mm in the depth dimension, and it was centered on the peak of the source or artifact wavefront.

Detections were classified as correct if the intersect-over-union (IoU) of the ground truth and detection bounding box was greater than 0.5 and their score was greater than an optimal value. This optimal value for each class and each network was found by first defining a line with a slope equal to the number of negative detections divided by the number of positive detections, where positive detections were defined as detections with a IoU greater than 0.5. This line was shifted from the ideal operating point (true positive rate of 1 and false positive rate of 0) down and to the right until it intersected the receiver operating characteristics (ROC) curve. The point at which this line first intersected the ROC curve was determined to be the optimal score threshold. The ROC curve was created by varying the confidence threshold and plotting the rate of true and false positives at each tested threshold. The ROC curve indicates the quality of object detections made by the network. Misclassifications were defined to be a source detected as an artifact or an artifact detected as a source, and missed detections were defined as a source or artifact being detected as neither a source nor artifact.

In addition to classification, misclassification, and missed detection rate, we also considered precision, recall, and area-under-the-curve (AUC). Precision is defined as the number of correct positive detections over the total number of positive detections, and recall is defined as the number of correct positive detections over the total number of objects which should have been detected (note that recall and classification rate are equivalent in this work). AUC was defined as the total area under the ROC curve.

C. Transfer Learning to Experimental Data

To determine the feasibility of training with simulated data for the eventual identification and removal of artifacts in real data acquired from patients in a clinical setting, we tested our networks on two types of experimental data. We consider training with simulated data and transferring the trained network to experimental data to to be a form of transfer learning. Fig. 6 shows a schematic diagram and corresponding photograph of the first experimental setup. A 1 mm core diameter optical fiber was inserted in a needle and placed in the imaging plane between the transducer and a sheet of acrylic. This setup was placed in a waterbath. The optical fiber was coupled to a Quantel (Bozeman, MT) Brilliant laser operating at 1064 nm and 2 mJ per pulse. When fired, the laser light from the fiber tip creates a photoacoustic signal in the water which propagates in all directions. This signal travels both directly to the transducer, creating the source signal, and to the acrylic which reflects the signal to the transducer, creating the reflection artifact. The acrylic plate represents a highly echoic structure in the body such as bone.

Fig. 6.

(a) Schematic diagram and (b) photograph of the experimental waterbath setup.

Seventeen channel data images were captured, each after changing the location of the transducer while maintaining the distance between the optical fiber tip and the acrylic plate. The transducer was attached to a Sawyer Robot (Rethink Robotics, Boston, MA), and it was translated in 5 mm increments in the depth dimension for 5–6 depths and 10 mm in the lateral dimension for 3 lateral positions. An Alpinion (Bothell, WA) E-Cube 12R scanner connected to an L3–8 linear array ultrasound transducer was used to acquire channel data during these experiments. Six of the previously described networks trained with the finely spaced sources were used to test the experimental waterbath data. The differences between these six networks included the noise levels, artifact shifting method, and receiver designs used during training, as described in more detail in Section III-D.

The second experiment was performed with a phantom containing 4 brachytherapy seeds and 2 air pockets as depicted in Fig. 7. This phantom was previously described in [16]. In order to generate a photoacoustic signal, the combination of brachytherapy seeds noted in Table III were illuminated with multiple separate optical fibers that were bundled together and connected to a single input source. The input end of the fibers was coupled to an Opotek (Carlsbad, CA) Phocus Mobile laser operating at 1064nm. The signals from the illuminated brachytherapy seeds were considered to be the true sources and all other signals were considered to be artifacts, including reflections from the air pockets and brachytherapy seeds. Fifteen images were captured in total by illuminating different combinations of the brachytherapy seeds and changing the orientation of the transducer as well as orientation of the phantom, as detailed in Table III. The phantom was imaged with an Alpinion (Bothell, WA) E-Cube 12R scanner connected to an L3-8 linear array ultrasound transducer which was held in place by a Sawyer Robot (Rethink Robotics, Boston, MA).

Fig. 7.

(a) Schematic diagram of the phantom with brachytherapy seeds labeled 1 through 4 and the two possible imaging sides for transducer placement noted as Side 1 and Side 2. Although the phantom extends beyond the dashed line, this region of the phantom was not included in the photoacoustic image. (b) Photograph of one version of the experimental setup for the phantom experiment, with the parameters for this setup noted as Image 3 in Table III.

TABLE III.

Brachytherapy Phantom Image Parameters

Image	Seeds Illuminated Indicies*	Transducer Orientation	Imaging Side*
1	1, 2	as shown	side 1
2	1, 2	flipped	side 1
3	1, 3	as shown	side 1
4	1, 3	flipped	side 1
5	3, 4	as shown	side 1
6	3, 4	flipped	side 1
7	1, 3, 4	as shown	side 1
8	1, 3, 4	as shown	side 1
9	1, 3, 4	flipped	side 1
10	3, 4	as shown	side 2
11	3, 4	flipped	side 2
12	1, 2, 3	as shown	side 1
13	1, 2, 3	flipped	side 1
14	1, 2, 3, 4	as shown	side 1
15	1, 2, 3, 4	flipped	side 1

^*The four seed number indicies and the two phantom imaging sides are indicated in Fig. 7(a).

When classifying sources and artifacts in channel data from the waterbath and phantom experiments, the confidence threshold was equivalent to the confidence threshold determined with simulated data.

D. Artifact Removal

After obtaining detection and classification results for the simulated and experimental data, three methods for artifact removal were tested. The first two methods replaced the pixels inside the detection bounding box in the channel data with either the average pixel value of the entire image or noise corresponding to the noise level of the image. The third method used the network outputs to display only the locations of the detected source signals in the image. Source detections were visualized as circles centered at the center of the detection bounding box with a radius corresponding to 2σ, where σ is the standard deviation of location errors found when testing the network.

For the first two artifact removal methods, delay-and-sum (DAS) beamforming was implemented replacing pixels in regions identified as artifacts with either noise or the average value. To implement DAS beamforming, the received channel data was delayed based on the distance between the receive element and a point in the image space. The delayed data was then summed across all receive elements to achieve a single scanline in a DAS photoacoustic image.

III. Results

A. Classification Accuracy

1) Classification Accuracy in the Presence of Channel Noise

The classification results from the initial noiseless data and the four noisy datasets are shown in Fig. 8(a). The results of testing show that the networks classified signals with greater than 98% accuracy when the noise level was less than −9dB SNR. For the −15dB SNR dataset, the classification accuracy fell to 82% accuracy, while classification accuracy dropped even further to 4.35% with −21dB channel SNR. Fig. 8(a) also shows that the rate of misclassification is less than 0.5% for all datasets. It is additionally observed that the rate of missed source and artifact detections increases greatly for higher noise levels (i.e., less than −9dB SNR).

Fig. 8.

(a) Classification results in the presence of various noise levels. The dark and medium blue bars show the accuracy of source and artifact detections, respectively. The light blue and green bars show the misclassification rate for sources and artifacts, respectively. The dark and light yellow bars show the missed detection rate for sources and artifacts, respectively. Corresponding (b) source and (c) artifact ROC curves demonstrate that performance degrades as channel SNR decreases.

Fig. 8(b) and (c) depict the ROC curves for the sources and artifacts, respectively. The results of each dataset is indicated by the different colored lines with true positive rate on the vertical axis and false positive rate on the horizontal axis. As noise increases the curves diverge from the ideal operating point.

2) Classification Accuracy for Previously Unseen Locations

Fig. 9 shows the results from testing with the shifted datasets, which were included to quantify performance when the network is presented with sources in previously unseen locations. The laterally shifted points yielded a classification accuracy of 100% for both sources and artifacts and a misclassification rate of 0%, which is identical performance to that of the initial, noiseless dataset. However, for the two trials that included depth shifts, the classification accuracy was 0%, indicating that the network fails when presented with depths that were not included during training. This result informs us that our network is not capable of generalizing to these untrained locations, however, because the network was trained with simulated data, we can remedy this limitation by simulating more points with finer depth spacing in order to achieve consistent classification performance across all depths, which is the primary purpose of the finely spaced network.

Fig. 9.

(a) Classification results for the shifted datasets after testing with networks that were trained with our initial noiseless dataset. The dark and medium blue bars show the accuracy of source and artifact detections, respectively. The light blue and green bars show the misclassification rate for sources and artifacts, respectively. The dark and light yellow bars show the missed detection rate for sources and artifacts, respectively. These results and the corresponding (b) source and (c) artifact ROC curves indicate poor generalization to depth positions that were not included during training.

3) Classification Accuracy With Finer Source Spacings

Results from the finely spaced datasets are shown in Fig. 10. The network trained with finely spaced sources and 5 mm artifact shifts behaved similarly to the network trained with the initial noiseless dataset in terms of source and artifact classification accuray, which measured 99.7% and 99.7%, respectively. The network derived from finely spaced, Euclidean-based shifting produced similar classification accuracy, but the misclassification rate increased to 10%. However, this network with Euclidean shifting implemented contains several special cases where the artifact and sources overlap, as shown in Fig. 11, and these special cases are not present when shifting artifacts by 5 mm only. The presence of overlapping wavefronts causes a significant overlap between source detections and the artifact ground truth bounding boxes. Similarly, artifact detections overlap with the source ground truth bounding boxes. These cases are incorrectly defined as misclassifications. Thus, when these overlapping sources and artifacts are excluded from the misclassification calculations, we obtain misclassification rates comparable to that of the finely spaced, 5 mm shifted network and performance is consistent across both shifting methods (5 mm and Euclidean), as shown in Fig. 10.

Fig. 10.

(a) Classification results for finely spaced datasets. The dark and medium blue bars show the accuracy of source and artifact detections, respectively. The light blue and turquoise bars show the misclassification rate for sources and artifacts, respectively. The dark green and light green bars show the missed detection rate for sources and artifacts, respectively. The dark yellow and light yellow bars show the misclassification rate for sources and artifacts, respectively, after removing overlapping sources and artifacts from calculations. These finely spaced networks exhibit performance levels comparable to the initial noiseless network, but can now correctly classify at a wider range of depths, corresponding (b) source and (c) artifact ROC curves are consistent with this observation.

Fig. 11.

Example of the overlapping of source and artifact wavefronts that occurs when shifting the artifact by the Euclidean distance.

The results for precision, recall, and AUC for the noiseless, noisy, and finely spaced datasets are reported in the first seven rows of Table IV. For noise levels below −9dB SNR, precision, recall, and AUC all exceed 0.97. For the −15dB SNR dataset precision, recall, and AUC drop to 0.76, 0.82, and 0.93, respectively, while for the −21dB SNR dataset precision, recall, and AUC drop even further to 0.64, 0.04, and 0.25, respectively. For the finely spaced datasets, precision, recall, and AUC exceed 0.99.

TABLE IV.

Summary of Classification Performance for Simulated Data

Dataset*	Source			Artifact
	Prec.	Recall	AUC	Prec.	Recall	AUC
Initial, Noiseless	1.000	1.000	1.000	1.000	1.000	1.000
−3dB SNR	1.000	1.000	1.000	1.000	1.000	1.000
−9dB SNR	1.000	0.993	0.999	0.999	0.974	0.995
−15dB SNR	0.885	0.885	0.976	0.766	0.823	0.964
−21dB SNR	0.707	0.085	0.831	0.647	0.044	0.804
Finely Spaced 5 mm shift	0.998	0.997	1.000	0.997	0.997	.999
Euclidean shift	0.999	0.997	1.000	0.990	0.992	0.984
Multiple Noise Levels 1 source	0.8721	0.9713	0.9018	0.9619	0.8618	0.9471
2 sources	0.9805	0.9723	0.9868	0.9746	0.9239	0.9837
3 sources	0.9876	0.9721	0.9869	0.9830	0.8756	0.9880
4 sources	0.9906	0.9636	0.9867	0.9847	0.8314	0.9890
5 sources	0.9914	0.9578	0.9856	0.9892	0.7852	0.9888
6 sources	0.9922	0.9433	0.9842	0.9880	0.7600	0.9871
7 sources	0.9900	0.9377	0.9851	0.9910	0.7157	0.9870
8 sources	0.9960	0.9282	0.9915	0.9485	0.6867	0.9836
9 sources	0.9935	0.9281	0.9857	0.9859	0.6868	0.9863
10 sources	0.9944	0.9146	0.9867	0.9840	0.6325	0.9864
Discrete Receiver 1 source	0.8939	0.9160	0.9167	0.8818	0.9316	0.9386

^*A11 datasets used the continuous receiver unless otherwise stated.

4) Classification Accuracy for Multiple Sources

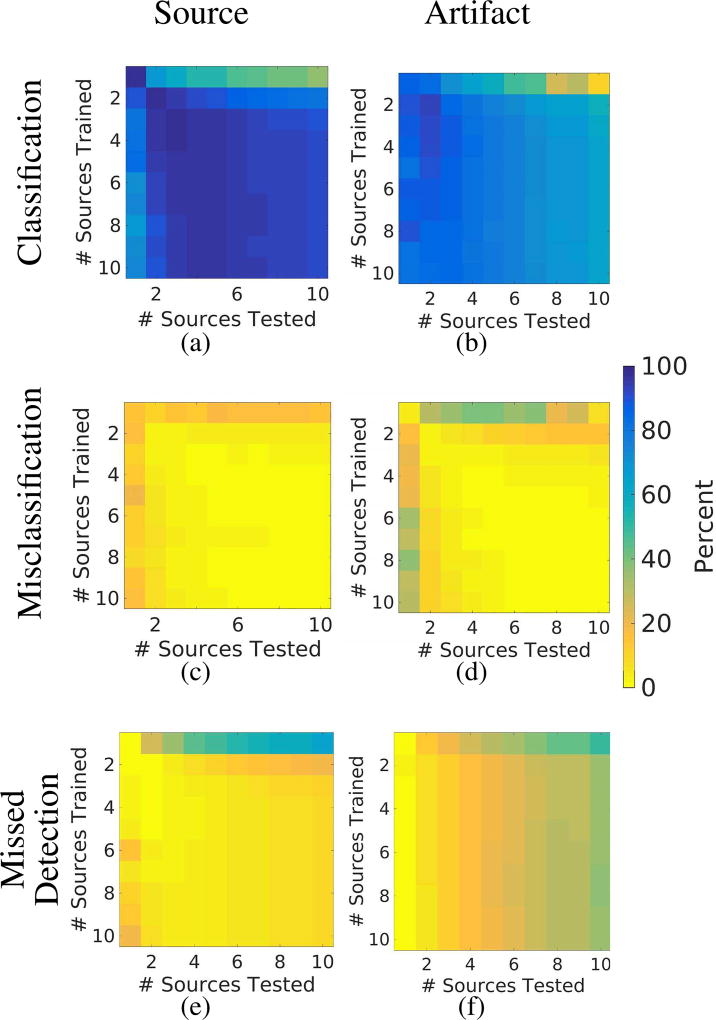
Fig. 12 shows source and artifact classification, misclassification, and missed detection rates for networks which were trained with 1 to 10 sources where the vertical axis indicates the number of sources in the datasets used for training the networks and the horizontal axis indicates the number of sources in the dataset used for testing each network. For example, the first row in Fig. 12(a) indicates the source classification rate for a network trained with only one source and tested against datasets containing 1 to 10 sources. In the first row of Fig. 12(a), the network suffers performance losses when tested with more sources than the network was trained to detect (i.e., 97.13% of sources were detected in the one source dataset and less than 68.00% of sources were detected in the multiple source datasets). For the remaining rows, the performance generally decreases moving left to right across columns (values ranging from 90.06% to 97.23% for the second column and 80.41% to 91.46% for the last column), with the first column of Fig. 12(a) presenting an exception to this general trend. In rows 2–10 of the first column of Fig. 12(a), the values ranged from 67.48% to 89.50%, which is substantially worse than the 97.13% performance noted in row 1 of this column. This result indicates that data containing one known source will have the best performance when only one source is included during training. In Fig. 12(b) the values generally decrease moving left to right across columns (82.18% to 89.41% for the first column and 9.38% to 63.31% for the final column). Fig. 12(c,d) show source and artifact misclassification rate, respectively, with the lowest rates generally occurring when both training and testing with more than one source. The misclassification rate for sources in the first two columns and rows of Fig. 12(c) ranged from 2.41% to 18.75% and the remaining values were less than 3.60%. The misclassification rate for artifacts in the first column and row of Fig. 12(d) ranged from 2.74% to 40.45% and the remaining values were less than 6.98%. Figs. 12(e) and 12(f) generally exhibit similar trends to Figs. 12(a) and 12(b), respectively, where the single-source network suffers significant performance losses with the multisource test sets (see first row). Otherwise, the missed detection rate generally increases from 6.64% to 19.56% in Fig.12(e) and 2.77% to 35.94% in Fig.12(f) when moving from left to right across the columns, with the exception of the first column in Fig. 12(e). The results for precision, recall, and AUC for these datasets containing multiple noise levels and multiple sources are reported in Table IV.

Fig. 12.

(a) Source and (b) artifact classification results for multisource datasets, where blue indicates better performance. (c) Source and (d) artifact misclassification results for multisource datasets, where yellow indicates better performance. (e) Source and (f) artifact missed detection results for multisource datasets, where yellow indicates better performance.

5) Classification Accuracy With Continuous vs. Discrete Receivers

Results comparing the performance for the continuous and discrete receivers are shown in Fig. 13 for a single photoacoustic source. We note that for the network trained and tested with the continuous receiver model, source and artifact accuracy measured 97.13% and 86.18%, respectively, and these results are the same as those shown in the first row and first column of each result in Fig. 12.. For the network trained and tested with the discrete receiver model, source and artifact accuracy measured 91.6% and 93.16%, respectively. In addition, source and artifact misclassification rates were 14.8% and 2.82%, respectively, for the network trained with the continuous receiver, and 11% and 12.63%, respectively for the network trained with the discrete receiver. For both networks, missed detection rates for both sources and artifacts were less than 0.7%. The results for precision, recall, and AUC for the dataset modeled with the discrete receiver are reported in Table IV.

Fig. 13.

(a) Classification results comparing the continuous and discrete receiver models. The dark and medium blue bars show the accuracy of source and artifact detections, respectively. The light blue and green bars show the misclassification rate for sources and artifacts, respectively. The dark and light yellow bars show the missed detection rate for sources and artifacts, respectively. Corresponding (b) source and (c) artifact ROC curves demonstrate that both networks perform similarly for sources with less agreement for artifacts. However, the ideal operating point differs for each ROC curve, thus the classification results are less similar.

B. Location Errors for Simulated Data

Table V lists the percent of correct detections which had errors below 1 mm and 0.5 mm for both sources and artifacts. Results indicate that within each dataset, location errors less than 1 mm were achieved in over 97% of the data. Location errors less than 0.5 mm were achieved in over 88%, with the exception of the finely spaced data.

TABLE V.

Summary of Euclidean Distance Errors for Simulated Data

Dataset*	Percentage of Total Errors ≤ 1mm		Percentage of Total Errors ≤ 0.5 mm
	Sources	Artifacts	Sources	Artifacts
Initial, Noiseless	100	100	93.43	94.03
−3dB SNR	100	100	97.55	95.47
−9dB SNR	99.94	100	94.89	96.38
−15dB SNR	100	100	89.12	89.79
−21dB SNR	100	100	92.41	88.74
Finely Spaced 5 mm shift	98.54	97.37	84.77	78.55
Euclidean shift	99.62	98.91	88.96	80.34
Multiple Noise Levels 1 source	99.82	99.73	89.88	89.23
2 sources	99.87	99.82	94.05	92.98
3 sources	99.81	99.78	93.04	92.13
4 sources	99.83	99.83	91.89	91.86
5 sources	99.77	99.84	92.90	92.34
6 sources	99.74	99.80	91.42	91.54
7 sources	99.50	99.86	92.47	93.09
8 sources	99.61	99.79	92.30	90.41
9 sources	99.66	99.89	91.98	91.33
10 sources	99.54	99.71	91.44	90.10
Discrete Receiver 1 source	100	100	93.83	92.77

^*A11 datasets used the continuous receiver unless otherwise stated.

The box-and-whiskers plots in Fig. 14 demonstrate the depth and lateral errors for sources and artifacts within each dataset. The top and bottom of each box represents the 75th and 25th percentiles of the measurements, respectively. The line inside each box represents the median measurement, and the whiskers (i.e., lines extending above and below each box) represent the range. Outliers were defined as any value greater than 1.5 times the interquartile range and are displayed as dots. Figs. 14 (a) and (b) show that the networks are more accurate in the depth dimension, where errors (including outliers) were frequently less than 0.6 mm, when compared to errors in the lateral dimension (Figs. 14 (c) and (d)), where outliers were as large as 1.5–2.0 mm. However, in both cases, the median values were consistently less than 0.1–0.5 mm, which is supported by the results reported in Table V.

Fig. 14.

Summary of distance errors for all tested simulated data in the depth (a,b) and lateral (c,d) dimensions for sources (a,c) and artifacts (b,d). Note that the depth errors are consistently lower than the lateral errors. For the multisource networks, distance errors were evaluated only for the number of sources for which the network was trained (i.e. the network which was trained with one source was only tested using the test set containing one source).

Figure 15 depicts the distribution of lateral errors for sources that were correctly classified with the noiseless, finely spaced, 5 mm shifted network. These errors are shown as a function of their depth in the image. These figures confirm that the majority of sources have lateral errors less than 0.5 mm. We also note that the for every source depth, the histograms have similar distributions.

Fig. 15.

Histograms of lateral errors of correctly classified sources for varying depths in the image for the noiseless, finely spaced, (a) 5 mm shifted network and (b) Euclidean shifted network. Note that the profiles of the histograms are similar with depth.

C. Artifact Removal for Simulated Data

Fig. 16 shows the result of our three methods to remove regions that were identified as artifacts. Sample channel data inputs to the network are shown in Figs. 16 (a)–(c) for three noise levels, and the corresponding B-mode images are shown in Fig. 16 (d)–(f). The average value substitution (Fig. 16 (g)–(i)) and the noise substitution (Fig. 16 (j)–(l)) methods successfully remove the center of the reflection artifact after beamforming. However, the tails of the reflection artifacts are still present in these new images. In addition, the noise substitution method further degrades image quality by exhibiting a blurring of these new values across the image. These two methods also pose a problem for cases where sources and artifacts overlap (e.g. Fig. 11) as they do no not take into consideration source locations in the image and could potentially remove a source in the process of removing an artifact.

Fig. 16.

Sample images from the noiseless, −3dB, and −9dB cases, shown from left to right, respectively, (a)–(c) before and (d)–(f) after applying traditional beamforming. Three artifact removal techniques are shown for each sample image: (g)–(i) average value substitution, (j)–(l) noise substitution, and (m)–(o) a CNN-based image that displays the location of the detected source based on the location of the bounding box. The yellow boxes in (a)–(c) indicate the portion of the images displayed in (d)–(o).

Another method for artifact removal is to only display objects which were classified as sources, as shown in Fig. 16 (m)–(o). This method was implemented by placing a disc-shaped object at the center of the detected bounding box and displaying it with a diameter of ±2σ, where σ refers to the standard deviation of the location errors for that particular noise level. One major benefit of this display method is that we can visualize true sources with an arbitrarily high contrast. In addition, this image is not corrupted by reflection artifacts because we do not display them, and we will not unintentionally remove sources in the process of removing artifacts with this method.

D. Experimental Results

The channel SNR in the experimental waterbath images was −3.3dB. Each image had one source signal and at least one reflection artifact, as seen in Fig. 17(a). The corresponding beamformed image and CNN-based image with the artifact removed are shown in Figs. 17(b) and (c), respectively.

Fig. 17.

(a, d, g) Sample images of experimental channel data where wavefronts labeled source indicate a true source and artifacts are unlabeled. The first row shows an example from the waterbath experiment while the second and third rows show examples from the phantom experiment. (b, e, h) The corresponding beamformed images where wavefronts labeled as sources indicate true sources and artifacts are unlabeled. (c, f, i) The corresponding image created with the CNN-based artifact removal method where source detections are displayed as white circles.

The channel SNR in the experimental phantom images was −4dB. Multiple source signals are present in each image along with multiple reflection artifacts, as noted in Table III and observed in Fig. 17(b) and (g). The corresponding beamformed images are shown in Fig. 17(e) and (h), respectively. The corresponding CNN-based images with artifacts removed are shown in Fig. 17(f) and (i) respectively.

The first six rows in Table VI show the percentage of correct, misclassified, and missed detections for sources and artifacts across the seventeen experimental waterbath images, revealing four notable observations. First, when the network was trained using Euclidean shifting, it performed better (100% source classification accuracy) when compared to 5mm shifting (88.24% source classification accuracy). Second, the best continuous receiver model correctly classified 70.27% of artifacts while the discrete model classified 89.74% of artifacts, indicating a performance increase with the discrete receiver model. Third, the network trained over a range of noise levels classified artifacts better (70.27% artifact classification accuracy), when compared to the network trained on one noise level (54.17% artifact classification accuracy). Fourth, contrary to Fig. 13, there is no decrease in source detection performance when switching from the continuous to discrete receiver. For visual comparison, the results from the two complementary continuous and discrete receiver models applied to experimental data are shown in Fig. 18.

TABLE VI.

Summary of Classification Performance for Experimental Data

Experiment	Network Model	Source			Artifact
		Correct	Misclassified	Missed	Correct	Misclassified	Missed
Waterbath	Noiseless, Fine, Continuous, 5 mm Shift	88.24%	11.67%	11.76%	0%	16.67%	87.50%
	−3dB Noise, Fine, Continuous, 5 mm Shift	35.29%	100%	0%	0%	41.67%	62.50%
	Noiseless, Fine, Continuous, Euclidean Shift	100%	5.88%	0%	0%	25%	79.17%
	−3dB Noise, Fine, Continuous, Euclidean Shift	100%	23.53%	0%	54.17%	8.33%	45.83%
	−5dB to +2dB Noise, Fine, Continuous, Euclidean Shift	100%	0%	0%	70.27%	10.81%	13.51%
	−5dB to +2dB Noise, Fine, Discrete, Euclidean Shift	100%	0%	0%	89.74%	0%	10.26%
Phantom	−5dB to +2dB Noise, Fine, Discrete, Euclidean Shift	74.36%	2.56%	25.64%	N/A	N/A	N/A
	−5 to +2dB Noise, Fine, Discrete, Euclidean Shift (only results within training range)	96.67%	3.33%	3.33%	N/A	N/A	N/A

Fig. 18.

Classification results for the experimental waterbath data when using the network trained with finely spaced point targets, −5dB to +2dB noise, and Euclidean shifting. Results from using networks trained with both the continuous and discrete receiver models (trained and tested with a single photoacoustic source) are shown for comparison.

When using the network trained with the discrete receiver, the mean absolute distance error between the peak location of the wavefront in channel data and the center of the detection bounding box for the waterbath dataset was was 0.40 mm with a standard deviation of 0.22 mm. For the same network, the mean absolute distance error for the phantom dataset was 0.38 mm with a standard deviation of 0.25 mm.

For the phantom dataset, only source detections were considered as it was difficult to quantify the number of artifacts in these experimental channel data images (see Fig. 17(b) and (d) for examples). The network trained with finely spaced point targets, −5dB to +2dB noise, Euclidean shifting, and discrete receiver correctly classified 74.35%, misclassified 2.56%, and missed 25.64% of sources across the 15 images, which included 39 source objects. These results are shown in Fig. 19 and reported in Table VI. These numbers show a marked decrease in performance when compared to the waterbath data. The main reason for this decrease in performance was due to the network only being trained at depths of 5 mm to 25 mm (as noted in Table I). When limiting our classification results to depths for which the network was trained, the same network classified 96.67%, misclassified 3.33%, and missed 3.33% of sources. This result agrees with the result from Section III-A2, where the trained networks failed to generalize to depths that were not included during training. Although Fig. 12 shows that networks trained with only one source do not transfer well to multisource test sets, it is interesting that the single source network used to test this experimental data set correctly classified multiple sources in 11 of the 15 total images.

Fig. 19.

Classification results for the experimental phantom data when using the network trained with finely spaced point targets, −5dB to +2dB noise, Euclidean shifting, and the discrete receiver. Blue bars indicate source classification accuracy, teal bars indicate source misclassification rate, and yellow bars indicate source missed detection rate. Results are compared for all illuminated sources and illuminated sources within depths at which the network was trained (5mm to 25 mm).

IV. Discussion

This work demonstrates the first use of CNNs as an alternative to traditional model-based photoacoustic beamforming techniques. In traditional beamforming, a wave propagation model is used to determine the location of signal sources. Existing models are insufficient when reflection artifacts deviate from the traditional geometric assumptions made by these models, which results in inaccurate output images. Instead, we train a CNN to distinguish between true point sources and artifacts in the channel data and use the network outputs to derive a new method of displaying artifact-free images with arbitrarily high contrast, resulting in improvements that exceed existing reflection artifact reduction approaches [21], [22].

We revealed several notable characteristics when applying CNNs to identify and remove highly problematic reflection artifacts in photoacoustic data. First, we learned that the classification accuracy is sufficient to differentiate sources from artifacts when the background noise is sufficiently low (Fig. 8), which is representative of photoacoustic signals generated from low-energy light sources. While our network is tailored to detecting point-like sources such as the circular cross-sections of needle or catheter tips (enabled by insertion of optical fibers in these needles and catheters), this approach could be extended to other types of photoacoustic targets through training with various initial pressure distribution sizes and geometries. We can potentially train these networks to learn other characteristics of the acoustic field, such as the medium sound speed and the signal amplitude.

We additionally demonstrated that this training requires incorporating many of the potential source locations in order to maximize classification accuracy, based on the poor results shown in Fig. 9 (i.e., when testing depth shifts that were not used during training). However, this initial network performed well at classifying sources when only the lateral positions were shifted, likely because wave shapes at the same depth are expected to be identical, regardless of their lateral positions. Based on these observations, it would be best to use our proposed machine learning approach when all possible depth locations are included during training, which is verified by the randomly selected training depths from the finely spaced network achieving better classification accuracy (see Fig. 10). This is also verified by the experimental phantom results failing in cases where depths were not trained (see Table VI). There is otherwise greater flexibility when choosing lateral training locations if we are primarily concerned with classification accuracy (and less concerned with location accuracy, for example, if we are only interested in knowing the number of sources present in an image).

It is highly promising that our networks were trained with simulated data, yet performed reasonably well when transferred to experimental data. Table VI and Fig. 18 demonstrate that as the simulations become more similar to experimental data (enabled by modeling the transducer, including several noise levels in the same network, etc.) the performance increases when transferring these networks to the experimental data domain. It is also promising that networks trained with only one simulated source and tested on the experimental data with multiple sources had increased performance when compared to testing this same network on simulated data with multiple sources (e.g., compare Fig. 12(a,c,e) with the phantom results in Table VI). This increased performance likely occurs because the sources are sufficiently separated from each other. A similar increased performance was observed when the discrete receiver model was applied to simulation versus experimental data (compare Figs. 13 and 18). While the reason for this increased performance with experimental data is unknown, one possible explanation is that the presence of a single sound speed in the experimental data versus the multiple sound speeds present in simulated data decreases the data complexity of the test data set, leading to increased performance in experimental data [35].

Fig. 12 suggests that there could be multiple optimal networks, depending on the desired weighting of the six performance metrics (i.e., classification accuracy, misclassification rates, and missed detection rates for both sources and artifacts), as network performance depends on the number of sources and thus complexity of the imaging field. Thus, future work will explore a multiple, ensemble network approach that combines the outputs of several independently trained networks.

The sub-millimeter location errors in simulation and experimental results can be related to traditional imaging system lateral resolution, which is proportional to target depth and inversely proportional to the ultrasound transducer bandwidth and aperture size [1], [5]. For example, traditional transabdominal imaging probes have a bandwidth of 1–5 MHz. To image a target at a depth of 5 cm with a 2 cm aperture width, the expected image resolution would be approximately 0.8–3.9 mm. Fig. 14 and Table V demonstrate that a large percentage of the location errors are better than the maximum achievable system resolution at this depth. Fig. 15 demonstrates that the lateral errors have a relatively constant distribution regardless of depth, indicating that the lateral resolution of our system is constant with depth. These observations suggest that our proposed machine learning approach has the potential to significantly outperform existing imaging system resolution at depths greater than 5 cm, thus making this a very attractive approach for interventional surgeries that require lower frequency probes because of the deeper acoustic penetration and the reduced signal attenuation (e.g. transabdominal, transcranial, and cardiac imaging applications).

Of the three artifact removal methods we explored, the CNN-based method was most promising, as it results in a noise-free, high contrast, high resolution image (e.g., Figs. 16(m)–(o)). This type of image could be used as a mask or scaling factor for beamformed images, or it could serve as a stand-alone image. The stand-alone image would be most useful for instrument or implant localization and isolation from reflection artifacts during interventional photoacoustic applications. To achieve greater accuracy, we can design specialized light delivery systems that attach to surgical tools (e.g., [17]) and learn their unique photoacoustic signatures. The results presented in this paper are additionally promising for other emerging approaches that apply deep learning to photoacoustic image reconstruction [40], [41]. Our trained code and a few of our datasets are freely available to foster future comparisons with the method presented in this paper [42].

V. Conclusion

The use of deep learning as a tool for reflection artifact detection and removal is a promising alternative to geometry-based beamforming models. We trained a CNN using simulated images of raw photoacoustic channel data containing multiple sources and artifacts. Our results show that the network can distinguish between a simulated source and artifact in the absence and presence of channel noise. In addition, we successfully determined the lateral and depth locations of the signal using the location of the bounding box. The network was successfully transferred to experimental data with similar classification accuracy to that of simulated data. Results are promising for distinguishing between photoacoustic sources and artifacts without relying on the inherent inaccuracies with traditional beamforming. This approach has additional potential to eliminate reflection artifacts from interventional photoacoustic images.