A study of Generalizability of Recurrent Neural Network-Based Predictive Models for Heart Failure Onset Risk using a Large and Heterogeneous EHR Data set

Abstract

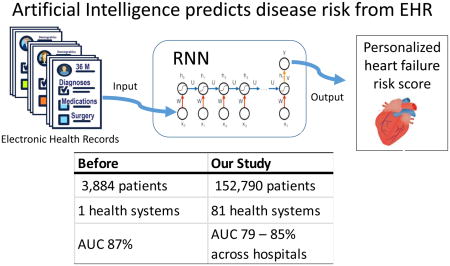
Recently, recurrent neural networks (RNNs) have been applied in predicting disease onset risks with Electronic Health Record (EHR) data. While these models demonstrated promising results on relatively small data sets, the generalizability and transferability of those models and its applicability to different patient populations across hospitals have not been evaluated. In this study, we evaluated an RNN model, RETAIN, over Cerner Health Facts® EMR data, for heart failure onset risk prediction. Our data set included over 150,000 heart failure patients and over 1,000,000 controls from nearly 400 hospitals. Convincingly, RETAIN achieved an AUC of 82% in comparison to an AUC of 79% for logistic regression, demonstrating the power of more expressive deep learning models for EHR predictive modeling. The prediction performance fluctuated across different patient groups and varied from hospital to hospital. Also, we trained RETAIN models on individual hospitals and found that the model can be applied to other hospitals with only about 3.6% of reduction of AUC. Our results demonstrated the capability of RNN for predictive modeling with large and heterogeneous EHR data, and pave the road for future improvements.

Graphical Abstract

1. Introduction

Cardiovascular diseases are the leading causes of mortality worldwide[1]. Among them, heart failure is a severe healthcare burden: per Centers of Disease Control and Prevention (CDC) and the American heart association (AHA), there were more than 5 million adult heart failure patients in the US in 2016, and that costs the nation more than $30 billion annually[2]. Estimating the risk for disease development can help early disease management and thus improving the health outcomes. Developing clinical event prediction models improves the quality of care especially when it is translated into real-time tools available at the bedside. Because of the wide adoption of Electronic Health Records (EHR) systems in the US over the past decade, Interests arises to leverage EHR data to build predictive models. Although the standard statistical regression models and traditional machine learning methods have been widely adopted, advanced deep learning techniques recently received more attention from many investigators because of their demonstrated superior prediction performance in various domains [3–7].

Deep learning often refers to artificial neural network models with multiple hidden layers that can be used to quantify the complex nonlinear relationships between inputs and outputs. Recurrent Neural Network (RNN) [4] is one class of the deep learning models that take into account the temporality in a sequence of events, and hence is well-suited for modeling and predicting a disease onset based on longitudinal observations of clinical events in a large population of subjects [3,4,8]. Long-short term memory (LSTM) and Gated recurrent units (GRU)[4,8] are two most popular types of RNN architectures and they have been applied to EHR and medical insurance claim databases to achieve the state-of-the-art accuracy of disease onset predictions[3,4,8].

Despite these successes, the generalizability of RNN based models remains a question. Generalizability is a key factor for the successful deployment of prediction models especially in the healthcare domain where there are variations in practice: demonstrating a high prediction accuracy only on the dataset used for model development is insufficient [9]. Especially for deep learning models with a large number of trainable parameters, overfitting is always a concern when models are developed over a single data set.

The REverse Time AttentIoN model (RETAIN)[3] is an RNN model that was shown to achieve high prediction accuracy and model interpretability. For a patient with a medical history consisting of a series of visits, each consisting of a number of medical codes and clinical events, RETAIN (or other RNN models) can be used to predict the onset of a certain disease for this patient. In addition, a neural attention mechanism can be used to calculate the contribution score for each medical code per hospital visit using the maximum activation in order to achieve clinical interpretability with its learned weights of medical codes. Choi et al. applied RETAIN on an EHR database and reported 87% AUC in the prediction of heart failure [3].

Like many RNN models, RETAIN was only tested on a relatively small data set from a single health system with nearly 4000 heart failure (HF) cases[3]. Moreover, it is unclear if the predicted risk scores can be reliably replicated based only on a relatively small EHR database. Thus, it is desirable to further test and more carefully investigate the deep learning models such as RETAIN over a larger EHR database with multiple hospitals and different features to evaluate if the good predictive properties of RNN models can be generalized.

In this work, we evaluate the RETAIN model using the Cerner Health Facts® EMR data that contains nearly 50 million patients across over 600 hospitals with more than 150,000 HF cases [10]. Our main goal is to validate and confirm the prediction accuracy of the RETAIN method on a large and heterogeneous EHR database. Moreover, we investigate the variability of prediction accuracy among different patient sub-populations and across different hospitals. Finally, we investigate if a model trained in one hospital can be applied to other hospitals.

2. Methods

2.1. A brief description of the Retain model

RETAIN is a two-level neural attention model on top of an RNN backbone. The model takes as input a patient’s history which includes a sequence of visits (encounters), each contains a set of medical events and outputs a binary prediction on whether the patient will have a heart failure onset in the future. The central feature of RETAIN is the use of two GRU RNNs to generate the attention weights for the purpose of interpretability [3]. The first RNN (RNNα) uses the Softmax function to calculate the visit-level attention weight notated as α (alpha) while the second RNN (RNNβ) uses the tanh function to calculate the event-level attention weight noted as β (beta). Those attention weights are used along with the initial linear embedding values of the input vectors representing the sequence of visits and the medical codes as the vector coordinates, to calculate the contribution score of each medical code in each visit. In this paper, we chose RETAIN model as a representative RNN model because the following: First, it is shown to have a performance on par of standard GRU models and compared favorably against logistic regression, a strong baseline method [3]; Second, it is providing a way for clinical interpretation compared to standard RNN models. Additionally, RETAIN source code is available as a Github Repo (https://github.com/mp2893/retain) with detailed documentation allowing reproducible research.

2.2. Cerner Healthfacts® database

Cerner Health Facts® EMR data [11] (version 2016) is derived from over 600 Cerner implementation throughout the United States. It contains clinical information for over 50 million unique patients with more than 10 years of records. In total there are more than 110 million patient visits (encounters) [12]. Data in Health Facts® is extracted directly from the EMR of hospitals with which Cerner has a data use agreement. Encounters may include pharmacy, clinical and microbiology laboratory, admission, and billing information from affiliated patient care locations. All admissions, medication orders and dispensing, laboratory orders, and specimens are date and time stamped, providing a temporal relationship between treatment patterns and clinical information. Cerner Corporation has established Health Insurance Portability and Accountability Act-compliant (HIPAA) operating policies to establish de-identification for Health Facts® [13]. These clinical data are mapped to the most common standards, for example, diagnoses and procedures are mapped to the International Classification of Diseases (ICD) codes, medications information include the national drug codes (NDCs), and laboratory tests are linked to their LOINIC codes.

2.3. Sample definition

We followed the case definition and case-control matching procedure described by Choi et al for heart failure prediction study [3] to construct our cohort dataset from Cerner Health Facts® EMR data. Cases were defined as patients who meet the following two criteria: (1) At least three heart failure related encounters had to occur within 12 months; (2) >=50 years old at the time of the first HF diagnose. The date of the first diagnosis is designated as the index date of the patient. For each case, up to 10 controls were matched by primary care hospital, sex, and age (five-year interval). Further, to match the time span of records in the Cerner Health Facts®, controls are required to have their first visit within one year of the first office visit of the matching case and have at least one visit a month before or any time after the diagnosis date of the matching case [14]. We further cleaned the extracted data to exclude all cases that showed any prior history of heart failure, as well as controls with any heart failure incidence before or after the index date with 180 days. In addition, we ensured that all the cases we use have at least one matched control and we cleaned up any redundant records. As a result, we obtained 152,790 cases and 1,152,517 controls.

2.4. Input variable definition

For medical codes in each visit, we included diagnoses, medication, and surgical procedures data. For that, we used the Cerner unique diagnoses identifiers that map to the International Classification of Diseases (ICD) (both ICD-9 and ICD-10) codes for medical Diagnoses [15], the same for surgical procedures, while we used the generic names for medication. We tested the effect of grouping the diagnoses codes using the Clinical Classification Software (CCS) [16] codes as well as the impact of adding demographic covariates.

2.5. Evaluation strategies

2.5.1. Searching for a model with optimal accuracy

Besides the extracted full cohort data and the selected hospitals’ datasets (Table 4), for development purpose, we prepared two subsets that share a randomly selected 14,500 cases. The first set having one control per case for a total of 14,500 controls hence we called the “balanced subset”, while the second set included all the assigned controls per case for a total of 109,079 controls and we refer to it as “unbalanced subset”. In each of our experiments we further subdivide the data into training, validation, and test sets with the ratio of 7:1:2, including the full cohort dataset. We evaluated the results mainly based on the area under the receiver operating characteristic curve (AUROC, or AUC) that represents the model prediction accuracy.

Table 4.

Descriptive analysis for the heterogeneity

Hospit al #	n	Census Region / Division	Case				Control
					Avg per Patient				Avg per Patient
			n	Visit	Diagnoses	Medication	n	Visit	Diagnoses	Medication
1	57,202	Northeast / 2	6,176	15	19	35	51,026	12	13	22
2	55,286	Northeast / 2	6,274	13	19	26	49,012	10	13	19
3	52,158	South / 7	6,545	8	12	30	45,613	6	10	24
4	44,277	Midwest / 4	6,257	12	19	25	38,020	10	15	20
5	42,729	South / 6	5,010	13	23	27	37,719	11	17	19
6	38,332	Northeast / 2	5,394	5	17	30	32,938	4	14	23
7	30,172	South / 5	3,352	6	27	30	26,820	5	19	21
8	28,440	Northeast / 2	3,075	8	13	35	25,365	6	9	22
9	24,913	South / 5	3,659	5	19	28	21,254	5	14	20
10	18,903	Northeast / 1	2,352	8	13	24	16,551	7	10	17

Our plan consisted of four main experiments. In the first experiment, we used the balanced subset to tune hyperparameters and evaluate the contribution of different medical code categories, demographic covariates, and time factors, through running the model either on individual category or different combination. In the second experiment, we compare the model performance of the balanced versus the unbalanced datasets using the optimal model obtained from the first experiment. In the third experiment, we compare different training curricula: In the original RETAIN method, patients are sorted by their number of visits before organized into mini-batches to allow efficient padding, while in each mini-match a case may not be fed together with matching controls. We compared the performance of the original curriculum against a modified curriculum where we enforced including the matched controls along with their cases within the same mini-batch. In the fourth and final experiment, we run the model on the full dataset using the optimal model selected in the first three experiments.

2.5.2. Evaluating Generalizability

Since Cerner Health Facts database includes data from multiple hospitals, we used all 10 hospitals that have at least 500 beds, provide care to acute cases, and have an HF cohort more than 18,000 patients (cases and controls combined) to evaluate the generalizability of RETAIN. For each hospital, we divide the patient cohorts into training, validation, and test sets with a ratio of 7:1:2. We evaluated the performances of the model trained on each hospital’s training (and validation) sets over the 10 hospitals’ test sets. We also evaluated the model that trained on all hospitals’ training sets over the 10 hospitals’ test sets. In addition, we stratified the model performance over subsets of the data with different characteristics such as the length of patient history.

2.5.3. Logistic regression as baseline model for performance comparison

In addition to the RETAIN model, we trained regularized logistic regressions using aggregated feature vector, where each dimension represents the occurrence of a specific code in any visit across the observation period for each patient without the temporality of sequential events (patients visits). Additionally, We calculated the prediction accuracy using the embedding of clinical codes obtained from the optimal epoch of RETAIN and we evaluated the performance with different regularization. All model’s hyperparameters were optimized by maximizing the AUC in the validation set.

3. Results

Table 1 shows a comparison between the cohort used for this paper (Cerner) and the one used for the initial evaluation of the RETAIN model (Sutter), while Table 2 is showing the descriptive analysis for the used cohort.

Table 1.

Comparison between Sutter [6] and Cerner Healthfacts® datasets Cohorts used for RETAIN evaluation

	Sutter	Cerner
Heart Failure Patients
Count (case + control)	3,884 + 28,903	152,790 + 1,152,517
Number of health systems	1	81
Number of hospitals	24	397
Avg. # of visits per patient	54	8
Avg. # of codes in a visit	3	16
Max # of codes in a visit	62	321
Max # of Dx on a visit	42	112
Avg. # of Dx codes in a visit	2	3
# of medical code groups:	615	15,815
Diagnose:	283	13,579
Medication:	94	1,892
Procedure:	238	325 (Surgical)
Demographic:		19

Table 2.

Study Cohort Descriptive Analysis. Means and standard deviations (in parentheses) of EHR variables and frequency of demographic variables are shown. P-values of the variables associated with case/control status is also included. For continuous variables, a t-test was used. For categorical variables, the chi-squared test is used.

		Case (n= 152,790)	Control (n= 1,152,517)	p-value
Number of Visits		9.08 (14.3)	7.51 (11.25)	< 0.0001
Diagnoses		18.17 (19.23)	13.55 (14.47)	< 0.0001
Medication		27.26 (21.9)	19.44 (18.02)	< 0.0001
Surgery		1.43 (0.84)	1.35 (0.72)	< 0.0001
Demographics
Gender	Female	53%	54%	0.0006232
	Male	47%	46%
Race	White	80%	83%	< 2.2e-16
	AfricanAmerican	18%	13%
	UnIdentified	2%	2%
	AsianPacific	1%	1%
Age Group	50–54 years	6%	8%	< 2.2e-16
	55–59 years	9%	10%
	60–64 years	10%	12%
	65–69 years	12%	14%
	70–74 years	14%	15%
	75–79 years	15%	15%
	80–84 years	15%	13%
	85+ years	19%	13%

As shown in table 2, except for surgery, cases are having 28% more visits on average than control, 37% more diagnoses code on average and 42% more medication. It is not surprising that demographic information is showing a similar distribution of cases and control as a result of the matching process. The slight imbalance is due to the fact that some categories have limited available controls. Some demographics records that nearly contribute to less than 0.05% such as Multiracial race are not shown in table 2.

3.1. Searching for model with optimal accuracy

In experiment 1 (Table 3), we found that using grouped diagnoses (CCS) codes showed relatively lower AUC than using Cerner codes that map to 5 digits ICD codes. Further, compared to the baseline model which only includes diagnosis codes, adding different categories of medical codes including medications and surgical procedures increased the model prediction accuracy by nearly 1%. It is interesting that adding demographic covariant improved by additional 1%, even though these variables are frequency-matched between cases and controls.

Table 3.

Effect of using different variable categories, datasets, and model variations on prediction accuracy, the Balanced subset is of (14,500 cases and controls), the Unbalanced subset is of (the same14,500 cases and 109,079 controls), whiles the full set consists of 152,790 cases and 1,152,517controls)

Experiment #	Model	AUC
1	RETAIN trained and tested on Balanced Subset – Diagnoses Data only	0.769
1	RETAIN trained and tested on Balanced Subset – Diagnoses Data grouped using CCS codes	0.759
1	RETAIN trained and tested on Balanced Subset – Diagnoses and Demographic Covariates (age, gender, race)	0.779
1	RETAIN trained and tested on Balanced Subset – Diagnoses, Demographic, and Medication	0.787
1 & 2	RETAIN trained and tested on Balanced Subset – All codes (Diagnoses, Demographic, Medication, and Surgery)	0.789
2	RETAIN trained and tested on Unbalanced Subset – All codes	0.79
2	RETAIN trained on Balanced Subset – All codes and tested on Unbalanced Subset – All codes	0.787
3	Forced Matching RETAIN trained and tested on Balanced Subset – Diagnoses Data only	0.762
3	Forced Matching RETAIN trained and tested on Balanced Subset – Diagnoses Data grouped using CCS codes	0.751
4	RETAIN trained and tested on the full cohort set	0.822
4	Logistic Regression with L2	0.766
4	Logistic Regression using embedding	0.782
4	Logistic Regression using embedding with L1	0.785
4	Logistic Regression using embedding with L2	0.786

For experiment 2, we found that the prediction AUC using the balanced subset was 0.789 while using the unbalanced subset was 0.79. While there was no significant difference in AUC, a single epoch duration using the balanced subset was 2 minutes versus 7 minutes for the unbalanced subset. Training on a balanced subset while testing on an unbalanced subset showing even a little lower AUC of 0.787.

For experiment 3, we found that forcing the inclusion of matched cases and controls within the same mini batch didn’t improve the prediction accuracy, it actually decreased by about 0.008, and it prolonged the epoch duration by 8 folds (16 minutes versus 2 minutes).

Finally, running RETAIN on the full cohort dataset using the optimized model showed prediction AUC of 0.822 in comparison to 0.766 using logistic regression and to 0.786 using the same embedding file used by RETAIN and duration per epoch of 72 minutes.

3.1.1. Factors influencing prediction accuracy

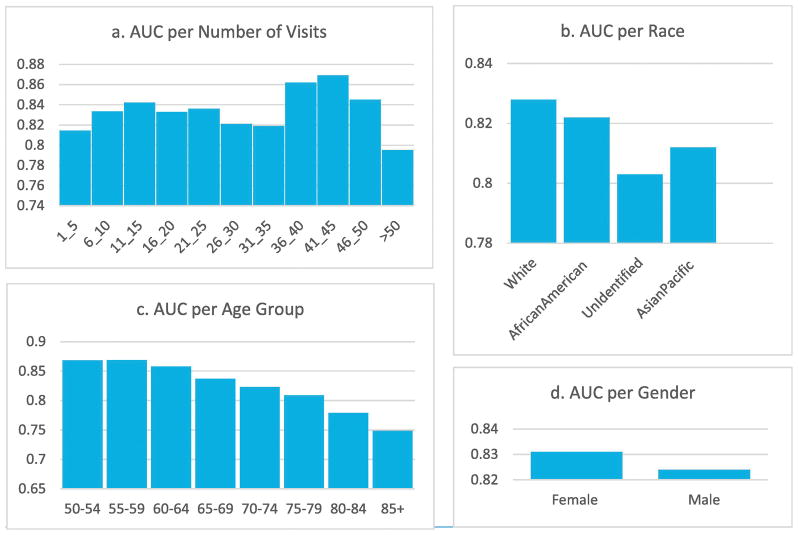
We stratified patients with different visit counts (Figure 1-a) and found that the model achieves the best performance for patients with 41–45 visits in our Cerner data set. We also calculated the stratified AUCs according to patients’ demographic covariates. Overall, females have 0.831 and males 0.824 (Figure 1-d). Interestingly RETAIN predicted better for young patients (0.87 for age 50–54) than older patients (0.75 for age 85+) (Figure 1-c). There is some difference in accuracy among different ethnicities: while Whites has the majority of the samples and has an AUC similar to the overall average, other ethnicities have smaller sample sizes and varied AUCs (Figure 1-b). The unidentified race has lowest AUC of 0.803, likely due to lower data quality.

Figure 1.

Generalizability: AUC stratified by different variables including gender, race, age group, and the length of patient history based on the number of visits

3.2. Generalizability

Another significant factor affecting accuracy is the heterogeneity of hospitals. It is unclear if varying practices in different hospitals would result in different performances. Our cohort has data from more than 390 hospitals and thus provide an excellent opportunity to evaluate the model performance over different hospitals. Based on our predefined selection criteria, we used the cohorts for ten largest hospitals (see 2.5.2. Evaluating Generalizability) described in Table 4 and tested the model on each hospital separately (Table 5). We also tested the impact of training the model on one hospital while testing on another to understand the transferability of a model trained on one hospital to other hospitals.

Table 5.

Heterogeneous prediction results across different hospitals.

Hospital #	Self-training data only	Full training data
1	0.817	0.845
2	0.802	0.834
3	0.782	0.794
4	0.783	0.815
5	0.838	0.851
6	0.778	0.789
7	0.812	0.825
8	0.819	0.827
9	0.830	0.841
10	0.774	0.806
Average AUC	0.804	0.823

As shown in Table 5, the prediction accuracy varies greatly by site. The prediction accuracy for models trained and tested on Hospital 5 was around 0.838 which is 2% better compared to the performance on the full dataset trained on all hospitals data, while Hospital 10 showed a much lower self-training AUC of 0.774. For almost all models trained on a single hospital, the model trained on the same hospital data is the one giving the best AUC, except for hospital 10, where the model trained on hospital 4 is giving a slightly better AUC by 0.1% (Supplemental Table 1). If the model trained in one hospital is directly applied to a different hospital, we can expect a reasonable generalization, but the prediction accuracy decreases on average by 3.6%. the most extreme case can show a loss in AUC for about 12%. However, the model trained on all hospitals’ training set is always giving a better AUC for samples at each hospital, demonstrating the value of big data, despite the heterogeneity.

4. Discussions

We found that the RNN model we tested, RETAIN, showed a superior prediction accuracy over the baseline model of logistic regression. In the full heterogeneous dataset, RNN model showed a better prediction AUC of 82% in comparison to 79% using logistic regression. Although logistic regression is known for better interpretability, the above AUC is achieved using a pre-trained embedding which would impact the model interpretability. The prediction accuracy of Logistic regression would be reduced to 77% without using the embedding. On the other hand, RETAIN is providing a way for interpretation through the calculation of the contribution score for each medical code within patients’ visits [3].

A main contribution of the paper is that we validated the generalizability of the deep learning approach developed in a small set of a single healthcare system on a large heterogeneous commercial EHR datasets. Interestingly, there is a gap between our performance and the 87% AUC reported by the authors of RETAIN on their dataset. Primarily, this may be due to that the Cerner data set, as a newly established commercial dataset, contains samples that are very different from the Sutter dataset where a smaller set of patients were followed through a long period of time. For example, although our dataset is significantly larger than the Sutter dataset, the average number of visits in our dataset is around 8 while for Sutter is around 54. The shorter and often incomplete patient history in Cerner may be a hurdle for predicting onset risks of chronical diseases such as heart failure. Additionally, the heterogeneity of samples from different hospitals in Cerner would introduce additional difficulty to predictive performance.

We observed that the prediction AUC among the ten largest hospitals is variable. This is expected as the quality of data and the different providers’ attitudes toward documenting patient clinical information in each practice. However, understand the factors responsible for the variable performance among hospitals is beyond the scope of current work and will be topic for future research. Performance variability across different hospitals we identified may have ramifications in terms of applicability of RNN-based predictive models in real practice. Adoption of a general predictive model trained on other data sets to a hospital should be a careful process.

In terms of generalizability, we found that the model trained in one hospital may be adopted by a different hospital, but we can expect an average of 3.6% decrease in the prediction accuracy. Overall, using the model that trained on the largest training set gives the best performance.

We have explored the applicability of the original RETAIN model in various datasets. First, we found that the prediction accuracy improved moderately with the training sample size, indicating that model may have reached saturation and more expressive model might be needed. Second, we found that inputs with more dimensions have better AUC. For example using over 10,000 Cerner Diagnoses unique identifiers that map to the 5-digits ICD codes, provided a better AUC than using the 285 single level CCS grouping categories, This is contrary to the evaluation done on Sutter [3]. This may be the results of the larger training set that allows training a bigger model. Third, we found that training on a balanced set or on an unbalanced set does not significantly change the AUC, therefore a balanced set may be more practical for model development as it offers higher efficiency. Forth, we found that forcing matched cases and controls within the same mini-batch does not improve AUC while leading to the longer training time per epoch. This suggests that the stochastic gradient descent algorithm used by a typical deep learning model such as RETAIN can effectively tolerate imbalances in mini-batches, and thus careful mini-batching may not be necessary.

For fair comparisons to the results in Choi et al. [3], we adopted a similar case-control matching procedure. However, we believe that it is not necessary to use the case-control matching in a predictive model if the imbalanced data between cases and controls do not affect the computational efficiency and performance. Since we have already included all the control factors such as race, sex, and age in the predictive model, in matter of fact the case-control matching reduces the predictive effect of these factors. We expect to obtain a higher predictive power without case-control matching.

5. Conclusion

Through extensive evaluation using a large and heterogeneous EHR dataset, we established the overall generalizability of RNN-based deep learning models across hospitals and clinics with different characteristics. However, the accuracy of RNN models varies in different patient groups, thus extensive testing is warranted before application of RNN models in practice.

Supplementary Material

supplement

Supplemental Table 1: 10 × 10 Hospitals Table

Highlights consist of a short collection of bullet points that convey the core findings of the article and should be submitted in a separate file in the online submission system. Please use ‘Highlights’ in the file name and include 3 to 5 bullet points (maximum 85 characters, including spaces, per bullet point)

• Accurate heart failure risk prediction of RNNs is validated in a large heterogeneous EHR data set.

• RNN (AUC 82%) outperforms logistic regression (AUC 79%) in our data set.

• RNN trained on one hospitals can be applied to other hospitals with only 3.6% reduction in AUC.

• Our results showed the promise of deep learning models for EHR predictive modeling.