Estimating the Distribution of Protein Post-Translational Modification States by Mass Spectrometry

Abstract

Post-translational modifications (PTMs) of proteins play a central role in cellular information encoding, but the complexity of PTM state has been challenging to unravel. A single molecule can exhibit a “modform” or combinatorial pattern of co-occurring PTMs across multiple sites, and a molecular population can exhibit a distribution of amounts of different modforms. How can this “modform distribution” be estimated by mass spectrometry (MS)? Bottom-up MS, based on cleavage into peptides, destroys correlations between PTMs on different peptides, but it is conceivable that multiple proteases with appropriate patterns of cleavage could reconstruct the modform distribution. We introduce a mathematical language for describing MS measurements and show, on the contrary, that no matter how many distinct proteases are available, the shortfall in information required for reconstruction worsens exponentially with increasing numbers of sites. Whereas top-down MS on intact proteins can do better, current technology cannot prevent the exponential worsening. However, our analysis also shows that all forms of MS yield linear equations for modform amounts. This permits different MS protocols to be integrated and the modform distribution to be constrained within a high-dimensional “modform region”, which may offer a feasible proxy for analyzing information encoding.

Graphical Abstract

INTRODUCTION

Individual amino acid residues in a protein may be chemically modified in multiple ways in response to physiological conditions, thereby giving rise to many potential “proteoforms”. ^1,2 Here we consider those proteoforms arising from reversible, enzymatically regulated post-translational modification (hereafter, “PTM”), such as phosphorylation, acetylation, ubiquitylation, and so on.³ Other proteoforms, such as those arising from alternative splicing or proteolytic cleavage, also have important functions, but PTMs, as defined above, have distinctive regulatory roles that are central to cellular information processing,^4,5 as discussed later.

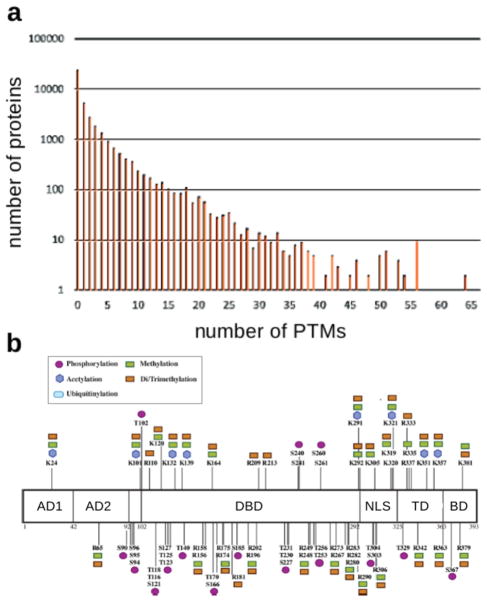
Proteomic studies show that many proteins carry PTMs and that the number of modified sites can vary substantially (Figure 1a). Nearly 40% of the proteins on the UniProt database are annotated with at least one modified site and proteins exist with more than 100 modification sites (Figure 1b). In particular, proteins with many interactions, so-called hub proteins, which integrate information from multiple biological pathways, can be heavily modified both in types of PTM and in numbers of modified sites for each PTM, as shown for the transcription factor and “guardian of the genome” p53 (Figure 1b).

Figure 1.

Protein post-translational modification. (a) Histogram generated from the 20 300 human SwissProt entries in the UniProt Knowledgebase, showing the number of proteins with annotated PTMs on up to 65 sites. (b) Schematic of the protein p53 showing the variety (inset) and number of novel PTMs identified in a recent mass spectrometry study, adapted from figure 6B of DeHart et al.⁶ In total, more than 100 modification sites have been reported on p53. Abbreviations: AD, activation domains; DBD, DNA binding domain; NLS, nuclear localization signal; TD, tetramerization domain; BD, basic domain.

It is increasingly appreciated that PTMs at distinct sites may interact to influence function,^7–11 thereby enabling sophisticated forms of cellular information processing.^5,12–14 In particular, it has been suggested that “PTM codes” occur in various biological contexts, of which the histone code is best known.^15–24 P53 offers a suggestive example: It differentially regulates a variety of downstream genes depending on physiological conditions that alter its PTMs.^18,25,26 These PTMs are found within the central DNA binding region, where they may influence genomic binding sites and affinities and within the N- and C-terminal regions, where they may modulate p53’s interactions with coregulators (Figure 1b). Substantial interplay between these widely separated modification sites would appear to be required for the intricate regulatory changes that are a hallmark of p53’s diverse functions.²⁷ However, the meaning of “code” has not been clearly defined and remains a matter of debate in the literature.^28,29

The potential interplay between PTMs at different sites makes it essential to keep track of PTMs across the entire protein. This is challenging for two reasons: PTMs on different sites can combine in various patterns, resulting in a combinatorial explosion with increasing numbers of sites, and different molecules in the population can exhibit different patterns of PTMs. In previous work we introduced the concepts of “modform” and “modform distribution” to address these problems.^5,30 A modform is a specific combinatorial pattern of co-occurring PTMs across a single protein molecule (Figure 2a). A binary modification like phosphorylation, which is present or absent at n modification sites, can have 2ⁿ potential phospho-modforms, whereas complex PTMs, like ubiquitylation or glycosylation, can yield much greater complexity.⁵ A protein’s modform distribution, which depends on its biological context, is the amount of each of its modforms present in the molecular population in that context (Figure 2b,c). The modform distribution provides the most complete quantitative estimate of a protein’s PTM state: It specifies which combinatorial patterns of co-occurring modifications are present, and, among these, which are most abundant and therefore most likely to have a substantial downstream impact. This paper is concerned with the principles underlying the estimation of modform distributions.

Figure 2.

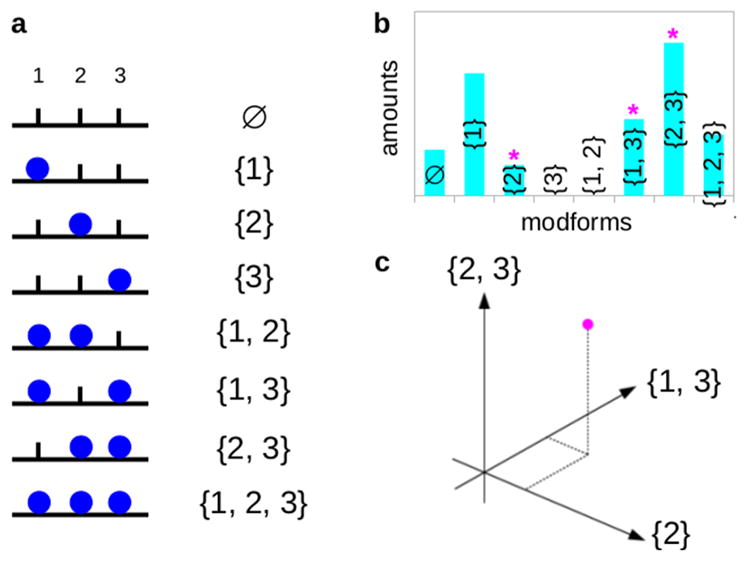
Modforms and modform distributions. (a) Eight modforms of a protein with three sites of binary modification (blue disc), with the corresponding modform subset shown in set notation on the right. The sites are numbered 1 to 3 from the left, as shown above the modforms. The symbol ø denotes the empty set, which has no elements. (b) Hypothetical modform distribution for the example in panel a, in the form of a histogram. Modforms {3} and {1,2} are absent, whereas the other modforms are present in varying amounts. The magenta asterisks indicate the components of the modform distribution that are pictured in the panel below. (c) Modform distribution in panel b as a vector (magenta dot), showing only the three components along the coordinate axes marked in the histogram above by the magenta asterisks. The complete modform distribution is a vector in eight dimensions.

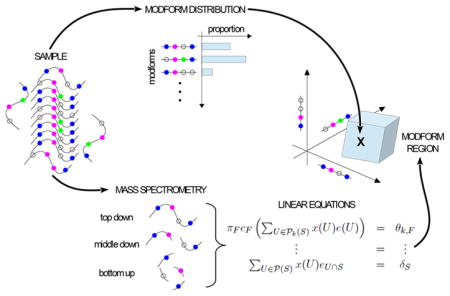
The development of mass spectrometry (MS) has made protein modform distributions far more experimentally accessible than modification-specific antibodies, which can only target a very limited number of PTM epitopes. MS approaches have provided decisive evidence of the interplay between PTMs at different sites, although such studies have up to now been largely focused on relatively small proteins.^9,31,32 The most widely used MS method is “bottom-up” (BU), in which proteins are first enzymatically cleaved by a protease into peptides, prior to reversed-phase liquid chromatography (RPLC) and mass spectrometry (MS). Modern spectrometers can detect differences in mass/charge ratio of a few parts in a million, allowing peptides to be sequenced and PTMs to be identified and localized on the sequence. Because peptides usually have many fewer modification sites than their parent proteins and because RPLC can often separate peptide modforms prior to MS, peptide modform distributions can, in principle, be determined.³³

However, proteolytic cleavage severs correlations between PTMs on different peptides. It is impossible to tell whether modform A on peptide 1 and modform B on peptide 2 came from a single protein modform carrying both A and B or from two protein modforms, one carrying A, but not B, and the other carrying B, but not A. The protein modform distribution is constrained by the peptide modform distributions, but, with only a single protease, the former cannot usually be reconstructed from the latter.

Nevertheless, it has seemed plausible that the modform distribution can be reconstructed, at least in principle, provided sufficiently many proteases are available with appropriate distinct patterns of cleavage, perhaps combining bottom-up with “middle down” (MD) approaches, in which larger peptides covering more sites are generated. However, this widely held belief has not been rigorously investigated and the question of precisely what we can learn about PTM state using MS remains open. To address this problem, we introduce here a mathematical language for describing MS measurements. We use this to show that reconstructing the protein modform distribution by cleavage-based MS is impossible, no matter what cleavage patterns are available and no matter what combinations of proteases are used. Furthermore, the shortfall in the information required for reconstructing the modform distribution worsens exponentially with the number of modification sites.

We also consider “top-down” (TD) MS, in which intact proteins are subject to mass analysis (TD MS¹) or to successive rounds of fragmentation prior to mass analysis (TD MS^k+1, after k rounds). We find that this can reduce the information shortfall, but, with current technology, the shortfall still increases exponentially with the number of modification sites.

Notwithstanding these limitations, our analysis also shows that all forms of MS (BU, MD, and TD) yield linear equations for modform amounts. This common mathematical format offers a way to integrate different MS protocols and workflows, thereby taking maximal advantage of all sources of data. We discuss how this can lead to a feasible strategy for constraining the modform distribution.

RESULTS

Linear Equations and Matrices for Peptide-Based MS

We first introduce a mathematical language for describing PTMs and MS procedures, through which MS data can be translated into a set of linear equations (eq 3). The language relies on several preliminary simplifying assumptions, which focus attention on the central problem. First, we consider only a binary PTM, such as phosphorylation, which may be present on up to n sites. Second, we assume that all proteases cleave with 100% efficiency. Third, we assume that after the protein is cleaved into peptides with fewer sites, each peptide modform distribution can be fully determined by MS. These assumptions are evidently unrealistic. However, they provide a best-case analysis: They allow us to ask if the problem of reconstructing the protein modform distribution is possible when everything works in its favor. If the protein modform distribution cannot be recovered with these assumptions, it certainly cannot be recovered without them. We note that some of these assumptions can be relaxed, which may be useful in subsequent studies.

Patterns of modification and cleavage can be described using either sequence or set notation. The former is widely used in bioinformatics but becomes increasingly opaque and difficult to manipulate for modforms. It is more productive to use set notation. Because this may be unfamiliar, new concepts are italicized when first used. Table 1 below gives concise definitions with further explanation in the Supporting Information (SI).

Table 1.

Explanations of Mathematical Concepts and Symbols

concept	explanation	example/notation
set	collection of entities (here, numbers)	U = {7, 2, 5, 3}
element	entity that is in a set	5 ∈ U, 1 ∉ U
standard form	distinct elements written in order	U = {2, 3, 5, 7}
empty set	set with no elements	ø
subset	set wholly contained in another	{2, 3} ⊆ U
power set	set of all subsets of a set	℘ ({1, 3}) = {ø, {1}, {3}, {1, 3}}
intersection	common subset	{2, 3} ∩ {3, 7} = {3}
union	merged set	{2, 3} ∪ {3, 7} = {2, 3, 7}

Sites of modification and cleavage are determined by their amino-acid positions in the primary protein sequence, but, for our purposes, it is only necessary to know the order of the modification sites (hereafter, “sites”). Let us identify these with the numbers 1, ..., n, in order along the primary sequence from, say, the N-terminal. Here n is the total number of sites. Let S be the set whose elements are all the sites, denoted in standard form by S = {1, ..., n}. If i is an element of S, denoted i ∈ S, then i corresponds to a site on the protein and must be one of the numbers between 1 and n inclusive. S will be the “universe” of sites in which we work.

A protein modform is defined by the sites that are modified. It therefore corresponds to a set, U, which is a subset of S, denoted U ⊆ S. For example, if n = 3, then U = {1, 3} corresponds to the modform with sites 1 and 3 modified and site 2 unmodified (Figure 2a). It is convenient to collect the protein modforms together into a new set, ℘(S), called the power set of S, consisting of all subsets of S. Because there are n sites in S, there are 2ⁿ subsets (modforms) in ℘(S).

A modform distribution is specified by the amount of each modform in the molecular population. If we denote a modform distribution by x, then for each modform U ∈ ℘(S), there is a number, x(U) ∈ ℝ, which gives the amount of modform U. Here ℝ denotes the real numbers, conventionally used for measurement. Because amounts cannot be negative, x(U) ≥ 0 for each modform U. A modform distribution can be thought of as a histogram over the modforms (Figure 2b).

A modform distribution can also be regarded as a vector, whose components are the modform amounts x(U) (Figure 2c). The notation ℝ^℘(S) denotes the vector space of all such vectors, which associate real numbers to modforms. This vector space has coordinate axes for each modform, U ∈ ℘(S). Let e_U ∈ ℝ^℘(S) denote the unit vector along the coordinate axis for the modform U. As a vector, e_U is defined by having the component 1 in the coordinate U and the component 0 in all other coordinates so that e_U(V) = 1 if V = U and e_U(V) = 0 otherwise. We can write each modform distribution as a linear combination of such unit vectors, so that

$$x=\sum _{U\in \mathcal{P}(S)}x(U)e_U$$ (1)

Equation 1 is analogous to the expression of a vector in 3D space, ℝ³, in terms of the unit vectors in the three Cartesian coordinate axes (Figure 2c). Modform distributions, however, exist in a space of dimension 2ⁿ, corresponding to the distinct modforms, rather than in a space of dimension 3.

Cleavage of a protein by a protease results in peptides that carry only certain modification sites of the original protein. Given a protease, let S₁ ⊆ S be the subset of sites carried on one of the peptides after cleavage. We will continue to use the same numbers to denote sites on the peptide as we did for sites on the protein. Under cleavage, the protein modform distribution in ℝ^℘(S) gives rise to a peptide modform distribution. Peptide modforms correspond to subsets of S₁ or elements of ℘(S₁), and peptide modform distributions are given by vectors in ℝ^℘(S₁). In this way, we get a cleavage map from protein modform distributions to peptide modform distributions

$$c_{S_1}:{ℝ}^{\mathcal{P}(S)}\to {ℝ}^{\mathcal{P}(S_1)}$$

It is not difficult to describe what such a cleavage map does on modforms. A given protein modform, represented by U ∈ ℘(S), gives rise to a peptide modified on those sites that are common to both the modform subset, U, and the cleavage subset, S₁. This common set is the intersection of U and S₁, denoted U ∩ S₁. Hence, c_S1(e_U) = e_U∩S1. Distinct protein modforms can give rise to the same peptide modform under cleavage, but they contribute additively, so that the cleavage map is linear. Hence, for a modform distribution, x, as in eq 1

$$c_{S_1}(x)=\sum _{U\in \mathcal{P}(S)}x(U)e_{U\cap S_1}$$ (2)

Note that cleavage can only produce subsets with contiguous sites: If S = {1, 2, 3}, then there is no protease whose cleavage subset is {1, 3}. However, we do not need this constraint immediately. It is more transparent to allow arbitrary cleavage subsets and to explain later how the practical nature of proteolytic cleavage influences the conclusions.

Because peptide modform distributions are assumed to be known, as discussed above, a cleavage map defines a system of linear equations

$$c_{S_1}(x)={\delta }_{S_1}$$ (3)

where δ_S1 ∈ ℝ^℘(S₁) is the peptide modform distribution vector measured by BU or MD MS, as described above. The problem of reconstructing the protein modform distribution is to solve for the unknown vector x ∈ ℝ^℘(S) in eq 3 and the similar equations arising from other cleavage subsets and proteases.

Because the cleavage map is linear, it can be represented by a matrix in terms of the unit vectors in ℝ^℘(S) and ℝ^℘(S₁). Examples matrices are shown in the SI. Cleavage matrices have a distinctive structure. Each entry is either 0 or 1; there is only a single 1 in each column. If the column corresponds to U ∈ ℘(S), then the row in which the sole 1 occurs corresponds to U ∩ S₁ ∈ ℘(S₁). Accordingly, the different rows are linearly independent; there are 2^p entries of 1 in each row, where p is the number of elements of S that are not in S₁.

Number of Linearly Independent Equations

Each row of a cleavage matrix gives a linear equation on the unknown components of the protein modform distribution through eq 3. Because there are 2ⁿ modforms, the same number of linearly independent equations is needed to determine the protein modform distribution. A single cleavage, however, does not provide enough equations. For n = 3 sites with a single cleavage between sites 1 and 2, we get two equations from the first peptide, represented by subset {1}, and four equations from the second peptide, represented by subset {2, 3}, giving only six equations for eight unknowns (SI).

Moreover, the equations must also be linearly independent. As noted above, the rows of any single cleavage matrix are always linearly independent. However, the column sums of a cleavage matrix are always 1, so that if two cleavage matrices are pooled, there is a linear dependency between the resulting equations. If the cleavage subsets are disjoint, as they are for subsets from a single cleavage, then there are no more linear dependencies (below). So, with the single cleavage for this example on n = 3 sites, there are, in fact, only five linearly independent equations for eight unknowns. The information shortfall is three equations.

This leaves open the possibility that with multiple proteases, each with a different pattern of cleavage, sufficiently many linearly independent equations can be found. For instance, with n = 3 sites as above, if a second protease cleaves between sites 2 and 3 only, then this would yield cleavage subsets S₃ = {1, 2} and S₄ = {3} and a further six equations, of which, once again, five are linearly independent. This gives 12 equations in total, and it may now seem very plausible that enough of these are linearly independent to recover all eight variables. Indeed, this is often informally suggested. But is it true?

Theorem 1

Let S₁, ..., S_N be the cleavage subsets arising from any number of proteases with any patterns of cleavage. The number of linearly independent equations arising from pooling the cleavage matrices is given by the number of distinct subsets of S consisting of all of the subsets of S_i, including S_i itself, for 1 ≤ i ≤ N.

This result was first proved in the field of algebraic statistics.³⁴ For convenience, and to keep this paper self-contained, we give an independent proof in the SI, where we also explain how this connection was discovered.

To see Theorem 1 at work, consider first the case where N = 1 of a single cleavage subset, S₁. Let us use the notation #U to denote the size of U. We know from the discussion above of the cleavage matrix that all rows are linearly independent. The number of rows is $2_1^{\#S}$, which is also the number of distinct subsets of S₁.

Now suppose that a single protease is used, which generates cleavage subsets S₁, ..., S_N. In this case, the subsets are pairwise disjoint, so that S_i ∩ S_j = ø for i ≠ j. Hence, each subset of S_i is distinct from any other subset of S_j, except for the empty set, which is common to all S_i. It follows from Theorem 1 that the number of linearly independent equations is 2^#S₁ + 2^#S₂ + ... + 2^#S_N − (N − 1), where the term N − 1 ensures that the empty set is counted only once. For n = 3 sites with a single cleavage between sites 1 and 2, we get N = 2, S₁ = {1}, and S₂ = {2, 3}, resulting in 2¹ + 2² − 1 = 5 linearly independent equations, as noted above.

If a second protease is used for a protein with three sites, as suggested above, it generates the cleavage subsets S₃ = {1, 2} and S₄ = {3}; these subsets are no longer disjoint from S₁ and S₂. The number of distinct subsets of S₁, ..., S₄ required for Theorem 1 is seen to be only 6. Hence, despite the 12 equations from two different proteases, Theorem 1 tells us that only six are linearly independent. There is still a shortfall of two equations.

There is no way of doing any better for a protein with three sites because any nontrivial protease (i.e., one that yields peptides with fewer sites than the protein) must cleave between sites 1 and 2 or sites 2 and 3 or both. The last possibility does not help because with S₅ = {1}, S₆ = {2}, and S₇ = {3} this protease would only give 2¹ + 2¹ + 2¹ − 2 = 4 linearly independent equations on its own, and, if combined with the first two proteases, it would not increase the number of distinct subsets required for Theorem 1 beyond 6 because S₅, S₆, and S₇ and their subsets have already been included in the count.

It is instructive, however, to consider what would happen if some other-worldly protease were able to yield the subset {1, 3}. If this was combined with the first two proteases, then the number of distinct subsets would rise to 7. The only subset missing from the count would be S = {1, 2, 3} itself.

Taking this reasoning a step further for a protein with n sites, if proteolytic cleavage was able to yield all subsets of size n − 1, then this would give 2ⁿ − 1 distinct subsets in Theorem 1, the only missing subset being S itself, which is enough linearly independent equations to almost determine the protein modform distribution. Perhaps this is some justification for the widely held belief that with sufficiently many proteases the protein modform distribution can be reconstructed. The problem is that of these n subsets of size n − 1, only {2, ..., n}, which misses site 1, and {1, ..., n − 1}, which misses site n, can arise from actual proteolytic cleavage.

It is not hard to see that a real, nontrivial protease that cleaves in a pattern other than these two extreme cases cannot do better in terms of Theorem 1. This is because the distinct subsets of any resulting cleavage subset are contained in either {2, ..., n} or {1, ..., n − 1}. It follows that, as far as the number of linearly independent equations is concerned, the best that can be done is to combine a protease that gives the cleavage subset {2, ..., n} with another that gives {1, ..., n − 1}. Because {2, ..., n} ∩ {1, ..., n − 1} = {2, ..., n − 1}, Theorem 1 tells us that the number of linearly independent equations is then 2ⁿ⁻¹ + 2ⁿ⁻¹ − 2ⁿ⁻² = 2ⁿ − 2ⁿ⁻². Hence, the shortfall from the 2ⁿ unknown quantities is at least 2ⁿ⁻².

Theorem 2

For a protein with n sites of binary modification, the number of linearly independent equations arising from any form of protein cleavage and peptide mass spectrometry, irrespective of how many proteases and patterns of cleavage are used, falls short of the number 2ⁿ, which is required to determine the modform distribution, by at least 2ⁿ⁻².

In practice, the extreme cleavages above leave all but one of the modification sites on a single peptide and therefore place the greatest burden on determining the peptide modform distribution. If these are to be fully determined, then the number of sites on the peptides must be reasonably low, which makes the shortfall much worse.

MS on Intact Proteins

Proteins can now be analyzed by “top-down” (TD) MS in an intact state, without cleavage into peptides. With TD MS¹, the amount of protein with exactly k modifications can be measured, but it is not possible to distinguish between positional isomers having the same number of modifications. TD MS¹ can therefore only provide n + 1 new equations. Although these are linearly independent, they can do little to counter the exponentially increasing shortfall of 2ⁿ⁻² (Figure 3).

Figure 3.

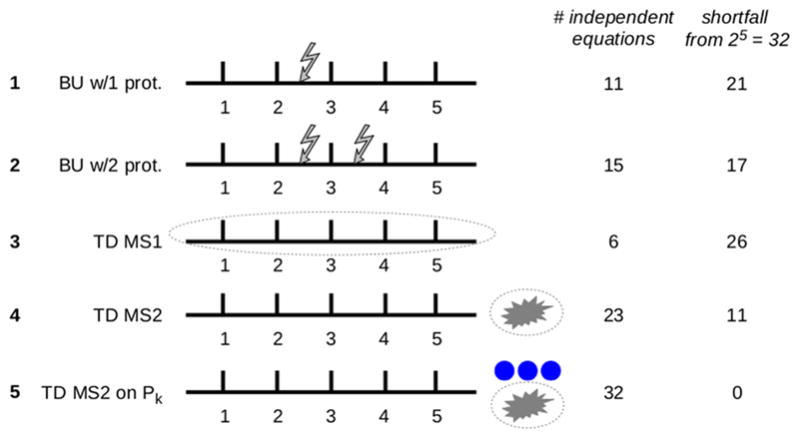
Reconstructing the modform distribution with various MS protocols. The results of the paper are illustrated for a hypothetical protein with five modification sites, subjected to five different MS protocols, as listed on the left: bottom-up with 1 and 2 proteases (jagged arrows show the cleavages), top-down MS1 (dotted oval around the intact protein), top-down MS2 (explosion symbol denotes fragmentation), and top-down MS2 after isolation of modforms with exactly k modifications, ℘_k(S), for all values from k = 0 to k = 5 (blue discs). The maximum number of linearly independent equations, which can be obtained under the assumptions used in the paper, are listed (right, first column) along with the shortfall required to fully determine the modform distribution (right, second column). The numbers of equations were determined from Theorem 1 (protocols 1 and 2), the discussion in the text (protocol 3), and by hand calculation (protocols 4 and 5).

More can be done, however, because the protein can be fragmented in the spectrometer and the masses of the fragment ions determined (TD MS²). Various techniques of fragmentation are available. Previous work has shown that with electron capture dissociation, the fragmentation efficiency is largely uniform across the protein backbone and is largely unaffected by the modification status of residues near the fragmentation site.³⁵ The resulting fragment ions (“fragments”) correspond to subsets of sites that are contiguous, such as F = {i, i + 1, ..., i + p}, where, in principle, i can run from 1 to n and p can be any number from 0 to n − i.

Mathematically speaking, fragments and cleavage peptides are similar: Both correspond to contiguous subsets of sites, both can have combinatorial patterns of PTMs or modforms, and both inherit a modform distribution from the parent protein. Fragmentation is subject to various biases and imperfections, but we will ignore these, as we did above for cleavage, so as to undertake a best-case analysis.

With MS², only those fragment modforms with different numbers of modifications can be distinguished. To express this, define the “counting map”, π_F: ℝ^℘(U) → ℝ^#F+1 by the matrix that has a 1 in row k only for those modforms with exactly k modifications and 0 elsewhere. Here k runs from 0 to #F. The overall result of undertaking TD MS² is then to yield the composition of the counting map π_F with the cleavage map c_F for the relevant fragment F. For the protein modform distribution x ∈ ℝ^℘(S), this composition yields the vectors π_Fc_F(x) ∈ ℝ^#F+1.

One important further step can be taken with TD MS. It is possible to efficiently isolate in the spectrometer those modforms with a given number of modifications.³² This determines a new distribution that is considerably simpler because it has many fewer modforms. To express this, let ℘_k(S) denote the set of those subsets of S of size k, corresponding to those modforms with exactly k modifications

$${\mathcal{P}}_k(S)=\{U\in \mathcal{P}(S)\text{such}\text{that}\#U=k\}$$

With this definition, ℘₀(S) = {ø}, ℘₁(S) = {{1}, ..., {n}}, and ℘_n(S) = {{1, ..., n}}. If x ∈ ℝ^℘(S) is a protein modform distribution, let x^(k) ∈ ℝ^℘_k(S) denote that part of x consisting only of those modforms with exactly k modifications

$$x^{(k)}=\sum _{U\in P_k(S)}x(U)e_U$$

The vector space ℝ^℘_k(S) can be regarded as the subspace of ℝ^℘(S) spanned by the unit vectors e_U with U ∈ ℘_k(S), so we can treat x^(k) as lying in ℝ^℘(S). The effect of isolating the modforms with k modifications and undertaking TD MS² is then to obtain the equations

$${\pi }_F{c}_F{x}^{(k)}={\theta }_{k,F}$$ (4)

where θ_k,F ∈ ℝ^#F+1 is the vector of measured amounts of fragment modforms having 0, ..., #F modifications, obtained from the protein modforms with exactly k modifications.

Equation 4 for TD MS² has several advantages over eq 3 for peptide-based MS. The original protein has 2ⁿ potential modforms, but the number of modforms with exactly k modifications is given by the binomial coefficient $\left(\begin{array}{c}n\\ k\end{array}\right)=n!/k!(n-k)!$. For fixed k, this number scales as n^k as n increases, which is much slower than the exponential increase in 2ⁿ for the total number of modforms. Furthermore, for different values of k, the equations in eq 4 are linearly independent of each other because they involve entirely different variables. This suggests that we may be able to do better using TD MS² to recover the protein modform distribution than with peptide-based MS (Figure 3).

The matrix corresponding to π_Fc_F is easily described: There is a 1 in the column corresponding to the modform subset U ∈ ℘(S) in the row whose index is #(U ∩ F), and there is 0 elsewhere in the column. As an example, consider a protein with n = 5 modification sites and suppose that we have isolated those modforms with k = 2 modifications. The fragment F = {2, 3, 4} gives rise to the fragment matrix

$${\pi }_F{c}_F=\begin{array}{|c|}\hline \begin{array}{ccccccccccc}& \{1,2\}& \{1,3\}& \{1,4\}& \{1,5\}& \{2,3\}& \{2,4\}& \{2,5\}& \{3,4\}& \{3,5\}& \{4,5\}\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 1& 1& 1& 1& 0& 0& 0& 1& 0& 1& 1\\ 2& 0& 0& 0& 0& 1& 1& 0& 1& 0& 0\\ 3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\\ \hline\end{array}.$$ (5)

Here the columns correspond to the $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$ modforms having exactly two modifications among five sites, as listed along the top row, and the rows correspond to the number of modifications found on fragment F after fragmentation, as listed in the first column.

As with the cleavage matrices arising in peptide-based MS, TD MS² fragment matrices like that in eq 5 have entries that are only 0 and 1, with a single 1 in each column. However, they differ from cleavage matrices in having different numbers of 1’s in each row, and some rows can even be 0. The nonzero rows are necessarily linearly independent. It is an interesting mathematical problem to find an analogue of Theorem 1 for the number of linearly independent rows when there are multiple fragments. This is work in progress, but an upper bound for this number is easily found and is already informative.

For modforms with exactly k modifications, the number of nonzero rows in any fragment matrix is at most k + 1. It is not difficult to see that there are n(n + 1)/2 contiguous subsets of the form {i, i + 1, ..., i + p}, which correspond to fragments. Hence the total number of nonzero rows is at most n(n + 1)(k + 1)/2. The number of linearly independent rows cannot be larger than this upper bound. For a given k, this bound scales as n², whereas the number of modforms with k modifications scales as n^k, as noted above. For k = 2, we have n(n − 1)/2 modforms with two modifications and no more than 3n(n + 1)/2 equations (not all of which will be linearly independent). The shortfall may be controlled in this case. Indeed, for n = 5 modification sites, for which modforms with k = 2 or k = 3 modifications are most important, TD MS2 after isolation of ℘_k(S) is sufficient to completely recover the modform distribution (Figure 3). However, this no longer holds for n = 6 (not shown), and the scaling causes the shortfall to inexorably worsen as n increases. TD MS² therefore offers an improvement over BU MS for small numbers of sites, but the information shortfall required to determine the protein modform distribution continues to worsen with increasing numbers of sites.

With a further round of fragmentation (MS³),³⁶ it may be possible to obtain the modform distribution of smaller fragments, which would increase the number of linearly independent equations. Whereas top-down MS¹, as noted above, is severely limited in what it can reveal about the modform distribution (Figure 3), top-down MS^N for N > 2 offers increasingly powerful capabilities as N increases. Greater depth of fragmentation may become available in the future, which raises the interesting question of whether the information shortfall can then be significantly reduced. The mathematical framework introduced here will enable this question to be rigorously addressed.

DISCUSSION

Figure 3 illustrates our results for a hypothetical protein with five modification sites. Whereas BU MS with multiple proteases is unable to recover the modform distribution, TD MS2 after isolation of ℘_k(S) is able to fully reconstruct it. However, as noted above, reconstruction by this method fails as soon as n > 5.

Despite the limits that we have derived, our results suggest how MS can still be feasibly exploited to estimate a protein’s PTM state. MS measurements, whether BU, MD, or TD, yield linear equations for the unknown modform amounts x(U) (eqs 3 and 4), so whatever data come from different protocols can be integrated in a common linear format. This suggests a way to constrain the modform distribution. Because modform amounts can never be negative, x(U) ≥ 0. Hence, if a linear equation specifies that x(U₁) + x(U₂) = δ, then it follows that x(U₁) and x(U₂) are confined within ranges: 0 ≤ x(U₁) ≤ δ and 0 ≤ x(U₂) ≤ δ. Each equation in which these variables appear further constrains them so that taking all of the equations together, from whatever MS measurements they come, may substantially limit the range of each of the variables. The modform amounts can be constrained, even if they cannot be exactly determined.

Because of the linear nature of the equations and the semilinear (inequality-based) constraints, we know that the modform distribution x is contained within a region bounded by flat sides in the high-dimensional space of all modforms. We call this the “modform region” (Figure 4). It represents the most knowledge that can be inferred about the modform distribution from whatever MS data is available. The shape of this region is potentially highly informative about which modforms, if any, dominate the distribution. This would indicate, in turn, which PTMs at which sites are influencing each other and suggest signatures of such influence that could be identified by targeted MS experiments. Furthermore, alterations to the pattern of PTMs arising from physiological perturbations are likely to change the shape of the region (Figure 4) and thereby link the perturbations to the interplay between PTMs and the resulting changes in PTM patterns. The modform region offers a data-centric proxy for the modform distribution and a way to visualize it in high-dimensional space. If there are protein PTM codes, as discussed in the Introduction, then the modform region offers a quantitative way to identify and analyze them.

Figure 4.

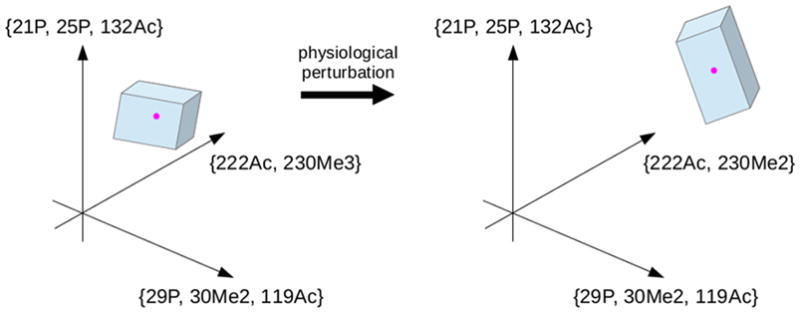
Modform region and perturbation. A hypothetical modform region is shown, with the high dimensional space ℝ^℘(S) restricted to three dimensions. The axes are labeled with hypothetical modform subsets using a notation that suggests how different types of PTMs—phosphorylation, acetylation, and methylation—can be described. The modform distribution, restricted to the three dimensions being shown, is the point (magenta) lying within the polyhedral modform region (blue). The position and shape of the modform region indicate what the MS data says about the modform distribution and the interplay between co-occurring PTMs. Physiological perturbations that alter the modform distribution can alter the position and shape of the modform region.

The methods of linear programming provide algorithms for determining regions defined by linear equations and semilinear constraints, and these algorithms are capable of efficiently dealing with thousands of variables. It seems, therefore, that modform regions can be feasibly estimated well beyond the examples previously studied with small numbers of modification sites.³⁰ The implementation of such methods is beyond the scope of the present paper, but we hope to report on it in subsequent work.

Our ability to determine protein PTM state and to make sense of how information is encoded by PTMs has been hampered by the difficulty of making quantitative measurements of modform distributions. Mass spectrometry currently offers the best methods for achieving this, but its capabilities and limitations have remained unclear. The mathematical language introduced here has allowed us to reason rigorously about MS measurements and to thereby determine both what is feasible with current technology and what is unattainable. As the number of modification sites increases, no current technology can keep up with the exponential increase in the information required to determine the modform distribution. At best, the distribution can be constrained within a high-dimensional modform region. Improvements to the depth of fragmentation in top-down MS may offer the best hope for achieving tighter constraints. We hope these general results will encourage further analysis of protein modforms, their distributions, and the biological information that may be encoded in them.