Deep Learning for Quantification of Epicardial and Thoracic Adipose Tissue from Non-Contrast CT

Abstract

Epicardial adipose tissue (EAT) is a visceral fat deposit related to coronary artery disease. Fully automated quantification of EAT volume in clinical routine could be a timesaving and reliable tool for cardiovascular risk assessment. We propose a new fully automated deep learning framework for EAT and thoracic adipose tissue (TAT) quantification from non-contrast coronary artery calcium CT scans. A first multi-task convolutional neural network (ConvNet) is used to determine heart limits and perform segmentation of heart and adipose tissues. A second ConvNet, combined with a statistical shape model (SSM), allows for pericardium detection. EAT and TAT segmentations are then obtained from outputs of both ConvNets. We evaluate the performance of the method on CT datasets from 250 asymptomatic individuals. Strong agreement between automatic and expert manual quantification is obtained for both EAT and TAT with median Dice score coefficients (DSC) of 0.823 (inter-quartile range (IQR): 0.779–0.860) and 0.905 (IQR: 0.862–0.928), respectively; with excellent correlations of 0.924 and 0.945for EAT and TAT volumes. Computations are performed in <26 seconds on a standard personal computer for one CT scan. Therefore, the proposed method may represent a tool for rapid fully automated quantification of adipose tissue and may improve cardiovascular risk stratification in patients referred for routine CT calcium scans.

I. INTRODUCTION

EPICARDIAL adipose tissue (EAT) is a local visceral fat depot contained by the pericardium, thus surrounding the coronary artery tree. This metabolically active fat depot—a recognized source of pro-inflammatory mediators— has been shown to promote the development of atherosclerosis in underlying coronary vasculature, through its direct contact with the coronary arteries [1–6]. Increased EAT volume has been shown to be independently related to major adverse cardiovascular events (MACE) [7–10], particularly in asymptomatic individuals, or to coronary artery diseases [11]. EAT can be manually measured from widely used coronary artery calcium (CAC) CT scans, performed for cardiovascular risk assessment [12, 13]. Thus, the quantification of EAT in clinical routine would be of great interest for a potential improvement in risk assessment and MACE prediction. However, it requires a time-consuming process. To date, measurement of EAT is not implemented in clinical practice, due to the absence of reliable, timesaving and fully-automated quantification methods. Quantification of EAT is technically a challenging task as it requires identification of the pericardium; quantification of thoracic adipose tissue (TAT, union of epicardial and paracardial adipose tissue (PAT)) is easier as it does not have this requirement. However, even if TAT and EAT volumes are correlated [14], previous studies shown EAT has a higher prognosis capability due to its immediate proximity to the heart and coronary arteries. Figure 1 shows the pericardium and adipose tissues around the heart in non-contrast CT.

Figure 1.

Pericardium and adipose tissues in calcium scoring non-contrast CT.

We propose a fast and fully automated algorithm for EAT and TAT volume quantification from non-contrast calcium scoring CT datasets, using a deep learning approach, based on convolutional neural networks (ConvNets) [15]. We first introduce previous work on EAT quantification, and ConvNets applied to medical imaging. We then describe the data used in this work and present the experiments performed. Finally, we conclude this paper with potential involvements suggested by the results and provide some ideas for further analyses. To our knowledge, this is the first application of deep learning for fully automated quantification of EAT and TAT from coronary calcium scoring CT scans.

II. RELATED WORK

A. Epicardial adipose tissue quantification in CT modality

Previous work on EAT quantification have been semi-automated and relied on expert manual measurements, following initial localization of the heart [16–18]. These approaches mainly consisted of identification of control points in transverse views. A spline was then interpolated to provide a segmentation of the pericardial sac for each axial slice. However, this time-consuming method is not suitable for clinical routine due to the tedious process required to quantify each dataset. Several solutions were then proposed to perform an automatic segmentation of the pericardium. In prior studies [14, 19], authors used the anatomy of the thoracic cavity and combined region-growing with adaptive thresholds to define a cardiac bounding box. This box allowed to define heart position in transverse views, but also to determine inferior and superior limits in the 3D CT volume. Atlas-based methods were also proposed to initialize the pericardium contour [20–23]. These initializations can limit the time required for the expert to analyze the whole 3D CT volume to define heart limits, and consequently also reduce expert variability; however, they do not identify automatically the pericardium border. A second step to detect the pericardial layer is required. To this end, a feature detector with an adapted kernel size only responding to the thin pericardium was proposed [20, 21]. When tested on 50 patients, this approach detected the mid-anterior region where the pericardial wall appears as a thin layer with higher Hounsfield units (HU) than the fat tissue. However, this approach had difficulties in detecting the pericardium in the superior and inferior parts of the heart where the adipose tissue distribution varies between patients. In [19], a radial sampling was performed on each transverse view, from the center of the heart. A detection of pericardium points was then performed along the direction of the sampling after a pre-processing step based on heart anatomy and intensity clustering. Recently, random forests were also proposed to classify voxels on the entire 3D pericardium shape [22]. Detection was performed along directions perpendicular to the pericardial surface, similarly to the radial sampling used in [19], which allows a rotational invariant feature detection, independently from the orientation with respect to the anatomy. This approach was validated on a small cohort of 30 coronary CT angiography (CTA) datasets.

Common methodologies were found among the studies proposed in the literature for automatic EAT quantification. To generalize the proposed approaches, automatic EAT quantification can be decomposed as a two-stage process: a first localization of the heart in the 3D CT volume, including inferior and superior heart limits definition, followed by a pericardium line detection. After these two steps, a final post-preprocessing was used in all the studies to exclude non-fat voxels with corresponding HU outside the adipose tissue attenuation range, defined in most of the studies from −190HU to −30HU.

To summarize, several approaches have been proposed for EAT quantification with promising initial results. However, there is still an unmet clinical need for a robust, fast and fully automated algorithm suitable for integration of EAT quantification from non-contract CT in clinical routine.

B. Convolutional neural network (ConvNets)

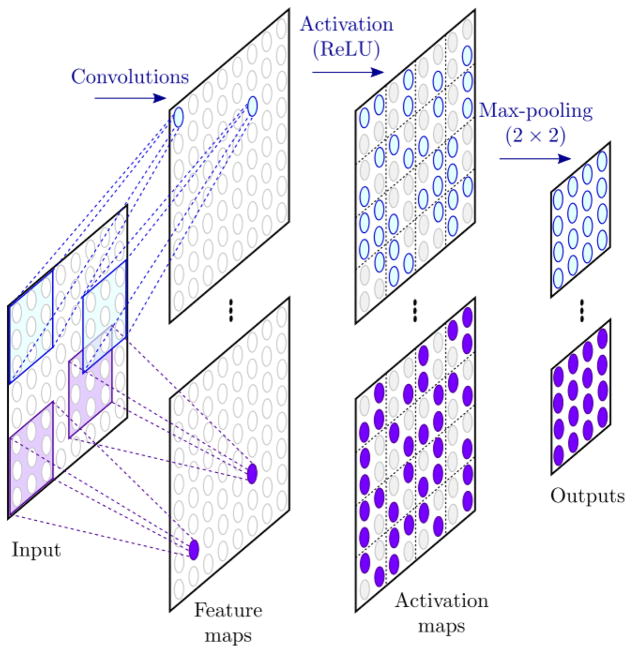
In the past few years, the popularity of deep learning methods has exponentially increased. These techniques have drastically improved the state-of-the-art performances for various tasks such as computer vision, speech recognition or natural language processing [15]. The popular AlexNet model proposed by Krizhevsky et al. [24], based on ConvNets, outperformed the results of previous works in the ImageNet classification challenge [25] and contributed to the interest for deep learning approaches. The development of ConvNets initially started three decades ago, inspired by the animal visual process, and one of their first applications was the recognition for handwritten digit [26]. ConvNets are variants of artificial neural networks in which the hidden layers are composed by convolution filters. These filters perform as feature extractors. Depending on the kernel size, each neuron in a layer responds only to a region of the previous layer, called receptive field. The filters are applied on the whole input of the layer with the same weights. Thus, each filter performs a feature detection independently from its position in the input and provide a feature map. Convolutional layers are usually combined with activation function, such as the rectified linear unit (ReLU), which add non-linearity in the network, and pooling layers which reduce the size of the input and ensure shift invariance in the feature detection. The sequence of consecutive convolutional, activation and pooling layers can be referred to hidden convolutional unit (HCU), as shown in Figure 2.

Figure 2.

Example of a hidden convolutional unit (HCU). Convolutions are performed on the input to provide feature maps. Each neuron in the feature maps responds only to its receptive field in the input, defined by the kernel size. Activation function is then applied to provide non-linearity in the network. Finally, a pooling layer reduces the dimension of the maps and increases the shift invariance of the feature detection.

Recently, ConvNets have found many applications in the field of medical imaging with an increasing number of publications. For example, ConvNets were used in cancer imaging for breast cancer [27, 28], brain tumor [29, 30] and lung nodule [31–33] detection, for classification of interstitial lung disease [34, 35] or for breast arterial calcifications [36]. In cardiac imaging, ConvNets have been widely used for ventricle and heart segmentation in MRI [37–40]. The second edition of the Annual Data Science Bowl (2016) held a competition on automated ejection fraction estimation from cine cardiac MRI, and thus has motivated the number of recent works proposed for ventricle segmentation. Previous studies have also described automatic coronary calcium scoring from both CTA and CT datasets [41, 42].

C. ConvNets and segmentation

Although ConvNets were historically developed for classification, several approaches have been proposed to allow segmentation tasks. A straightforward solution is to perform a patch-based pixelwise classification. The network is fed with a patch centered at the pixel to be classified and provides an output probability of the pixel of belonging to each class. The repetition across the whole image results in image segmentation. Although this approach has been efficiently used in several studies [34, 36], it only focuses on the neighborhood of the specified pixel, depending on the patch size, and thus limits the information used by the network for the global representation of the input. In [43], authors proposed fully convolutional networks (FCN), a variant of ConvNets, for semantic segmentation. This approach upsamples maps from intermediate HCU to the input resolution. These upsampled maps are then used to provide output probability maps for each class. FCN are fed with the entire image and only one forward pass is required to perform the segmentation. All the information contained within the input image can thus be used by the network to perform a more global representation. Each HCU are associated to a level of abstraction and their combination provide a multiresolution description of the image. Based on this work, several other segmentation networks have been proposed, such as the famous U-Net [44] and SegNet [45], and shown to be efficient for both non-medical and medical images segmentation. The main difference between these networks lies in the combination of the different layers and how the upsampled feature maps are concatenated. This approach is particularly interesting in medical imaging as it allows for the utilization of the whole anatomy and, by doing so, may provide a superior localization of the region of interest.

While deep learning methods, and especially ConvNets, have been widely used in medical imaging to tackle various problems, to the best of our knowledge, they have not been used yet for automatic pericardium identification and robust EAT quantification from non-contrast CT datasets.

III. MATERIAL

A. Datasets

The cohort used in this study comprised 250 consecutive non-contrast ECG-triggered CT datasets acquired for standard CAC scoring. These datasets were randomly collected from the prospective EISNER trial acquired at Cedars-Sinai Medical Center [46]. The patient population was composed by asymptomatic subjects with no previously known coronary artery disease but with cardiovascular risk factors. The population is described in Table 1. No scans were excluded due to poor image quality or artefacts. The average number of transverse slices per scan was 55, with a slice spacing equal to 2.5 mm or 3 mm. The dimension of each axial slice was 512×512 pixels of 0.684 mm × 0.684 mm. A total of 13756 transverse views were used in this study.

Table 1.

Patient characteristics

Characteristics	Data
No. of patients	250
Sex
No. of women†	103(41.2)
No. of men†	147(58.8)
Age (years)*	59.8±7
Body mass index (kg/m2)**	26.6[18.3–57]
Current smoker†	20(8)
Diabetes†	17(6.8)
Hypercholesterolemia†	171(68.4)
Calcium score**	5.2[0–2296]

^†Data provided as number of patients (percentage)

^*Data provided as mean ± standard deviation

^**Data provided as median and range

B. Ground truth generation

The evaluation of the ConvNet procedure for EAT quantification requires the definition of a reference gold standard. With this purpose, an imaging cardiologist certified in cardiac CT (level III reader) with over 3 years of experience in reading CAC scoring CT, manually drew a closed contour on every axial slice to identify the pericardium, encompassing the heart and EAT. A second closed contour was drawn around the first to include the PAT (external to the pericardium). Delineations were made using semi-automated QFAT research software (version 2, developed at Cedars-Sinai Medical Center). Binary masks were then generated for the EAT and heart, PAT and the thoracic mask defined as their union. Finally, as described in the related works, a threshold was used to exclude pixels with corresponding HU outside the fat attenuation range [−190HU, −30HU]. A median filter was also applied on each slice with a 3×3 kernel size to limit the influence of artefacts in the fat quantification. The inferior limit was defined as the axial slice below the posterior descending artery, while the superior limit was identified by the bifurcation of the pulmonary trunk [47].

IV. METHODS

A. Overall framework

Our proposed method is depicted in Figure 3. The fat segmentation is performed in axial slices, which are given as input of a first network Net₁. This network is composed by a convolutional architecture whose objective is to capture hierarchical features from the input. From this step, multiple tasks are performed. Firstly, fully connected (dense) layers are stacked to the architecture to determine if the input slice is located within the heart limits (Task 1). Secondly, up-sampling was done on the HCU of the convolutional architecture to perform two segmentation tasks: one for the union of intra and extra pericardial structures (Task 2), defining the thoracic mask, and one for their differentiation (Task 3), defining epicardial and paracardial masks, respectively. One of the novelty in our approach is the combination of dense layers and up-sampling blocks to perform a conjoint optimization of the convolutional architecture used for both slice classification and segmentation. A pericardium detection is then done by a second network Net₂. The epicardial mask resulting from Net₁ is firstly used to perform a radial sampling and transform the input CT slice from Cartesian to cylindrical coordinates. The transformed input is then given to the Net₂ which provides an output probability map of the pericardial sac. The maximal probabilities are then used to define a contour whose shape is regularized with a statistical shape model (SSM). The SSM was built by performing a singular value decomposition (SVD) on expert manual contours to extract main shape variabilities. Finally, the post-processing, including the HU threshold ([−190HU, −30HU]) to remove non-fat pixels and the median filtering, provides the binary fat images for adipose tissue quantification.

Figure 3.

Framework of the proposed method. An axial slice is given as input of the first network Net₁, which performs 3 simultaneous tasks: (1) slice prediction of being located between heart limits, (2) thoracic mask segmentation and (3) epicardial-paracardial masks segmentation. A second network Net₂ is used to perform pericardium line detection after atransformation of the input in cylindrical coordinates. A SSM shape regularization is then performed to obtain the final masksegmentation. A post-processing step, including Hounsfield unit threshold and median filtering, provides the adipose tissue masks.

B. Convolutional architecture

The convolutional architecture used in Net₁, described in Table 2, consisted in 6 stacked HCU. Each HCU was composed by convolutional, ReLU and max-pooling layers. The first HCU captured neighborhood texture information at pixel location with a kernel size of 5×5. A stride parameter equal to 2 was used for both convolution and pooling, reducing the input size from 512×512 to 128×128. The 5 others HCU were identical: a 3×3 convolutional kernel size and stride parameters equal to 1 and 2 for convolution and pooling, respectively, were used. As the depth increases, the feature maps size decreases. The high-level layers captured global information from the previous maps, describing the anatomical organization and providing localization information, and were used for slice selection.

Table 2.

Convolutional architecture of Net₁ (for slice classification and segmentation)

	Kernel size	Stride	Number of feature maps	Output size
Input	-	-	-	512×512
HCU 1	5×5	2	16	128×128
HCU 2	3×3	1	64	64×64
HCU 3	3×3	1	128	32×32
HCU 4	3×3	1	256	16×16
HCU 5	3×3	1	512	8×8
HCU 6	3×3	1	512	4×4

C. Slice selection using dense layers

Dense layers were concatenated to the convolutional architecture to perform the slice selection (Task 1). Two first layers were connected to the HCU 6. Each one was composed by 1024 neurons. These layers combined the information from the convolutional architecture to provide two scores, one for each class: selection or rejection of the current input slice. A final SoftMax layer was used to normalize the 2 output scores and provide probabilities for the axial slice to be located inside or outside the heart limits. The input slice was then selected if the associated probability to belongs within the limits was superior or equal to a threshold t_s (section V.D).

D. Segmentation using upsampling layers

When the input slice was selected, the results from binary mask segmentations (Tasks 2 and 3) were considered. Two upsampling blocks were added to the convolutional architecture. The first block was used to perform the thoracic mask segmentation. In each unit from HCU 2 to HCU 6, the feature maps were firstly combined to provide a score map: each pixel of the score map was assigned with the result of a weighted sum of corresponding pixels in all the feature maps. The weighted sum was done by a convolutional layer with a F×1×1 kernel size, where F is the number of feature maps. Five upsampling layers were then used to transform the score maps to the input size. Instead of using learnable weights in the upsampling layers, we fixed the weights to perform a bilinear interpolation, thus reducing the dimensionality of the optimization problem. Another convolutional layer with a 5×1×1 kernel size was used to combine the upsampled maps from the 5 HCU and provide 2 output maps. Again, a SoftMax function normalized the scores, for each pixel, to obtain probabilities of being inside or outside the thoracic mask. The binary mask segmentation was obtained, as in the previous task, by applying a threshold t_Tho on the thoracic probability map (section 0).

Similarly, a second upsampling block was used for the epicardial/paracardial masks segmentation. In this case, 3 output probability maps were obtained, one for each of the 3 classes to predict: epicardial mask, paracardial mask or the background. Because the thoracic mask was defined as the union of both epicardial and paracardial masks, we used it as a stencil for the segmentation. Epicardial and paracardial masks were defined by pixels inside the thoracic mask with greater epicardial or paracardial probabilities, respectively. From these definition, we ensured there was no overlap between epicardial and paracardial masks, and that their union was equal to the thoracic mask.

The first network Net₁ performed a first initialization of the pericardium which can be defined as the boundary between epicardial and paracardial masks. However, this definition is prone to shape irregularities. Discrepancies are likely to appear as the convolutional architecture performed a global representation of the input with respect to the anatomy but does not focus on the thin pericardium layer.

E. Pericardium identification

We performed a pericardium detection to regularize and improve the previous segmentation. Firstly, a radial sampling from the centroid of the segmented epicardial mask was performed to transform the input CT slice from Cartesian (x, y) to cylindrical (ρ,θ) coordinates. Sampling parameters were chosen to obtain a squared transformed image as input to the second ConvNet. A total of 256 rays were used to sample the image from 0° to 360° with an angle step Δθ≈1.4°. In each direction, 256 sampled points were obtained from ρ=0mm (centroid) to ρ=100mm, with a radius step Δρ≈0.39mm. The size of the transformed slice was 256×256. The transformed CT slice was given as input of a second FCN Net₂ whose convolutional architecture is presented in Table 3. Again, upsampling was performed from HCU 2 to HCU 5, and 2 output probability maps were provided, one for the pericardium line and one for the background. Each of the 256 columns of the pericardium probability map corresponded to a direction θ of the radial sampling. Along each direction, the pixel associated to the maximum probability was defined as a contour point (ρ,θ). The 256 points were used to define a new pericardium contour.

Table 3.

Convolutional architecture of Net₂

	Kernel size	Stride	Number of outputs	Output size
Input	-	-	-	256×256
HCU 1	5×5	1	16	128×128
HCU 2	3×3	1	64	64×64
HCU 3	3×3	1	128	32×32
HCU 4	3×3	1	256	16×16
HCU 5	3×3	1	512	8×8

F. Pericardium SSM and regularization

To limit the influence of misclassifications of Net₂, a shape regularization was performed with a SSM on the contour identified in the previous step. To build the SSM, a radial sampling was firstly used to transform manual pericardium contours from training datasets into vectors of cylindrical coordinates, with the same previous parameters (Δθ from 0° to 360°). A SVD was then performed on the sampled contours to extract shape variabilities among the training population. The new contour from Net₂ was projected to the space spanned by the left singular vectors (components of the model) obtained from the SVD. The regularization was then performed by reconstructing the new contour as a weighted sum of the SSM components. By limiting the components used in the reconstruction to the K first singular vectors, high frequencies corresponding to shape discrepancies, and encoded in last components, were removed. The regularized pericardium contour was finally rasterized to provide the final binary epicardial mask.

G. Post processing

Finally, the post processing step provided the binary fat segmentation. As used in the generation of the reference, a standard adipose tissue HU range [−190HU, −30HU] threshold was used on binary masks, and a median filter was applied.

V. EXPERIMENTS

In this section, we present all the experiments that were used to train, parameterize and evaluate the proposed method.

A. Evaluation and statistical analysis

The proposed method was evaluated in two ways. Firstly, the overlap ratio between expert and automatic fat segmentation was measured with the Dice score coefficient (DSC), defined as:

$$\mathit{DSC}(Fa{t}_{ex},Fa{t}_{DL})=\frac{2\mid Fa{t}_{ex}\cap Fa{t}_{DL}\mid }{\mid Fa{t}_{ex}\mid +\mid Fa{t}_{DL}\mid }$$

where Fat_ex and Fat_DL are the binary fat segmentation from the expert and the proposed deep learning algorithm, respectively. The volumes from both measures were compared using Pearson’s correlation coefficient, Bland-Altman analysis [48], and Wilcoxon signed-rank tests.

B. 10-fold cross validation

To perform a robust non-biased evaluation of the framework, a 10-fold cross validation was used. The whole cohort of 250 cases was split in 10 subsets of 25 cases each one. For each fold of the 10-fold cross validation, the following datasets were used: (1) training dataset - 8 subsets (200 cases) were used to train the ConvNets and create the SSM, (2) validation dataset - one subset (25 cases) was defined to tune the networks, select the optimal number of components in the SSM regularization and verify there was no over-fitting, (3) test dataset - the last subset (25 cases) was used for the evaluation of the method. The final results were then concatenated from 10 separated subsets. Thus, the overall test population was 250 subjects with 10 different models.

C. Networks training

Our networks architectures are based on initially proposed FCN [43] and have been optimized through multiple experiments. The number of layers, numbers of kernels per layer, numbers of neurons in dense layers and numbers of upsampling layers, as well as optimization parameters, were then determined as the ones maximizing the performances over the validation subsets. Thus, the configuration providing the best training convergence and optimal generalization error (error obtained on the validation dataset) was used for the evaluation on the test subsets.

In a first attempt, the three tasks of Net₁ were trained independently with the same 10 folds. However, the slice classification task (Task 1) trained alone provided a poor accuracy in detecting inferior and superior limits. Similarly, the epicardial/paracardial segmentation (Task 3) did not provide a good differentiation between the two classes. By combining all the task together in a simultaneous training, we noticed a drastic improvement for both classification and segmentation.

The optimization of Net₁ was thus performed as a multi-task training (Task 1–3, Figure 3). Backpropagations for each loss function of the three tasks described in section IV were done simultaneously. The global loss and gradients of the network were defined as a weighted sum of the losses and gradients of the three tasks. The optimal set of weight values, defined as the one leading to the best generalization on the validation dataset, was obtained by a grid search with steps equal to 0.1.

The second network Net₂ was trained until the convergence of the validation loss was reached. The same architecture of the first network (5 last HCU) was used.

For each network, the training was performed by minimizing the cross-entropy loss function using a stochastic gradient descent optimizer. For optimization parameters, the starting learning rate was set to 0.005, with a rate decay of 0.5 every 20000 iterations. A momentum parameter equal to 0.9 and a batch size of 20 were also added to regularize the optimization. Finally, to limit overfitting, drop out layers [49] were used before each score computation with a drop out ratio equal to 0.5. The training slices where randomly shuffled to prevent the networks from learning over similar epochs.

D. Segmentations

Three parameters were used in the segmentation definition: the probability thresholds t_s and t_Tho used for the slice selection and the thoracic segmentation, respectively, and the number of components K used in the pericardium shape regularization. The influence of these three parameters was assessed on the validation subset. For each fold, the threshold values t_s and t_Tho maximizing the slice classification accuracy and the DSC between expert manual and automatic measurements for TAT, respectively, were then used for the segmentation of the test subset. Similarly, the number of components K which maximized the DSC for EAT on the validation subset was also used to regularize segmentations on the test subset.

E. Implementation

The proposed method was implemented in python using the Caffe library [50] for the processes involving ConvNets. The other parts of the method were implemented in C++ and python. All experiments were done on a Linux OS, with an Intel Core i7-6800K CPU @ 3.40GHz, 2 NVIDIA 1080 GPU and 32GB of RAM. The time required for the training in each fold of the cross validation was approximatively 11 hours. After the development, the method was tested on a standard personal computer on a Windows 10 OS with CPU computation only (Intel Core i7-6700 CPU @ 3.40GHz and 16GB or RAM). The mean time required to quantify EAT and TAT on the 250 cases was 25.63±3.72 seconds per case, using CPU computation only and 3.26±0.87 seconds with GPU computation, compared to approximatively 10–11 minutes for EAT and TAT quantifications performed by the expert.

VI. RESULTS

We present in this section all the results from the experiments.

A. Multi-task optimization

The optimization on the first fold is presented in figure 4. The global loss function is equal to a weighted sum of the 3 tasks; (1) slice classification, (2) thoracic segmentation and (3) epicardial segmentation. The optimal weights for the 3 tasks, according to the grid search, were 0.2, 0.4 and 0.4, respectively.

Figure 4.

Multi-task loss evolution during the first fold optimization. Plain and dash lines represent loss of the training and validation datasets, respectively.

B. Slice selection

Performance for the slice classification task (Net₁, of being within the heart limits) was evaluated by receiver operating characteristic (ROC) curves performed on the test dataset for each of the 10 folds. Net₁ provided a very high performance in the slice selection with a mean area under the curve (AUC) of 0.992±0.002. The maximal classification accuracy of 0.953±0.005 was obtained for a threshold t_s=0.531±0.051. The low standard deviation of the optimal threshold demonstrated a coherence between the 10 Net₁ trained in each cross-validation fold. The model has proved to correctly identify heart limits with mean slice position errors per scan of 0.22±0.287 and 0.132±0.316, in slice units, for the inferior and superior limits, respectively. No misclassified slices were found in the median zone or outside the heart far from limits. We observed a slightly lower error obtained for the superior limit compared to the inferior limit.

C. Thoracic segmentation and fat quantification

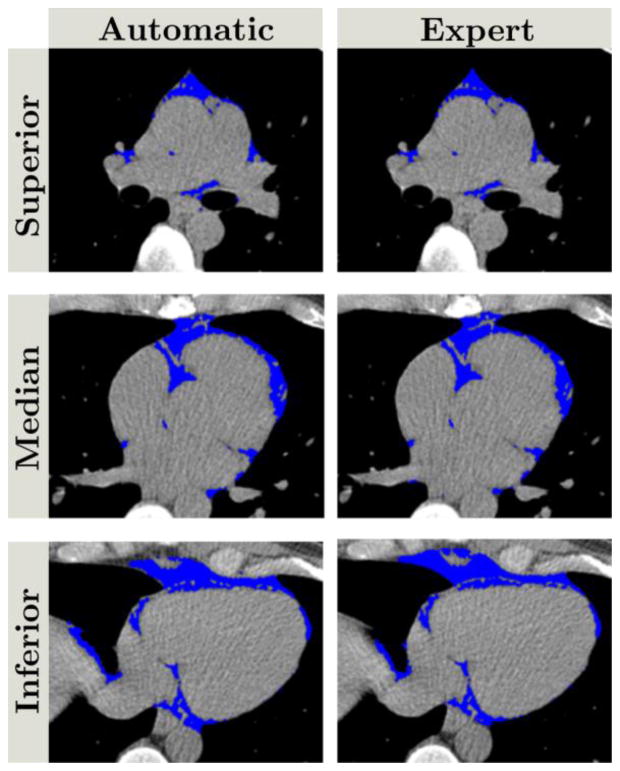
The second task of the Net₁ consisted in the segmentation of the thoracic mask, providing the TAT segmentation after the post-processing. Across the 10 test datasets, a median DSC of 0.905 (IQR: 0.862–0.928) was obtained for a probability threshold t_Tho=0.214±0.008. The optimal threshold provided for each fold a high correlation between automatic and manual TAT volume quantifications (correlation coefficient R=0.945, p<0.00001) as presented in figure 5. The Bland-Altman analysis (figure 6) demonstrated a bias between the two measures equal to 0.12 cm³ (95% Confidence Interval (CI): [−3.29,3.28]). No significant differences were found between the two measurements (expert vs. automatic, p=0.92). The median TAT volume was 130.35cm³ (IQR: 89.12–198.18) and 130.94cm³ (IQR: 87.24–193.69) for expert and automatic quantification, respectively. This high agreement between our proposed method and expert measurement is very promising for clinical routine consideration and for further analyses. A comparison between expert and automatic segmentation is presented in figure 7.

Figure 5.

Automatic vs. expert TAT quantifications. An excellent agreement was obtained with a high correlation (R=0.945).

Figure 6.

Bland-Altman analysis of automatic vs. expert TAT quantifications. The analysis demonstrated a non-significant bias between the two measures (0.12 cm³, p=0.92).

Figure 7.

Comparison of automatic (left column) and expert (right column) thoracic fat segmentation. Blue pixels correspond to fat pixels obtained after post-processing the thoracic mask from Net₁. Top, middle and bottom rows correspond to superior, median, and inferior parts of the heart, respectively. The DSC was 0.905.

D. Epicardial segmentation and fat quantification

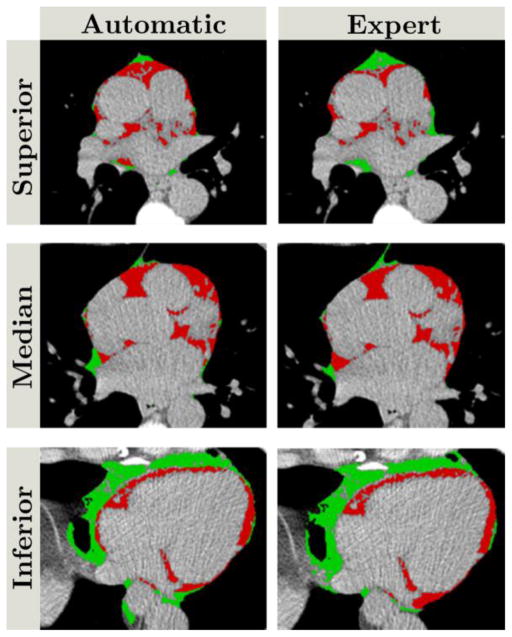
The second network Net₂ and the SSM regularization allowed for an accurate pericardium identification. A comparison of the pericardium defined by Net₁ and the pericardium after SSM regularization is presented in figure 8. From this example, while the initial definition (green) does not provide a reliable contour, the final definition of the pericardium (red) ensures a robust contour similar to the expert manual delineation (white). The resulting DSC for the epicardial mask (before the fat threshold) and for EAT were 0.926 (IQR: 0.914–0.937) and 0.823 (IQR: 0.779–0.860), respectively. They were obtained for K=4 components used in the shape regularization. The median EAT volume was 78.03cm³ (IQR: 57.08–105.79) and 78.64cm³ (IQR: 54.48–106.58) for expert and automatic quantifications, respectively. An excellent correlation was obtained (0.926, p<0.00001) (figure 9). The Bland-Altman analysis demonstrated a low bias of −1.41cm³ (95% CI:[−3.08,0.26]) (figure 10). No significant differences were found between the two distributions (p=0.79). An example of EAT segmentation (after the post-processing to remove non-fat pixels) is presented in figure 11 and compared to expert manual delineation. For comparison, when not considering the combination of the Net₂ and SSM for EAT quantification, the DSC and volume correlation were 0.727 (IQR: 0.693–0.765) and 0.894. A significant difference was obtained between expert and Net₁ quantifications (p<0.0001). When considering the pericardium detection from Net₂ but not the shape regularization, a median DSC of 0.814 (IQR: 0.762–0.847) was obtained, showing no significant difference with the full method (p=0.09). However, when comparing the Hausdorff distances for the pericardium contours without SSM regularization [7.61mm (IQR:6.48–9.12)] and with [5.03mm (IQR: 4.34–7.20)], a significant difference was observed (p<0.001). These results show the interest of the second step for pericardium identification and regularization.

Figure 8.

Pericardium defined by Net₁ (green) and after SSM regularization (red), compared to the expert delineation (white). While the green line presents a non-reliable shape, the combination of the Net₂ and the SSM ensures a smooth pericardium contour closer to the expert delineation.

Figure 9.

Automatic vs. expert EAT quantifications. A very high correlation was obtained between both measurements (R=0.926

Figure 10.

Bland-Altman analysis of automatic vs. expert EAT quantifications. A non-significant bias of −1.41 cm³ was obtained (p=0.79).

Figure 11.

Comparison of automatic (left column) and expert (right column) epicardial (red)/paracardial (green) adipose tissue segmentations. Top, middle and bottom rows correspond to superior, median, and inferior parts of the heart, respectively. The DSC was 0.823.

E. Interest of the multi-task learning

To assess the interest of using multi-task learning for Net₁, especially combining the slice classification with the mask segmentations, we compared TAT segmentations when separating the tasks during the training to those previously presented (section VI. C.). TAT was segmented on each slice using single task learning, and independently, slices predicted outside the limits were then removed. The median DSC was 0.863 (IQR: 0.823–0.890), showing a significant difference compared to DSC from multi-task learning according to the Wilcoxon test (p<0.00001). The average errors on limit prediction, when doing single task learning, were 1.24±0.652 and 1.03±0.476, in slice units, for inferior and superior limits, respectively.

F. Comparison to the state-of-the-art: U-Net

To compare our proposed approach to a reference segmentation method from the literature, we performed a comparative study with the U-Net architecture [44]. The originally proposed architecture was used for the comparison and dense layers were concatenated to the deepest layer for slice classification supervision. The same meta-parameters were used for the training of the U-Net networks. Results were evaluated using the same 10 folds. As for our proposed approach, the U-Net segmentation target were the binary masks, and the post-processing was applied to remove non-fat pixels. For TAT quantification, the modified U-Net architecture provided DSC and volume correlation of 0.822 (IQR: 0.779–0.852) and 0.874 (p<0.0001), respectively, with a significant difference from expert quantification (p=0.041). For EAT quantification, DSC and correlation were 0.719 (IQR: 0.633–0.762) and 0.829 (p<0.0001). Again, a significant difference was obtained with the expert measures (p<0.0001).

G. Accuracy

In both tissues quantification, we observed a decrease in the accuracy when the volume increases. This observation may have several explanations such as higher adipose tissue around the diaphragm or anatomical variations leading to specific adipose tissue distributions as presented in figure 12. A weak correlation was found between EAT errors and BMI (r=0.229, p=0.0003). However, no correlations were obtained between other patient’s characteristics reported in Table 1 and errors in percentage (relatively to expert measures).

Figure 12.

Axial slice from an outlier case (68-year old male) with BMI 31.1. We observe larger amount of adipose tissue in the superior and anterior part of the heart (yellow arrow). The pericardium is also invisible in this part, which explains the failure of the algorithm to provide a contour (red) close to the expert delineation (white). This pattern is present in most of the outliers in our results.

H. Comparison to inter-observer variability

Finally, to fully assess the performance of the proposed approach, a second expert performed manual measurements on 30 cases randomly selected among the initial 250 cases. The second expert was blinded from results from the first expert and from the automated approach. We compared the automated quantifications with the manual measurements from both experts on the 30 cases. Table 4 summarize the results.

Table 4.

Automated quantification and inter-observer variability

		DSC	Correlation	Wilcoxon (p-value)
TAT	O1 vs. O2	0.906	0.96	0.88
	O1 vs. DL	0.917	0.98	0.79
	O2 vs. DL	0.895	0.97	1
EAT	O1 vs. O2	0.89	0.97	0.65
	O1 vs. DL	0.808	0.98	0.80
	O2 vs. DL	0.801	0.94	0.76

O1: first observer, O2: second observer, DL: automated method

VII. DISCUSSION

We developed and evaluated a novel multi-task deep convolutional neural network approach for fully automatic quantification of epicardial and thoracic adipose tissues from non-contrast calcium scoring CT datasets. To our knowledge, multi-task ConvNets for both heart classification and segmentation with shape regularization for pericardium detection has not been applied before to clinical cardiac CT data. We demonstrated that automatic adipose tissue volume quantifications by the proposed method show strong agreement with expert manual measurements. In addition, deep learning estimations of epicardial contours also showed strong agreement to expert manual delineations. The proposed method may offer a timesaving tool for fully automated EAT and TAT quantification in clinical routine which, when integrated with calcium scoring from non-contrast CT scans, could improve cardiovascular risk stratification, without additional radiation exposure for the patient or additional interaction for the physician. The runtime for segmentation and quantification of volumetric adipose tissues is <26 seconds for a whole 3D scan on a standard computer compared to approximatively 10–11 minutes for EAT and TAT quantification performed by the expert, which potentially facilitates TAT and EAT volume quantification in clinical routine for improved cardiovascular risk assessment.

Our fully automated approach correlated highly with standard manual measurements of EAT. The variability between automatic quantification and expert manual measurement reported in our study is similar to the inter-expert variability as reported in a previous study on the EISNER cohort [18] and in other cohort [51]. Notably, the segmentation results were statistically equivalent between our approach and either expert reader. The results obtained on 30 cases and compared to the measurements from two expert readers demonstrated the proposed approach can be considered as a third expert reader for TAT and EAT quantification. The novel aspect of this approach is fully automated, high performance segmentation of EAT and TAT from standard coronary calcium scoring CT, which offers immediate translational value and enhances the clinical impact of this work.

Our approach has been evaluated on the largest cohort to date for EAT and TAT volumetric quantification with N=250 CT scans. We used a multi-task training approach for the quantification of EAT and TAT. In a previous study, multi-task training has also provided equivalent or higher performances for medical image segmentation compared to task specific training [52]. In our approach, we enhanced the multi-task procedure by combining different architectures, namely dense layers and upsampling blocks, that are trained simultaneously to derive a unique deep learning model that performs cardiac CT slice classification and tissue segmentation at the same time. The multitask learning performed better than single task learning, tried in a first attempt. It improved performances of both heart limits detection and epicardial segmentation. The improvement of the epicardial segmentation allowed to provide a more robust identification of the centroid for the radial sampling. This robustness was important to not introduce variability in the SSM which was related to centroid position and not to pericardium shape. Moreover, the proposed deep learning framework incorporated a probability map computation for pericardial contour pixels followed by a statistical pericardial shape model to enhance the delineation of the pericardium to a smooth contour. Finally, we compared our proposed approach to a modified version of U-Net with slice classification supervision. For TAT quantification, U-Net provided lower results than our method, for both DSC and volume quantification. A significant difference was also observed between the U-Net TAT quantifications and the expert manual measurements. For EAT quantification, U-Net performed also worse than our approach, even when considering only the results from the first step, without pericardium identification and shape regularization. Again, a significant difference was obtained with the expert manual measurement. The reason for the lower performances obtained by U-Net may potentially be the upsampling process combined with the skip connections. In U-Net, the upsampling is performed on the second half, with consecutive up-convolutions, from the lowest resolution to the input resolution. In parallel, the skip connections transport the information directly to the second half of the architecture. Thus, the direct transport of the very early layers, especially the first one directly connected to the output, gives more importance to high resolution signals, attenuating the signal from deep layers. In our proposed approach, upsampling is used to connect the intermediate layers directly to the output (Figure 3, section IV. D.), unlike U-Net skip connections which go through the consecutive up-convolutions, especially the deepest ones. We also removed the connection of the first layer, to limit high variations in the output.

There are some limitations in our study. We used single-center CT datasets with one expert reader as the reference standard for training data. In future work, we plan to evaluate our framework on larger multicenter cohorts with multiple expert readers. We observed lower accuracy for both TAT and EAT as the volume increases. This observation can be explained by anatomical variations in patients with higher BMI. In most of outlier cases, a larger amount of adipose tissue was observed in the superior and anterior part of the heart (Figure 12). Moreover, in these cases, the pericardium line was barely visible, which explain the low accuracy of the automatic delineation and quantification. In future work, more cases with such anatomical variations will be included in the training dataset to allow the ConvNets to learn this adipose tissue pattern and improve the accuracy. Finally, a 2D approach was considered instead of using 3D ConvNets. This choice was motivated by several reasons. Firstly, the complexity of the network increases when considering 3D convolutions, while the number of observations decreases. Indeed, a whole 3D scan would be considered as a single observation, compared to an average of 55 observations (2D slices) per scan for the 2D approach. The number of training data would then be reduced from >11000 to 200. Also, the anisotropy of the data, as well as the different number of slices between scans, are other reasons which motivated us to consider 2D ConvNets in a first attempt. A preprocessing step would be required to reshape the scan and may lead to missing information in some observations due to the difference in the field of view between scans. In future work, we will increase the number of data and use a reshape preprocessing to evaluate a 3D convolutional approach.

VIII. CONCLUSION

We propose and evaluate a new multi-task framework based on deep convolutional neural networks for fully automated quantification of epicardial and thoracic adipose tissue volumes from non-contract CT datasets. The proposed method provided fast segmentation with strong agreement with expert manual volume measurements. The proposed approach may represent a tool for rapid measurement of EAT volume as an imaging biomarker for future clinical use, offering promise for improved prediction of adverse cardiac events.