Abstract
Automatic segmentation of abdominal anatomy on computed tomography (CT) images can support diagnosis, treatment planning and treatment delivery workflows. Segmentation methods using statistical models and multi-atlas label fusion (MALF) require inter-subject image registrations which are challenging for abdominal images, but alternative methods without registration have not yet achieved higher accuracy for most abdominal organs. We present a registration-free deep-learning-based segmentation algorithm for eight organs that are relevant for navigation in endoscopic pancreatic and biliary procedures, including the pancreas, the GI tract (esophagus, stomach, duodenum) and surrounding organs (liver, spleen, left kidney, gallbladder). We directly compared the segmentation accuracy of the proposed method to existing deep learning and MALF methods in a cross-validation on a multi-centre data set with 90 subjects. The proposed method yielded significantly higher Dice scores for all organs and lower mean absolute distances for most organs, including Dice scores of 0.78 vs. 0.71, and 0.74 for the pancreas, 0.90 vs 0.85, 0.87 and 0.83 for the stomach and 0.76 vs 0.68, 0.69 and 0.66 for the esophagus. We conclude that deep-learning-based segmentation represents a registration-free method for multi-organ abdominal CT segmentation whose accuracy can surpass current methods, potentially supporting image-guided navigation in gastrointestinal endoscopy procedures.
Index Terms: Abdominal CT, Segmentation, Deep learning, Pancreas, Gastrointestinal tract, Stomach, Duodenum, Esophagus, Liver, Spleen, Kidney, Gallbladder
I. Introduction
Segmentation of organs in abdominal images can support clinical workflows in multiple domains, including diagnostic interventions, treatment planning and treatment delivery. Organ segmentation is a crucially important step for computer-assisted diagnostic and biomarker measurement systems [1]. Segmentations of treatment volumes and organs-at-risk are also central to planning radiation therapies [2]. More generally, segmentation-based patient-specific anatomical models can support surgical planning and delivery via intra-operative image-guidance systems [3].
In endoscopic pancreatobiliary procedures, an endoscope is inserted orally and navigated through the gastrointestinal tract to specific positions on the stomach or duodenal wall to allow pancreatobiliary imaging and intervention. Due to the small endoscopic field of view and the lack of visual orientation cues, this navigation task is challenging, particularly for novice endoscopists [4]. Image-guidance showing registered anatomical models would provide orientation and targeting cues that are outside of the endoscopic field of view or challenging to see on endoscopic images. To support targeting and navigation, segmentations of multiple organs are needed: the pancreas, gastrointestinal organs (esophagus, stomach and duodenum), and nearby organs used as navigational landmarks (liver, gallbladder, spleen and left kidney).
Manual segmentation of 3D abdominal images is laborintensive and impractical for most clinical workflows, motivating (semi-)automated segmentation tools [2]. Research into such tools has focused on computed tomography (CT), due to its clinical prevalence, and on three methodologies: statistical models (SM) [5], [6], multi-atlas label fusion (MALF) [6]–[10] and registration-free methods [11]–[14]. SM and MALF, reviewed in more detail in Section I-A1, rely on establishing anatomic correspondences between images from different subjects, a task that remains challenging due to high inter-subject variability in organ shape and appearance as well as soft tissue deformation [15]. Registration-free methods trade registration challenges for the challenges of constructing variability- and deformation-invariant features (”hand-tuned” or learnt) that characterize anatomy in an unregistered training data set. Despite the claimed advantage of this approach, registration-free methods have achieved less accurate multi-organ segmentations than the registration-based approaches [16].
Recent advances in machine learning, computational power and data availability, however, have enabled the training of more complex registration-free methods, including deep fully convolutional networks (FCNs), promising increased segmentation accuracy [17]. FCNs, discussed in detail in Section I-A2, are particularly well-suited to multi-organ abdominal segmentation because they require neither explicit anatomical correspondences nor hand-tuned image features. In multi-organ abdominal segmentation, they have been used alone [18] or with pre- or post-processing, such as level sets [19] and MALF [20], demonstrating their potential value. However, these pipelines still have not achieved higher accuracies than the most accurate registration-based methods for most organs [16].
This study presents the dense V-network FCN (DenseVNet) and its application to multi-organ segmentation on abdominal CT, yielding higher accuracies than three existing methods. The contributions of this work are four-fold:
-
1)
The DenseVNet segmentation network is presented, which enables high-resolution activation maps through memory-efficient dropout and feature reuse.
-
2)
A batch-wise spatial dropout scheme is proposed, which lowers the memory and computational costs of dropout.
-
3)
The accuracy of DenseVNet for multi-organ segmentation from abdominal CT is evaluated using a cross-validation over 90 manually segmented images from multiple centres. The results indicate that higher segmentation accuracy can be achieved than a state-of-the-art MALF method and two existing FCNs.
-
4)
The parts of DenseNet critical for accuracy are identified by comparing the accuracies of network variants.
This builds on our preliminary work [21], with an improved network architecture, a larger data set, and more extensive comparisons with other algorithms and network variants.
A. Related work
1). Common multi-organ segmentation methodologies
Statistical models [5], [6] involve co-registering images in a training data set to estimate anatomical correspondences, constructing a statistical model of the distribution of shapes [22] and/or appearances [23] of corresponding anatomy in the training data, and fitting the resulting model to new images to generate segmentations. Multi-atlas label fusion methods [6]–[10] register images in a training data set to each new image and combine propagated reference segmentations to generate new segmentations. Statistical models and multi-atlas methods are limited by image registration accuracy. This registration, while extensively studied, remains challenging [15]. The size, shape, appearance, and relative positions of abdominal organs vary considerably between patients due to natural variability, disease status and previous treatments and within each patient due to soft tissue deformation. To avoid challenging registrations, registration-free methods train a voxel-wise classifier on unregistered images. Some methods have relied on handcrafted organ-specific image features [11], [12], but many recent approaches involve training classifiers on selected (but typically organ-agnostic) image features [13], [14]. Registration challenges notwithstanding, MALF has yielded more accurate multi-organ abdominal CT segmentations than registration free methods for most organs [16]. However, recent advances in registration-free methods may change this.
2). FCNs for segmentation
FCNs are compositions of simple image-to-image functions with trainable parameters, including convolution with linear kernels and voxelwise non-linearities. FCNs are efficient architectures for deep-learning-based tasks that require image outputs like segmentation.
FCNs have recently been applied to segmentation of volumetric images in medical image analysis [18], [19], [24]–[26] where such images are common. Segmentation of volumetric images face particular challenges, mainly due to the need to process large volumetric images under memory constraints.
One strategy to constrain the memory usage is to process smaller images: small patches of a larger image or lower resolution images. Image-patch segmentations consider various patch types – single 2D slices, slabs of adjacent 2D slices or smaller cropped regions – and orientations – single axis-aligned slices, multiple slices from multiple axes, or oblique slices. These methods gain memory efficiency but lose spatial context. In contrast, Milletari et al. [25] and Çiçek et al. [24] used 3D representations of the entire image by downsampling the image sequentially so that most image features are only represented at low resolution. Our previous work [21] used 3D representations with fewer, but higher-resolution, features by using dense blocks [27], stacks of convolutional units in which the input of each layer comprises the outputs of all preceding stack layers, compensating for using fewer features.
Another strategy to constrain the memory usage is to limit the network depth. However, this affects the FCN receptive field (i.e. the size of the image region affecting each output voxel), which grows linearly with the network depth. Larger convolutional kernels mitigate this by increasing the linear growth rate; however, this can result in a very high parameter count (which grows as the cube of kernel size in 3D). Sequential downsampling, mentioned above, also mitigates this effect, as the receptive field grows exponentially with the number of downsampling stages. Dilated convolutions [28], used in our previous work [21], instead use large, but sparse kernels to give exponential receptive field size with few parameters.
Multi-organ segmentation poses additional challenges. First, more information must be propagated through the network, exacerbating the aforementioned memory challenges. The relative weighting of the losses for different organs (with high volume imbalance) can have unpredictable effects on convergence and final errors; using the Dice coefficient is common but remains poorly characterized. Imposing shape [29] and topological [30] constraints between specified organs also remains challenging. Despite these challenges, deep learning has been used in multi-organ abdominal CT segmentation alone [18], [31] or as part of a larger segmentation pipeline [19], [20]. Zhou et al. [18] segmented 19 abdominal organs on 2D slices in axial, sagittal and coronal views and combined the results using majority-voting label fusion. Roth et al. [31] segmented 7 organs using a two-stage hierarchical pipeline based on 3D UNet [24]. Hu et al. [19] segmented 4 organs using a 3D FCN to generate organ probability maps as features for a level-set-based segmentation. Larsson et al. [20] used MALF to identify a region of interest for each organ and a 3D FCN with hand-tuned input features to complete the segmentation. Compared to registration-based methods in a recent segmentation challenge [16], these methods were substantially more accurate (>2% Dice score improvement) for gallbladder, achieved parity (within 2% Dice score) for the liver, left kidney, right adrenal gland and aorta, but have lower accuracy for the pancreas, gastrointestinal tract (esophagus, stomach) and other organs (spleen, right kidney, vena cava, portal/splenic vein, and left adrenal gland).
II. Data
Ninety abdominal CT images and corresponding reference standard segmentations of the spleen, left kidney, gallbladder, esophagus, liver, stomach, pancreas and duodenum were used for this study. The CT images and some of the segmentations were drawn from two publicly available data sets: forty-three subjects from the Cancer Imaging Archive Pancreas-CT data set [26], [32], [33] with pancreas segmentations and 47 subjects from the ‘Beyond the Cranial Vault’ (BTCV) segmentation challenge [16] with segmentations of all organs except duodenum. The remaining reference standard segmentations were performed at our centre. The completed segmentations and subject identifiers have been made publicly available (DOI:http://doi.org/10.5281/zenodo.1169361).
A. Image data
The Pancreas-CT data set comprises abdominal CT acquired at the National Institutes of Health Clinical Center from pre-nephrectomy healthy kidney donors or patients with neither major abdominal pathologies nor pancreatic cancer lesions [33]. The BTCV data set comprises abdominal CT acquired at the Vanderbilt University Medical Center from metastatic liver cancer patients or post-operative ventral hernia patients [15]. Images had voxel sizes from 0.6–0.9 mm in the anterior-posterior (AP) and left-right (LR) axes and 0.5–5.0 mm in the inferior-superior (IS) axis. Images were manually cropped to the rib-cage and abdominal cavity transversely, to the superior extent of the liver or spleen and the inferior extent of the liver or kidneys, resulting in fields of view ranging from 172–318mm AP, 246–367mm LR and 138–283mm IS.
B. Reference standard segmentations
Segmentations from the Pancreas-CT and BTCV datasets were used where available. An imaging research fellow (E.G.), under the supervision of a board-certified radiologist with 8 years of experience in gastrointestinal CT and MRI image interpretation (F.G.), interactively segmented the unsegmented organs on both data sets and edited the segmented organs to ensure a consistent segmentation protocol, using Matlab 2015b and ITK-SNAP 3.2 (http://itksnap.com).
III. Methods
This study compares our proposed algorithm to multiple automated segmentation algorithms in two experiments. First, to evaluate the improvements to the state of the art in segmentation accuracy due to our algorithm, we compare three distinct algorithms detailed below: the multi-atlas-label-fusion-based DEEDS+JLF [34], [35], the deep-learning-based VoxResNet [36], and the proposed deep-learning-based DenseVNet. Second, to clarify the architectural factors contributing to these improvements, we compare variations of the proposed DenseVNet architecture.
A. Proposed algorithm: Dense V-network segmentation
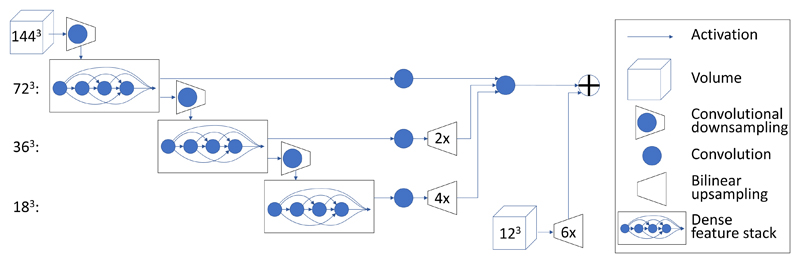
The proposed segmentation method uses a fully-convolutional neural network [37] based on convolutional units composed as shown in Figure 1. The architecture design can be understood in terms of 5 key features described below: batch-wise spatial dropout, dense feature stacks, V-network downsampling and upsampling, dilated convolutions, and an explicit spatial prior. For clarity and precision, each of these will be described conceptually and specified mathematically. The supplementary material, available in the multimedia tab online, has guidance for implementing the network.
Fig. 1.
DenseVNet network architecture. First, 723 feature maps are computed using a strided convolution. Second, a cascade of dense feature stacks and strided convolutions generate activation maps at three resolutions. Third, a convolution unit is applied at each resolution reducing the number of features. Fourth, after bilinear upsampling back to 723, the maps are concatenated and a final convolution generates the likelihood logits. Finally, these are added to the upsampled spatial prior to generate the segmentation logit. Parameters for individual components are given in Table II.
Each convolutional unit comprised three functions: (1) a 3D convolution with a learned kernel, (2) a batch normalization [38] to facilitate robust gradient propagation, and (3) a rectified linear unit (ReLU) non-linearity [39] to represent non-linear functions. Specifically, convolutional units are denoted,
| (1) |
where W is a convolutional kernel; batch normalization b(X, γ) transforms the mean of each channel to 0 and the variance to a learned per-channel scale parameter γ, and the rectified linear unit r(X) = max(0, X) induces non-linearity.
For computational and memory efficiency, we introduce our new batch-wise spatial dropout. In regular spatial dropout [40], to regularize the network, random channels are dropped (i.e. set to zero) with an independent specified probability,
| (2) |
where ô(X, BO) sets channels masked by stochastic binary mask BO to zero, and X̂i−1 = ô(Xi−1, BI) is the previous unit’s output after dropout with mask BI. Standard implementations calculate and store the dropped activations that do not affect subsequent layers. Our proposed batch-wise spatial dropout avoids computing these activations by modifying the convolution kernels instead of the activation maps, denoted
| (3) |
where ō(W, BI, BO) is a new kernel without input and output channels masked by BI and BO, X̄i−1 is the output of the previous unit after batch-wise spatial dropout, and γ̄ is the scale parameter of undropped channels. Note that X̄i is identical to the undropped channels of X̂i but does not compute or store the dropped channels, and that subsequent convolutions are unaffected if their kernel is similarly modified. To realize the efficiency gains, two further changes are made. First, the same channels are dropped for all images in each mini-batch, so that the same convolution kernels can be used for the whole minibatch. Second, the distribution of dropped channels is changed to limit the maximum memory usage. In spatial dropout, the probability distribution of keeping k out of n channels is a binomial distribution although the expected value E[K = k] = pn, the maximum value (corresponding to the maximum memory usage) is n. Instead the proposed batch-wise spatial dropout drops channels using dependent Bernoulli distributions, such that a fixed number of channels ⌈pn⌉ are kept. Segmentation inference can use all features by scaling the convolutional unit outputs by nf/⌈nfp⌉ this requires more memory per subject than training, as all nf feature maps are generated. Alternatively, Monte-Carlo inference [41] can be used (increasing the computation cost but lowering the memory usage) by inferring multiple segmentation samples using dropout, and combining them. Both of these approaches are evaluated in the experiments below. An implementation of batch-wise spatial dropout is available in the NiftyNet platform1.
Dense feature stacks, adapted from the dense block defined by Huang et al. [27], are a sequence of composite functions where the input of each function is the concatenated output of all preceding functions. In contrast to Huang’s dense block, our composite function use our batch-wise spatial dropout for regularization, and do not use 1 × 1 bottleneck layers. Specifically, the output of an m-layer dense feature stack fm(X0) = [X0; X1; …; Xm] where
| (4) |
| (5) |
where [A; B] denotes channel-wise concatenation; Wa,nf,di is an a×a×a convolution kernel (a = 3) with nf output channels (4, 8 and 16 for high, medium and low resolution dense feature stacks) and dilation rate di (d2 = 3, d3 = 9, di∉{2,3} = 1); selects all previously computed channels, selects all channels from X0 and otherwise is sampled stochastically such that ⌈pnf⌉ channels are selected (p = 0.5). This structure has several advantages. First, like residual networks [42], the feature stacks inherently encode identity functions, as the final output channels include the inputs. Second, they combine multiple network depths within a single network [43] allowing both effective propagation of gradients through the network (every kernel weight lies in a shallow sub-graph of depth 1) and representation of complex functions (every kernel weight lies in multiple deeper sub-graphs with depths 2 to m). Finally, when memory constraints limit the number of activation maps, information from earlier layers is stored only once in memory, but accessed by later layers. Memory-efficient dense blocks [44], where a careful implementation of feature concatenation avoids storing multiple copies of feature maps, can achieve O(m) memory usage. The improvements of batch-wise spatial dropout can be combined with those of memory-efficient dense blocks by only allocating shared memory storage for the number of computed activation maps, which is fixed for our dependent Bernoulli distributions.
A V-network architecture comprises downsampling and upsampling subnetworks, with skip connections to propagate higher resolution information to the final segmentation. Previous V-networks [24], [25], typically use shallow strided-convolution downsampling units followed by shallow transpose-convolutional upsampling units with additive or concatenating skip connections within each resolution. DenseVNet differs in several ways: the downsampling subnetwork is a sequence of three dense feature stacks connected by downsampling strided convolutions; each skip connection is a single convolution of the corresponding dense feature stack output, and the upsampling network comprises bilinear upsampling to the final segmentation resolution. Memory efficiencies of dense feature stacks and batch-wise spatial dropout enable deeper networks at higher resolutions, which is advantageous for segmentation of smaller structures. The bilinear upsampling of skip connections to the segmentation resolution (723) limits artifacts induced by transpose convolution [45]. The V-network generates a logit label prediction L with 9 classes.
Dilated convolutions use sparse convolution kernels to represent functions with large receptive fields but few trainable parameters. Specifically, a dilated kernel Wa,k,d is a (d(a − 1) + 1)3 kernel with a trainable parameter every d elements in each dimension and 0 elsewhere. For the i-th convolutional layer of a FCN, the relative resolution is and the receptive field size, expressed recursively, is where di, si and ai are the dilation rate, stride and kernel size (before dilation) of layer i. Because both resolution and receptive field size depend on si, sequential downsampling can generate either local high-resolution features in early layers or global low-resolution features after the downsampling layers. In contrast, by increasing di exponentially with si = 1, dilated convolutions can generate high-resolution features with exponentially growing receptive fields in the early layers. This allows more complex functions of these features to be computed in later layers. The high-resolution large-receptive-field features in lower layers may help the segmentation of small structures (e.g. esophagus) whose location can be inferred from large structures nearby.
Finally, we use an explicit spatial prior introduced in our previous work [21]. Medical images are frequently acquired in standard anatomically aligned views with relatively consistent organ positions and orientations, motivating spatial segmentation priors. Spatial priors can be encoded implicitly, due to boundary effects of convolution or by providing image coordinates as an input channel [46]. Our previous work [21] introduced an explicit spatial prior. The spatial prior P is a low-resolution 3D map of trainable parameters, which is bilinearly upsampled to the segmentation resolution and added to the outputs of the V-network (i.e. L′ = u(P) + L). Conceptually, this could represent the posterior log-probability L′ = logp(L|x, I) of the class label L at voxel x given image I as the sum of a log-likelihood L = logp(I|x,L) generated by the V-network and a prior log-probability u(P) = logp(L|x) generated by the spatial prior. However, the spatial prior parameters are trained as part of the end-to-end gradient-based optimization and may not represent the true prior probability.
1). Implementation details
The loss function was the weighted sum of an L2 regularisation loss with label-smoothed [47] probabilistic Dice scores for each organ l averaged across subjects in each minibatch,
| (6) |
where vectors and Rl are the algorithm’s probabilistic segmentation and the binary reference standard segmentation for organ l for each subject, respectively. To further mitigate the extreme class imbalance (e.g. esophagus averaged 0.09% of the image and liver averaged 11.7%), Dice score hinge losses heavily penalizing Dice scores below 0.01 and 0.10 were introduced after warm up periods of 25 and 100 iterations, respectively. The loss function at iteration i was
| (7) |
| (8) |
| (9) |
where w ∈ W are kernel values, l is the Dice loss, v is the hinge loss threshold, and t is the delay in iterations.
The network was trained using the Adam optimizer with ϵ = 0.001 and mini-batch size 10 for 5000 iterations (i.e. 625 epochs). Training each instance of the network took approximately 6 hours using Titan X Pascal or P100 GPUs (NVIDIA Corporation, Los Alamitos, CA). A Tensorflow implementation of a trained DenseVNet network is available in the NiftyNet platform model zoo (http://niftynet.io/model_zoo).
The cropped region of interest, ranging from 209–471 voxels (172–367mm) transversely and 32–450 voxels (138–283mm) in the IS axis, was resampled to a 1443-voxel volume. During training, for data augmentation, affine perturbations were applied yielding skewed subregions 0% to 10% smaller in each dimension. For the baseline DenseVNet used in the algorithm comparison, we used Monte Carlo inference using the mode of 30 723 segmentation samples (chosen heuristically apriori), taking approximately 8–15 seconds per image. In post-processing, the 723 segmentation labels were resampled to the original cropped region at the original image resolution in Matlab using curvature flow smoothing [48] with 2 iterations (chosen visually a priori to avoid quantization artifacts). Then, for each organ, the union of all connected components comprising >10% (chosen ad hoc, a priori) of the segmented organ volume was taken as the final mask.
B. Evaluation metrics and statistical methods
We compared the accuracy of segmentation algorithms using a 9-fold cross-validation over 90 subjects. For each test image in each fold, we compared each organ segmentation to the reference standard segmentation using three metrics:
Dice coefficient – 2|A ∩ B|/(|A| + |B|)
symmetric mean boundary distance – and
symmetric 95% Hausdorff distance − (P95(D(A, B)) + P95(D(B, A)))/2,
where A and B are the algorithm and reference segmentations, D(A, B) is the set of distances from boundary pixels of A, ΩA, to the nearest boundary pixel in ΩB (i.e. and P95(D) is the 95-th percentile of D. The Dice coefficient measures the relative volumetric overlap between segmentations. The mean boundary and 95% Hausdorff distances reflect the agreement between segmentation boundaries, with the latter being more sensitive to localized disagreements.
In each analysis, we compared the accuracy of the proposed algorithm to each comparator using a sign test for correlated data [49], which is insensitive to the skewed distribution of accuracy differences observed in our data, and accounts for the correlation between values within each fold due to the shared training set. We used Benjamini–Hochberg false-discovery-rate multiple-comparison correction (α = 0.05) for pairwise tests. This correction was performed separately for the primary analysis comparing algorithms and the secondary analysis comparing architecture variants. In several subjects, one or more organs were not present in the images due to prior surgeries; these organs (7 gallbladders, 1 left kidney and 1 esophagus) were excluded from the aggregate descriptive statistics and statistical comparisons above as the measures used are not meaningful in this scenario. In these cases, we reported the segmented volume (ideally 0) for these organs (Supplementary material Table II, available in the multimedia tab online).
C. Primary analysis: algorithm comparison
We compared the segmentation accuracy of our algorithm to those of two existing algorithms: the deep-learning-based VoxResNet [36] method and the MALF-based DEEDS+JLF method [34], [35], described below.
1). Comparison algorithm 1: deep-learning-based VNet
To evaluate our specific architecture, we compare it to a baseline V-network architecture for 3D image segmentation, VNet [25], which has been widely used and adapted, and has a publicly available implementation (https://github.com/faustomilletari/VNet). Because the original VNet was designed for binary segmentation, we modified the loss gradient to support multiple labels and missing organs, from where Ul and Il are the volumes of the union and intersection of Rl and respectively, and ϵ = 0.01 is a constant for numerical stability when there are missing organs. VNet uses a parametric rectified linear unit activation function and does not use batch-normalization. The downsampling subnetwork comprises a residual unit (i.e. one or more convolutional units in series added back to the input) at 5 resolutions with strided convolution for downsampling. The upsampling subnetwork concatenates features upsampled using transpose convolution with ’skip’ features directly from downsampling subnetwork and applies a residual unit. We trained VNet using Caffe and our adaptation of the reference implementation and applied the same post-processing as for DenseVNet.
2). Comparison algorithm 2: deep-learning-based VoxRes-Net
To further evaluate our specific architecture, we compare it to an existing off-the-shelf FCN for multi-class segmentation, VoxResNet [36]. VoxResNet has been evaluated for segmentation of multiple tissue types in the brain, but was adapted to multi-organ segmentation by adding output channels.
VoxResNet is more similar to our architecture than VNet, using batch normalization and rectified-linear-unit non-linearities, and combining all upsampled features together instead of incrementally at each resolution. The downsampling subnetwork includes a combination of convolutional units and residual network units. The upsampling subnetwork comprises, for each of 4 resolutions, a transpose convolution to upsample the network to the segmentation resolution followed by a convolutional unit; these upsampled logits are summed to yield the segmentation. We trained VoxResNet using the same loss function and optimization protocol and applied the same post-processing as for DenseVNet.
3). Comparison algorithm 3: MALF-based DEEDS+JLF
To evaluate our proposed method relative to the current state of the art, we compare its segmentation accuracy to an existing MALF-based method [34], [35], abbreviated as DEEDS+JLF. First, atlas images from the training data were registered to the input image using dense displacement sampling (DEEDS) [34]. Then, transformed reference labels were combined using joint label fusion (JLF) [35]. DEEDS minimizes the self-similarity context metric under an affine transformation then under free-form deformation with diffusion-based regularization using a discretised search space. DEEDS was shown to yield the highest registration accuracies in a direct comparison of 6 publicly available algorithms [15]. Joint label fusion computes the weighted average of the transformed labels, where the weights are a function of the image similarity between the atlas images and target image compensating for correlations between atlas images. A combination of DEEDS and JLF achieved the highest accuracies in the BTCV segmentation challenge [16]. DEEDS and JLF computations were performed using the publicly available deedsRegSSC (http://www.mpheinrich.de/software.html) and PICSL Multi-Atlas Segmentation Tool (https://www.nitrc.org/projects/picsl_malf) implementations, respectively, using published abdominal CT registration parameters for DEEDS [15] and default parameters for JLF. Segmentations were post-processed as for DenseVNet.
D. Secondary analysis: architecture features
To isolate and quantify the contribution of each element of the proposed architecture, we conducted a series of ‘ablation’ experiments, wherein we altered key concepts underlying the architecture: the dense feature stacks, V-network structure, hinge loss, dilated convolutions, spatial prior, batch-wise spatial dropout, Monte Carlo inference, and receptive field size.
To evaluate the dense feature stacks, we compared DenseVNet to variants with regular inter-layer connections: NoDenseLow, where dense feature stacks were replaced with regular convolutional unit stacks (each unit connected only to its immediate predecessor) with the same number of channels as DenseVNet, but lower trainable parameter count (due to connectivity); and NoDenseHigh, with regular convolutional unit stacks but more channels (12, 24 and 48) to match the parameter count of DenseVNet.
Evaluating the V-network structure is challenging, as it induces several properties: representations at multiple scales, increased layer count, larger receptive field size, higher numbers of channels, and more learnable parameters. Because these properties interact, it is not feasible to manipulate them independently while holding the others constant. Instead, we evaluate these factors together by comparing our four-resolution network to 3 alternatives: ShallowV, with three resolutions (1443, 723, and 363); NoVLow, with only two resolutions (1443 and 723) and correspondingly low trainable parameter count; and NoVHigh, with two resolutions but more channels per convolution (nf = 35 and 75 features in the skip connection) to match the parameter count of DenseVNet.
To evaluate the hinge loss, dilated convolutions, explicit spatial prior, batch-wise spatial dropout, we compared our network to four corresponding alternative networks:
hinge loss: a network replacing the hinge loss with the simpler Dice score abbreviated as NoHinge.
dilated convolutions: a network with each dilated convolution replaced with a standard 3 × 3 × 3 convolution, abbreviated as NoDil.
the explicit spatial prior: a network with the spatial prior layer omitted, abbreviated as NoPrior.
batch-wise spatial dropout: a network using standard Bernoulli distributed channel-wise spatial dropout [40] within the dense feature stacks with probability p = 0.5, abbreviated as NoBSDO.
To evaluate Monte Carlo inference, the trained DenseVNet was used, but inference was performed with no dropout, using all features; these results are abbreviated as Deterministic.
To further evaluate the impact of receptive field size, we compared our network to one with the ShallowV architecture without dilated convolutions, abbreviated as NoDilShallowV.
In these experiments, the batch size was reduced from 10 to 8, so that DenseVNet and the less memory efficient NoBSDO could be directly compared using the same batch size.
IV. Results
A. Primary analysis: algorithm comparison
For the algorithm comparison, the medians of the segmentation evaluation metrics for each organ are reported in Table III and whisker plots are shown in Figure 3, respectively. Representative segmentations from the 25th, 50th and 75th percentiles of Dice scores shown in Figure 2.
Table III.
Median segmentation metrics from the algorithm comparison (whisker plots in Figure 3). Boldface denotes statistically significant findings where the median metric differed from DenseVNet (Confidence intervals are given in Table VI).
| Spl. | L. Kid. | Gallb. | Esoph. | Liv. | Stom. | Panc. | Duod. | |
|---|---|---|---|---|---|---|---|---|
| Dice coefficient (%) | ||||||||
| DEEDS+JLF | 0.89 | 0.92 | 0.67 | 0.66 | 0.94 | 0.83 | 0.74 | 0.62 |
| VoxResNet | 0.91 | 0.91 | 0.79 | 0.69 | 0.95 | 0.87 | 0.74 | 0.59 |
| VNet | 0.94 | 0.92 | 0.72 | 0.68 | 0.94 | 0.85 | 0.71 | 0.58 |
| DenseVNet | 0.96 | 0.95 | 0.84 | 0.76 | 0.96 | 0.90 | 0.78 | 0.63 |
| Mean boundary distance (mm) | ||||||||
| DEEDS+JLF | 2.1 | 1.3 | 3.0 | 2.3 | 2.1 | 3.6 | 2.3 | 3.9 |
| VoxResNet | 1.8 | 1.6 | 1.9 | 2.2 | 2.0 | 3.0 | 2.2 | 4.1 |
| VNet | 1.2 | 1.3 | 2.8 | 2.4 | 2.2 | 3.8 | 2.9 | 4.7 |
| DenseVNet | 0.8 | 0.9 | 1.6 | 1.7 | 1.6 | 2.5 | 1.9 | 4.1 |
| 95% Hausdorff distance (mm) | ||||||||
| DEEDS+JLF | 5.1 | 3.4 | 8.5 | 6.4 | 6.2 | 12.1 | 7.0 | 15.3 |
| VoxResNet | 3.8 | 4.2 | 5.0 | 6.0 | 5.2 | 9.1 | 6.3 | 13.9 |
| VNet | 3.6 | 3.7 | 7.5 | 6.5 | 6.4 | 12.6 | 9.5 | 16.0 |
| DenseVNet | 2.4 | 3.1 | 4.6 | 5.6 | 4.9 | 9.1 | 5.9 | 15.0 |
Fig. 3.
Box and whisker plots of segmentation metrics for the algorithm comparison. Boxes show 25th to 75th percentiles, whiskers show inliers within 1.5 inter-quartile ranges, markers show outliers beyond that range. High Dice scores are better and low distance scores are better.
Fig. 2.
Top: Posterior view of segmentations from three patients with Dice scores closest to the 25th, 50th, and 75th percentile: pancreas (cyan), esophagus (purple), stomach (yellow), duodenum (pink), liver (orange), spleen (red), left kidney (brown) and gallbladder (green). Bottom: Segmentations overlaid on CT.
Excluding the duodenum (discussed below), the proposed network yielded higher Dice scores than VNet, VoxResNet and DEEDS+JLF (all statistically significant) and lower mean boundary distances (all statistically significant except for pancreas segmentations with DEEDS+JLF). The 95% Hausdorff distance had higher variability, likely due to the poor robustness of 95% quantiles; consequently, while the proposed method had lower observed distances in 20/21 comparisons, the difference only reached statistical significance in 15/21.
The duodenum segmentations were the least accurate for all algorithms and all metrics. DenseVNet had higher Dice scores than other algorithms, and lower mean boundary distance than VNet, but no other comparisons were statistically significant. Although partially attributable to higher variability due to high interpatient anatomical variation and poor image contrast with distal intestines, the observed differences in median accuracy metrics are generally smaller than for other organs.
B. Secondary analysis: architecture features
For the evaluation of architecture features, the medians of the segmentation evaluation metrics for each organ are reported in Table IV. The accuracy differences when eliminating dilated convolutions and the explicit spatial prior were not statistically significant in any comparisons. Eliminating batch-wise spatial dropout or one downsampling unit of the V-structure yielded a small loss in accuracy by all metrics for most organs, but differences for the gallbladder or esophagus, the smallest organs (0.17% and 0.09% of voxels on average), were not significant. Eliminating the dense connections or eliminating the V-network entirely yielded substantially less accurate segmentations for all comparisons.
Table IV.
Median segmentation metrics for the evaluation of architecture features. Boldface denotes statistically significant findings where the median metric for the variant differed from DenseVNet.
| Param. | Spl. | L. Kid. | Gallb. | Esoph. | Liv. | Stom. | Panc. | Duod. | |
|---|---|---|---|---|---|---|---|---|---|
| Dice coefficient (%) | |||||||||
| NoDenseLow | 142k | 0.74 | 0.77 | 0.21 | 0.37 | 0.79 | 0.49 | 0.40 | 0.35 |
| NoDenseHigh | 865k | 0.78 | 0.78 | 0.22 | 0.43 | 0.83 | 0.50 | 0.44 | 0.39 |
| NoVLow | 51k | 0.90 | 0.85 | 0.67 | 0.59 | 0.91 | 0.69 | 0.52 | 0.40 |
| NoVHigh | 858k | 0.94 | 0.92 | 0.78 | 0.72 | 0.94 | 0.81 | 0.64 | 0.50 |
| ShallowV | 277k | 0.95 | 0.94 | 0.81 | 0.75 | 0.95 | 0.88 | 0.74 | 0.63 |
| NoDilShallowV | 277k | 0.95 | 0.94 | 0.82 | 0.75 | 0.94 | 0.86 | 0.75 | 0.60 |
| NoBSDO | 879k | 0.96 | 0.95 | 0.82 | 0.75 | 0.95 | 0.90 | 0.78 | 0.64 |
| NoDil | 879k | 0.96 | 0.95 | 0.82 | 0.75 | 0.95 | 0.90 | 0.77 | 0.66 |
| NoPrior | 864k | 0.96 | 0.95 | 0.81 | 0.76 | 0.95 | 0.90 | 0.78 | 0.65 |
| NoHinge | 879k | 0.96 | 0.95 | 0.81 | 0.74 | 0.95 | 0.89 | 0.78 | 0.64 |
| Deterministic | 879k | 0.96 | 0.95 | 0.83 | 0.76 | 0.95 | 0.90 | 0.79 | 0.68 |
| DenseVNet | 879k | 0.96 | 0.95 | 0.82 | 0.74 | 0.95 | 0.89 | 0.78 | 0.66 |
| Mean boundary distance (mm) | |||||||||
| NoDenseLow | 142k | 5.9 | 4.3 | 10.6 | 6.4 | 12.7 | 11.0 | 7.8 | 8.5 |
| NoDenseHigh | 865k | 5.1 | 4.0 | 9.8 | 4.9 | 7.8 | 10.1 | 7.0 | 7.8 |
| NoVLow | 51k | 2.0 | 2.7 | 3.2 | 3.2 | 3.5 | 6.9 | 5.3 | 7.2 |
| NoVHigh | 858k | 1.2 | 1.3 | 1.9 | 1.9 | 2.5 | 4.6 | 3.4 | 6.0 |
| ShallowV | 277k | 0.9 | 1.0 | 1.7 | 1.7 | 2.0 | 3.0 | 2.3 | 4.0 |
| NoDilShallowV | 277k | 1.0 | 1.0 | 1.7 | 1.7 | 2.1 | 3.2 | 2.3 | 4.5 |
| NoBSDO | 879k | 0.8 | 0.9 | 1.7 | 1.7 | 1.7 | 2.5 | 2.0 | 3.7 |
| NoDil | 879k | 0.8 | 0.8 | 1.7 | 1.7 | 1.7 | 2.4 | 2.0 | 3.7 |
| NoPrior | 864k | 0.8 | 0.9 | 1.7 | 1.7 | 1.6 | 2.2 | 2.0 | 3.7 |
| NoHinge | 879k | 0.8 | 0.9 | 1.7 | 1.8 | 1.7 | 2.3 | 2.1 | 4.0 |
| Deterministic | 879k | 0.8 | 0.9 | 1.5 | 1.7 | 1.7 | 2.3 | 2.0 | 3.5 |
| DenseVNet | 879k | 0.8 | 0.9 | 1.7 | 1.7 | 1.7 | 2.7 | 1.9 | 3.6 |
| 95% Hausdorff distance (mm) | |||||||||
| NoDenseLow | 142k | 18.5 | 14.8 | 23.2 | 15.8 | 42.7 | 29.1 | 21.6 | 23.2 |
| NoDenseHigh | 865k | 17.3 | 14.4 | 22.8 | 11.9 | 26.2 | 27.6 | 18.0 | 21.7 |
| NoVLow | 51k | 7.4 | 10.7 | 8.3 | 10.8 | 13.3 | 21.9 | 17.1 | 23.4 |
| NoVHigh | 858k | 4.2 | 5.0 | 5.4 | 6.1 | 10.2 | 17.3 | 12.8 | 20.1 |
| ShallowV | 277k | 2.7 | 3.8 | 4.8 | 5.4 | 7.1 | 11.0 | 7.1 | 15.9 |
| NoDilShallowV | 277k | 3.0 | 4.1 | 5.0 | 5.7 | 7.4 | 12.4 | 6.9 | 16.3 |
| NoBSDO | 879k | 2.4 | 2.9 | 4.8 | 5.3 | 5.3 | 9.5 | 5.9 | 13.7 |
| NoDil | 879k | 2.5 | 2.8 | 4.7 | 5.2 | 5.2 | 8.0 | 5.9 | 13.5 |
| NoPrior | 864k | 2.4 | 3.0 | 4.5 | 5.3 | 5.2 | 8.2 | 5.9 | 14.0 |
| NoHinge | 879k | 2.5 | 2.9 | 4.7 | 5.4 | 5.2 | 7.9 | 6.1 | 14.3 |
| Deterministic | 879k | 2.5 | 3.3 | 4.3 | 5.2 | 5.2 | 8.5 | 6.0 | 12.8 |
| DenseVNet | 879k | 2.4 | 3.0 | 4.8 | 5.4 | 5.1 | 8.6 | 5.9 | 13.8 |
V. Discussion
In this paper, we present a registration-free deep-learning-based algorithm to segment multiple organs from abdominal CT. To facilitate intraprocedural navigation in endoscopic pancreatobiliary interventions, eight organs were segmented: the pancreas, three organs from the gastrointestinal tract (esophagus, stomach and duodenum) where the endoscope is navigated, and four nearby organs for use as navigational landmarks (liver, gallbladder, spleen and left kidney).
Clinically acceptable segmentation accuracies have yet to be defined for guiding abdominal interventions, and depend on the intervention and guidance system. However, accuracy improvements for the pancreas (containing clinically important targets) and the gastrointestinal tract (where the endoscope is navigated) should be prioritized over navigational landmarks as an endoscope can be oriented without precise boundaries.
A direct comparison of our proposed method with two existing deep-learning based methods and a recent MALF-based method demonstrated improved overlap for all eight organs and improved boundary accuracy for seven of the eight. The largest improvements were for the smallest organs (gallbladder and esophagus). This may be due in part to the challenges in registering small organs for MALF, which is avoided with registration-free methods and in part due to the deeper high-resolution features in DenseVNet. Segmentation accuracy for the duodenum, which has been less well studied, was much lower than other organs, but interestingly was very similar across all four algorithms. FCN methods were also found to be faster (<1s for deterministic and 8–15s for Monte Carlo inference). DEEDS+JLF took 60s per pairwise registrations and 78 minutes to fuse labels from 80 registered atlases. Although these times would not be a limiting factor in a clinical workflow for fully-automated segmentation, the deep learning methods are fast enough to use for more accurate semi-automatic segmentations.
Many previous studies have proposed methods for multiorgan segmentation of abdominal CT. Some of the required organs (pancreas, liver, kidney and spleen) are included in many of these studies; however, gastrointestinal tract segmentation has received much less attention. Only one other study [18] has reported duodenal segmentation (pooled with the stomach as a single segmentation). Comparing segmentation accuracy to previous literature is challenging; quantitative metrics are not directly comparable due to differences in data set sizes, imaging protocols and quality and reference segmentation protocols and quality. This notwithstanding, Table V shows mean Dice scores for the segmented organs from many reported methods. In most previous work and our proposed method, liver, spleen and kidney segmentations have consistently yielded higher Dice scores than other anatomy. On these organs, many segmentations yield segmentations with Dice scores within 0.02 of the highest reported scores (ours for spleen, Hu et al. [19] for left kidney and liver). It is unlikely that these differences are statistically or meaningfully different, given the data variability. Segmentation accuracies for the other organs have been more variable. Notably, Cerrolaza et al. [5] reported some of the highest accuracies for gallbladder, stomach and pancreas segmentations, but much lower accuracies for organ segmentations that are commonly very accurate: spleen, left kidney and liver. Our method yielded the highest mean Dice scores for spleen, esophagus, stomach and pancreas, and mean Dice scores within 0.02 of the highest for liver and left kidney. However, the mean Dice score for the gallbladder were lower than several other methods with a highly skewed distribution (the median Dice score was 0.84, but 13/84 had scores less than 0.50). This may be due to 6 patients in our data set without gallbladders; while gallbladder segmentations for these patients were excluded from the scores, they were included in the training data and may have affected training.
Table V.
Mean Dice scores for previous abdominal CT multi-organ segmentation methods. Different data sets and segmentation of unlisted organs preclude direct comparisons.
| Reference | Method | Mean Dice scores %; higher is better | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Spl. | L.Kid. | Gall. | Esoph. | Liv. | Stom. | Panc. | Duod. | ||
| Cerrolaza [5] | SM | 0.86 | 0.69 | 0.83 | 0.82 | 0.87 | 0.74 | ||
| Heinrich [34] [50] | MA | 0.92 | 0.92 | 0.60 | 0.69 | 0.95 | 0.80 | 0.74 | |
| Hu [19] | DL+ | 0.94 | 0.95 | 0.96 | |||||
| Kechichian [51] | MA+ | 0.84 | 0.86 | 0.14 | 0.93 | 0.35 | |||
| Larsson [20] | MADL | 0.93 | 0.91 | 0.62 | 0.66 | 0.95 | 0.78 | 0.60 | |
| Oda [52] | MA+ | 0.88†† | 0.90†† | 0.94†† | 0.62†† | ||||
| Okada [6] | SM+ | 0.93 | 0.94 | 0.67 | 0.73 | ||||
| Roth [31] | DL | 0.91 | 0.71 | 0.93 | 0.84 | 0.63 | |||
| Shimizu [10] | MA | 0.91† | 0.88† | 0.77† | 0.37† | 0.94† | 0.55† | 0.53† | |
| Suzuki [9] | MA | 0.88† | 0.65† | 0.25† | 0.85† | 0.07† | 0.46† | ||
| Tong [8] | MA | 0.92 | 0.93 | 0.95 | 0.70 | ||||
| Wang [53] | MA | 0.93 | 0.92 | 0.95 | 0.66 | ||||
| Xu [7] | MA | 0.90 | 0.84 | 0.27 | 0.43 | 0.91 | 0.55 | 0.45 | |
| Zhou [18] | DL | 0.92† | 0.91† | 0.65† | 0.43† | 0.95† | 0.60†‡ | 0.62† | 0.60†‡ |
| Zografos [54] | RF | 0.92† | 0.92† | 0.91† | 0.59† | ||||
| DEEDS+JLF | MA | 0.87 | 0.90 | 0.60 | 0.64 | 0.93 | 0.81 | 0.72 | 0.56 |
| VoxResNet | DL | 0.90 | 0.89 | 0.69 | 0.65 | 0.94 | 0.84 | 0.72 | 0.60 |
| VNet | DL | 0.92 | 0.90 | 0.64 | 0.65 | 0.94 | 0.81 | 0.67 | 0.56 |
| Proposed | DL | 0.95 | 0.93 | 0.73 | 0.71 | 0.95 | 0.87 | 0.75 | 0.63 |
MA=multi-atlas label fusion; SM=statistical shape/appearance model; RF=registration-free; DL=deep learning.
denotes processing with methods commonly used in registration-free methods.
estimated from mean Jaccard index;
estimated from mean precision and recall.
Stomach and duodenum were segmented as one class.
The architecture experiments identified two features that were critical to the segmentation accuracy: the dense connections and the multi-scale V-network structure significantly improved the performance. First, the dense connections yielded the largest improvement. The relatively small difference between NoDenseHigh and NoDenseLow suggests that this improvement is not due to the additional trainable parameters, but rather due to the connectivity structure that supports gradient propagation and feature reuse. Second, the four-resolution DenseVNet with the multi-scale V-network structure outperformed the two-resolution NoVLow network without it. Some of the differences can be attributed to having fewer trainable parameters, as NoVHigh recovered 38–82% of the difference depending on the organ; however, NoVHigh still substantially underperformed DenseVNet. DenseVNet yielded significant but very small improvements over the three-resolution ShallowV for most organs, suggesting that even minimal multiscale structure delivers the vast majority of the benefit. Although one purported advantage of multi-scale networks is that the receptive field of the network is larger, ShallowV, where the receptive field covers 50–100% of the image, and NoDilShallowV, where the receptive field covers 5–50% of the image, yielded very similar performance, suggesting that the entire image is not necessary for accurate segmentation.
To avoid biased performance estimates due to selecting the best of multiple variants for baseline comparisons, the network architecture for algorithm comparisons was specified a priori. It included the following features where the observed accuracy differences did not reach statistical significance: dilated convolutions, the explicit spatial prior, and the hinge loss. This suggests that these features may be omitted from DenseVNet with minimal change in segmentation performance. Additionally, our experiments in which these features were omitted give the following insights into information propagation within the architecture. The dilated convolutions increase the receptive field of the features early in the network, particularly the high resolution features; the receptive field of the high resolution features spans half the image in the network with dilated convolutions, while it spans less than a quarter of the image in the network without them. The small performance difference without dilated convolutions suggests that high resolution global information is either incorporated late in the network, or is unnecessary to achieve the observed segmentation accuracy. Our spatial prior, which encoded the voxel-wise label probability, is suitable for coarsely aligned images (via standardized acquisition or pre-processing). Our results suggest that this simple spatial information can be implicitly encoded in learned features when the prior is excluded, perhaps using features from nearby organs or image-boundary artifacts. However, forms of spatial prior that encode global dependencies, such as topological [30] or shape-representation [29] loss functions, may still improve performance, and merit investigation. Two features were introduced to reduce memory costs without affecting performance: batch-wise spatial dropout and Monte Carlo inference. Differences from these additions did not reach statistical significance for 46/48 comparisons. Our findings suggest that batch-wise spatial dropout should be used in DenseVNet implementations and that the inference method can be chosen based on memory or computation time constraints.
While our experiments focused on the network architecture, the data pipeline also included pre- and post-processing. First, to constrain memory, images were cropped manually to the abdominal cavity. Altering the cropping protocol for the test data sufficiently (i.e. beyond the variability generated by data augmentation) can impact segmentation accuracy. Specifically, when the cropped region was adjusted outward by 5% in each axis (outside the data augmentation variability), the Dice scores decreased by 0.03 ± 0.06 (mean±SD); however, when the cropped regions on the test data were adjusted inward by the same 5% (within the data augmentation variability), the Dice scores changed by 0.00 ± 0.04. This suggests that data augmentation variability should cover the anticipated cropping variability. Second, the data were post-processed to filter out small false positive regions and upsample the segmentations smoothly. In post hoc comparisons, removing the connected component filter or using bilinear upsampling instead of our smoothing upsampling scheme generally had minimal impact on the segmentation performance, with median Dice, MAD and Hausdorff distance scores changing by less than 0.005, 0.1 mm and 1.1 mm, respectively.
Our conclusions are qualified by some limitations. Authors were not blinded to the manual segmentations during algorithm development; although the cross-validation was only run after algorithm development was complete, design decisions may have been influenced by data observations. Algorithm parameters for the FCN methods were not extensively optimized for this application; the reported performance of DenseVNet, VNet and VoxResNet methods may underestimate their potential performance. The statistical comparison accounts for correlation within each fold, but not between folds due to partial overlap of the training data; an independent evaluation on a disjoint data set would be valuable. The evaluation metrics measure segmentation fidelity with the manual reference, and not the clinical utility of the resulting segmentations for aiding endoscopic navigation; future work will evaluate whether the proposed algorithm is accurate enough to provide a 3D patient-specific anatomical model to aid endoscopic navigation.
In conclusion, the proposed deep-learning-based DenseVNet can segment the pancreas, esophagus, stomach, liver, spleen, gallbladder, left kidney and duodenum more accurately than previous methods using deep learning or multi-atlas label fusion. The densely linked layers and a shallow V-network architecture are critical to the segmentation accuracy of this network. The use of dilated convolutions was not necessary, suggesting that global high-resolution non-linear features are not critical for abdominal CT organ segmentation. The use of an explicit spatial prior was also not necessary, suggesting that convolutional neural networks are implicitly encoding spatial priors, despite their purported translational invariance. The automatically generated segmentations of abdominal anatomy have the potential to support image-guided navigation in pancreatobiliary endoscopy procedures.
Supplementary Material
Table I.
Table of Symbols
| Tensors | |
| L | logit segmentation from V-network |
| P | logit spatial prior |
| L′, L″, | logit and probabilistic segmentation and l-th channel |
| Rl | l-th channel on reference standard segmentation |
| stochastic binary masks for dropout | |
| W | convolution kernel |
| Operators | |
| c(X, W, s, γ) | convolutional unit |
| r(X) | rectified linear non-linearity |
| b(X, γ) | channel-wise batch normalization |
| ō(X, BI, BO) | batch-wise spatial dropout |
| fm(X) | dense feature stack |
| u(X) | bilinear upsampling |
| Operator parameters (operator: parameters) | |
| c: s, γ | stride, scale parameter |
| f: m, a, di, nf | # layers, kernel size, i-th layer dilation rate, # features in each unit |
| Other notation† | |
| p | approximate probability of keeping each channel |
| x, y, z | voxel coordinates |
Symbols used within one paragraph are omitted for brevity.
Table II.
Detailed parameters for DenseVNet architecture.
| Layer | Input | Output | Kernel | Stride | Subunits m × nf |
|---|---|---|---|---|---|
| Feature | 1443 × 1 | 723 × 24 | 53 | 2 | |
| DFS 1 | 723 × 24 | 723 × 20 | 33 | 1 | 5 × 4 |
| Skip 1 | 723 × 20 | 723 × 12 | 33 | 1 | |
| Down 1-2 | 723 × 20 | 363 × 24 | 33 | 2 | |
| DFS 2 | 363 × 24 | 363 × 80 | 33 | 1 | 10 × 8 |
| Skip 2 | 363 × 80 | 363 × 24 | 33 | 1 | |
| Up 2 | 363 × 24 | 723 × 24 | |||
| Down 2-3 | 363 × 80 | 183 × 24 | 33 | 2 | |
| DFS 3 | 183 × 24 | 183 × 160 | 33 | 1 | 10 × 16 |
| Skip 3 | 183 × 160 | 183 × 24 | 33 | 1 | |
| Up 3 | 183 × 24 | 723 × 24 | |||
| Up Prior | 123 × 9 | 723 × 9 |
Table VI.
Confidence intervals on the change in segmentation metrics (positive for Dice scores and negative for the boundary distances when DenseVNet is better) for the algorithm comparison.
| Spleen | Left Kidney | Gallbladder | Esophagus | Liver | Stomach | Pancreas | Duodenum | |
|---|---|---|---|---|---|---|---|---|
| Dice coefficient (%) | ||||||||
| DEEDS+JLF | 0.03,0.09 | 0.01,0.03 | 0.03,0.18 | 0.04,0.12 | 0.01,0.03 | 0.02,0.08 | -0.00,0.08 | -0.01,0.09 |
| VoxResNet | 0.04,0.05 | 0.03,0.05 | 0.00,0.05 | 0.03,0.09 | 0.01,0.01 | 0.02,0.04 | 0.02,0.05 | 0.01,0.05 |
| VNet | 0.01,0.03 | 0.01,0.03 | 0.04,0.12 | 0.02,0.09 | 0.01,0.02 | 0.02,0.07 | 0.04,0.10 | 0.03,0.09 |
| Mean boundary distance (mm) | ||||||||
| DEEDS+JLF | -1.8,-0.5 | -0.5,-0.2 | -1.5,-0.1 | -0.7,-0.1 | -0.9,-0.1 | -1.3,-0.2 | -0.8,0.1 | -0.9,0.3 |
| VoxResNet | -1.1,-0.8 | -0.8,-0.5 | -0.5,-0.1 | -0.7,-0.3 | -0.5,-0.2 | -0.8,-0.3 | -0.5,-0.2 | -0.5,0.2 |
| VNet | -0.5,-0.2 | -0.4,-0.2 | -1.4,-0.4 | -0.7,-0.2 | -0.8,-0.3 | -1.7,-0.2 | -1.1,-0.4 | -1.1,-0.1 |
| 95% Hausdorff distance (mm) | ||||||||
| DEEDS+JLF | -3.5,-0.7 | -0.7,0.2 | -4.2,-1.1 | -1.6,0.0 | -1.2,0.1 | -4.9,-0.0 | -1.7,0.1 | -1.9,1.9 |
| VoxResNet | -1.7,-1.0 | -1.2,-0.5 | -1.0,0.3 | -1.0,-0.0 | -0.6,0.1 | -1.2,0.2 | -1.3,-0.1 | -1.7,2.1 |
| VNet | -1.7,-0.5 | -1.2,-0.1 | -3.4,-0.7 | -1.5,-0.3 | -1.8,-0.5 | -5.0,-0.3 | -4.1,-1.1 | -3.0,0.4 |
Acknowledgements
This publication presents independent research supported by Cancer Research UK (Multidisciplinary C28070/A19985) and the National Institute for Health Research UCL/UCL Hospitals Biomedical Research Centre.
Footnotes
niftynet.layer.channel_sparse_convolution.Channel SparseConvolutionalLayer in the http://niftynet.io code repositories
References
- [1].van Ginneken B, Schaefer-Prokop CM, Prokop M. Computer-aided diagnosis: how to move from the laboratory to the clinic. Radiology. 2011;261(3):719–732. doi: 10.1148/radiol.11091710. [DOI] [PubMed] [Google Scholar]
- [2].Sykes J. Reflections on the current status of commercial automated segmentation systems in clinical practice. Journal of Medical Radiation Sciences. 2014;61(3):131–134. doi: 10.1002/jmrs.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Howe RD, Matsuoka Y. Robotics for surgery. Annual Review of Biomedical Engineering. 1999;1(1):211–240. doi: 10.1146/annurev.bioeng.1.1.211. [DOI] [PubMed] [Google Scholar]
- [4].Eisen GM, Dominitz JA, Faigel DO, Goldstein JA, Petersen BT, Raddawi HM, Ryan ME, Vargo JJ, Young HS, Wheeler-Harbaugh J, et al. Guidelines for credentialing and granting privileges for endoscopic ultrasound. Gastrointestinal endoscopy. 2001;54(6):811–814. doi: 10.1016/s0016-5107(01)70082-x. [DOI] [PubMed] [Google Scholar]
- [5].Cerrolaza JJ, Reyes M, Summers RM, González-Ballester MÁ, Linguraru MG. Automatic multi-resolution shape modeling of multi-organ structures. MedIA. 2015;25(1):11–21. doi: 10.1016/j.media.2015.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Okada T, Linguraru MG, Hori M, Summers RM, Tomiyama N, Sato Y. Abdominal multi-organ segmentation from CT images using conditional shape–location and unsupervised intensity priors. MedIA. 2015;26(1):1–18. doi: 10.1016/j.media.2015.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Xu Z, Burke RP, Lee CP, Baucom RB, Poulose BK, Abramson RG, Landman BA. Efficient multi-atlas abdominal segmentation on clinically acquired CT with SIMPLE context learning. MedIA. 2015;24(1):18–27. doi: 10.1016/j.media.2015.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Tong T, Wolz R, Wang Z, Gao Q, Misawa K, Fujiwara M, Mori K, Hajnal JV, Rueckert D. Discriminative dictionary learning for abdominal multi-organ segmentation. MedIA. 2015;23(1):92–104. doi: 10.1016/j.media.2015.04.015. [DOI] [PubMed] [Google Scholar]
- [9].Suzuki M, Linguraru MG, Okada K. MICCAI. Springer; 2012. Multi-organ segmentation with missing organs in abdominal CT images; pp. 418–425. [DOI] [PubMed] [Google Scholar]
- [10].Shimizu A, Ohno R, Ikegami T, Kobatake H, Nawano S, Smutek D. Segmentation of multiple organs in non-contrast 3D abdominal CT images. IJCARS. 2007;2(3):135–142. [Google Scholar]
- [11].Casiraghi E, Campadelli P, Pratissoli S, Lombardi G. Automatic abdominal organ segmentation from CT images. ELCVIA. 2009;8 [Google Scholar]
- [12].Saxena S, Sharma N, Sharma S, Singh S, Verma A. An automated system for atlas based multiple organ segmentation of abdominal CT images. BJMCS. 2016;12:1–14. [Google Scholar]
- [13].Lombaert H, Zikic D, Criminisi A, Ayache N. MICCAI. Springer; 2014. Laplacian forests: semantic image segmentation by guided bagging; pp. 496–504. [DOI] [PubMed] [Google Scholar]
- [14].He B, Huang C, Jia F. Fully automatic multi-organ segmentation based on multi-boost learning and statistical shape model search. VISCERAL Challenge@ ISBI. 2015:18–21. [Google Scholar]
- [15].Xu Z, Lee CP, Heinrich MP, Modat M, Rueckert D, Ourselin S, Abramson RG, Landman BA. Evaluation of six registration methods for the human abdomen on clinically acquired CT. IEEE Trans Biomed Eng. 2016;63(8):1563–1572. doi: 10.1109/TBME.2016.2574816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Landman B, Xu Z, Igelsias JE, Styner M, Langerak TR, Klein A. MICCAI multi-atlas labeling beyond the cranial vault - workshop and challenge. 2015 accessed July 2017. [Google Scholar]
- [17].Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, van der Laak JAWM, van Ginneken B, Snchez CI. A survey on deep learning in medical image analysis. arXiv:1702.05747v1. 2017 doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- [18].Zhou X, Ito T, Takayama R, Wang S, Hara T, Fujita H. MICCAI Workshop on Large-Scale Annotation of Biomedical Data and Expert Label Synthesis. Springer; 2016. Three-dimensional CT image segmentation by combining 2D fully convolutional network with 3D majority voting; pp. 111–120. [Google Scholar]
- [19].Hu P, Wu F, Peng J, Bao Y, Chen F, Kong D. Automatic abdominal multi-organ segmentation using deep convolutional neural network and time-implicit level sets. IJCARS. 2016:1–13. doi: 10.1007/s11548-016-1501-5. [DOI] [PubMed] [Google Scholar]
- [20].Larsson M, Zhang Y, Kahl F. Robust abdominal organ segmentation using regional convolutional neural networks. Scandinavian Conference on Image Analysis; Springer; 2017. pp. 41–52. [Google Scholar]
- [21].Gibson E, Giganti F, Hu Y, Bonmati E, Bandula S, Gurusami K, Davidson BR, Pereira S, Clarkson MJ, Barratt DC. Towards image-guided pancreas and biliary endoscopy: automatic multi-organ segmentation on abdominal CT with dense dilated networks. MICCAI. 2017 Sep; doi: 10.1109/TMI.2018.2806309. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Heimann T, Meinzer H-P. Statistical shape models for 3D medical image segmentation: a review. Medical image analysis. 2009;13(4):543–563. doi: 10.1016/j.media.2009.05.004. [DOI] [PubMed] [Google Scholar]
- [23].Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. IEEE Trans Pattern Anal Mach Intell. 2001;23(6):681–685. [Google Scholar]
- [24].Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. MICCAI. Springer; 2016. 3D U-net: learning dense volumetric segmentation from sparse annotation; pp. 424–432. [Google Scholar]
- [25].Milletari F, Navab N, Ahmadi S-A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. IEEE 3D Vis. 2016:565–571. [Google Scholar]
- [26].Roth HR, Lu L, Farag A, Shin H-C, Liu J, Turkbey EB, Summers RM. MICCAI. Springer; 2015. Deeporgan: Multi-level deep convolutional networks for automated pancreas segmentation; pp. 556–564. [Google Scholar]
- [27].Huang G, Liu Z, Weinberger KQ, van der Maaten L. Densely connected convolutional networks. arXiv:1608.06993. 2016 [Google Scholar]
- [28].Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions. arXiv:1511.07122. 2015 [Google Scholar]
- [29].Oktay O, Ferrante E, Kamnitsas K, Heinrich M, Bai W, Caballero J, Guerrero R, Cook S, de Marvao A, Dawes T, O’Regan D, et al. Anatomically constrained neural networks (acnn): Application to cardiac image enhancement and segmentation. 2017 doi: 10.1109/TMI.2017.2743464. [DOI] [PubMed] [Google Scholar]
- [30].BenTaieb A, Hamarneh G. Topology aware fully convolutional networks for histology gland segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer; 2016. pp. 460–468. [Google Scholar]
- [31].Roth HR, Oda H, Hayashi Y, Oda M, Shimizu N, Fujiwara M, Misawa K, Mori K. Hierarchical 3d fully convolutional networks for multi-organ segmentation. 2017 doi: 10.1016/j.compmedimag.2018.03.001. [DOI] [PubMed] [Google Scholar]
- [32].Clark K, Vendt B, Smith K, Freymann J, Kirby J, Koppel P, Moore S, Phillips S, Maffitt D, Pringle M, Tarbox L, et al. The cancer imaging archive (TCIA): Maintaining and operating a public information repository. Journal of Digital Imaging. 2013;26(6):1045. doi: 10.1007/s10278-013-9622-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Roth HR, Farag A, Turkbey EB, Lu L, Liu J, Summers RM. Data from TCIA Pancreas-CT. 2016 [Google Scholar]
- [34].Heinrich MP, Jenkinson M, Brady M, Schnabel JA. MRF-based deformable registration and ventilation estimation of lung CT. IEEE Trans Med Imag. 2013;32(7):1239–1248. doi: 10.1109/TMI.2013.2246577. [DOI] [PubMed] [Google Scholar]
- [35].Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich PA. Multi-atlas segmentation with joint label fusion. IEEE TPAMI. 2013;35(3):611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Chen H, Dou Q, Yu L, Qin J, Heng P-A. VoxResNet: Deep voxelwise residual networks for brain segmentation from 3D MR images. NeuroImage. 2017 doi: 10.1016/j.neuroimage.2017.04.041. [DOI] [PubMed] [Google Scholar]
- [37].Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. IEEE CVPR. 2015:3431–3440. doi: 10.1109/TPAMI.2016.2572683. [DOI] [PubMed] [Google Scholar]
- [38].Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv:1502.03167. 2015 [Google Scholar]
- [39].Nair V, Hinton GE. Rectified linear units improve restricted Boltzmann machines. In: Fürnkranz J, Joachims T, editors. Proc ICML. Omnipress; 2010. pp. 807–814. [Google Scholar]
- [40].Tompson J, Goroshin R, Jain A, LeCun Y, Bregler C. Efficient object localization using convolutional networks. IEEE CVPR. 2015:648–656. [Google Scholar]
- [41].Gal Y, Ghahramani Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. CoRR. 2015 vol. abs/1506.02142. [Google Scholar]
- [42].He K, Zhang X, Ren S, Sun J. Identity mappings in deep residual networks. arXiv:1603.05027. 2016 [Google Scholar]
- [43].Veit A, Wilber MJ, Belongie S. Residual networks behave like ensembles of relatively shallow networks. NIPS. 2016:550–558. [Google Scholar]
- [44].Pleiss G, Chen D, Huang G, Li T, van der Maaten L, Weinberger KQ. Memory-efficient implementation of densenets. arXiv preprint arXiv:1707.06990. 2017 [Google Scholar]
- [45].Odena A, Dumoulin V, Olah C. Deconvolution and checkerboard artifacts. Distill. 2016 [Online]. Available: http://distill.pub/2016/deconv-checkerboard. [Google Scholar]
- [46].Brust C-A, Sickert S, Simon M, Rodner E, Denzler J. Efficient convolutional patch networks for scene understanding. CVPR Scene Understanding Workshop. 2015 [Google Scholar]
- [47].Pereyra G, Tucker G, Chorowski J, Kaiser Ł, Hinton G. Regularizing neural networks by penalizing confident output distributions. arXiv:1701.06548. 2017 [Google Scholar]
- [48].Kroon D-J. Smooth triangulated mesh. [accessed 07/04/2017];MATLAB Central File Exchange. 2010 [Online]. Available: mathworks.com/matlabcentral/fileexchange/26710. [Google Scholar]
- [49].Gerard PD, Schucany WR. An enhanced sign test for dependent binary data with small numbers of clusters. Computational statistics & data analysis. 2007;51(9):4622–4632. [Google Scholar]
- [50].Landman B, Warfield S, editors. MICCAI 2012 Grand Challenge and Workshop on Multi-Atlas Labeling; 2012. [Google Scholar]
- [51].Kéchichian R, Valette S, Desvignes M. Cloud-Based Benchmarking of Medical Image Analysis. Springer; 2017. Automatic multiorgan segmentation using hierarchically registered probabilistic atlases; pp. 185–201. [Google Scholar]
- [52].Oda M, Nakaoka T, Kitasaka T, Furukawa K, Misawa K, Fujiwara M, Mori K. MICCAI Workshop on Computational and Clinical Challenges in Abdominal Imaging. Springer; 2011. Organ segmentation from 3D abdominal CT images based on atlas selection and graph cut; pp. 181–188. [Google Scholar]
- [53].Wang Z, Bhatia KK, Glocker B, Marvao A, Dawes T, Misawa K, Mori K, Rueckert D. MICCAI. Springer; 2014. Geodesic patch-based segmentation; pp. 666–673. [DOI] [PubMed] [Google Scholar]
- [54].Zografos V, Valentinitsch A, Rempfler M, Tombari F, Menze B. MICCAI Workshop on Medical Computer Vision. Springer; 2015. Hierarchical multi-organ segmentation without registration in 3D abdominal CT images; pp. 37–46. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.